Implementation of Non-Isolated High Gain Interleaved DC-DC Converter for Fuel Cell Electric Vehicle Using ANN-Based MPPT Controller
Abstract
:1. Introduction
- A high voltage gain (of about 12.33) is attained by engaging voltage gain extension methods. The coupled inductor improves the voltage gain by altering the number of turns of inductor coils, and further additional voltage gain is provided by switched capacitor cells.
- In order to achieve a higher voltage gain, the switches are operated at a minimal duty ratio of 0.45.
- With a phase shift of 180°, the two interleaved phases can produce ripple-free input current. The ripple on the input current is reduced since the entire input current is split throughout the interleaved segments.
- The lossless clamp circuit recirculates the coupled inductors’ leakage inductance to the output side, effectively suppressing the reverse-recovery concern of diodes.
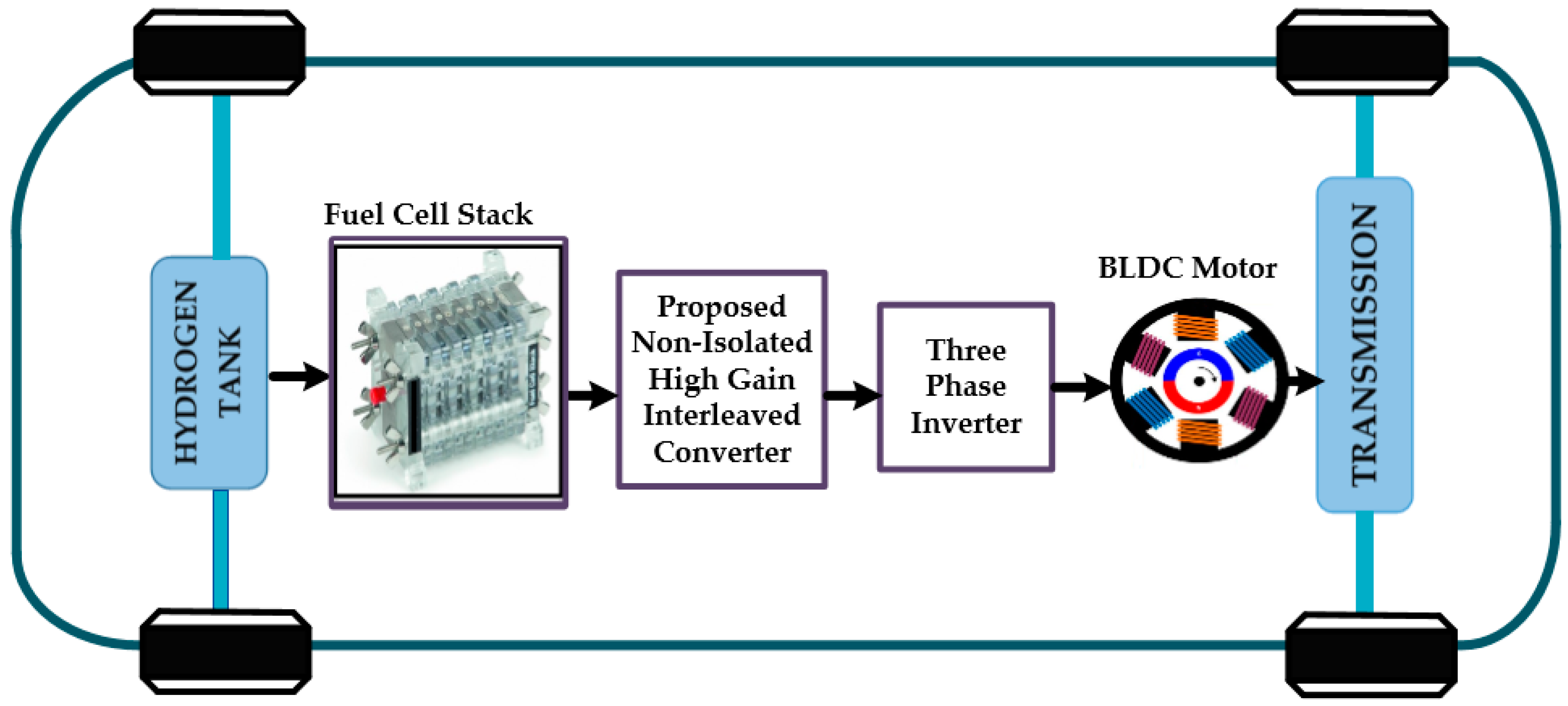
2. Architecture of the FCEV System
Modeling of PEMFC
3. Non-Isolated High Gain Interleaved Converter
- Stage I [t0–t1]
- Stage II [t1–t2]
- Stage III [t2–t3]
- Stage IV [t3–t4]
- Stage V [t4–t5]
- Stage VI [t5–t6]
3.1. Analysis of the Proposed Converter
3.2. Comparison of the Proposed Converter
4. Design of RBFN-Based MPPT Controller
5. Electronic Commutation of the BLDC Motor
6. Simulation Results and Discussions
7. Hardware Results and Discussions
8. Conclusions
- The suggested converter has a conversion ratio of 12.33
- The duty ratio of the MOSFETs is 0.45
- The arrangement of switches is an interleaved structure that will provide a smooth, ripple-free input current.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, F.-K.; Amogne, Z.E.; Chou, J.-H. A Hybrid Method for Remaining Useful Life Prediction of Proton Exchange Membrane Fuel Cell Stack. IEEE Access 2021, 9, 40486–40495. [Google Scholar] [CrossRef]
- Emadi, A.; Williamson, S.S. Fuel cell vehicles: Opportunities and challenges. In Proceedings of the IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004; Volume 2, pp. 1640–1645. [Google Scholar] [CrossRef]
- Refaat, S.S.; Ellabban, O.; Bayhan, S.; Abu-Rub, H.; Blaabjerg, F.; Begovic, M.M. Smart Transportation. In Smart Grid and Enabling Technologies; IEEE: Piscataway, NJ, USA, 2021; pp. 169–193. [Google Scholar] [CrossRef]
- Moghadari, M.; Kandidayeni, M.; Boulon, L.; Chaoui, H. Operating Cost Comparison of a Single-Stack and a Multi-Stack Hybrid Fuel Cell Vehicle Through an Online Hierarchical Strategy. IEEE Trans. Veh. Technol. 2023, 72, 267–279. [Google Scholar] [CrossRef]
- Petrovic, S.; Hossain, E. Development of a Novel Technological Readiness Assessment Tool for Fuel Cell Technology. IEEE Access 2020, 8, 132237–132252. [Google Scholar] [CrossRef]
- Yuan, H.-B.; Zou, W.-J.; Jung, S.; Kim, Y.-B. A Real-Time Rule-Based Energy Management Strategy With Multi-Objective Optimization for a Fuel Cell Hybrid Electric Vehicle. IEEE Access 2022, 10, 102618–102628. [Google Scholar] [CrossRef]
- Ali, A.; Almutairi, K.; Padmanaban, S.; Tirth, V.; Algarni, S.; Irshad, K.; Islam, S.; Zahir, M.H.; Shafiullah, M.; Malik, M.Z. Investigation of MPPT Techniques Under Uniform and Non-Uniform Solar Irradiation Condition–A Retrospection. IEEE Access 2020, 8, 127368–127392. [Google Scholar] [CrossRef]
- Chu, C.; Chen, C. Robust maximum power point tracking method for photovoltaic cells: A sliding mode control approach. Solar Energy 2009, 83, 1370–1378. [Google Scholar] [CrossRef]
- Esram, T.; Chapman, P.L. Comparison of Photovoltaic Array Maximum Power Point Tracking Techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef]
- Ram, J.; Rajasekar, N.; Miyatake, M. Design and overview of maximum power point tracking techniques in wind and solar photovoltaic systems: A review. Renew. Sustain. Energy Rev. 2017, 73, 1138–1159. [Google Scholar] [CrossRef]
- Tao, F.; Zhu, L.; Fu, Z.; Si, P.; Sun, L. Frequency Decoupling-Based Energy Management Strategy for Fuel Cell/Battery/Ultracapacitor Hybrid Vehicle Using Fuzzy Control Method. IEEE Access 2020, 8, 166491–166502. [Google Scholar] [CrossRef]
- Ali, M.N.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. An Efficient Fuzzy-Logic Based Variable-Step Incremental Conductance MPPT Method for Grid-Connected PV Systems. IEEE Access 2021, 9, 26420–26430. [Google Scholar] [CrossRef]
- Aly, M.; Rezk, H. A Differential Evolution-Based Optimized Fuzzy Logic MPPT Method for Enhancing the Maximum Power Extraction of Proton Exchange Membrane Fuel Cells. IEEE Access 2020, 8, 172219–172232. [Google Scholar] [CrossRef]
- Goyal, V.K.; Shukla, A. Isolated DC–DC Boost Converter for Wide Input Voltage Range and Wide Load Range Applications. IEEE Trans. Ind. Electron. 2021, 68, 9527–9539. [Google Scholar] [CrossRef]
- Singh, B.; Kushwaha, R. A PFC Based EV Battery Charger Using a Bridgeless Isolated SEPIC Converter. IEEE Trans. Ind. Appl. 2020, 56, 477–487. [Google Scholar] [CrossRef]
- Tseng, K.-C.; Huang, C.-C.; Cheng, C.-A. A Single-Switch Converter With High Step-Up Gain and Low Diode Voltage Stress Suitable for Green Power-Source Conversion. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 363–372. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, T.; He, Y. A Switched-Capacitor-Based Active-Network Converter With High Voltage Gain. IEEE Trans. Power Electron. 2014, 29, 2959–2968. [Google Scholar] [CrossRef]
- Baddipadiga, B.P.; Ferdowsi, M. A high-voltage-gain dc-dc converter based on modified dickson charge pump voltage multiplier. IEEE Trans. Power Electron. 2017, 32, 7707–7715. [Google Scholar] [CrossRef]
- Wu, B.; Li, S.; Liu, Y.; Smedley, K.M. A New Hybrid Boosting Converter for Renewable Energy Applications. IEEE Trans. Power Electron. 2016, 31, 1203–1215. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, J.; Yang, P. A single-switch high gain quadratic boost converter based on voltage-lift-technique. In Proceedings of the 2012 10th International Power & Energy Conference (IPEC), Ho Chi Minh City, Vietnam, 12–14 December 2012; pp. 71–75. [Google Scholar] [CrossRef]
- Tseng, K.-C.; Cheng, C.-A.; Chen, C.-T. High Step-Up Interleaved Boost Converter for Distributed Generation Using Renewable and Alternative Power Sources. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 713–722. [Google Scholar] [CrossRef]
- Hassan, W.; Lu, D.D.-C.; Xiao, W. Single-Switch High Step-Up DC–DC Converter With Low and Steady Switch Voltage Stress. IEEE Trans. Ind. Electron. 2019, 66, 9326–9338. [Google Scholar] [CrossRef]
- Meier, M.B.; da Silva, S.A.; Badin, A.A.; Romaneli, E.F.R.; Gules, R. Soft-Switching High Static Gain DC–DC Converter Without Auxiliary Switches. IEEE Trans. Ind. Electron. 2018, 65, 2335–2345. [Google Scholar] [CrossRef]
- Sathyan, S.; Suryawanshi, H.M.; Shitole, A.B.; Ballal, M.S.; Borghate, V.B. Soft-Switched Interleaved DC/DC Converter as Front-End of Multi-Inverter Structure for Micro Grid Applications. IEEE Trans. Power Electron. 2018, 33, 7645–7655. [Google Scholar] [CrossRef]
- Lai, C.-M.; Pan, C.-T.; Cheng, M.-C. High-Efficiency Modular High Step-Up Interleaved Boost Converter for DC-Microgrid Applications. IEEE Trans. Ind. Appl. 2012, 48, 161–171. [Google Scholar] [CrossRef]
- Kumar, P.H.; Somasekhar, V.T. An Enhanced Fault-Tolerant and Auto reconfigurable BLDC Motor Drive for Electric Vehicle Applications. IEEE J. Emerg. Sel. Top. Ind. Electron. 2023, 4, 368–380. [Google Scholar] [CrossRef]
- Naseri, F.; Farjah, E.; Ghanbari, T. An Efficient Regenerative Braking System Based on Battery/Supercapacitor for Electric, Hybrid, and Plug-In Hybrid Electric Vehicles with BLDC Motor. IEEE Trans. Veh. Technol. 2017, 66, 3724–3738. [Google Scholar] [CrossRef]
- Benyahia, N.; Denoun, H.; Zaouia, M.; Rekioua, T.; Benamrouche, N. Power system simulation of fuel cell and supercapacitor based electric vehicle using an interleaving technique. Int. J. Hydrogen Energy 2015, 40, 15806–15814. [Google Scholar] [CrossRef]
- Gong, W.; Cai, Z. Accelerating parameter identification of proton exchange membrane fuel cell model with ranking-based differential evolution. Energy 2013, 59, 356–364. [Google Scholar] [CrossRef]
- Reddy, K.J.; Sudhakar, N. High Voltage Gain Interleaved Boost Converter with Neural Network Based MPPT Controller for Fuel Cell Based Electric Vehicle Applications. IEEE Access 2018, 6, 3899–3908. [Google Scholar] [CrossRef]
- Czarnowski, I.; Jędrzejowicz, J.; Jędrzejowicz, P. Designing RBFNs Structure Using Similarity-Based and Kernel-Based Fuzzy C-Means Clustering Algorithms. IEEE Access 2021, 9, pp. 4411–4422. [Google Scholar] [CrossRef]
- Seghouane, A.-K.; Shokouhi, N. Adaptive Learning for Robust Radial Basis Function Networks. IEEE Trans. Cybern. 2021, 51, 2847–2856. [Google Scholar] [CrossRef]
- Afzal, A.; Navid, K.M.Y.; Saidur, R.; Razak, R.K.A.; Subbiah, R. Back Propagation Modeling of Shear Stress and Viscosity of Aqueous Ionic—MXene Nanofluids. J. Therm. Anal. Calorim. 2021, 145, 2129–2149. [Google Scholar] [CrossRef]
- Afzal, A.; Buradi, A.; Jilte, R.; Sundara, V.; Shaik, S.; Ağbulut, Ü.; Alwetaishi, M.; Saleel, C.A. Use of Modern Algorithms for Multi-Parameter Optimization and Intelligent Modelling of Sustainable Battery Performance. J. Energy Storage 2023, 73, 108910. [Google Scholar] [CrossRef]
- Khandal, S.V.; Razak, A.; Veza, I.; Afzal, A.; Alwetaishi, M.; Shaik, S.; Ağbulut, Ü.; Rashedi, A. Hydrogen and Dual Fuel Mode Performing in Engine with Different Combustion Chamber Shapes: Modelling and Analysis Using RSM-ANN Technique. Int. J. Hydrogen Energy 2024, 52, 973–1005. [Google Scholar] [CrossRef]
- Mokashi, I.; Afzal, A.; Khan, S.A.; Abdullah, N.A.; Bin Azami, M.H.; Jilte, R.D.; Samuel, O.D. Nusselt Number Analysis from a Battery Pack Cooled by Different Fluids and Multiple Back-Propagation Modelling Using Feed-Forward Networks. Int. J. Therm. Sci. 2021, 161, 106738. [Google Scholar] [CrossRef]
- Huddar, V.B.; Razak, A.; Cuce, E.; Gadwal, S.; Alwetaishi, M.; Afzal, A.; Saleel, C.A.; Shaik, S. Thermal Performance Study of Solar Air Dryers for Cashew Kernel: A Comparative Analysis and Modelling Using Response Surface Methodology (RSM) and Artificial Neural Network (ANN). Int. J. Photoenergy 2022, 2022, 4598921. [Google Scholar] [CrossRef]
- Afzal, A.; Khan, S.A.; Islam, T.; Jilte, R.D.; Khan, A.; Soudagar, M.E.M. Investigation and Back-Propagation Modeling of Base Pressure at Sonic and Supersonic Mach Numbers. Phys. Fluids 2020, 32, 096109. [Google Scholar] [CrossRef]


































| Parameters | Rating |
|---|---|
| Maximum power (Pmax) | 1.26 kW |
| Maximum current (Imax) | 52 A |
| Maximum voltage P (max) | 34.8 V |
| No. of cells | 42 |
| Temperature (T) | 54 °C |
| Fuel cell response time (s) | 1 s |
| Nominal air flow rate | 2400 IPM |
| Reference | Number of Switches | Number of Diodes | Number of Capacitors | Number of Cores | Voltage Gain | Voltage Stress of Switches |
|---|---|---|---|---|---|---|
| Converter in [16] | 1 | 5 | 5 | 1 | ||
| Converter in [17] | 2 | 3 | 3 | 2 | ||
| Converter in [18] | 2 | 5 | 5 | 2 | ||
| Converter in [19] | 1 | 4 | 4 | 1 | ||
| Converter in [20] | 1 | 3 | 3 | 1 | ||
| Converter in [21] | 2 | 2 | 3 | 1 | ||
| Converter in [22] | 1 | 5 | 5 | 1 | ||
| Converter in [23] | 2 | 4 | 2 | 1 | ||
| Converter in [24] | 2 | 3 | 8 | 1 | ||
| Converter in [25] | 2 | 4 | 3 | 4 | ||
| Proposed Converter | 2 | 4 | 3 | 2 |
| Parameters | Values |
|---|---|
| Input variables | VFC, IFC |
| Input variables | Duty ratio |
| Spread factor | 0.01 |
| Training algorithm | Ordinary least squares |
| Maximum limit of the hidden neurons | 529 |
| θ (Degree) | Hall Signals | VSI Switching States | |||||||
|---|---|---|---|---|---|---|---|---|---|
| HA | HB | HC | S3 | S4 | S5 | S6 | S7 | S8 | |
| NA | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0–60 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 60–120 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 120–180 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 180–240 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 240–300 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 300–360 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| NA | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Components | Parameters |
|---|---|
| Input voltage VFC | 30–35 V |
| Output voltage V0 | 370 V |
| Switching frequency | 10 kHz |
| Duty cycle | 0.6 |
| Turns ratio | 1 |
| The capacitors C1, C2 | 4 μF |
| The capacitors C3 | 2.2 μF |
| The capacitors C4, C5 | 650 nF |
| The capacitor C0 | 470 μF |
| Parameters | PEMFC with RBFN-Based MPPT | PEMFC with Fuzzy-Based MPPT | ||||||
|---|---|---|---|---|---|---|---|---|
| Time Period (S) | 0 to 0.3 | 0.3 to 0.5 | 0.5 to 0.7 | 0.7 to 0.9 | 0 to 0.3 | 0.3 to 0.5 | 0.5 to 0.7 | 0.7 to 0.9 |
| Fuel Cell Temperature (°K) | 340 | 320 | 360 | 350 | 340 | 320 | 360 | 350 |
| Output voltage VDC (V) | 258 | 226 | 368 | 344 | 253 | 222 | 374 | 340 |
| Output current IDC (A) | 4.6 | 4.1 | 6.7 | 6.1 | 3.3 | 2.8 | 4.7 | 4.3 |
| Output power PDC (W) | 1197 | 900 | 2503 | 2155 | 868 | 645 | 1788 | 1536 |
| Components | Parameters |
|---|---|
| The power MOSFET’s S1, S2 | IXTK 62N 25 |
| The diodes D1, D2, D3, D4 | RF1001 |
| The diodes D5, D6, D0 | MUR1560 |
| The capacitors C0 | 470 μF |
| The capacitors C1, C2 | 4 μF |
| The capacitors C3 | 2.2 μF |
| The capacitors C4, C5 | 650 nF |
| Coupled inductors | EPCOS B66344 |
| Motor | BLDC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Subbulakshmy, R.; Palanisamy, R.; Alshahrani, S.; Saleel, C.A. Implementation of Non-Isolated High Gain Interleaved DC-DC Converter for Fuel Cell Electric Vehicle Using ANN-Based MPPT Controller. Sustainability 2024, 16, 1335. https://doi.org/10.3390/su16031335
Subbulakshmy R, Palanisamy R, Alshahrani S, Saleel CA. Implementation of Non-Isolated High Gain Interleaved DC-DC Converter for Fuel Cell Electric Vehicle Using ANN-Based MPPT Controller. Sustainability. 2024; 16(3):1335. https://doi.org/10.3390/su16031335
Chicago/Turabian StyleSubbulakshmy, R., R. Palanisamy, Saad Alshahrani, and C Ahamed Saleel. 2024. "Implementation of Non-Isolated High Gain Interleaved DC-DC Converter for Fuel Cell Electric Vehicle Using ANN-Based MPPT Controller" Sustainability 16, no. 3: 1335. https://doi.org/10.3390/su16031335
APA StyleSubbulakshmy, R., Palanisamy, R., Alshahrani, S., & Saleel, C. A. (2024). Implementation of Non-Isolated High Gain Interleaved DC-DC Converter for Fuel Cell Electric Vehicle Using ANN-Based MPPT Controller. Sustainability, 16(3), 1335. https://doi.org/10.3390/su16031335








