Spatial Downscaling of ERA5 Reanalysis Air Temperature Data Based on Stacking Ensemble Learning
Abstract
:1. Introduction
2. Materials and Methods
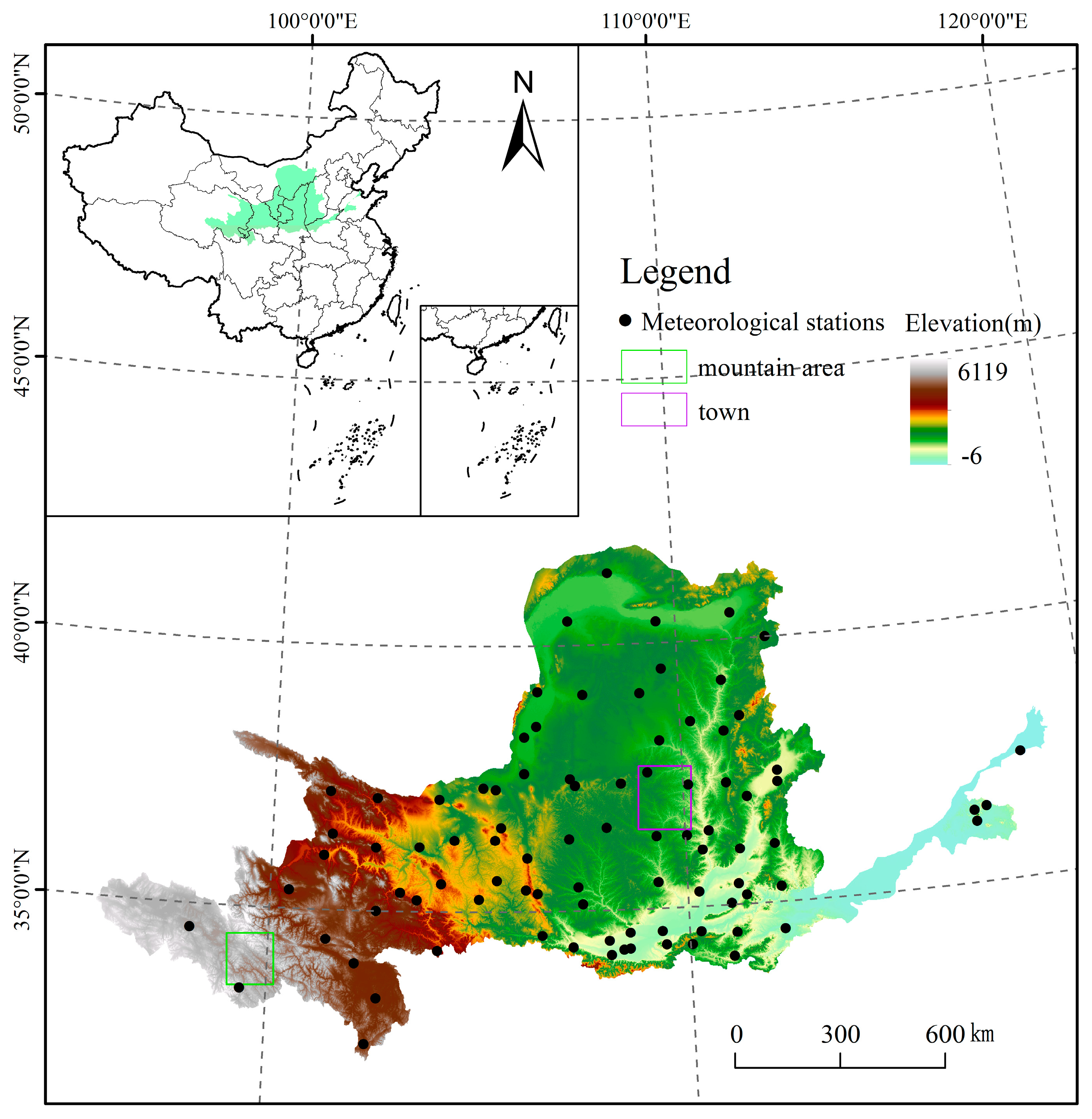
2.1. Study Area
2.2. Data Sources and Preprocessing
- (1)
- ERA5-Land reanalysis air temperature data
- (2)
- Meteorological station data
- (3)
- MODIS data
- (4)
- DEM data
2.3. Research Methods
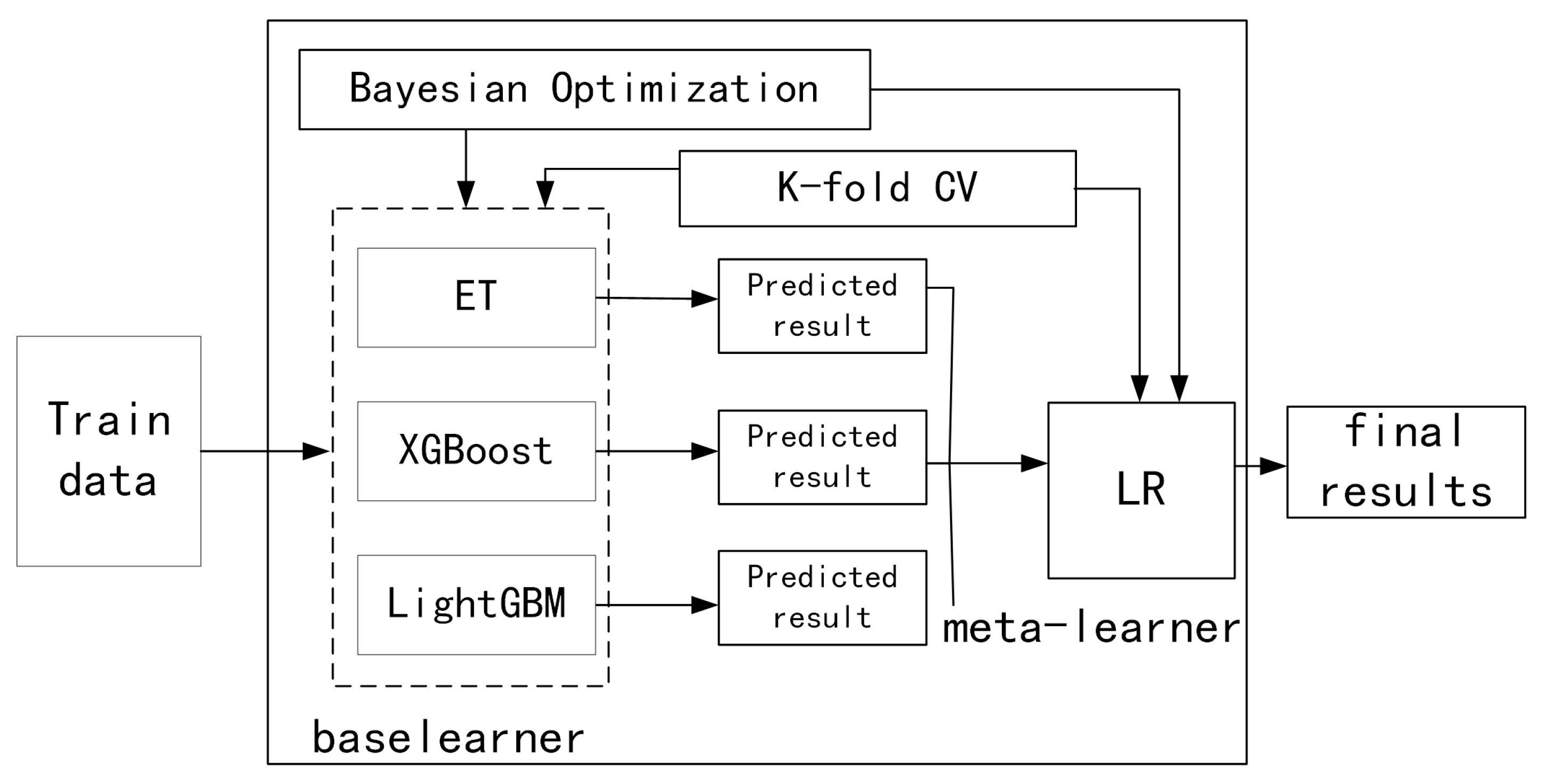
2.3.1. Stacking Ensemble Learning
- (1)
- Stacking ensemble learning principles
- (2)
- Building a stacking ensemble learning framework
2.3.2. Bayesian Optimization
2.3.3. Using K-Fold CV for Model Accuracy Validation
2.3.4. Evaluation Methods
2.3.5. Correlation Analysis
3. Results
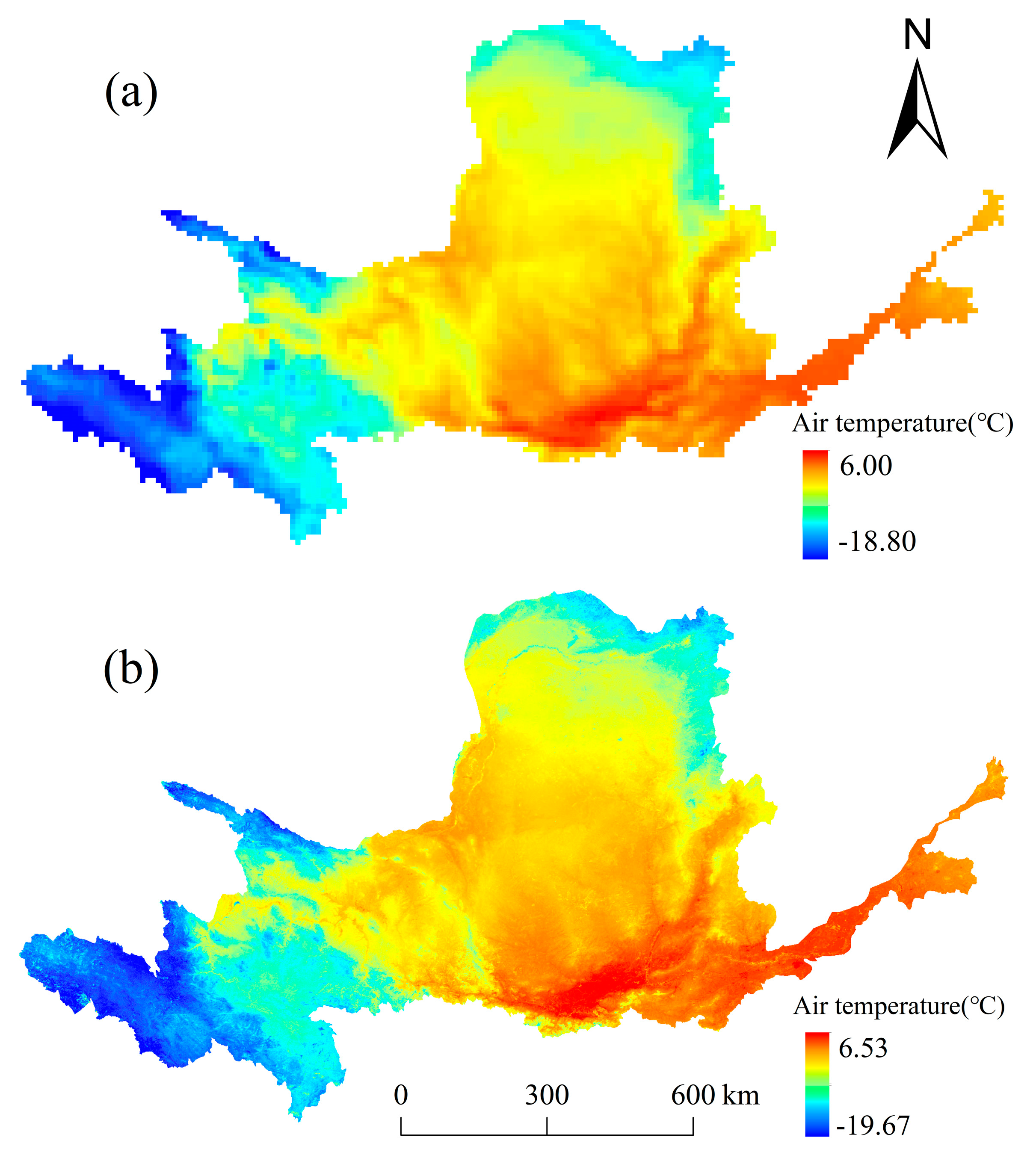
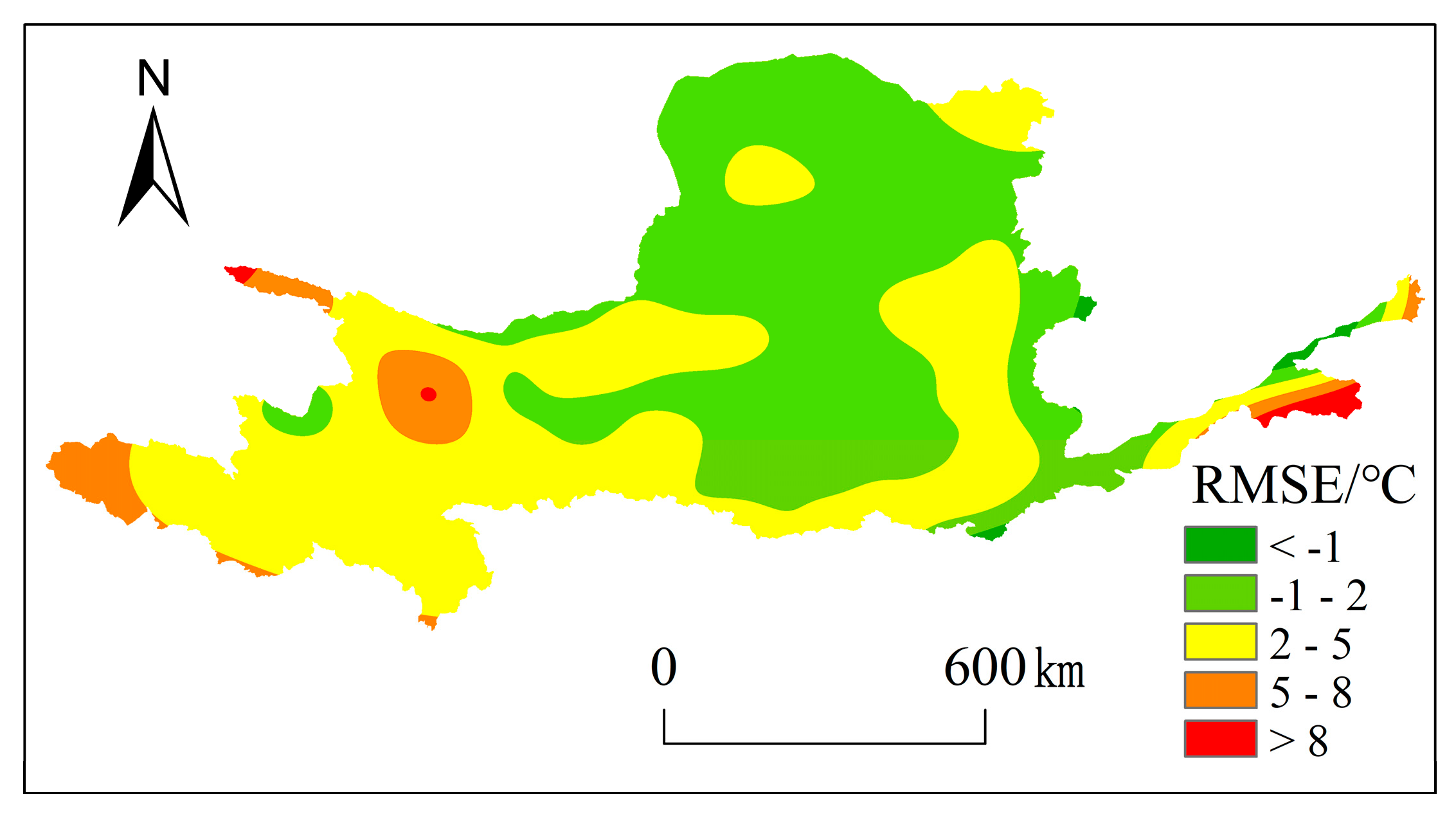
3.1. ERA5-Land Reanalysis Air Temperature Data Accuracy Analysis
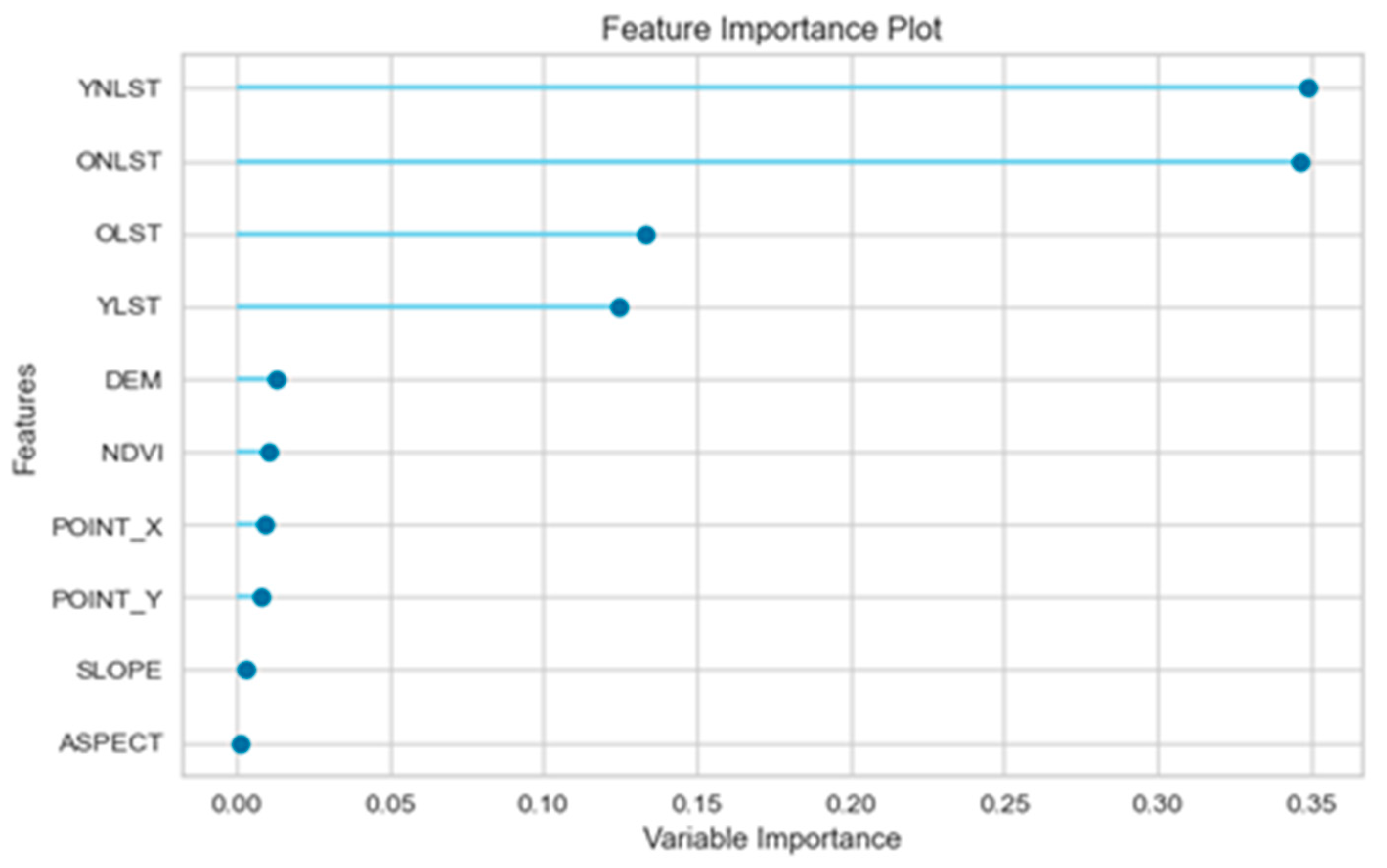
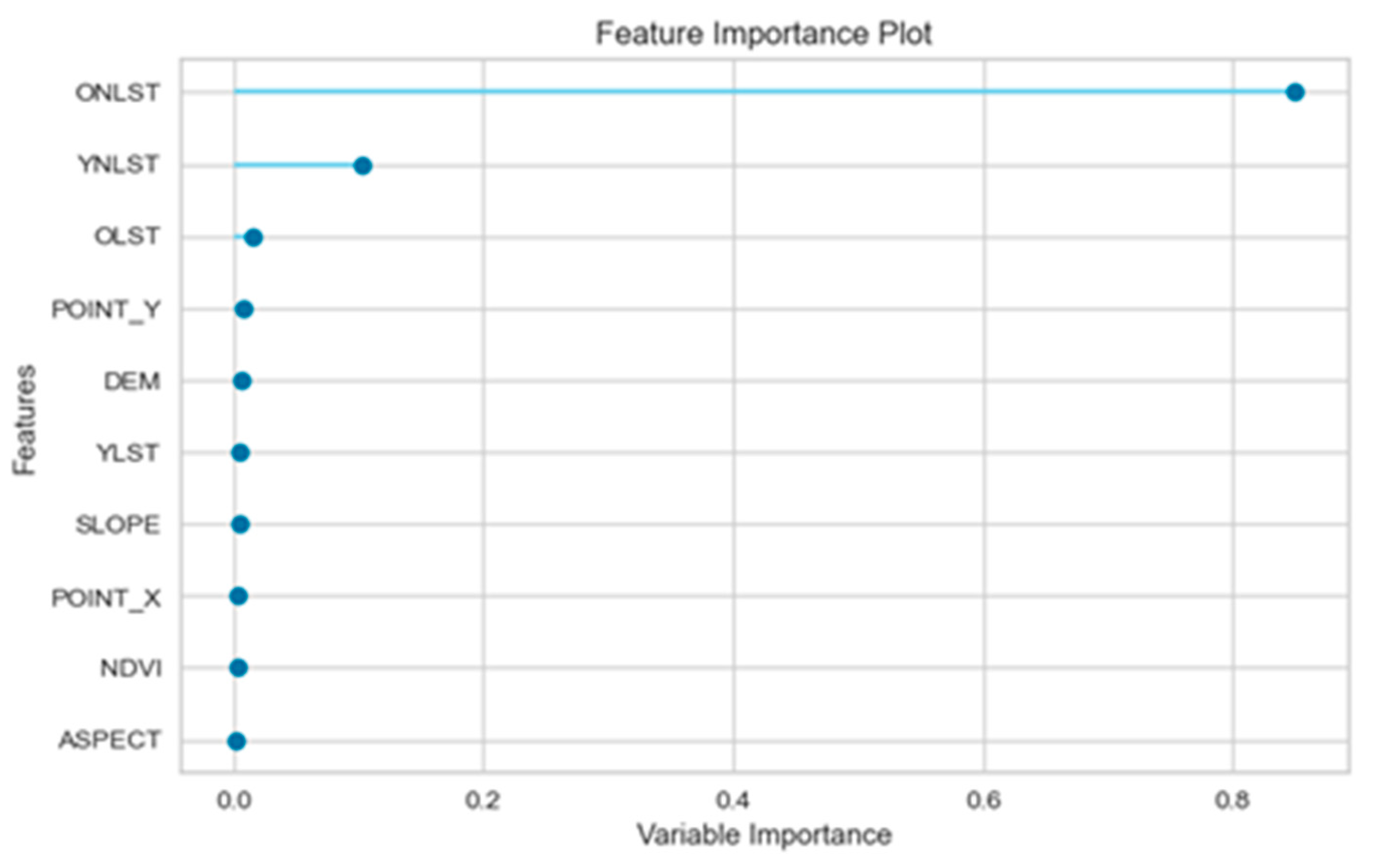
3.2. Variable Selection
3.3. Model Performance Evaluation
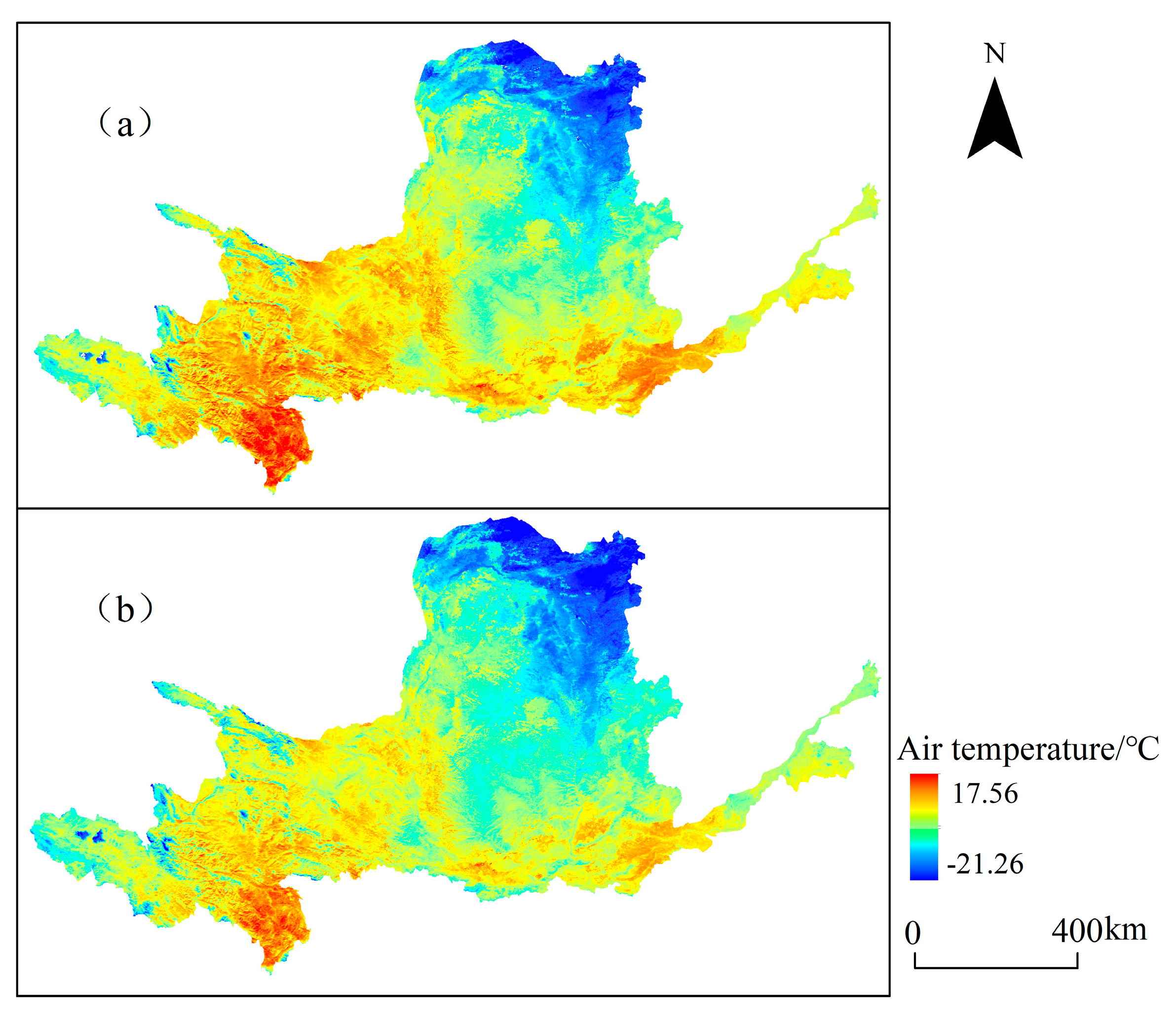
3.4. Analysis of Stacking Ensemble Model Downscaling Results
4. Discussion
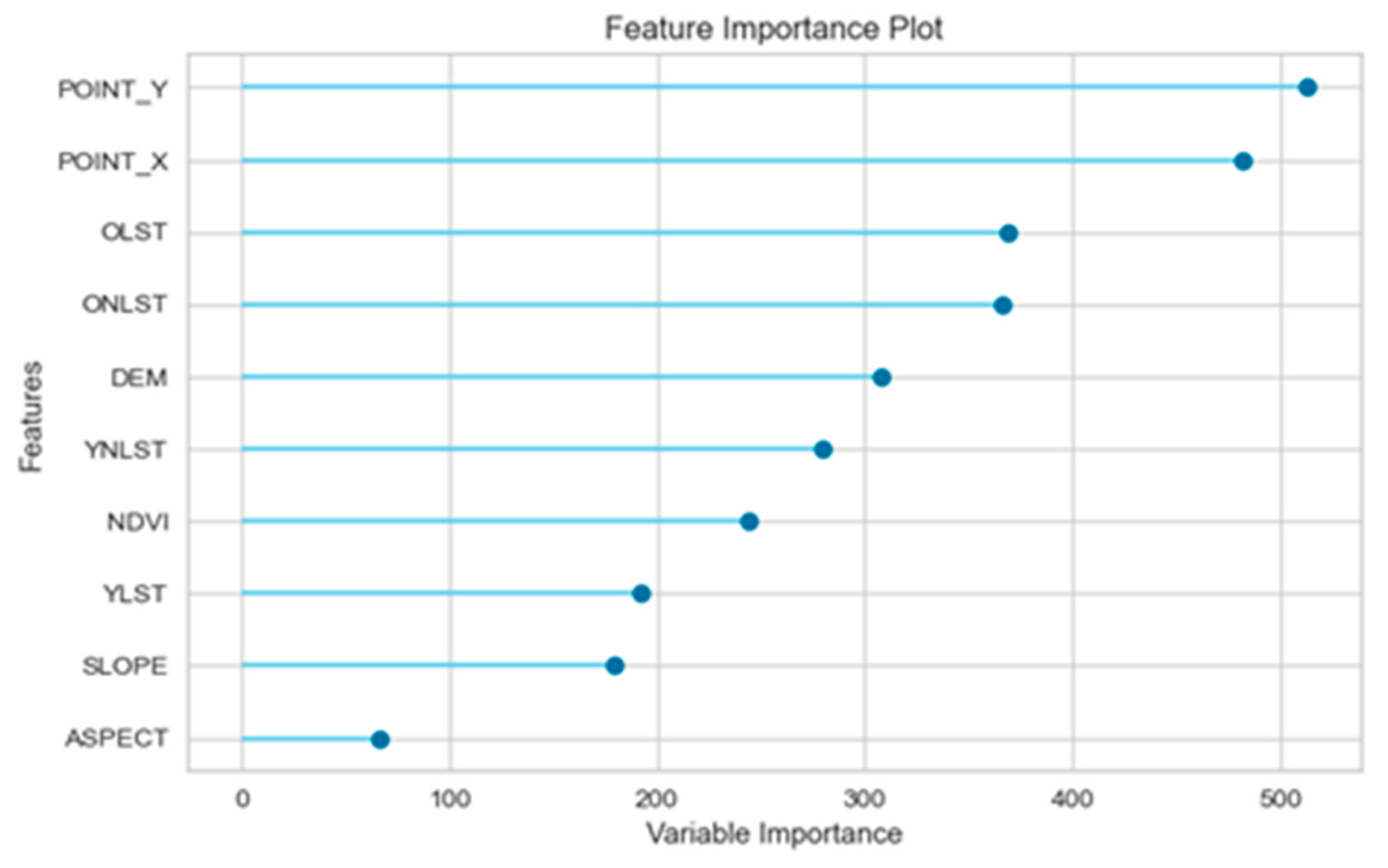
4.1. Variable Importance
4.2. The Limitation of This Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Suggitt, A.; Wilson, R.; Isaac, N.; Beale, C.; Auffret, A.; August, T.; Bennie, J.; Crick, H.; Duffield, S.; Fox, R.; et al. Extinction risk from climate change is r-educed by microclimatic buffering. Nat. Clim. Chang. 2018, 8, 713–717. [Google Scholar] [CrossRef]
- Nieto, H.; Sandholt, I.; Aguado, I.; Chuvieco, E.; Stisen, S. Air temperature estimation with MSG-SEVIRI data: Calibration and validation of the TVX algorithm for the Iberian Peninsula. Remote Sens. Environ. 2011, 115, 107–116. [Google Scholar] [CrossRef]
- Chen, S.; Chen, W.; Wu, R.; Yu, B.; Song, L. Performance of the IPCC AR6 models in simulating the relation of the western North Pacific subtropical high to the spring northern tropical Atlantic SST. Int. J. Climatol. 2020, 41, 725. [Google Scholar] [CrossRef]
- Howarth, C.; Viner, D. Integrating adaptation practice in assessments of climate change science: The case of IPCC Working Group II reports. Environ. Sci. Policy 2022, 135, 1–5. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, S.; Wang, N.; Huang, C.; Wang, X. Prolonged duration and increased severity of agricultural droughts during 1978 to 2016 detected by ESA CCI SM in the humid Yunnan Province, Southwest China. Catena 2021, 198, 105036. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Q.; Ge, Q.; Dai, J.; Qin, Y.; Dai, L.; Zou, X.; Chen, J. Modelling the impacts of climate change and crop management on phenological trends of spring and winter wheat in China. Agric. For. Meteorol. 2018, 248, 518–526. [Google Scholar] [CrossRef]
- Gerlitz, L. Using fuzzified regression trees for statistical downscaling and regionalization of near surface tempera tures in complex terrain: A case study from Khumbu Hi mal. Theor. Appl. Climatol. 2015, 122, 337–352. [Google Scholar] [CrossRef]
- Vittorio, A.; Miller, N. Evaluating a modified point-based method to downscale cell-based climate variable data to high-resolution grids. Theor. Appl. Climatol. 2013, 112, 495–519. [Google Scholar] [CrossRef]
- Wang, Y.; Tan, D.; Han, L.; Li, D.; Wang, X.; Lu, G.; Lin, J. A Review of Climate Change Research in the Yellow River Basin. J. Desert Res. 2021, 41, 235–246. [Google Scholar]
- Zhang, L.; Huang, J.; Liang, J.; Yu, H.; Guan, X.; Ma, J.; Shen, Y.; Deng, J.; Huang, N.; Meng, X.; et al. Impacts of Climate Change on the Yellow River Basin and Countermeasures. Sci. Technol. Rev. 2020, 38, 42–51. [Google Scholar]
- Dirksen, M.; Knap, W.; Steeneveld, G.; Holtslag, A.; Tank, A. Downscaling daily air temperature measurements in the Nether lands. Theor. Appl. Climatol. 2020, 142, 751–767. [Google Scholar] [CrossRef]
- Tang, G.; Ali, B.; Ma, Z.; Di, L.; Hong, L. Downscaling of ERA-interim temperature in the contiguous United States and its implications for rain–snow partitioning. J. Hydrometeorol. 2018, 19, 1215–1233. [Google Scholar] [CrossRef]
- Wang, S.; Xu, T.; Nie, W.; Zhen, Z. Evaluation of Precipitable Water Vapor from Five Reanalysis Products with Ground-Based GNSS Observations. Remote Sens. 2020, 12, 1817. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, S.; Yan, J.; Chen, Z.; Ruan, X. A comparison of atmospheric temperature over China between adiosonde observations and multiple reanalysis datasets. Acta Meteorol. Sin. 2016, 74, 71–284. [Google Scholar]
- Wang, T.; Wu, T.; Li, R.; Xie, C.; Zou, D.; Qin, Y.; Yu, W.; Wang, W. Evaluation of Monthly Air Temperature from Two Reanalysis Datasets in Mongolia. Plateau Meoteorology 2016, 35, 651–661. [Google Scholar]
- Kumar, A.; Yadav, J.; Mohan, R. Seasonal sea-ice variability and its trend in the Weddell Sea sector of West Antarctica. Environ. Res. Lett. 2021, 16, 24–46. [Google Scholar] [CrossRef]
- Ding, M.; Du, J.; Xiao, T. Applicability of the four reanalysis temperature data in Chang Tang Nature Reserve. J. Glaciol. Geocryol. 2020, 42, 1046–1056. [Google Scholar]
- Zhang, L.; Yu, Y.; Su, L.; Hao, T.; Zheng, H. Effects of Land Use Change on Air Temperature of Heilongjiang Province in 1960–2010. Sci. Geogr. Sin. 2017, 37, 952–959. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Thepaut, J. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Miao, W.; Liu, S.; Zhu, Y.; Duan, S.; Han, F. Spatio-temporal differentiation and altitude dependence of temperature and precipitation in Meili Snow Mountains. Clim. Chang. Res. 2022, 18, 328–342. [Google Scholar]
- Zou, J.; Lu, N.; Jiang, H.; Qin, J.; Yao, L.; Xin, Y.; Su, F. Performance of air temperature from ERA5-Land reanalysis in coastal urban agglomeration of Southeast China. Sci. Total Environ. 2022, 828, 154459. [Google Scholar] [CrossRef]
- Tang, H.; Wang, X.; Chen, F.; Jiang, L.; He, C.; Long, A. Simulation of Manas River runoff based on ERA5-Land dataset. Earth Sci. Front. 2022, 29, 271–283. [Google Scholar]
- Zhang, H.; Gao, Y. Projected Changes of Precipitation over the Qinghai-Tibetan Plateau Based on Dynamical Downscaling. Plateau Meteorol. 2020, 39, 477–485. [Google Scholar]
- Xu, Z.; Han, Y.; Yang, Z. Dynamical downscaling of regional climate: A review of methods and limitations. Sci. China Earth Sci. 2019, 62, 365–375. [Google Scholar] [CrossRef]
- Shu, J.; Jiang, X.; Huang, X.; Wu, Q. Statistical Downscaling Modeling Analysis of Summer Precipitation in Southwest China. Plateau Meteorol. 2019, 38, 349–358. [Google Scholar]
- Kustas, W.; Norman, J.; Anderson, M.; French, A. Estimating subpixel surface temperatures and energy fluxes from the vegetation index-radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Zhu, X.; Song, X.; Leng, P.; Hu, R. Research on Downscaling of Land Surface Temperature using Multi-Scale Geographic Weighted Regression. J. Remote Sens. 2021, 25, 1749–1766. [Google Scholar]
- Gong, Y.; Ma, S.; Liu, W. A comparative study of machine learning and statistical models in climate downscaling in the Shiyang River Basin. J. Desert Res. 2022, 42, 196–210. [Google Scholar]
- Jing, W.; Feng, M.; Yang, Y. A Statistical Downscaling Approach of NCEP/NCAR Reanalysis Temperature Data. J. Geo-Inf. Sci. 2013, 15, 819–828. [Google Scholar] [CrossRef]
- Li, X.; Yuan, Z.; Deng, W.; Yang, L.; Zhou, X.; Hu, L. Spatial downscaling methods for the 2-meter air temperature grid data based on multiple machine learning models. Remote Sens. Nat. Resour. 2023, 35, 57–65. [Google Scholar]
- Wang, R.; Gao, W.; Peng, W. Spatial downscaling method for air temperature through the correlation between land use/land cover and microclimate: A case study of the Greater Tokyo Area, Japan. Urban Clim. 2021, 40, 101003. [Google Scholar] [CrossRef]
- Yu, F.; Zhu, S.; Zhang, G.; Zhu, J.; Zhang, N.; Xu, Y. A Downscaling Method for Land Surface Air Temperature of ERA5 Reanalysis Dataset under Complex Terrain Conditions in Mountainous Areas. J. Geo-Inf. Sci. 2022, 24, 750–765. [Google Scholar]
- Wolpert, D. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Sikora, R.; Al-Laymoun, O. A Modified Stacking Ensemble Machine Learning Algorithm Using Genetic Algorithms; Springer: New Delhi, India, 2017. [Google Scholar]
- Wang, R.; Bao, T.; Li, Y.; Song, B.; Xiang, Z. Combination Prediction Model for Dam Deformation Based on Multi-Factor Fusion and Stacking Ensemble Learning. J. Hydraul. Eng. 2023, 54, 497–506. [Google Scholar]
- Gall, J.; Yao, A.; Razavi, N.; Van Gool, L.; Lempitsky, V. Hough Forests for Object Detection, Tracking, and Action Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2188–2202. [Google Scholar] [CrossRef]
- Liu, X.; Huang, W.; Jiang, Y.; Guo, R.; Huang, Y.; Song, Q.; Yang, Y. Research on Classification and Recognition of Severe Convective Weather Based on the LightGBM Algorithm. Plateau Meteorol. 2021, 40, 909–918. [Google Scholar]
- Xue, D. Reconstruction of All-Weather Daytime and Nighttime MODIS Aqua-Terra Land Surface Temperature Products Using an XGBoost Approach. Remote Sens. 2021, 13, 4723. [Google Scholar]
- Brochu, E.; Cora, V.; Freitas, N. A Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning. Comput. Sci. 2010. [Google Scholar] [CrossRef]
- Wu, Y. Assessment of machine learning classifiers for global lake ice cover mapping from MODIS TOA reflectance data. Remote Sens. Environ. 2021, 253, 112206. [Google Scholar] [CrossRef]
- Davis, P. Estimation of shelter temperature from operational satellite sounder data. Clim. Appl. Meteorol. 1983, 22, 369–376. [Google Scholar] [CrossRef]
- Vogt, J.; Viau, A.; France, P. Mapping regional air temperature fields using satellite-derived surface skin temperatures. Int. J. Climatol. 1997, 17, 1559–1579. [Google Scholar] [CrossRef]
- Jing, J.; Liu, J.; Qin, C.; Mioa, Y.; Zhu, A. Near-surface air temperature lapse rates and seasonal and type differences in China. Prog. Geogr. 2016, 35, 1538–1548. [Google Scholar]
- Lookingbill, T.; Urban, D. Spatial estimation of air temperature differences for landscape-scale studies in montane environments. Agric. For. Meteorol. 2003, 114, 141–151. [Google Scholar] [CrossRef]
- Huang, H.; Xu, H.; Lin, T.; Xia, G. Spatiotemporal Variation Characteristics of Normalized Vegetation Index in Altay Region of Xinjiang from 2001 to 2020 and Its Response to Climate Change. Acta Ecol. Sin. 2022, 42, 2798–2809. [Google Scholar]
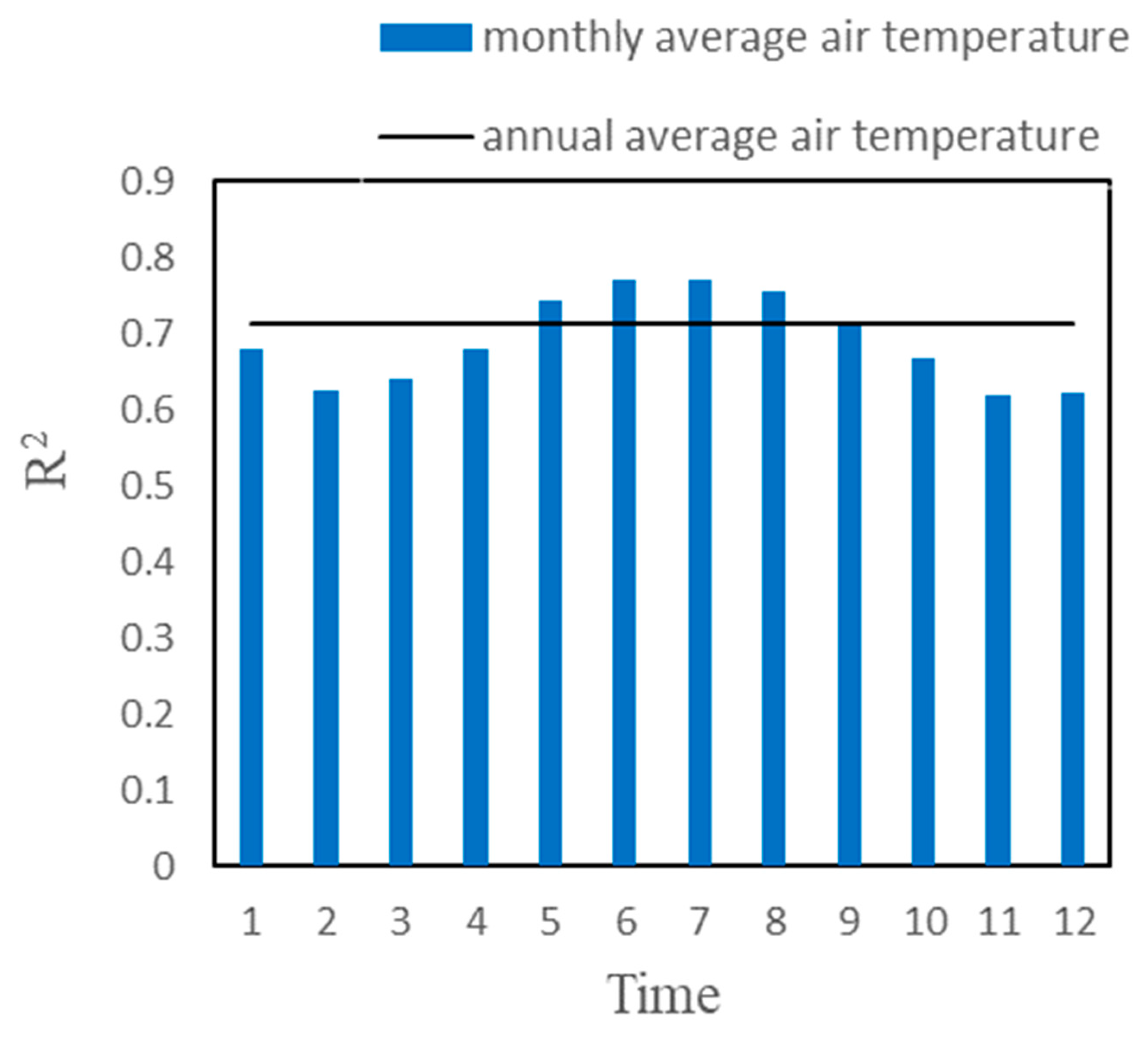



| Indicator | Monthly Average Air Temperature | Annual Average Air Temperature |
|---|---|---|
| R2 | 0.69 | 0.71 |
| MAE | 2.07 | 1.89 |
| RMSE | 2.95 | 2.72 |
| Variable Types | Variable Abbreviation | Variable Description |
|---|---|---|
| Independent variable | YLST | Aqua satellite (1:30 PM) surface land temperature |
| YNLST | Aqua satellite (1:30 AM) surface land temperature | |
| OLST | Aqua satellite (1:30 AM) surface land temperature | |
| ONLST | Aqua satellite (1:30 AM) surface land temperature | |
| POINT_X | longitude | |
| POINT_Y | latitude | |
| DEM | altitude | |
| SLOPE | slope | |
| ASPECT | aspect | |
| NDVI | Normalized Difference Vegetation Index |
| Algorithm | Train Set | Test Set | ||||
|---|---|---|---|---|---|---|
| R2 | MAE | RMSE | R2 | MAE | RMSE | |
| Stacking | 0.986 | 0.761 | 1.274 | 0.987 | 0.741 | 1.215 |
| ET | 0.985 | 0.773 | 1.306 | 0.987 | 0.755 | 1.248 |
| XGBoost | 0.983 | 0.911 | 1.416 | 0.984 | 0.899 | 1.360 |
| LightGBM | 0.981 | 1.010 | 1.499 | 0.982 | 0.998 | 1.455 |
| Data | MAE | RMSE |
|---|---|---|
| 0.1° Reanalyzed air temperature | 1.855 | 2.524 |
| Downscaled 1 km air temperature | 1.810 | 2.519 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Li, J.; Liu, D. Spatial Downscaling of ERA5 Reanalysis Air Temperature Data Based on Stacking Ensemble Learning. Sustainability 2024, 16, 1934. https://doi.org/10.3390/su16051934
Zhang Y, Li J, Liu D. Spatial Downscaling of ERA5 Reanalysis Air Temperature Data Based on Stacking Ensemble Learning. Sustainability. 2024; 16(5):1934. https://doi.org/10.3390/su16051934
Chicago/Turabian StyleZhang, Yuna, Jing Li, and Deren Liu. 2024. "Spatial Downscaling of ERA5 Reanalysis Air Temperature Data Based on Stacking Ensemble Learning" Sustainability 16, no. 5: 1934. https://doi.org/10.3390/su16051934
APA StyleZhang, Y., Li, J., & Liu, D. (2024). Spatial Downscaling of ERA5 Reanalysis Air Temperature Data Based on Stacking Ensemble Learning. Sustainability, 16(5), 1934. https://doi.org/10.3390/su16051934





