Determination of the Shear Strength of Unsaturated Loess Samples from Conventional Triaxial Shear Tests Applying Rubber Membrane Correction
Abstract
1. Introduction
- (i)
- Change the force conditions: Filling the space between the rubber membrane and the specimen with the liquid rubber, copper, or other materials [12,13,14] to reduce the embedded volume. However, this technique also has an impact on the test results by reducing the actual influence of the axial force conditions of the specimen, triggering new errors;
- (ii)
- Instrumental compensation method: Water is replenished within the specimen [15,16,17] or between a special dual membrane [18] to compensate for the embedded volume of the rubber membrane. This method compensates for the localized drainage of the specimen due to the embedded rubber membrane and is believed to eliminate 100% of the effect [19];
- (iii)
- Optimization of measurement systems: Typically, water is continuously injected or withdrawn either by using manual techniques [20] or by using computerized control techniques [15,21,22] to compensate for the effect of membrane compliance. Copper rods of different diameters and the same height are placed in the specimen, and the embedded volume is estimated by the linear relationship between the change of total volume and diameter of copper rods [23]. The copper rod method has been subsequently improved by many scholars [24,25,26]. Various empirical calculations for determining the embedded volume have also been proposed [27,28];
- (iv)
- Analytical derivation method: Martin et al. [29] proposed a theoretical and computational method based on the generation and development of pore pressure. The analytical expression of the embedded volume has been derived by the elasto-mechanical method used in calibration and applied to correct the measured data. However, this technique is found to not be suitable for well-graded coarse-grained soil samples [6].
2. Experiments and Methods
2.1. Soil Samples and Physical Properties
2.2. Experiments
2.3. Methods
2.3.1. Method 1
2.3.2. Method 2
3. Results
3.1. Loess Shear Strength
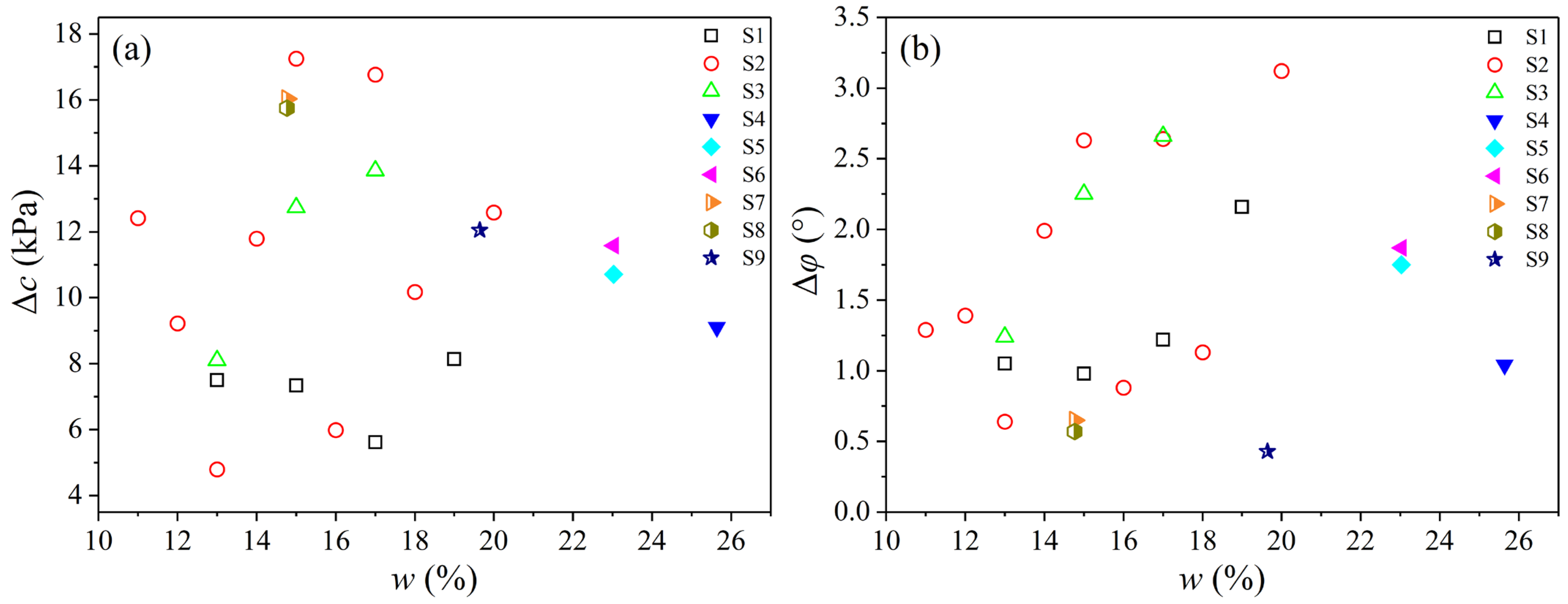
3.2. Calculation of Shear Strength Error under the Influence of a Rubber Membrane
4. Discussions
4.1. Factors Affecting the Error of Shear Strength Index
4.1.1. Types of Soil Sample
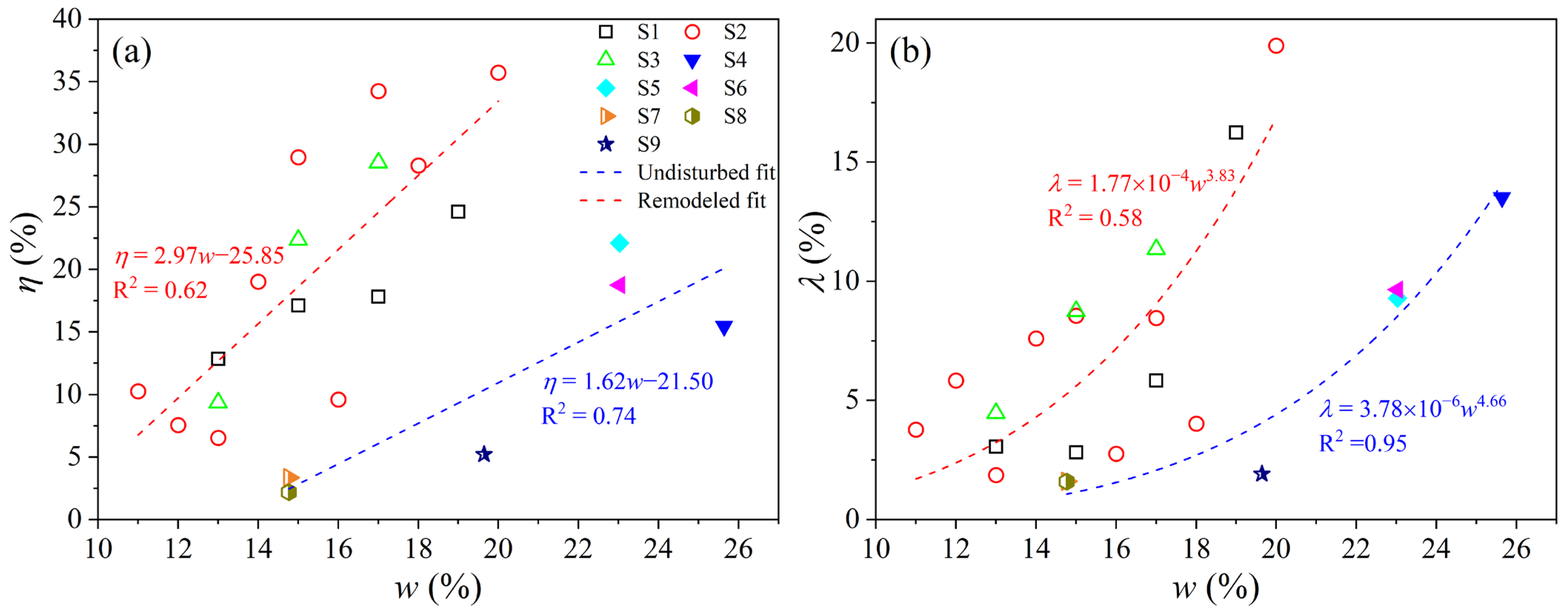
4.1.2. Water Content
- (a)
- Relationship to the change amount of shear strength
- (b)
- Relationship to the change rate of shear strength
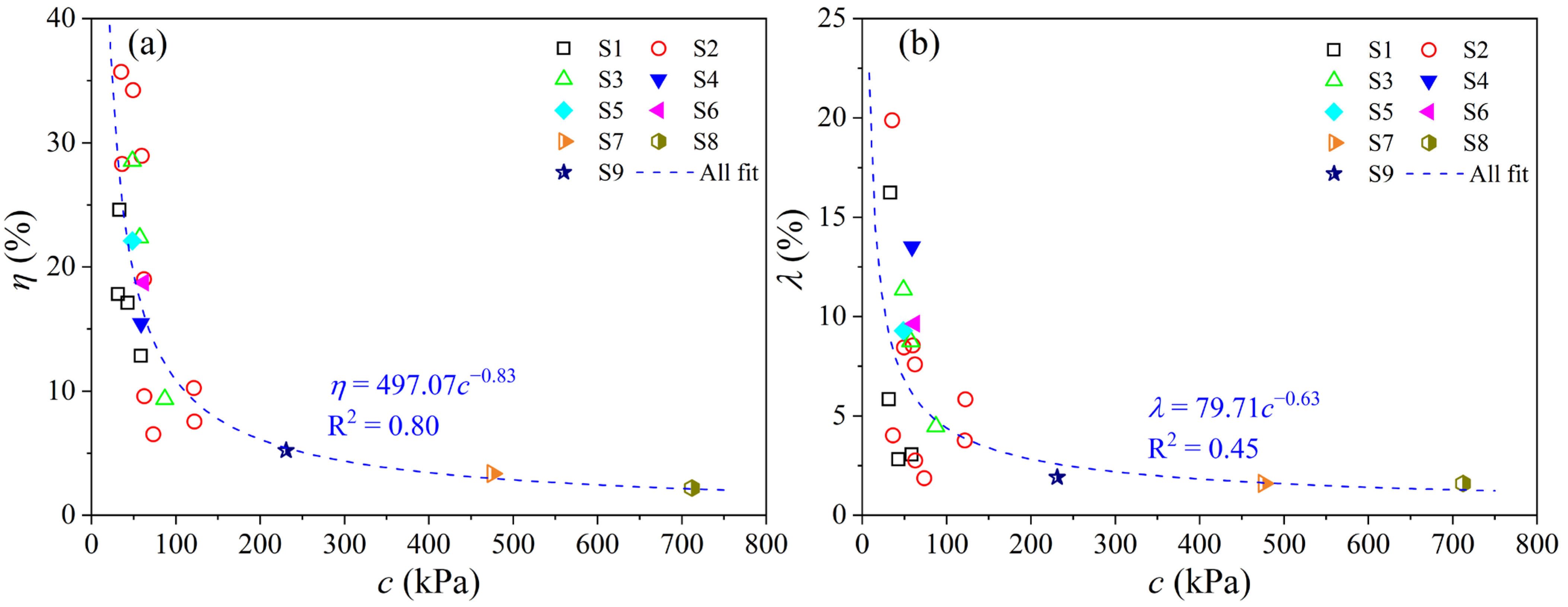
4.1.3. Measured Cohesion cu
4.1.4. Measured Internal Friction Angle φu
4.2. Correction for Measured Shear Strength Index
4.2.1. Remolded Loess
4.2.2. Undisturbed Loess
- (a)
- Corrections based on measured shear strength indices
- (b)
- Corrections based on measured water content
5. Conclusions
- (1)
- The measured undrained cohesion, cu, from the UU test with a rubber membrane is significantly larger than the corrected value, cu0, and the differentials are 5–17.5 kPa. The rate of change ranges from 2.21% to 35.74%. Meanwhile, the measured internal friction angle, φu, is less than the corrected value, φu0, with the amount being 0.43–3.12°. The rate of change ranges from 1.60% to 19.89%, which is significantly less compared to the undrained cohesion;
- (2)
- The influence degree of the rubber membrane on the measured cohesion, cu, and internal friction angle, φu, of loess in the UU test is inversely proportional to the loess shear strength. The loss rate of cohesion shows a power function decay law with the measured cohesion, while the increased rate of the internal friction angle illustrates a negative linear correlation with the measured internal friction angle. Both the change rate of cohesion and the internal friction angle of undisturbed loess increased linearly with the increase in water content;
- (3)
- Based on the test data, the relationship between the shear strength indices and influencing factors of types of loess was fitted with the determination coefficient R2 basically being more than 0.8. Empirical correction formulae for the measured shear strength indices developed from the UU tests with a rubber membrane of remolded loess, Q3 undisturbed loess, and Q2 undisturbed loess were established, respectively. The proposed correction formulae can be used for correcting the mechanical parameters of loess in engineering practice applications and designing sustainable infrastructure in problematic loess deposits of northwest China.
- (4)
- The proposed correction method in this study can be extended to other soils to develop new relationships. However, it is important to note that the proposed correction relationships are valid only for the mechanical parameters of loess samples from northwest China.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cai, G.; Li, J.; Liu, S.; Li, J.; Han, B.; He, X.; Zhao, C. Simulation of Triaxial Tests for Unsaturated Soils under a Tension–Shear State by the Discrete Element Method. Sustainability 2022, 14, 9122. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Ly, H.-B.; Ho, L.S.; Al-Ansari, N.; Van Le, H.; Tran, V.Q.; Prakash, I.; Pham, B.T. Influence of Data Splitting on Performance of Machine Learning Models in Prediction of Shear Strength of Soil. Math. Probl. Eng. 2021, 2021, 4832864. [Google Scholar] [CrossRef]
- Peng, P.; Li, Z.; Zhang, X.; Liu, W.; Sui, S.; Xu, H. Slope Failure Risk Assessment Considering Both the Randomness of Groundwater Level and Soil Shear Strength Parameters. Sustainability 2023, 15, 7464. [Google Scholar] [CrossRef]
- Liu, H.; Lyu, X.; Wang, J.; He, X.; Zhang, Y. The Dependence between Shear Strength Parameters and Microstructure of Subgrade Soil in Seasonal Permafrost Area. Sustainability 2020, 12, 1264. [Google Scholar] [CrossRef]
- Soldo, A.; Miletić, M. Study on Shear Strength of Xanthan Gum-Amended Soil. Sustainability 2019, 11, 6142. [Google Scholar] [CrossRef]
- Xu, W.; Chen, S.; Fu, Z.; Ji, E. Measuring Method for Membrane Penetration Capacity of Coarse-Grained Soil in Triaxial Tests. Chin. J. Geotech. Eng. 2021, 43, 1536–1541. [Google Scholar] [CrossRef]
- Newland, P.L.; Allely, B.H. Volume Changes in Drained Triaxial Tests on Granular Materials. Geotechnique 1957, 7, 17–34. [Google Scholar] [CrossRef]
- Evans, M.D.; Seed, H.B. Undrained Cyclic Triaxial Testing of Gravels: The Effect of Membrane Compliance; College of Engineering, University of California: Oakland, CA, USA, 1987. [Google Scholar]
- Noor, M.J.M.; Nyuin, J.D.; Derahman, A. A Graphical Method for Membrane Penetration in Triaxial Tests on Granular Soils. J. Inst. Eng. Malays. 2012, 73, 23–30. [Google Scholar]
- Chen, C.; Zang, H. Some Problems in Triaxial Test on Saturated Sands. Chin. J. Geotech. Eng. 2000, 22, 659–663. [Google Scholar]
- Alhani, I.J.; Noor, M.J.M.; Albadri, W.M. Membrane Penetration Effects on Shear Strength and Volume Change of Soil during Triaxial Test. AIP Conf. Proc. 2018, 2020, 020008. [Google Scholar]
- Raghunandan, M.E.; Sharma, J.S.; Pradhan, B. A Review on the Effect of Rubber Membrane in Triaxial Tests. Arab. J. Geosci. 2015, 8, 3195–3206. [Google Scholar] [CrossRef]
- Tsoi, W.-Y.; Lee, K.-M. Membrane Penetration Remedy for the Testing of Lightly Cemented Scrap Rubber Tire Chips. Geotech. Test. J. 2008, 32, 55–63. [Google Scholar] [CrossRef]
- Choi, J.W.; Ishibashi, I. An Experimental Method for Determining Membrane Penetration. Geotech. Test. J. 1992, 15, 413–417. [Google Scholar] [CrossRef]
- Ramana, K.V.; Raju, V.S. Constant-Volume Triaxial Tests to Study the Effects of Membrane Penetration. Geotech. Test. J. 1981, 4, 117–122. [Google Scholar] [CrossRef]
- Tokimatsu, K.; Nakamura, K. A Liquefaction Test without Membrane Penetration Effects. Soils Found. 1986, 26, 127–138. [Google Scholar] [CrossRef]
- Seed, R.B.; Hossain, A. Development of a Laboratory Technique for Correcting Results of Undrained Triaxial Shear Tests on Soils Containing Coarse Particles for Effects of Membrane Compliance; US Army Engineer Waterways Experiment Station, Geotechnical Laboratory: Vicksburg, MS, USA, 1987. [Google Scholar]
- Kramer, S.L.; Sivaneswaran, N. A Nondestructive, Specimen-Specific Method for Measurement of Membrane Penetration in the Triaxial Test. Geotech. Test. J. 1989, 12, 50–59. [Google Scholar] [CrossRef]
- Wang, L.; Sun, R.; Liu, H.; Yuan, X.; Wang, Y. New Method to Compensate for Membrane Compliance in Dynamic Triaxial Liquefaction Tests on Gravelly Soils. Chin. J. Geotech. Eng. 2020, 42, 2281–2290. [Google Scholar] [CrossRef]
- Sivathayalan, S.; Vaid, Y.P. Truly Undrained Response of Granular Soils with No Membrane-Penetration Effects. Can. Geotech. J. 1998, 35, 730–739. [Google Scholar] [CrossRef]
- Nicholson, P.G.; Seed, R.B.; Anwar, H.A. Elimination of Membrane Compliance in Undrained Triaxial Testing. II. Mitigation by Injection Compensation. Can. Geotech. J. 1993, 30, 739–746. [Google Scholar] [CrossRef]
- Tokimatsu, K.; Nakamura, K. A Simplified Correction for Membrane Compliance in Liquefaction Tests. Soils Found. 1987, 27, 111–122. [Google Scholar] [CrossRef]
- Roscoe, K.H.; Schofield, A.N.; Thurairajah, A. An Evaluation of Test Data for Selecting a Yield Criterion for Soils; ASTM International: West Conshohocken, PA, USA, 1964. [Google Scholar]
- Raju, V.S.; Sadasivan, S.K. Membrane Penetration in Triaxial Tests on Sands. J. Geotech. Eng. Div. 1974, 100, 482–489. [Google Scholar] [CrossRef]
- Bopp, P.A.; Lade, P. V Membrane Penetration in Granular Materials at High Pressures. Geotech. Test. J. 1997, 20, 272–278. [Google Scholar] [CrossRef]
- Ji, E.; Zhu, J.; Wang, Q.; Jiang, M. Experiment of Membrane Penetration on Coarse Grained Soil. J. Geotech. Eng. 2018, 40, 346–352. [Google Scholar]
- Vaid, Y.P.; Negussey, D. A Critical Assessment of Membrane Penetration in the Triaxial Test. Geotech. Test. J. 1984, 7, 70–76. [Google Scholar] [CrossRef]
- Frydman, S.; Zeitlen, J.G.; Alpan, I. The Membrane Effect in Triaxial Testing of Granular Soils. J. Test. Eval. 1973, 1, 37–41. [Google Scholar] [CrossRef]
- Martin, G.R.; Seed, H.B.; Finn, W.D.L. Effects of System Compliance on Liquefaction Tests. J. Geotech. Eng. Div. 1978, 104, 463–479. [Google Scholar] [CrossRef]
- Li, Y.; Shi, W.; Aydin, A.; Beroya-Eitner, M.A.; Gao, G. Loess Genesis and Worldwide Distribution. Earth-Sci. Rev. 2020, 201, 102947. [Google Scholar] [CrossRef]
- Peng, J.; Wang, S.; Wang, Q.; Zhuang, J.; Huang, W.; Zhu, X.; Leng, Y.; Ma, P. Distribution and Genetic Types of Loess Landslides in China. J. Asian Earth Sci. 2019, 170, 329–350. [Google Scholar] [CrossRef]
- Fu, B.; Wang, S.; Liu, Y.; Liu, J.; Liang, W.; Miao, C. Hydrogeomorphic Ecosystem Responses to Natural and Anthropogenic Changes in the Loess Plateau of China. Annu. Rev. Earth Planet. Sci. 2017, 45, 223–243. [Google Scholar] [CrossRef]
- Nouaouria, M.S.; Guenfoud, M.; Lafifi, B. Engineering Properties of Loess in Algeria. Eng. Geol. 2008, 99, 85–90. [Google Scholar] [CrossRef]
- Wei, J.-Z.; Zheng, K.; Zhang, F.; Fang, C.; Zhou, Y.-Y.; Li, X.-C.; Li, F.-M.; Ye, J.-S. Migration of Rural Residents to Urban Areas Drives Grassland Vegetation Increase in China’s Loess Plateau. Sustainability 2019, 11, 6764. [Google Scholar] [CrossRef]
- Lv, Y.; Zhang, C.; Zhao, J. Collapsibility Mechanisms and Water Diffusion Morphologies of Loess in Weibei Area. Sustainability 2023, 15, 8573. [Google Scholar] [CrossRef]
- Gong, B. Study of PLSR-BP Model for Stability Assessment of Loess Slope Based on Particle Swarm Optimization. Sci. Rep. 2021, 11, 17888. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Xue, Y.; Qu, C.; Qiu, D.; Liu, Q.; Ma, X. Stability Classification Probability Model of Loess Deposits Based on MCS-Cloud. Environ. Sci. Pollut. Res. 2023, 30, 31218–31230. [Google Scholar] [CrossRef]
- Zhou, W.-H.; Xu, X.; Garg, A. Measurement of Unsaturated Shear Strength Parameters of Silty Sand and Its Correlation with Unconfined Compressive Strength. Measurement 2016, 93, 351–358. [Google Scholar] [CrossRef]
- Chen, S.-L.; Wang, X. A Graphical Method for Undrained Analysis of Cavity Expansion in Mohr–Coulomb Soil. Géotechnique 2022, 1–13. [Google Scholar] [CrossRef]
- Tang, J.; Chen, X.; Cui, L.; Liu, Z. Strain Localization of Mohr-Coulomb Soils with Non-Associated Plasticity Based on Micropolar Continuum Theory. J. Rock Mech. Geotech. Eng. 2023, 15, 3316–3327. [Google Scholar] [CrossRef]
- Yu, L.; Lyu, C.; Wang, M.; Xu, T. Three-Dimensional Upper Bound Limit Analysis of a Deep Soil-Tunnel Subjected to Pore Pressure Based on the Nonlinear Mohr-Coulomb Criterion. Comput. Geotech. 2019, 112, 293–301. [Google Scholar] [CrossRef]
- Pei, Q.; Zou, W.; Han, Z.; Wang, X.; Xia, X. Compression Behaviors of a Freeze–Thaw Impacted Clay under Saturated and Unsaturated Conditions. Acta Geotech. 2024, 1–18. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, P.; Zou, W.; Fan, K.; Vanapalli, S.K.; Wan, L. At-Rest Lateral Earth Pressure of Compacted Expansive Soils: Experimental Investigations and Prediction Approach. J. Rock Mech. Geotech. Eng. 2024. [Google Scholar] [CrossRef]
- Fan, K.; Yang, G.; Zou, W.; Han, Z.; Shen, Y. Lateral Earth Pressure of Granular Backfills on Retaining Walls with Expanded Polystyrene Geofoam Inclusions under Limited Surcharge Loading. J. Rock Mech. Geotech. Eng. 2023. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development, P.R. of China. Standard for Geotechnical Testing Method; Ministry of Housing and Urban-Rural Development: Beijing, China, 2019; 684p. [Google Scholar]




| Sample NO. | Loess Types | Age | Sampling Location | w (%) | ρd (g/cm3) | e | Sr (%) | IP |
|---|---|---|---|---|---|---|---|---|
| S1-1-R | Remolded loess | / | Lanzhou | 13.00 | 1.70 | 0.59 | 59.67 | 13.95 |
| S1-2-R | 15.00 | 68.85 | ||||||
| S1-3-R | 17.00 | 78.03 | ||||||
| S1-4-R | 19.00 | 87.21 | ||||||
| S2-1-R | Wangjiagou tunnel | 11.00 | 1.70 | 0.59 | 50.49 | 15.56 | ||
| S2-2-R | 12.00 | 55.08 | ||||||
| S2-3-R | 13.00 | 59.67 | ||||||
| S2-4-R | 14.00 | 64.26 | ||||||
| S2-5-R | 15.00 | 68.85 | ||||||
| S2-6-R | 16.00 | 73.44 | ||||||
| S2-7-R | 17.00 | 78.03 | ||||||
| S2-8-R | 18.00 | 82.62 | ||||||
| S2-9-R | 20.00 | 91.80 | ||||||
| S3-1-R | Beiershilipu tunnel | 13.00 | 1.70 | 0.59 | 59.67 | 13.51 | ||
| S3-2-R | 15.00 | 68.85 | ||||||
| S3-3-R | 17.00 | 78.03 | ||||||
| S4-UD | Undisturbed loess | Q3 | Weijiazui tunnel | 25.64 | 1.55 | 0.74 | 93.31 | 13.12 |
| S5-UD | Wangjiagou tunnel | 23.03 | 1.65 | 0.64 | 97.71 | 15.56 | ||
| S6-UD | ||||||||
| S7-UD | Q2 | Xujiachuan tunnel | 14.77 | 1.92 | 0.41 | 98.16 | 17.76 | |
| S8-UD | ||||||||
| S9-UD | Xinbantashan tunnel | 19.64 | 1.68 | 0.61 | 87.34 | 15.95 |
| Sample No. | Kf | Kf0 | Sample No. | Kf | Kf0 | ||||
|---|---|---|---|---|---|---|---|---|---|
| tanφu | cu | tanφu0 | cu0 | tanφu | cu | tanφu0 | cu0 | ||
| S1-1-R | 0.68 | 58.32 | 0.71 | 50.82 | S2-8-R | 0.66 | 35.94 | 0.69 | 25.77 |
| S1-2-R | 0.69 | 42.87 | 0.72 | 35.53 | S2-9-R | 0.28 | 35.2 | 0.34 | 22.62 |
| S1-3-R | 0.38 | 31.52 | 0.41 | 25.9 | S3-1-R | 0.52 | 86.67 | 0.55 | 78.56 |
| S1-4-R | 0.24 | 25.08 | 0.24 | 24.94 | S3-2-R | 0.48 | 56.93 | 0.53 | 44.2 |
| S2-1-R | 0.68 | 121.09 | 0.71 | 108.68 | S3-3-R | 0.43 | 48.51 | 0.49 | 34.67 |
| S2-2-R | 0.44 | 121.82 | 0.47 | 112.6 | S4-UD | 0.19 | 58.85 | 0.21 | 49.75 |
| S2-3-R | 0.68 | 73.25 | 0.7 | 68.46 | S5-UD | 0.34 | 48.42 | 0.38 | 37.71 |
| S2-4-R | 0.49 | 61.95 | 0.54 | 50.16 | S6-UD | 0.35 | 61.72 | 0.39 | 50.14 |
| S2-5-R | 0.59 | 59.55 | 0.66 | 42.3 | S7-UD | 0.85 | 474.97 | 0.87 | 458.94 |
| S2-6-R | 0.62 | 62.34 | 0.64 | 56.35 | S8-UD | 0.72 | 711.72 | 0.73 | 695.97 |
| S2-7-R | 0.61 | 48.92 | 0.67 | 32.16 | S9-UD | 0.4 | 230.82 | 0.41 | 218.77 |
| Soil Types | Parameters | cu (kPa) | φu (°) | cu0 (kPa) | φu0 (°) | Δc (kPa) | Δφ (°) | η (%) | λ (%) |
|---|---|---|---|---|---|---|---|---|---|
| Remolded loess | Range | 31.52–121.82 | 13.30–34.75 | 22.62–112.60 | 15.46–35.73 | 4.79–17.25 | 0.64–3.12 | 6.54–35.74 | 2.76–19.89 |
| 61.12 | 27.57 | 50.86 | 29.29 | 10.26 | 1.72 | 19.56 | 7.21 | ||
| s | 27.95 | 6.76 | 28.22 | 6.37 | 3.82 | 0.78 | 9.71 | 5.06 | |
| cv | 0.46 | 0.25 | 0.55 | 0.22 | 0.37 | 0.46 | 0.50 | 0.70 | |
| Undisturbed Q3 | Range | 48.42–61.72 | 10.58–19.38 | 37.71–50.14 | 12.01–21.25 | 9.10–11.58 | 1.04–1.87 | 15.46–22.12 | 9.30–13.52 |
| 56.33 | 16.09 | 45.87 | 17.94 | 10.46 | 1.85 | 18.78 | 12.72 | ||
| s | 7.00 | 5.22 | 7.07 | 5.15 | 1.26 | 0.10 | 3.33 | 5.62 | |
| cv | 0.12 | 0.32 | 0.15 | 0.29 | 0.12 | 0.05 | 0.18 | 0.44 | |
| Undisturbed Q2 | Range | 230.82–711.72 | 21.67–40.28 | 218.77–695.97 | 22.10–40.93 | 12.05–16.03 | 0.43–0.65 | 2.21–5.22 | 1.60–1.92 |
| 472.50 | 32.51 | 457.89 | 33.06 | 14.61 | 0.55 | 3.60 | 1.71 | ||
| s | 240.46 | 10.24 | 238.60 | 9.79 | 2.22 | 0.11 | 1.52 | 0.18 | |
| cv | 0.51 | 0.31 | 0.52 | 0.30 | 0.15 | 0.20 | 0.42 | 0.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, R.; Zhou, Z.; Vanapalli, S.; Wu, X. Determination of the Shear Strength of Unsaturated Loess Samples from Conventional Triaxial Shear Tests Applying Rubber Membrane Correction. Sustainability 2024, 16, 2120. https://doi.org/10.3390/su16052120
He R, Zhou Z, Vanapalli S, Wu X. Determination of the Shear Strength of Unsaturated Loess Samples from Conventional Triaxial Shear Tests Applying Rubber Membrane Correction. Sustainability. 2024; 16(5):2120. https://doi.org/10.3390/su16052120
Chicago/Turabian StyleHe, Ruixia, Ziwen Zhou, Sai Vanapalli, and Xuyang Wu. 2024. "Determination of the Shear Strength of Unsaturated Loess Samples from Conventional Triaxial Shear Tests Applying Rubber Membrane Correction" Sustainability 16, no. 5: 2120. https://doi.org/10.3390/su16052120
APA StyleHe, R., Zhou, Z., Vanapalli, S., & Wu, X. (2024). Determination of the Shear Strength of Unsaturated Loess Samples from Conventional Triaxial Shear Tests Applying Rubber Membrane Correction. Sustainability, 16(5), 2120. https://doi.org/10.3390/su16052120









