Analytical Modeling of Unsaturated Soil Shear Strength during Water Infiltration for Different Initial Void Ratios
Abstract
:1. Introduction
2. Literature Review
2.1. Unsaturated Water Retention and Water Flow
2.2. Void Ratio Effect on Water Retention and Unsaturated Hydraulic Conductivity
2.3. Unsaturated Soil Shear Strength
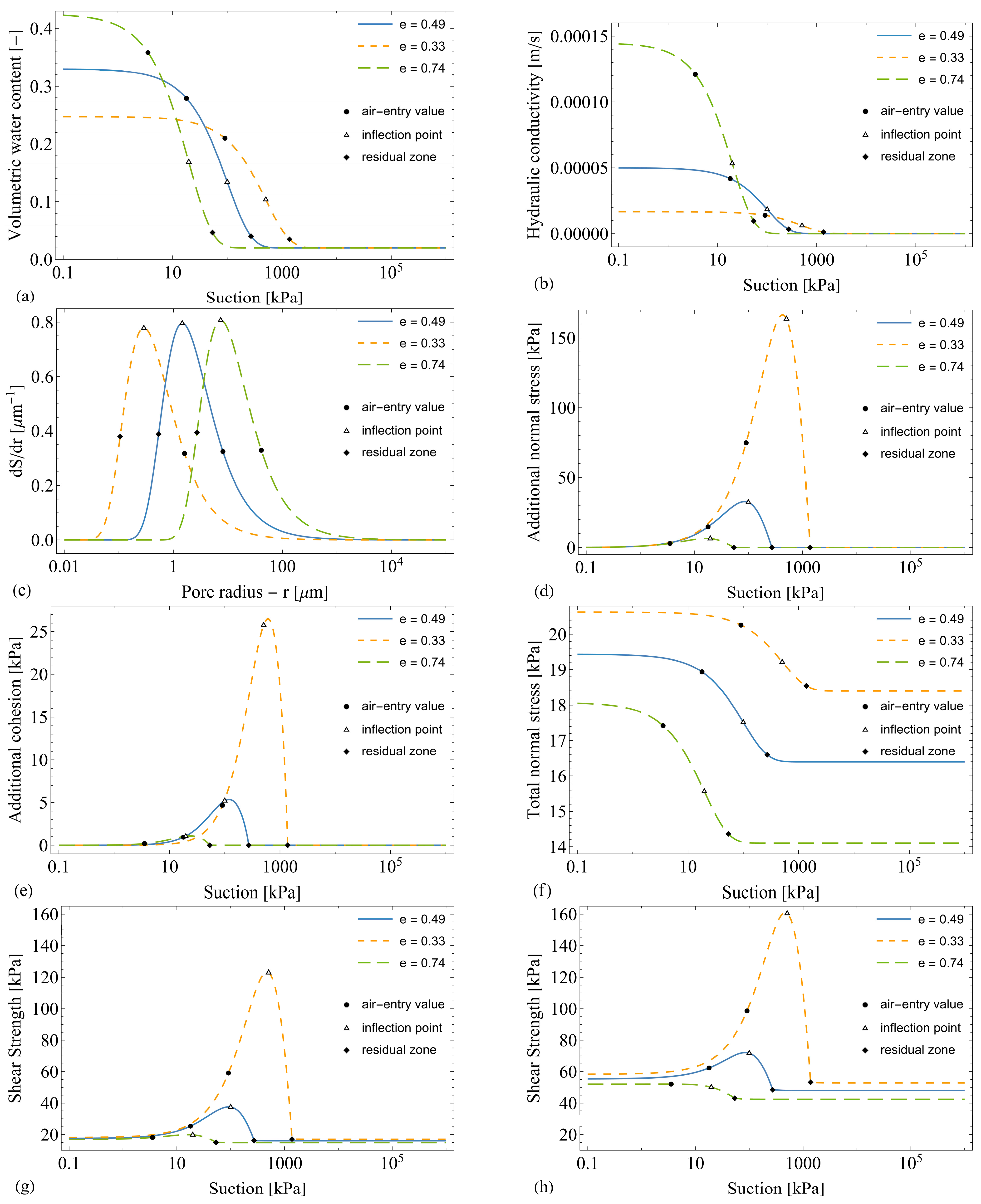
3. Unsaturated Shear Strength Modeling for Different Initial Void Ratios
4. Shear Strength Variation Simulation
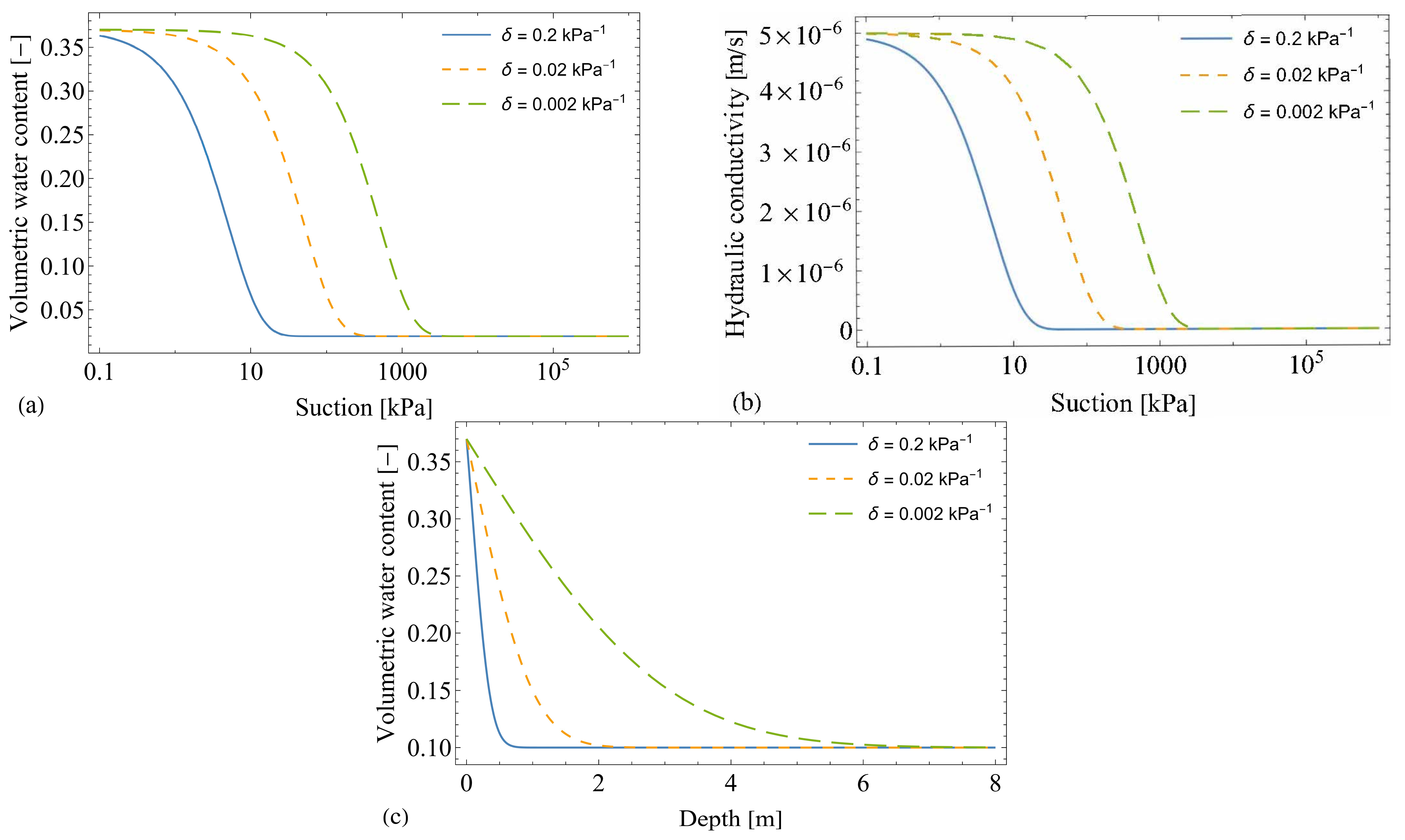
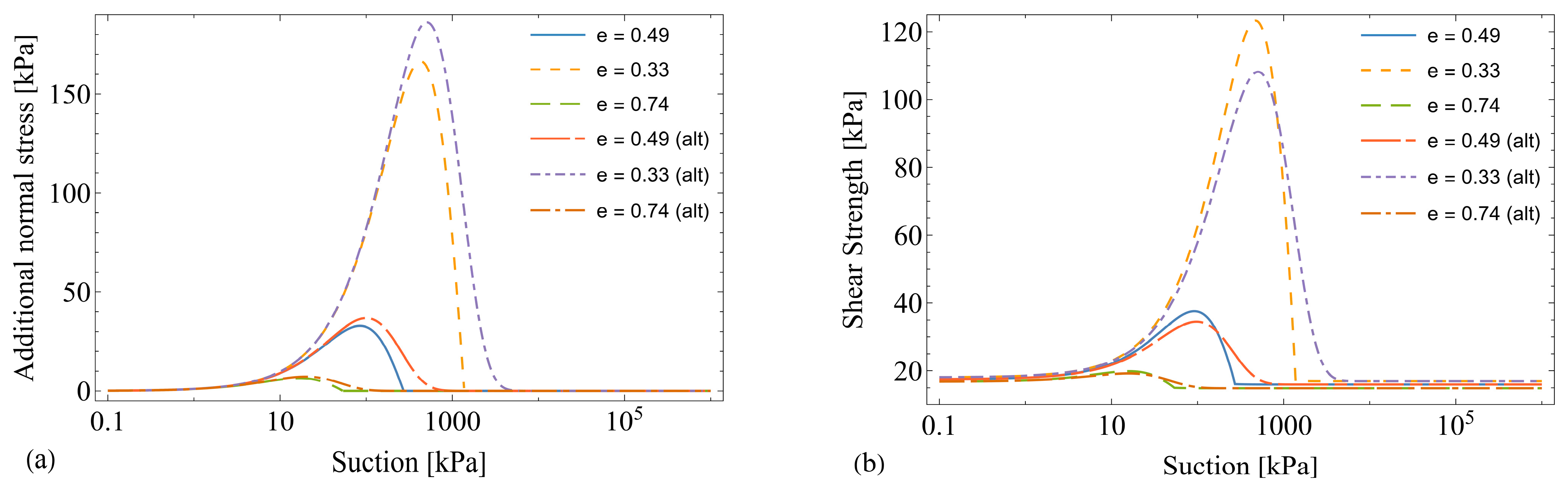
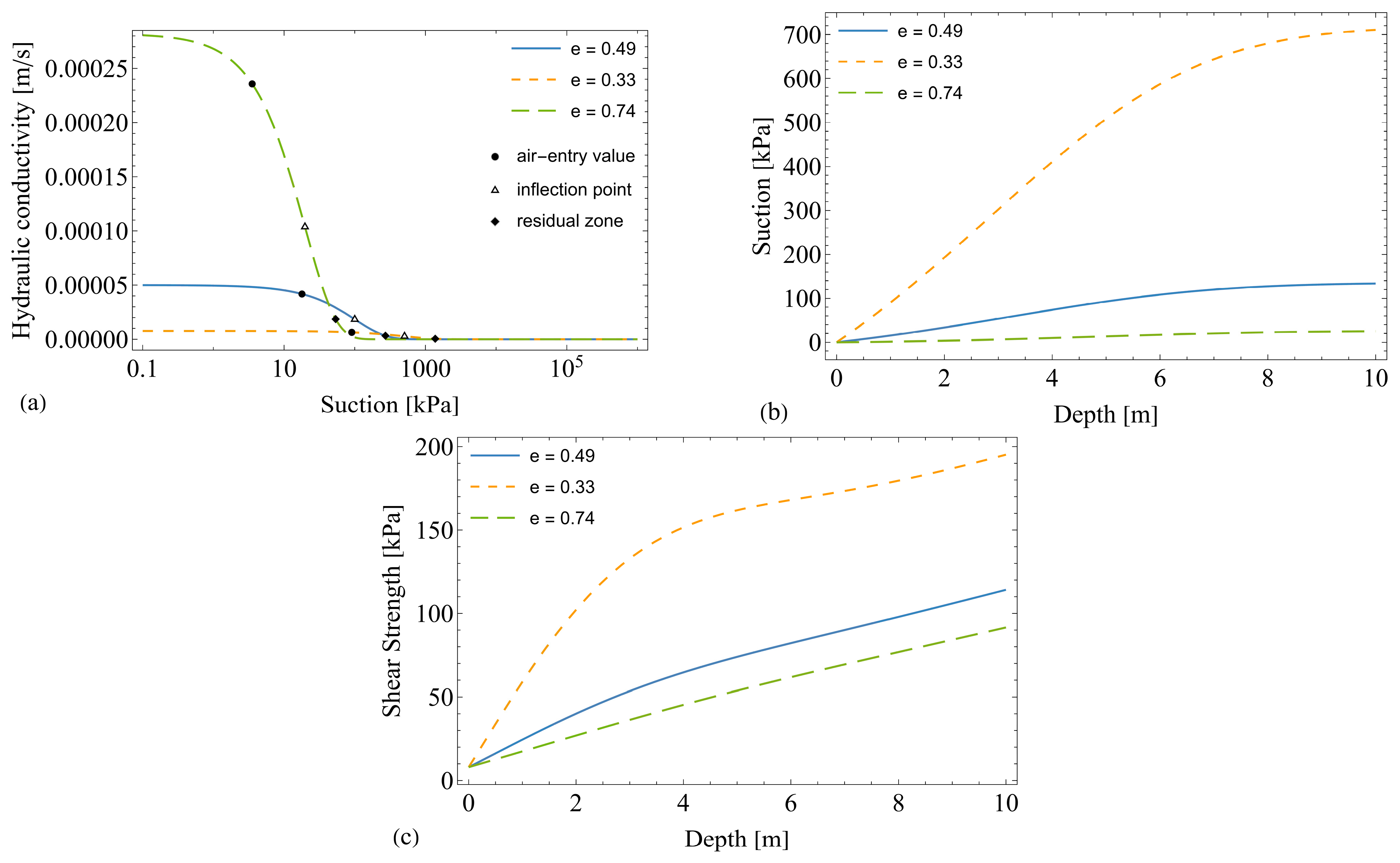
4.1. Effect of Suction for Different Void Ratios
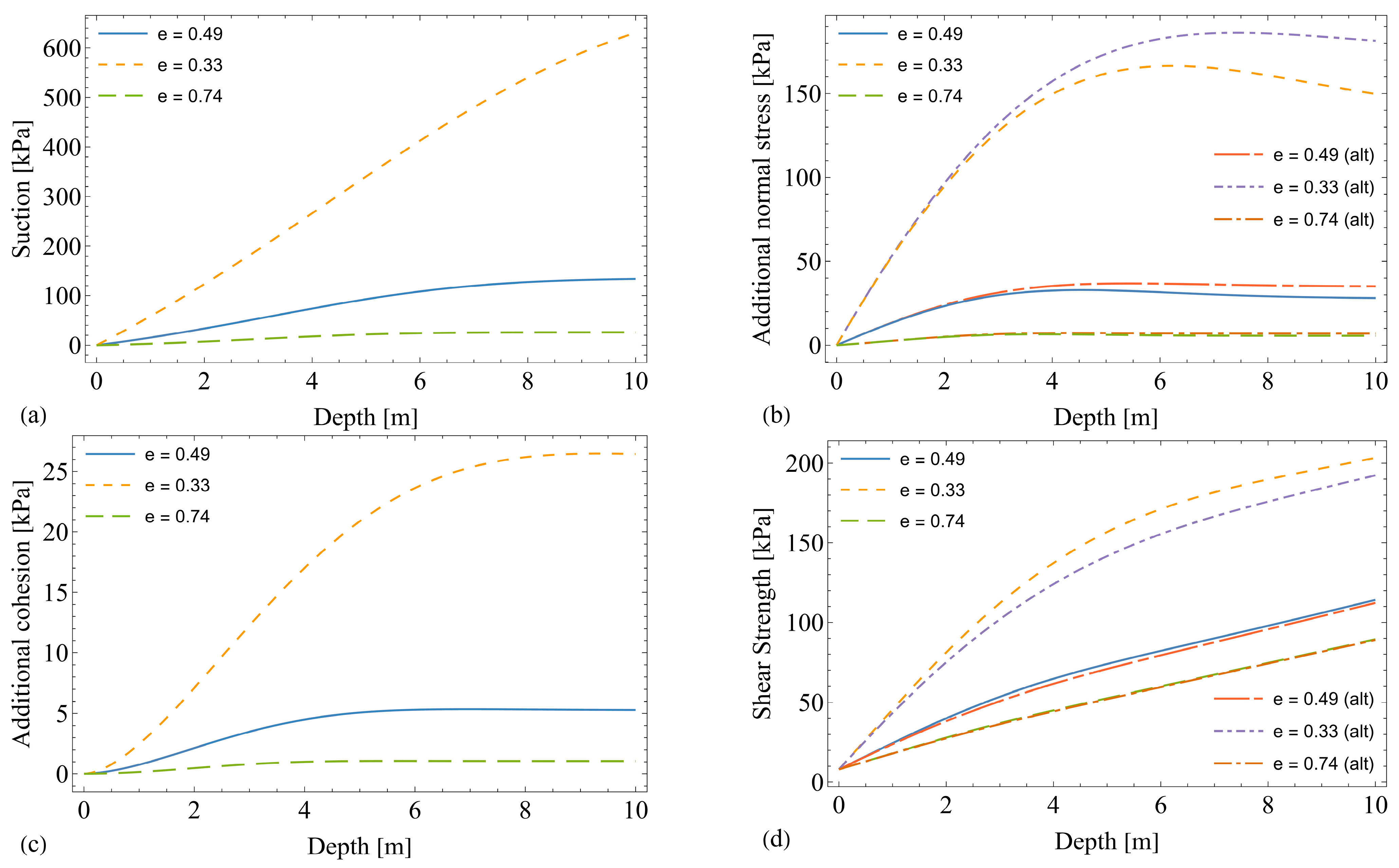
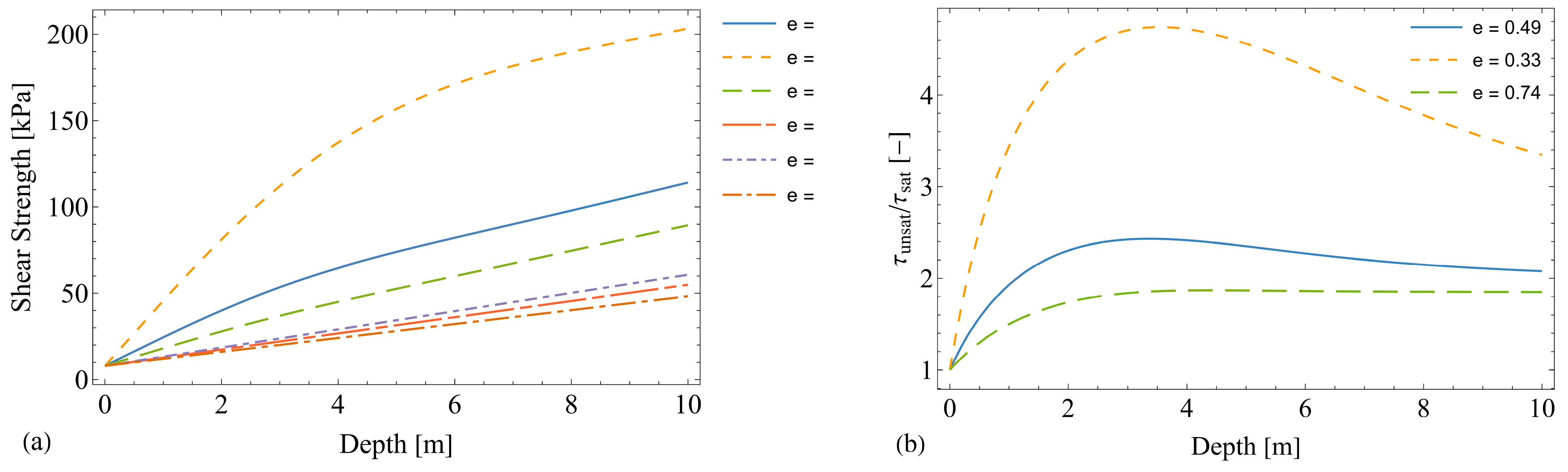
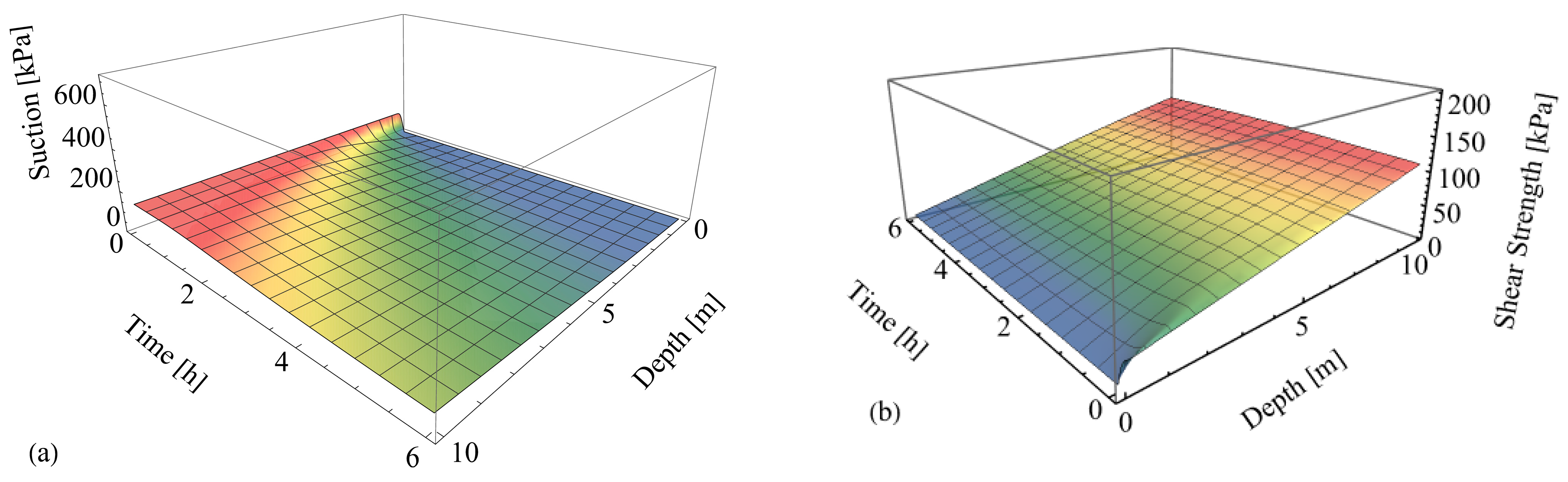
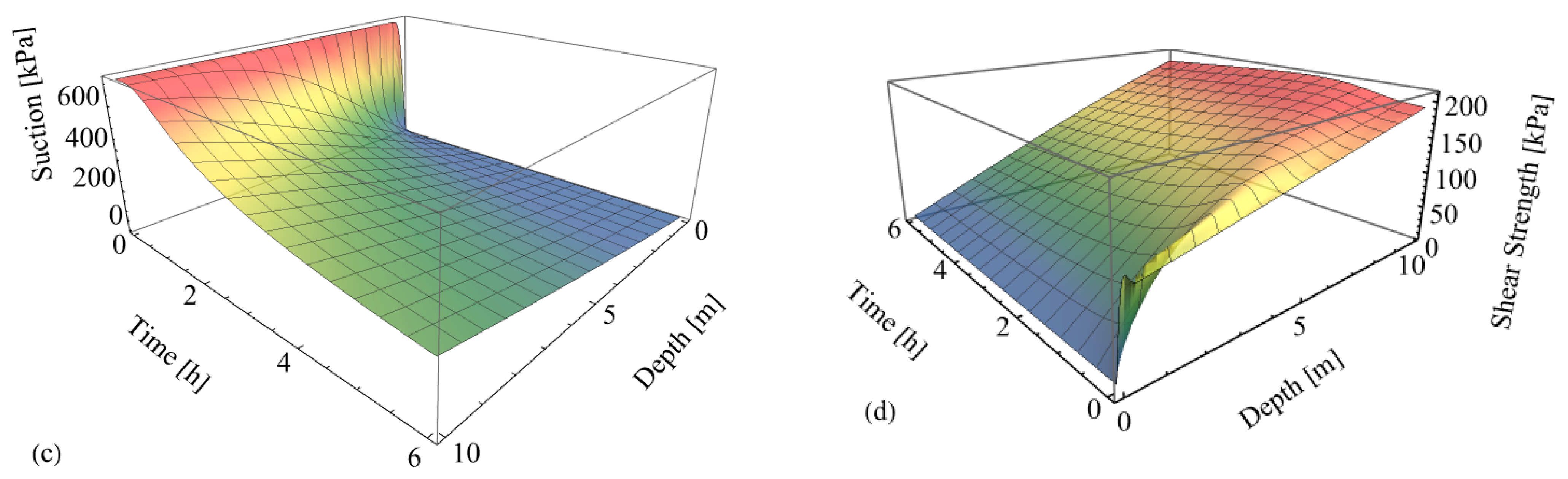
4.2. Effect of Water Infiltration for Different Initial Void Ratios
4.3. Concluding Remarks
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Residual Suction
Appendix B. Continuous Function for the Additional Cohesion
References
- Stefanow, D.; Dudziński, P.A. Soil Shear Strength Determination Methods—State of the Art. Soil. Tillage Res. 2021, 208, 104881. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H.; Fredlund, M.D. Unsaturated Soil Mechanics in Engineering Practice; Wiley: Hoboken, NJ, USA, 2012; ISBN 9781118133590. [Google Scholar]
- Dantas, A.P.d.N.; Cavalcante, A.L.B. Evaluation of Antecedent Rainfall Effects in the Analysis of the Probability of Transient Failure in Unsaturated Slopes. MATEC Web Conf. 2021, 337, 3016. [Google Scholar] [CrossRef]
- Costa, K.R.C.B.d.; Dantas, A.P.d.N.; Cavalcante, A.L.B.; Assis, A.P.d. Probabilistic Approach to Transient Unsaturated Slope Stability Associated with Precipitation Event. Sustainability 2023, 15, 15260. [Google Scholar] [CrossRef]
- Vanapalli, S.K.; Fredlund, D.G.; Pufahl, D.E.; Clifton, A.W. Model for the Prediction of Shear Strength with Respect to Soil Suction. Can. Geotech. J. 1996, 33, 379–392. [Google Scholar] [CrossRef]
- Tran, T.P.A.; Fredlund, D.G. Verification of the Fredlund (2019) Unsaturated Shear Strength Function. Geosciences 2021, 11, 151. [Google Scholar] [CrossRef]
- Macedo, E.S.d.; Sandre, L.H. Deaths from Landslides in Brazil: 1988 to 2022. Rev. Bras. Geol. Eng. Ambient. 2022, 12, 110–117. [Google Scholar]
- Ben Sim, K.; Lee, M.L.; Wong, S.Y. A Review of Landslide Acceptable Risk and Tolerable Risk. Geoenviron. Disasters 2022, 9, 3. [Google Scholar]
- Petley, D. Global Patterns of Loss of Life from Landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Shi, Q. Influence of Rainfall Intensity and Duration on Slope Stability in Unsaturated Soils. Q. J. Eng. Geol. 1998, 31, 105–113. [Google Scholar] [CrossRef]
- Ray, R.L.; Jacobs, J.M.; de Alba, P. Impacts of Unsaturated Zone Soil Moisture and Groundwater Table on Slope Instability. J. Geotech. Geoenviron. Eng. 2010, 136, 1448–1458. [Google Scholar] [CrossRef]
- Cho, S.E.; Lee, S.R. Instability of Unsaturated Soil Slopes Due to Infiltration. Comput. Geotech. 2001, 28, 185–208. [Google Scholar] [CrossRef]
- Batali, L.; Andreea, C. Slope Stability Analysis Using the Unsaturated Stress Analysis. Case Study. Proc. Procedia Eng. 2016, 143, 284–291. [Google Scholar]
- Oh, S.; Lu, N. Slope Stability Analysis under Unsaturated Conditions: Case Studies of Rainfall-Induced Failure of Cut Slopes. Eng. Geol. 2015, 184, 96–103. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Gao, Z.; Xiang, K.; Zhai, Q.; Satyanaga, A.; Chua, Y.S. Evaluation of the Performance of the Horizontal Drain in Drainage of the Infiltrated Water from Slope Soil under Rainfall Conditions. Sustainability 2023, 15, 14163. [Google Scholar] [CrossRef]
- Toli, A.; Giudici, M. Modeling Water Flow in Variably Saturated Porous Soils and Alluvial Sediments. Sustainability 2023, 15, 15723. [Google Scholar] [CrossRef]
- Wu, X.; Vanapalli, S.K. Three-Dimensional Modeling of the Mechanical Behavior of a Single Pile in Unsaturated Expansive Soils during Infiltration. Comput. Geotech. 2022, 145, 104696. [Google Scholar] [CrossRef]
- Liu, Y.; Vanapalli, S.K. Mechanical Behavior of a Floating Model Pile in Unsaturated Expansive Soil Associated with Water Infiltration: Laboratory Investigations and Numerical Simulations. Soils Found. 2021, 61, 929–943. [Google Scholar] [CrossRef]
- Liu, Y.; Vanapalli, S.K. Modified Shear Displacement Method for Analysis of Piles in Unsaturated Expansive Soils Considering Influence of Environmental Factors. Int. J. Geomech. 2022, 22, 04022069. [Google Scholar] [CrossRef]
- Tan, M.; Vanapalli, S.K. Foundation Bearing Capacity Estimation on Unsaturated Soil Slope under Transient Flow Condition Using Slip Line Method. Comput. Geotech. 2022, 148, 104804. [Google Scholar] [CrossRef]
- Kong, X.; Cai, G.; Cheng, Y.; Zhao, C. Numerical Implementation of Three-Dimensional Nonlinear Strength Model of Soil and Its Application in Slope Stability Analysis. Sustainability 2022, 14, 5127. [Google Scholar] [CrossRef]
- Nguyen, T.S.; Likitlersuang, S. Reliability Analysis of Unsaturated Soil Slope Stability under Infiltration Considering Hydraulic and Shear Strength Parameters. Bull. Eng. Geol. Environ. 2019, 78, 5727–5743. [Google Scholar] [CrossRef]
- Kim, Y.; Jeong, S.; Kim, J. Coupled Infiltration Model of Unsaturated Porous Media for Steady Rainfall. Soils Found. 2016, 56, 1071–1081. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A. Effect of Infiltration on Single-Pile and Monopile–Raft Foundation Embedded in Unsaturated Sand. Int. J. Geomech. 2023, 23, 04022288. [Google Scholar] [CrossRef]
- Aventian, G.D.; Satyanaga, A.; Sagu, A.; Serikbek, B.; Pernebekova, G.; Aubakirova, B.; Zhai, Q.; Kim, J. Analytical and Finite-Element-Method-Based Analyses of Pile Shaft Capacity Subjected to Rainfall Infiltration. Sustainability 2024, 16, 313. [Google Scholar] [CrossRef]
- Cavalcante, A.L.B.; Zornberg, J.G. Efficient Approach to Solving Transient Unsaturated Flow Problems. I: Analytical Solutions. Int. J. Geomech. 2017, 17, 04017013. [Google Scholar] [CrossRef]
- Costa, M.B.A.d.; Cavalcante, A.L.B. Novel Approach to Determine Soil–Water Retention Surface. Int. J. Geomech. 2020, 20, 4020054. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W.; Wu, D.T. A Closed-Form Equation for Effective Stress in Unsaturated Soil. Water Resour. Res. 2010, 46, W05515. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A.; Dai, G. Estimation of Unsaturated Shear Strength from Soil–Water Characteristic Curve. Acta Geotech. 2019, 14, 1977–1990. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary Conduction of Liquids through Porous Mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H. Determination of Soil-Water Characteristic Curve Variables. Comput. Geotech. 2012, 42, 37–43. [Google Scholar] [CrossRef]
- Soltani, A.; Azimi, M.; Deng, A.; Taheri, A. A Simplified Method for Determination of the Soil–Water Characteristic Curve Variables. Int. J. Geotech. Eng. 2017, 13, 316–325. [Google Scholar] [CrossRef]
- Costa, M.B.A.d.; Cavalcante, A.L.B. Bimodal Soil–Water Retention Curve and k-Function Model Using Linear Superposition. Int. J. Geomech. 2021, 21, 04020054. [Google Scholar] [CrossRef]
- Tschapek, M.; Scoppa, C.O.; Wasowski, C. The Surface Tension of Soil Water. J. Soil. Sci. 1978, 29, 17–21. [Google Scholar] [CrossRef]
- Otalvaro, I.F.; Neto, M.P.C.; Delage, P.; Caicedo, B. Relationship between Soil Structure and Water Retention Properties in a Residual Compacted Soil. Eng. Geol. 2016, 205, 73–80. [Google Scholar] [CrossRef]
- Kozeny, J. Uber Kapillare Leitung Der Wasser in Boden. Sitzungsber. Akad. Wiss. Wien. 1927, 136, 271–306. [Google Scholar]
- Carman, P.C. Fluid Flow through Granular Beds. Trans. Inst. Chem. Eng. 1937, 15, 32–48. [Google Scholar] [CrossRef]
- Costa, A. Permeability-Porosity Relationship: A Reexamination of the Kozeny-Carman Equation Based on a Fractal Pore-Space Geometry Assumption. Geophys. Res. Lett. 2006, 33, L02318. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J.; Xu, G.; Zheng, Y.; Kang, X. Improved Model for Predicting the Hydraulic Conductivity of Soils Based on the Kozeny-Carman Equation. Hydrol. Res. 2021, 52, 719–733. [Google Scholar] [CrossRef]
- Ren, X.; Zhao, Y.; Deng, Q.; Kang, J.; Li, D.; Wang, D. A Relation of Hydraulic Conductivity—Void Ratio for Soils Based on Kozeny-Carman Equation. Eng. Geol. 2016, 213, 89–97. [Google Scholar] [CrossRef]
- Bishop, A.W. The Principle of Effective Stress. Tek. Ukebl. 1959, 39, 859–863. [Google Scholar]
- Jommi, C. Remarks on the Constitutive Modeling of Unsaturated Soils. In Experimental Evidence and Theoretical Approaches in Unsaturated Soils; Tarantino, A., Mancuso, C., Eds.; Balkema: Rotterdam, The Netherlands, 2000; pp. 139–153. ISBN 9058091864. [Google Scholar]
- Cavalcante, A.L.B.; Mascarenhas, P.V.S. Efficient Approach to Modeling Unsaturated Soils Shear Strength Using the Soil Water Retention Curve. Acta Geotech. 2021, 16, 3177–3186. [Google Scholar] [CrossRef]
- Santos, D.B.; Lemos, M.A.d.C.; Cavalcante, A.L.B. Transient Unsaturated Shaft Resistance of a Single Pile during Water Flow. MATEC Web Conf. 2021, 337, 03007. [Google Scholar] [CrossRef]
- Li, K.Q.; Li, D.Q.; Liu, Y. Meso-Scale Investigations on the Effective Thermal Conductivity of Multi-Phase Materials Using the Finite Element Method. Int. J. Heat. Mass. Transf. 2020, 151, 119383. [Google Scholar] [CrossRef]
- Li, K.Q.; Liu, Y.; Yin, Z.Y. An Improved 3D Microstructure Reconstruction Approach for Porous Media. Acta Mater. 2023, 242, 118472. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, D.B.; Sousa, P.F.d.; Cavalcante, A.L.B. Analytical Modeling of Unsaturated Soil Shear Strength during Water Infiltration for Different Initial Void Ratios. Sustainability 2024, 16, 1394. https://doi.org/10.3390/su16041394
Santos DB, Sousa PFd, Cavalcante ALB. Analytical Modeling of Unsaturated Soil Shear Strength during Water Infiltration for Different Initial Void Ratios. Sustainability. 2024; 16(4):1394. https://doi.org/10.3390/su16041394
Chicago/Turabian StyleSantos, Daniel Batista, Patrícia Figuereido de Sousa, and André Luís Brasil Cavalcante. 2024. "Analytical Modeling of Unsaturated Soil Shear Strength during Water Infiltration for Different Initial Void Ratios" Sustainability 16, no. 4: 1394. https://doi.org/10.3390/su16041394
APA StyleSantos, D. B., Sousa, P. F. d., & Cavalcante, A. L. B. (2024). Analytical Modeling of Unsaturated Soil Shear Strength during Water Infiltration for Different Initial Void Ratios. Sustainability, 16(4), 1394. https://doi.org/10.3390/su16041394





