Consideration of Carbon Emissions in Multi-Trip Delivery Optimization of Unmanned Vehicles
Abstract
:1. Introduction
1.1. Background
1.2. Literature Review
- Given the common issue in the logistics industry of not being able to provide a sufficient number of unmanned vehicles to meet all customer demands, this paper addresses the multi-trip vehicle routing problem (MT-CVRP) with a consideration of carbon emissions. A mathematical optimization model has been developed, incorporating constraints such as maximum service time, the number of vehicles, and their rated load capacities, along with the minimization of the unmanned vehicle startup costs, transportation costs, fuel costs, and environmental costs associated with carbon emissions, as its objectives.
- Given the inherent NP-hard nature of the model, this paper employs heuristic algorithms for its resolution. A solution mapping process is designed based on the integer combination encoding of the trip, vehicle, and customer numbers. Extending beyond the traditional GA, this paper incorporates an SA to bolster its global search capability. An IGA is also devised to address and solve the MT-CVRP.
- The simulation was divided into small-scale, medium-scale, and large-scale cases using the Solomon RC 208 series international standard dataset. A sensitivity analysis was also conducted using the E-n51-k5 standard dataset. The experimental results demonstrated that the IGA is more advantageous in solving the MT-CVRP problem compared to the GA and SA. This experimental validation confirms the effectiveness of this model and algorithm and provides theoretical guidance and experimental methods for logistics companies to achieve low-carbon transportation and reduce their energy consumption and environmental pollution.
2. Optimization Modeling
2.1. State the Research Question and Hypothesis
2.1.1. Describe the Problem to Be Solved
2.1.2. Model Assumptions
- Each unmanned vehicle trip starts from the distribution center; the vehicle serves the customer and then returns to the distribution center.
- The vehicles are of the same type and their total transportation quantity cannot exceed their carrying capacity.
- The location coordinates and demands of each customer are known.
- Each customer must and can only be visited once.
- The speed of the unmanned vehicle is known and fixed, without considering traffic congestion.
- The total delivery time for all trips of each unmanned vehicle does not exceed their maximum service duration.
- The start time for each trip of the unmanned vehicle is the end time of the previous trip of the delivery vehicle.
- Assuming that the unmanned vehicle is a fuel vehicle, its fuel consumption per km is proportional to its carbon dioxide emissions, regardless of the effects of driving speed, road conditions, and other factors on fuel consumption.
2.2. Description of Symbols and Variables
2.3. Formatting of Mathematical Components
3. IGA
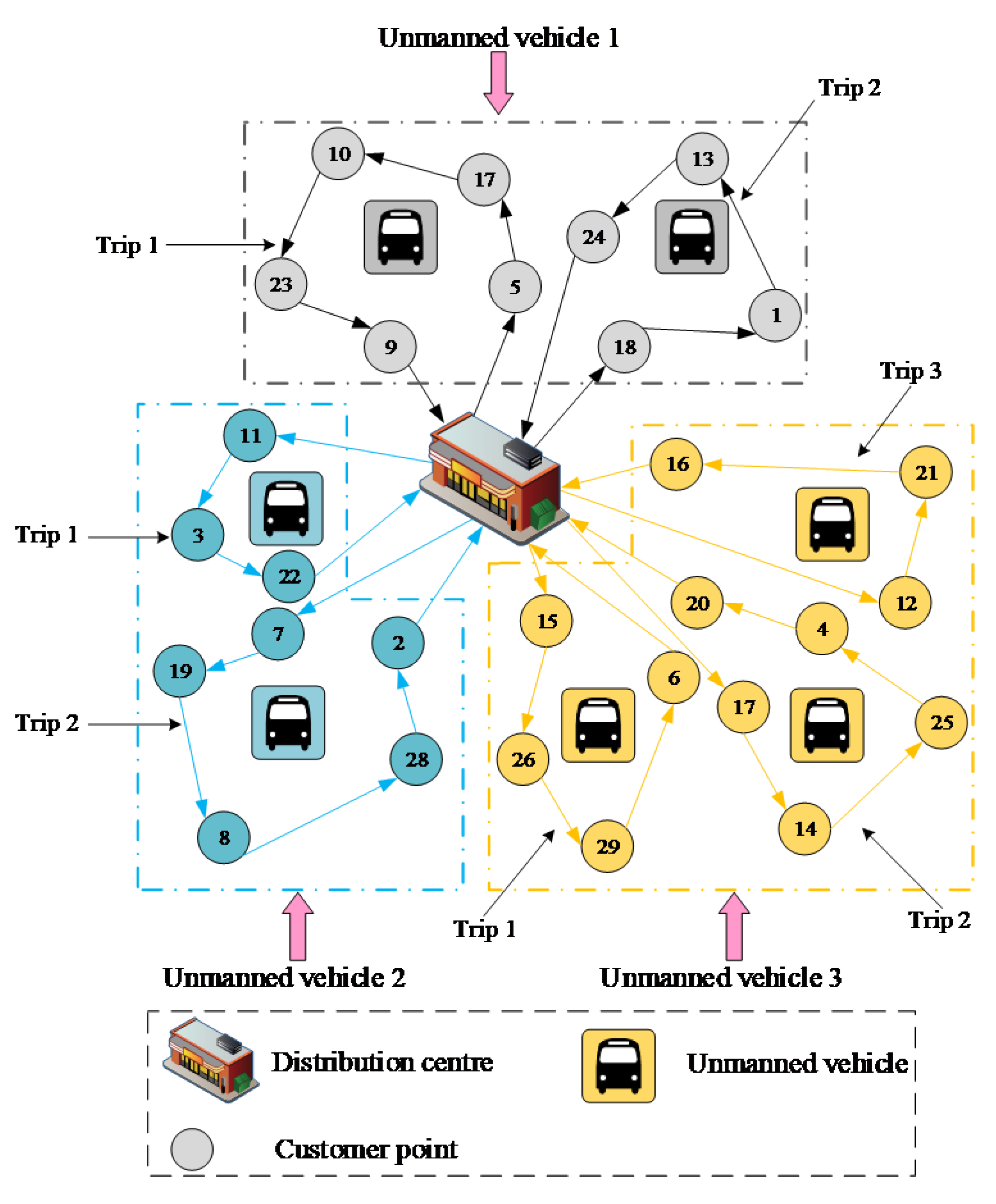
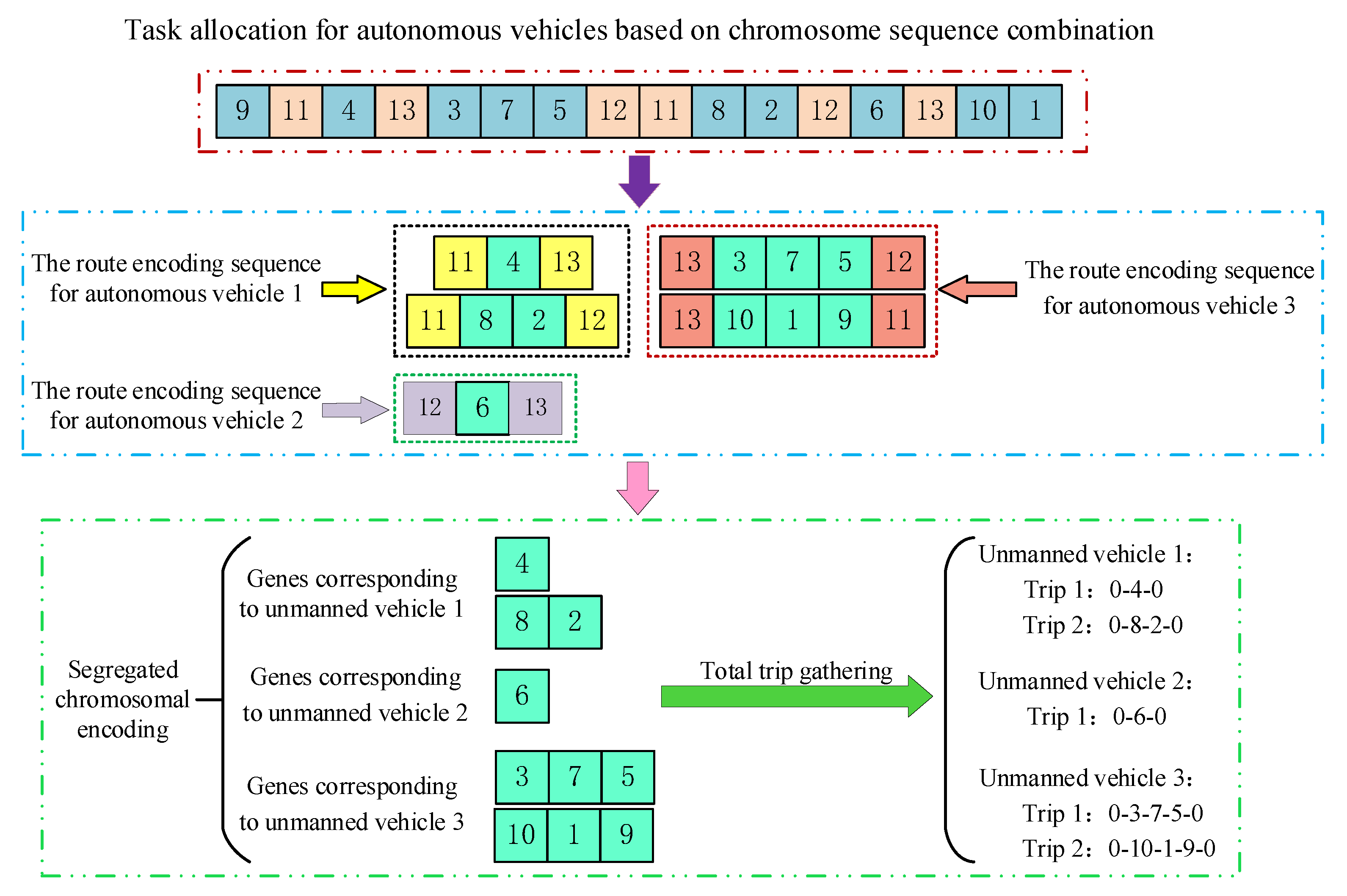
3.1. Decoding and Coding
3.2. Calculation of Adaptation
3.3. Selection
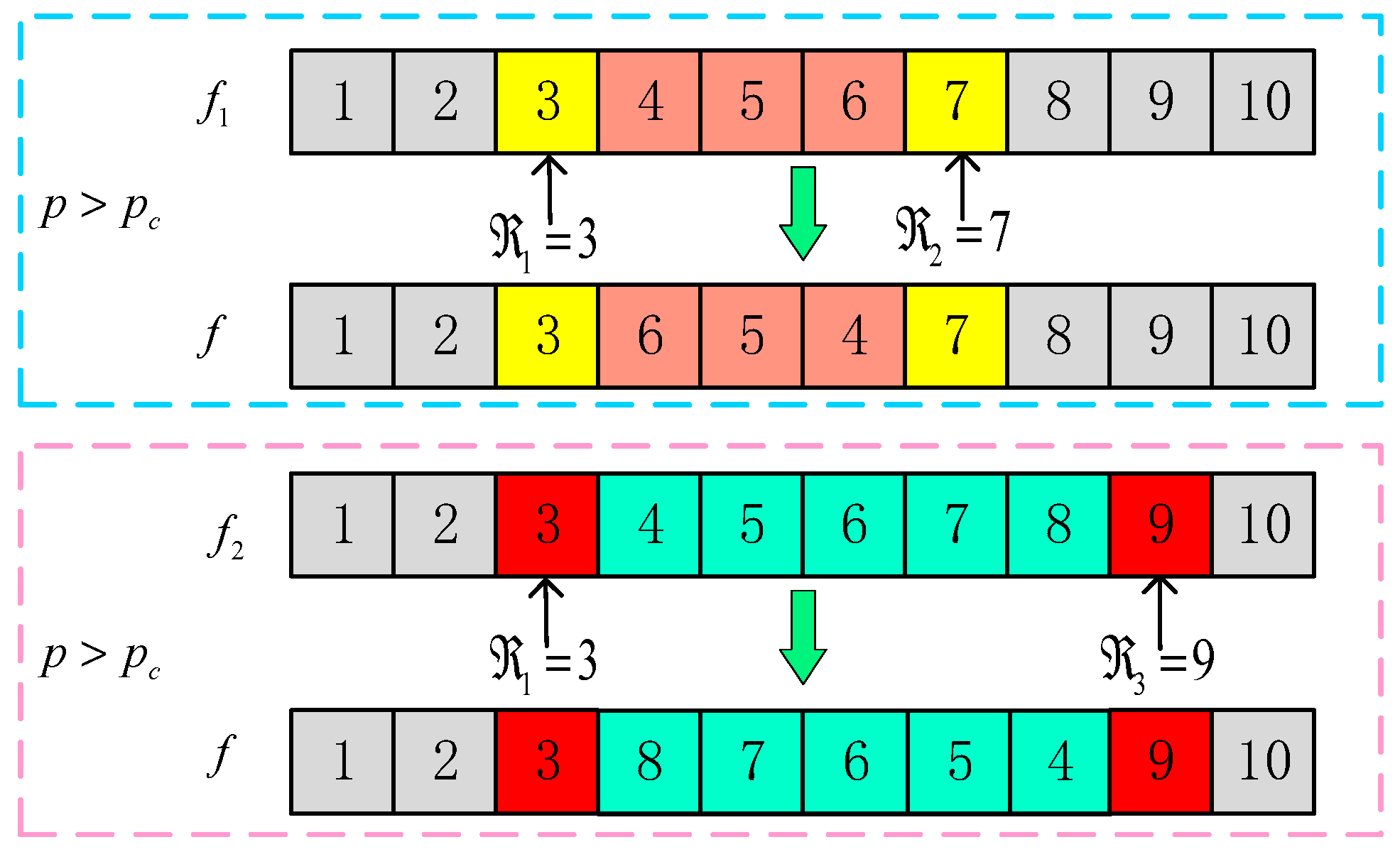
3.4. Crossing
- Randomly select a gene spot in the paternal chromosome , e.g., ;
- Generate a random decimal number within the range of [0, 1]; if , then select a second gene point in the parent chromosome , such as . Invert the partial chromosome sequence between gene point and gene point to produce a new chromosome , which does not include the and gene points, which is similar to the principle of 2-Opt algorithm operation;
- If is selected, then another paternal chromosome is selected from the population to determine the location of , and the next gene point . If the gene point is selected from chromosome , the previous gene point will be taken if it is out of bounds; similarly, the portion of the chromosome between the gene point and the gene point will be inverted to exclude the and gene points.
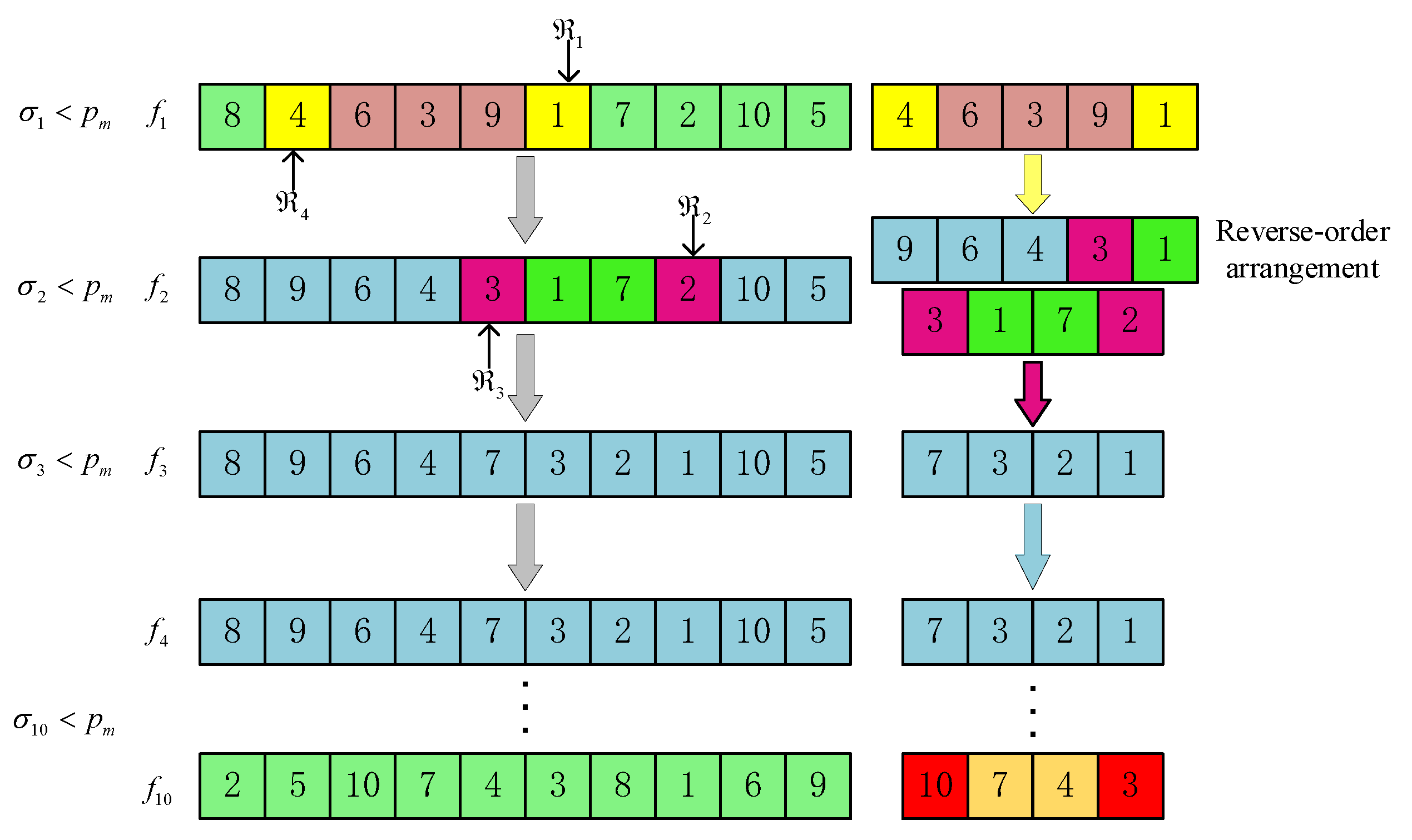
3.5. Mutation
- Assuming that the length of chromosome is , firstly, for the 1st gene , generate a random number , if , generate a random number of , , , mapped to gene , which forms the sequence of genes between alleles of the chromosome, in accordance with their subscripts, from smallest to largest, in order, and, after the reverse order of the sequence is embedded in (including , ), at this time observe the chromosome ; if , then do not generate a random number, and do not do anything with the gene;
- For the gene , if the random number , a random number is generated . is mapped to the gene , and the chromosome allele between is embedded in after a reverse-ordering process, at which point the chromosome is ; if , no random number is generated, and no processing is carried out for the gene;
- Continue to repeat the above steps until all the alleles of the entire chromosome have been traversed to complete the mutation operation.
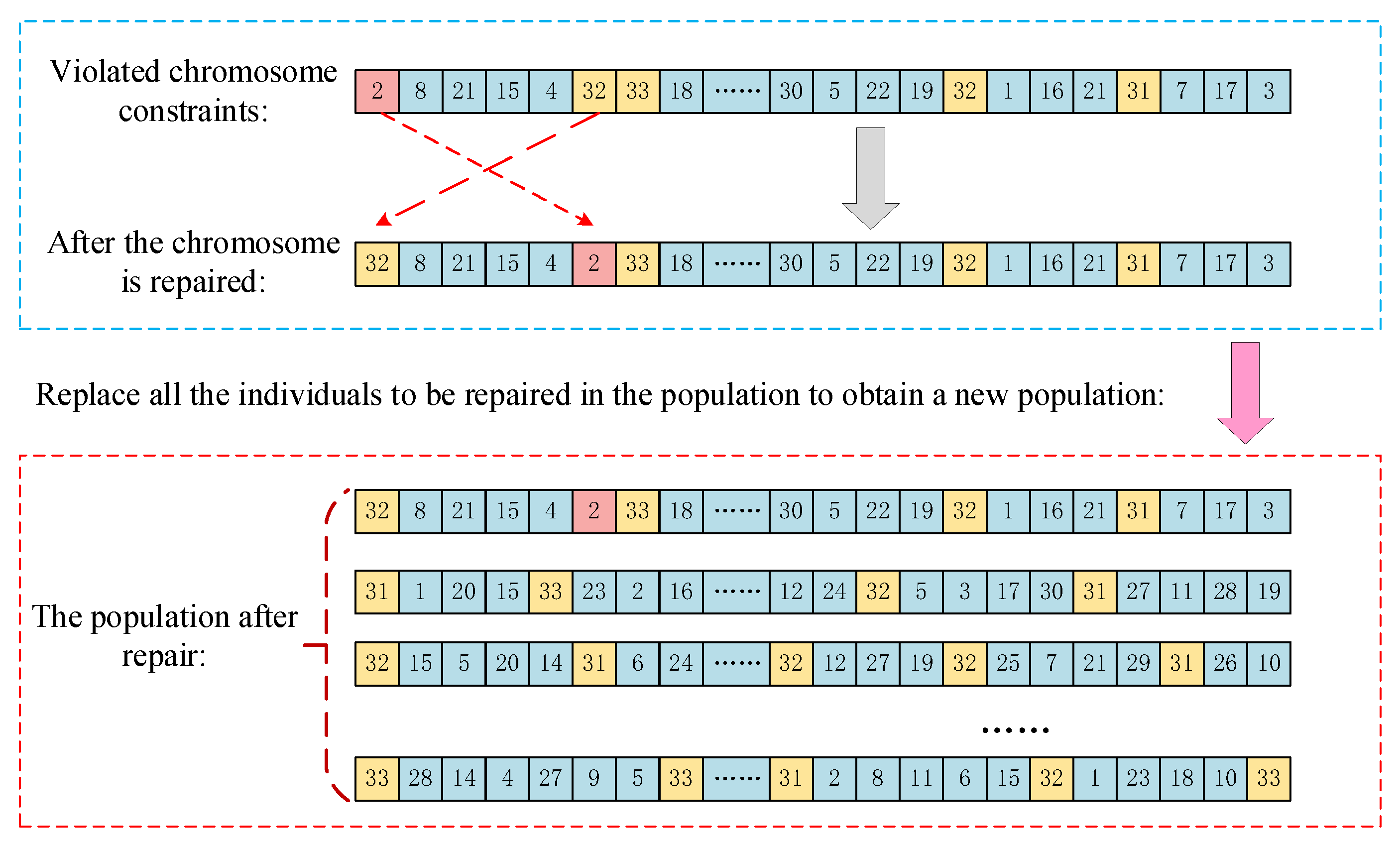
3.6. Repair Operation
3.7. Simulated Annealing Algorithm
3.8. Elite Retention Strategies
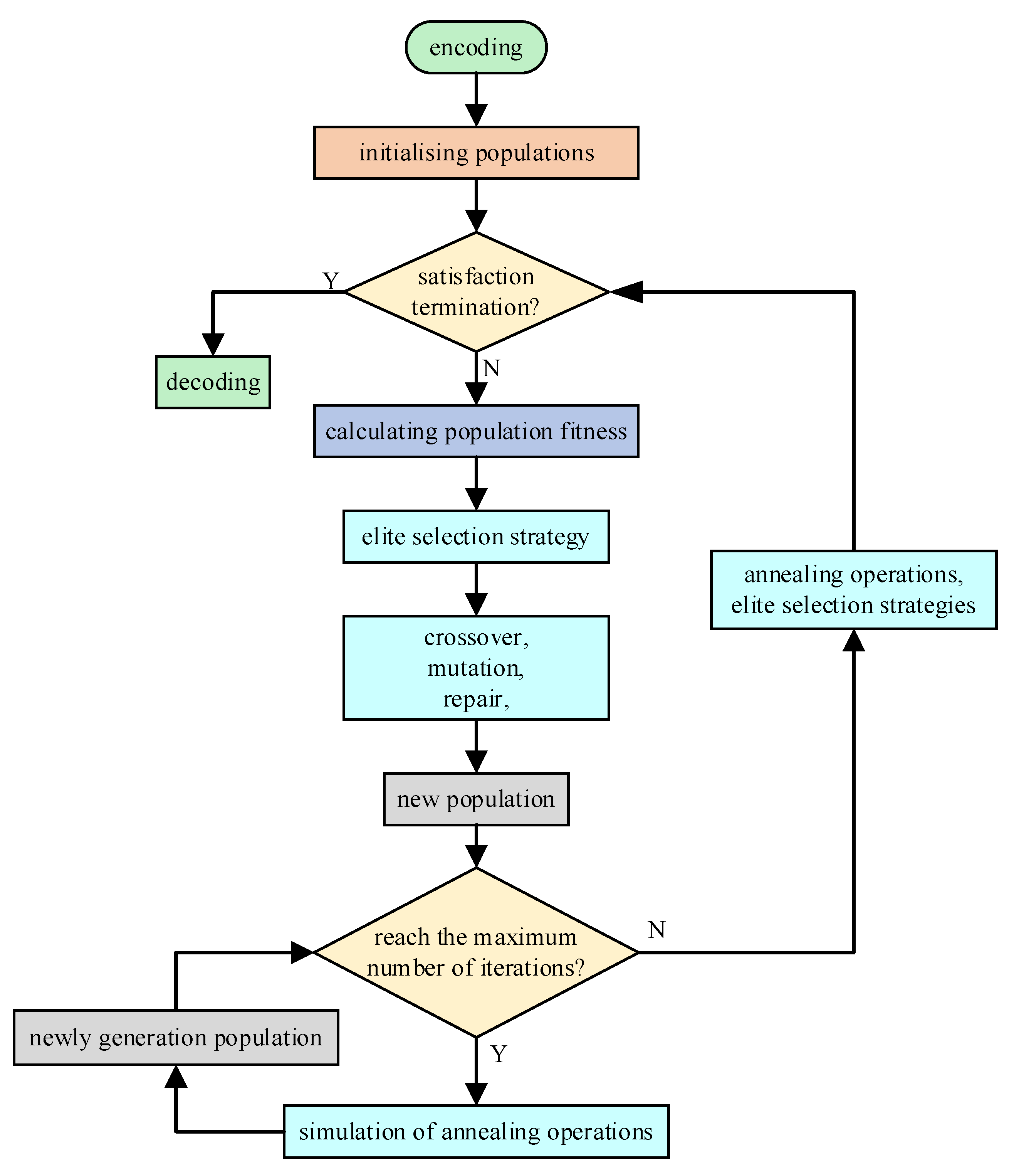
3.9. Algorithmic Flow
| Algorithm 1 IGA |
| Input: Algorithm-related parameters and simulation base data |
| Output: Multi-trip solutions for unmanned vehicles |
| 1. encoding, initializing the IGA algorithm and setting parameters |
| 2. mapping the problem and randomly generating a certain size of the population |
| 3. if the initialization scheme satisfies the set constraints, then |
| 4. decoding |
| 5. else |
| 6. calculating the fitness value and performing elite selection, crossover, mutation, and repair operations |
| 7. else |
| 8. if the maximum number of iterations is reached, then performing cooling and elite selection |
| 9. else |
| 10. implementation of simulated annealing operations |
| 11. end if |
| 12. break |
| 13. end if |
4. Simulation Test and Result Analysis
4.1. Calculations and Parameterizations
4.2. Simulation of Small-Scale Cases
4.3. Simulating Medium-Scale Cases
4.4. Simulation of Large-Scale Cases
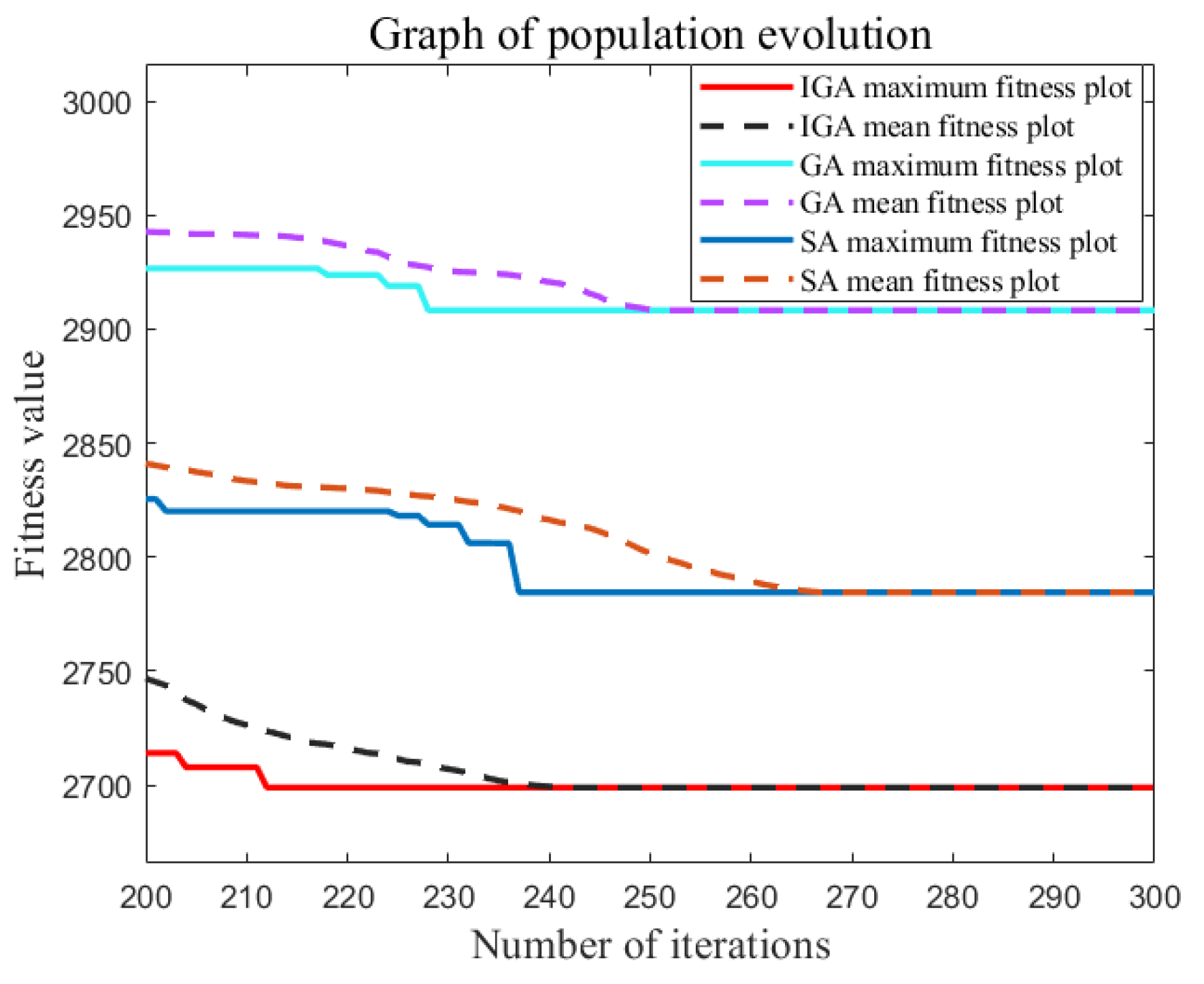
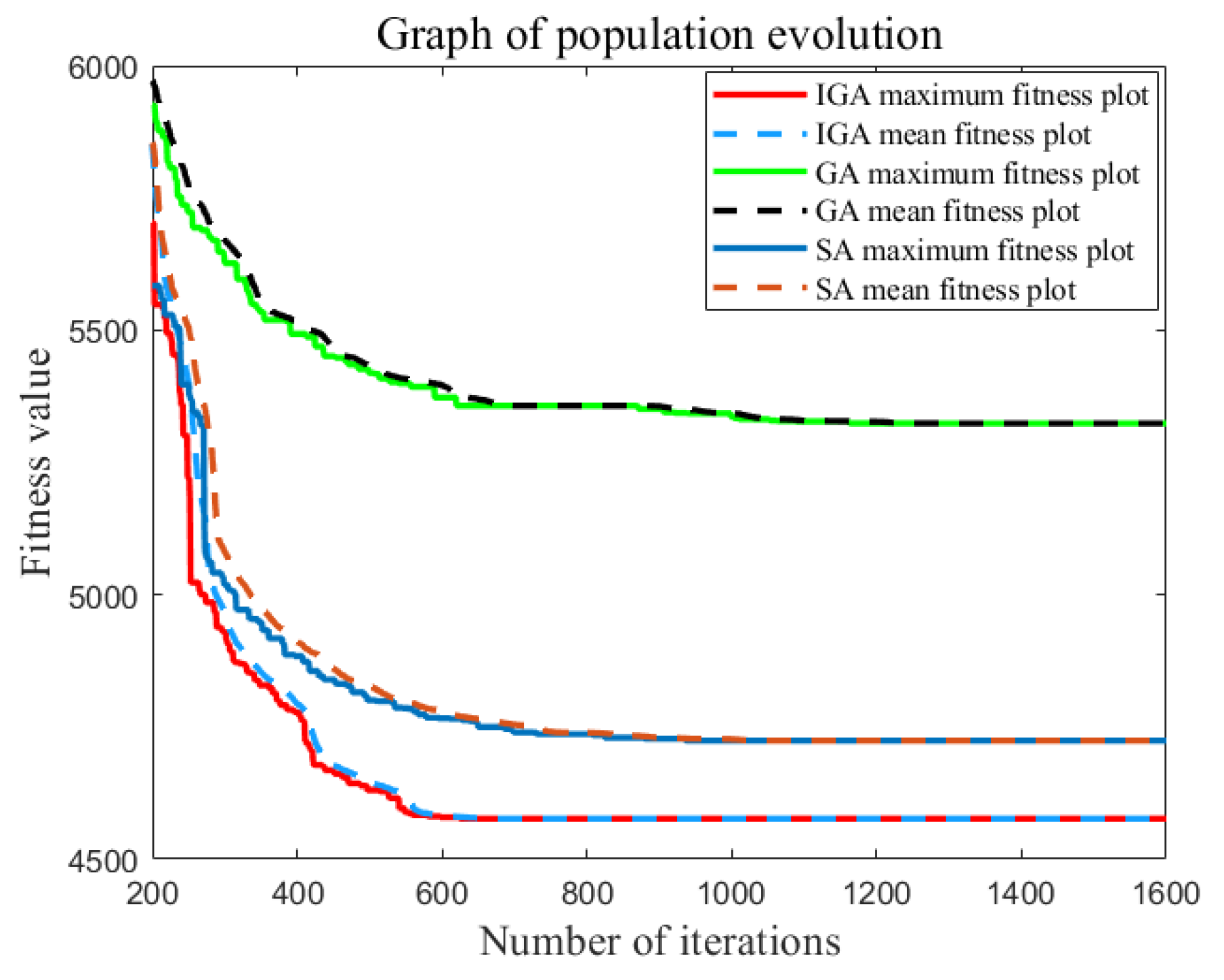
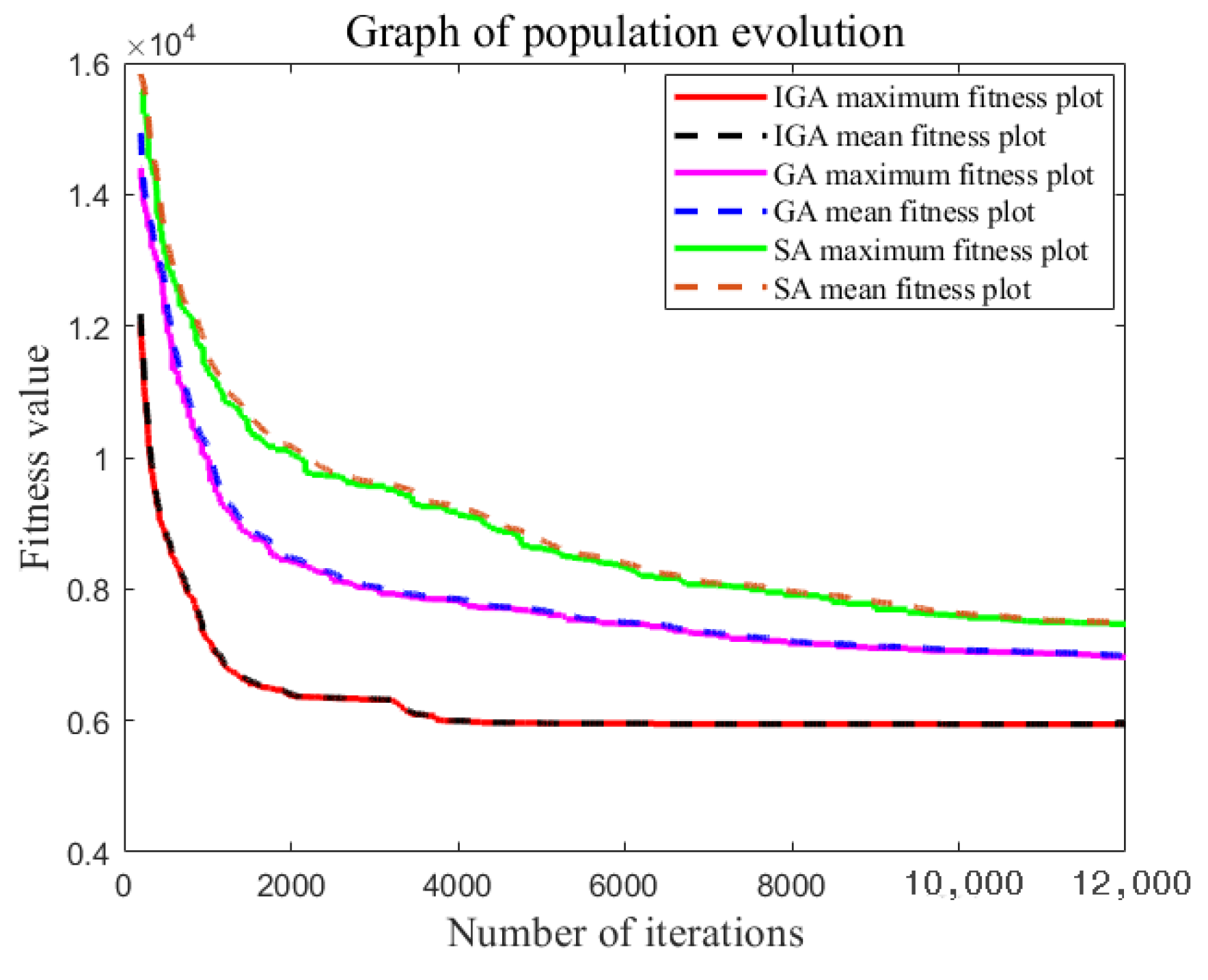
- Based on graphs 8, 10, and 12, it can be observed that the IGA achieves convergence at a faster rate than the GA and SA. In these graphs, the fitness value remains unchanged at the 212th, 580th, and 3850th iterations of the IGA, respectively. Additionally, as the problem size increases, the difference in fitness values becomes more pronounced, indicating that the IGA not only provides better solutions but also exhibits good convergence speed.
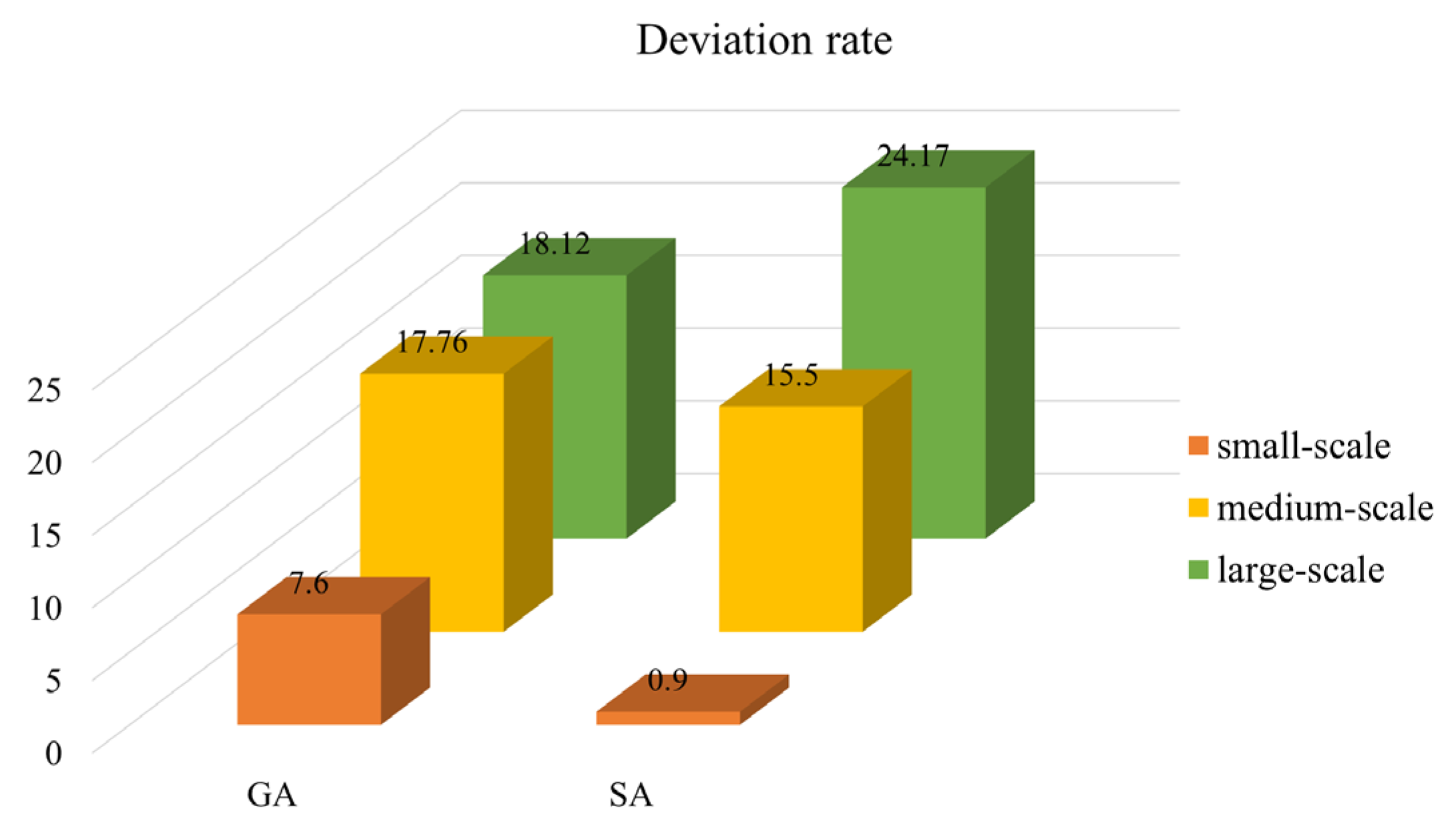
- Analyzing the total cost deviation rate in Figure 13, it can be seen that, compared to the GA, the IGA yields lower deviation rates of 7.6%, 17.76%, and 18.12% for small, medium, and large problem sizes, respectively. Similarly, compared to the SA, the deviation rates for the IGA are 0.97%, 15.5%, and 24.17% for those respective problem sizes. These results demonstrate that the IGA consistently outperforms the other two algorithms. In smaller and medium-sized problems, the SA performs better than the GA, while in larger problems the GA outperforms the SA.
- With the same problem size, the number of autonomous vehicles may vary, leading to different startup costs. In the simulations of small to large problems, the startup costs of the vehicles account for 22.23%, 21.43%, and 19.95% of the total cost, respectively. This ratio gradually decreases with an increase in the number of customers. Additionally, due to the varying number of autonomous vehicles and their routes during the delivery process, the fuel cost, environmental cost (CO2 emissions), and total delivery duration also vary significantly.
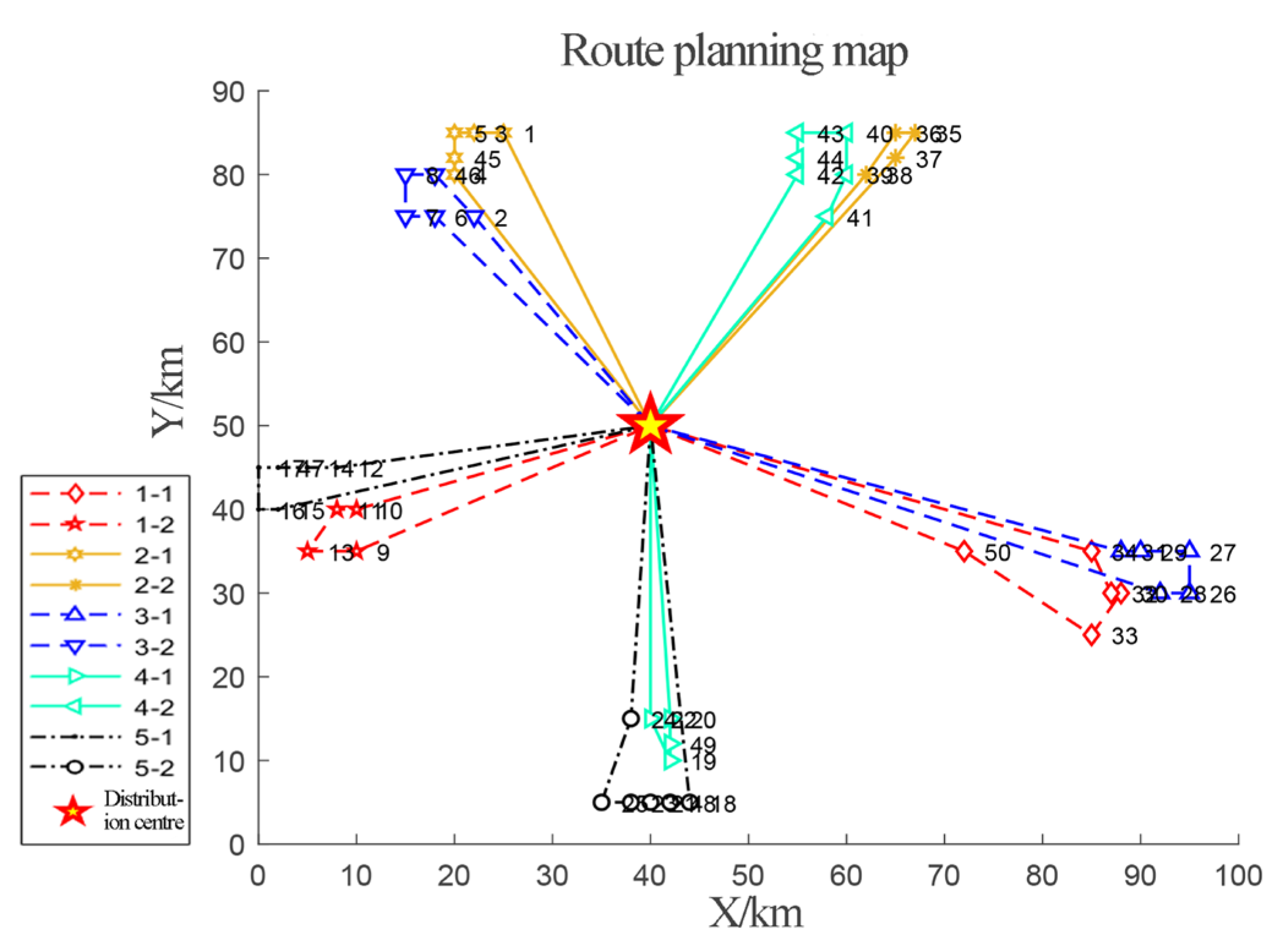
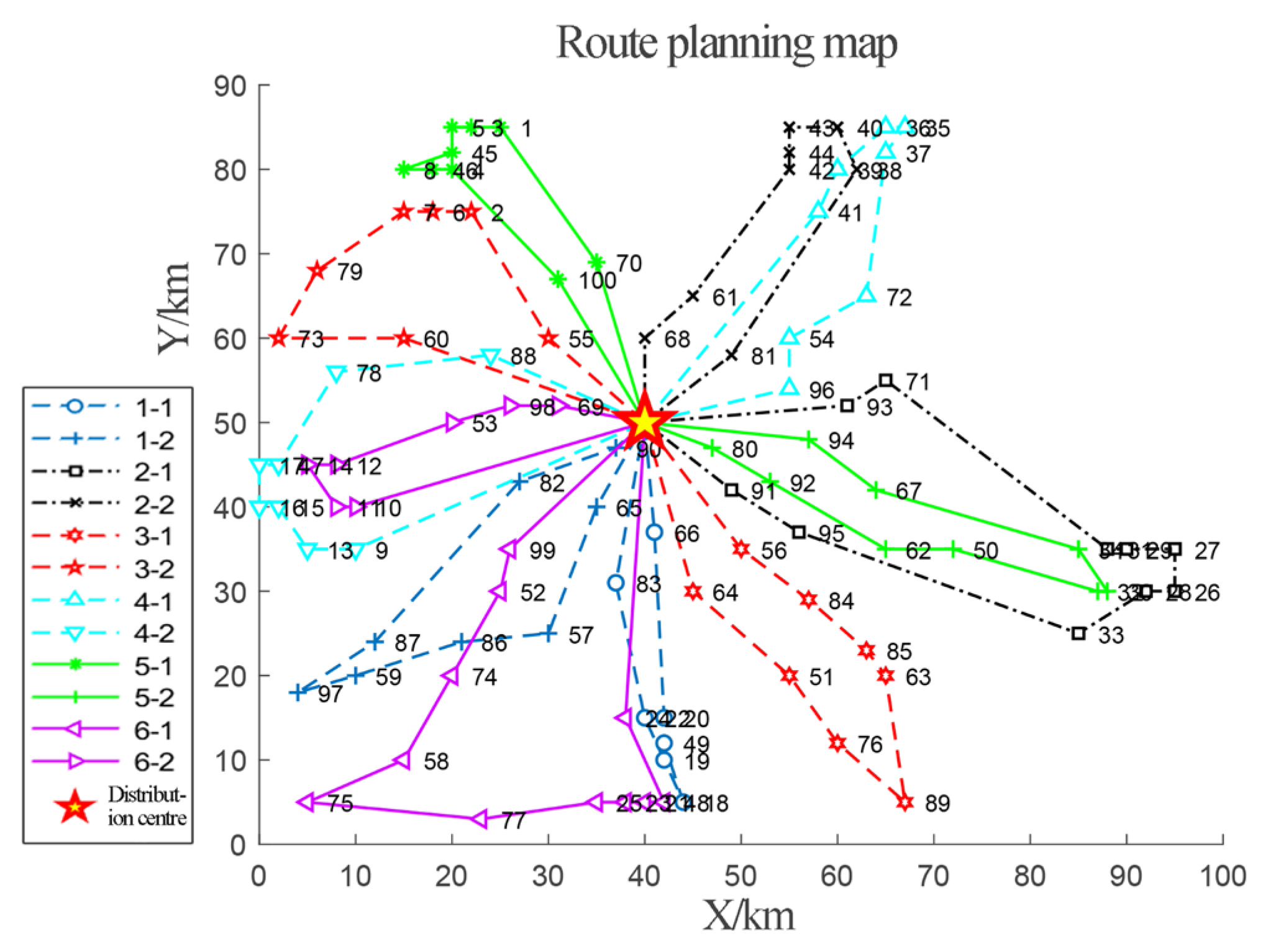
- Table 4, Table 6 and Table 8 provide the optimal delivery plans obtained, using the IGA, for different problem sizes. These tables include the plans, lengths, and load capacities of each route, as well as the total route length and overall delivery duration. As the problem size increases, the number of dominated autonomous vehicles also increases. However, whether for small, medium, or large problem sizes, all autonomous vehicle delivery trips adhere to the constraints of the vehicles’ load capacity and maximum delivery duration. This indicates that the algorithm effectively considers the constraints of the model during the optimization process, without adding penalty costs to the total cost.
5. Sensitivity Analysis
5.1. Compared with Single-Route Delivery by Unmanned Vehicles
5.2. Deliveries Using Different Vehicle Models
5.3. Consideration of the Impact of Carbon Emissions
6. Conclusions
- Using the Solomon RC 208 international standard dataset, simulations were conducted for small-, medium-, and large-scale scenarios, comparing the IGA with the GA and SA. Firstly, the IGA is capable of providing high-quality results in a shorter period of time. Secondly, varying the startup numbers of the autonomous vehicles for different scale distributions leads to differences in their total delivery costs, as well as their fuel expenses, environmental costs (CO2 emissions), and overall delivery durations. Lastly, from the perspective of algorithm effectiveness, by observing the optimal delivery plans generated by the IGA, it is evident that the algorithm satisfies its predetermined constraints across all three scales of scenarios, while possessing strong global search capabilities and high computational efficiency.
- By employing the E-n51-k5 standard dataset and comparing it with the existing literature [44], multi-trip delivery proves advantageous over single-trip delivery, especially with respect to vehicle startup costs. The choice of delivery strategy hinges on the costs and transportation expenses linked to unmanned vehicles. Unmanned vehicles with a high load capacity can curtail their total number of trips and overall delivery duration. In delivery plans that account for carbon emissions, the routes of unmanned vehicles are optimized.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Niu, Y.; Guo, C.; Jia, S. A Vehicle Routing Optimization Model for Community Group Buying Considering Carbon Emissions and Total Distribution Costs. Energies 2023, 16, 931. [Google Scholar] [CrossRef]
- Severino, A.; Curto, S.; Barberi, S.; Arena, F.; Pau, G. Unmanned vehicles: An Analysis Both on Their Distinctiveness and the Potential Impact on Urban Transport Systems. Appl. Sci. 2021, 11, 3604. [Google Scholar] [CrossRef]
- Zhang, S.; Markos, C.; James, J.Q. Autonomous vehicle intelligent system: Joint ride-sharing and parcel delivery strategy. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18466–18477. [Google Scholar] [CrossRef]
- Vlachos, I.P.; Pascazzi, R.M.; Zobolas, G.; Repoussis, P.; Giannakis, M. Lean manufacturing systems in the area of Industry 4.0: A lean automation plan of AGVs/IoT integration. Prod. Plan. Control 2023, 34, 345–358. [Google Scholar] [CrossRef]
- Wang, N.; Lyu, Y.; Jia, S.; Zheng, C.; Meng, Z.; Chen, J. A dynamic graph-based many-to-one ride-matching approach for shared autonomous electric vehicles. Transportation 2023, 4, 1–27. [Google Scholar] [CrossRef]
- Hakak, S.; Gadekallu, T.R.; Maddikunta, P.K.R.; Ramu, S.P.; Parimala, M.; De Alwis, C.; Liyanage, M. Unmanned vehicles in 5G and beyond: A Survey. Veh. Commun. 2022, 39, 100551. [Google Scholar] [CrossRef]
- Parekh, D.; Poddar, N.; Rajpurkar, A.; Chahal, M.; Kumar, N.; Joshi, G.P.; Cho, W. A Review on Unmanned vehicles: Progress, Methods and Challenges. Electronics 2022, 11, 2162. [Google Scholar] [CrossRef]
- Liu, S.; Gao, X.; Chen, L.; Zhou, S.; Peng, Y.; Yu, D.Z.; Ma, X.; Wang, Y. Multi-Traveler Salesman Problem for Unmanned Vehicles: Optimization through Improved Hopfield Neural Network. Sustainability 2023, 15, 15118. [Google Scholar] [CrossRef]
- Zhang, C.; Tang, L.; Zhang, J.; Gou, L. Optimizing Distribution Routes for Chain Supermarket Considering Carbon Emission Cost. Mathematics 2023, 11, 2734. [Google Scholar] [CrossRef]
- Chen, X.; Li, Q.; Li, R.; Cai, X.; Wei, J.; Zhao, H. UAV Network Path Planning and Optimization Using a Vehicle Routing Model. Remote Sens. 2023, 15, 2227. [Google Scholar] [CrossRef]
- Ito, S.; Akaiwa, K.; Funabashi, Y.; Nishikawa, H.; Kong, X.; Taniguchi, I.; Tomiyama, H. Load and Wind Aware Routing of Delivery Drones. Drones 2022, 6, 50. [Google Scholar] [CrossRef]
- Saksuriya, P.; Likasiri, C. Hybrid Heuristic for Vehicle Routing Problem with Time Windows and Compatibility Constraints in Home Healthcare System. Appl. Sci. 2022, 12, 6486. [Google Scholar] [CrossRef]
- Guan, Y.; Wang, Y.; Yan, X.; Guo, H.; Zhao, Y. The One E-Ticket Customized Bus Service Mode for Passengers with Multiple Trips and the Routing Problem. Sustainability 2022, 14, 2124. [Google Scholar] [CrossRef]
- Cataldo-Díaz, C.; Linfati, R.; Escobar, J.W. Mathematical Model for the Electric Vehicle Routing Problem Considering the State of Charge of the Batteries. Sustainability 2022, 14, 1645. [Google Scholar] [CrossRef]
- Baek, D.; Chen, Y.; Chang, N.; Macii, E.; Poncino, M. Battery-Aware Electric Truck Delivery Route Exploration. Energies 2020, 13, 2096. [Google Scholar] [CrossRef]
- Zhao, M.; Lu, Y. A Heuristic Approach for a Real-World Electric Vehicle Routing Problem. Algorithms 2019, 12, 45. [Google Scholar] [CrossRef]
- Chen, S.; Chen, R.; Gao, J. A Monarch Butterfly Optimization for the Dynamic Vehicle Routing Problem. Algorithms 2017, 10, 107. [Google Scholar] [CrossRef]
- Song, R.; Qin, W.; Shi, W.; Xue, X. Optimizing Freight Vehicle Routing in Dynamic Time-Varying Networks with Carbon Dioxide Emission Trajectory Analysis. Sustainability 2023, 15, 15504. [Google Scholar] [CrossRef]
- Hachiya, D.; Mas, E.; Koshimura, S. A Reinforcement Learning Model of Multiple UAVs for Transporting Emergency Relief Supplies. Appl. Sci. 2022, 12, 10427. [Google Scholar] [CrossRef]
- Cattaruzza, D.; Absi, N.; Feillet, D.; Vigo, D. An iterated local search for the multi-commodity multi-trip vehicle routing problem with time windows. Comput. Oper. Res. 2014, 51, 257–267. [Google Scholar] [CrossRef]
- Tan, K.; Liu, W.; Xu, F.; Li, C. Optimization Model and Algorithm of Logistics Vehicle Routing Problem under Major Emergency. Mathematics 2023, 11, 1274. [Google Scholar] [CrossRef]
- Hou, B.; Zhang, K.; Gong, Z.; Li, Q.; Zhou, J.; Zhang, J.; de La Fortelle, A. SoC-VRP: A Deep-Reinforcement-Learning-Based Vehicle Route Planning Mechanism for Service-Oriented Cooperative ITS. Electronics 2023, 12, 4191. [Google Scholar] [CrossRef]
- Zheng, X.; Gao, F.; Tong, X. Research on Green Vehicle Path Planning of AGVs with Simultaneous Pickup and Delivery in Intelligent Workshop. Symmetry 2023, 15, 1505. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, H.; Ma, J.; Yue, B.; Guan, Y.; Shi, J.; Shangguan, L. Improved Genetic Algorithm for Solving Green Path Models of Concrete Trucks. Appl. Sci. 2023, 13, 9256. [Google Scholar] [CrossRef]
- Fleischmann, B. The Vehicle Routing Problem with Multiple Use of Vehicles. Ph.D. Thesis, Fachbereich Wirtschaftswissenschaften, Universität Hamburg, Hamburg, Germany, 1990. [Google Scholar]
- Hernandez, F.; Feillet, D.; Giroudeau, R.; Naud, O. An exact method to solve the multitrip vehicle routing problem with time windows and limited duration. TRISTAN 2010, 7, 366–369. [Google Scholar] [CrossRef]
- Azi, N.; Gendreau, M.; Potvin, J.Y. An exact algorithm for a vehicle routing problem with time windows and multiple use of vehicles. Eur. J. Oper. Res. 2010, 202, 756–763. [Google Scholar] [CrossRef]
- Munari, P.; Morabito, R. A branch-price-and-cut algorithm for the vehicle routing problem with time windows and multiple deliverymen. Top 2018, 26, 437–464. [Google Scholar] [CrossRef]
- Marques, G.; Sadykov, R.; Dupas, R.; Deschamps, J.C. A branch-cut-and-price approach for the single-trip and multi-trip two-echelon vehicle routing problem with time windows. Transp. Sci. 2022, 56, 1598–1617. [Google Scholar] [CrossRef]
- Huang, N.; Li, J.; Zhu, W.; Qin, H. The multi-trip vehicle routing problem with time windows and unloading queue at depot. Transp. Res. Part E Logist. Transp. Rev. 2021, 152, 102370. [Google Scholar] [CrossRef]
- Bettinelli, A.; Cacchiani, V.; Crainic, T.G.; Vigo, D. A branch-and-cut-and-price algorithm for the multi-trip separate pickup and delivery problem with time windows at customers and facilities. Eur. J. Oper. Res. 2019, 279, 824–839. [Google Scholar] [CrossRef]
- Karimi, L.; Nawrin Ferdous, C. Branch and Price Algorithm for Multi-Trip Vehicle Routing with a Variable Number of Wagons and Time Windows. Algorithms 2022, 15, 412. [Google Scholar] [CrossRef]
- Karoonsoontawong, A.; Kobkiattawin, O.; Xie, C. Efficient insertion heuristic algorithms for multi-trip inventory routing problem with time windows, shift time limits and variable delivery time. Netw. Spat. Econ. 2019, 19, 331–379. [Google Scholar] [CrossRef]
- Petch, R.J.; Salhi, S. A multi-phase constructive heuristic for the vehicle routing problem with multiple trips. Discret. Appl. Math. 2003, 133, 69–92. [Google Scholar] [CrossRef]
- Brandao, J.; Mercer, A. A tabu search algorithm for the multi-trip vehicle routing and scheduling problem. Eur. J. Oper. Res. 1997, 100, 180–191. [Google Scholar] [CrossRef]
- Olivera, A.; Viera, O. Adaptive memory programming for the vehicle routing problem with multiple trips. Comput. Oper. Res. 2007, 34, 28–47. [Google Scholar] [CrossRef]
- Babaee Tirkolaee, E.; Abbasian, P.; Soltani, M.; Ghaffarian, S.A. Developing an applied algorithm for multi-trip vehicle routing problem with time windows in urban waste collection: A case study. Waste Manag. Res. 2019, 37, 4–13. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Hosseinabadi, A.A.R.; Soltani, M.; Sangaiah, A.K.; Wang, J. A Hybrid Genetic Algorithm for Multi-Trip Green Capacitated Arc Routing Problem in the Scope of Urban Services. Sustainability 2018, 10, 1366. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Goli, A.; Bakhsi, M.; Mahdavi, I. A robust multi-trip vehicle routing problem of perishable products with intermediate depots and time windows. Numer. Algebra Control. Optim. 2017, 7, 417–433. [Google Scholar] [CrossRef]
- Zhang, X.N.; Fan, H. Multi-trip fuzzy demand vehicle path optimization with time window preferences. Comput. Integr. Manuf. Syst. 2018, 24, 2461–2477. Available online: https://kns.cnki.net/kcms/detail/11.5946.TP.20180108.1722.004.html (accessed on 25 April 2017).
- Zhen, L.; Ma, C.; Wang, K.; Xiao, L.; Zhang, W. Multi-depot multi-trip vehicle routing problem with time windows and release dates. Transp. Res. Part E Logist. Transp. Rev. 2020, 135, 101866. [Google Scholar] [CrossRef]
- Chen, D.; Pan, S.; Chen, Q.; Liu, J. Vehicle routing problem of contactless joint distribution service during COVID-19 pandemic. Transp. Res. Interdiscip. Perspect. 2020, 8, 100233. [Google Scholar] [CrossRef]
- Song, Q. Application of an optimized beam-PSO algorithm in multi-trip vehicle routing problem. Comput. Eng. Sci. 2019, 41, 1882–1891. Available online: https://kns.cnki.net/dm/manage/export.html?filename=CJFDLAST2019!JSJK201910024!1!0&displaymode=NEW&uniplatform=NZKPT (accessed on 13 August 2018).
- Song, Q.; Liu, L.X. Research on Multi-Trip Vehicle Routing Problem and Distribution Center Location Problem. Math. Pract. Underst. 2016, 46, 103–113. Available online: https://www.cqvip.com/qk/93074x/201607/668483120.html (accessed on 7 November 2015).
- Wassan, N.; Wassan, N.; Nagy, G.; Salhi, S. The multiple trip vehicle routing problem with backhauls: Formulation and a two-level variable neighbourhood search. Comput. Oper. Res. 2017, 78, 454–467. [Google Scholar] [CrossRef]
- Neira, D.A.; Aguayo, M.M.; De la Fuente, R.; Klapp, M.A. New compact integer programming formulations for the multi-trip vehicle routing problem with time windows. Comput. Ind. Eng. 2020, 144, 106399. [Google Scholar] [CrossRef]
- Anggodo, Y.; Ariyani, A.; Ardi, M.; Mahmudy, W. Optimization of multi-trip vehicle routing problem with time windows using genetic algorithm. J. Environ. Eng. Sustain. Technol. 2017, 3, 92–97. [Google Scholar] [CrossRef]
- Janinhoff, L.; Klein, R.; Scholz, D. Multitrip vehicle routing with delivery options: A data-driven application to the parcel industry. OR Spectrum 2023, 1–54. [Google Scholar] [CrossRef]
- Sahoo, B.M.; Pandey, H.M.; Amgoth, T. A genetic algorithm inspired optimized cluster head selection method in wireless sensor networks. Swarm. Evol. Comp. 2022, 75, 101151. [Google Scholar] [CrossRef]
- Han, J.; Liu, Y.; Li, Y. Vehicle Routing Problem with Drones Considering Time Windows and Dynamic Demand. Appl. Sci. 2023, 13, 13086. [Google Scholar] [CrossRef]
- Wang, F.; Ge, X.; Li, Y.; Zheng, J.; Zheng, W. Optimising the Distribution of Multi-Cycle Emergency Supplies after a Disaster. Sustainability 2023, 15, 902. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the vehicle routing and scheduling problems with time window constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
| Papers | Optimization Models | Solution Method | ||||
|---|---|---|---|---|---|---|
| Research Topics | Research Object | Objective Function | Precision Algorithms | Heuristics Algorithms | Others | |
| Zhang et al. [9] | A vehicle routing problem with time windows (VRPTW) | Family medical services | Minimize travel costs | Particle Swarm Optimization (PSO) | ||
| Chen et al. [10] | VRP | Task assignment | Minimize the maximum observation time | CPLEX and Gurobi solvers | ||
| Guan et al. [13] | VRP | Customized bus | Maximizing profits | GA | ||
| Zhao et al. [16] | Electric Vehicle Routing Problem (EVRP) | Electric vehicle services | Minimize operating costs | Adaptive large neighborhood search (ALNS) | ||
| Hachiya et al. [19] | VRP | Unmanned aerial vehicle (UAV) | Minimizing total costs | Q-learning (QL) | ||
| Zheng et al. [23] | Green Vehicle Routing Problem Involving Simultaneous Pickup and Delivery with Time Windows (GVRPSPDTWs) | The green automated guided vehicle (AGV)’s energy consumption | Minimizing total energy costs | Hybrid differential evolution algorithm based on large neighborhood search (DE-LNS) | ||
| Yang et al. [24] | The Green VRP | Commercial concrete distribution | Minimizing total fuel consumption | GA | ||
| Hernandez et al. [26] | MTVRP | Vehicle delivery | Minimize time spent visiting customers | Branching and pricing algorithms | ||
| Marques et al. [29,31] | A multi-trip vehicle routing problem with time windows (MTVRPTW) | Delivery of goods to customers | Minimization of transport costs | Branch-Cut-and-Price approach | ||
| Brandao et al. [35] | A multi-trip vehicle routing and scheduling problem (MTVRSP) | Real distribution problems | Access to all customers and minimal time spent | Tabu search heuristic | ||
| Babaee et al. [37] | MTVRP | Municipal waste recycling | Minimize total cost of ownership | SA | ||
| Tirkolaee et al. [38] | The multi-trip Green Capacitated Arc Routing Problem (G-CARP) | Environmentally friendly emissions of greenhouse gases | Minimizing the cost of greenhouse gas emissions | Hybrid Genetic Algorithm (HGA) | ||
| Tirkolaee et al. [39] | MTVRP | Perishable products | Minimizing total distance traveled and total cost | CPLEX solver | ||
| Chen et al. [42] | Multi-vehicle multi-trip routing problem | Community courier delivery service | Residents’ satisfaction with food delivery services | Artificial bee colony algorithm (ABC) | ||
| Wassan et al. [45] | A Multiple Trip Vehicle Routing Problem with Backhauls (MT-VRPB) | Arranging shipments from distribution centers | CPLEX solver | The Two-Level VNS algorithm | ||
| Neira et al. [46] | A multi-trip vehicle routing problem with time windows, service-dependent loading times, and limited trip durations (MTVRPTW-SDLT) | Vehicle deliveries | Reduce costs | Two integer programming (IP) models | ||
| Anggodo et al. [47] | A multi-trip vehicle routing problem with time windows (MTVRPTW) | Travel route issues | Minimal commuting time | GA | ||
| Janinhoff et al. [48] | A multi-trip vehicle routing problem with delivery options (MT-VRPDO) | Express delivery | Minimizing delivery costs | Adaptive large neighborhood search (ALNS) | Data-driven framework | |
| Parameter Symbols | Specific Meaning | Units |
|---|---|---|
| Set: | ||
| The set of customers, denoted as | - | |
| The set of vehicles, denoted as | - | |
| The set of all points, denoted as | - | |
| The set of all edges, denoted as | - | |
| Parameters: | ||
| The carrying capacity of the unmanned vehicle | kg | |
| The demand of customer | kg | |
| The distance between customer and customer | km | |
| The time at which the unmanned vehicle has passed through customer and customer | h | |
| The cost per unit distance traveled by the unmanned vehicle | USD/km | |
| The startup cost for each unmanned vehicle | USD | |
| Cost per liter of fuel | USD | |
| The environmental cost of emitting 1 kg of CO2 | USD/kg CO2 | |
| The vehicle’s fuel consumption per kilometer | L/km | |
| The fuel conversion coefficient | Kg CO2/L | |
| The penalty cost for the unmanned vehicle’s total delivery time exceeding its maximum driving time | USD/h | |
| The penalty cost per unit for exceeding the vehicle’s rated load capacity | USD/kg | |
| A large positive number | - | |
| The maximum delivery time for each trip during unmanned vehicle delivery | H | |
| The maximum number of vehicles that can be used for unmanned vehicle delivery | vehicles | |
| Intermediate variables: | ||
| The sequence in which customers are to be serviced by unmanned vehicle on trip | - | |
| All trips of unmanned vehicle | - | |
| The departure time of unmanned vehicle on trip | H | |
| The travel time of unmanned vehicle on trip | H | |
| The load capacity of unmanned vehicle on trip | Kg | |
| The distance traveled by unmanned vehicle | Km | |
| The set of all trips of unmanned vehicle | - | |
| Decision variables | ||
| Is 1 if unmanned vehicle is activated, otherwise 0 | - | |
| Is 1 if unmanned vehicle serves customer and on trip , otherwise 0 | - |
| Algorithm | Total Cost (USD) | Vehicle Startup Cost (USD) | Fuel Cost (USD) | Environmental Cost (USD) | Total Distance (km) | Number of Unmanned Vehicles | Total Number of Trips | Total Delivery Time (h) | Deviation Rate (%) |
|---|---|---|---|---|---|---|---|---|---|
| IGA | 2698.87 | 600 | 1100.70 | 458.61 | 539.56 | 3 | 6 | 10.78 | - |
| GA | 2903.77 | 800 | 1103.27 | 459.68 | 540.82 | 4 | 6 | 10.82 | 7.60 |
| SA | 2725.16 | 600 | 1114.49 | 464.35 | 546.32 | 3 | 6 | 10.93 | 0.97 |
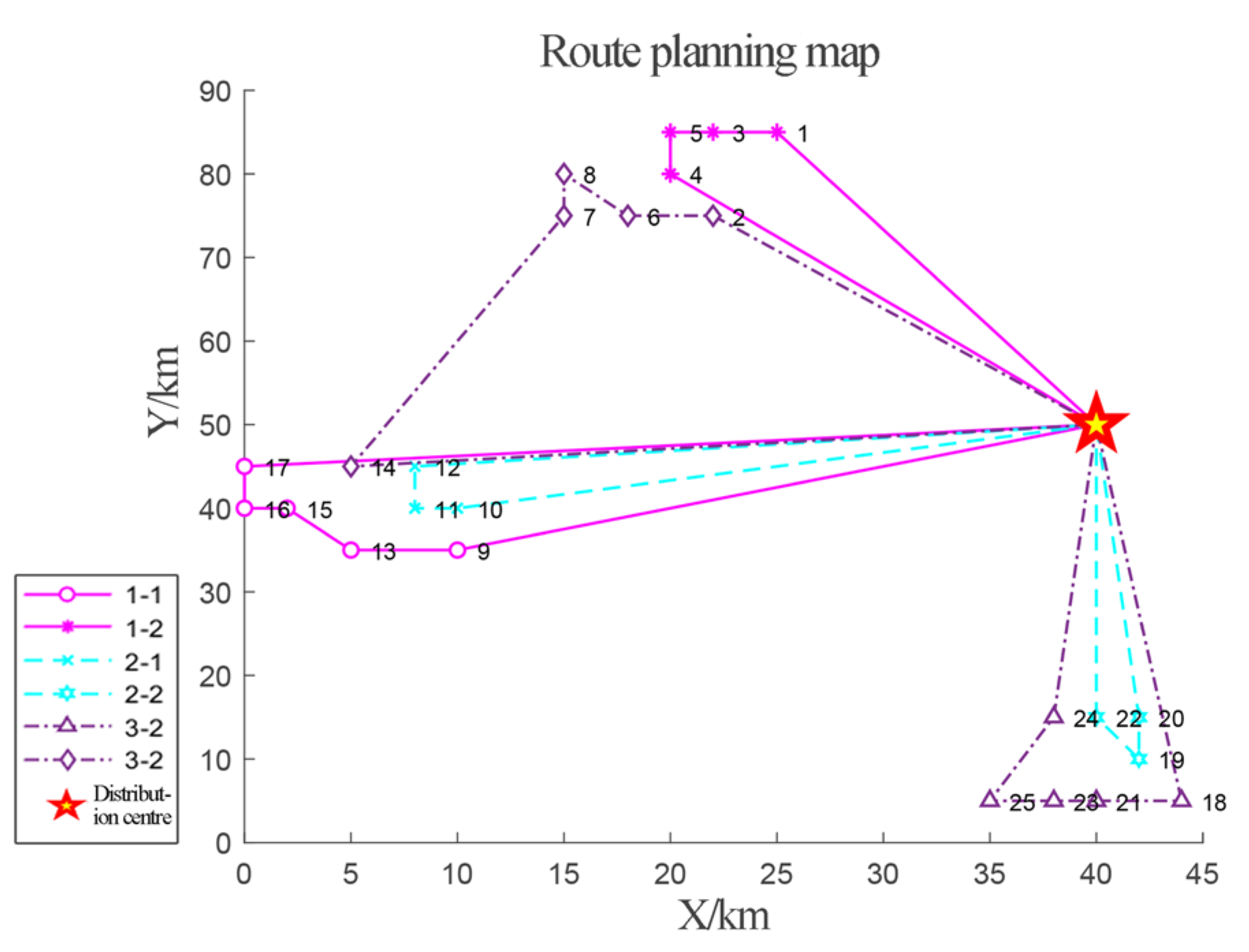
| Unmanned Vehicle | Route Programs | Route Capacity (kg) | Route Length (km) | Total Line Length (km) | Route Distribution Time (h) | Total Distribution Time (h) |
|---|---|---|---|---|---|---|
| 1 | 0-9-13-15-16-17-0 0-4-5-3-1-0 | 90 90 | 91.68 84.13 | 175.81 | 1.83 1.68 | 3.51 |
| 2 | 0-10-11-12-0 020-19-22-0 | 90 90 | 71.01 80.44 | 151.45 | 1.42 1.61 | 3.03 |
| 3 | 0-24-25-23-21-18-0 02-6-8-7-14-0 | 90 90 | 99.67 112.61 | 212.28 | 1.99 2.25 | 4.24 |
| Algorithm | Total Cost (USD) | Vehicle Startup Cost (USD) | Fuel Cost (USD) | Environmental Cost (USD) | Total Distance (km) | Number of Unmanned Vehicles | Total Number of Trips | Total Delivery Time (h) | Deviation Rate (%) |
|---|---|---|---|---|---|---|---|---|---|
| IGA | 4665.83 | 1000 | 1869.57 | 778.95 | 916.46 | 5 | 10 | 18.31 | - |
| GA | 5494.65 | 1000 | 2292.27 | 955.07 | 1123.66 | 5 | 11 | 22.48 | 17.76 |
| SA | 4738.17 | 1000 | 1887.59 | 786.46 | 925.29 | 5 | 11 | 18.51 | 15.50 |
| Unmanned Vehicle | Route Programs | Route Loading Capacity (kg) | Route Length (km) | Total Line Length (km) | Route Distribution Time (h) | Total Distribution Time (h) |
|---|---|---|---|---|---|---|
| 1 | 0-1-3-5-45-4-0 | 100 | 84.13 | 84.13 | 1.68 | 1.68 |
| 2 | 0-50-34-31-0 0-9-13-15-16-17-47-0 | 80 100 | 101.63 91.7 | 193.3 | 2.03 1.83 | 3.86 |
| 3 | 0-33-32-30-28-26-27-29-0 0-38-36-35-37-0 | 100 100 | 127.06 89.25 | 216.31 | 2.54 1.78 | 4.32 |
| 4 | 0-42-44-43-40-39-41-0 0-2-46-8-7-6-0 0-12-14-11-10-0 | 100 90 100 | 84.73 81.51 74.84 | 241.08 | 1.69 1.63 1.50 | 4.82 |
| 5 | 0-24-19-49-22-0 0-20-18-48-21-23-25-0 | 100 100 | 82.07 99.53 | 181.6 | 1.64 1.99 | 3.63 |
| Algorithm | Total Cost (USD) | Vehicle Startup Cost (USD) | Fuel Cost (USD) | Environmental Cost (USD) | Total Distance (km) | Number of Unmanned Vehicles | Total Number of Trips | Total Delivery Time (h) | Deviation Rate (%) |
|---|---|---|---|---|---|---|---|---|---|
| IGA | 6015.11 | 1200 | 2525.17 | 1052.11 | 1237.83 | 6 | 12 | 24.74 | - |
| GA | 7104.89 | 1200 | 2965.33 | 1235.50 | 1453.59 | 6 | 13 | 29.07 | 18.12 |
| SA | 7468.86 | 1200 | 3136.43 | 1306.78 | 1537.46 | 6 | 14 | 30.75 | 24.17 |
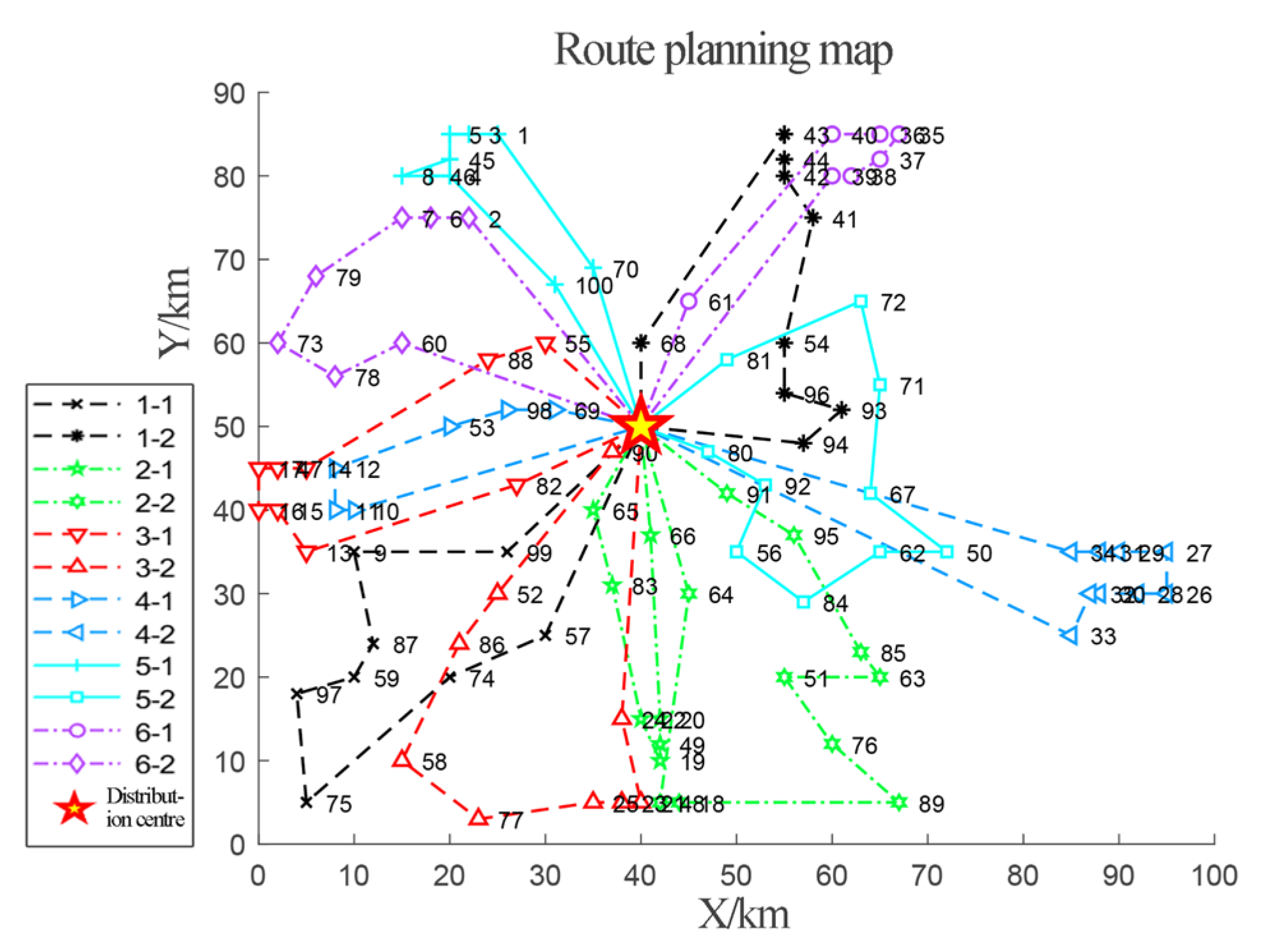
| Unmanned Vehicle | Route Programs | Route Loading Capacity (kg) | Route Length (km) | Total Line Length (km) | Route Distribution Time (h) | Total Distribution Time (h) |
|---|---|---|---|---|---|---|
| 1 | 0-66-20-49-18-19-22-83-0 0-90-82-87-59-86-57-65-0 | 150 110 | 91.63 103.30 | 194.93 | 1.83 2.07 | 3.9 |
| 2 | 0-91-95-33-28-26-27-29-31-93-0 0-81-38-40-43-44-42-61-68-0 | 122 130 | 132.21 88.08 | 220.29 | 2.64 1.76 | 4.4 |
| 3 | 0-64-51-76-89-63-85-84-56-0 0-55-2-6-7-79-73-60-0 | 137 138 | 108.56 98.41 | 206.97 | 2.17 1.97 | 4.14 |
| 4 | 0-96-54-72-37-35-36-39-41-0 0-88-78-47-17-16-15-13-9-0 | 150 146 | 96.94 99.91 | 196.85 | 1.94 2.00 | 3.94 |
| 5 | 0-70-1-3-5-45-8-46-4-100-0 0-80-92-62-50-32-30-34-67-94-0 | 126 142 | 93.16 107.36 | 200.52 | 1.86 2.15 | 4.01 |
| 6 | 0-24-48-21-23-25-77-75-58-74-52-99-0 0-69-98-53-12-14-11-10-0 | 149 141 | 142.26 76.00 | 218.26 | 2.85 1.52 | 4.02 |
| Single-Trip Delivery (E-n51-k5) | Multi-Trip Delivery | |||
|---|---|---|---|---|
| Literature [44] | IGA | Deviation Rate (%) | ||
| Number of unmanned vehicles (vehicles) | 5 | 3 | 2 | −150 |
| Total distance traveled (km) | 521 | 600 | 558.73 | 6.75 |
| Unmanned vehicle startup costs (USD) | 1500 | 900 | 600 | −150 |
| Transportation costs (USD) | 2605 | 3000 | 2793.65 | 6.75 |
| Fuel costs (USD) | 1062.84 | 1224 | 1139.82 | 6.75 |
| Environmental costs (USD) | 442.83 | 509.98 | 474.90 | 6.75 |
| Total cost (USD) | 4110.67 | 4733.98 | 5008.41 | 17.92 |
| Total duration (h) | 8.68 | 10 | 9.31 | 6.77 |
| 100 kg | 150 kg | 180 kg | Deviation Rate (%) | |
|---|---|---|---|---|
| Number of unmanned vehicles (vehicles) | 5 | 4 | 3 | 66.67 |
| Total number of trips | 10 | 7 | 5 | 100 |
| Average number of journeys | 2 | 1.75 | 1.67 | 19.76 |
| Total distribution hours (h) | 18.45 | 15.21 | 10.37 | 77.92 |
| Total distance (km) | 917.29 | 769.98 | 518.5 | 76.91 |
| Vehicle startup costs (USD) | 1000 | 1200 | 1500 | 50 |
| Fuel costs (USD) | 1871.27 | 1570.77 | 1057.74 | 76.91 |
| Environmental costs (USD) | 779.66 | 654.46 | 440.70 | 76.91 |
| Transportation costs (USD) | 917.29 | 2309.94 | 3111 | 239.15 |
| Total cost (USD) | 4566.25 | 5735.22 | 6109.46 | 34 |
| Running time (seconds) | 20.82 | 20.08 | 21.28 | 5.98 |
| Consideration of Carbon Emissions | Carbon Emissions Not Taken into Account | Deviation Rate (%) | |
|---|---|---|---|
| Number of unmanned vehicles (vehicles) | 6 | 6 | 0 |
| Total number of trips (pcs) | 12 | 12 | 0 |
| Average number of journeys (in) | 2 | 2 | 0 |
| Total distribution hours (h) | 25.42 | 25.84 | 1.63 |
| Total distance (km) | 1271.72 | 1292.05 | 1.57 |
| Vehicle startup costs (USD) | 1200 | 1200 | 0 |
| Fuel costs (USD) | 2594.32 | 2635.78 | 1.57 |
| Environmental costs (USD) | 1080.92 | - | - |
| CO2 emissions (kg) | 900.76 | - | - |
| Transportation costs (USD) | 1271.722 | 1292.05 | 1.57 |
| Total cost (USD) | 6286.896 | 5127.82 | −22.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Liu, S.; Wang, Y.; Yu, D.Z.; Peng, Y.; Ma, X. Consideration of Carbon Emissions in Multi-Trip Delivery Optimization of Unmanned Vehicles. Sustainability 2024, 16, 2357. https://doi.org/10.3390/su16062357
Gao X, Liu S, Wang Y, Yu DZ, Peng Y, Ma X. Consideration of Carbon Emissions in Multi-Trip Delivery Optimization of Unmanned Vehicles. Sustainability. 2024; 16(6):2357. https://doi.org/10.3390/su16062357
Chicago/Turabian StyleGao, Xinhua, Song Liu, Yan Wang, Dennis Z. Yu, Yong Peng, and Xianting Ma. 2024. "Consideration of Carbon Emissions in Multi-Trip Delivery Optimization of Unmanned Vehicles" Sustainability 16, no. 6: 2357. https://doi.org/10.3390/su16062357
APA StyleGao, X., Liu, S., Wang, Y., Yu, D. Z., Peng, Y., & Ma, X. (2024). Consideration of Carbon Emissions in Multi-Trip Delivery Optimization of Unmanned Vehicles. Sustainability, 16(6), 2357. https://doi.org/10.3390/su16062357







