Development of Methodology for Estimation of Energy-Efficient Building Renovation Using Application of MINLP-Optimized Timber–Glass Upgrade Modules
Abstract
1. Introduction
1.1. Current Advancements and Achievements in the Vertical Addition of Buildings
1.2. Objectives
2. Design Strategies and Measures
2.1. Renovation Approaches and Measures
- Partial renovations are made up of only one or a few actions, which typically improve a building’s appearance and functionality to a moderate degree.
- The deep renovation approach involves renovation actions that produce higher levels of overall efficiency.
- The highest level of building enhancement can be attained by comprehensive renovation techniques that include all pertinent measures needed to address the technical, functional, social, environmental, and economic aspects of a renovation.
- Building additions (horizontal additions, balconies, upgrade modules, etc.);
- A different ecological system (gathering of rainwater, etc.);
- Taking accessibility into consideration.
2.2. Daylighting Recommendations and Design Strategies
3. Materials and Methods
3.1. Description of Case Study Buildings
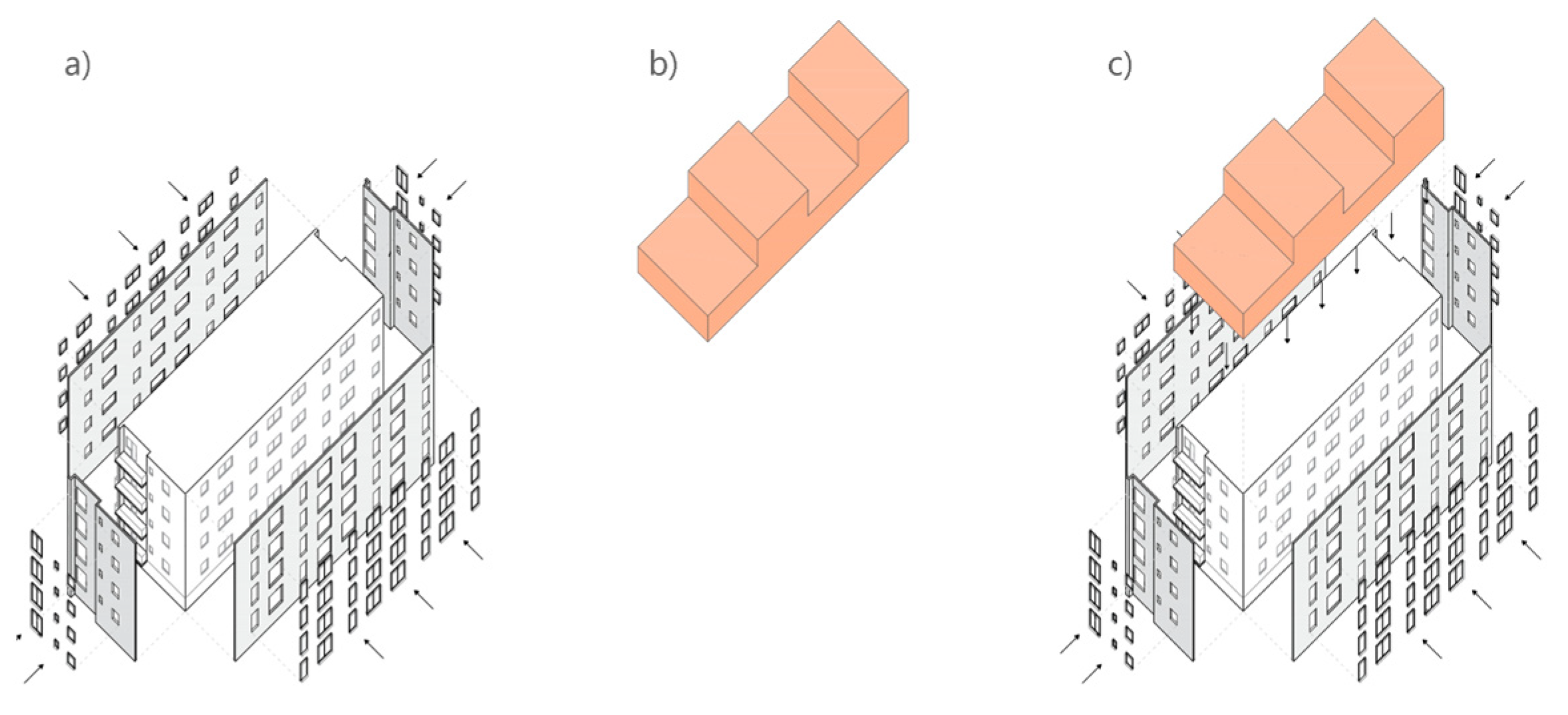
3.2. Timber–Glass Upgrade Module Design
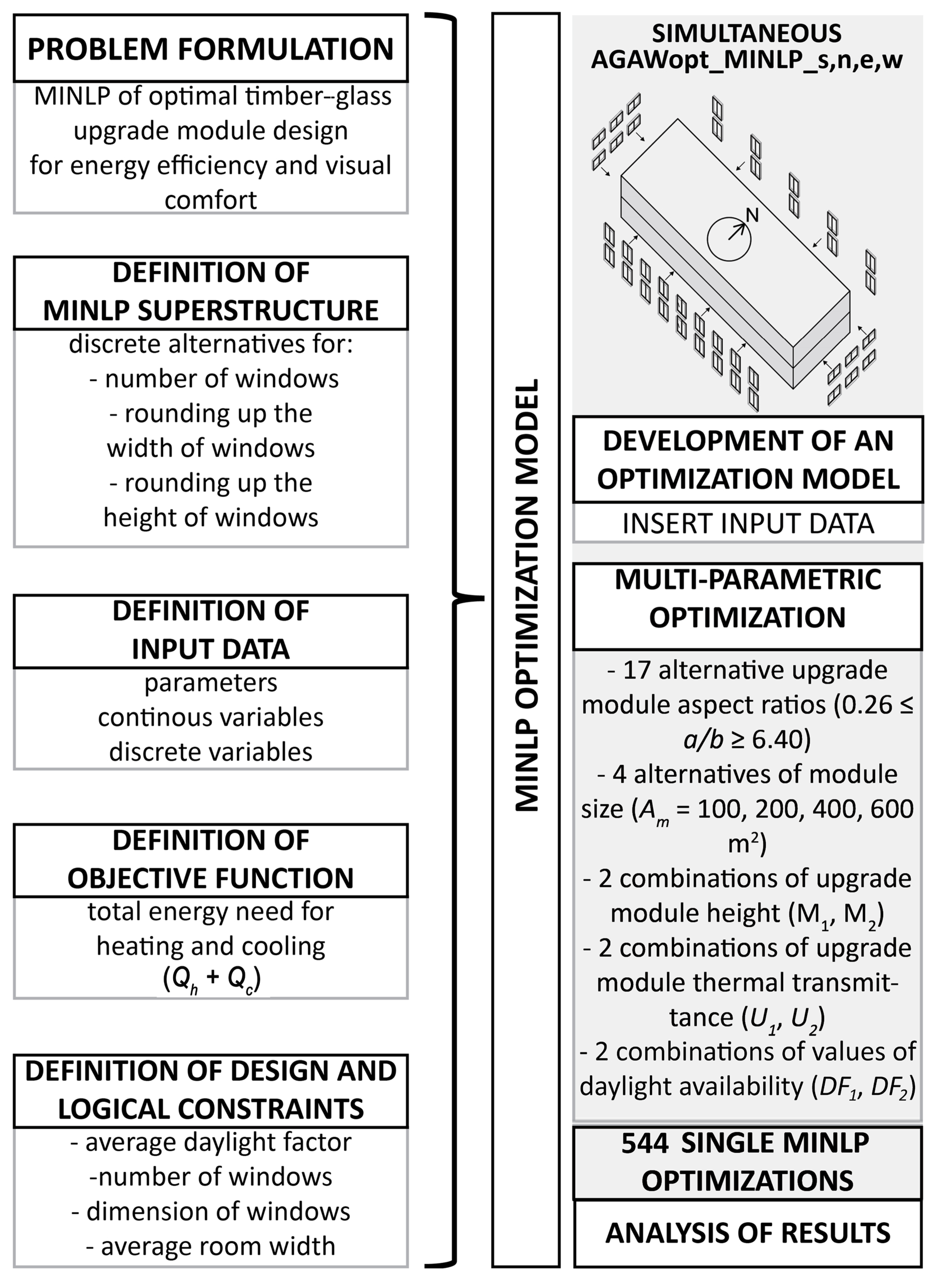
MINLP Design Optimization of Timber–Glass Upgrade Modules
- l, l ∈ L, discrete options for rounding alternatives for widths of north-facing windows;
- m, m ∈ M, discrete options for rounding alternatives for heights of north-facing windows;
- n, n ∈ N, discrete options for determining the suitable quantity of north-facing windows;
- o, o ∈ O, discrete options for rounding alternatives for widths of east- and west-facing windows;
- p, p ∈ P, discrete options for rounding alternatives for heights of east- and west-facing windows;
- r, r ∈ R, discrete options for determining the suitable quantity of east- and west-facing windows.
3.3. Basic Limitations of Study
- The climate of Maribor, Central Europe, is considered.
- This research does not cover the ventilation, heating, and cooling systems’ designs in the REBs and upgrade modules.
- It is believed there exists no heat exchange between the upgrade module and the final REB level via the contact zone (floor slab) (Qt,floor = 0, no heat flow).
- The assessment of global structural analysis is not part of any analysis within this research. Owing to the gap between the generally higher actual load-bearing capacities of the structures and the lower theoretical load-bearing capacities required by the standards, most of the existing structures are likely to have sufficient load-bearing ability to support the addition of one or two upgrading stories constructed with a lightweight timber-framed construction method.
- Instead of being measured as a decrease in the amount of energy required for electric lights, visual comfort was evaluated as a boundary condition. Setting lower bounds for a DF is predicated on the assumption that the rooms receive sufficient daylight during the day.
- Energy costs are an important consideration that can influence the choice of building renovation strategies. However, the proposed method, which is not influenced by energy costs, considers energy consumption as a performance parameter.
3.4. Software
4. Results and Discussion
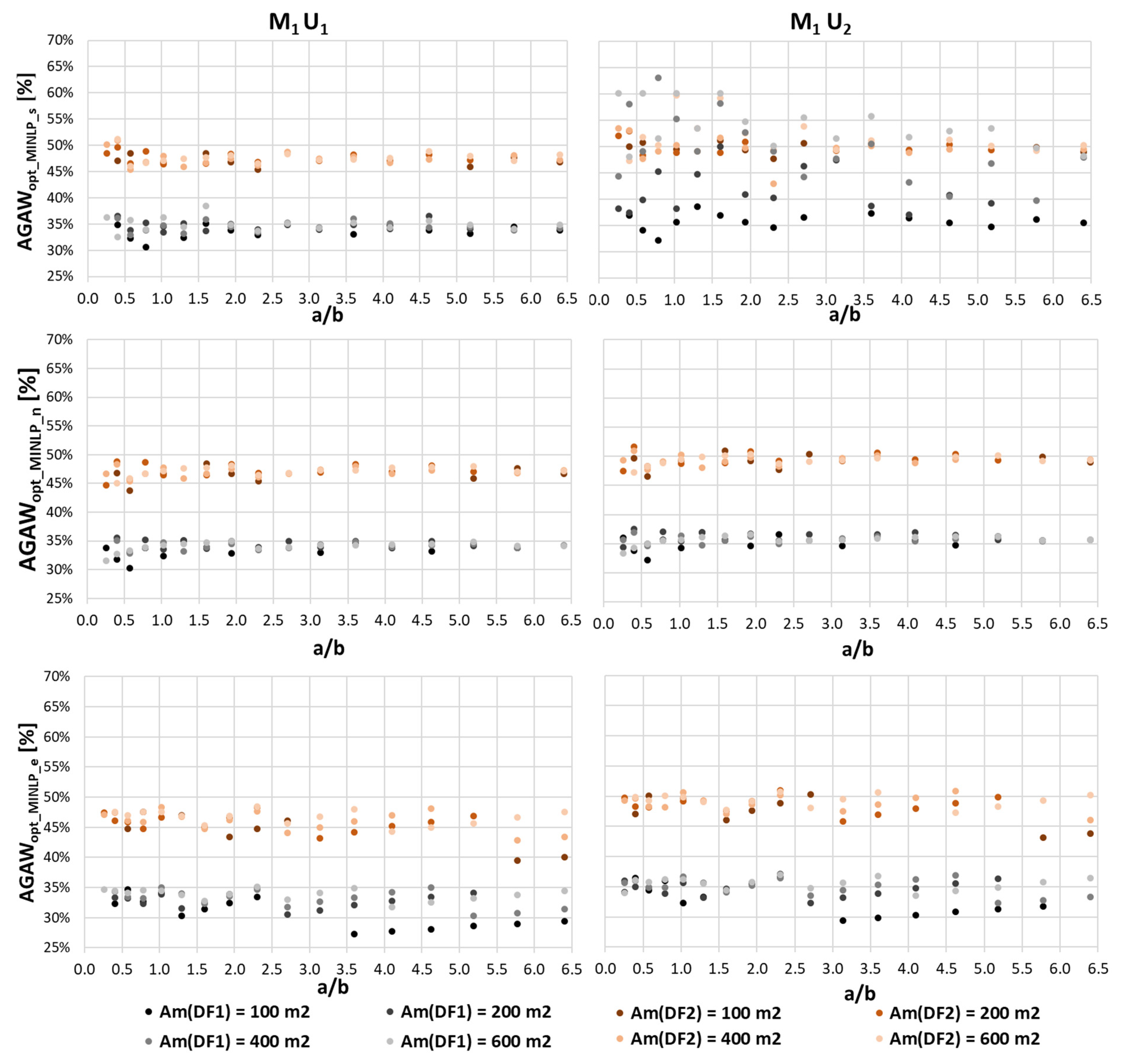
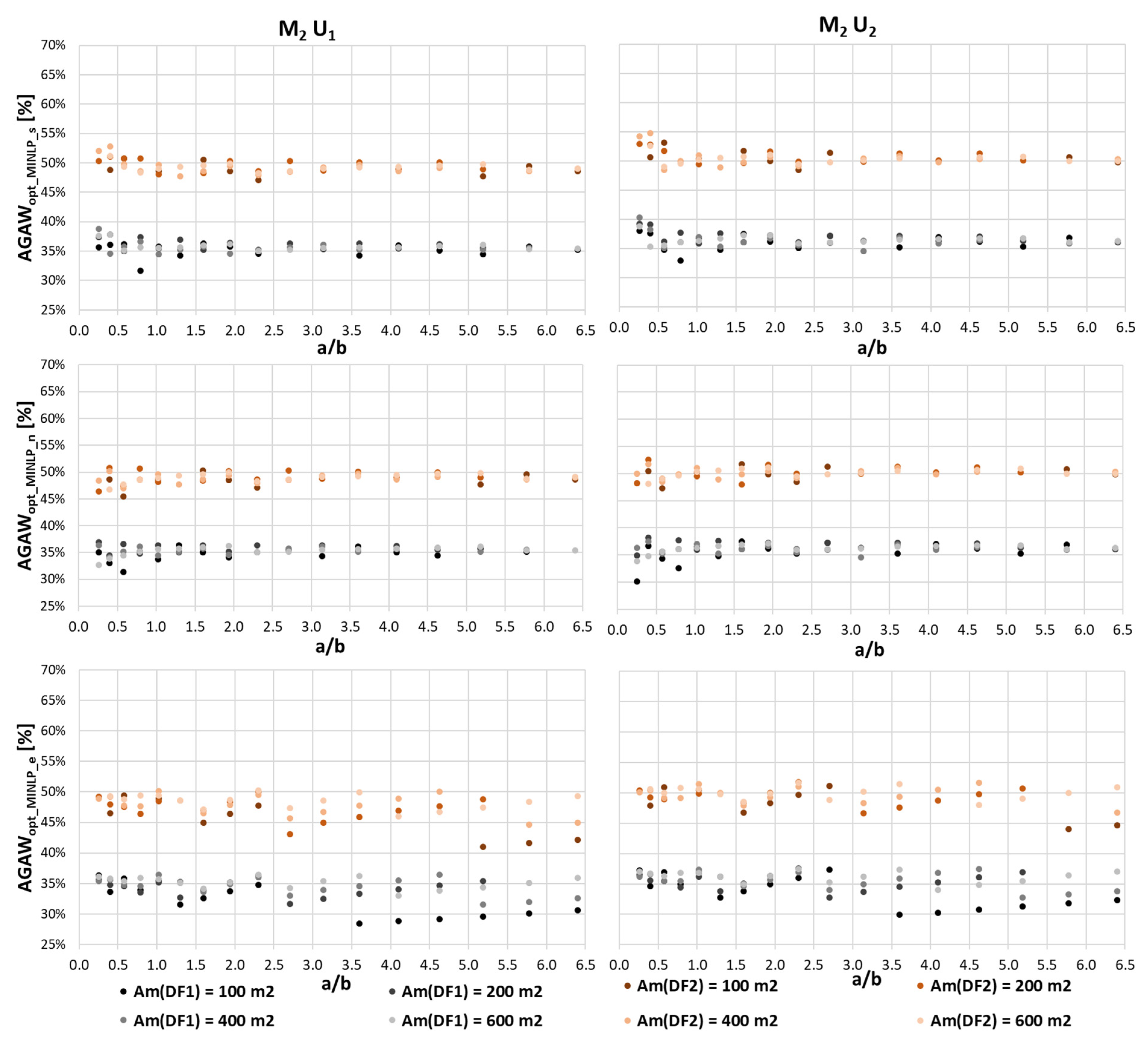
4.1. Redefinition of Timber–Glass Upgrade Modules with the Best Possible Design
Defined Ideal Proportions of Glazing for the Developed Upgrade Module Types Covering the Entire Roof Area of REBs
4.2. Vertical Addition to a Building Incorporating Energy-Efficient Timber–Glass Upgrade Modules
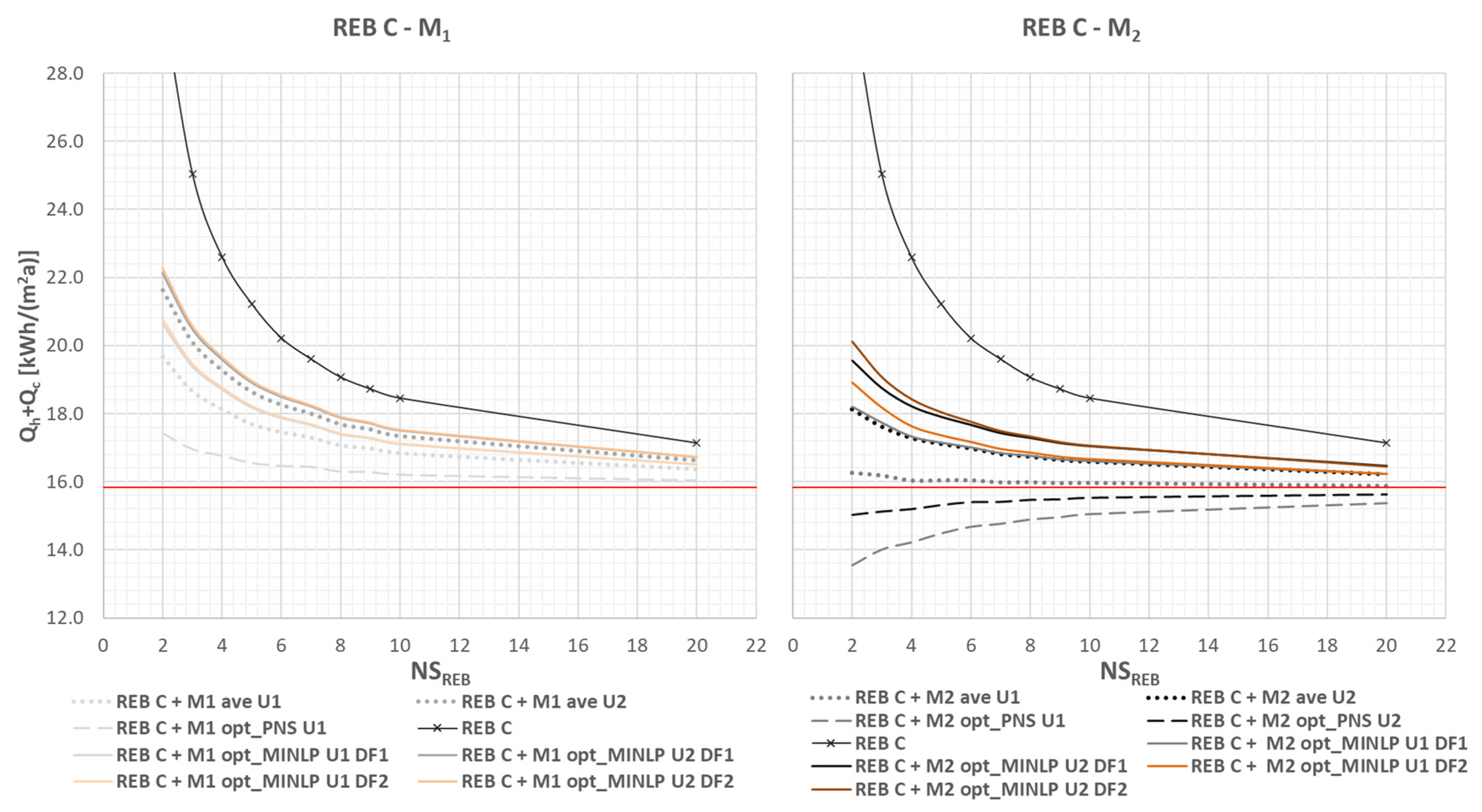
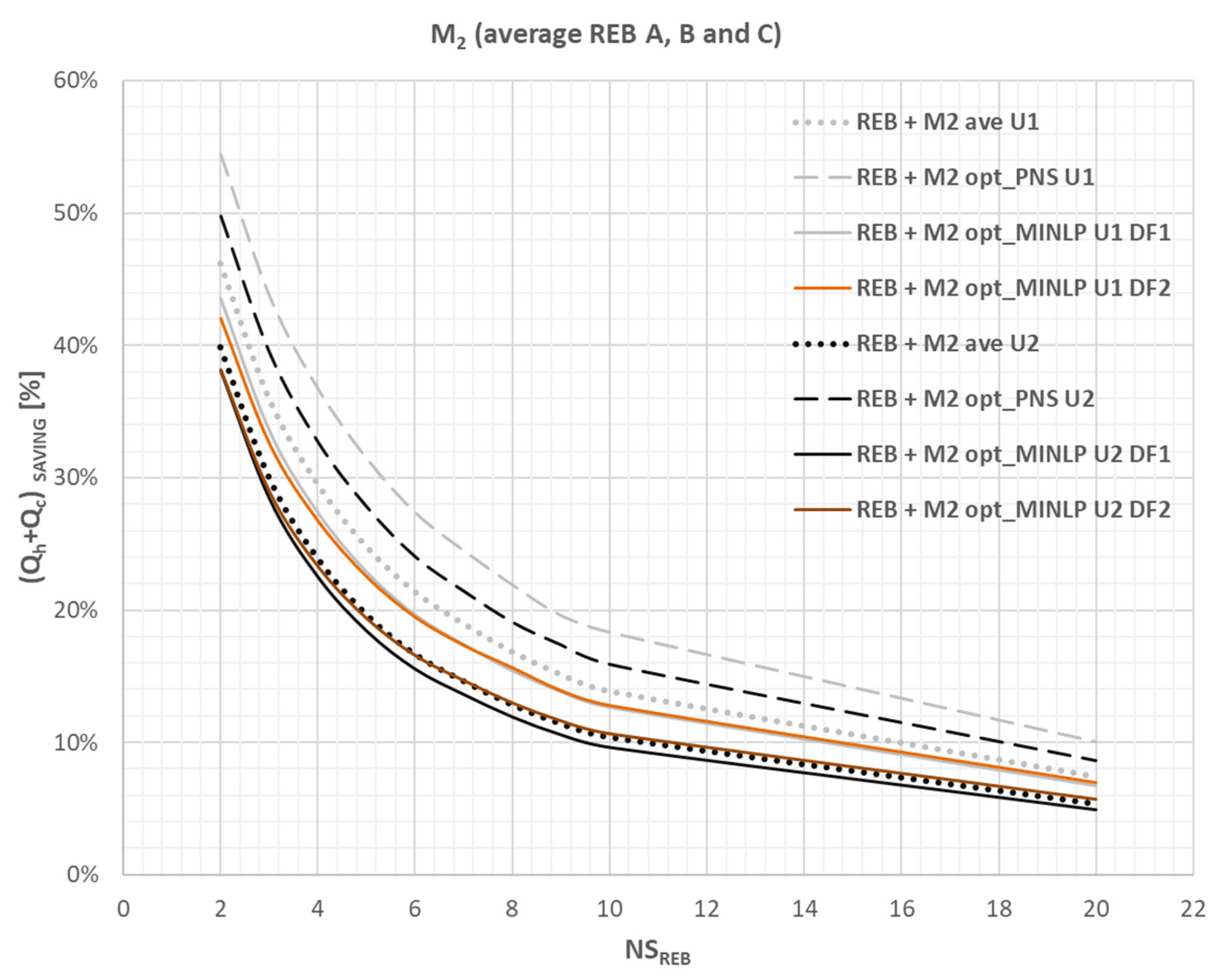
4.3. Methodology for Estimating Energy-Efficient Building Renovation with Building Upgrade Modules
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency. Net Zero RoadmapWe: A Global Pathway to Keep the 1.5 °C Goal in Reach—2023 Update; International Energy Agency: Paris, France, 2023. [Google Scholar]
- Hermelink, A.; Schimschar, S.; Offermann, M.; John, A.; Reiser, M.; Pohl, A.; Grözinger, J.; Esser, A.; Dunne, A.; Meeusen, T.; et al. Comprehensive Study of Building Energy Renovation Activities and the Uptake of Nearly Zero-Energy Buildings in the EU; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar]
- Aparicio-Gonzalez, E.; Domingo-Irigoyen, S.; Sánchez-Ostiz, A. Rooftop Extension as a Solution to Reach NZEB in Building Renovation. Application through Typology Classification at a Neighborhood Level. Sustain. Cities Soc. 2020, 57, 102109. [Google Scholar] [CrossRef]
- Economidou, M.; Atanasiu, B.; Despret, C.; Maio, J.; Nolte, I.; Rapf, O. Europe’s Buildings Under the Microscope: A Country-by-Country Review of the Performance of the Buildings; Buildings Performance Institute Europe BPIE: Brussels, Belgium, 2011. [Google Scholar]
- Amer, M.; Mustafa, A.; Teller, J.; Attia, S.; Reiter, S. A Methodology to Determine the Potential of Urban Densification through Roof Stacking. Sustain. Cities Soc. 2017, 35, 677–691. [Google Scholar] [CrossRef]
- Puglisi, V.; Invernale, A. Mansard Roof, Attics and Garrets and the Convenience of Investment in Order to Contain Land Consumption. In Procedia Engineering; Elsevier Ltd.: Amsterdam, The Netherlands, 2016; Volume 161, pp. 1428–1432. [Google Scholar]
- Pukhkal, V.; Murgul, V.; Garifullin, M. Reconstruction of Buildings with a Superstructure Mansard: Options to Reduce Energy Intensity of Buildings. In Procedia Engineering; Elsevier Ltd.: Amsterdam, The Netherlands, 2015; Volume 117, pp. 624–627. [Google Scholar]
- Jaksch, S.; Franke, A.; Österreicher, D.; Treberspurg, M. A Systematic Approach to Sustainable Urban Densification Using Prefabricated Timber-Based Attic Extension Modules. Energy Procedia 2016, 96, 638–649. [Google Scholar] [CrossRef][Green Version]
- Sundling, R.; Blomsterberg, Å.; Landin, A. Enabling Energy-Efficient Renovation: The Case of Vertical Extension to Buildings. Constr. Innov. 2019, 19, 2–14. [Google Scholar] [CrossRef]
- Žegarac Leskovar, V.; Premrov, M. Energy-Efficient Timber-Glass Houses; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Rissetto, R.; Pont, U.; Mahdavi, A. Performance Comparison of Timber-Based Assemblies and Other Construction Solutions for Rooftop Extensions. Int. Rev. Appl. Sci. Eng. 2019, 9, 153–161. [Google Scholar] [CrossRef]
- Artés, J.; Wadel, G.; Martí, N. Vertical Extension and Improving of Existing Buildings. Open Constr. Build. Technol. J. 2017, 11, 83–94. [Google Scholar] [CrossRef]
- Mikučioniene, R.; Martinaitis, V.; Keras, E. Evaluation of Energy Efficiency Measures Sustainability by Decision Tree Method. Energy Build. 2014, 76, 64–71. [Google Scholar] [CrossRef]
- Tan, B.; Yavuz, Y.; Otay, E.N.; Çamlibel, E. Optimal Selection of Energy Efficiency Measures for Energy Sustainability of Existing Buildings. Comput. Oper. Res. 2016, 66, 258–271. [Google Scholar] [CrossRef]
- Abdul Hamid, A.; Farsäter, K.; Wahlström, Å.; Wallentén, P. Literature Review on Renovation of Multifamily Buildings in Temperate Climate Conditions. Energy Build. 2018, 172, 414–431. [Google Scholar] [CrossRef]
- Bertone, E.; Sahin, O.; Stewart, R.A.; Zou, P.; Alam, M.; Blair, E. State-of-the-Art Review Revealing a Roadmap for Public Building Water and Energy Efficiency Retrofit Projects; The Gulf Organisation for Research and Development: Doha, Qatar, 2016; Volume 5, pp. 526–548. [Google Scholar]
- Oropeza-Perez, I.; Østergaard, P.A. Active and Passive Cooling Methods for Dwellings: A Review. Renew. Sustain. Energy Rev. 2018, 82, 531–544. [Google Scholar] [CrossRef]
- Galatioto, A.; Ciulla, G.; Ricciu, R. An Overview of Energy Retrofit Actions Feasibility on Italian Historical Buildings. Energy 2017, 137, 991–1000. [Google Scholar] [CrossRef]
- Webb, A.L. Energy Retrofits in Historic and Traditional Buildings: A Review of Problems and Methods. Renew. Sustain. Energy Rev. 2017, 77, 748–759. [Google Scholar] [CrossRef]
- Guarino, F.; Rincione, R.; Mateu, C.; Teixidó, M.; Cabeza, L.F.; Cellura, M. Renovation Assessment of Building Districts: Case Studies and Implications to the Positive Energy Districts Definition. Energy Build. 2023, 296, 113414. [Google Scholar] [CrossRef]
- Dodoo, A.; Yao Ayikoe Tettey, U.; Gustavsson, L. On Input Parameters, Methods and Assumptions for Energy Balance and Retrofit Analyses for Residential Buildings. Energy Build. 2017, 137, 76–89. [Google Scholar] [CrossRef]
- Niemelä, T.; Kosonen, R.; Jokisalo, J. Cost-Effectiveness of Energy Performance Renovation Measures in Finnish Brick Apartment Buildings. Energy Build. 2017, 137, 60–75. [Google Scholar] [CrossRef]
- Husiev, O.; Campos-Celador, A.; Álvarez-Sanz, M.; Terés-Zubiaga, J. Why District Renovation Is Not Leading the Race? Critical Assessment of Building Renovation Potential under Different Intervention Levels. Energy Build. 2023, 295, 113288. [Google Scholar] [CrossRef]
- Abdallah, M.; El-Rayes, K. Optimizing the Selection of Building Upgrade Measures to Minimize the Operational Negative Environmental Impacts of Existing Buildings. Build. Environ. 2015, 84, 32–43. [Google Scholar] [CrossRef]
- Andrić, I.; Pina, A.; Ferrão, P.; Lacarrière, B.; Le Corre, O. The Impact of Renovation Measures on Building Environmental Performance: An Emergy Approach. J. Clean. Prod. 2017, 162, 776–790. [Google Scholar] [CrossRef]
- Kang, Y.; Xu, W.; Wu, J.; Li, H.; Liu, R.; Lu, S.; Rong, X.; Xu, X.; Pang, F. Study on Comprehensive Whole Life Carbon Emission Reduction Potential and Economic Feasibility Impact Based on Progressive Energy-Saving Targets: A Typical Renovated Ultra-Low Energy Office. J. Build. Eng. 2022, 58, 105029. [Google Scholar] [CrossRef]
- Dominguez, C.; Kakkos, E.; Gross, D.; Hischier, R.; Orehounig, K. Renovated or Replaced? Finding the Optimal Solution for an Existing Building Considering Cumulative CO2 Emissions, Energy Consumption and Costs—A Case Study. Energy Build. 2024, 303, 113767. [Google Scholar] [CrossRef]
- Alonso, C.; Oteiza, I.; Frutos, B.; Martín-Consuegra, F.; Frutos, B. Methodological Proposal for Monitoring Energy Refurbishment. Indoor Environmental Quality in Two Case Studies of Social Housing in Madrid, Spain. Energy Build. 2017, 155, 492–502. [Google Scholar] [CrossRef]
- Du, L.; Leivo, V.; Prasauskas, T.; Turunen, M.; Kiviste, M.; Martuzevicius, D.; Haverinen-Shaughnessy, U. Energy Retrofits in Multi-Family Buildings in North-East Europe: The Impacts on Thermal Conditions. Energy Procedia 2015, 78, 860–864. [Google Scholar] [CrossRef][Green Version]
- Craft, W.; Ding, L.; Prasad, D.; Partridge, L.; Else, D. Development of a Regenerative Design Model for Building Retrofits. Procedia Eng. 2017, 180, 658–668. [Google Scholar] [CrossRef]
- Koops—Van Hoffen, H.E.; van Lenthe, F.J.; Poelman, M.P.; Droomers, M.; Borlée, F.; Vendrig—De Punder, Y.M.R.; Jambroes, M.; Kamphuis, C.B.M. Understanding the Mechanisms Linking Holistic Housing Renovations to Health and Well-Being of Adults in Disadvantaged Neighbourhoods: A Realist Review. Health Place 2023, 80, 102995. [Google Scholar] [CrossRef]
- Amer, M.; Attia, S. Roof Stacking: Learned Lessons from Architects; SBD Lab, Liege University: Liege, Belgium, 2017; ISBN 9782930909035. [Google Scholar]
- Floerke, P.; Weiß, S.; Stein, L.; Wagner, M. Catalogue of Typologies—Rooftop Extensions; Bauforumstahl e.V.: Düsseldorf, Germany, 2014. [Google Scholar]
- Tichelmann, K.U.; Groß, K. Wohnraumpotentiale Durch Aufstockungen; Technische Universität Darmstadt: Darmstadt, Germany, 2016. [Google Scholar]
- Jaksch, S.; Franke, A.; Treberspurg, M. A Timber Based Attic Extension System for Sustainable Urban Densification. In Proceedings of the WCTE 2016—World Conference on Timber Engineering, Vienna, Austria, 22–25 August 2016; pp. 5598–5606. [Google Scholar]
- Wijnants, L.; Allacker, K.; De Troyer, F. Environmental and Financial Life Cycle Assessment of “Open-Renovation-Systems”: Methodology and Case Study. Energy Procedia 2016, 96, 529–539. [Google Scholar] [CrossRef]
- Wijnants, L.; Allacker, K.; Troyer, F. De Life Cycle Assessment of Prefabricated Timber Frame ‘Open-Renovation-Systems’ for Rooftop Extensions. In Proceedings of the 33 International Conference PLEA2017: Design to Thrive, Edinburgh, Scotland, 2–5 July 2017; Volume I, pp. 1612–1619. [Google Scholar]
- Amoruso, F.M.; Schuetze, T. Hybrid Timber-Based Systems for Low-Carbon, Deep Renovation of Aged Buildings: Three Exemplary Buildings in the Republic of Korea. Build. Environ. 2022, 214, 108889. [Google Scholar] [CrossRef]
- Žegarac Leskovar, V.; Premrov, M. Integrative Approach to Comprehensive Building Renovations; Springer: Berlin/Heidelberg, 2019; ISBN 9783030114756. [Google Scholar]
- Amer, M.; Mustafa, A.; Attia, S. Conceptual Framework for Off-Site Roof Stacking Construction. J. Build. Eng. 2019, 26, 100873. [Google Scholar] [CrossRef]
- Argenziano, M.; Faiella, D.; Bruni, F.; De Angelis, C.; Fraldi, M.; Mele, E. Upwards—Vertical Extensions of Masonry Built Heritage for Sustainable and Antifragile Urban Densification. J. Build. Eng. 2021, 44, 102885. [Google Scholar] [CrossRef]
- Soikkeli, A. Additional Floors in Old Apartment Blocks. Energy Procedia 2016, 96, 815–823. [Google Scholar] [CrossRef]
- Jančar, J. Nadgradnje Obstoječih Stavb z Lahkimi Lesenimi Konstrukcijami s Stališča Potresne Odpornosti. Ph.D. Thesis, University of Maribor, Maribor, Slovenia, 2016. [Google Scholar]
- Špegelj, T. Development of the Timber-Glass Upgrade Module for the Purpose of Energy-Efficient Refurbishment of the Existing Multi-Family Buildings. Ph.D. Thesis, University of Maribor, Maribor, Slovenia, 2016. [Google Scholar]
- Špegelj, T.; Žegarac Leskovar, V.; Premrov, M. Application of the Timber-Glass Upgrade Module for Energy Refurbishment of the Existing Energy-Inefficient Multi-Family Buildings. Energy Build. 2016, 116, 362–375. [Google Scholar] [CrossRef]
- Špegelj, T.; Premrov, M.; Žegarac Leskovar, V. Development of the Timber-Glass Upgrade Module for the Purpose of Its Installation on Energy-Inefficient Buildings in the Refurbishment Process. Energy Effic. 2017, 10, 973–988. [Google Scholar] [CrossRef]
- Lešnik, M.; Premrov, M.; Žegarac Leskovar, V. Design Parameters of the Timber-Glass Upgrade Module and the Existing Building: Impact on the Energy-Efficient Refurbishment Process. Energy 2018, 162, 1125–1138. [Google Scholar] [CrossRef]
- Lešnik, M.; Žegarac Leskovar, V.; Premrov, M. Scientific Research Related to Building Renovation. In Integrative Approach to Comprehensive Building Renovations; Springer Verlag: Berlin/Heidelberg, 2019; pp. 69–159. [Google Scholar]
- Lešnik, M.; Kravanja, S.; Premrov, M.; Žegarac Leskovar, V. Optimal Design of Timber-Glass Upgrade Modules for Vertical Building Extension from the Viewpoints of Energy Efficiency and Visual Comfort. Appl. Energy 2020, 270, 115173. [Google Scholar] [CrossRef]
- SIST EN 17037:2019; Daylight of Buildings. Slovenski institut za standardizacijo (SIST): Ljubljana, Slovenia, 2019.
- Langston, C.; Wong, F.K.W.; Hui, E.C.M.; Shen, L.Y. Strategic Assessment of Building Adaptive Reuse Opportunities in Hong Kong. Build. Environ. 2008, 43, 1709–1718. [Google Scholar] [CrossRef]
- Ministrstvo Za Infrastrukturo. Dolgoročna Strategija Za Spodbujanje Naložb Energetske Prenove Stavb (Long-Term Strategy for Mobilising Investments in the Energy Renovation of Buildings) (DSEPS); Ministrstvo Za Infrastrukturo: Ljubljana, Slovenia, 2015.
- Lechner, N. Heating, Cooling, Lighting: Sustainable Design Methods for Architects, 4th ed.; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Šijanec Zavrl, M.; Rakušček, A.; Stegnar, G. Tipologija Stavb Energetska Učinkovitost in Tipične Stavbe v Sloveniji; Gradbeni Inštitut ZRMK d.o.o.: Ljubljana, Slovenia, 2012. [Google Scholar]
- Pinterić, M. Building Physics: From Physical Principles to International Standards; Springer International Publishing: Cham, Switzerland, 2017; ISBN 9783319574844. [Google Scholar]
- Grossmann, I.E.; Viswanathan, J. DICOPT—Discrete and Continuous Optimizer; Design Research Center (EDRC) at Carnegie Mellon University: Pittsburgh, PA, USA, 2002. [Google Scholar]
- Passive House Planning Package (PHPP). Available online: https://passivehouse.com/04_phpp/04_phpp.htm (accessed on 27 December 2024).
- SIST EN ISO 13790:2008; Energy Performance of Buildings—Calculation of Energy Use for Space Heating and Cooling. Slovenski Institut za Standardizacijo (SIST): Ljubljana, Slovenia, 2008.
- ISO 52016-1:2017; Energy performance of buildings—Energy needs for heating and cooling, internal temperatures and sensible and latent heat loads, Part 1: Calculation procedures. International Organization for Standardization (ISO): Geneva, Switzerland, 2017.
- Premrov, M.; Žigart, M.; Žegarac Leskovar, V. Influence of the Building Shape on the Energy Performance of Timber- Glass Buildings Located in Warm Climatic Regions. Energy 2018, 149, 496–504. [Google Scholar] [CrossRef]



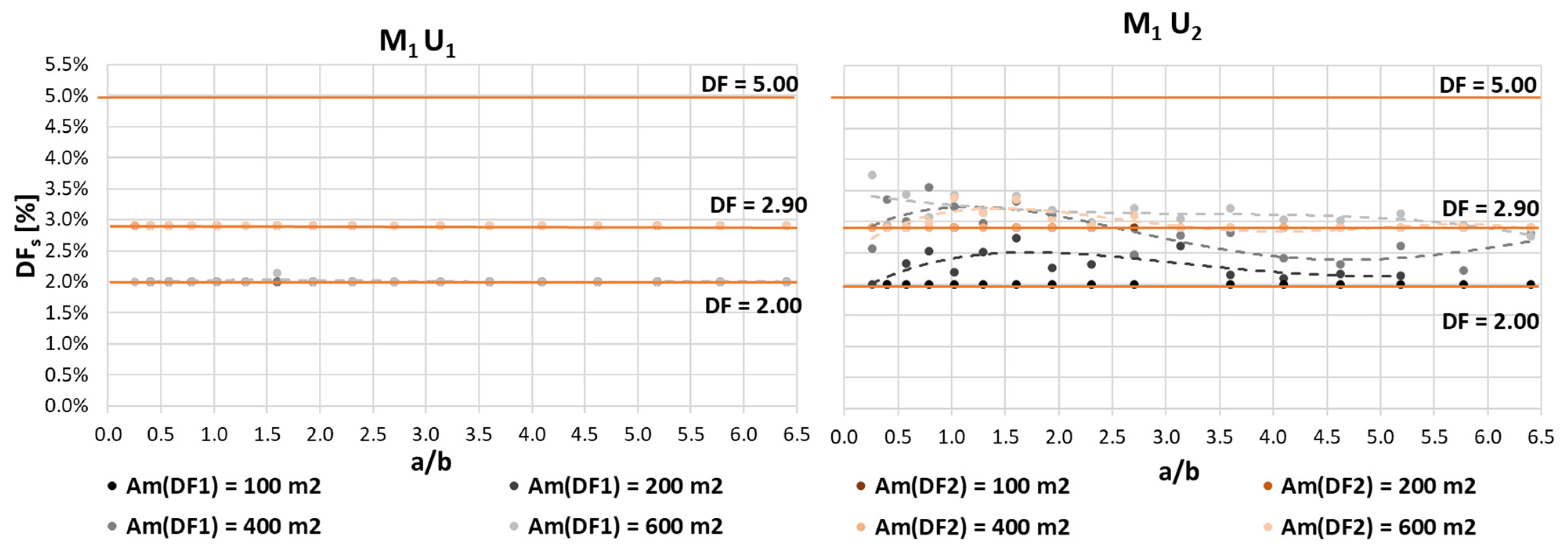
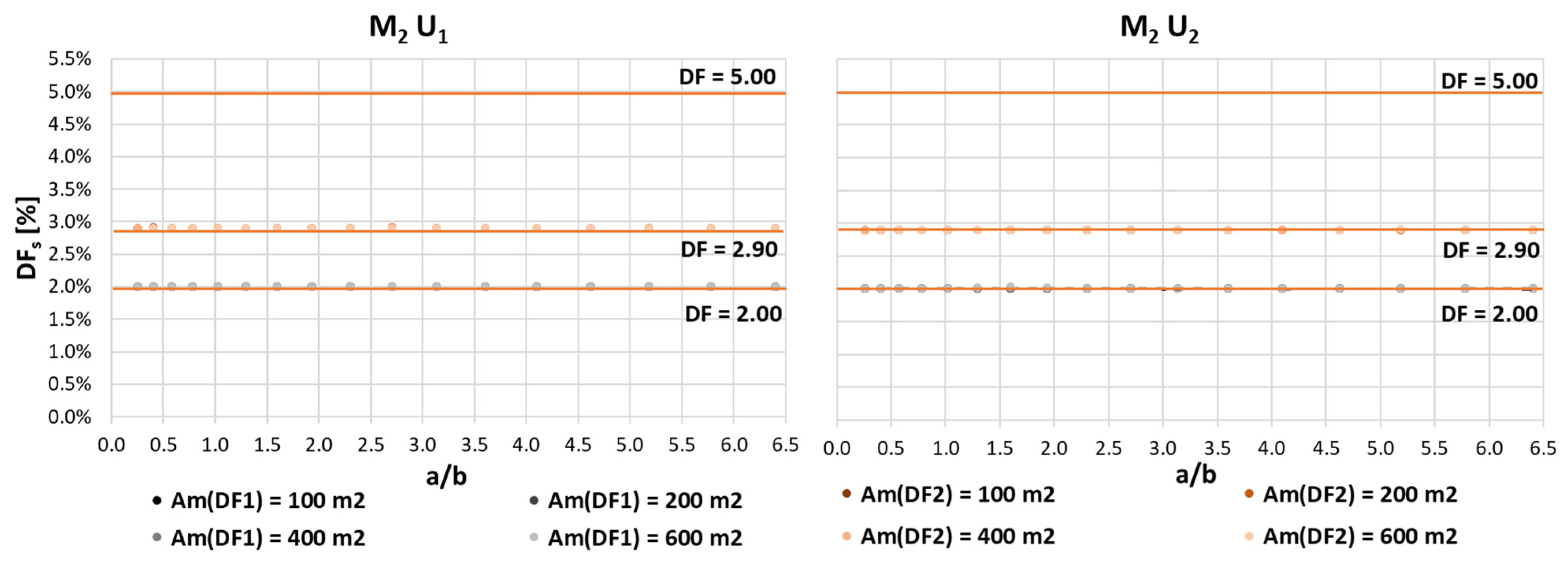
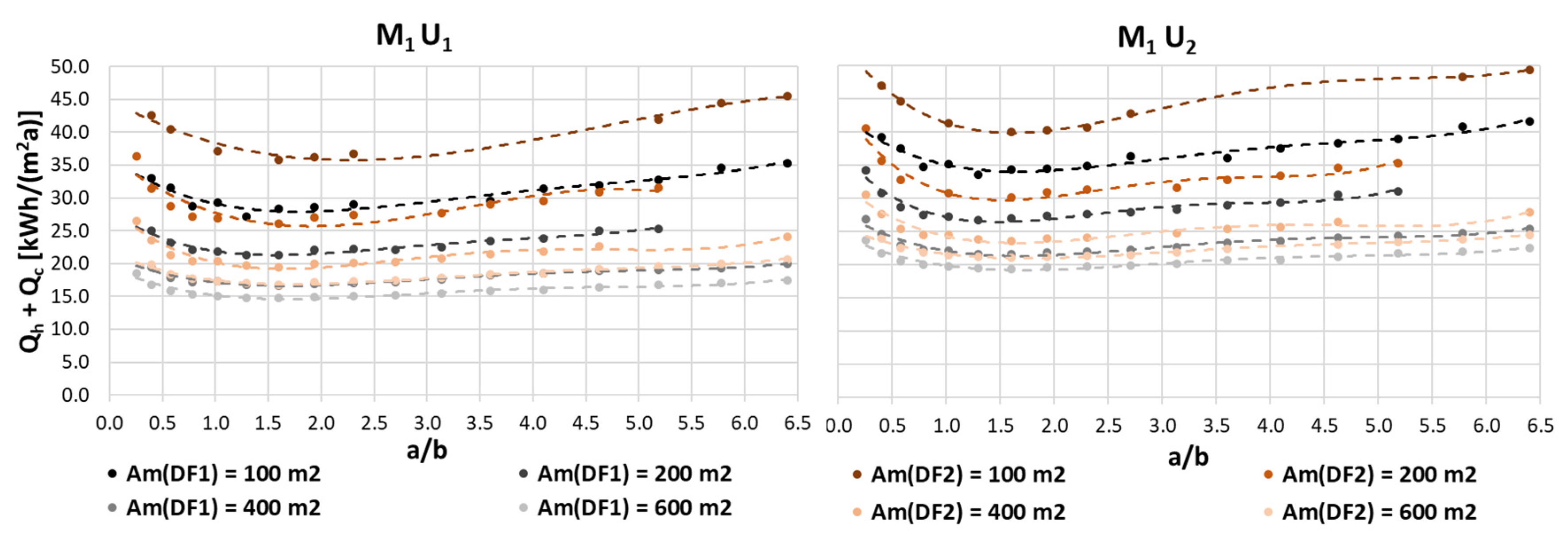

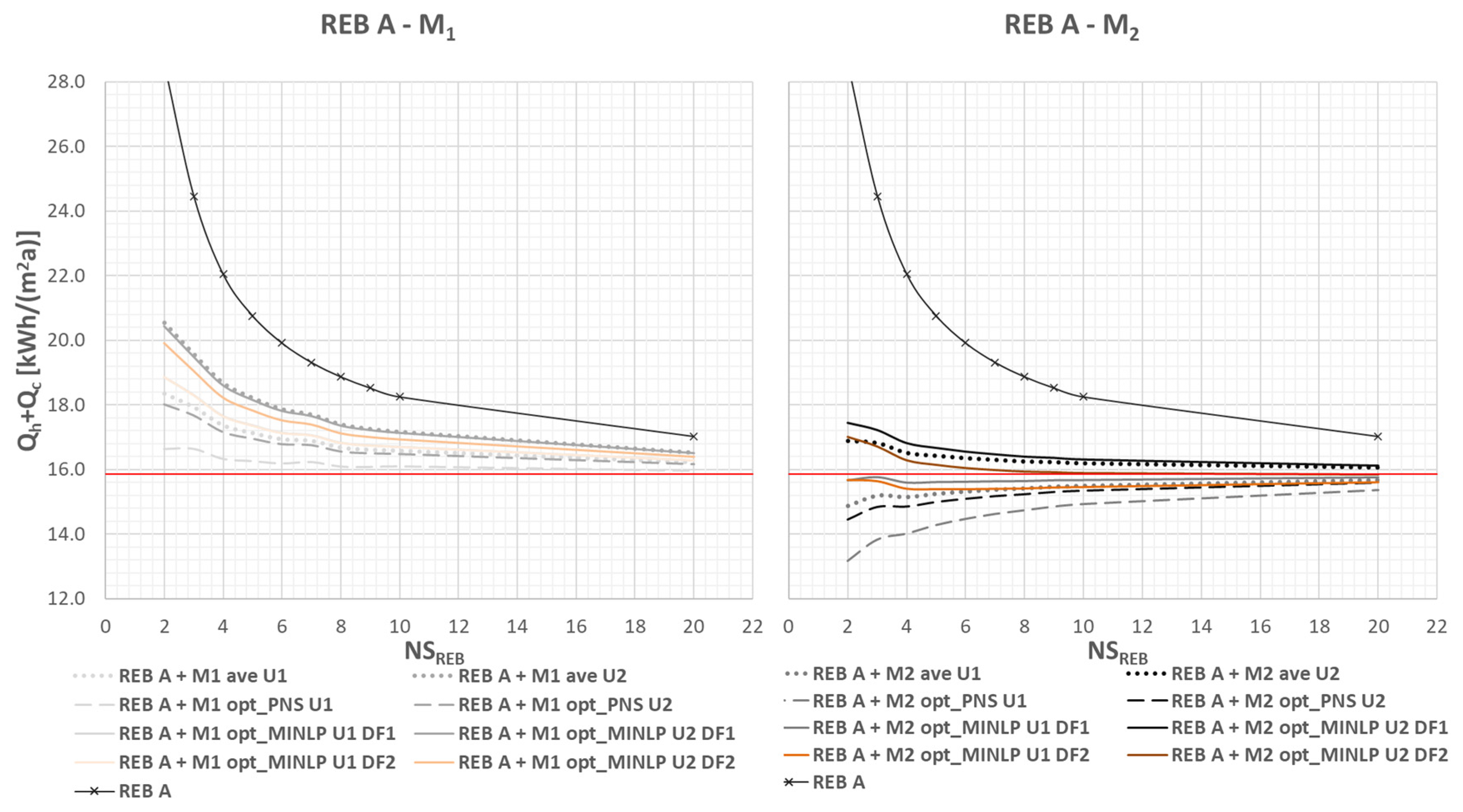


| Capital | Geographical Latitude (°) | Median External Diffuse Illuminance Ev,d,med | DF to Exceed 100 lx | DF to Exceed 300 lx | DF to Exceed 500 lx | DF to Exceed 750 lx |
|---|---|---|---|---|---|---|
| Ljubljana | 46.22 | 17,000 | 0.6% | 1.8% | 2.9% | 4.4% |
| Module Type | AGAWopt_MINLP_s (%) | AGAWopt_MINLP_n (%) | AGAWopt_MINLP_e (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| REB A | REB B | REB C | REB A | REB B | REB C | REB A | REB B | REB C | ||
| M1 | U1 | 34.5 | 32.3 | 35.0 | 34.5 | 32.3 | 35.0 | 33.7 | 34.7 | 34.6 |
| U2 | 46.9 | 46.6 | 44.5 | 36.3 | 34.0 | 36.9 | 35.6 | 36.4 | 36.5 | |
| M2 | U1 | 35.9 | 37.4 | 37.3 | 35.9 | 33.5 | 36.4 | 35.1 | 36.0 | 36.0 |
| U2 | 36.8 | 34.8 | 37.6 | 36.8 | 34.5 | 37.5 | 36.2 | 36.9 | 37.1 | |
| Module Type | AGAWopt_MINLP_s (%) | AGAWopt_MINLP_n (%) | AGAWopt_MINLP_e (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| REB A | REB B | REB C | REB A | REB B | REB C | REB A | REB B | REB C | ||
| M1 | U1 | 47.7 | 46.1 | 48.5 | 47.7 | 46.1 | 48.3 | 46.5 | 45.6 | 47.8 |
| U2 | 50.0 | 51.2 | 51.1 | 50.0 | 51.0 | 50.9 | 49.1 | 50.1 | 50.3 | |
| M2 | U1 | 49.7 | 50.6 | 50.3 | 49.7 | 46.4 | 50.2 | 48.4 | 49.8 | 49.6 |
| U2 | 50.8 | 49.2 | 51.8 | 50.9 | 45.4 | 51.6 | 50.0 | 48.5 | 51.0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lešnik Nedelko, M.; Kravanja, S.; Premrov, M.; Žegarac Leskovar, V. Development of Methodology for Estimation of Energy-Efficient Building Renovation Using Application of MINLP-Optimized Timber–Glass Upgrade Modules. Sustainability 2025, 17, 319. https://doi.org/10.3390/su17010319
Lešnik Nedelko M, Kravanja S, Premrov M, Žegarac Leskovar V. Development of Methodology for Estimation of Energy-Efficient Building Renovation Using Application of MINLP-Optimized Timber–Glass Upgrade Modules. Sustainability. 2025; 17(1):319. https://doi.org/10.3390/su17010319
Chicago/Turabian StyleLešnik Nedelko, Maja, Stojan Kravanja, Miroslav Premrov, and Vesna Žegarac Leskovar. 2025. "Development of Methodology for Estimation of Energy-Efficient Building Renovation Using Application of MINLP-Optimized Timber–Glass Upgrade Modules" Sustainability 17, no. 1: 319. https://doi.org/10.3390/su17010319
APA StyleLešnik Nedelko, M., Kravanja, S., Premrov, M., & Žegarac Leskovar, V. (2025). Development of Methodology for Estimation of Energy-Efficient Building Renovation Using Application of MINLP-Optimized Timber–Glass Upgrade Modules. Sustainability, 17(1), 319. https://doi.org/10.3390/su17010319









