Deposit–Refund System as a Strategy to Drive Sustainable Energy Transition on the Example of Poland
Abstract
:1. Introduction
- The application of the balanced center of gravity method (using rectangular, Euclidean and network metrics) enables the development of an effective reverse logistics model.
- Optimal placement of logistics centers in the deposit–refund system can reduce energy expenditures and transportation costs.
- A deposit–refund logistics model elaborated for Poland can be successfully adapted to other countries with a similar level of economic development.
- Development and presentation of a model for the distribution of logistics facilities for the newly created deposit–refund system in Poland, developed using the balanced center of gravity method, taking into account the minimization of energy inputs.
- Identification of key factors affecting the energy efficiency of the deposit–refund system, such as the geographic distribution of collection points and the intensity of material flows.
- Development of optimization methodologies in the context of green logistics with an emphasis on sustainability and environmental concerns.
- Proposing practical recommendations for decision-makers and designers of the deposit–refund system in Poland, allowing the effective planning of infrastructure and logistics operations.
2. Literature Review and Key Concepts
- achieving the required level of recycling of packaging waste;
- achieving the required level of separate collection of packaging and packaging waste;
- achieving the required levels of recycled plastic share by weight in single-use bottles of up to three liters:
- -
- from 2025—25% recycled plastic for PET bottles,
- -
- from 2030—30% of recycled plastics;
- reducing the number of caps as separate waste:
- -
- obligation to permanently fix plastic caps and lids with a capacity of up to three liters;
- reducing the problem of public space pollution.
- Entities introducing packaged beverages.
- Entities directly introducing packaged beverages.
- Retail outlets, wholesalers, and other collection points.
- Store customers.
- Deposit–refund system operator.
3. Materials and Methods
- Locations of waste supplier distribution centers: and forecast delivery volumes to the planned metering center .
- Location of the deposit–refund system operator’s sorting facility: and forecast capacity of facilities .
- Unit, calculated cost of carriage. The rate for routes from the i-th delivery points to the warehouse is denoted by , while the rate for routes from the warehouse to the j-th sales points is denoted by (e.g., for transporting 1 ton per 1 km).
- Volume of waste stream size .
- The distance in the rectangular metric was calculated using the following formula:
- The distance in the Euclidean metric was calculated from the following formula:
- The distance in the network metric was calculated based on the length of the road between facilities (according to the actual shape of the transportation infrastructure) .
4. Results
4.1. Waste Value Stream Assumptions in the Logistics Network
- For central Poland (:
- For southwestern Poland (:
- For northwestern Poland (:
4.2. Determination of the Location of Metering Centers Using the Balanced Center of Gravity Method Based on the Euclidean Metric
- For central Poland:
- For southwestern Poland:
- For northwestern Poland:
4.3. Determination of the Location of Metering Centers Using the Balanced Center of Gravity Method Based on the Rectangular Metric
- For southwestern Poland:
- For northwestern Poland:
4.4. Determination of the Location of Metering Centers Using the Balanced Center of Gravity Method Based on the Network Metric (According to the Actual Shape of the Transportation Infrastructure)
- For central Poland:
- For southwestern Poland:
- For northwestern Poland:
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bórawski, P.; Wyszomierski, R.; Bełdycka-Bórawska, A.; Mickiewicz, B.; Kalinowska, B.; Dunn, J.W.; Rokicki, T. Development of Renewable Energy Sources in the European Union in the Context of Sustainable Development Policy. Energies 2022, 15, 1545. [Google Scholar] [CrossRef]
- Fatimah, Y.A.; Govindan, K.; Murniningsih, R.; Setiawan, A. Industry 4.0 based sustainable circular economy approach for smart waste management system to achieve sustainable development goals: A case study of Indonesia. J. Clean. Prod. 2020, 269, 122263. [Google Scholar] [CrossRef]
- Fan, Z.; Luo, Y.; Liang, N.; Li, S. A Novel Sustainable Reverse Logistics Network Design for Electric Vehicle Batteries Considering Multi-Kind and Multi-Technology. Sustainability 2023, 15, 10128. [Google Scholar] [CrossRef]
- Al-Thani, H.; Koç, M.; Isaifan, R.J.; Bicer, Y. A Review of the Integrated Renewable Energy Systems for Sustainable Urban Mobility. Sustainability 2022, 14, 10517. [Google Scholar] [CrossRef]
- Bataille, C.G. Physical and policy pathways to net-zero emissions industry. Wiley Interdiscip. Rev. Clim. Chang. 2020, 11, e633. [Google Scholar] [CrossRef]
- Vågerö, O.; Zeyringer, M. Can we optimise for justice? Reviewing the inclusion of energy justice in energy system optimisation models. Energy Res. Soc. Sci. 2023, 95, 102913. [Google Scholar] [CrossRef]
- Yu, J.; Hao, S.; Han, J. Optimizing Virtual Energy Hub’s for Enhanced Market Participation and Operational Resilience. Eksploat. Niezawodn.–Maint. Reliab. 2025, 27, 193171. [Google Scholar] [CrossRef]
- Frampton, D.M.F.; Haque, N.; Verrelli, D.I.; Dumsday, G.J.; Lee-Chang, K.J. Process Design Guided by Life Cycle Assessment to Reduce Greenhouse Gas-Related Environmental Impacts of Food Processing. Sustainability 2021, 13, 6864. [Google Scholar] [CrossRef]
- Gholami, M.; Karimi Ghaleh Jough, F.; Gholami, A. Streamlining Smart Grids Reliability Assessment: An Innovative Mapping Approach. Eksploat. Niezawodn.–Maint. Reliab. 2025, 27, 195258. [Google Scholar] [CrossRef]
- Coronado, M.; Kadoch, B.; Contreras, J.; Kristjanpoller, F. Reliability and availability modelling of a retrofitted Diesel-based cogeneration system for heat and hot water demand of an isolated Antarctic base. Eksploat. Niezawodn.–Maint. Reliab. 2023, 25, 169779. [Google Scholar] [CrossRef]
- Zarębski, A.; Zarębska, J.; Marosek, K. Implementation of the Deposit System in Poland as a Tool for Implementing the Circular Economy. Energies 2024, 17, 5489. [Google Scholar] [CrossRef]
- Borucka, A.; Kozłowski, E.; Antosz, K.; Parczewski, R. A New Approach to Production Process Capability Assessment for Non-Normal Data. Appl. Sci. 2023, 13, 6721. [Google Scholar] [CrossRef]
- Borucka, A.; Grzelak, M. Application of Logistic Regression for Production Machinery Efficiency Evaluation. Appl. Sci. 2019, 9, 4770. [Google Scholar] [CrossRef]
- Ma, R.; Zhao, Y.; Li, J. Enhancing Distribution System Flexibility through Network Restructuring and Optimal Planning of Distributed Energy Resources. Eksploat. Niezawodn.–Maint. Reliab. 2025, 27, 19065. [Google Scholar] [CrossRef]
- Szymańska, E.J.; Mroczek, R.; Drożdż, J. A Closed-Loop Economy in the Meat Industry for Generating Alternative Energy from Biogas Plants. Energies 2024, 17, 6172. [Google Scholar] [CrossRef]
- Liu, Y. Enhancing Flexibility and Reliability in Smart Distribution Networks: A Self-Healing Approach. Eksploat. Niezawodn.–Maint. Reliab. 2025, 27, 195269. [Google Scholar] [CrossRef]
- Bibri, S.E. The eco-city and its core environmental dimension of sustainability: Green energy technologies and their integration with data-driven smart solutions. Energy Inf. 2020, 3, 4. [Google Scholar] [CrossRef]
- Krzywda, D. Closing the loop-packaging waste management and the deposit system in Poland. Pol. J. Manag. Stud. 2022, 26, 233–247. [Google Scholar] [CrossRef]
- Broniewicz, E.; Larsson, A.; Piontek, W.; Sidorczuk-Pietraszko, E. Economic effects of introducing a deposit-return system for packaging in Poland. Econ. Environ. 2023, 86, 169–185. [Google Scholar] [CrossRef]
- Zhou, K.; Liu, Q.; Feng, J.; Chang, T.; Liu, J. Comprehensive environmental performance of bottle-to-bottle recycling of PET bottles based on deposit-refund system in China. Waste Manag. 2023, 172, 90–100. [Google Scholar] [CrossRef]
- Bobek-Nagy, J.; Kurdi, R.; Kovács, A.; Simon-Stőger, L.; Szigeti, M.; Varga, C. How introduction of deposit-refund system (DRS) changes recycling of non-drinking bottle PET wastes. Express Polym. Lett. 2023, 17, 1166–1179. [Google Scholar] [CrossRef]
- Martinho, G.; Santos, P.; Alves, A.; Ramos, M. Indicators and characteristics of PET packaging collected in a Deposit and Refund System pilot project. Heliyon 2024, 10, e25182. [Google Scholar] [CrossRef] [PubMed]
- Ustawa z dnia 13 lipca 2023 r. o zmianie ustawy o gospodarce opakowaniami i odpadami opakowaniowymi oraz innych ustaw (Dz.U. z 2023 r. poz. 1852) zwana ustawą kaucyjną. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20230001852 (accessed on 9 December 2024).
- Document 32019L0904; Directive (EU) 2019/904 of the European Parliament and of the Council of 5 June 2019 on the Reduction of the Impact of Certain Plastic Products on the Environment. EU: New York, NY, USA, 2019.
- Schnurr, R.E.; Alboiu, V.; Chaudhary, M.; Corbett, R.A.; Quanz, M.E.; Sankar, K.; Srain, H.S.; Thavarajah, V.; Xanthos, D.; Walker, T.R. Reducing marine pollution from single-use plastics (SUPs): A review. Mar. Pollut. Bull. 2018, 137, 157–171. [Google Scholar] [CrossRef]
- Chen, Y.; Awasthi, A.K.; Wei, F.; Tan, Q.; Li, J. Single-use plastics: Production, usage, disposal, and adverse impacts. Sci. Total Environ. 2021, 752, 141772. [Google Scholar] [CrossRef]
- System kaucyjny w Polsce ogłoszony w Dzienniku Ustaw. Available online: https://rekopol.pl/newsletter/system-kaucyjny-w-polsce-ogloszony-w-dzienniku-ustaw/ (accessed on 10 December 2024).
- Agnusdei, G.P.; Gnoni, M.G.; Sgarbossa, F. Are deposit-refund systems effective in managing glass packaging? State of the art and future directions in Europe. Sci. Total Environ. 2022, 851, 158256. [Google Scholar] [CrossRef]
- System kaucyjny w Europie. Available online: https://kaucyjny.pl/przyklady-z-zagranicy/ (accessed on 10 December 2024).
- Zhou, G.; Gu, Y.; Wu, Y.; Gong, Y.; Mu, X.; Han, H.; Chang, T. A systematic review of the deposit-refund system for beverage packaging: Operating mode, key parameter and development trend. J. Clean. Prod. 2020, 251, 119660. [Google Scholar] [CrossRef]
- Kozar, Ł.J. The financial sector and sustainable development-a review of selected environmental practices implemented in financial institutions operating in Poland between 2016 and 2020. Finans. Prawo Finans. 2022, 1, 143–157. [Google Scholar] [CrossRef]
- Dmitrieva, D.; Romasheva, N. Sustainable development of oil and gas potential of the Arctic and its shelf zone: The role of innovations. J. Mar. Sci. Eng. 2020, 8, 1003. [Google Scholar] [CrossRef]
- Zabaniotou, A. Redesigning a bioenergy sector in EU in the transition to circular waste-based Bioeconomy-A multidisciplinary review. J. Clean. Prod. 2018, 177, 197–206. [Google Scholar] [CrossRef]
- Vukovic, N.; Makogon, E. Waste-to-Energy Generation: Complex Efficiency Analysis of Modern Technologies. Sustainability 2022, 14, 13814. [Google Scholar] [CrossRef]
- Reijonen, H.; Bellman, S.; Murphy, J.; Kokkonen, H. Factors related to recycling plastic packaging in Finland’s new waste management scheme. Waste Manag. 2021, 131, 88–97. [Google Scholar] [CrossRef] [PubMed]
- Kozłowski, E.; Borucka, A.; Oleszczuk, P.; Leszczyński, N. Evaluation of readiness of the technical system using the semi-Markov model with selected sojourn time distributions. Eksploat. Niezawodn.–Maint. Reliab. 2024, 26, 191545. [Google Scholar] [CrossRef]
- Oszczypała, M.; Ziółkowski, J.; Małachowski, J. Semi-Markov approach for reliability modelling of light utility vehicles. Eksploat. Niezawodn.–Maint. Reliab. 2023, 25, 161859. [Google Scholar] [CrossRef]
- Borucka, A.; Kozłowski, E.; Parczewski, R.; Antosz, K.; Gil, L.; Pieniak, D. Supply Sequence Modelling Using Hidden Markov Models. Appl. Sci. 2023, 13, 231. [Google Scholar] [CrossRef]
- Marchi, B.; Zanoni, S. Supply Chain Management for Improved Energy Efficiency: Review and Opportunities. Energies 2017, 10, 1618. [Google Scholar] [CrossRef]
- Park, A.; Li, H. The Effect of Blockchain Technology on Supply Chain Sustainability Performances. Sustainability 2021, 13, 1726. [Google Scholar] [CrossRef]
- Xie, P.; Li, C. Dynamic Modeling and Optimization of Energy Storage in Peer-to-Peer Energy Trading Systems. Eksploat. Niezawodn.–Maint. Reliab. 2025, 27, 195761. [Google Scholar] [CrossRef]
- Silva, C.; Ribeiro, R.; Gomes, P. Algorithmic Optimization Techniques for Operations Research Problems. In Data Analytics in System Engineering: Proceedings of the Computational Methods in Systems and Software; Springer: Cham, Switzerland, 2023; pp. 331–339. [Google Scholar] [CrossRef]
- Rahmaniperchkolaei, B.; Taeeb, Z.; Shahriari, M.; Lotfi, F.H.; Saati, S. Applied optimization problems. In Decision-Making Models; Academic Press: Washington, DC, USA, 2024; pp. 237–299. [Google Scholar] [CrossRef]
- Soleimani, H.; Kannan, G. A hybrid particle swarm optimization and genetic algorithm for closed-loop supply chain network design in large-scale networks. Appl. Math. Model. 2015, 39, 3990–4012. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A comprehensive survey on particle swarm optimization algorithm and its applications. Math. Probl. Eng. 2015, 2015, 931256. [Google Scholar] [CrossRef]
- Gad, A.G. Particle swarm optimization algorithm and its applications: A systematic review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Tako, A.A.; Robinson, S. The application of discrete event simulation and system dynamics in the logistics and supply chain context. Decis. Support Syst. 2012, 52, 802–815. [Google Scholar] [CrossRef]
- Gyulai, D.; Bergmann, J.; Lengyel, A.; Kádár, B.; Czirkó, D. Simulation-based digital twin of a complex shop-floor logistics system. In Proceedings of the 2020 Winter Simulation Conference (WSC), Orlando, FL, USA, 14–18 December 2020; IEEE: New York, NY, USA, 2020; pp. 1849–1860. [Google Scholar] [CrossRef]
- Frej, D.; Jaśkiewicz, M. Comparison of Volunteers’ Head Displacement with Computer Simulation—Crash Test with Low Speed of 20 km/h. Sensors 2022, 22, 9720. [Google Scholar] [CrossRef] [PubMed]
- Coelho, F.; Relvas, S.; Barbosa-Póvoa, A.P. Simulation-based decision support tool for in-house logistics: The basis for a digital twin. Comput. Ind. Eng. 2021, 153, 107094. [Google Scholar] [CrossRef]
- Li, X.; Song, K.; Shi, J. Degradation generation and prediction based on machine learning methods: A comparative study. Eksploat. Niezawodn.–Maint. Reliab. 2025, 27, 192168. [Google Scholar] [CrossRef]
- Azzedine, A.; Nouri, F.Z.; Bouhouche, S. A new hybrid approach based on probability distribution and an improved machine learning for multivariate risk assessment. Diagnostyka 2024, 25, 2024213. [Google Scholar] [CrossRef]
- Kozłowski, M.; Racewicz, S.; Wierzbicki, S. Image Analysis in Autonomous Vehicles: A Review of the Latest AI Solutions and Their Comparison. Appl. Sci. 2024, 14, 8150. [Google Scholar] [CrossRef]
- Rane, N.L.; Desai, P.; Rane, J.; Paramesha, M. Artificial intelligence, machine learning, and deep learning for sustainable and resilient supply chain and logistics management. In Trustworthy Artificial Intelligence in Industry and Society; Deep Science Publishing: London, UK, 2024; pp. 156–184. [Google Scholar] [CrossRef]
- Abdullah, A.G.; Ibrahim, M.A.; Ibrahim, W.K. Detection and identification of fault in transmission lines based on ANN. Diagnostyka 2024, 25, 2024206. [Google Scholar] [CrossRef]
- Retail Market 2021. Structure, Number of Establishments, Trends. Available online: https://foodfakty.pl/rynek-detaliczny-2021-struktura-liczebnosc-placowek-trendy-wyniki-badania-liczebnosci-i-struktury-handlu-w-czerwcu-2021-wg-nielseniq (accessed on 11 December 2024).
- Gawałkiewicz, M. Implementation of the Deposit-Refund System in Poland Using Remondis as an Example. Bachelor’s Thesis, Warszawa, Poland, 2024. [Google Scholar]
- Krawczyk, S. Quantitative Methods in Logistics (Enterprises); t. II; C.H. BECK: Warszawa, Poland, 2021. [Google Scholar]
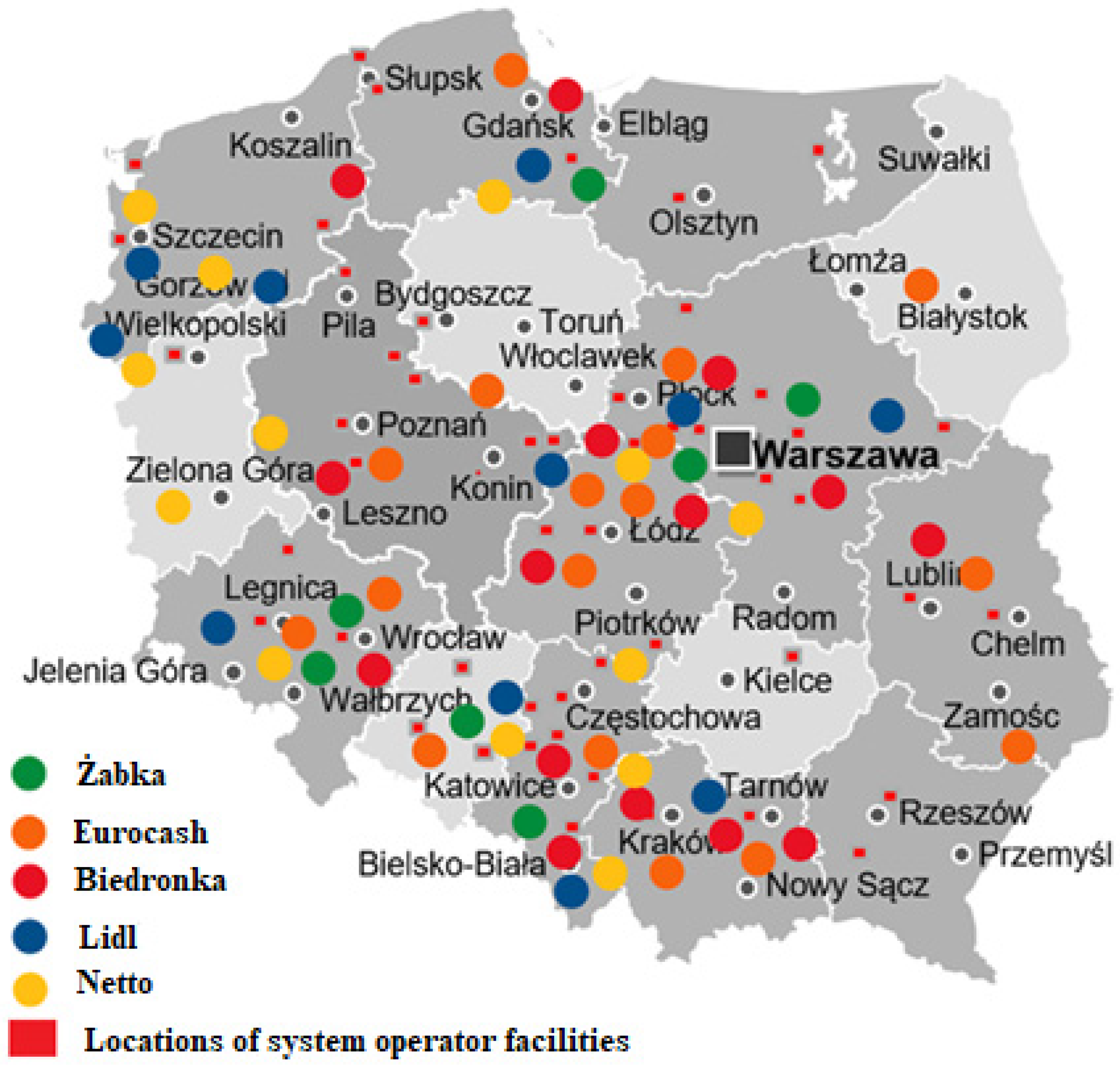
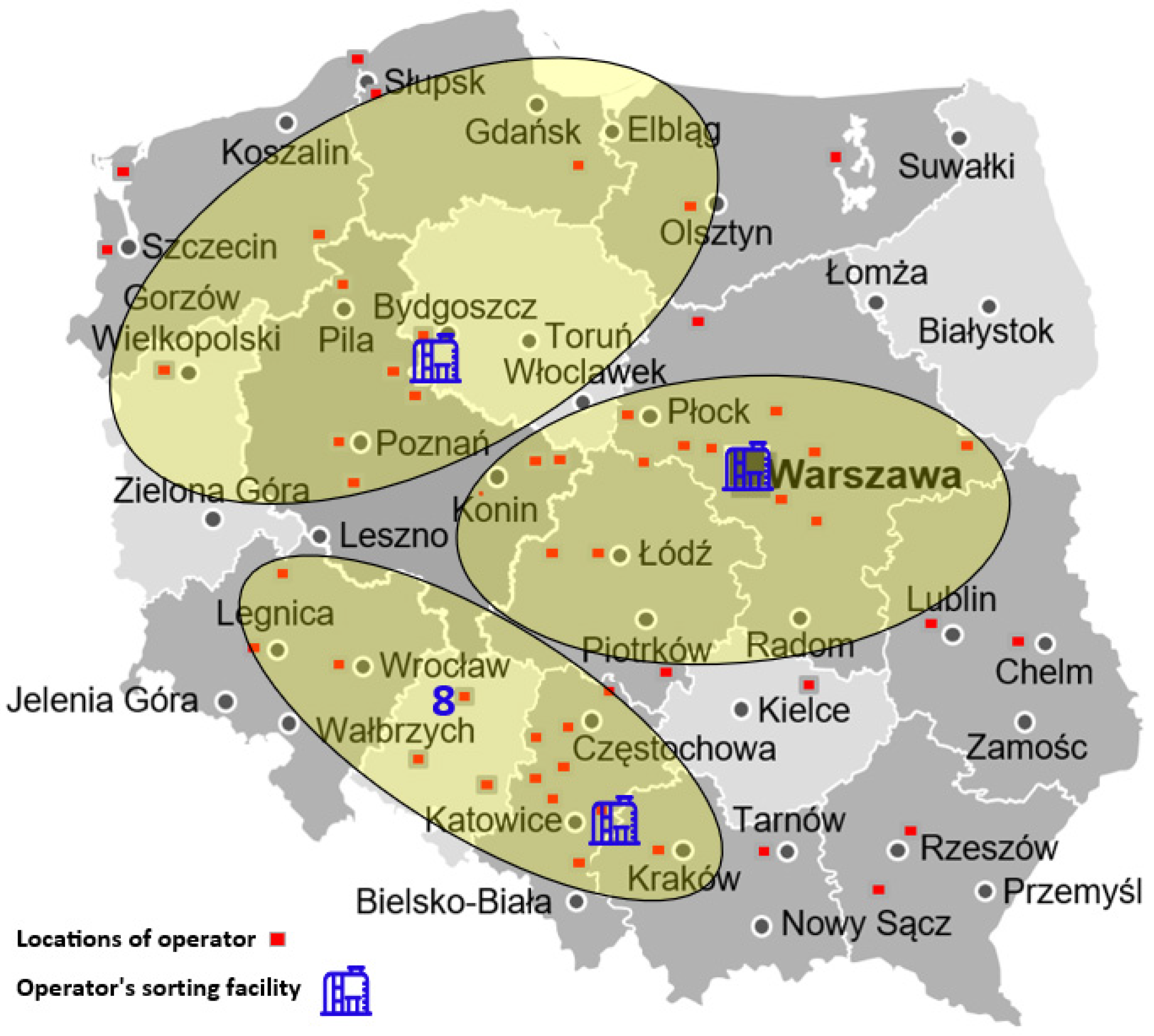
| Item | Type of Packaging | Levels of Separate Collection of Packaging and Packaging Waste in % by Year | ||||
|---|---|---|---|---|---|---|
| 2025 | 2026 | 2027 | 2028 | 2029 and Beyond | ||
| 1 | Disposable plastic beverage bottles up to and including 3 L with plastic caps and lids, excluding glass or metal beverage bottles with plastic caps and lids | 77 | 81 | 84 | 87 | 90 |
| 2 | Metal cans with a capacity of up to 1 L | 77 | 81 | 84 | 87 | 90 |
| 3 | Reusable glass bottles with a capacity of up to one and a half liters | 77 | 81 | 84 | 87 | 90 |
| Name of Locality | Number of Distribution Centers | Waste Weight [t] per Month | Longitude x | Latitude y |
|---|---|---|---|---|
| Suppliers | ||||
| Central Poland | ||||
| Płock | 5 | 110 | 19.70 | 52.55 |
| Konin | 4 | 88 | 18.25 | 52.23 |
| Warszawa | 8 | 176 | 21.07 | 52.23 |
| Lublin | 2 | 44 | 22.57 | 51.25 |
| Łódź | 4 | 88 | 19.46 | 51.77 |
| Southwestern Poland | ||||
| Legnica | 3 | 66 | 16.16 | 51.21 |
| Kraków | 5 | 110 | 19.94 | 50.06 |
| Wrocław | 3 | 66 | 17.04 | 51.11 |
| Częstochowa | 7 | 154 | 19.11 | 50.81 |
| Wałbrzych | 3 | 66 | 16.28 | 50.77 |
| Northwestern Poland | ||||
| Elbląg | 5 | 110 | 19.40 | 54.16 |
| Szczecin | 6 | 132 | 14.55 | 53.43 |
| Poznań | 4 | 88 | 16.93 | 52.41 |
| Gorzów Wielkopolski | 2 | 44 | 15.24 | 52.73 |
| Toruń | 3 | 66 | 18.60 | 53.01 |
| Recipients | ||||
| Sorting plant Warsaw | 1 | 506 | 21.09 | 52.18 |
| Sorting plant Gliwice | 1 | 462 | 18.67 | 50.29 |
| Sorting plant Bydgoszcz | 1 | 440 | 18.00 | 53.12 |
| Name of Locality | Waste Weight [t] per Month | x | y | (xi − x1)2 | (y1 − yi)2 | dj1 | dj1 [km] |
|---|---|---|---|---|---|---|---|
| Central Poland | |||||||
| Płock | 110 | 19.70 | 52.55 | 1.36 | 0.10 | 1.21 | 134.41 |
| Konin | 88 | 18.25 | 52.23 | 6.83 | 0.00 | 2.61 | 290.61 |
| Warszawa | 176 | 21.07 | 52.23 | 0.04 | 0.00 | 0.21 | 22.89 |
| Lublin | 44 | 22.57 | 51.25 | 2.91 | 0.95 | 1.96 | 218.21 |
| Łódź | 88 | 19.46 | 51.77 | 1.98 | 0.21 | 1.48 | 164.57 |
| Sorting plant Warsaw | 506 | 21.09 | 52.18 | 0.04 | 0.00 | 0.21 | 22.89 |
| Total: | 853.59 | ||||||
| Southwestern Poland | |||||||
| Legnica | 66 | 16.16 | 51.21 | 6.19 | 0.68 | 2.62 | 291.29 |
| Kraków | 110 | 19.94 | 50.06 | 1.66 | 0.10 | 1.33 | 147.83 |
| Wrocław | 66 | 17.04 | 51.11 | 2.60 | 0.52 | 1.77 | 196.36 |
| Częstochowa | 154 | 19.11 | 50.81 | 0.22 | 0.18 | 0.63 | 70.23 |
| Wałbrzych | 66 | 16.28 | 50.77 | 5.59 | 0.14 | 2.40 | 266.35 |
| Sorting plant Gliwice | 462 | 18.67 | 50.29 | 0.00 | 0.01 | 0.09 | 10.37 |
| Total: | 982.42 | ||||||
| Northwestern Poland | |||||||
| Elbląg | 110 | 19.40 | 54.16 | 2.54 | 1.10 | 1.91 | 212.09 |
| Szczecin | 132 | 14.55 | 53.43 | 10.62 | 0.10 | 3.27 | 364.13 |
| Poznań | 88 | 16.93 | 52.41 | 0.78 | 0.49 | 1.13 | 125.20 |
| Gorzów Wielkopolski | 44 | 15.24 | 52.73 | 6.60 | 0.14 | 2.60 | 288.84 |
| Toruń | 66 | 18.60 | 53.01 | 0.63 | 0.01 | 0.80 | 89.08 |
| Sorting plant Bydgoszcz | 440 | 18.00 | 53.12 | 0.04 | 0.00 | 0.19 | 21.22 |
| Total: | 1100.55 | ||||||
| No. | Location of the Facility | xi | vi | vr |
|---|---|---|---|---|
| 1 | Konin | 18.25 | 88 | 88.00 |
| 2 | Łódź | 19.46 | 88 | 176.00 |
| 3 | Płock | 19.70 | 110 | 286.00 |
| 4 | Warszawa | 21.07 | 176 | 462.00 |
| 5 | Sorting plant Warsaw | 21.09 | 506 | 968.00 |
| 6 | Lublin | 22.57 | 44 | 1012.00 |
| No. | Location of the Facility | xi | vi | vr |
|---|---|---|---|---|
| 1 | Lublin | 51.25 | 44 | 44.00 |
| 2 | Łódź | 51.77 | 88 | 132.00 |
| 3 | Konin | 52.23 | 88 | 220.00 |
| 4 | Warszawa | 52.23 | 176 | 396.00 |
| 5 | Warszawa | 52.18 | 506 | 902.00 |
| 6 | Płock | 52.55 | 110 | 1012.00 |
| No. | Location of the Facility | xi | yi | |x1 − xj| | |y1 − yj| | di [Degrees]. | di [km]. |
|---|---|---|---|---|---|---|---|
| 1 | Płock | 19.70 | 52.55 | 1.37 | 0.32 | 1.70 | 188.49 |
| 2 | Konin | 18.25 | 52.23 | 2.82 | 0.01 | 2.83 | 314.41 |
| 3 | Warszawa | 21.07 | 52.23 | 0.00 | 0.01 | 0.01 | 1.34 |
| 4 | Lublin | 22.57 | 51.25 | 1.50 | 0.97 | 2.47 | 274.66 |
| 5 | Łódź | 19.46 | 51.77 | 1.62 | 0.45 | 2.07 | 230.13 |
| 6 | Warszawa | 21.09 | 52.18 | 0.01 | 0.04 | 0.05 | 5.76 |
| Total: | 1014.79 | ||||||
| Name of Locality | Waste Weight [t] per Month | x | y | lj [km] |
|---|---|---|---|---|
| Central Poland | ||||
| Płock | 110 | 19.70 | 52.55 | 84.30 |
| Konin | 88 | 18.25 | 52.23 | 197.00 |
| Warszawa | 176 | 21.07 | 52.23 | 44.30 |
| Lublin | 44 | 22.57 | 51.25 | 208.00 |
| Łódź | 88 | 19.46 | 51.v77 | 111.00 |
| Sortownia Warszawa | 506 | 21.09 | 52.v18 | 47.00 |
| Suma | 691.60 | |||
| Southwestern Poland | ||||
| Legnica | 66 | 16.16 | 51.21 | 210.00 |
| Kraków | 110 | 19.94 | 50.06 | 149.00 |
| Wrocław | 66 | 17.04 | 51.11 | 148.00 |
| Częstochowa | 154 | 19.11 | 50.81 | 71.60 |
| Wałbrzych | 66 | 16.28 | 50.77 | 218.00 |
| Sortownia Gliwice | 462 | 18.67 | 50.29 | 43.40 |
| Suma | 840.00 | |||
| Northwestern Poland | ||||
| Elbląg | 110 | 19.40 | 54.16 | 260.00 |
| Szczecin | 132 | 14.55 | 53.43 | 224.00 |
| Poznań | 88 | 16.93 | 52.41 | 145.00 |
| Gorzów Wielkopolski | 44 | 15.24 | 52.73 | 176.00 |
| Toruń | 66 | 18.60 | 53.01 | 98.00 |
| Sortownia Bydgoszcz | 440 | 18.00 | 53.12 | 43.50 |
| Suma | 946.50 | |||
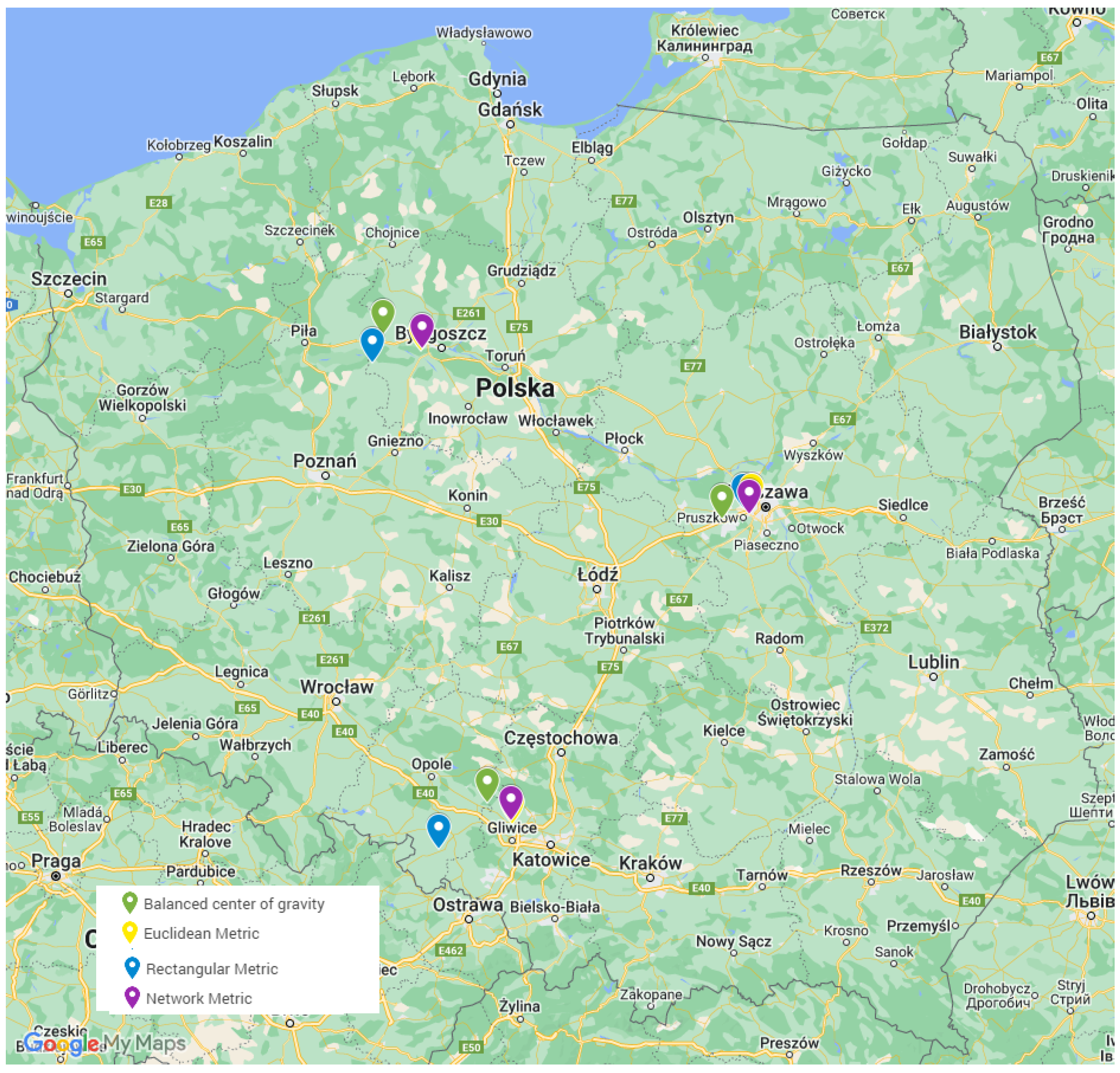
| Area | Gravity Method | Euclidean Metric | Rectangular Metric | Network Metric | ||||
| x | y | x | y | x | y | x | y | |
| Central Poland | 20.60 | 52.16 | 20.87 | 52.22 | 20.80 | 52.22 | 20.85 | 52.19 |
| Southwestern Poland | 18.42 | 50.51 | 18.65 | 50.39 | 17.97 | 50.24 | 18.64 | 50.41 |
| Northwestern Poland | 17.46 | 53.20 | 17.81 | 53.11 | 17.36 | 53.04 | 17.82 | 53.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borucka, A.; Grzelak, M. Deposit–Refund System as a Strategy to Drive Sustainable Energy Transition on the Example of Poland. Sustainability 2025, 17, 1030. https://doi.org/10.3390/su17031030
Borucka A, Grzelak M. Deposit–Refund System as a Strategy to Drive Sustainable Energy Transition on the Example of Poland. Sustainability. 2025; 17(3):1030. https://doi.org/10.3390/su17031030
Chicago/Turabian StyleBorucka, Anna, and Małgorzata Grzelak. 2025. "Deposit–Refund System as a Strategy to Drive Sustainable Energy Transition on the Example of Poland" Sustainability 17, no. 3: 1030. https://doi.org/10.3390/su17031030
APA StyleBorucka, A., & Grzelak, M. (2025). Deposit–Refund System as a Strategy to Drive Sustainable Energy Transition on the Example of Poland. Sustainability, 17(3), 1030. https://doi.org/10.3390/su17031030







