Tidal Current Modeling Using Shallow Water Equations Based on the Finite Element Method: Case Studies in the Qiongzhou Strait and Around Naozhou Island
Abstract
:1. Introduction
2. Numerical Method
2.1. Governing Equations
2.2. Numerical Discretization
2.3. Tidal Open Boundary Conditions
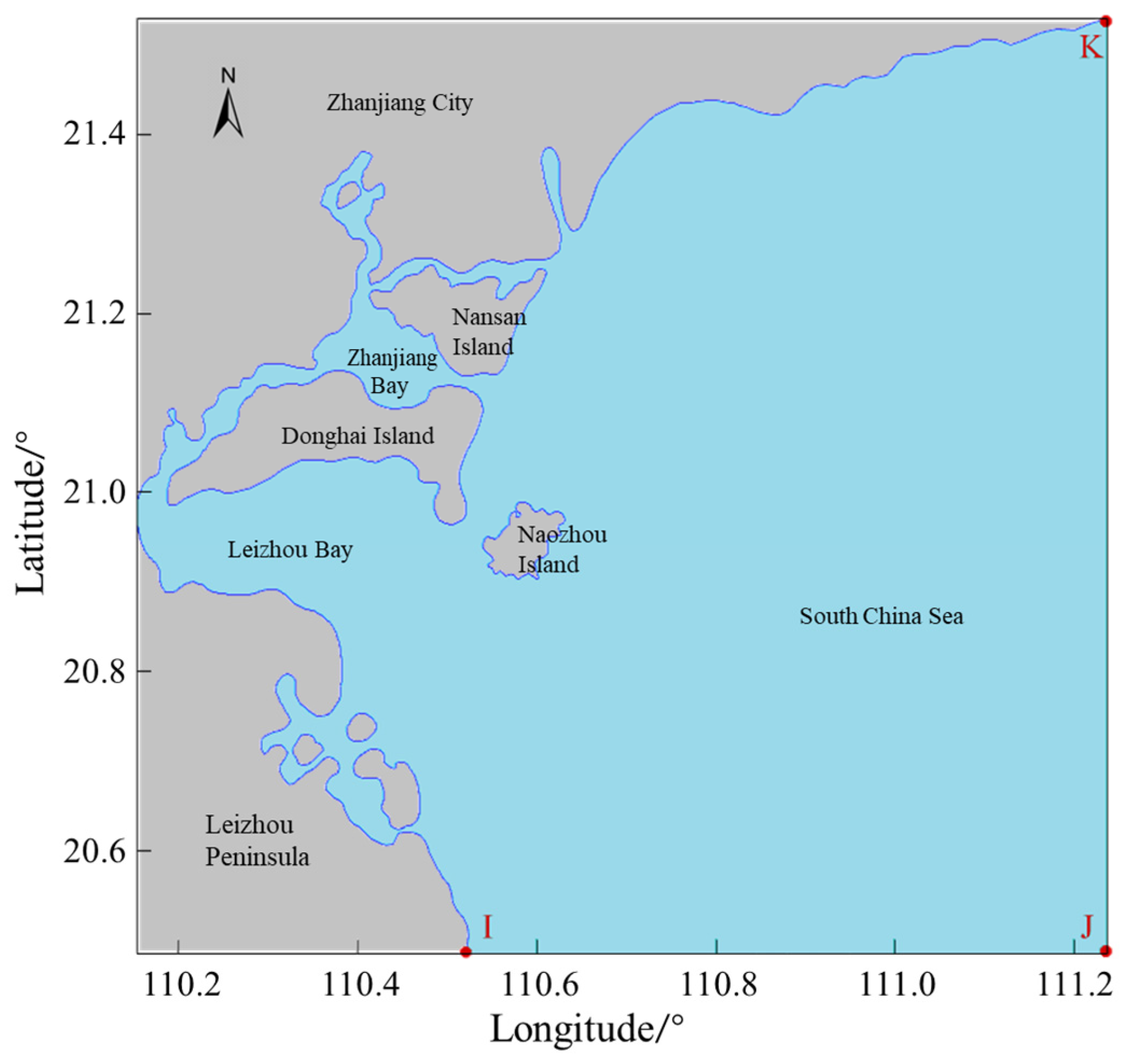
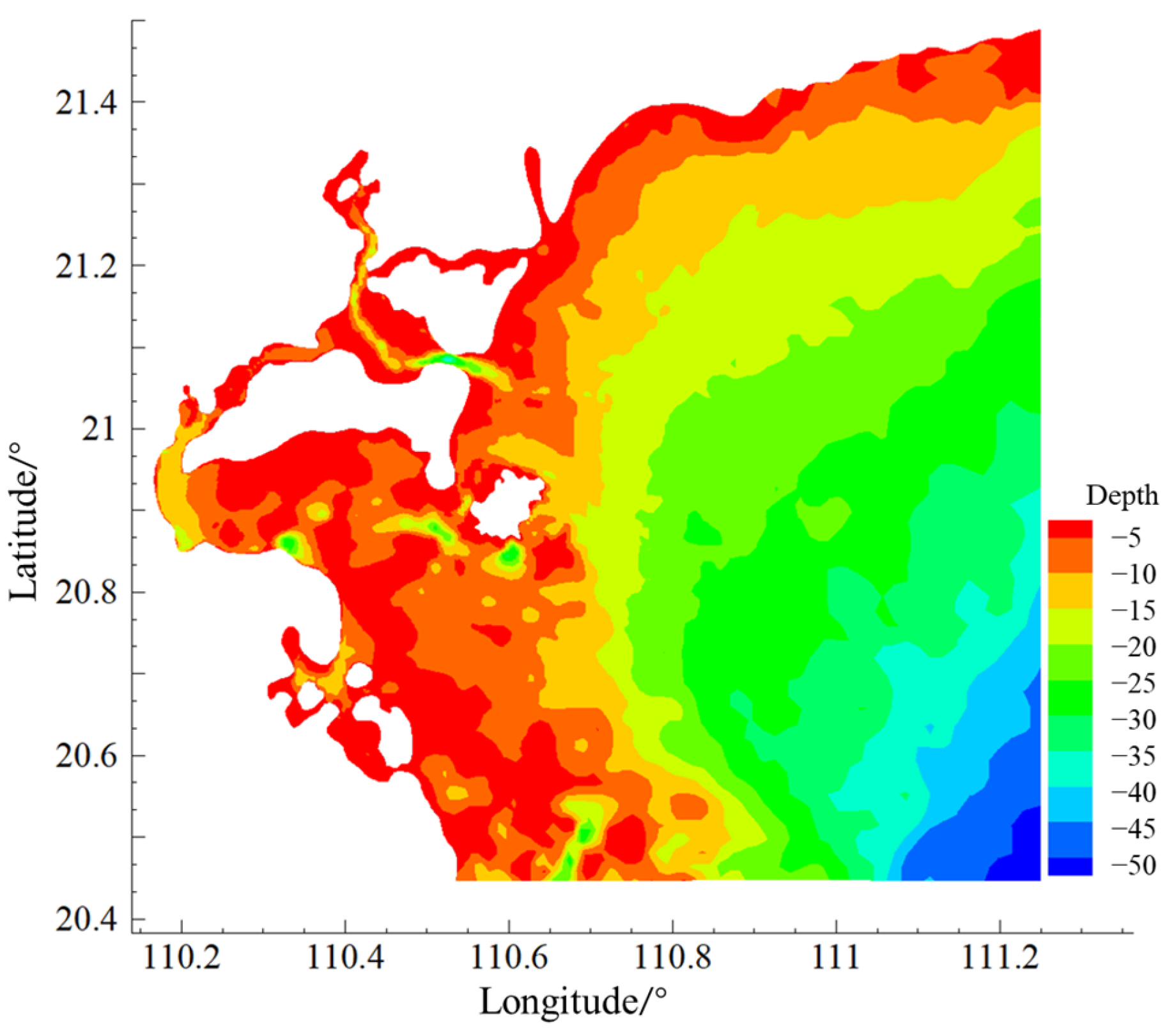
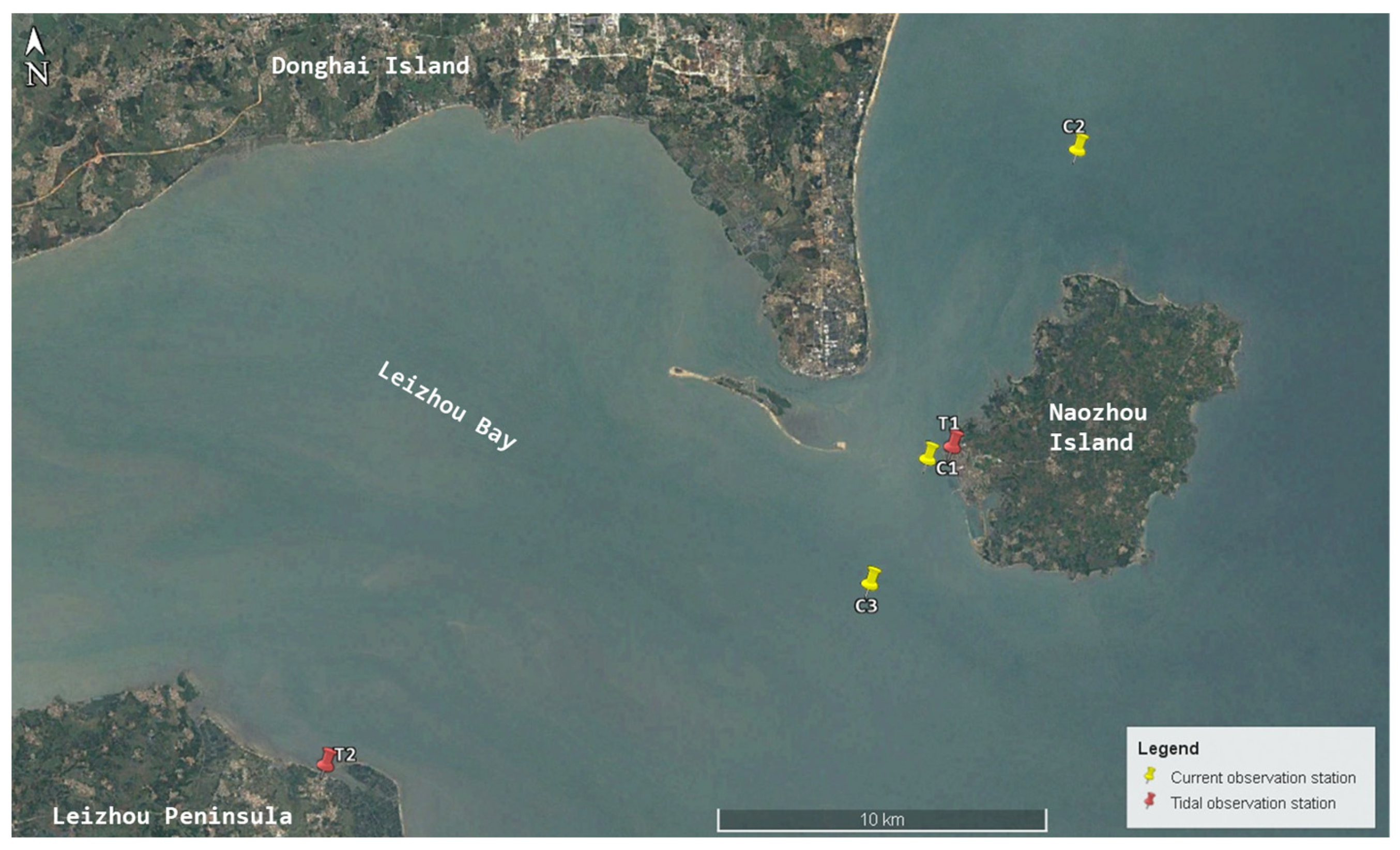
3. Research Area and Data Sources
4. Numerical Experiments
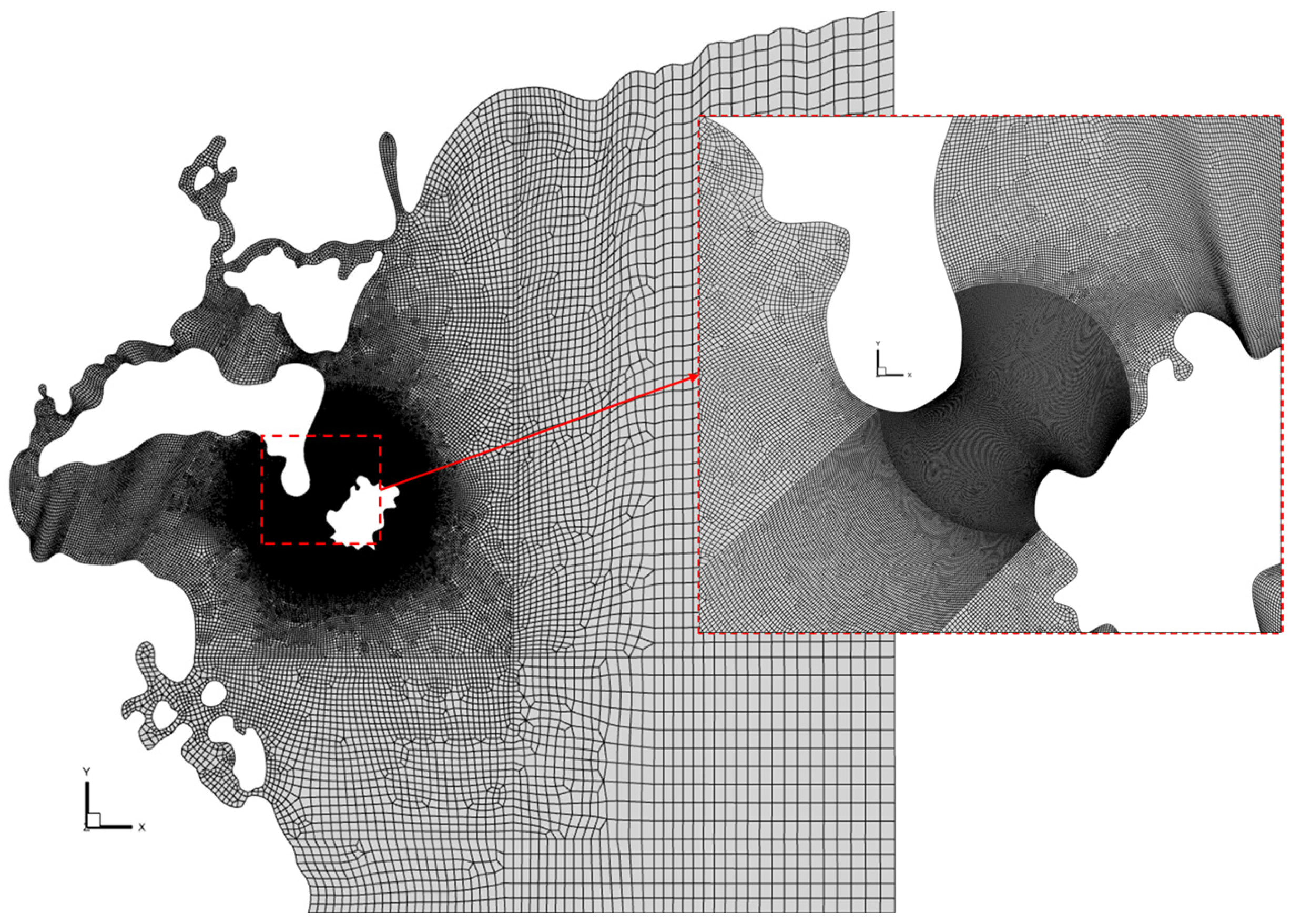
4.1. Qiongzhou Strait
4.2. Naozhou Island
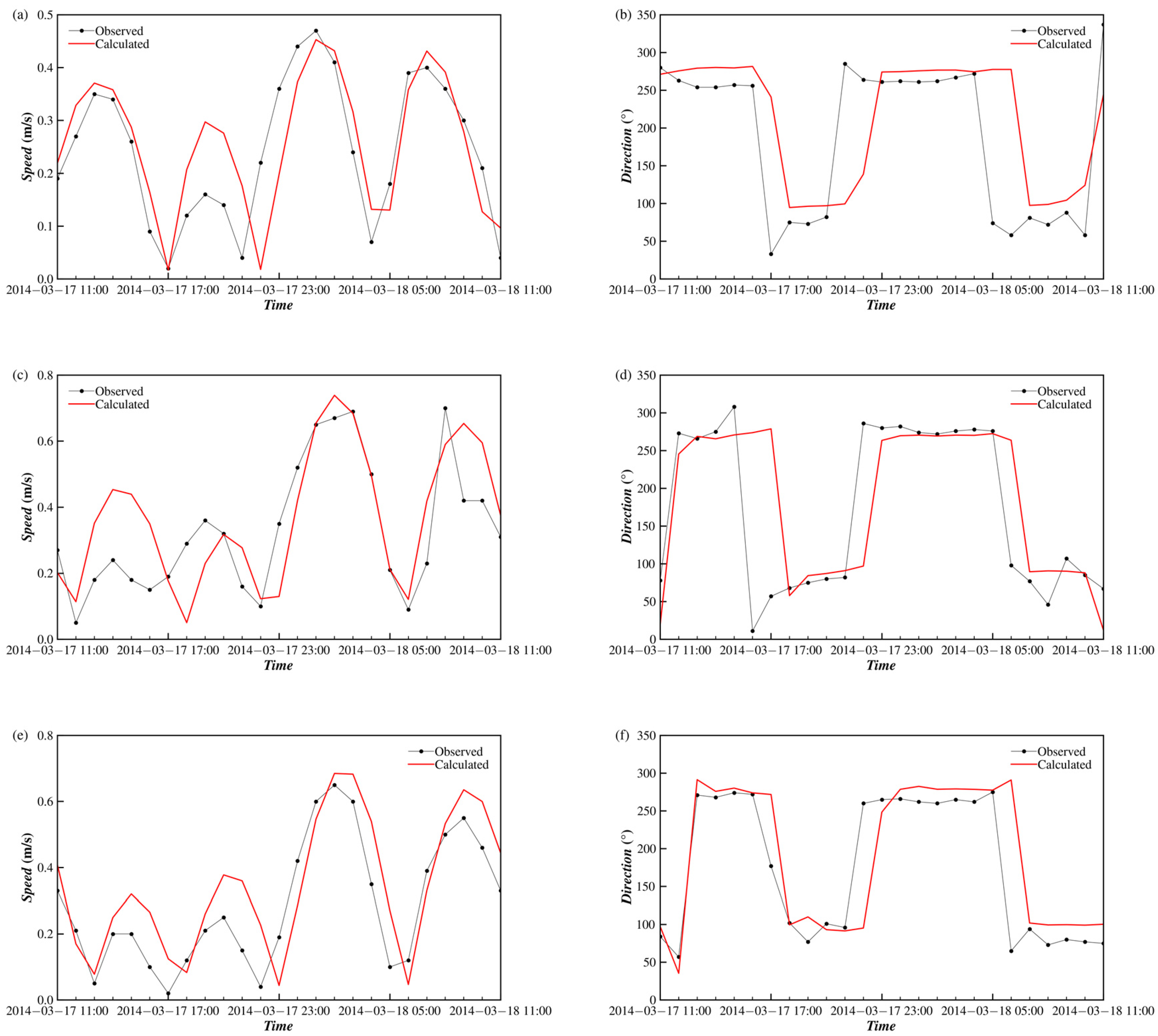
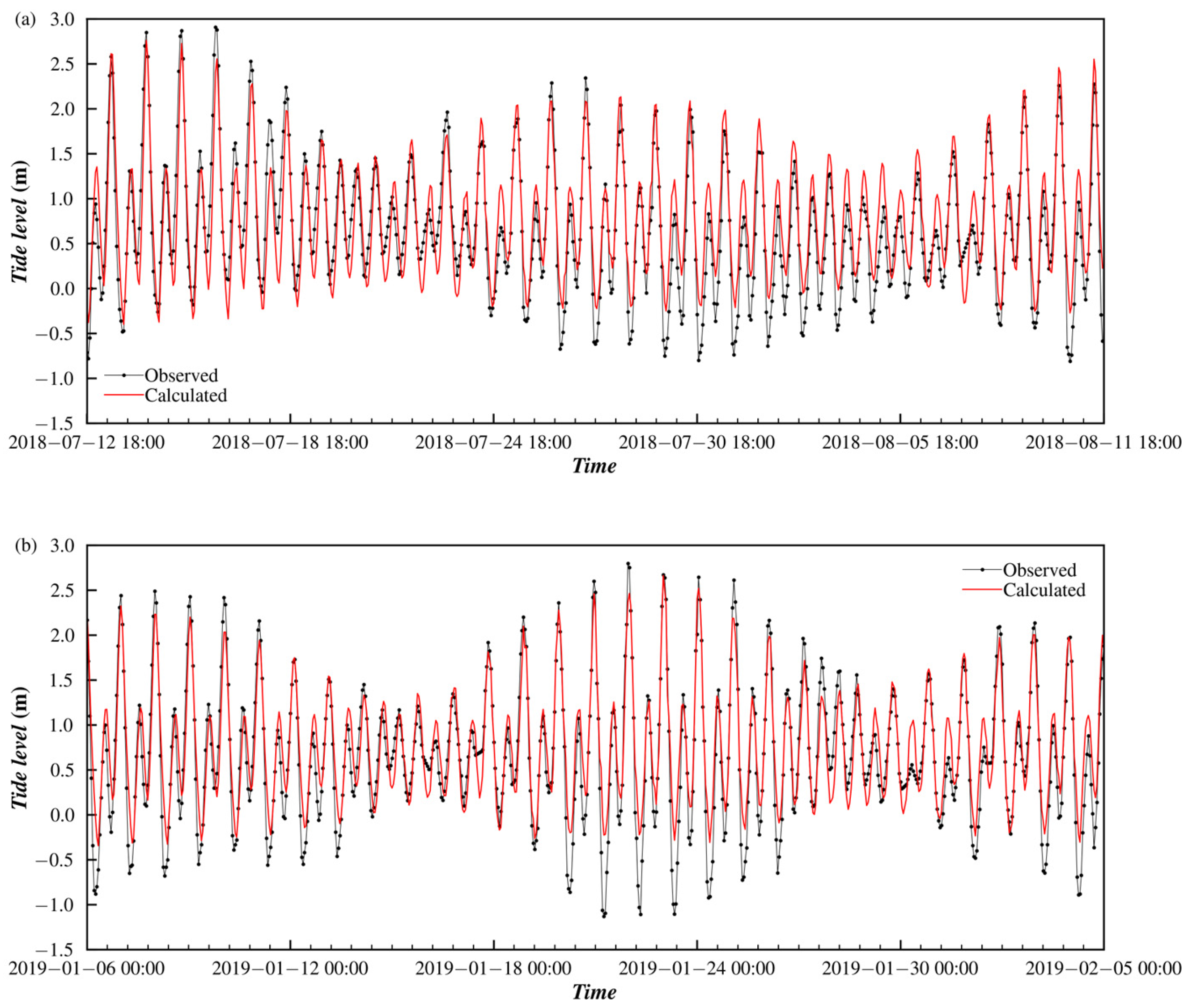
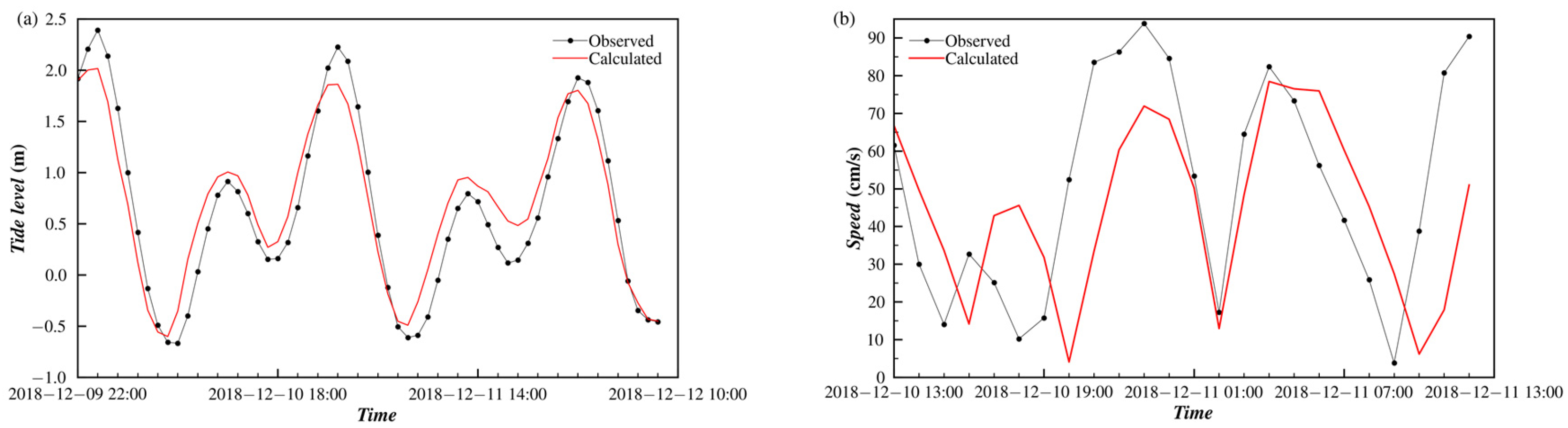
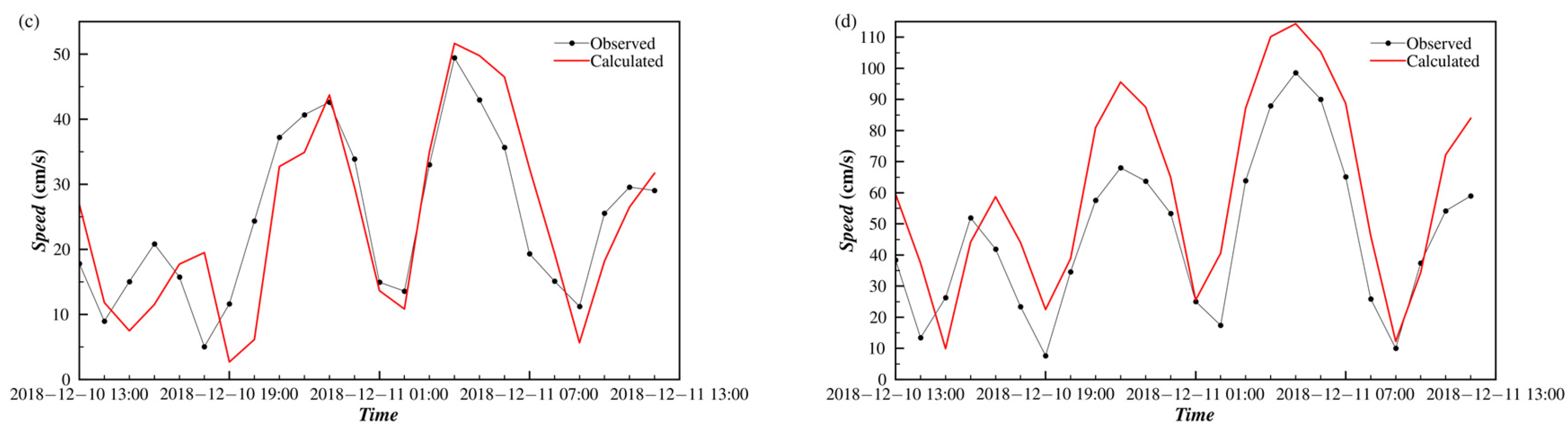
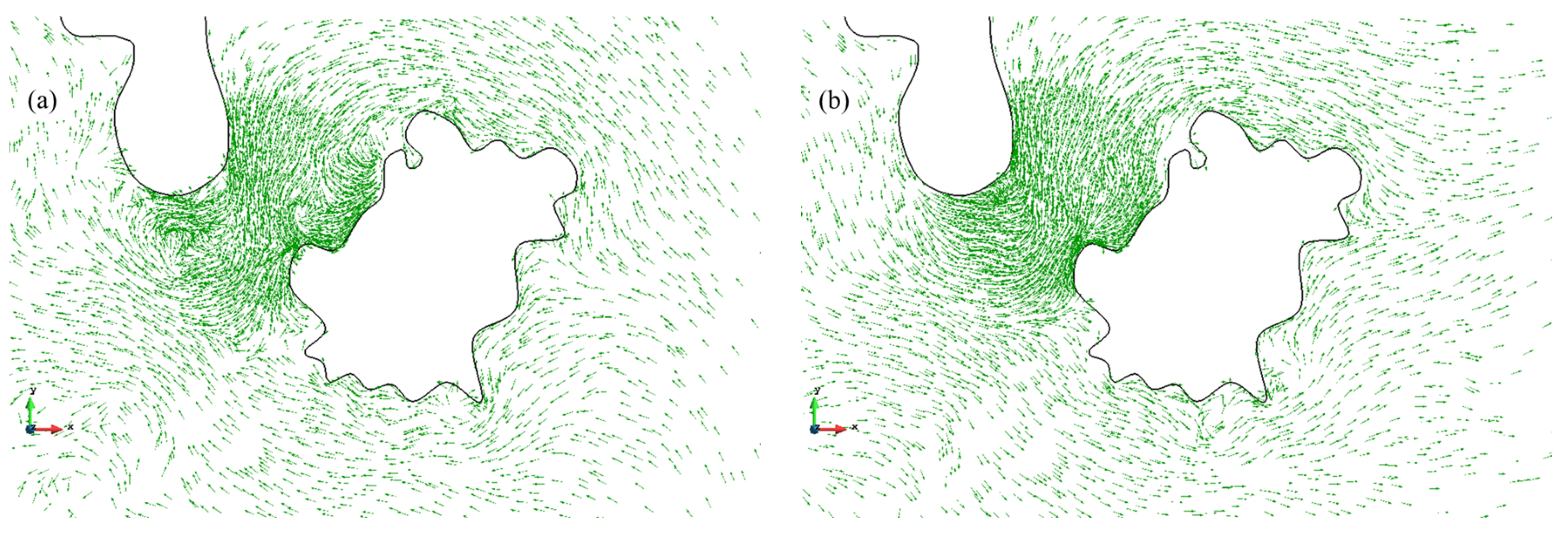
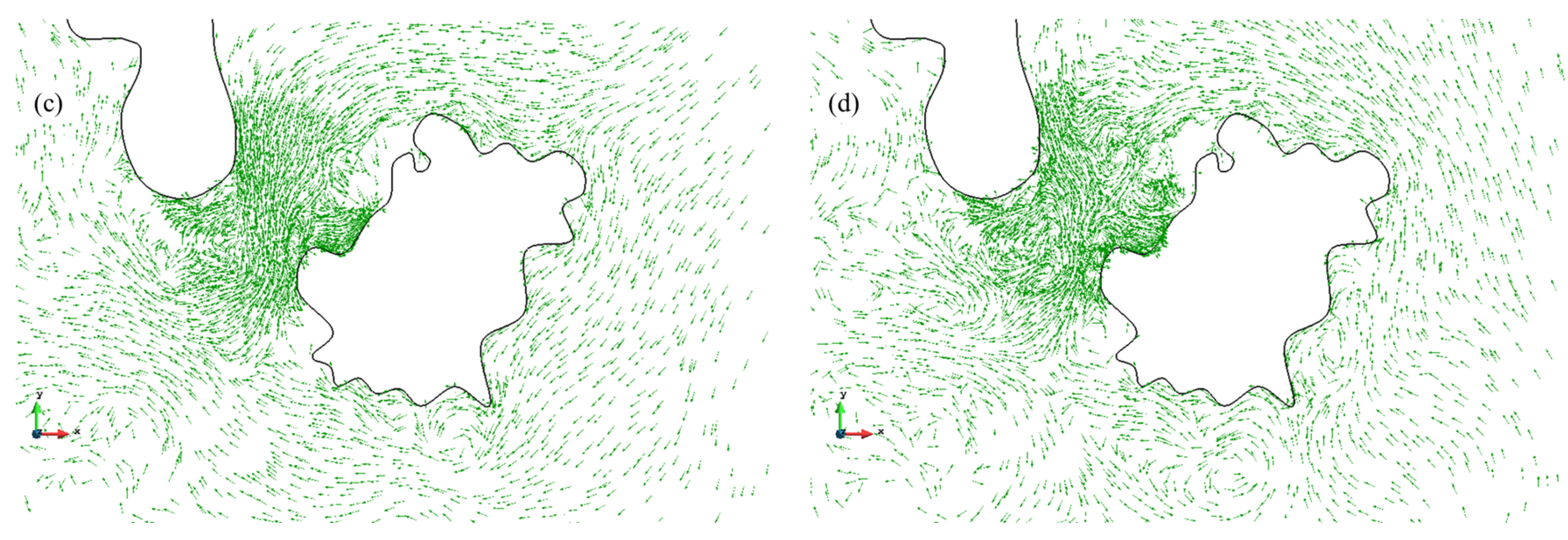
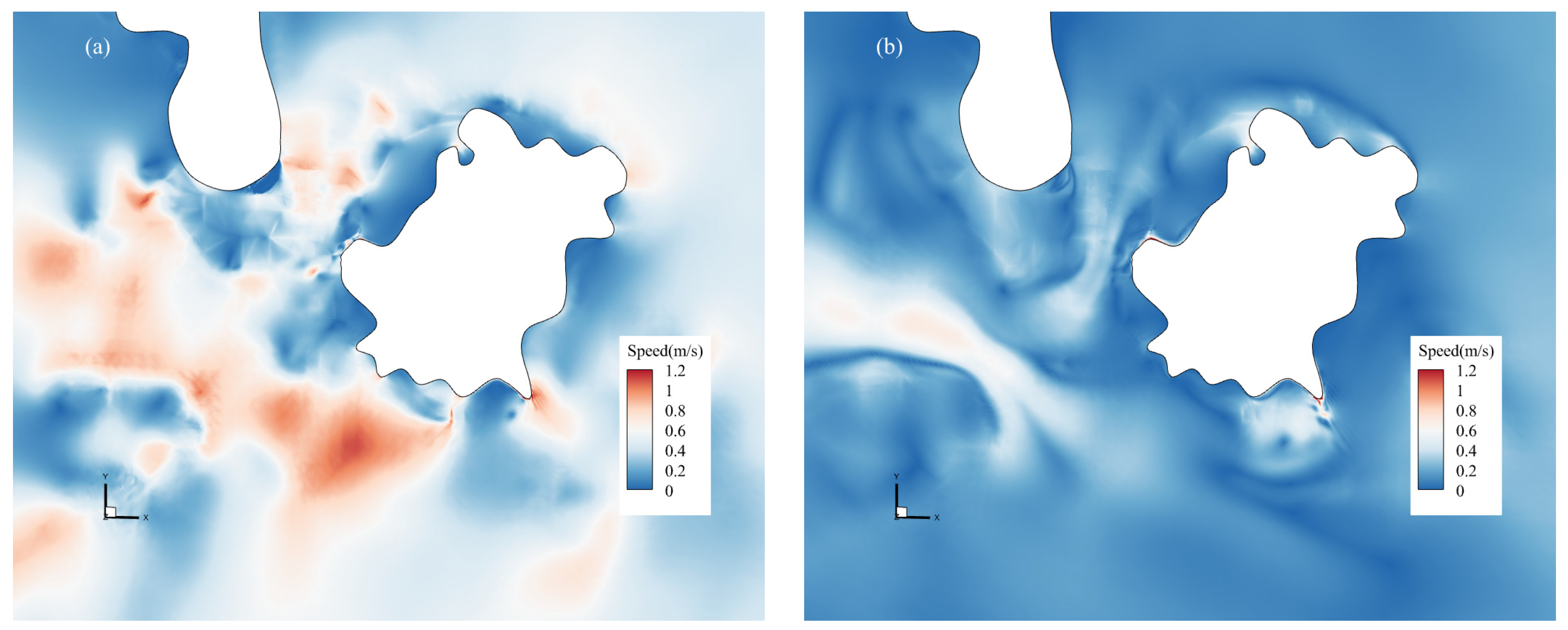
4.2.1. Numerical Results
4.2.2. Analysis of Tidal Current Characteristics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Egbert, G.D.; Ray, R.D. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature 2000, 405, 775–778. [Google Scholar] [CrossRef] [PubMed]
- Xing, Y.; Shu, C.-W. High-order well-balanced finite difference WENO schemes for a class of hyperbolic systems with source terms. J. Sci. Comput. 2006, 27, 477–494. [Google Scholar] [CrossRef]
- Ren, B.F.; Gao, Z.; Gu, Y.G.; Xie, S.S.; Zhang, X.X. A Positivity-Preserving and Well-Balanced High Order Compact Finite Difference Scheme for Shallow Water Equations. Commun. Comput. Phys. 2024, 35, 524–552. [Google Scholar] [CrossRef]
- Lukáčová-Medvid’ová, M.; Vlk, Z. Well-balanced finite volume evolution Galerkin methods for the shallow water equations with source terms. Int. J. Numer. Methods Fluids 2005, 47, 1165–1171. [Google Scholar] [CrossRef]
- Noelle, S.; Pankratz, N.; Puppo, G.; Natvig, J.R. Well-balanced finite volume schemes of arbitrary order of accuracy for shallow water flows. J. Comput. Phys. 2006, 213, 474–499. [Google Scholar] [CrossRef]
- Ern, A.; Piperno, S.; Djadel, K. A well-balanced Runge–Kutta discontinuous Galerkin method for the shallow-water equations with flooding and drying. Int. J. Numer. Methods Fluids 2008, 58, 1–25. [Google Scholar] [CrossRef]
- Xing, Y.; Shu, C.-W. High order well-balanced finite volume WENO schemes and discontinuous Galerkin methods for a class of hyperbolic systems with source terms. J. Comput. Phys. 2006, 214, 567–598. [Google Scholar] [CrossRef]
- Umgiesser, G.; Canu, D.M.; Cucco, A.; Solidoro, C. A finite element model for the Venice Lagoon. Development, set up, calibration and validation. J. Mar. Syst. 2004, 51, 123–145. [Google Scholar] [CrossRef]
- Mandelman, I.; Ferrari, M.A.; Fernández, D.R. Evaluation of a finite element formulation for the shallow water equations with numerical smoothing in the Gulf of San Jorge. Comput. Appl. Math. 2023, 43, 5. [Google Scholar] [CrossRef]
- Kawahara, M.; Hirano, H.; Tsubota, K.; Inagaki, K. Selective lumping finite element method for shallow water flow. Int. J. Numer. Methods Fluids 1982, 2, 89–112. [Google Scholar] [CrossRef]
- Jiang, C.; Yang, C.; Liang, D. Computation of shallow wakes with the fractional step finite element method. J. Hydraul. Res. 2009, 47, 127–136. [Google Scholar] [CrossRef]
- Grotkop, G. Finite element analysis of long-period water waves. Comput. Methods Appl. Mech. Eng. 1973, 2, 147–157. [Google Scholar] [CrossRef]
- Mao, J.; Zhao, L.; Bai, X.; Guo, B.; Liu, Z.; Li, T. A novel well-balanced scheme for modeling of dam break flow in drying-wetting areas. Comput. Fluids 2016, 136, 324–330. [Google Scholar] [CrossRef]
- Bermudez, A.; Vazquez, M.E. Upwind methods for hyperbolic conservation laws with source terms. Comput. Fluids 1994, 23, 1049–1071. [Google Scholar] [CrossRef]
- Kuiry, S.N.; Sen, D.; Ding, Y. A high-resolution shallow water model using unstructured quadrilateral grids. Comput. Fluids 2012, 68, 16–28. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, X.; Shu, C.-W. Positivity-preserving high order well-balanced discontinuous Galerkin methods for the shallow water equations. Adv. Water Resour. 2010, 33, 1476–1493. [Google Scholar] [CrossRef]
- Gourgue, O.; Comblen, R.; Lambrechts, J.; Kärnä, T.; Legat, V.; Deleersnijder, E. A flux-limiting wetting–drying method for finite-element shallow-water models, with application to the Scheldt Estuary. Adv. Water Resour. 2009, 32, 1726–1739. [Google Scholar] [CrossRef]
- Bunya, S.; Kubatko, E.J.; Westerink, J.J.; Dawson, C. A wetting and drying treatment for the Runge–Kutta discontinuous Galerkin solution to the shallow water equations. Comput. Methods Appl. Mech. Eng. 2009, 198, 1548–1562. [Google Scholar] [CrossRef]
- Kärnä, T.; de Brye, B.; Gourgue, O.; Lambrechts, J.; Comblen, R.; Legat, V.; Deleersnijder, E. A fully implicit wetting–drying method for DG-FEM shallow water models, with an application to the Scheldt Estuary. Comput. Methods Appl. Mech. Eng. 2011, 200, 509–524. [Google Scholar] [CrossRef]
- Rompas, P.T.D.; ManongkoFaculty, J.D.I. Numerical simulation of marine currents in the Bunaken Strait, North Sulawesi, Indonesia. Iop. Conf. Ser.-Mat. Sci. 2016, 128, 012003. [Google Scholar] [CrossRef]
- Barth, A.; Alvera-Azcárate, A.; Beckers, J.M.; Weisberg, R.H.; Vandenbulcke, L.; Lenartz, F.; Rixen, M. Dynamically constrained ensemble perturbations—Application to tides on the West Florida Shelf. Ocean Sci. 2009, 5, 259–270. [Google Scholar] [CrossRef]
- Walters, R.A.; Gillibrand, P.A.; Bell, R.G.; Lane, E.M. A study of tides and currents in Cook Strait, New Zealand. Ocean Dyn. 2010, 60, 1559–1580. [Google Scholar] [CrossRef]
- Le, H.-A.; Lambrechts, J.; Ortleb, S.; Gratiot, N.; Deleersnijder, E.; Soares-Frazão, S. An implicit wetting–drying algorithm for the discontinuous Galerkin method: Application to the Tonle Sap, Mekong River Basin. Environ. Fluid Mech. 2020, 20, 923–951. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, Z.; Zhang, D.; Hu, D.; Yu, Z.; Yue, S. Tide–Surge Interactions in Lingdingyang Bay, Pearl River Estuary, China: A Case Study from Typhoon Mangkhut, 2018. Estuaries Coasts 2024, 47, 330–351. [Google Scholar] [CrossRef]
- Hu, P.; Zhao, Z.; Ji, A.; Li, W.; He, Z.; Liu, Q.; Li, Y.; Cao, Z. A GPU-Accelerated and LTS-Based Finite Volume Shallow Water Model. Water 2022, 14, 922. [Google Scholar] [CrossRef]
- Chen, Z.R.; Zhang, Q.H.; Ran, G.Q.; Nie, Y. A Wetting and Drying Approach for a Mode-Nonsplit Discontinuous Galerkin Hydrodynamic Model with Application to Laizhou Bay. J. Mar. Sci. Eng. 2024, 12, 147. [Google Scholar] [CrossRef]
- Su, M.D.; Xu, X.; Zhu, J.L.; Hon, Y.C. Numerical simulation of tidal bore in Hangzhou Gulf and Qiantangjiang. Int. J. Numer. Methods Fluids 2001, 36, 205–247. [Google Scholar] [CrossRef]
- He, A.; He, X.; Bai, Y.; Zhu, Q.; Gong, F.; Huang, H.; Pan, D. Simulation of Sedimentation in Lake Taihu with Geostationary Satellite Ocean Color Data. Remote Sens. 2019, 11, 379. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Wu, J. A general explicit or semi-explicit algorithm for compressible and incompressible flows. Int. J. Numer. Meth. Eng. 1992, 35, 457–479. [Google Scholar] [CrossRef]
- Chorin, A.J. A numerical method for solving incompressible viscous flow problems (Reprinted from the Journal of Computational Physics, vol 2, pg 12-26, 1997). J. Comput. Phys. 1997, 135, 118–125. [Google Scholar] [CrossRef]
- Le Provost, C.; Genco, M.L.; Lyard, F.; Vincent, P.; Canceil, P. Spectroscopy of the world ocean tides from a finite element hydrodynamic model. J. Geophys. Res. Ocean. 1994, 99, 24777–24797. [Google Scholar] [CrossRef]
- Shi, M.; Chen, C.; Xu, Q.; Lin, H.; Liu, G.; Wang, H.; Wang, F.; Yan, J. The Role of Qiongzhou Strait in the Seasonal Variation of the South China Sea Circulation. J. Phys. Oceanogr. 2002, 32, 103–121. Available online: https://journals.ametsoc.org/view/journals/phoc/32/1/1520-0485_2002_032_0103_troqsi_2.0.co_2.xml (accessed on 25 January 2025). [CrossRef]
- Li, M.; Xie, L.; Zong, X.; Li, J.; Li, M.; Yan, T.; Han, R. Tidal currents in the coastal waters east of Hainan Island in winter. J. Oceanol. Limnol. 2022, 40, 438–455. [Google Scholar] [CrossRef]
- Zu, T.; Gan, J.; Erofeeva, S.Y. Numerical study of the tide and tidal dynamics in the South China Sea. Deep-Sea Res. Pt. I 2008, 55, 137–154. [Google Scholar] [CrossRef]
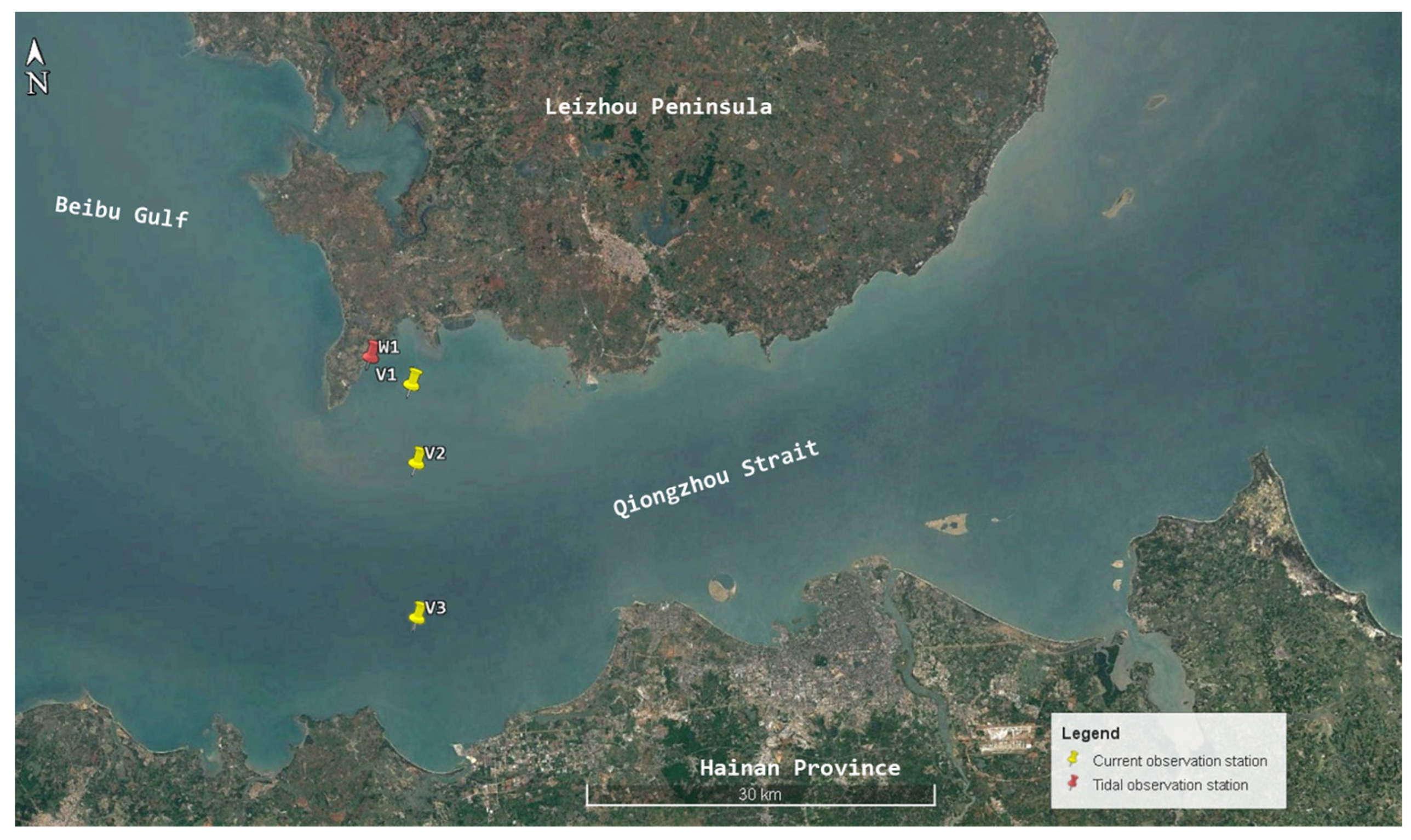
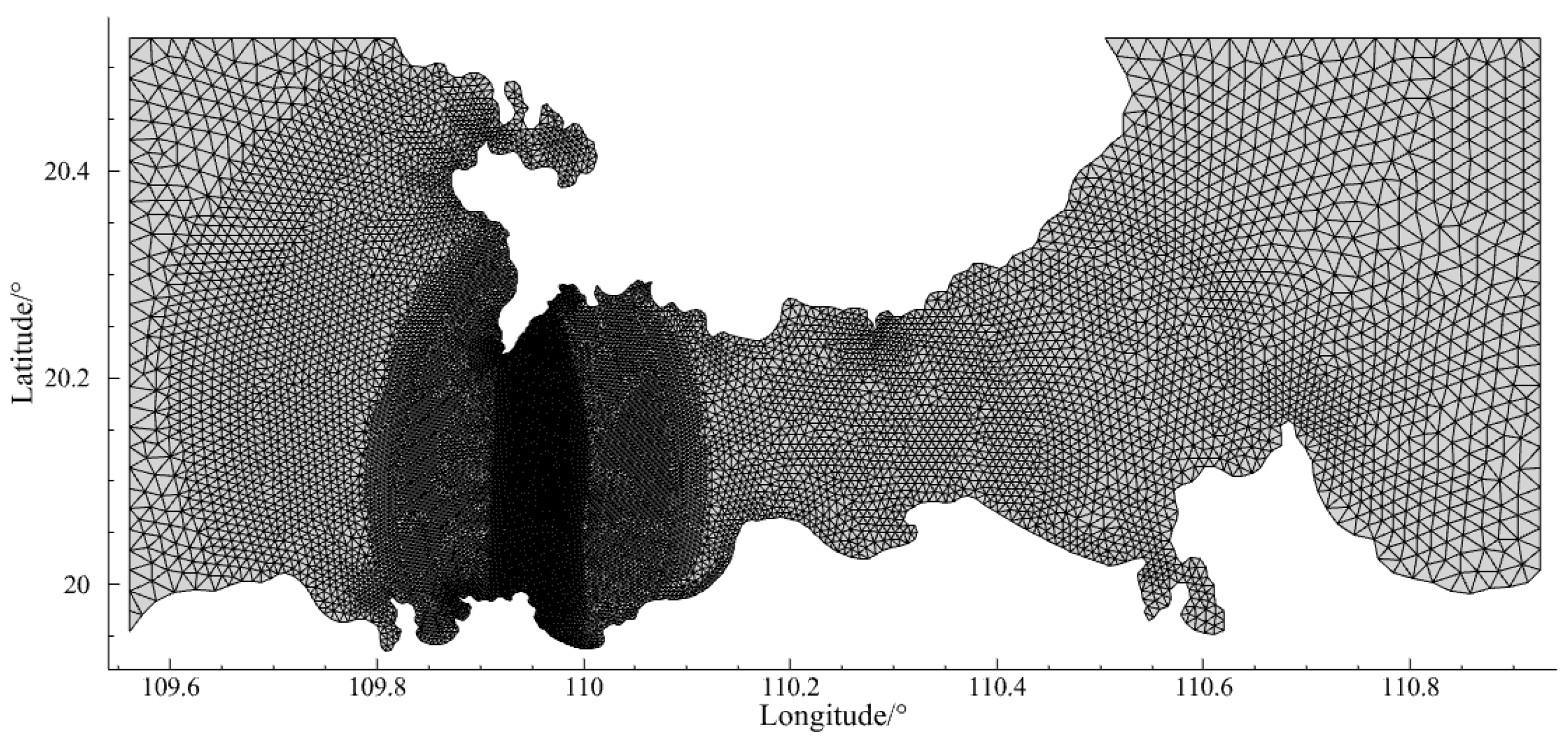
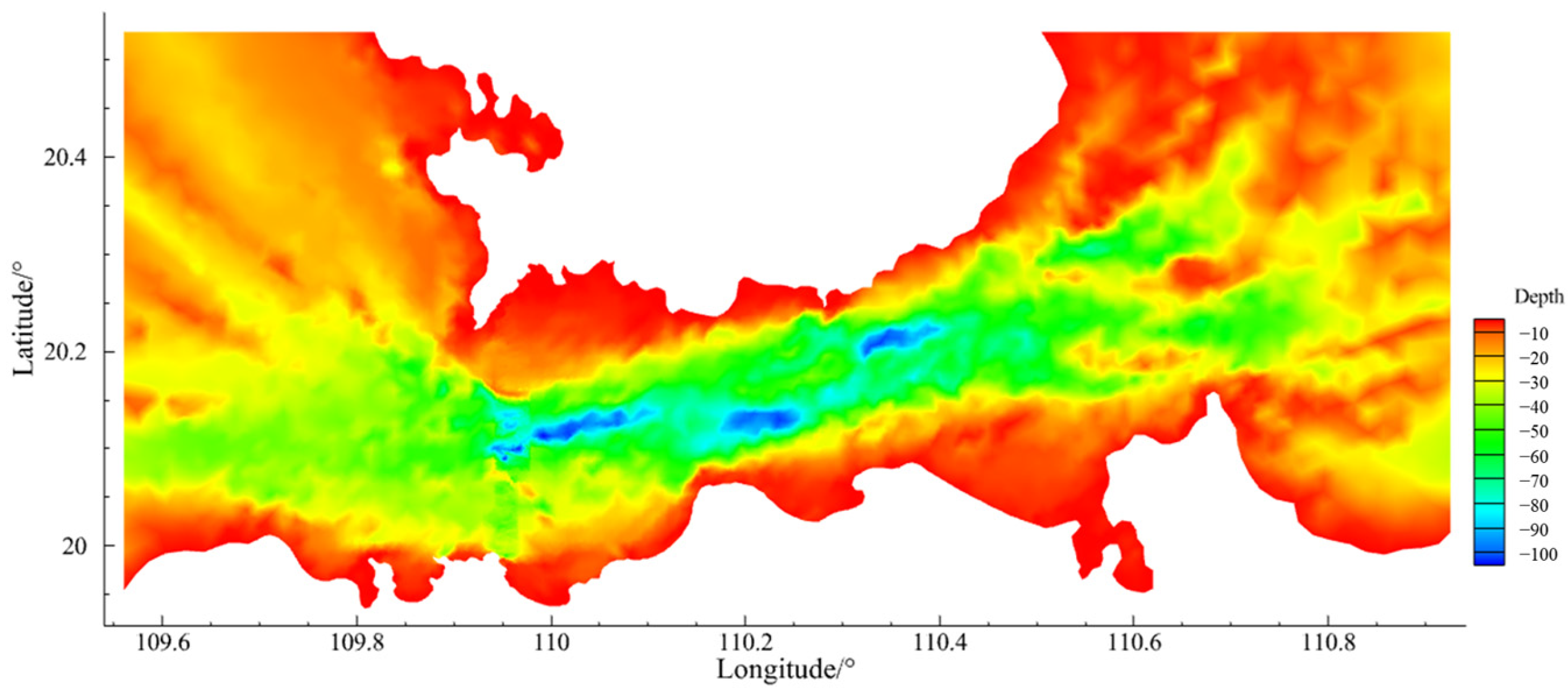
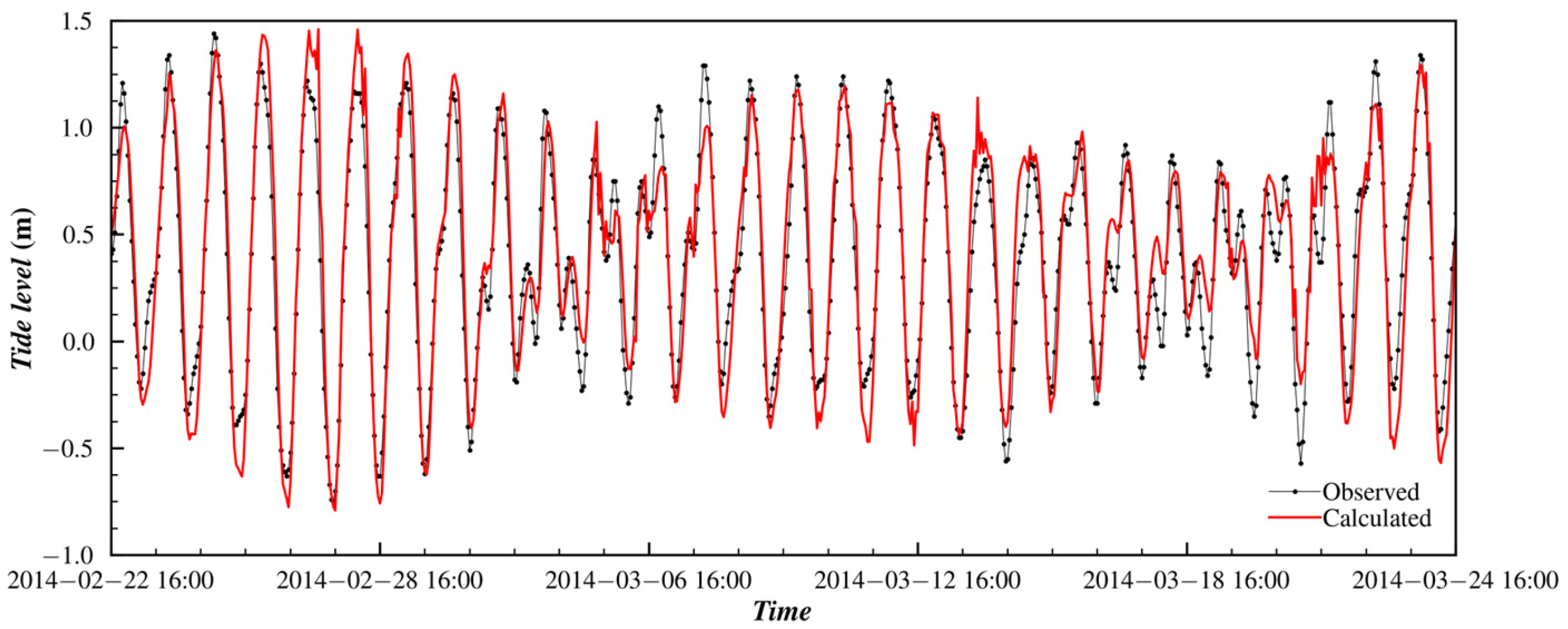

| Station | Coordinates | Observation Parameters and Time | |
|---|---|---|---|
| W1 | 109°57.113′ E, 20°15.104′ N | Tide level | From 22 Feb. 16:00 to 24 Mar. 15:00, 2014 |
| V1 | 109°59.064′ E, 20°13.741′ N | Flow speed and direction | Spring tide: From 23 Mar. 11:00 to 24 Mar. 12:00, 2014 Neap tide: From 17 Mar. 11:00 to 24 Mar. 12:00, 2014 |
| V2 | 109°59.142′ E, 20°10.103′ N | Flow speed and direction | |
| V3 | 109°58.829′ E, 20°02.952′ N | Flow speed and direction | |
| Forecast Points | Longitude | Latitude |
|---|---|---|
| I | 110°31.18′ E | 20°29.97′ N |
| J | 111°14.97′ E | 20°29.97′ N |
| K | 111°14.97′ E | 21°29.56′ N |
| Station | Coordinates | Time |
|---|---|---|
| T1 | 110°33.000′ E, 20°54.000′ N | From 22:00 on 9 Dec. 2018, to 09:00 on 12 Dec. 2018 |
| T2 | 110°21.786′ E, 20°49.270′ N | Summer: From 18:00 on 12 Jul. 2018, to 23:00 on 11 Aug. 2018 Winner: From 00:00 on 6 Jan. 2019, to 23:00 on 6 Feb. 2109 |
| C1 | 110°32.562′ E, 20°53.819′ N | From 13:00 on 10 Dec. 2018 to 14:00 on 11 Dec. 2018 |
| C2 | 110°35.434′ E, 20°58.759′ N | |
| C3 | 110°31.450′ E, 20°51.826′ N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, D.; Mao, J.; Li, J.; Zhao, L. Tidal Current Modeling Using Shallow Water Equations Based on the Finite Element Method: Case Studies in the Qiongzhou Strait and Around Naozhou Island. Sustainability 2025, 17, 1256. https://doi.org/10.3390/su17031256
Peng D, Mao J, Li J, Zhao L. Tidal Current Modeling Using Shallow Water Equations Based on the Finite Element Method: Case Studies in the Qiongzhou Strait and Around Naozhou Island. Sustainability. 2025; 17(3):1256. https://doi.org/10.3390/su17031256
Chicago/Turabian StylePeng, Dawei, Jia Mao, Jianhua Li, and Lanhao Zhao. 2025. "Tidal Current Modeling Using Shallow Water Equations Based on the Finite Element Method: Case Studies in the Qiongzhou Strait and Around Naozhou Island" Sustainability 17, no. 3: 1256. https://doi.org/10.3390/su17031256
APA StylePeng, D., Mao, J., Li, J., & Zhao, L. (2025). Tidal Current Modeling Using Shallow Water Equations Based on the Finite Element Method: Case Studies in the Qiongzhou Strait and Around Naozhou Island. Sustainability, 17(3), 1256. https://doi.org/10.3390/su17031256





