Machine Learning-Based Carbon Emission Predictions and Customized Reduction Strategies for 30 Chinese Provinces
Abstract
1. Introduction
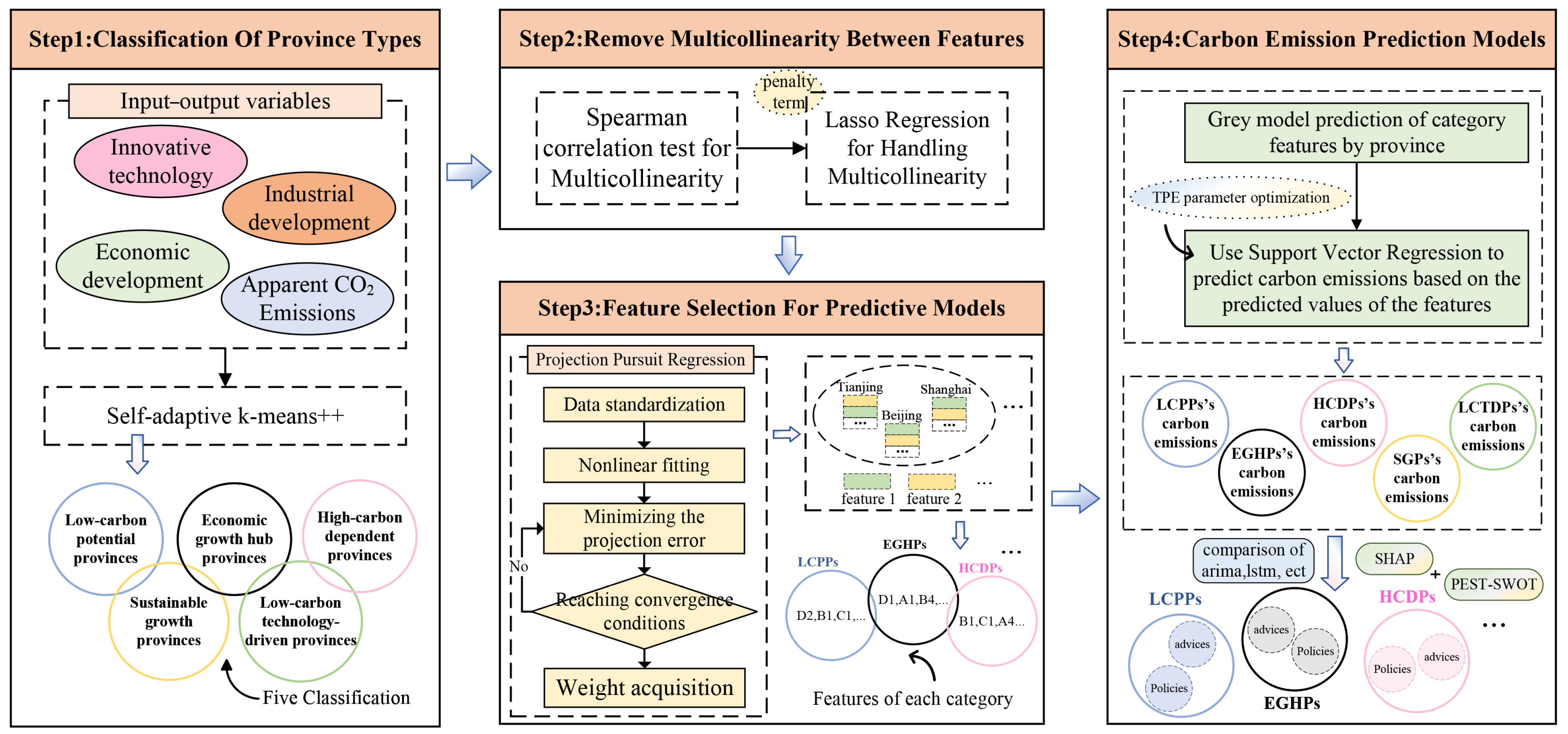
2. Materials and Methods
2.1. Province Clusters
2.1.1. Classification Data Processing
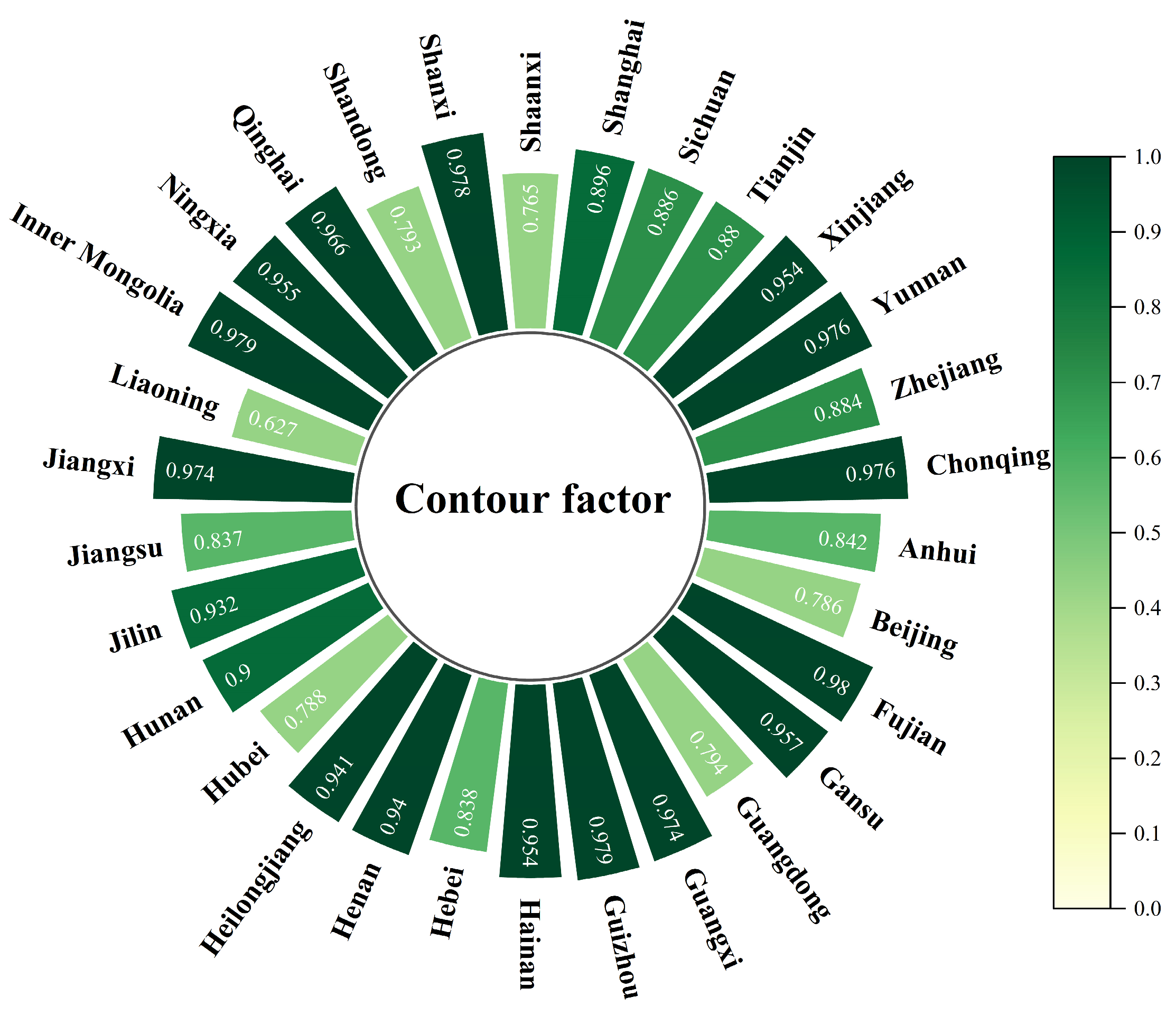
2.1.2. Self-Adaptive k-Means++ Algorithm
2.2. Lasso Regression
2.3. Carbon Emission Prediction Algorithm
2.3.1. GM Algorithm
2.3.2. SVR Prediction Algorithm with TPE Bayesian Parameter Optimization
- 1.
- TPE-based Bayesian Parameter Optimization
- 2.
- SVR
2.4. Data Sources and Selection
2.4.1. Data Sources
2.4.2. Data Selection
3. Results
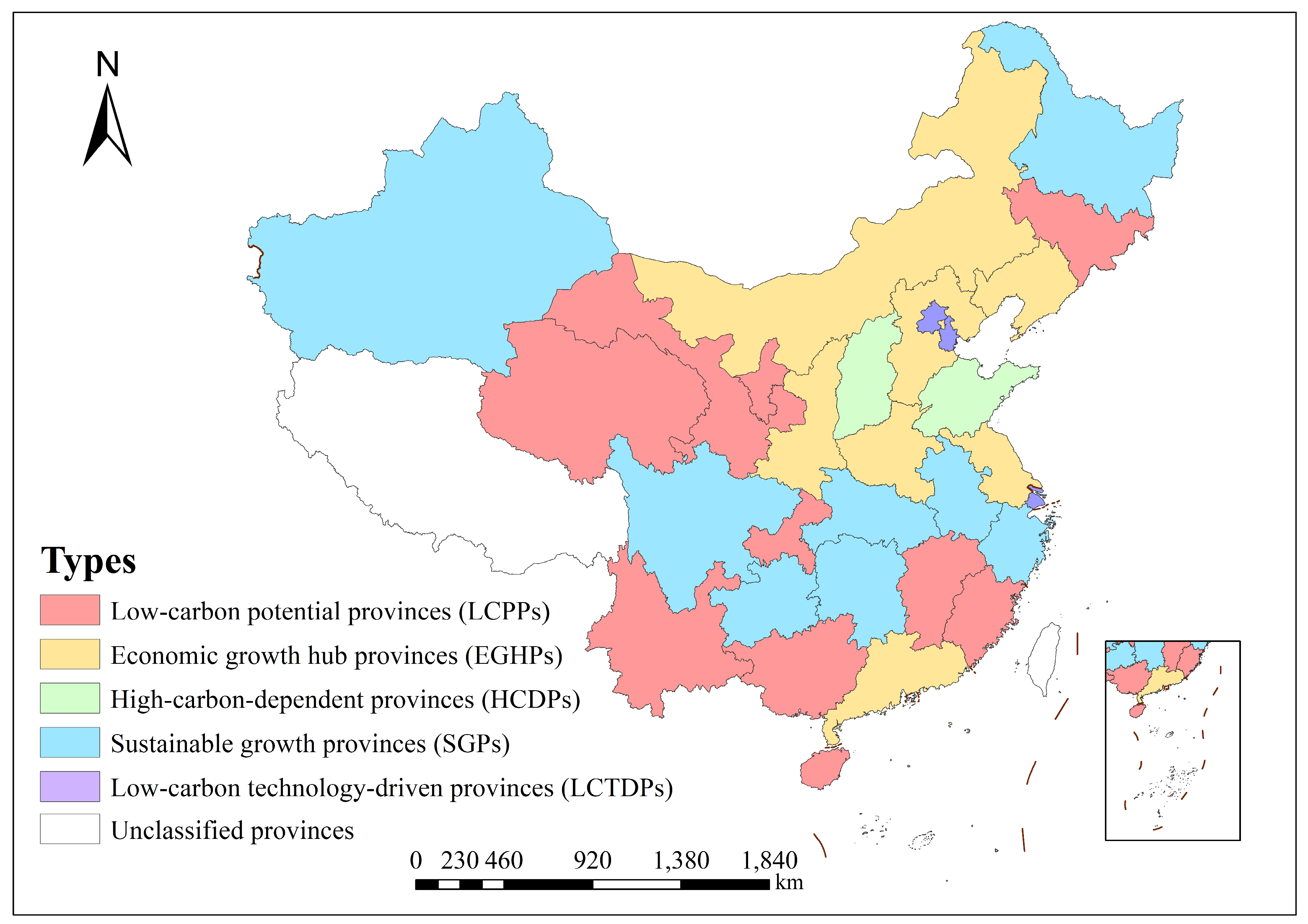
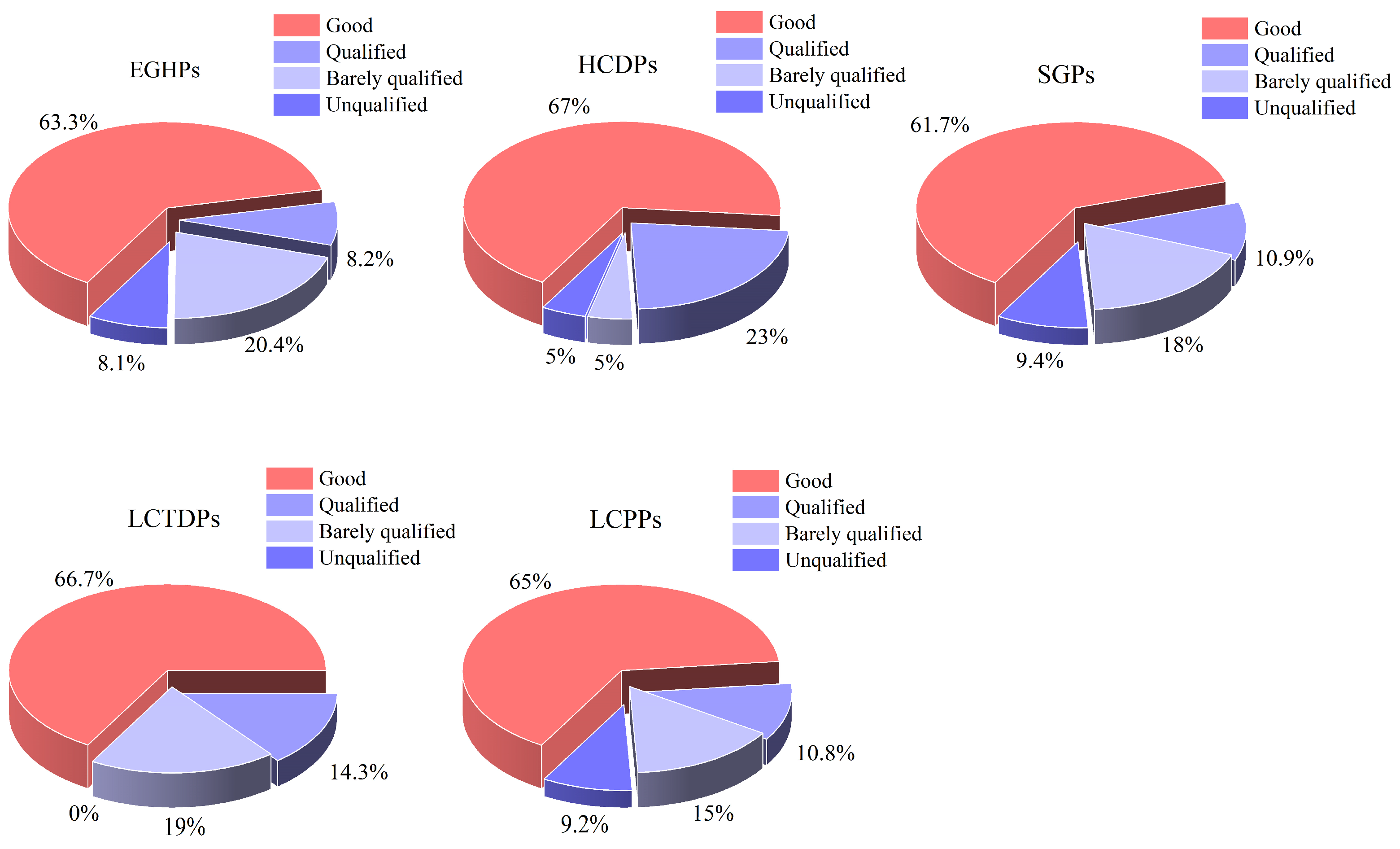
3.1. Provincial Classification
Spatial Distribution of Four Driving Factors
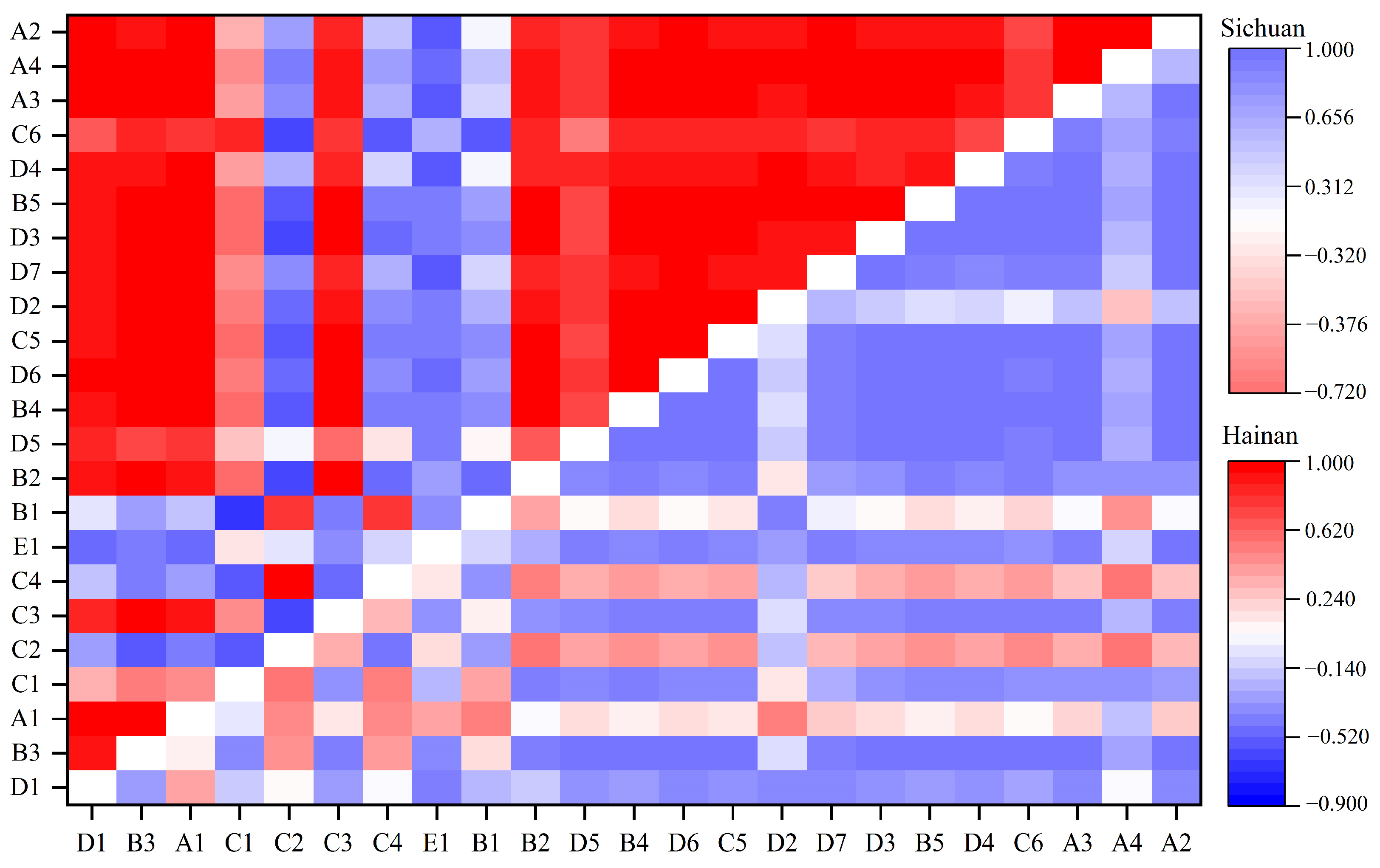
3.2. Handling Multicollinearity
3.2.1. Multicollinearity Analysis of the Driving Factors
3.2.2. Lasso Regression to Address Multicollinearity
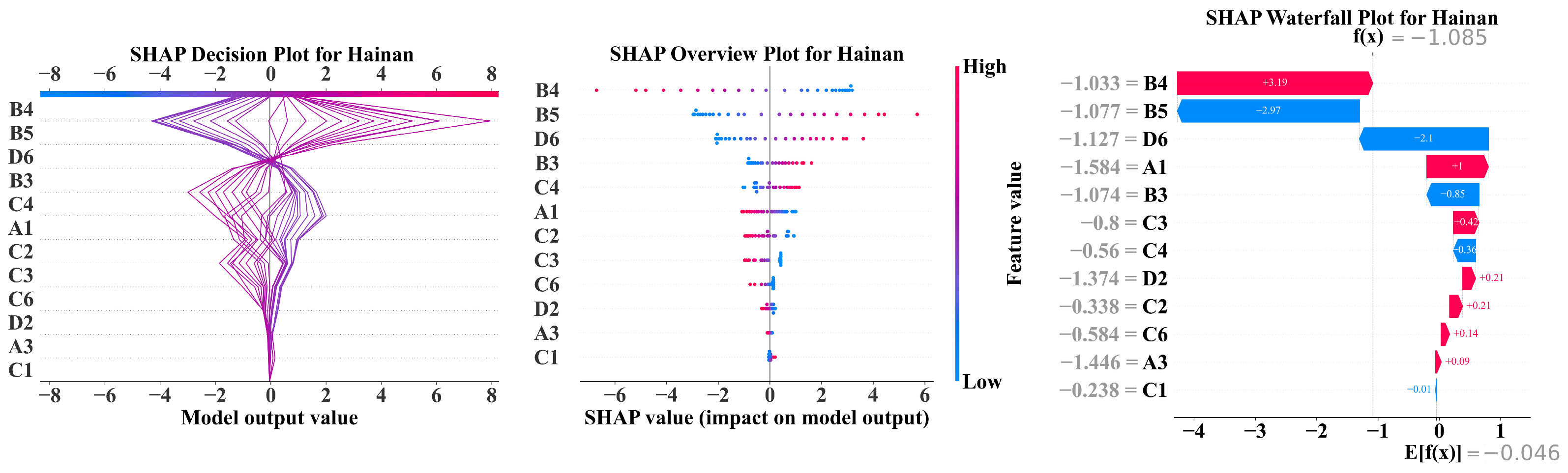
3.3. PPR for Driving Factor Selection
3.4. GM-SVR Carbon Emission Prediction Model
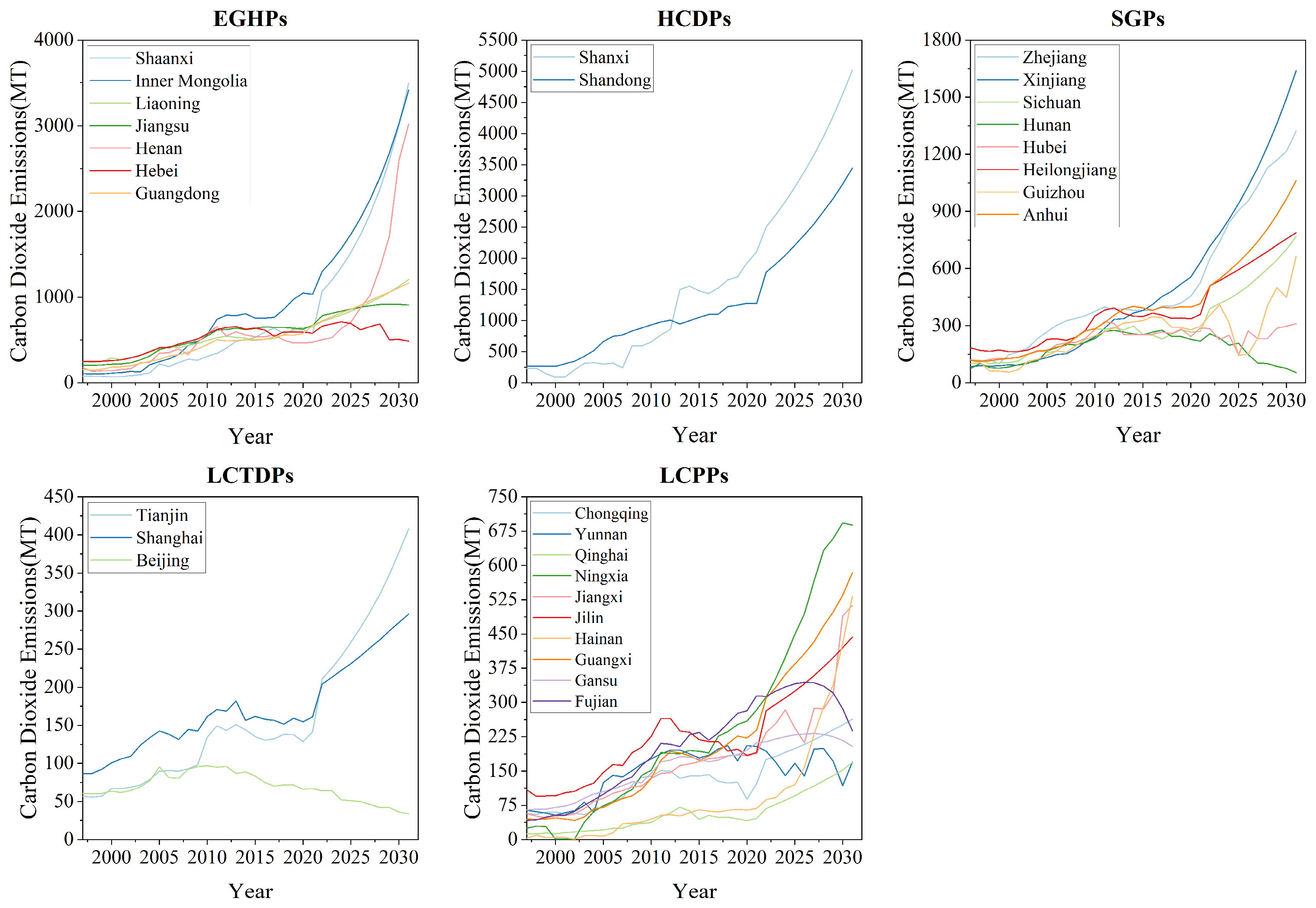
3.4.1. Driving Factor Prediction
3.4.2. Carbon Emission Prediction
3.5. Comparative Analysis of Multiple Prediction Models
4. Discussion
4.1. Heterogeneity Analysis of Regional Carbon Emissions
4.1.1. Political Factors
- LCPPs: The political will of the government to promote low-carbon policies and reduce carbon emissions plays a critical role in shaping regional carbon emission trends. For instance, policies focused on clean energy development and energy efficiency improvements to reduce coal and electricity consumption. Additionally, the government’s political stability and emphasis on environmental protection influence the control and reduction of high-carbon energy sources. Policies such as energy consumption caps, green tax incentives, and support for renewable energy projects could be crucial in decreasing the reliance on coal. Furthermore, government initiatives can influence factors such as railway passenger volume and urban population distribution by promoting public transportation and urban development in environmentally friendly ways;
- EGHPs: In this category, the government’s adoption of strict energy control policies directly influences carbon emissions. Specific policies include carbon tax regulations, energy consumption quotas, and incentives for energy efficiency improvements in industries. The government may also provide financial support and subsidies to foster technological innovation, particularly in clean technologies such as renewable energy, carbon capture, and energy storage solutions. Support for domestic patent applications in green technologies also contributes to reducing carbon emissions by promoting local innovation in low-carbon solutions. These regions might also focus on green infrastructure to manage urban growth and reduce emissions;
- HCDPs: Government policies aimed at green development are particularly significant in reducing carbon emissions in these high-carbon-dependent provinces. For instance, policies may involve phasing out coal plants, incentivizing renewable energy adoption, and promoting energy-efficient technologies. Political transparency and public participation in environmental decision making can enhance the effectiveness of these policies. Furthermore, local governance plays an important role in the implementation of environmental protection laws, such as stricter emission standards and environmental impact assessments for industrial projects. Policies supporting electricity consumption reduction and public education on energy conservation are likely to be emphasized in these regions;
- SGPs: Political decisions regarding energy consumption directly influence carbon emissions, especially in the management of coal and electricity use. Governments may adopt energy transition policies that focus on reducing the share of coal in energy production and increasing the use of renewable energy sources. In addition, the government might introduce green technology support policies, such as subsidies for electric vehicles, solar power projects, and carbon emission reduction targets. These measures are designed to reduce the carbon footprint of key industries, particularly in manufacturing and transportation sectors. By focusing on low-carbon technology adoption, these provinces can further their goals of reducing emissions;
- LCTDPs: Policy guidance is vital in promoting an increase in the share of the secondary industry while reducing diesel consumption. For example, tax incentives for green technologies, subsidies for electric transportation, and carbon credit systems can play a central role. Governments may also provide strong support for education, promoting green technologies through research funding and the development of training programs for low-carbon industries. Additionally, transportation policies focusing on public transit and electric vehicle infrastructure could contribute to overall carbon reduction efforts. Technology development policies might include research and development (R&D) grants for low-carbon innovation, ensuring that these provinces maintain a technological edge in reducing their carbon emissions.
4.1.2. Economic Factors
- LCPPs: Economic transformation and industrial upgrading impact carbon emissions significantly. Also, high GDP regions are often accompanied by higher energy consumption and carbon emissions, especially in areas relying on traditional high-carbon energy. However, economic efficiency helps reduce carbon emission pressure;
- EGHPs: Economic openness, market transaction volume, and patent application volume are key economic factors driving green innovation and low-carbon technology application. Also, accelerated economic development can increase energy demand, leading to higher carbon emissions. However, the development of a green economy and environmental investments can mitigate this growth;
- HCDPs: The speed of economic growth is highly correlated with carbon emissions. Excessive reliance on heavy industry or high-carbon industries will increase emissions, while optimizing economic structure can help reduce emissions. In addition, the increase in per capita GDP has a noticeable effect on driving carbon emissions;
- SGPs: In this category, the proportion of coal and electricity consumption is directly linked to the stage of economic development. Economic development often leads to increased energy demand, resulting in higher carbon emissions. However, restructuring to rely on low-carbon technologies and clean energy may help reduce emissions;
- LCTDPs: The proportion of the secondary industry in the economic structure and energy consumption patterns impact carbon emissions. However, economic growth, especially industrialization, will increase carbon emissions unless there is a transition to clean energy technologies.
4.1.3. Social Factors
- LCPPs: Urban population density and demographic changes impact energy consumption and carbon emissions significantly. During urbanization, energy demand tends to rise, leading to higher carbon emissions. However, increased social awareness of environmental protection and energy conservation can alleviate this impact;
- EGHPs: Social culture, education levels, and environmental awareness affect carbon emissions significantly. As society deepens its understanding of the low-carbon economy, residents’ low-carbon lifestyles will contribute to reducing emissions. Meanwhile, social behavior and policy support will promote the application of low-carbon technologies;
- HCDPs: Urban population and urbanization have a particularly strong effect on carbon emissions. What is more, increased population density may lead to more energy demand, with transportation, buildings, and industries raising emissions. Additionally, social support and participation in environmental policies will influence the application of low-carbon technologies and emission reduction;
- SGPs: The public’s acceptance of low-carbon lifestyles is closely related to carbon emissions. As environmental policies and green technologies become more popular, social support for reducing energy consumption and carbon emissions gradually increases, facilitating a society-wide low-carbon transition;
- LCTDPs: Social structure, population mobility, and urbanization are closely related to carbon emissions. As per capita GDP and social welfare increase, energy demand typically rises, which may lead to higher carbon emissions.
4.1.4. Technological Factors
- LCPPs: Technological progress affects energy consumption patterns and carbon emissions directly, especially breakthroughs in clean energy and energy-saving technologies. Therefore, the adoption of advanced green technologies can significantly reduce coal and electricity consumption, thereby lowering emissions;
- EGHPs: Technological innovation, especially in the areas of energy savings, emission reduction, and low-carbon technologies, plays a crucial role in reducing carbon emissions. As market transaction volumes and patent applications increase, the research and application of low-carbon technologies will help control emissions;
- HCDPs: Technological advancements can improve energy efficiency effectively, especially in electricity consumption and building sectors. Additionally, the widespread use of green technologies in energy-saving, environmental protection, and clean production reduces carbon emissions directly;
- SGPs: Technological advancements are crucial in reducing carbon emissions. Emerging technologies will drive the green transformation of the energy structure to reduce dependence on high-carbon energy sources like coal and electricity, including high-efficiency energy, clean energy, and low-carbon production processes;
- LCTDPs: Innovations in green technologies for industrial production and energy consumption affect carbon emissions directly. Thanks to green technologies, the reduction in diesel consumption and improved energy efficiency in the secondary industry will reduce carbon emissions. Advances in sustainable energy will drive the transition to a low-carbon economy.
4.1.5. SWOT-Analysis
- 1.
- LCPPs
- (1)
- Strengths
- Government Policy Support: policies such as clean energy development and energy efficiency improvements help reduce coal and electricity consumption;
- Political Stability: strong policy stability is conducive to achieving long-term low-carbon goals;
- High Public Awareness of Environmental Protection: with the improvement of environmental awareness, public support for low-carbon living and energy conservation helps in the implementation of policies.
- (2)
- Weaknesses
- High Dependency on Coal: despite government green energy policies, certain regions remain heavily dependent on coal, with a slow transition process;
- Economic Transition Challenges: some low-carbon potential provinces still lag in industrial restructuring and technological innovation, leading to high energy demand for economic growth.
- (3)
- Opportunities
- National-Level Policy Support: policies such as green tax incentives and renewable energy project support help accelerate the application of green technologies in these regions;
- Emerging Green Technologies: technological innovations can effectively reduce dependence on coal and electricity, driving regional low-carbon transitions.
- (4)
- Threats
- External Economic Competitive Pressure: during the low-carbon transition, there may be competitive pressure from other provinces or countries in the development of green technologies;
- Inconsistent Policy Implementation: local governments may have differences in implementing green policies, leading to uneven transition progress.
- 2.
- EGHPs
- (1)
- Strengths
- Government Promotion of Green Technologies: the government supports the popularization of low-carbon technologies through policies such as green infrastructure construction and innovation subsidies;
- Strong Market Activity and Patent Applications: these factors promote local innovation and the application of green technologies.
- (2)
- Weaknesses
- Increased Energy Demand from Economic Growth: rapid economic development leads to higher energy consumption and carbon emissions, especially in high-carbon industries that rely on traditional energy sources.
- (3)
- Opportunities
- Green Economic Investment: investment and support for green technologies, both domestic and international, provide opportunities for these regions to develop low-carbon industries;
- Renewable Energy: government support for clean energy technologies can accelerate the pace of green transition.
- (4)
- Threats
- Structural Dependence on High-Carbon Industries: despite green policies, reliance on traditional high-carbon industries may limit the effectiveness of the low-carbon transition;
- Inconsistency in Local Government Policy Implementation: differences in local government execution of low-carbon policies may affect the overall emission reduction results.
- 3.
- HCDPs
- (1)
- Strengths
- Government Policies Shifting Toward Low Carbon: policies aimed at promoting green technologies and improving energy efficiency are gradually being implemented;
- Significant Potential for Technological Advancements: particularly in energy efficiency and building energy conservation, there is considerable room for improvement.
- (2)
- Weaknesses
- Reliance on Heavy Industry or High-Carbon Industries: the transformation pressure is substantial due to the reliance on these industries;
- High Energy Consumption in Densely Populated Areas: this leads to higher carbon emissions.
- (3)
- Opportunities
- National Policy Support and Local Government Green Development Projects: these can help accelerate the low-carbon transition;
- Widespread Application of Green Technologies: clean energy and energy-saving technologies can effectively reduce carbon emissions.
- (4)
- Threats
- Competition from High-Carbon Industries: the difficulty in reforming traditional industries may increase the pressure on low-carbon transition;
- Policy Implementation Effectiveness: local government execution of policies may not meet expectations, especially if local governments lack sufficient enforcement.
- 4.
- SGPs
- (1)
- Strengths
- Active Government Policies on Energy Consumption Management and Reducing Coal Use: the government has taken proactive steps in managing energy consumption and reducing coal use;
- Market Transactions and Technological Innovation Support: these support the promotion of low-carbon technologies, contributing to carbon emissions control.
- (2)
- Weaknesses
- Dependency on High-Carbon Energy in Industrial Structure: economic growth could lead to increased energy demand and carbon emissions;
- Low Public Awareness of Low-Carbon Living: this hinders the widespread adoption of low-carbon technologies.
- (3)
- Opportunities
- Energy Structure Transformation: government efforts to promote low-carbon energy and technologies enhance the green transformation of industrial structures;
- Low-Carbon Technology Support Policies: subsidies and green technology incentives help accelerate industrial transformation.
- (4)
- Threats
- Over-reliance on Coal and Traditional Energy: this could obstruct the low-carbon transition process;
- External Market and Policy Changes: changes in the global green economy and intense competition could heighten transition pressure.
- 5.
- LCTDPs
- (1)
- Strengths
- Strong Government Green Policies: these policies focus on energy structure adjustments and the application of low-carbon technologies;
- Market Activity and Technological Innovation: these factors help promote low-carbon technologies and the development of local green industries.
- (2)
- Weaknesses
- Challenges in Industrial Restructuring: difficulties remain in transforming high-carbon industries, leading to pressure in transitioning the economy;
- Limited Green Technology Diffusion: the popularization of green technologies is still constrained by technology maturity and insufficient funding.
- (3)
- Opportunities
- Technological Innovation and Increased Market Transactions: these push the application of low-carbon technologies, especially in electric transportation and clean energy;
- National Policy Support: national-level policies provide more green investment opportunities for these regions.
- (4)
- Threats
- Rapid Technological Iteration: the fast pace of green technology advancement may leave some regions behind in terms of technology updates;
- Short-Term Goals of Local Governments and Markets: inconsistent implementation of low-carbon policies may affect overall results due to the focus on short-term objectives.
4.2. Future Development Suggestions
4.2.1. LCPPs
4.2.2. EGHPs
4.2.3. HCDPs
4.2.4. SGPs
4.2.5. LCTDPs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Algorithm A1 self-adaptive k-means++ | |
| 1: | Input: Features |
| 2: | Output: Categorized results by province |
| 3: | Initialize cluster centers randomly from data |
| 4: | For each k in the given range of cluster numbers do |
| 5: | For each iteration in the range of Max number of iterations do |
| 6: | Compute distances from each data point to each cluster center |
| 7: | For each data point do |
| 8: | Assign to the nearest cluster based on distance |
| 9: | End for |
| 10: | Update cluster centers based on assigned points |
| 11: | Check for convergence based on the center change threshold |
| 12: | Calculate the silhouette score for the current k and save |
| 13: | End for |
| 14: | End for |
| 15: | Determine the best k based on the maximum silhouette score |
References
- Fang, J.; Zhu, J.; Wang, S.; Yue, C.; Shen, H. Global warming, human-induced carbon emissions, and their uncertainties. Sci. China Earth Sci. 2011, 54, 1458–1468. [Google Scholar] [CrossRef]
- Sun, W.; Huang, C. Predictions of carbon emission intensity based on factor analysis and an improved extreme learning machine from the perspective of carbon emission efficiency. J. Clean. Prod. 2022, 338, 130414. [Google Scholar] [CrossRef]
- Fang, K.; Tang, Y.; Zhang, Q.; Song, J.; Wen, Q.; Sun, H.; Ji, C.; Xu, A. Will China peak its energy-related carbon emissions by 2030? Lessons from 30 Chinese provinces. Appl. Energy 2019, 255, 113852. [Google Scholar] [CrossRef]
- Lin, C.; Li, X. Carbon peak prediction and emission reduction pathways exploration for provincial residential buildings: Evidence from Fujian Province. Sustain. Cities Soc. 2024, 102, 105239. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, J.; Xu, Z.; Hu, X.; Hu, D.; Yang, G. Does the setting of local government economic growth targets promote or hinder urban carbon emission performance? Evidence from China. Environ. Sci. Pollut. Res. 2023, 30, 117404–117434. [Google Scholar] [CrossRef]
- Zheng, Y.; Tang, J.; Huang, F. The impact of industrial structure adjustment on the spatial industrial linkage of carbon emission: From the perspective of climate change mitigation. J. Environ. Manag. 2023, 345, 118620. [Google Scholar] [CrossRef]
- Zhao, J.; Ji, G.; Yue, Y.; Lai, Z.; Chen, Y.; Yang, D.; Yang, X.; Wang, Z. Spatio-temporal dynamics of urban residential CO2 emissions and their driving forces in China using the integrated two nighttime light datasets. Appl. Energy 2019, 235, 612–624. [Google Scholar] [CrossRef]
- Caiado, R.G.G.; Filho, W.L.; Quelhas, O.L.G.; Nascimento, D.L.M.; Ávila, L.V. A literature-based review on potentials and constraints in the implementation of the sustainable development goals. J. Clean. Prod. 2018, 198, 1276–1288. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, L. Research on carbon peak prediction of various prefecture-level cities in Jiangsu Province based on factors influencing carbon emissions. Sustainability 2024, 16, 7105. [Google Scholar] [CrossRef]
- Wei, Z.; Wei, K.; Liu, J.; Zhou, Y. The relationship between agricultural and animal husbandry economic development and carbon emissions in Henan Province, the analysis of factors affecting carbon emissions, and carbon emissions prediction. Mar. Pollut. Bull. 2023, 193, 115134. [Google Scholar] [CrossRef]
- Zhao, J.; Kou, L.; Wang, H.; He, X.; Xiong, Z.; Liu, C.; Cui, H. Carbon emission prediction model and analysis in the Yellow River Basin based on a machine learning method. Sustainability 2022, 14, 6153. [Google Scholar] [CrossRef]
- Dai, D.; Zhou, B.; Zhao, S.; Lu, K.; Liu, Y. Research on industrial carbon emission prediction and resistance analysis based on CEI-EGM-RM method: A case study of Bengbu. Sci. Rep. 2023, 13, 14528. [Google Scholar] [CrossRef] [PubMed]
- Yan, R.; Chen, M.; Xiang, X.; Feng, W.; Ma, M. Heterogeneity or illusion? Track the carbon Kuznets curve of global residential building operations. Appl. Energy 2023, 347, 121441. [Google Scholar] [CrossRef]
- Zou, C.; Ma, M.; Zhou, N.; Feng, W.; You, K.; Zhang, S. Toward carbon free by 2060: A decarbonization roadmap of operational residential buildings in China. Energy 2023, 277, 127689. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, M.; Zhu, H.; Jiang, H.; Liu, J. Impact factors and peaking simulation of carbon emissions in the building sector in Shandong Province. J. Build Eng. 2024, 87, 109141. [Google Scholar] [CrossRef]
- Yang, J.; Cai, W.; Ma, M.; Li, L.; Liu, C.; Ma, X.; Li, L.; Chen, X. Driving forces of China’s CO2 emissions from energy consumption based on Kaya-LMDI methods. Sci. Total Environ. 2020, 711, 134569. [Google Scholar] [CrossRef]
- Zhu, B.; Ye, S.; Han, D.; Wang, P.; He, K.; Wei, Y.; Xie, R. A multiscale analysis for carbon price drivers. Energy Econ. 2019, 78, 202–216. [Google Scholar] [CrossRef]
- Yu, Y.; Xu, W. Impact of FDI and R&D on China’s industrial CO2 emissions reduction and trend prediction. Atmos. Pollut. Res. 2019, 10, 1627–1635. [Google Scholar]
- Sapnken, F.E.; Hong, K.R.; Noume, H.C.; Tamba, J.G. A grey prediction model optimized by meta-heuristic algorithms and its application in forecasting carbon emissions from road fuel combustion. Energy 2024, 302, 131922. [Google Scholar] [CrossRef]
- Zhong, W.; Zhai, D.; Xu, W.; Gong, W.; Yan, C.; Zhang, Y.; Qi, L. Accurate and efficient daily carbon emission forecasting based on improved ARIMA. Appl. Energy 2024, 376, 12432. [Google Scholar] [CrossRef]
- Ye, L.; Du, P.; Wang, S. Industrial carbon emission forecasting considering external factors based on linear and machine learning models. J. Clean. Prod. 2024, 434, 140010. [Google Scholar] [CrossRef]
- Luo, C.; Gao, Y.; Jiang, Y.; Zhao, C.; Ge, H. Predictive modeling of carbon emissions in Jiangsu Province’s construction industry: An MEA-BP approach. J. Build Eng. 2024, 86, 108903. [Google Scholar] [CrossRef]
- Jiang, X. Prediction method of carbon emissions of intelligent buildings based on secondary decomposition BAS-LSTM. Clean. Technol. Environ. Policy 2024. [Google Scholar] [CrossRef]
- Niu, D.; Wang, K.; Wu, J.; Sun, L.; Liang, Y.; Xu, X.; Yang, X. Can China achieve its 2030 carbon emissions commitment? Scenario analysis based on an improved general regression neural network. J. Clean. Prod. 2020, 243, 118558. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, J. Analysis influence factors and forecast energy-related CO2 emissions: Evidence from Hebei. Environ. Monit. Assess 2020, 192, 665. [Google Scholar] [CrossRef]
- Yao, Y.; Sun, Z.; Li, L.; Cheng, T.; Chen, D.; Zhou, G.; Liu, C.; Kou, S.; Chen, Z.; Guan, Q. CarbonVCA: A cadastral parcel-scale carbon emission forecasting framework for peak carbon emissions. Cities 2023, 138, 104354. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, Q.; Tan, T. Prediction of carbon dioxide emissions in China using shallow learning with cross validation. Energies 2022, 15, 8642. [Google Scholar] [CrossRef]
- Green, F.; Stern, N. China’s changing economy: Implications for its carbon dioxide emissions. Clim. Policy 2016, 17, 423–442. [Google Scholar] [CrossRef]
- Wang, A.; Hu, S.; Lin, B. Emission abatement cost in China with consideration of technological heterogeneity. Appl. Energy 2021, 290, 116748. [Google Scholar] [CrossRef]
- Wang, Q.; Li, L. The effects of population aging, life expectancy, unemployment rate, population density, per capita GDP, urbanization on per capita carbon emissions. Sustain. Prod. Consum. 2021, 28, 760–774. [Google Scholar] [CrossRef]
- Wang, Y.; Niu, Y.; Li, M.; Yu, Q.; Chen, W. Spatial structure and carbon emission of urban agglomerations: Spatiotemporal characteristics and driving forces. Sustain. Cities Soc. 2021, 78, 103600. [Google Scholar] [CrossRef]
- Zhou, J.; Hu, T.; Wei, Z.; Ji, D. Evaluation of high-quality development level of regional economy and exploration of index obstacle degree: A case study of Henan Province. J. Knowl. Econ. 2024, 129, 107994. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X. A comparative study of statistical and machine learning models on carbon dioxide emissions prediction of China. Environ. Sci. Pollut. Res. 2023, 30, 117485–117502. [Google Scholar] [CrossRef] [PubMed]
- Baldassi, C. Recombinator-k-means: An evolutionary algorithm that exploits k-means++ for recombination. IEEE Trans. Evol. Comput. 2022, 26, 991–1003. [Google Scholar] [CrossRef]
- Geng, X.; Mu, Y.; Mao, S.; Ye, J.; Zhu, L. An improved k-means algorithm based on fuzzy metrics. IEEE Access 2020, 8, 217416–217424. [Google Scholar] [CrossRef]
- McNeish, D.M. Using Lasso for predictor selection and to assuage overfitting: A method long overlooked in behavioral sciences. Multivariate Behav. Res. 2015, 50, 471–484. [Google Scholar] [CrossRef]
- Gao, C.; Hu, Z.; Xiong, Z.; Su, Q. Grey prediction evolution algorithm based on accelerated even grey model. IEEE Access 2020, 8, 107941–107957. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Zhang, H.; Xiong, L.; Lei, H.; Deng, S. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Raghavendra, S.N.; Deka, P.C. Support vector machine applications in the field of hydrology: A review. Appl. Soft. Comput. 2014, 19, 372–386. [Google Scholar] [CrossRef]
- Shan, Y.; Guan, D.; Zheng, H.; Ou, J.; Li, Y.; Meng, J.; Mi, J.; Zhu, L.; Zhang, Q. China CO2 emission accounts 1997–2015. Sci. Data 2018, 5, 170201. [Google Scholar] [CrossRef]
- Shan, Y.; Huang, Q.; Guan, D.; Hubacek, K. China CO2 emission accounts 2016–2017. Sci. Data 2020, 7, 54. [Google Scholar] [CrossRef] [PubMed]
- Shan, Y.; Liu, J.; Liu, Z.; Xu, X.; Shao, S.; Wang, P.; Guan, D. New provincial CO2 emission inventories in China based on apparent energy consumption data and updated emission factors. Appl. Energy 2016, 184, 742–750. [Google Scholar] [CrossRef]
- Guan, Y.; Shan, Y.; Huang, Q.; Chen, H.; Wang, D.; Hubacek, K. Assessment to China’s recent emission pattern shifts. Earths Future 2021, 9, 11. [Google Scholar] [CrossRef]
- Xu, J.; Guan, Y.; Oldfield, J.; Guan, D.; Shan, Y. China carbon emission accounts 2020–2021. Appl. Energy 2024, 360, 122837. [Google Scholar] [CrossRef]
- Wang, A.; Hu, S.; Lin, B. Can environmental regulation solve pollution problems? Theoretical model and empirical research based on the skill premium. Energy Econ. 2020, 94, 105068. [Google Scholar] [CrossRef]
- Andrée, B.P.J.; Chamorro, A.; Spencer, P.; Koomen, E.; Dogo, H. Revisiting the relation between economic growth and the environment; a global assessment of deforestation, pollution and carbon emission. Renew. Sustain. Energy Rev. 2019, 114, 109221. [Google Scholar] [CrossRef]
- Yang, W.; Feng, L.; Wang, Z.; Fan, X. Carbon emissions and national sustainable development goals coupling coordination degree study from a global perspective: Characteristics, heterogeneity, and spatial effects. Sustainability 2023, 15, 9070. [Google Scholar] [CrossRef]
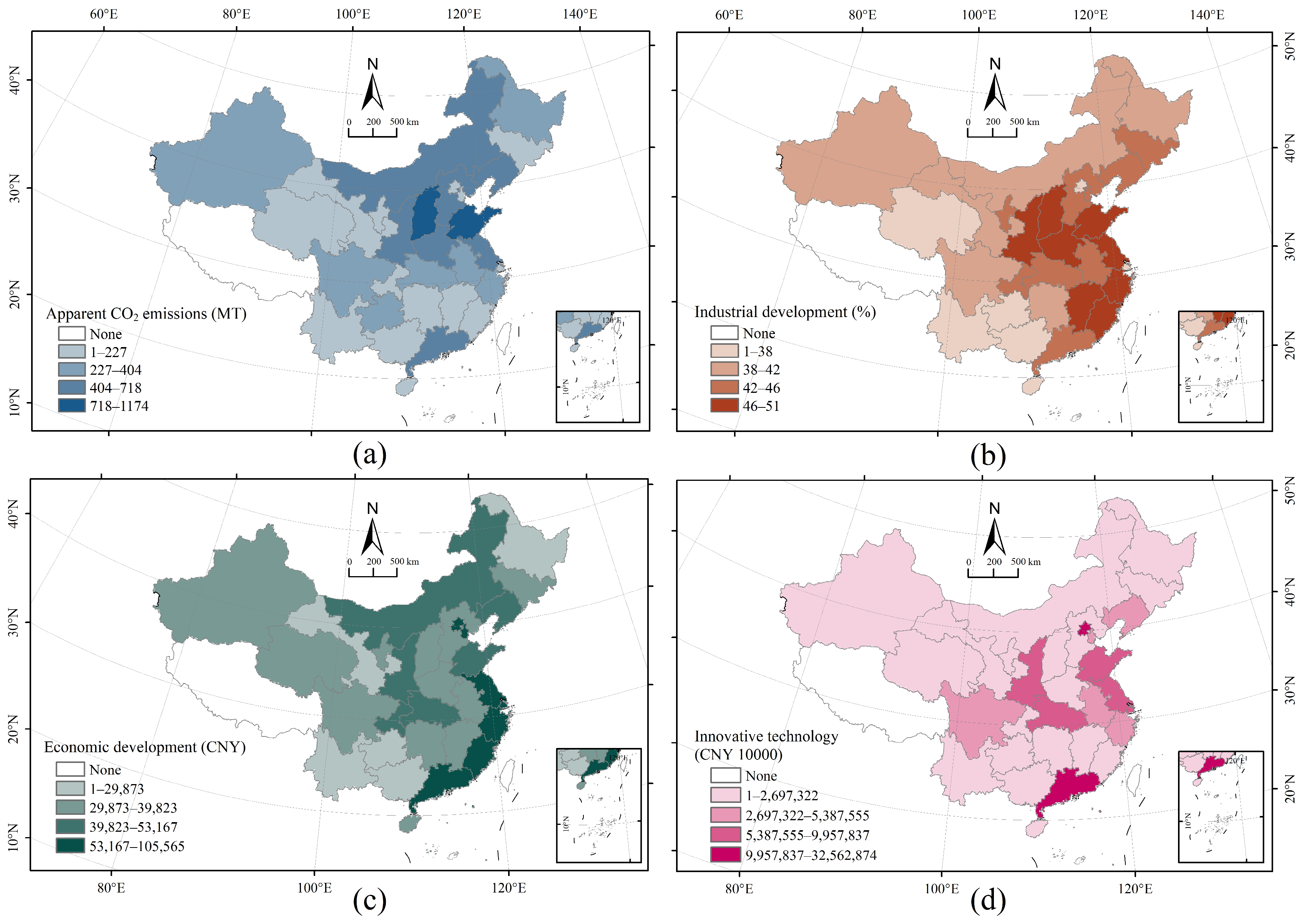

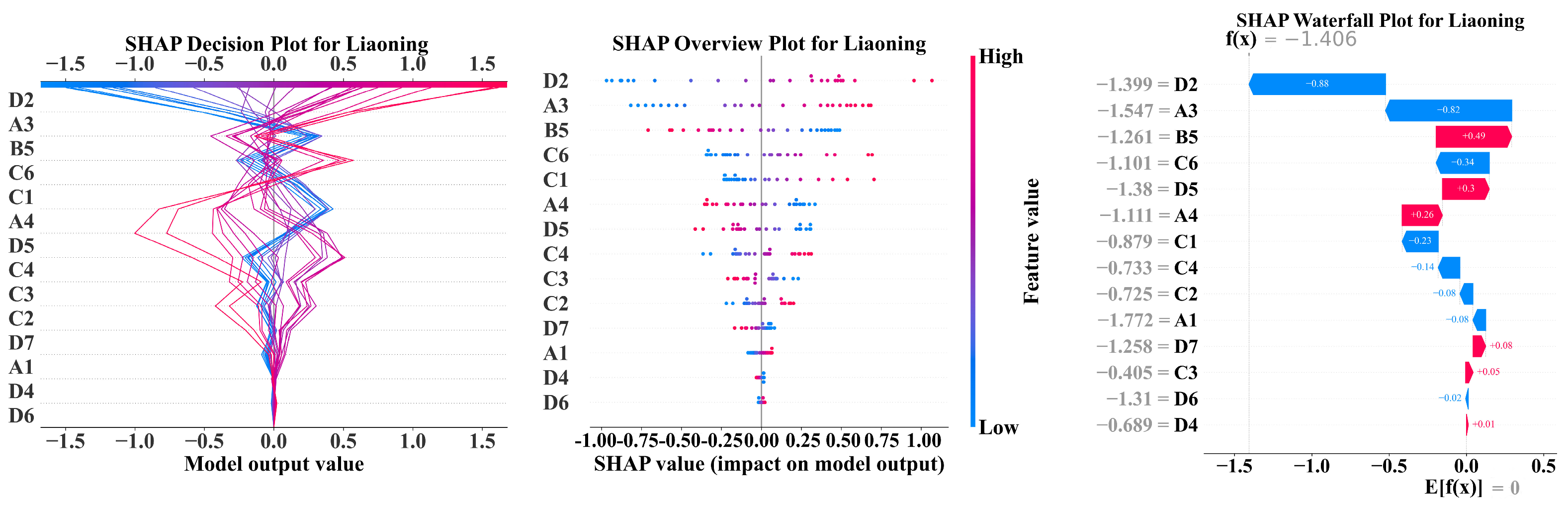

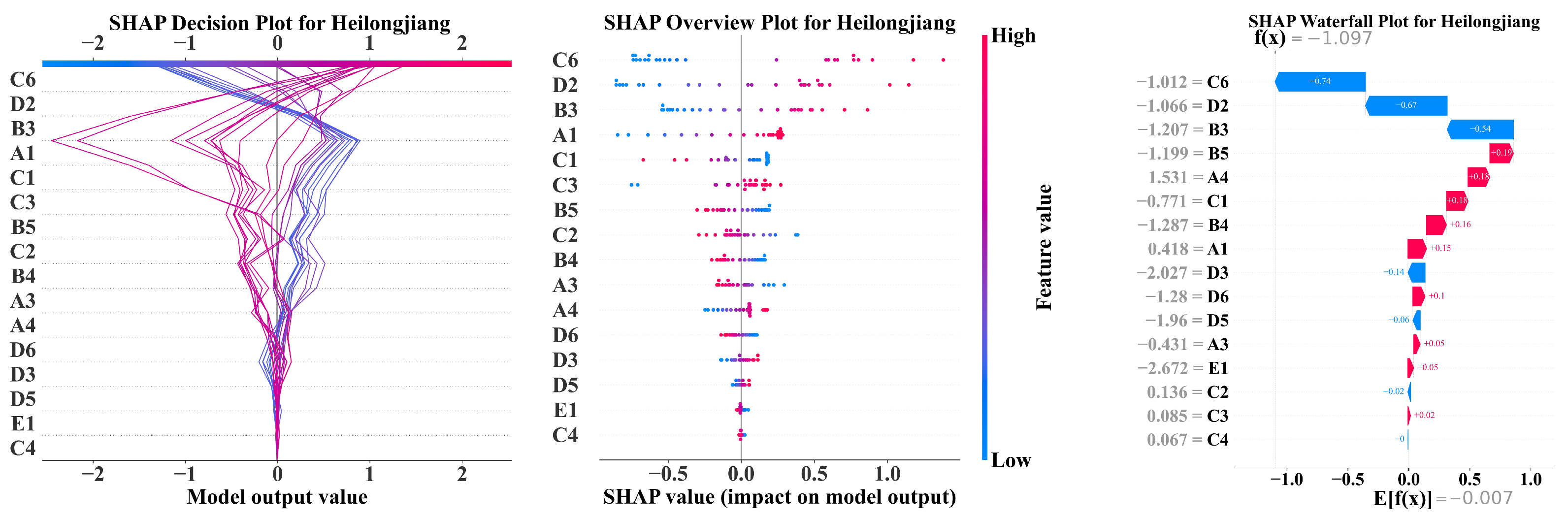
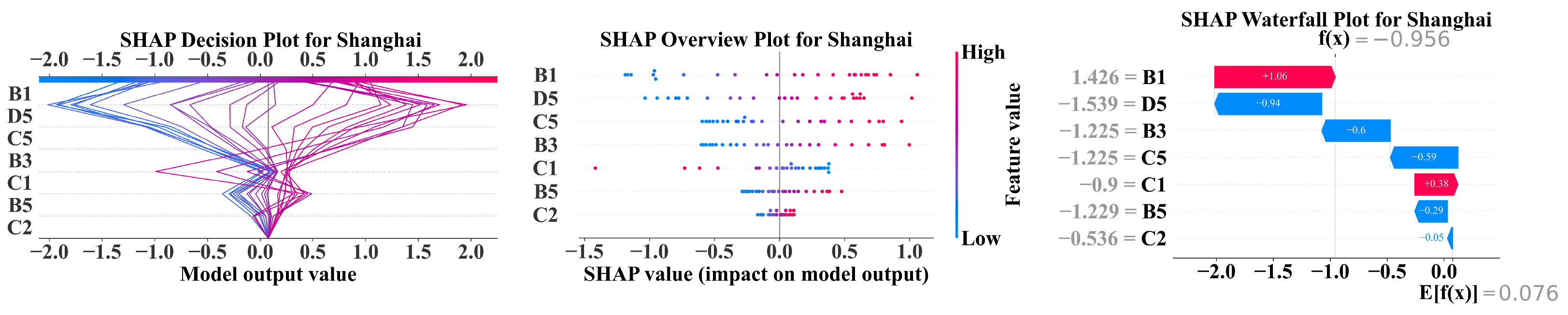
| Primary Feature | Secondary Feature | Unit | Code |
|---|---|---|---|
| Population | Total Population | Ten thousand people | A1 |
| Urbanization Rate | % | A2 | |
| Urban Population | Ten thousand people | A3 | |
| Resident Population at Year-End | Ten thousand people | A4 | |
| Economy | Proportion of Secondary Industry in GDP | % | B1 |
| Proportion of Tertiary Industry in GDP | % | B2 | |
| GDP per Capita | CNY | B3 | |
| Gross Regional Product | Hundred million CNY | B4 | |
| GDP per Capita of Region | CNY/person | B5 | |
| Social Factors | Technology Market Transaction Value | Ten thousand CNY | C1 |
| Road Passenger Traffic | Ten thousand CNY | C2 | |
| Rail Passenger Traffic | Ten thousand CNY | C3 | |
| Passenger Traffic | Ten thousand passenger trips | C4 | |
| Education Expenditure | Ten thousand CNY | C5 | |
| Domestic Patent Applications Received | Items | C6 | |
| Energy Factors | Carbon Dioxide Emissions | MT | D1 |
| Coal Consumption | Ten thousand tons | D2 | |
| Gasoline Consumption | Ten thousand tons | D3 | |
| Natural Gas Consumption | Hundred million cubic meters | D4 | |
| Diesel Consumption | Ten thousand tons | D5 | |
| Electricity Consumption | Billion kWh | D6 | |
| Kerosene Consumption | Ten thousand tons | D7 | |
| Environmental Factors | Green Coverage Rate in Built-up Areas | % | E1 |
| Province | B3 | A1 | C1 | C2 | C3 | C4 | E1 |
|---|---|---|---|---|---|---|---|
| Shanghai | 0.006 | −0.023 | 0 | −0.01 | −0.008 | 0 | 0.319 |
| Yunnan | 0 | −0.292 | 0 | 0 | 0.005 | −0.001 | −0.404 |
| Inner Mongolia | 0.037 | 0.794 | 0 | −0.023 | 0.041 | 0.022 | −0.675 |
| Beijing | 0 | 0.059 | 0 | 0 | 0.001 | 0 | −0.303 |
| Jilin | 0.001 | 0.234 | 0 | −0.006 | −0.001 | 0.006 | 0.101 |
| Sichuan | −0.001 | −0.046 | 0 | −0.002 | −0.002 | 0.002 | −4.88 |
| Tianjin | −0.003 | 0 | 0 | 0.028 | 0.039 | −0.028 | 0 |
| Ningxia | 0.003 | 3.242 | 0 | −0.02 | 0.053 | 0.018 | 1.854 |
| Anhui | −0.006 | −0.041 | 0 | 0.004 | 0.011 | −0.004 | −0.61 |
| Shandong | 0.026 | 1.441 | 0 | −0.003 | 0.009 | 0.003 | 4.257 |
| Shanxi | −0.384 | −0.576 | 0.001 | 0.127 | 0.176 | −0.155 | −19.819 |
| Guangdong | 0 | −0.017 | 0 | 0.001 | 0 | −0.001 | −2.114 |
| Guangxi | 0.006 | −0.027 | 0 | 0.004 | 0.005 | −0.003 | 0.076 |
| Xinjiang | 0.01 | −0.039 | 0 | 0 | −0.002 | 0 | 2.185 |
| Jiangsu | 0 | −0.625 | 0 | −0.005 | −0.006 | 0.005 | −0.761 |
| Jiangxi | 0.001 | −0.098 | 0 | −0.001 | 0 | 0.001 | −0.299 |
| Hebei | −0.094 | 0.772 | 0 | 0 | 0.02 | −0.001 | 0 |
| Henan | −0.05 | 0.125 | 0 | −0.021 | −0.03 | 0.02 | 0.19 |
| Zhejiang | 0.01 | −0.011 | 0 | 0.011 | 0.01 | −0.011 | 2.707 |
| Hainan | −0.002 | −0.222 | 0 | −0.012 | −0.02 | 0.012 | 0.139 |
| Hubei | −0.001 | −0.008 | 0 | 0 | 0.003 | 0 | −0.453 |
| Hunan | 0.005 | 0.142 | 0 | 0 | −0.001 | 0 | −11.551 |
| Gansu | −0.002 | −0.019 | 0 | 0.004 | 0.007 | −0.004 | 0.306 |
| Fujian | 0.004 | −0.069 | 0 | 0.001 | 0 | −0.001 | −3.901 |
| Guizhou | 0.02 | 0.02 | 0 | 0 | −0.019 | 0 | −0.809 |
| Liaoning | −0.064 | 0.344 | 0 | 0.009 | 0.004 | −0.008 | 0.254 |
| Chongqing | −0.002 | −0.126 | 0 | 0 | 0.013 | 0 | −1.078 |
| Shaanxi | 0.016 | 2.562 | 0 | 0.012 | 0.021 | −0.012 | −1.566 |
| Qinghai | 0.007 | 0.418 | 0 | −0.015 | 0.007 | 0.015 | −0.24 |
| Heilongjiang | −0.004 | 0.399 | 0 | −0.002 | 0.016 | 0 | 0.04 |
| Category | Effective Driving Factors |
|---|---|
| Low-carbon potential provinces (LCPPs) | C2, B3, D2, A3, A1, C1, D6, C4, C6, C3, B5, B4 |
| Economic growth hub provinces (EGHPs) | C1, B5, D5, D7, C6, C2, C3, D2, C4, D4, D6, A4, A1, A3 |
| High-carbon-dependent provinces (HCDPs) | A4, B3, C1, C2, D6, B4, C6, A3, D7, E1, B1 |
| Sustainable growth provinces (SGPs) | C1, A3, A4, B5, C6, C2, B3, C3, E1, D5, B4, D3, D2, C4, D6, A1 |
| Low-carbon technology-driven provinces (LCTDPs) | C2, C1, B5, C5, D5, B1, B3 |
| Province | Factor | 2027 | 2028 | 2029 | 2030 | 2031 |
|---|---|---|---|---|---|---|
| Hainan (LCPPs) | C1 | 70,003.93 | 76,783.04 | 84,218.63 | 92,374.28 | 101,319.70 |
| C2 | 26,654.30 | 28,043.98 | 29,506.10 | 31,044.46 | 32,663.03 | |
| D5 | 455.33 | 468.52 | 482.10 | 496.07 | 510.44 | |
| Liaoning (EGHPs) | C1 | 15,186,425.47 | 17,646,268.75 | 20,504,548.71 | 23,825,802.71 | 27,685,021.65 |
| C2 | 74,335.99 | 75,319.90 | 76,316.83 | 77,326.95 | 78,350.45 | |
| D5 | 2371.90 | 2532.60 | 2704.17 | 2887.38 | 3082.99 | |
| Shandong (HCDPs) | C1 | 59,327,768.93 | 65,207,510.88 | 77,094,826.87 | 87,512,060.07 | 90,219,269.12 |
| C2 | 114,268.81 | 114,535.20 | 114,802.20 | 115,069.82 | 115,338.07 | |
| B1 | 41.08 | 40.68 | 40.29 | 39.90 | 39.51 | |
| Heilongjiang (SGPs) | C1 | 8,159,351.428 | 9,517,661.358 | 11,102,092.92 | 12,950,289.21 | 15,106,159.89 |
| C2 | 21,797.98 | 21,228.48 | 20,673.87 | 20,133.75 | 19,607.74 | |
| D5 | 483.43 | 485.75 | 488.08 | 490.42 | 492.77 | |
| Shanghai (LCTDPs) | C1 | 38,685,401.75 | 44,225,406.57 | 50,558,776.64 | 57,799,127.11 | 66,076,343.53 |
| C2 | 4075.18 | 4163.22 | 4253.17 | 4345.06 | 4438.93 | |
| B1 | 24.31 | 23.68 | 23.07 | 22.47 | 21.89 |
| Fold | RMSE | MAE | R2 |
|---|---|---|---|
| 1 | 0.158 | 0.150 | 0.952 |
| 2 | 0.165 | 0.154 | 0.957 |
| 3 | 0.160 | 0.152 | 0.954 |
| 4 | 0.159 | 0.153 | 0.956 |
| 5 | 0.164 | 0.156 | 0.955 |
| Avg | 0.161 | 0.153 | 0.955 |
| Algorithm | RMSE | MAE | R2 |
|---|---|---|---|
| GM | 0.345 | 0.351 | 0.671 |
| LSTM | 0.315 | 0.342 | 0.678 |
| SVR | 0.315 | 0.234 | 0.684 |
| X-GBOOST | 0.475 | 0.443 | 0.618 |
| Random Forest | 0.272 | 0.254 | 0.765 |
| GM-SVR | 0.161 | 0.153 | 0.955 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, S.; Fu, T.; Dai, M. Machine Learning-Based Carbon Emission Predictions and Customized Reduction Strategies for 30 Chinese Provinces. Sustainability 2025, 17, 1786. https://doi.org/10.3390/su17051786
Hong S, Fu T, Dai M. Machine Learning-Based Carbon Emission Predictions and Customized Reduction Strategies for 30 Chinese Provinces. Sustainability. 2025; 17(5):1786. https://doi.org/10.3390/su17051786
Chicago/Turabian StyleHong, Siting, Ting Fu, and Ming Dai. 2025. "Machine Learning-Based Carbon Emission Predictions and Customized Reduction Strategies for 30 Chinese Provinces" Sustainability 17, no. 5: 1786. https://doi.org/10.3390/su17051786
APA StyleHong, S., Fu, T., & Dai, M. (2025). Machine Learning-Based Carbon Emission Predictions and Customized Reduction Strategies for 30 Chinese Provinces. Sustainability, 17(5), 1786. https://doi.org/10.3390/su17051786






