The Source–Knowledge–Use-Based Interdisciplinary Teaching Framework for Enhancing Sustainability: A Humanities–Science–Technology Model for Fuzzy Mathematics as a Case

Abstract

Interdisciplinary teaching is a pivotal strategy for deepening disciplinary theory and broadening students’ cognitive boundaries, crucial for the sustainability of education. By considering scientific knowledge’s humanistic background and technological evolution, this study proposes a novel interdisciplinary teaching framework based on the Source–Knowledge–Use (SKU) paradigm. Then, taking fuzzy mathematics as a case, the Humanities–Science–Technology Model (HSTM), based on a tripartite progression from humanistic foundations to scientific principles and then to technological applications, was established. This study systematically expounds the HSTM’s framework, contents, and implementation design, while critically examining potential challenges and corresponding mitigation strategies. The proposed SKU-based interdisciplinary teaching framework not only provides methodological guidance for interdisciplinary instruction in fuzzy mathematics but also offers transferable insights for cognate disciplines seeking to implement sustainable educational practices.

1. Introduction

1.1. Background

The world is undergoing unprecedented change, presenting significant opportunities as well as formidable challenges. Sustainable development has become a global consensus [1,2]. Education is a major force for social progress, and innovation in teaching models is particularly critical [3]. Especially when faced with complex and ever-changing challenges, the traditional teaching mode based on a single discipline has struggled to meet the demands of sustainable development.

Against this background, the use of a novel interdisciplinary paradigm has emerged as a key issue to be addressed [4,5,6]. Interdisciplinary teaching, an innovative educational concept, emphasizes breaking down the boundaries of traditional disciplines and promoting the organic integration of multidisciplinary knowledge [7,8,9]. Its core idea is that, in the face of increasingly complex societal problems and real needs, it is often difficult to provide solutions with knowledge of a single discipline, while interdisciplinary teaching can cultivate students’ ability to use multidisciplinary knowledge comprehensively, improve their depth of thinking, and enhance their ability to solve complex problems [10,11].

Scholars have engaged in in-depth discussions on interdisciplinary teaching. Kelly-Irving et al. [12] bring together researchers and participants from different disciplinary backgrounds to work within a course framework. Filler et al. [13] explored how interdisciplinary teaching can be implemented through the Internet. In view of the problems in teaching “Transport Economics”, Hang et al. [14] discussed the need to introduce problem-based learning (PBL), teaching organization, and implementation methods. Hu et al. [15] constructed a three-dimensional integrated interdisciplinary teaching design based on the science curriculum standard of junior high school in China, and explained the design ideas, methods, and key strategies by taking the teaching of a water-related topic in junior high school as an example. Jiang and Wang [16] analyzed the practical dilemma and transformative approach of interdisciplinary subject teaching. Relevant research shows that current interdisciplinary teaching mainly focuses on using multidisciplinary knowledge to solve a specific problem or task, but the underlying logic and basic paradigm are not sufficiently considered.

We believe that the birth of a discipline serves at least a dual function: describing the world and serving humanity. Therefore, its most basic foundation should be the interpretation of practical problems and human knowledge. On this basis, through logical reasoning and empirical research, the mysteries and laws of nature are revealed, forming a series of scientific systems. How does science serve mankind? Thus, technology must be developed. Technology is the practical application of scientific principles, which not only promotes the progress and development of society, but also deepens people’s understanding of the world and benefits humanity.

1.2. The Objective of This Study

Humanities, science, and technology complement each other and, together, form a complete system of human cognition and world transformation. Therefore, the construction of an interdisciplinary teaching model “from humanities to science and then to technology (HSTM)” is of great value in improving students’ expansion of thinking and innovation ability. However, the current practice of interdisciplinary teaching rarely includes the integration of humanities, science, and technology.

In view of the above analysis, this study attempts to explore a new interdisciplinary teaching idea called “Source–Knowledge–Use (SKU)” based on the whole development process of a scientific knowledge. Then, focusing on the fuzzy mathematics course, the HSTM is applied and modeled, and several related issues are discussed.

2. Concepts and Model

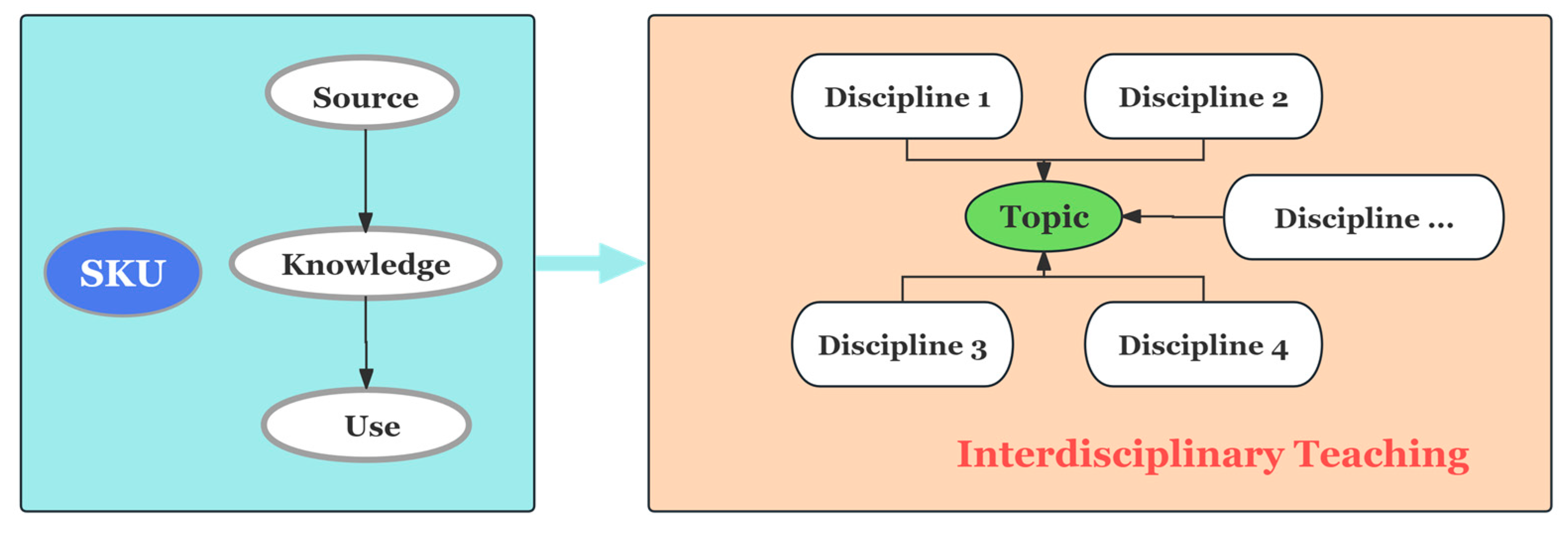
2.1. Interdisciplinary Teaching and Source–Knowledge–Use (SKU)

The concept of interdisciplinarity was first proposed in the mid-1920s with the aim of transcending the boundaries of a single discipline and using multidisciplinary knowledge to solve complex problems [17]. Bruce et al. [18] pointed out that interdisciplinarity is not a standalone disciplinary approach, but a comprehensive treatment of the same problem from different disciplinary perspectives and the provision of systematic results. Zhang [19] believes that interdisciplinary research is not only the pursuit of value and the spirit of the times, but also the epistemology and methodology of disciplinary research that emphasizes interactive construction and cooperative exploration. Based on the understanding of interdisciplinarity, some scholars have proposed that interdisciplinary teaching is a teaching that centers on one discipline, selects a core topic, and uses different disciplinary knowledge to process and design the common topic [20,21,22]. Some scholars have also pointed out that the core feature of interdisciplinary teaching is to design and implement around a “theme” on the basis of spanning a single discipline [23,24,25,26]. To sum up, interdisciplinary teaching is a kind of problem-solving-oriented teaching activity with a theme or topic as the carrier, integrating the knowledge and methods of more than two disciplines. In this process, we take problem solving as the goal and carry out thematic research on the effectiveness of problem solving by discovering the relevance between the knowledge of multiple disciplines. By integrating multidisciplinary knowledge to solve a specific problem, this teaching mode is obviously helpful in cultivating students’ comprehensive knowledge competence and problem solving ability.

Constructivist learning theory holds that knowledge is constructed by learners through active exploration, practice, and social interaction, rather than being passively received [27]. This requires learners to understand the source, creation, and application of knowledge and to form a comprehensive understanding of knowledge, from its origin to its application. In this process, the emphasis on knowledge construction necessitates multidisciplinary integration and reflects the social and cross-context transfer characteristics of knowledge. Thus, it should be emphasized that the teaching of a discipline’s knowledge must be conducted on the basis of a development chain. That is, it must answer three questions: What is the source of knowledge? How is knowledge created? And how is knowledge applied? From the origin of knowledge to the establishment of the knowledge system, and then to the practice of its corresponding application technology, this represents a teaching and learning mode that encompasses the full life cycle of knowledge. In this mode, learners will gain a comprehensive understanding of relevant knowledge, which undoubtedly involves the integration of multiple disciplines. For learners, this not only allows them to master the knowledge but also to understand the humanistic and practical problems it stems from, the questions it can answer, and how to put it into practice.

Based on constructivist learning theory, in this study, we condense the above consideration as the “Source–Knowledge–Use (SKU)” framework, and then propose a new teaching mode named SKU-based interdisciplinary teaching. This mode integrates SKU into interdisciplinary teaching. The framework is illustrated in Figure 1.

On the right side of Figure 1, Discipline 1, Discipline 2, etc., represent multiple different disciplines (such as philosophy, management, mathematics, etc.) that collaborate to solve a specific topic. We propose integrating the SKU concept on the left into this aspect, forming a new interdisciplinary teaching model based on SKU.

In traditional interdisciplinary teaching, this was often based on a project-based problem or issue, and then teaching and problem solving were integrated by drawing on knowledge from different disciplines that could be used to address the problem. In contrast, in the SKU philosophy we propose, this involves teaching knowledge by exploring the source of that knowledge together with an emphasis on how that knowledge can be used. Through SKU, we can present knowledge in a systematic way, which enhances students’ ability to think creatively and systematically about problems. In the process of SKU, multidisciplinary knowledge is inevitably involved, and through SKU, multidisciplinary knowledge is naturally linked or synthesized, and its applicability to problem solving becomes clear. Therefore, the SKU-based interdisciplinary teaching model teaches students a fundamental method or paradigm for dealing with a particular type of problem, rather than a solution to a particular problem.

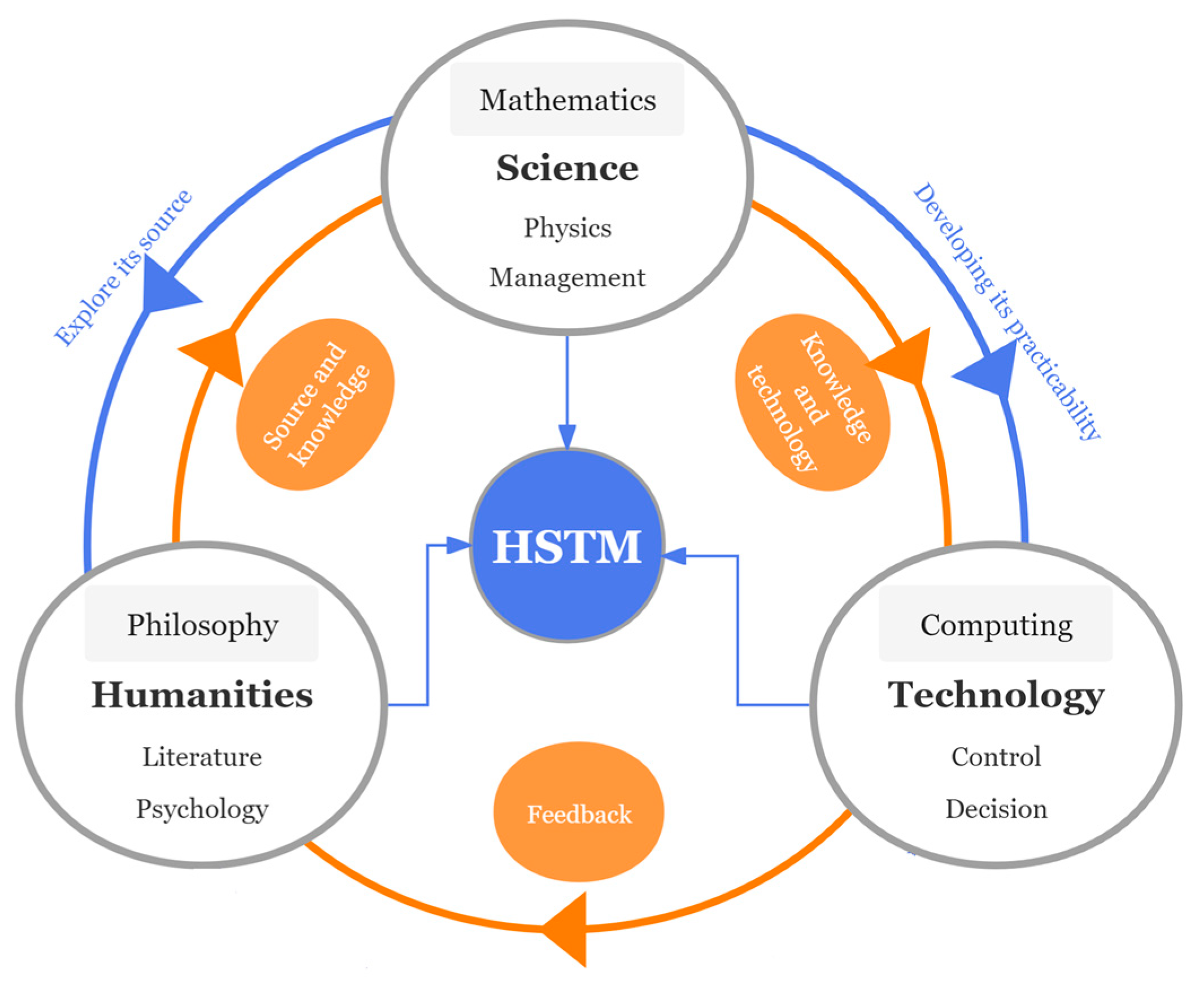
2.2. Humanities–Science–Technology Model (HSTM)

According to the SKU-based interdisciplinary teaching framework, a new interdisciplinary teaching mode has been constructed from the perspective of integrating humanities, science, and technology: HSTM. The basic framework of HSTM is shown in Figure 2.

In HSTM, H (humanities) corresponds to the S (source) in SKU, which focuses on the origin of knowledge, i.e., the philosophical problems it specifically describes. S (science) corresponds to the K (knowledge) in SKU, emphasizing the establishment of a scientific system and systematically describes the laws or problems in humanities subjects. T (technology) corresponds to the U (use) in SKU, which focuses on the application of knowledge in practice, and its core is the development of technology.

The HSTM focuses on establishing an SKU-based interdisciplinary teaching framework, emphasizing the process from humanities to science and then to technology. In humanities teaching, the main content may involve philosophy, literature, and psychology. Philosophy reflects objective reality, literature tends towards social life, and psychology is concerned with human cognition. In science teaching, this may include subjects such as mathematics, physics, and management, primarily teaching concepts, theorems, and methods. In the subsequent process of technology teaching, the emphasis is on how to apply knowledge to solve practical problems, such as computation (deriving results through mathematical deduction), control (adaptive adjustment strategies), and decision-making (selecting schemes under multi-objective constraints). Thus, a teaching chain has been formed. Furthermore, in the process of putting knowledge into practice through technology, new objective phenomena may be discovered, which require deeper humanistic knowledge for explanation (feedback mechanism). Ultimately, this forms a cycle that enhances the sustainability of discipline teaching through continuous development and accumulation.

3. HSTM for Fuzzy Mathematics

This section systematically analyzes the interdisciplinary characteristics of fuzzy mathematics from the three dimensions of humanities, science, and technology, and then proposes the framework, content, teaching methods, and implementation strategies of the HSTM of fuzzy mathematics, based on SKU-based interdisciplinary teaching.

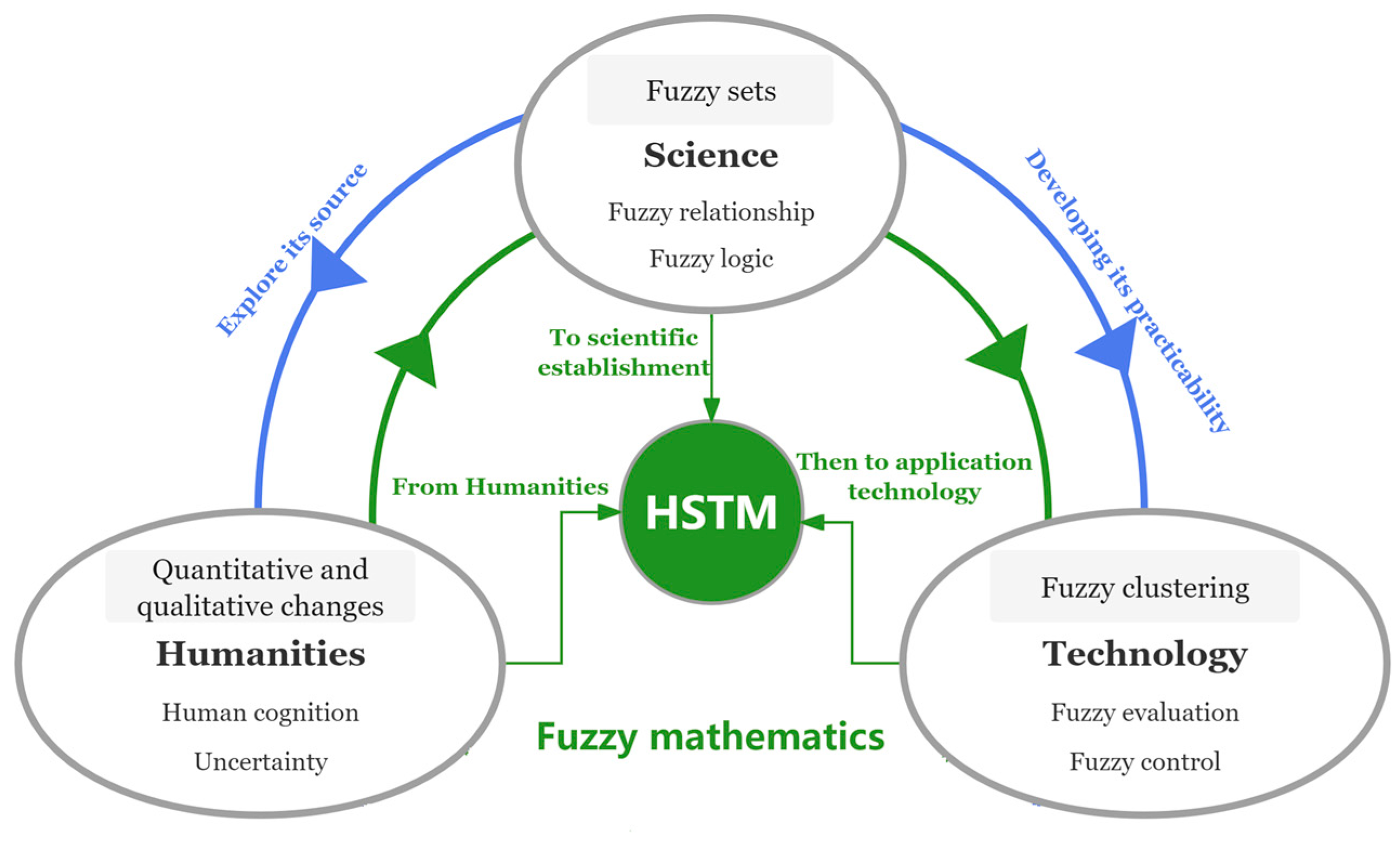
3.1. The Interdisciplinary Nature of Fuzzy Mathematics

Since the concept of fuzzy sets was proposed by Zadeh in the 1960s [28], fuzzy mathematics has rapidly evolved into an emerging discipline and has found widespread application in various fields. This section explores the interdisciplinary nature of fuzzy mathematics, considering it from three dimensions: humanities, science, and technology.

3.1.1. The Humanistic Background of Fuzzy Mathematics

The emergence and development of fuzzy mathematics have a deep philosophical background [29]. Classical mathematics is grounded in certainty and accuracy, and utilizing theoretical tools such as set theory to abstract and formalize complex phenomena in the real world. However, there are many ambiguous phenomena in the real world, such as concepts like “old age”, “tall”, “beauty”, and “intelligence”, whose boundaries are not clearly defined and cannot be strictly described by classical mathematics. The advent of fuzzy mathematics is precisely to solve such fuzzy problems, and its philosophical foundations are mainly reflected in the following aspects.

Quantitative and qualitative changes: Fuzzy mathematics fosters philosophical reflection on the transition from quantitative to qualitative changes [30]. In fuzzy sets, the degree to which elements belong to the set changes gradually, without clear boundaries. This process of change reflects the philosophical idea that things move from one state to another, embodying the transformation from quantitative to qualitative change. The similarity between fuzziness and human thinking: Fuzzy mathematics has similarities to human thinking. Fuzzy mathematics simulates and reflects the fuzziness that is often present in human thought processes. Through fuzzy mathematics, we can gain a deeper understanding of the complexity and diversity of human thought.

Fuzzy mathematics breaks the precision and certainty of traditional mathematics by introducing concepts of ambiguity and uncertainty. Consequently, it promotes the diversity and inclusiveness of human culture. The application of fuzzy mathematics has not only altered our way of thinking, but has also influenced our lifestyles and values.

3.1.2. The Scientific Value of Fuzzy Mathematics

The core concepts of fuzzy mathematics revolve around fuzzy sets, which represent an extension of the traditional set and possess several scientific attributes.

A fuzzy set is a mathematical model that captures the degree of uncertainty in an item’s categorization. Membership functions are employed to describe the extent to which elements belong to a set. By incorporating membership functions, fuzzy mathematics can more accurately describe the fuzziness in the real world. The proposal of fuzzy sets breaks the limitation of classical set theory that the membership relationship between elements and sets can only be either “yes” or “no”. In fuzzy sets, elements can possess any real number between 0 and 1 as their degree of membership, mirroring the inherent characteristics of fuzzy phenomena in reality.

Fuzzy logic leverages fuzzy set theory to investigate the reasoning of fuzzy thinking, along with the forms and laws governing fuzzy language [31]. It constitutes a multi-valued logic that challenges the traditional binary principle and the laws of contradiction and the excluded middle. The focus of fuzzy logic is on fuzzy entities that can be quantified in uncertain things, and can be used in many fields such as control theory, information theory, systems engineering, etc. The advent of fuzzy logic provides a new mathematical tool for addressing fuzzy problems.

As a branch of modern mathematics, fuzzy mathematics is closely related to other branches of mathematics. For example, fuzzy topology, fuzzy group theory, fuzzy convexity theory, fuzzy probability, etc., are all important research areas in fuzzy mathematics. The development of these sub-disciplines not only enriches the theoretical system of fuzzy mathematics, but also promotes the development of other branches of mathematics. In addition, fuzzy mathematics is closely related to classical mathematics, stochastic mathematics, and so on. Classical mathematics has achieved significant results in dealing with deterministic problems, but it has shortcomings in dealing with fuzzy problems. The introduction of fuzzy mathematics addresses this limitation, providing fresh tools and methods for managing fuzzy problems.

3.1.3. The Technical Application of Fuzzy Mathematics

The application technology of fuzzy mathematics has strong practicality and has been widely used in many areas of daily production and life.

Fuzzy clustering analysis permits a data point to belong to multiple categories simultaneously, and each data point can have different degrees of membership to each category [32]. This method has a wide range of applications in fields such as data mining, image segmentation and pattern recognition. For example, in image segmentation, fuzzy clustering analysis can segment the image into different regions based on features such as pixel greyscale values and colors, thus achieving automatic segmentation and recognition of the image.

Based on fuzzy set theory, the fuzzy control system uses fuzzy logic to fuzzify the input, state, and output of the system, and controls the system according to fuzzy inference rules. This control system has strong robustness, adaptability, and fault tolerance, and can handle more complex and uncertain control problems [33]. Fuzzy control systems have been widely applied in fields such as industrial automation and traffic control.

Fuzzy optimization technology is used for dealing with optimization problems that contain fuzziness and uncertainty. It uses fuzzy set to fuzzify the objective function of problems, and obtains the optimal or satisfactory solution through fuzzy reasoning and solving algorithms. Fuzzy optimization technology has a wide range of applications in engineering design, economic planning, and production management [34].

Fuzzy comprehensive evaluation uses fuzzy sets to quantify multiple indicators and comprehensively evaluate the object based on membership functions and weight coefficients [35]. This method has the advantages of simple evaluation process and objective and accurate evaluation results, and has been widely used in fields such as enterprise management, environmental evaluation, and educational evaluation.

3.2. The Framework and Contents of HSTM for Fuzzy Mathematics

3.2.1. The Basic Framework

According to Section 3.1, it is not difficult to find that fuzzy mathematics has rich connotations in the three dimensions of humanities, science, and technology. In fact, many disciplines serve people and should start from describing the humanistic source, to forming a scientific system, and then to developing practical technology.

It is key to know what it is and why it matters, and how to apply what you have learned. Therefore, the fuzzy mathematics course reflects the integration of multiple disciplines and also lays the foundation for interdisciplinary teaching and learning based on the integration of humanities, science, and technology.

The basic framework of the HSTM for fuzzy mathematics is shown in Figure 3.

Based on the HSTM framework, the content of a fuzzy mathematics course is discussed in terms of three dimensions: humanities, science, and technology.

3.2.2. Humanistic Dimension Content

In the humanistic dimension, the fuzzy set has a wide compatibility and has wide-ranging and deep connotations in philosophy, psychology, sociology, etc.

In materialistic dialectics, quantitative change and qualitative change are regarded as two basic states of development and change of things. Quantitative change is the gradual increase or decrease in the quantity of things, and it is the change in the relative static state of things in the process of development, which reflects the continuity of the existence and development of things, and is the necessary preparation for qualitative change. Qualitative change is the fundamental change of things and the interruption of the gradual process of things, which is manifested as a fundamental and significant change. A fuzzy set describes the fuzzy properties of things through a membership function, which is itself a manifestation of quantitative change. When the degree of membership gradually increases and reaches a certain critical value, the nature of things can change qualitatively and enter a new category of fuzzy set.

From a psychological point of view, the cognitive process of human beings is full of uncertainty. The cognitive process consists of the human brain reflecting on the nature of objective objects and the relationship between objects through the forms of sensation, perception, image, memory, thought, speech, and imagination. In this process, sensation is the individual reflection of the human brain on the objective things that directly affect the sensory organs, while perception is the grasping of the general attributes of things. The application of fuzzy sets in psychology is reflected in the description and analysis of human cognitive fuzziness. For example, when people evaluate something, they often use vague language such as “very good”, “average”, “bad”, and so on. There is no clear boundary between these evaluations, but there is a certain transition zone. A fuzzy set describes this transition state by a membership function, which makes people’s perception of things more subtle and comprehensive. In addition, with the continuous increase in information and deepening of cognition, people’s evaluation of things may also undergo qualitative changes, from vague to clear, or from one fuzzy set to another fuzzy set, which is very consistent with the cognitive change process in psychology.

In sociology, uncertainty as an essential feature of modern society has become a practical problem and an academic issue that cannot be ignored. Fuzzy sets provide a powerful tool for evaluating uncertainty. With the drastic change in social structures and the transformation from traditional society to modern society, the uncertainty of social development has emerged. Fuzzy sets can quantitatively analyze and comprehensively evaluate social phenomena with uncertainty through membership function and fuzzy operation. For example, in human resource management, employee performance evaluation often involves several fuzzy indicators, such as work ability, work attitude, teamwork, and so on. These indicators are difficult to measure with precise numbers, but fuzzy sets can transform these fuzzy indicators into quantifiable membership degrees for comprehensive evaluation. In addition, fuzzy sets can also deal with multi-factor and multi-level complex problems, such as logistics location, quality, and economic benefit evaluation, which are also full of uncertainty.

3.2.3. Scientific Dimension Content

In terms of the scientific dimension, fuzzy set combines the classical set theory method with the common phenomenon of this and that. It expands the category of set concepts, and derives fuzzy relations, fuzzy logic, and other reasoning methods, thereby laying a foundation for the application of fuzzy mathematics.

Fuzzy set theory is an important branch of modern mathematics dedicated to the description and treatment of phenomena involving fuzziness. The concept of a fuzzy set extends traditional set theory, where the relationship between an element and a set is clear: either belonging or not. However, in reality, many concepts such as “young”, “tall”, and “warm” have fuzziness that is difficult to define with a simple “yes” or “no”.

Fuzzy sets introduce a membership function to describe this fuzziness, mapping elements in the universe of discourse to the interval [0,1], representing the degree to which an element belongs to the set. Let U be the universe of discourse, and A be a fuzzy set on U. For any u ∈ U, there exists a membership function:

μ_A(u) ∈ [0,1]

(1)

where μ_A(u) = 1 indicates that u fully belongs to A; μ_A(u) = 0 indicates that u does not belong to A; and 0 < μ_A(u) < 1 indicates that u partially belongs to A. Fuzzy set theory provides mathematical tools for dealing with such fuzzy phenomena, widely applied in artificial intelligence, decision support systems, control systems, and other fields.

Fuzzy relations extend traditional relations to describe associations between elements with fuzziness. In ordinary relations, the relationship between elements is clear-cut, either existing or not. However, in reality, many relations such as “similarity” and “proximity” possess fuzziness. Fuzzy relations introduce a membership function to describe this fuzziness. Given the universes of discourse U and V, a fuzzy subset R of their Cartesian product U × V is called a fuzzy relation from U to V. The fuzzy relation R is fully determined by its membership function μ_R, which, for any (u,v) ∈ U × V, reflects the degree to which u relates to v according to R.

Fuzzy logic extends traditional Boolean logic to handle propositions and reasoning with fuzziness. In Boolean logic, the truth value of a proposition can only be 0 or 1, true or false. In reality, however, many propositions, such as “This room is warm”, have fuzziness, with truth values that are difficult to define with a simple true or false. Fuzzy logic introduces a membership function to describe this fuzziness, allowing propositional truth values to be any value in the interval [0,1], representing the degree to which a proposition is true. The core of fuzzy logic is fuzzy reasoning based on IF-THEN fuzzy rules, using fuzzy relations for reasoning and decision-making. Fuzzy reasoning includes fuzzification, inference, and defuzzification steps. Fuzzification maps actual inputs to fuzzy sets and calculates their membership degrees. Reasoning determines the output based on the degree of agreement between fuzzy rules and inputs. Defuzzification converts fuzzy outputs into definite output values.

3.2.4. Technical Dimension Content

In terms of technology, the applications of fuzzy sets mainly include fuzzy cluster analysis, fuzzy comprehensive evaluation and fuzzy control, which have been widely and successfully applied in many fields.

Fuzzy clustering is widely applied in fields such as data mining, image processing and bioinformatics, especially when dealing with datasets with fuzzy boundaries and complex characteristics, such as market segmentation, gene expression pattern recognition, and image segmentation. It effectively reveals the inherent structure and patterns in the data. In fuzzy clustering, the degree to which a sample does not belong to a cluster is considered to be gradual, rather than an absolute 0 or 1. The core idea is to construct a fuzzy similarity matrix that reflects the similarity between samples and perform clustering through fuzzy equivalence relations. The specific steps include (1) determining the sample set and constructing sample feature vectors; (2) computing the similarity between samples to construct a fuzzy similarity matrix; (3) clustering the fuzzy similarity matrix based on fuzzy equivalence relations or λ-cut methods; and (4) analyzing the clustering results to reveal the inherent structure and patterns within the data. The Fuzzy C-Means (FCM) algorithm is a typical representative of fuzzy clustering, with an objective function to minimize the weighted squared error sum between samples and cluster centers, where the weighting coefficients are membership degrees.

Fuzzy comprehensive evaluation is widely used in fields such as environmental assessment, business management, and risk assessment, especially when dealing with complex problems characterized by multiple factors, multiple levels, and fuzziness, such as water quality evaluation, supply chain performance evaluation, and project investment risk assessment. It provides comprehensive, objective, and scientific evaluation results. Fuzzy comprehensive evaluation treats evaluation objects, evaluation factors, and evaluation grades as fuzzy sets. Through fuzzy operation rules, it comprehensively considers the effects of various factors on the evaluation object and provides a comprehensive evaluation result. Its core idea is to construct a fuzzy evaluation matrix that reflects the fuzzy relationship between evaluation factors and evaluation grades, and to obtain a comprehensive evaluation vector through synthetic operations. Specific steps include the following: (1) determining the evaluation factor set and evaluation grade set; (2) constructing a fuzzy evaluation matrix reflecting the membership degree of each evaluation factor to the evaluation grades; (3) determining the weight vector of evaluation factors; (4) calculating the comprehensive evaluation vector based on fuzzy synthetic operation rules; (5) determining the grade or score of the evaluation object based on the comprehensive evaluation vector.

Fuzzy control is widely used in areas such as industrial control, robot navigation, and autonomous driving, especially when dealing with complex systems characterized by non-linearity, time-varying behavior, and uncertainty, such as temperature control, path planning, and obstacle avoidance strategies. It provides robust and adaptive control strategies. Fuzzy control treats the input and output variables of the controlled object as fuzzy sets. It realizes the formulation and execution of control strategies through fuzzy rules and fuzzy reasoning. Its core idea is to construct a fuzzy controller, which includes three core components: fuzzification, fuzzy reasoning, and defuzzification. Specific steps include (1) determining the input variables and output variables of the controlled object; (2) designing the fuzzy controller, including the fuzzy rule base, fuzzy inference engine, and defuzzification method; (3) designing fuzzy rules and membership functions based on the control requirements; (4) calculating the fuzzy set of the output variable by fuzzy reasoning based on the fuzzy set of the input variables; and (5) converting the fuzzy set of the output variable into specific control instructions by defuzzification methods.

3.3. The Implementation of HSTM for Fuzzy Mathematics

The implementation of the HSTM requires the support and cooperation of many aspects, as well as the integration of knowledge from several disciplines, so connecting knowledge is its focus and difficulty. In addition, the utilization of various teaching methods is necessary, including discussion-based teaching, project-based teaching, independent innovation practice, and so on.

For fuzzy mathematics, integrating knowledge from multiple disciplines in the teaching process is also a challenge. However, we have found that one can explore its origin from the dialectical concept and the principle of quantitative and qualitative change in philosophy. The scientific knowledge system of fuzzy mathematics is already relatively comprehensive, and multiple technologies have been developed and applied in many fields. Based on the above analysis, we hereby propose a preliminary implementation scheme of the HSTM for fuzzy mathematics, as shown in

Table 1. An implementation scheme of HSTM for fuzzy mathematics.

Processes	Contents	Methods	Objectives
Humanities	Principle of quantitative and qualitative change: How to quantify the process of change	Discussion-based method Group discussion Discover problem Seek a solution	Break through the traditional binary logic and realize the transformation of logic paradigm from {0,1} to [0,1]
	Uncertainty: The opposite of necessity and precision. Randomness? Fuzziness?
	Human cognition: difficult to have a clear definition of something
Science	Fuzzy sets: the definition, properties, characteristic functions, and membership functions of fuzzy sets.	Teaching-based method Student: Self-study Teacher: Teaching Teacher and student: Q&A	Proficient in mastering the basic theories and methods of fuzzy mathematics, understanding its scientific value, and application prospects
	Fuzzy relationship: differences and connections with classical binary relationships, cut-set, synthesis, similarity relationships.
	Fuzzy logic: expansion from binary logic to fuzzy logic, fuzzy rules, fuzzy reasoning
Technology	Fuzzy clustering: the principle and steps of fuzzy clustering; assign fuzzy clustering projects (clustering problem with multiple attributes and samples)	Project-based method Teacher releases project Students explore solutions Reflection and innovation	Proficient in using fuzzy clustering methods to solve problems, practicing pattern recognition independently
	Fuzzy evaluation: the principle and steps of fuzzy comprehensive evaluation; assign fuzzy comprehensive evaluation projects (multisample evaluation problem with multiple indicators)		Proficient in using fuzzy comprehensive evaluation methods to handle problems, independently discovering topics and conducting research
	Fuzzy control: The principle of fuzzy control; Guide students to think about cases of fuzzy control; Encourage students to read literature on fuzzy control carefully		Understand the basic concepts and processes of fuzzy control, and master the basic essentials of academic paper writing
Summary	Summarize the humanistic background, basic concepts, concepts, scientific methods, and application technologies of fuzzy mathematics, and explore its development frontiers	Teaching and discussion	Master the basic content system of HSTM and have a comprehensive and profound understanding of fuzzy mathematics

.

4. Challenge and Countermeasure

HSTM provides a cyclic teaching mechanism that can simultaneously enhance the depth and breadth of cognitive understanding of teaching content by both educators and learners, while allowing subjects to discover new problems, establish new knowledge, and provide new solutions, thereby enhancing the sustainability of education and teaching. However, the implementation of the HSTM for fuzzy mathematics faces many difficulties, including the issues of teaching evaluation, resource dispersion, and the lack of interdisciplinary ability of teachers. To overcome these difficulties, it is necessary to build a diversified evaluation system, integrate curriculum resources organically, and cultivate the interdisciplinary ability of the teaching team.

4.1. Construction of a Diversified Evaluation System

To do justice to the interdisciplinary nature of the course, the assessment criteria must include not only mathematical skills, but also problem solving abilities, critical thinking, and the ability to apply fuzzy mathematical concepts across disciplines. The inclusion of peer and self-assessment mechanisms provides a more comprehensive perspective of student performance. Peer evaluation motivates students to assess their peers’ understanding and use of fuzzy sets in interdisciplinary contexts, fostering a collaborative learning atmosphere. Self-assessment enables students to reflect on their learning and identify areas for improvement. Project-based assessment, in which students apply fuzzy mathematics to solve real-world problems spanning multiple disciplines, is a powerful assessment tool.

4.2. Organic Integration of Course Resources

The integration and dissemination of course resources is a notable obstacle to the implementation of an interdisciplinary teaching mode for HSTM fuzzy mathematics. To overcome this problem, facilitating the seamless integration of course resources is paramount. A careful curriculum mapping exercise should be undertaken to identify and synchronize resources from different disciplines with the core principles of fuzzy mathematics. This includes the creation of a repository of interdisciplinary case studies, scientific articles, and projects that exemplify the application of fuzzy mathematics in different fields. The creation of a collaborative online platform can facilitate the sharing and accessibility of resources among students and faculty.

4.3. Enhancing the Interdisciplinary Ability of the Teaching Team

The effectiveness of interdisciplinary teaching depends on the ability of the teaching team to navigate and integrate knowledge from different fields. Therefore, it is imperative to enhance the interdisciplinary skills of the teaching team. Routine professional development programs specifically tailored to interdisciplinary teaching should be organized. These programs should include topics such as interdisciplinary curriculum design, teaching methods, and the latest advances in fuzzy mathematics and its applications in different domains. Encouraging teachers to participate in collaborative research projects that bridge fuzzy mathematics with other disciplines can foster a deeper understanding and appreciation of interdisciplinary connections. Such initiatives can also lead to the creation of innovative teaching materials and case studies that highlight the real-world relevance of fuzzy mathematics.

5. Conclusions

In this study, the humanistic heritage and the technological derivation of scientific knowledge are considered in a chain, and a new interdisciplinary teaching concept and model are explored from the development perspective of origin, formation, and application. The fuzzy mathematics course is taken as an example to conduct specific research, and the main conclusions are as follows:

(1)

Interdisciplinary teaching is one of the most important ways to promote the sustainable development of education, but its interdisciplinary consideration based on knowledge itself is still insufficient, and it needs to change from “solving specific problems” to “forming a universal basic paradigm”;

(2)

By considering the humanistic background and development source of scientific knowledge, exploring the establishment process of its system, and then how to use the knowledge for technical application, we established the framework of SKU teaching, which is conducive to promoting the deepening of interdisciplinary education;

(3)

Fuzzy mathematics possesses excellent interdisciplinary capabilities. From humanities to science and then to technology, it is crucial to develop an HSTM teaching mode. However, it faces numerous challenges that need to be addressed from various aspects, such as resource reconstruction, teacher training, and multiple assessments.

In conclusion, the implementation of the SKU-based interdisciplinary teaching mode based on knowledge itself rather than problems is of great significance to the deepening of course teaching and the cultivation of students’ comprehensive ability. By systematically studying the humanistic background of knowledge generation, the establishment of knowledge science systems, and the corresponding technological applications, this is expected to form a feedback loop mechanism while learning and applying interdisciplinary knowledge. This process helps to enhance learners’ comprehensive grasp of knowledge, further improving their ability to identify and solve problems, which plays an important supporting role in the sustainability of teaching and even education. However, it still faces many challenges and needs relevant educators to continue their efforts in the future. In addition, further and ongoing research is needed on how to define indicators to evaluate the effectiveness of the proposed framework in supporting interdisciplinary teaching, as well as how to implement feedback and review processes to continuously improve this framework.