A Novel Adaptive Fault-Tolerant Cooperative Control for Multi-PMLSMs of Low-Carbon Urban Rail Linear Traction Systems
Abstract
1. Introduction
- A cooperative approach based on sliding mode control (SMC) is proposed for multi-PMLSMs in this study. At the core of the devised control scheme, the estimated values shape the sliding manifold. Furthermore, the controller incorporates an adaptive parameter and a sophisticated adaptive mechanism, both of which significantly contribute to enhancing the convergence properties and overall robustness of the proposed method.
- An adaptive fault-tolerant controller based on a composite observer is designed for multi-PMLSMs, which aims to stabilize the system under the condition of actuator stuck faults.
- An event-trigger mechanism is constructed for multi-PMLSMs. In this article, the tracking error and estimation error are utilized to design a time-varying trigger threshold, enhancing the controller’s robustness.
2. Preliminaries and Problem Formulation
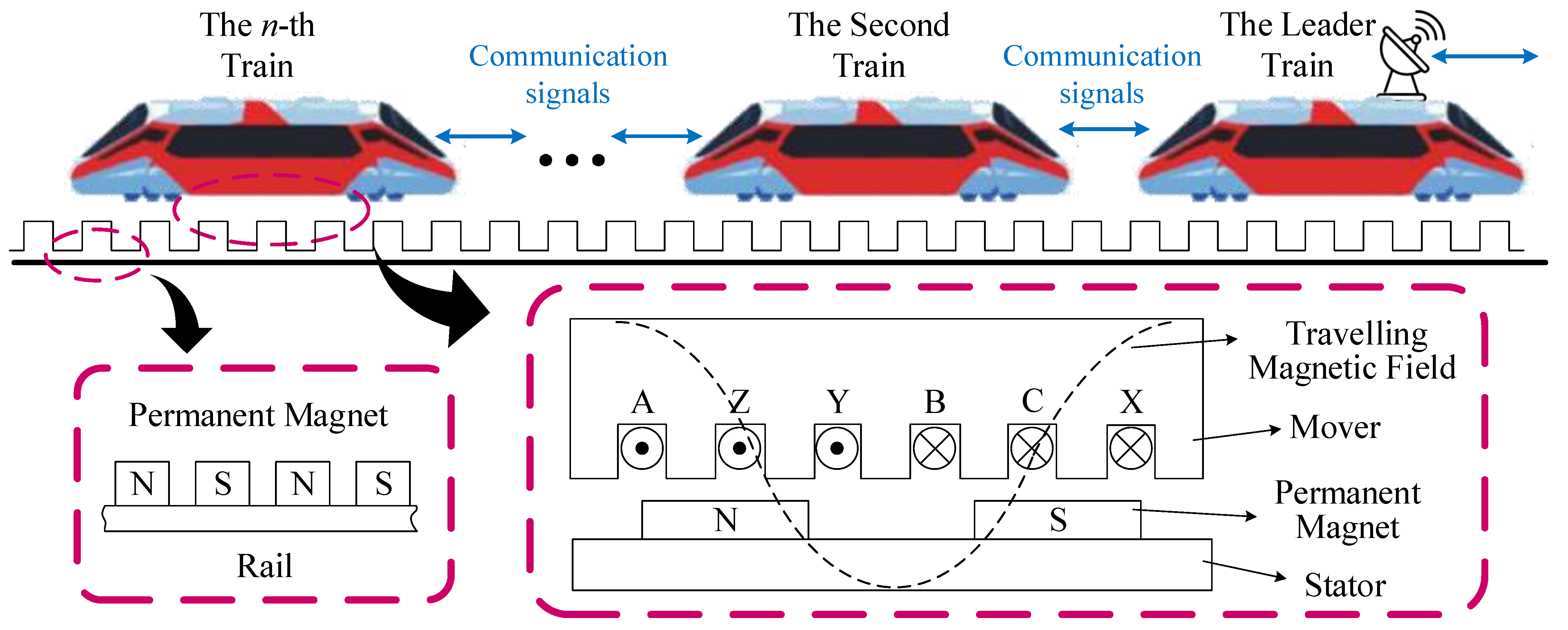
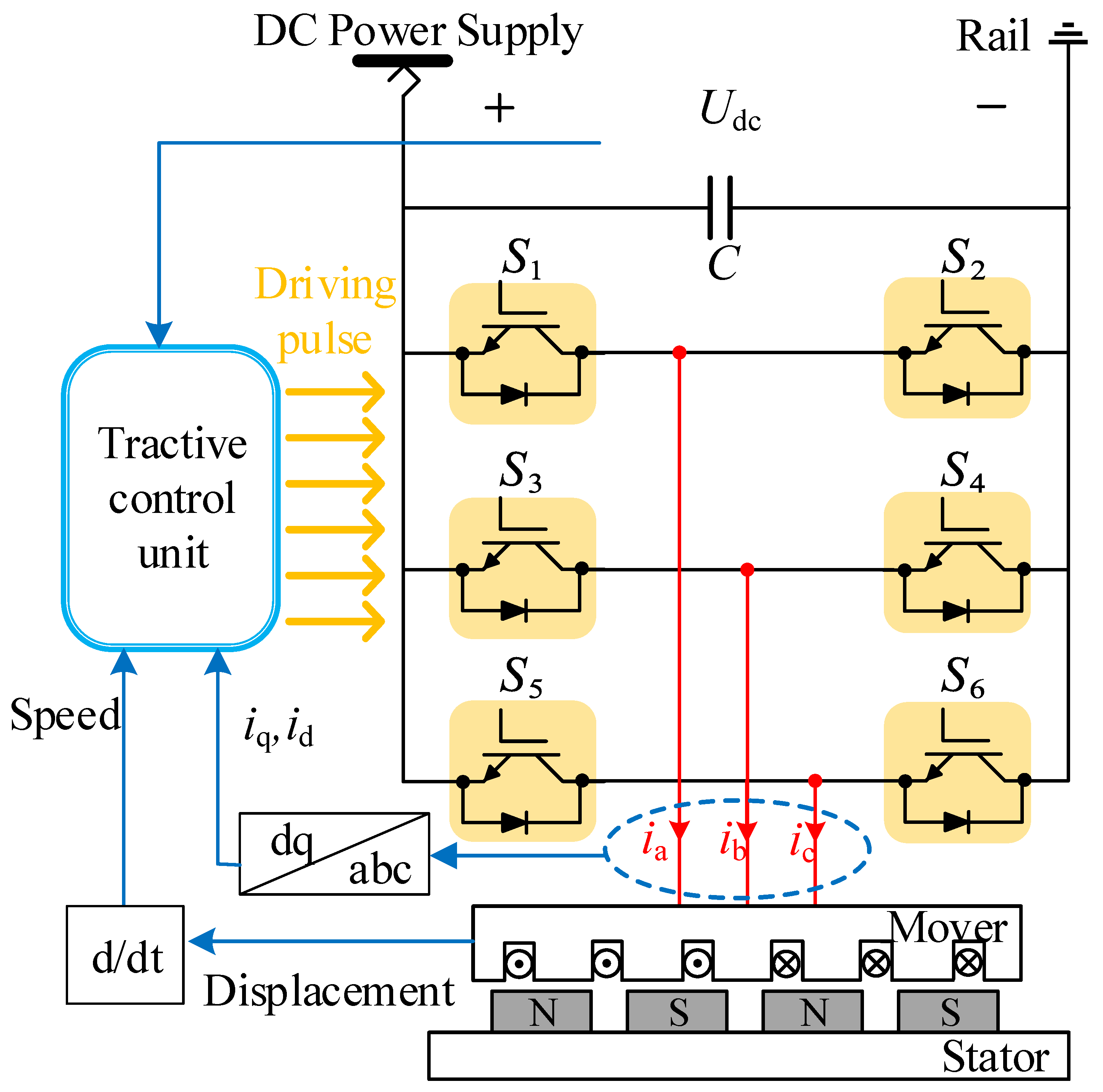
2.1. System Description
2.2. Dynamic Model of Multi-PMLSMs
2.3. Directed Graph Theory
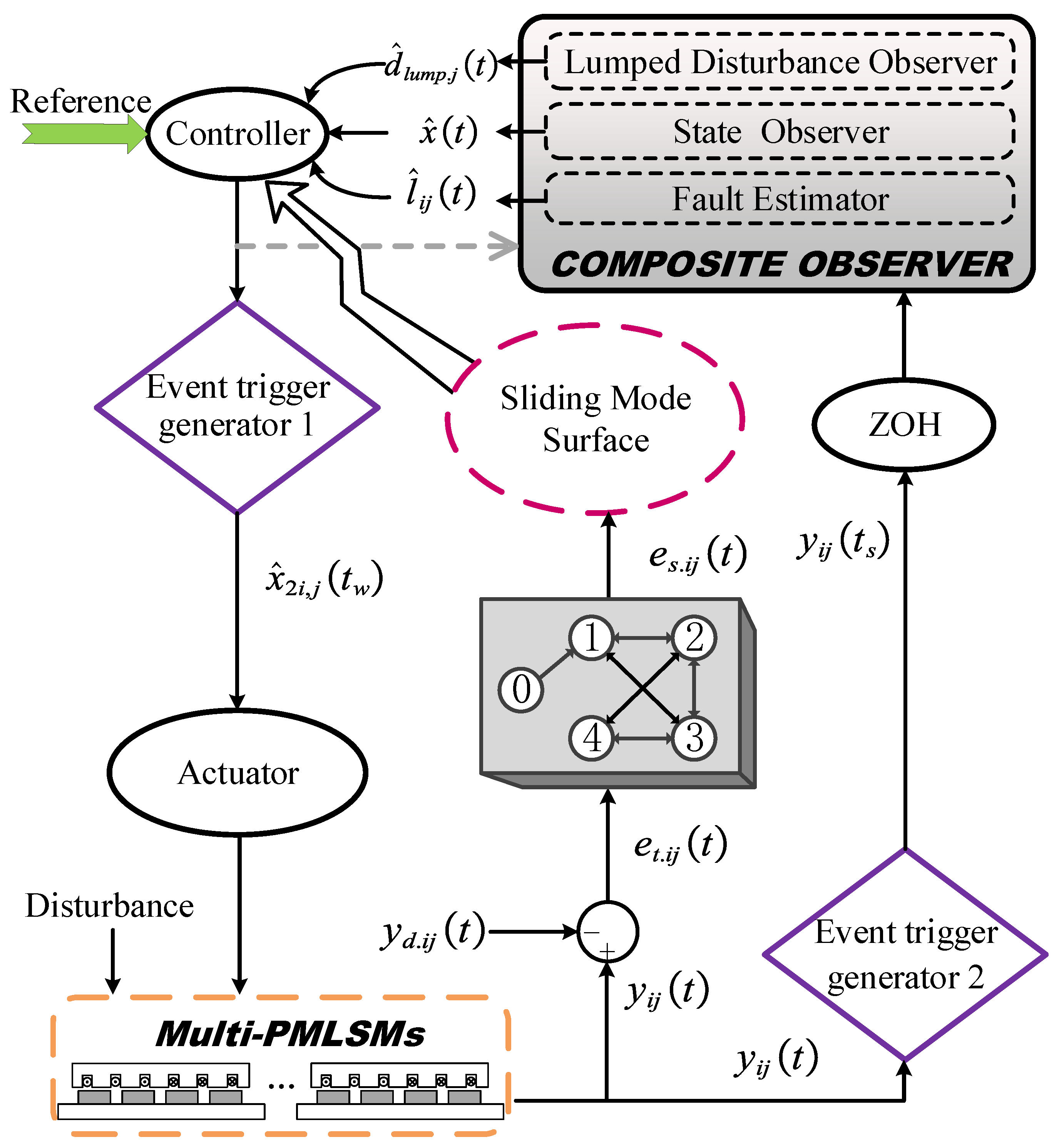
3. Proposed Method
3.1. Event-Trigger Condition Design
3.2. Composite Observer Design
3.3. Adaptive Fault-Tolerant Controller Design
3.4. Event-Triggered Adaptive Fault-Tolerant Controller Design
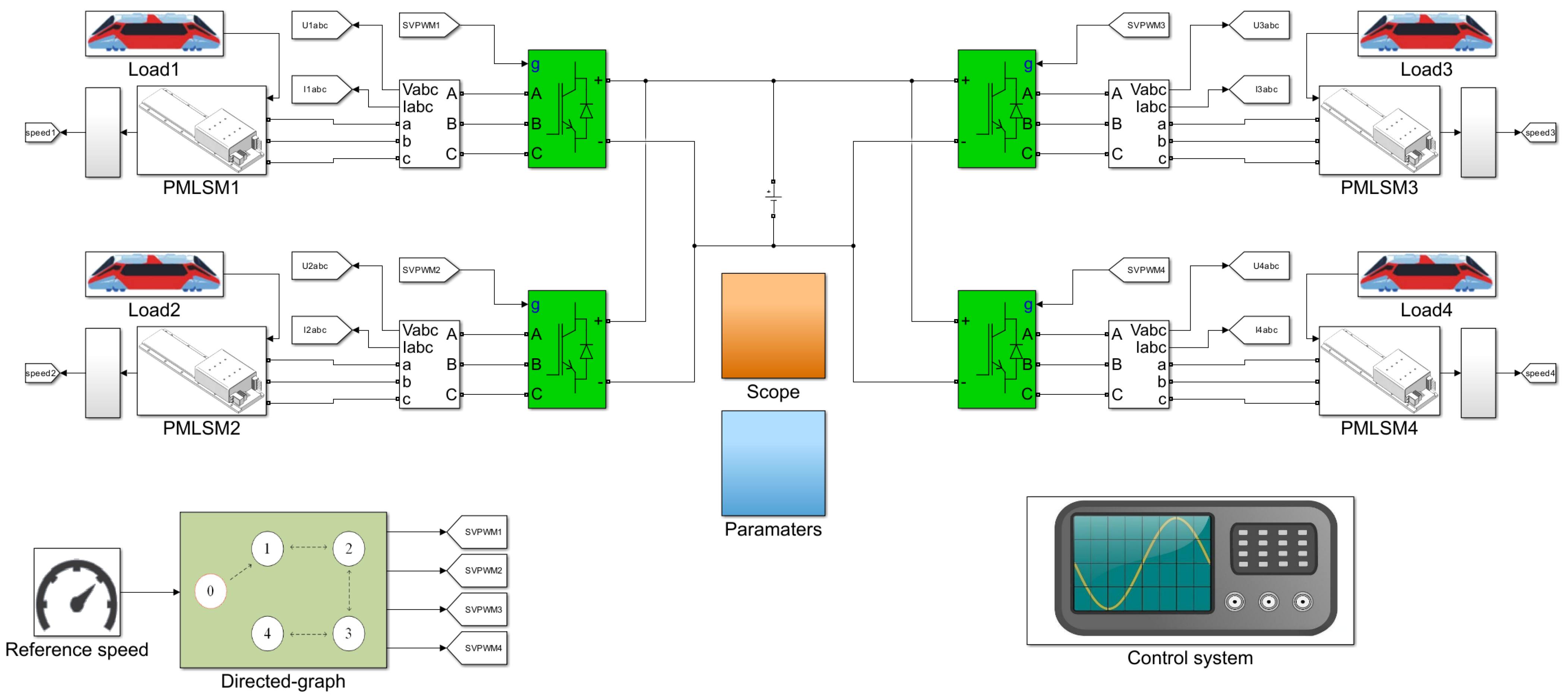
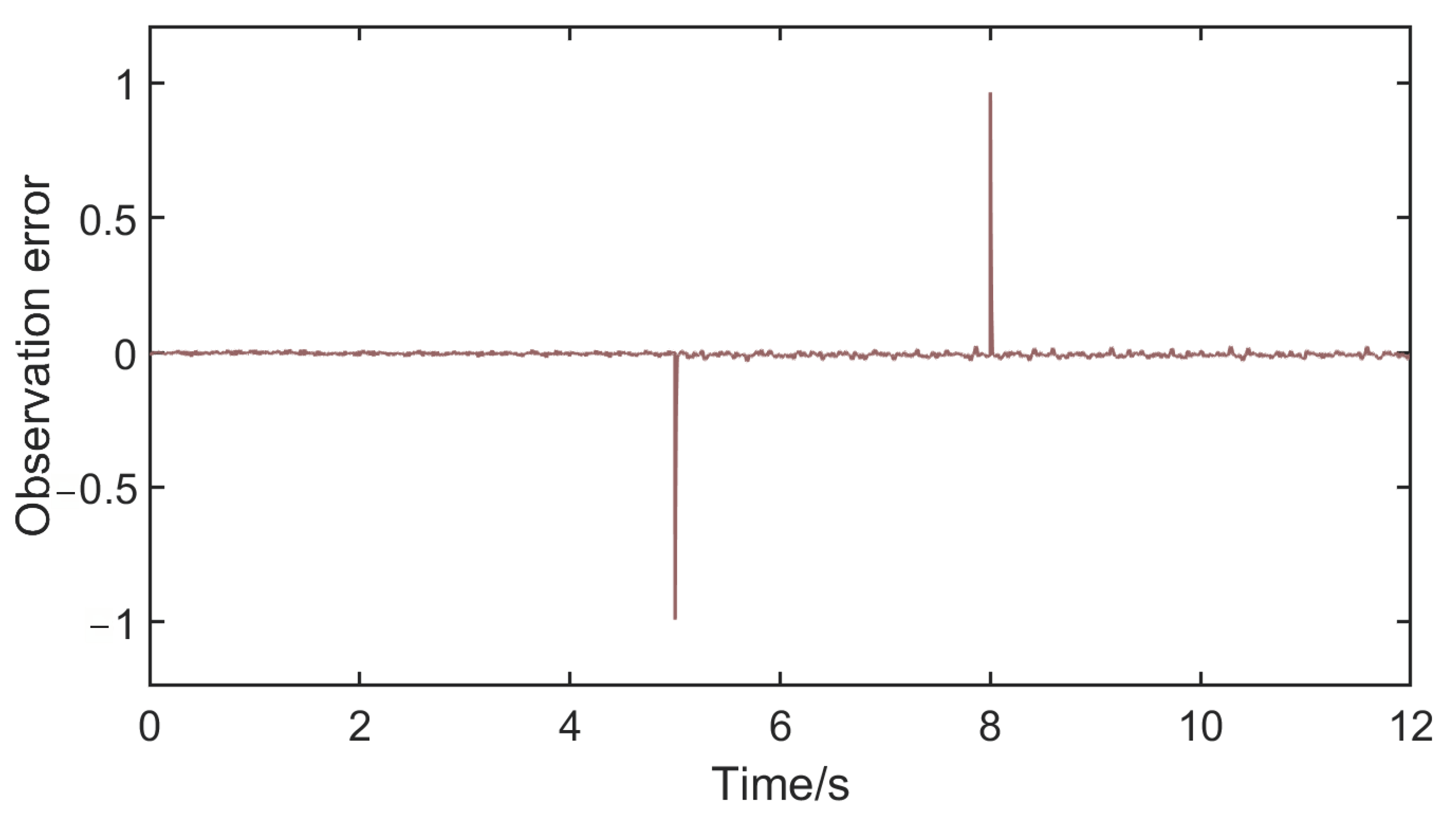
4. Results and Analysis
5. Conclusions
- The composite observer effectively estimates lumped disturbances, which include external disturbances. This enables the adaptive sliding mode controller to compensate for these disturbances and maintain high tracking accuracy under actuator stuck faults and bias faults.
- The event-triggered mechanism reduces the communication burden by transmitting control signals only when necessary, while ensuring that Zeno behavior is avoided. This makes the method suitable for high-density urban rail networks with limited communication resources.
- The proposed method demonstrates promising application prospects in modern urban rail systems. For instance, the energy-saving performance of PMLSMs, combined with the event-triggered mechanism, can reduce energy consumption contributing to the development of low-carbon transit networks.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| , | d-q axis inductance |
| , | d-q axis current |
| , | d-q axis voltage |
| v | speed of the motor |
| electrical angular velocity of the mover | |
| armature resistance | |
| permanent magnet flux | |
| M | mass of motor |
| a | acceleration |
| B | viscous friction coefficient |
| resistance force | |
| displacement of motor | |
| , | the quantity of electric charge |
| the control gains | |
| the input | |
| the loss of effectiveness | |
| , | upper and lower bound |
| the designed control input | |
| constant parameter | |
| bias fault | |
| system uncertainty | |
| disturbance | |
| directed topological graph | |
| the set of nodes | |
| the set of edges | |
| adjacency matrix | |
| the current output | |
| the trigger output signal | |
| W | weighting matrix |
| constant parameter | |
| the observer gain | |
| the estimation error compensator | |
| a designed matrix | |
| the estimation of | |
| the lumped disturbance | |
| the lumped disturbance | |
| a positive constant | |
| P | a positive symmetric matrix |
| the tracking error | |
| the neighborhood synchronization error | |
| the sliding mode | |
| the estimation of | |
| the estimation of | |
| the interval between two triggering instances |
References
- Song, L.; Zhang, J.; Liu, Q.; Zhang, L.; Wu, X. Characteristics of Noise Caused by Trains Passing on Urban Rail Transit Viaducts. Sustainability 2025, 17, 94. [Google Scholar] [CrossRef]
- Liu, X.; Dabiri, A.; Wang, Y.; Schutter, B.D. Modeling and Efficient Passenger-Oriented Control for Urban Rail Transit Networks. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3325–3338. [Google Scholar] [CrossRef]
- Chen, Z.; Liang, Y.; Tian, T.; Peng, P. Sustainable Transportation: Exploring the Node Importance Evolution of Rail Transit Networks during Peak Hours. Sustainability 2024, 16, 6726. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, C.; Wang, H.; Yu, F.R.; Tang, T. Machine Learning in Urban Rail Transit Systems: A Survey. IEEE Trans. Intell. Transp. Syst. 2023, 25, 2182–2207. [Google Scholar] [CrossRef]
- Shen, X.; Wei, H.; Lie, T.T. Management and Utilization of Urban Rail Transit Regenerative Braking Energy Based on the Bypass DC Loop. IEEE Trans. Transp. Electrif. 2021, 7, 1699–1711. [Google Scholar] [CrossRef]
- Huang, Y.; Gao, X.; Song, Z.; Liu, X.; Liu, C. A Novel Wireless Motor Based on Three-Phase Six-Stator-Winding PMSM. IEEE Trans. Ind. Electron. 2024, 71, 7590–7598. [Google Scholar] [CrossRef]
- Dai, Y.; Zhang, L.; Xu, D.; Chen, Q.; Yan, X.-G. Anti-Disturbance Cooperative Fuzzy Tracking Control of Multi-PMSMs Low-Speed Urban Rail Traction Systems. IEEE Trans. Transp. Electrif. 2024, 8, 1040–1052. [Google Scholar] [CrossRef]
- Wang, D.; Peng, C.; Li, J.; Wang, C. Comparison and Experimental Verification of Different Approaches to Suppress Torque Ripple and Vibrations of Interior Permanent Magnet Synchronous Motor for EV. IEEE Trans. Ind. Electron. 2023, 70, 2209–2220. [Google Scholar] [CrossRef]
- Zhou, X.; Li, H.; Wang, L.; Peng, C.; Wang, S.; Liang, L.; Deng, Z. Vertical Dynamic Response Analysis of HTS Maglev Vehicle Excited by a Designed Coreless-Typed PMLSM. IEEE Trans. Transp. Electrif. 2023, 9, 3421–3433. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, H.; Li, B.; Wang, Q.; Ding, D.; Wang, G.; Xu, D. Auxiliary Model Compensated RESO-Based Proportional Resonant Thrust Ripple Suppression for PMLSM Drives. IEEE Trans. Transp. Electrif. 2023, 9, 2141–2152. [Google Scholar] [CrossRef]
- Dong, F.; Zhao, J.; Zhao, J.; Song, J.; Chen, J.; Zheng, Z. Robust Optimization of PMLSM Based on a New Filled Function Algorithm With a Sigma Level Stability Convergence Criterion. IEEE Trans. Ind. Inform. 2021, 17, 4743–4754. [Google Scholar] [CrossRef]
- Xu, W.; Liao, K.; Ge, J.; Qu, G.; Cheng, S.; Wang, A.; Boldea, I. Improved Position Sensorless Control for PMLSM via an Active Disturbance Rejection Controller and an Adaptive Full-Order Observer. IEEE Trans. Ind. Appl. 2023, 59, 1742–1753. [Google Scholar] [CrossRef]
- Xiang, B.; Wen, T.; Liu, H. Cooperative Control of Multiple PM Actuators in PMLSM With Segmented Windings. IEEE Trans. Transp. Electrif. 2024, 10, 5570–5580. [Google Scholar] [CrossRef]
- Song, H.; Gao, S.; Li, Y.; Liu, L.; Dong, H. Train-Centric Communication Based Autonomous Train Control System. IEEE Trans. Intell. Veh. 2023, 8, 721–731. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.; Tang, T.; Yang, L. Event-Triggered Predictive Control for Automatic Train Regulation and Passenger Flow in Metro Rail Systems. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1782–1795. [Google Scholar] [CrossRef]
- Xu, D.; Huang, J.; Su, X.; Shi, P. Adaptive command-filtered fuzzy backstepping control for linear induction motor with unknown end effect. Inf. Sci. 2019, 477, 118–131. [Google Scholar] [CrossRef]
- Hu, D.; Xu, W.; Dian, R.; Liu, Y.; Zhu, J. Loss minimization control of linear induction motor drive for linear metros. IEEE Trans. Ind. Electron. 2018, 65, 6870–6880. [Google Scholar] [CrossRef]
- Li, H.; Sheng, H.; Shen, L. Iterative learning PID controller for permanent magnet linear synchronous motor. J. Phys. Conf. Ser. 2021, 1852, 032044. [Google Scholar] [CrossRef]
- Li, L.; Cheung, N.; Yang, G.; Wang, C.; Fu, P.F.; Li, G.C.; Pan, J.F. Design of a variable-gain adjacent cross-coupled controller for coordinated motion of multiple permanent magnet linear synchronous motors. Comput. Electron. Agric. 2022, 192, 106561. [Google Scholar] [CrossRef]
- Zhu, H.; Shi, L.; Zhang, M. A Novel Thrust Control Based on Total Resistance Force Observation for Long Primary Linear Induction Motor. In Proceedings of the 2021 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Republic of Korea, 31 October–3 November 2021; pp. 1798–1801. [Google Scholar]
- Pan, J.; Fu, P.; Niu, S.; Wang, C.; Zhang, X. High-Precision Coordinated Position Control of Integrated Permanent Magnet Synchronous Linear Motor Stations. IEEE Access 2020, 8, 126253–126265. [Google Scholar] [CrossRef]
- Fu, P.; Pan, J.; Wang, C.; Huang, R. Research on Coordinated Control of Multi-PMSLM Based on Sliding Mode Variable Structure Deviation Coupling Algorithm. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar]
- Mao, Z.; Yan, X.-G.; Jiang, B.; Chen, M. Adaptive Fault-Tolerant Sliding-Mode Control for High-Speed Trains With Actuator Faults and Uncertainties. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2449–2460. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, Q.; Sun, P.; Feng, X. Distributed Adaptive Fault-Tolerant Control for High-Speed Trains Using Multi-Agent System Model. IEEE Trans. Veh. Technol. 2020, 73, 3277–3286. [Google Scholar] [CrossRef]
- Shi, P.; Wang, X.; Meng, X.; He, M.; Mao, Y.; Wang, Z. Adaptive Fault-Tolerant Control for Open-Circuit Faults in Dual Three-Phase PMSM Drives. IEEE Trans. Power Electron. 2023, 38, 3676–3688. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Z. Fault Estimation and Tolerant Control of a Class of Nonlinear Systems and Its Application in High-Speed Trains. IEEE Trans. Control. Syst. Technol. 2023, 31, 2903–2911. [Google Scholar] [CrossRef]
- Lin, X.; Bai, W.; Wang, Q.; Yu, S. Virtual Coupling-Based H Active Fault-Tolerant Cooperative Control for Multiple High-Speed Trains With Unknown Parameters and Actuator Faults. IEEE J. Emerg. Sel. Top. Circuits Syst. 2023, 13, 780–788. [Google Scholar] [CrossRef]
- Zheng, J.; Hou, Z. Model Free Adaptive Iterative Learning Control Based Fault-Tolerant Control for Subway Train With Speed Sensor Fault and Over-Speed Protection. IEEE Trans. Autom. Sci. Eng. 2024, 21, 168–180. [Google Scholar] [CrossRef]
- Guo, X.; Wei, G.; Ding, D. Fault-Tolerant Consensus Control for Discrete-Time Multi-Agent Systems: A Distributed Adaptive Sliding-Mode Scheme. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2515–2519. [Google Scholar] [CrossRef]
- Yu, W.; Huang, D.; Wang, Q.; Cai, L. Distributed Event-Triggered Iterative Learning Control for Multiple High-Speed Trains With Switching Topologies: A Data-Driven Approach. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10818–10829. [Google Scholar] [CrossRef]
- Bai, W.; Dong, H.; Lü, J.; Li, Y. Event-Triggering Communication Based Distributed Coordinated Control of Multiple High-Speed Trains. IEEE Trans. Veh. Technol. 2021, 70, 8556–8566. [Google Scholar] [CrossRef]
- Wang, J.; Pan, H.; Sun, W. Event-Triggered Adaptive Fault-Tolerant Control for Unknown Nonlinear Systems With Applications to Linear Motor. IEEE/ASME Trans. Mechatron. 2022, 27, 940–949. [Google Scholar] [CrossRef]
- Wang, J.; Ma, J.; Pan, H.; Sun, W. Event-Triggered Adaptive Saturated Fault-Tolerant Control for Unknown Nonlinear Systems With Full State Constraints. IEEE Trans. Autom. Sci. Eng. 2024, 21, 1837–1849. [Google Scholar] [CrossRef]
- Zhao, X.M.; Gong, Y.W.; Jin, H.Y.; Xu, C. Adaptive super-twisting-based nonsingular fast terminal sliding mode control of permanent magnet linear synchronous motor. Trans. Inst. Meas. Control. 2023, 45, 3057–3066. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, W.; Shi, P.; Jiang, B. Model-Free cooperative adaptive sliding-mode-constrained-control for multiple linear induction traction systems. IEEE Trans. Cybern. 2020, 50, 4076–4086. [Google Scholar] [CrossRef]


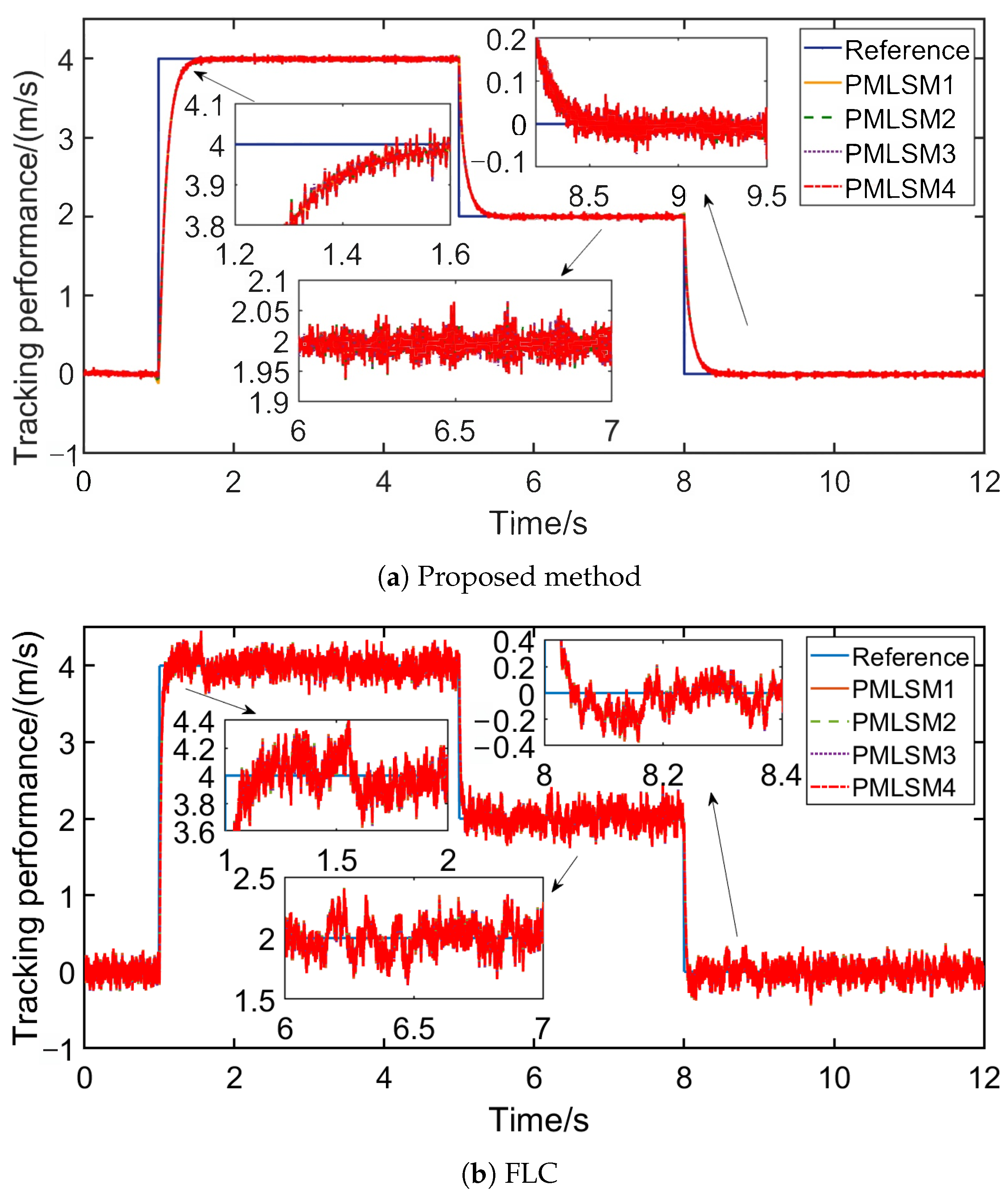
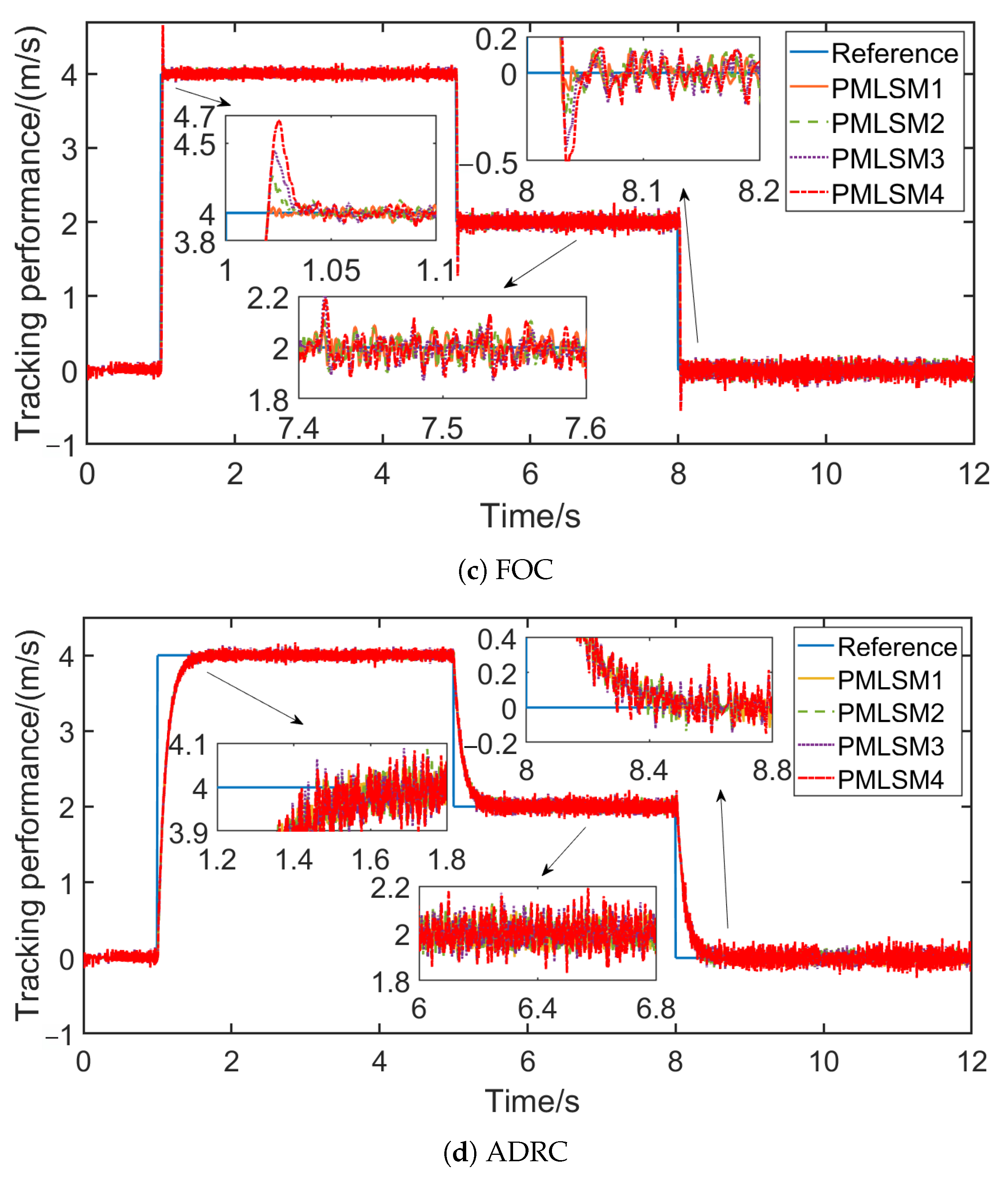

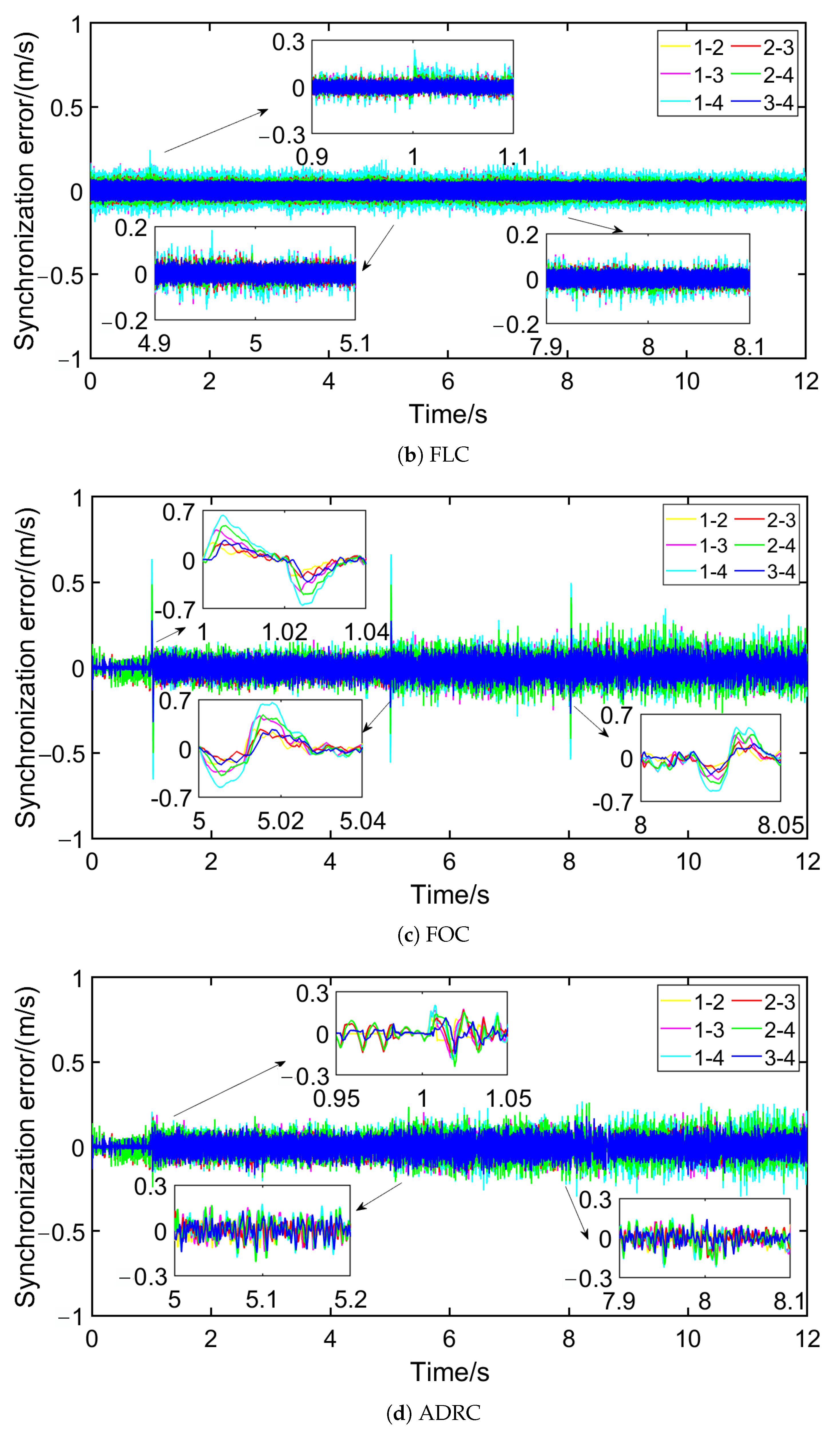
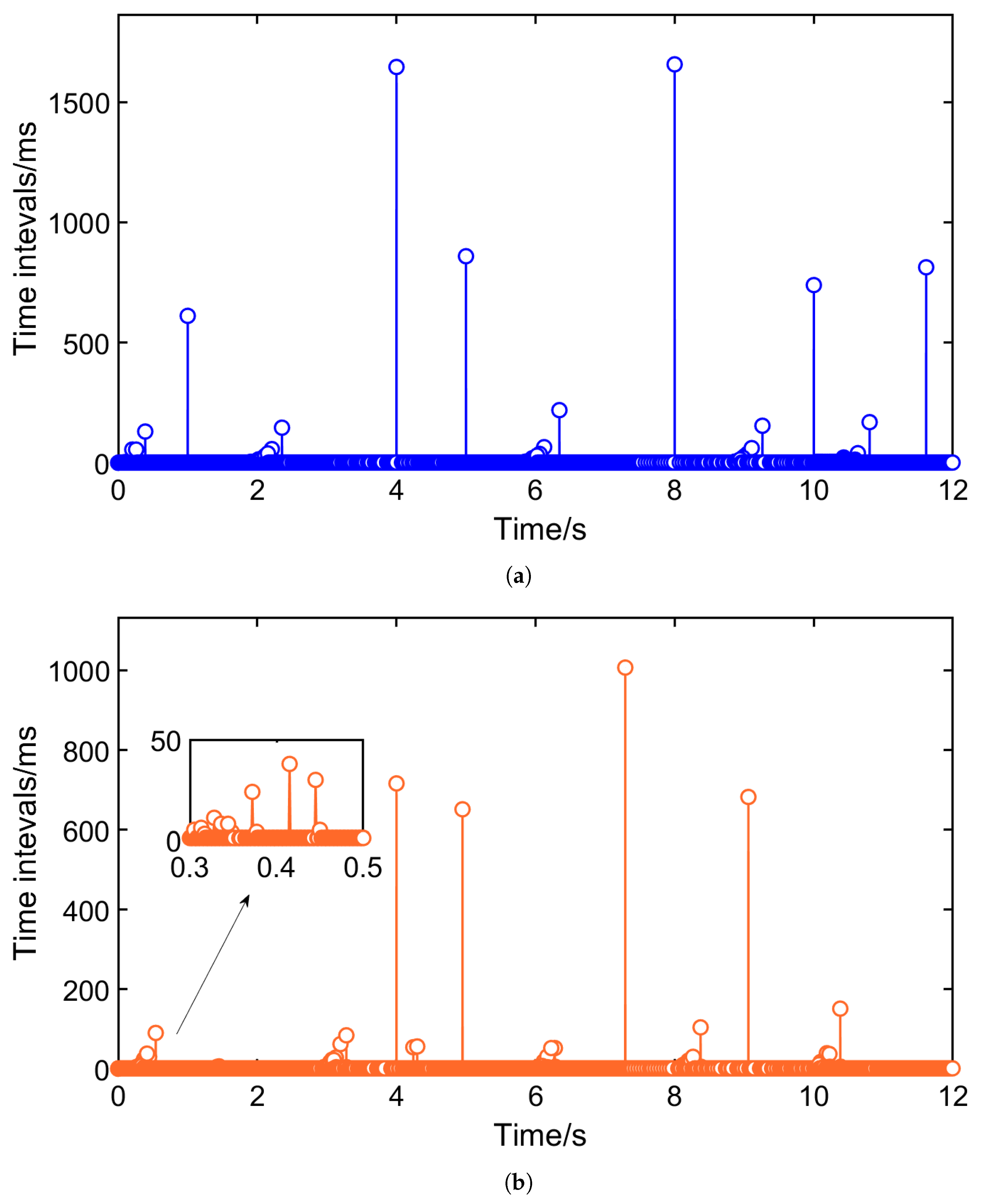
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| 0.071 | 0.0038 H | ||
| 0.131 | 0.0044 H | ||
| M | 351.745 kg | 0.333 Wb | |
| B | 41.01 kg/s | 97.5 N/A |
| Parameters | Value | Parameters | Value | Parameters | Value |
|---|---|---|---|---|---|
| 0.01 | 0.1 | 0.3 | |||
| 3 | 4.5 | 0.49 | |||
| 12 | 0.98 | 0.9 | |||
| 0.015 | 0.55 | 0.88 |
| ITAE | Proposed | FLC | FOC | ADRC |
|---|---|---|---|---|
| 1–2 | 0.0600 | 0.2348 | 0.3062 | 0.2734 |
| 1–3 | 0.1319 | 0.3348 | 0.5345 | 0.5002 |
| 1–4 | 0.1465 | 0.3668 | 0.6238 | 0.5765 |
| 2–3 | 0.0822 | 0.2281 | 0.4033 | 0.3674 |
| 2–4 | 0.0980 | 0.2395 | 0.5495 | 0.5123 |
| 3–4 | 0.0971 | 0.2070 | 0.4024 | 0.3778 |
| SUM | 0.6157 | 1.6110 | 2.8197 | 2.6076 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Dai, Y.; Liu, Y.; Li, L.; Huang, X. A Novel Adaptive Fault-Tolerant Cooperative Control for Multi-PMLSMs of Low-Carbon Urban Rail Linear Traction Systems. Sustainability 2025, 17, 2367. https://doi.org/10.3390/su17062367
Chen H, Dai Y, Liu Y, Li L, Huang X. A Novel Adaptive Fault-Tolerant Cooperative Control for Multi-PMLSMs of Low-Carbon Urban Rail Linear Traction Systems. Sustainability. 2025; 17(6):2367. https://doi.org/10.3390/su17062367
Chicago/Turabian StyleChen, Hongtao, Yuchen Dai, Yuhan Liu, Lei Li, and Xiaoning Huang. 2025. "A Novel Adaptive Fault-Tolerant Cooperative Control for Multi-PMLSMs of Low-Carbon Urban Rail Linear Traction Systems" Sustainability 17, no. 6: 2367. https://doi.org/10.3390/su17062367
APA StyleChen, H., Dai, Y., Liu, Y., Li, L., & Huang, X. (2025). A Novel Adaptive Fault-Tolerant Cooperative Control for Multi-PMLSMs of Low-Carbon Urban Rail Linear Traction Systems. Sustainability, 17(6), 2367. https://doi.org/10.3390/su17062367






