Principal Component Random Forest for Passenger Demand Forecasting in Cooperative, Connected, and Automated Mobility
Abstract
1. Introduction
2. Related Work
2.1. Statistical-Based Methodologies
2.2. AI-Based Methodologies
2.3. Research Gap and Novelty of the Proposed Work
3. Methodology
3.1. Overview
3.2. Algorithmic Procedure
3.3. Dataset Collection and Splitting
3.4. Evaluation Metrics
4. Results
- Tampere, Finland (two different running phases).
- Frankfurt, Germany.
- Carinthia, Austria.
- Trikala, Greece.
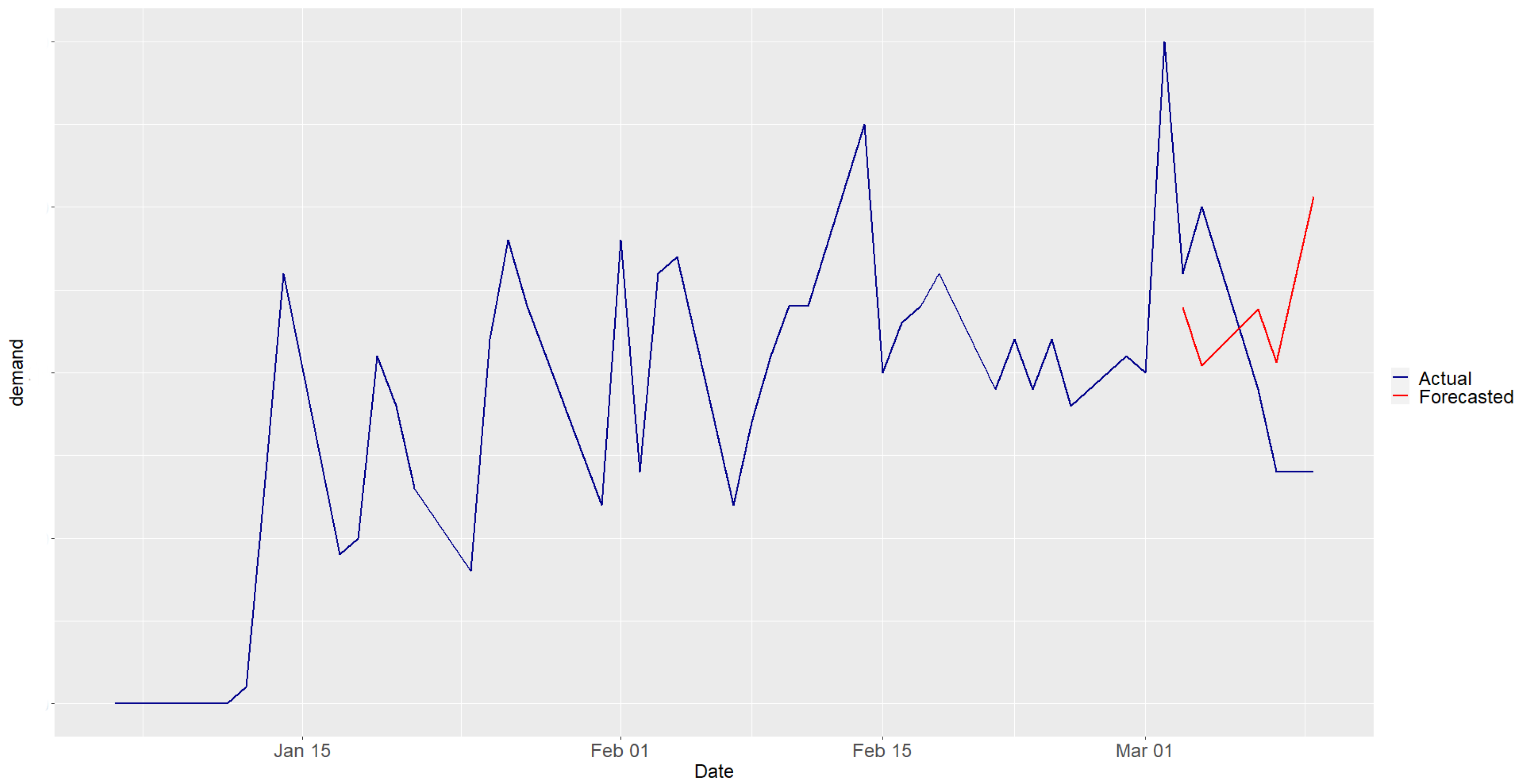
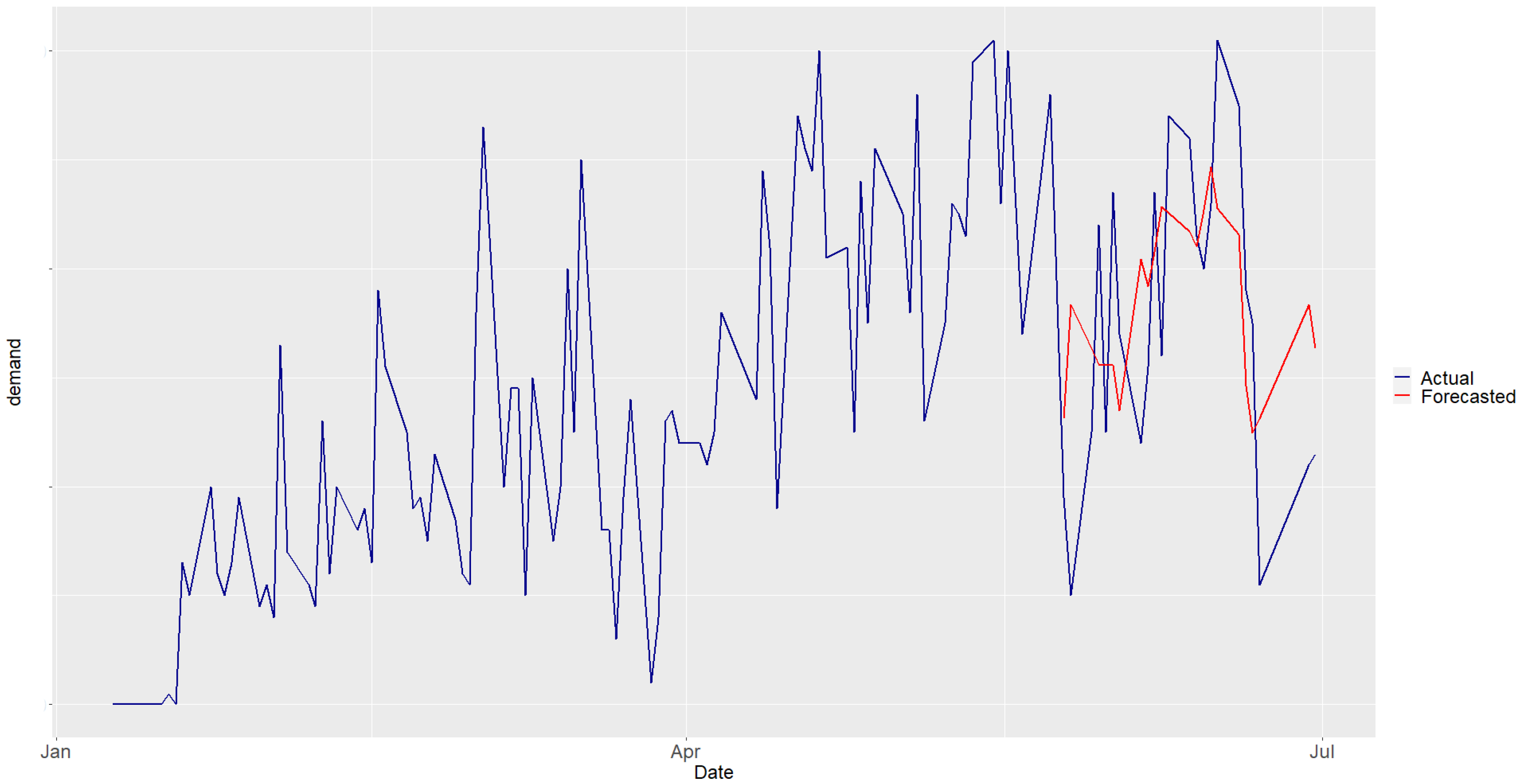
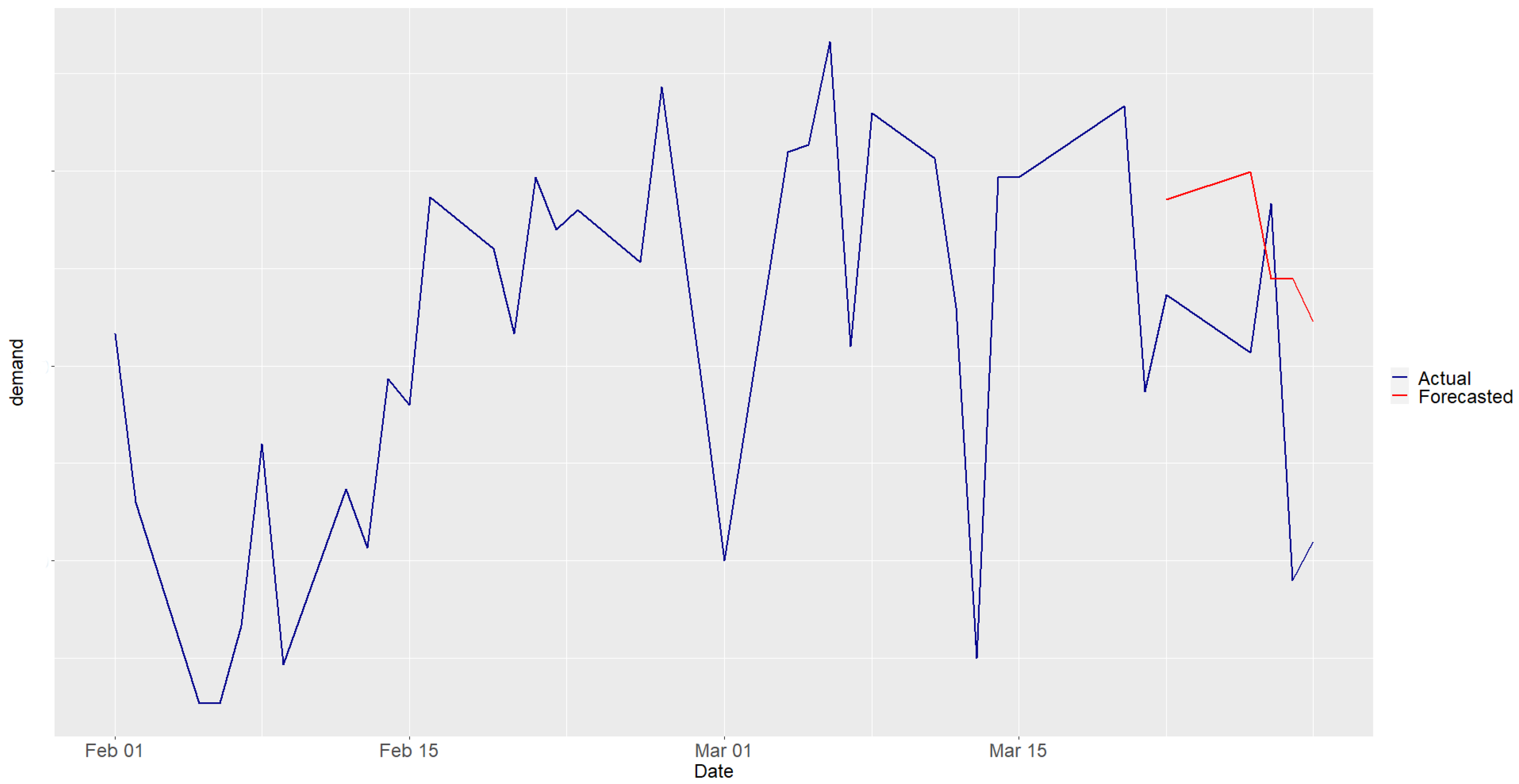
4.1. Tampere 1st Phase
4.2. Tampere 2nd Phase
4.3. Frankfurt
4.4. Carinthia
4.5. Trikala
4.6. Evaluation Results
4.7. Comparative Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gruyer, D.; Orfila, O.; Glaser, S.; Hedhli, A.; Hautière, N.; Rakotonirainy, A. Are connected and automated vehicles the silver bullet for future transportation challenges? Benefits and weaknesses on safety, consumption, and traffic congestion. Front. Sustain. Cities 2021, 2, 607054. [Google Scholar] [CrossRef]
- Hák, T.; Janoušková, S.; Moldan, B. Sustainable Development Goals: A need for relevant indicators. Ecol. Indic. 2016, 60, 565–573. [Google Scholar] [CrossRef]
- Chehri, A.; Mouftah, H.T. Autonomous vehicles in the sustainable cities, the beginning of a green adventure. Sustain. Cities Soc. 2019, 51, 101751. [Google Scholar] [CrossRef]
- Taiebat, M.; Brown, A.L.; Safford, H.R.; Qu, S.; Xu, M. A review on energy, environmental, and sustainability implications of connected and automated vehicles. Environ. Sci. Technol. 2018, 52, 11449–11465. [Google Scholar] [CrossRef]
- Lazarus, J.; Shaheen, S.; Young, S.E.; Fagnant, D.; Voege, T.; Baumgardner, W.; Fishelson, J.; Sam Lott, J. Shared Automated Mobility and Public Transport; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Obschonka, M.; Audretsch, D.B. Artificial intelligence and big data in entrepreneurship: A new era has begun. Small Bus. Econ. 2020, 55, 529–539. [Google Scholar] [CrossRef]
- Benke, K.; Benke, G. Artificial intelligence and big data in public health. Int. J. Environ. Res. Public Health 2018, 15, 2796. [Google Scholar] [CrossRef]
- Wolfert, S.; Ge, L.; Verdouw, C.; Bogaardt, M.J. Big data in smart farming—A review. Agric. Syst. 2017, 153, 69–80. [Google Scholar] [CrossRef]
- Li, J.; Herdem, M.S.; Nathwani, J.; Wen, J.Z. Methods and applications for Artificial Intelligence, Big Data, Internet of Things, and Blockchain in smart energy management. Energy AI 2023, 11, 100208. [Google Scholar] [CrossRef]
- Samara, D.; Magnisalis, I.; Peristeras, V. Artificial intelligence and big data in tourism: A systematic literature review. J. Hosp. Tour. Technol. 2020, 11, 343–367. [Google Scholar] [CrossRef]
- Rijwani, T.; Kumari, S.; Srinivas, R.; Abhishek, K.; Iyer, G.; Vara, H.; Dubey, S.; Revathi, V.; Gupta, M. Industry 5.0: A review of emerging trends and transformative technologies in the next industrial revolution. Int. J. Interact. Des. Manuf. (IJIDEM) 2024, 19, 667–679. [Google Scholar] [CrossRef]
- Eshetu, A.; Valilai, O.F.; Wicaksono, H. Unveiling the Potential of Artificial Intelligence in Cooperative, Connected, and Automated Mobility (CCAM) Solutions: A Systematic Literature Review. In Proceedings of the 2024 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 15–18 December 2024; pp. 1272–1276. [Google Scholar]
- Spanos, G.; Siomos, A.; Schmidt, C.; Tygesen, M.; Salanova, J.M.; Rodrigues, F.; Papadopoulos, A.; Antypas, E.; Sersemis, A.; Gemou, M.; et al. Services for Connected, Cooperated, and Automated Mobility based on Big Data and Artificial Intelligence: The SHOW project paradigm. Open Res. Eur. 2025, 5, 24. [Google Scholar] [CrossRef]
- Antypas, E.; Spanos, G.; Lalas, A.; Votis, K.; Tzovaras, D. A time series approach for estimated time of arrival prediction in autonomous vehicles. Transp. Res. Procedia 2024, 78, 166–173. [Google Scholar] [CrossRef]
- Papadopoulos, A.; Sersemis, A.; Spanos, G.; Lalas, A.; Liaskos, C.; Votis, K.; Tzovaras, D. Lightweight accident detection model for autonomous fleets based on GPS data. Transp. Res. Procedia 2024, 78, 16–23. [Google Scholar] [CrossRef]
- Banister, D. Sustainable transport: Challenges and opportunities. Transportmetrica 2007, 3, 91–106. [Google Scholar] [CrossRef]
- Banerjee, N.; Morton, A.; Akartunalı, K. Passenger demand forecasting in scheduled transportation. Eur. J. Oper. Res. 2020, 286, 797–810. [Google Scholar] [CrossRef]
- Higgoda, R.; Madurapperuma, M. Dynamic Nexus between Air-Transportation and Economic Growth: A Systematic Literature Review. J. Transp. Technol. 2019, 9, 156–170. [Google Scholar] [CrossRef]
- Xu, M.; Ma, X.; Zhao, Y.; Qiao, W. A Systematic Literature Review of Maritime Transportation Safety Management. J. Mar. Sci. Eng. 2023, 11, 2311. [Google Scholar] [CrossRef]
- Sogbe, E.; Susilawati, S.; Pin, T.C. Scaling up public transport usage: A systematic literature review of service quality, satisfaction and attitude towards bus transport systems in developing countries. Public Transp. 2024, 1–44. [Google Scholar] [CrossRef]
- Lyu, T.; Wang, P.S.; Gao, Y.; Wang, Y. Research on the big data of traditional taxi and online car-hailing: A systematic review. J. Traffic Transp. Eng. Engl. Ed. 2021, 8, 1–34. [Google Scholar] [CrossRef]
- Zachariah, R.A.; Sharma, S.; Kumar, V. Systematic review of passenger demand forecasting in aviation industry. Multimed. Tools Appl. 2023, 82, 46483–46519. [Google Scholar] [CrossRef]
- Ingle, C.; Bakliwal, D.; Jain, J.; Singh, P.; Kale, P.; Chhajed, V. Demand forecasting: Literature review on various methodologies. In Proceedings of the 2021 12th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kharagpur, India, 6–8 July 2021; pp. 1–7. [Google Scholar]
- Nithin, K.S.; Mulangi, R.H. Spatio-Temporal Factors Affecting Short-Term Public Transit Passenger Demand Prediction: A Review. In Proceedings of the International Conference on Transportation Planning and Implementation Methodologies for Developing Countries, Mumbai, India, 18–20 December 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 421–430. [Google Scholar]
- Xue, R.; Sun, D.; Chen, S. Short-term bus passenger demand prediction based on time series model and interactive multiple model approach. Discret. Dyn. Nat. Soc. 2015, 2015, 682390. [Google Scholar] [CrossRef]
- Tang, J.; Zuo, A.; Liu, J.; Li, T. Seasonal decomposition and combination model for short-term forecasting of subway ridership. Int. J. Mach. Learn. Cybern. 2022, 13, 145–162. [Google Scholar] [CrossRef]
- Tao, S.; Corcoran, J.; Rowe, F.; Hickman, M. To travel or not to travel:‘Weather’is the question. Modelling the effect of local weather conditions on bus ridership. Transp. Res. Part C Emerg. Technol. 2018, 86, 147–167. [Google Scholar] [CrossRef]
- Hao, S.; Lee, D.H.; Zhao, D. Sequence to sequence learning with attention mechanism for short-term passenger flow prediction in large-scale metro system. Transp. Res. Part C Emerg. Technol. 2019, 107, 287–300. [Google Scholar] [CrossRef]
- Liu, L.; Chen, R.C.; Zhu, S. Impacts of weather on short-term metro passenger flow forecasting using a deep LSTM neural network. Appl. Sci. 2020, 10, 2962. [Google Scholar] [CrossRef]
- Liu, Y.; Lyu, C.; Liu, X.; Liu, Z. Automatic feature engineering for bus passenger flow prediction based on modular convolutional neural network. IEEE Trans. Intell. Transp. Syst. 2020, 22, 2349–2358. [Google Scholar] [CrossRef]
- Koutroumanidis, T.; Sylaios, G.; Zafeiriou, E.; Tsihrintzis, V.A. Genetic modeling for the optimal forecasting of hydrologic time series: Application in Nestos River. J. Hydrol. 2009, 368, 156–164. [Google Scholar] [CrossRef]
- Caliwag, A.C.; Lim, W. Hybrid VARMA and LSTM method for lithium-ion battery state-of-charge and output voltage forecasting in electric motorcycle applications. IEEE Access 2019, 7, 59680–59689. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Chen, W.; Wang, L.Y.; Qu, C. Online joint-prediction of multi-forward-step battery SOC using LSTM neural networks and multiple linear regression for real-world electric vehicles. J. Energy Storage 2020, 30, 101459. [Google Scholar] [CrossRef]
- Athanasakis, E.; Spanos, G.; Papadopoulos, A.; Lalas, A.; Votis, K.; Tzovaras, D. A Comprehensive Leakage-Free Forecasting Pipeline for Segmented Time Series: Application to Cross-Trip State-of-Charge Prediction in Automated Electric Vehicles. IEEE Trans. Intell. Veh. 2024; early access. [Google Scholar] [CrossRef]
- Greenacre, M.; Groenen, P.J.; Hastie, T.; d’Enza, A.I.; Markos, A.; Tuzhilina, E. Principal component analysis. Nat. Rev. Methods Primers 2022, 2, 100. [Google Scholar] [CrossRef]
- Spanos, G.; Giannoutakis, K.M.; Votis, K.; Viaño, B.; Augusto-Gonzalez, J.; Aivatoglou, G.; Tzovaras, D. A lightweight cyber-security defense framework for smart homes. In Proceedings of the 2020 International Conference on INnovations in Intelligent SysTems and Applications (INISTA), Novi Sad, Serbia, 24–26 August 2020; pp. 1–7. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Antoniadis, A.; Lambert-Lacroix, S.; Poggi, J.M. Random forests for global sensitivity analysis: A selective review. Reliab. Eng. Syst. Saf. 2021, 206, 107312. [Google Scholar] [CrossRef]
- Aivatoglou, G.; Anastasiadis, M.; Spanos, G.; Voulgaridis, A.; Votis, K.; Tzovaras, D.; Angelis, L. A RAkEL-based methodology to estimate software vulnerability characteristics & score-an application to EU project ECHO. Multimed. Tools Appl. 2022, 81, 9459–9479. [Google Scholar]
- Jolliffe, I.T. Principal Component Analysis for Special Types of Data; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Parmar, A.; Katariya, R.; Patel, V. A review on random forest: An ensemble classifier. In Proceedings of the International Conference on Intelligent Data Communication Technologies and Internet of Things (ICICI), Coimbatore, India, 7–8 August 2018; Springer: Berlin/Heidelberg, Germany, 2019; pp. 758–763. [Google Scholar]
- Polymeni, S.; Pitsiavas, V.; Spanos, G.; Matthewson, Q.; Lalas, A.; Votis, K.; Tzovaras, D. Toward sustainable mobility: AI-enabled automated refueling for Fuel Cell Electric Vehicles. Energies 2024, 17, 4324. [Google Scholar] [CrossRef]
- Wang, W.C.; Chau, K.W.; Xu, D.M.; Chen, X.Y. Improving forecasting accuracy of annual runoff time series using ARIMA based on EEMD decomposition. Water Resour. Manag. 2015, 29, 2655–2675. [Google Scholar] [CrossRef]
- Mahjoub, S.; Chrifi-Alaoui, L.; Marhic, B.; Delahoche, L. Predicting energy consumption using LSTM, multi-layer GRU and drop-GRU neural networks. Sensors 2022, 22, 4062. [Google Scholar] [CrossRef]
- Brownlee, J. Introduction to Time Series Forecasting with Python: How to Prepare Data and Develop Models to Predict the Future; Machine Learning Mastery: Dorado, CA, USA, 2017. [Google Scholar]
- Xu, Y.; Goodacre, R. On splitting training and validation set: A comparative study of cross-validation, bootstrap and systematic sampling for estimating the generalization performance of supervised learning. J. Anal. Test. 2018, 2, 249–262. [Google Scholar] [CrossRef]
- Zhou, J.; Shi, J.; Li, G. Fine tuning support vector machines for short-term wind speed forecasting. Energy Convers. Manag. 2011, 52, 1990–1998. [Google Scholar] [CrossRef]
- Suradhaniwar, S.; Kar, S.; Durbha, S.S.; Jagarlapudi, A. Time series forecasting of univariate agrometeorological data: A comparative performance evaluation via one-step and multi-step ahead forecasting strategies. Sensors 2021, 21, 2430. [Google Scholar] [CrossRef] [PubMed]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Hyndman, R. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]



| MAE | MdAE | RMSE | NMAE | NMdAE | NRMSE | |
|---|---|---|---|---|---|---|
| Tampere (1st period) | 5.4 | 4.08 | 6.03 | 13.50% | 10.20% | 15.10% |
| Tampere (2nd period) | 10.55 | 10.03 | 12.98 | 17.30% | 16.40% | 21.30% |
| Frankfurt | 20 | 17.67 | 23.45 | 12.40% | 11% | 14.60% |
| Carinthia | 8.62 | 6.42 | 10.97 | 7.80% | 5.80% | 9.90% |
| Trikala | 26.89 | 27.95 | 29.77 | 26.40% | 27.40% | 29.20% |
| Tampere (1st Period) | Tampere (2nd Period) | Frankfurt | Carinthia | Trikala | ||
|---|---|---|---|---|---|---|
| NMAE | 13.50% | 17.30% | 12.40% | 7.80% | 26.40% | |
| PCRF | NMdAE | 10.20% | 16.40% | 11.00% | 5.80% | 27.40% |
| NRMSE | 15.10% | 21.30% | 14.60% | 9.90% | 29.20% | |
| NMAE | 17% | 19.67% | 12.09% | 6.85% | 21.76% | |
| NAIVE | NMdAE | 12.50% | 19.67% | 7.45% | 8.11% | 14.71% |
| NRMSE | 21.15% | 22.82% | 17.46% | 7.67% | 28.53% | |
| NMAE | 14.53% | 23.15% | 13.74% | 11.62% | 19.27% | |
| AVERAGE | NMdAE | 11.55% | 23.01% | 15.12% | 10.19% | 20.70% |
| NRMSE | 17.32% | 27.54% | 15.92% | 13.29% | 23.34% | |
| NMAE | 17.97% | 19.87% | 12.11% | 6.85% | 22.19% | |
| DRIFT | NMdAE | 13.66% | 19.98% | 7.31% | 8.11% | 14.98% |
| NRMSE | 22.52% | 22.94% | 17.53% | 7.43% | 28.86% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spanos, G.; Lalas, A.; Votis, K.; Tzovaras, D. Principal Component Random Forest for Passenger Demand Forecasting in Cooperative, Connected, and Automated Mobility. Sustainability 2025, 17, 2632. https://doi.org/10.3390/su17062632
Spanos G, Lalas A, Votis K, Tzovaras D. Principal Component Random Forest for Passenger Demand Forecasting in Cooperative, Connected, and Automated Mobility. Sustainability. 2025; 17(6):2632. https://doi.org/10.3390/su17062632
Chicago/Turabian StyleSpanos, Georgios, Antonios Lalas, Konstantinos Votis, and Dimitrios Tzovaras. 2025. "Principal Component Random Forest for Passenger Demand Forecasting in Cooperative, Connected, and Automated Mobility" Sustainability 17, no. 6: 2632. https://doi.org/10.3390/su17062632
APA StyleSpanos, G., Lalas, A., Votis, K., & Tzovaras, D. (2025). Principal Component Random Forest for Passenger Demand Forecasting in Cooperative, Connected, and Automated Mobility. Sustainability, 17(6), 2632. https://doi.org/10.3390/su17062632







