Evolution of Disruption Resilience in the Wood Forest Products Trade Network, Considering the Propagation of Disruption Risks and Underload Cascading Failure
Abstract
:1. Introduction
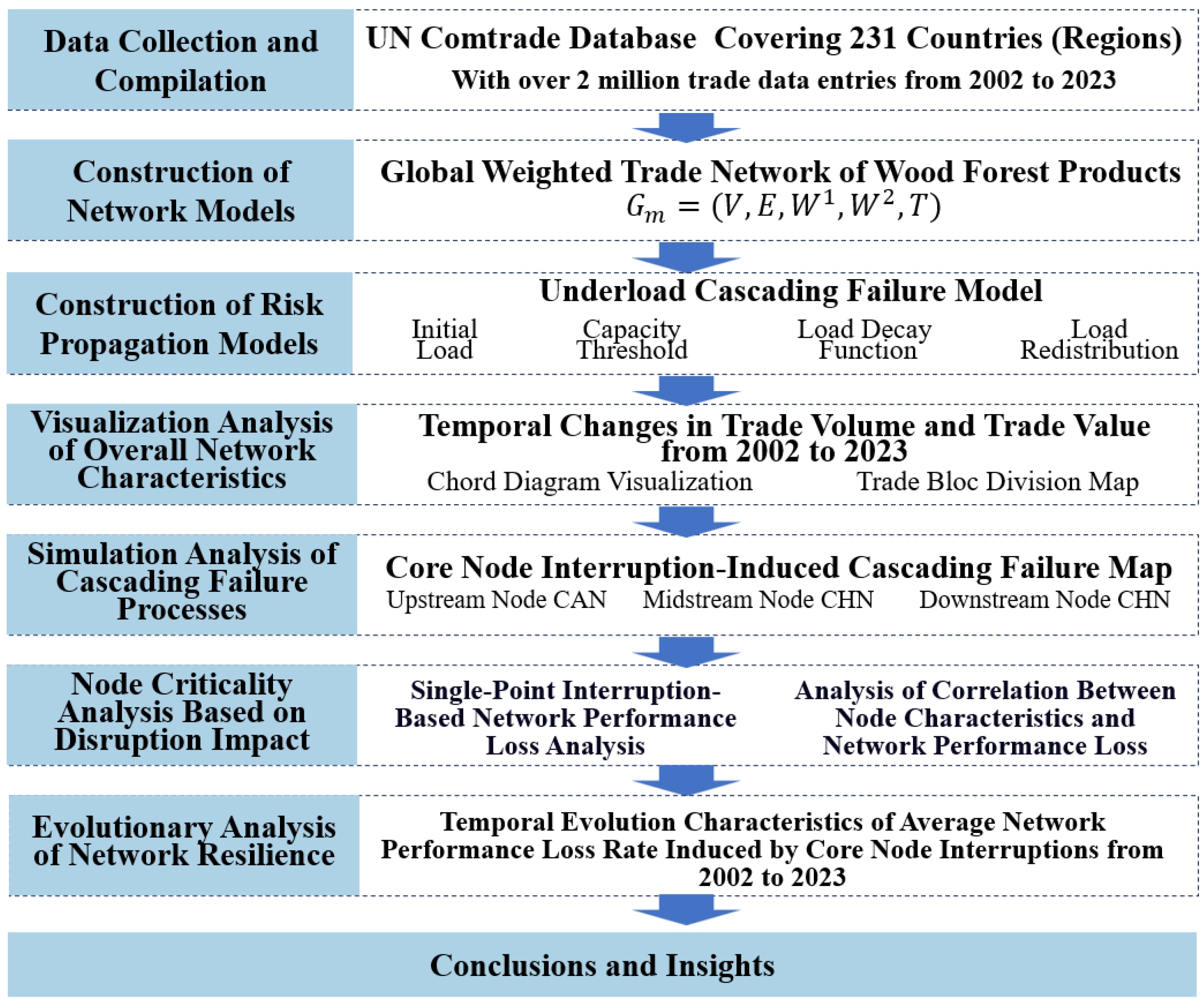
2. Data Sources and Research Methodology
2.1. Data Sources and Research Framework
2.2. Graph Theory Model Construction
2.3. Key Indicators for Analyzing Complex Network Models
2.4. Disruption Resilience Evaluation Metrics
3. Construction of the Disruption Risk Propagation Model
3.1. Model Selection
3.2. Initial Load Configuration
3.3. Decay Capacity and Failure Capacity
3.4. Export Load Decay Function
- (1)
- Export Load Decay Function for Type 1 (Import-Dominant) Nodes
- (2)
- Export Load Decay Function for Type 2 (Balanced Import–Export) Nodes
- (3)
- Export Load Decay Function for Type 3 (Export-Dominant) Nodes
3.5. Export Load Redistribution
4. Results Analysis
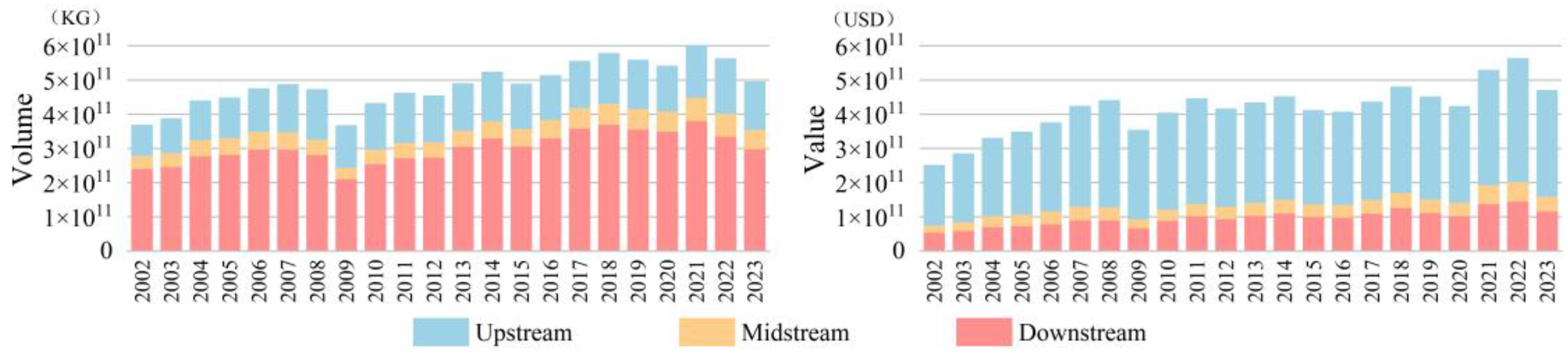
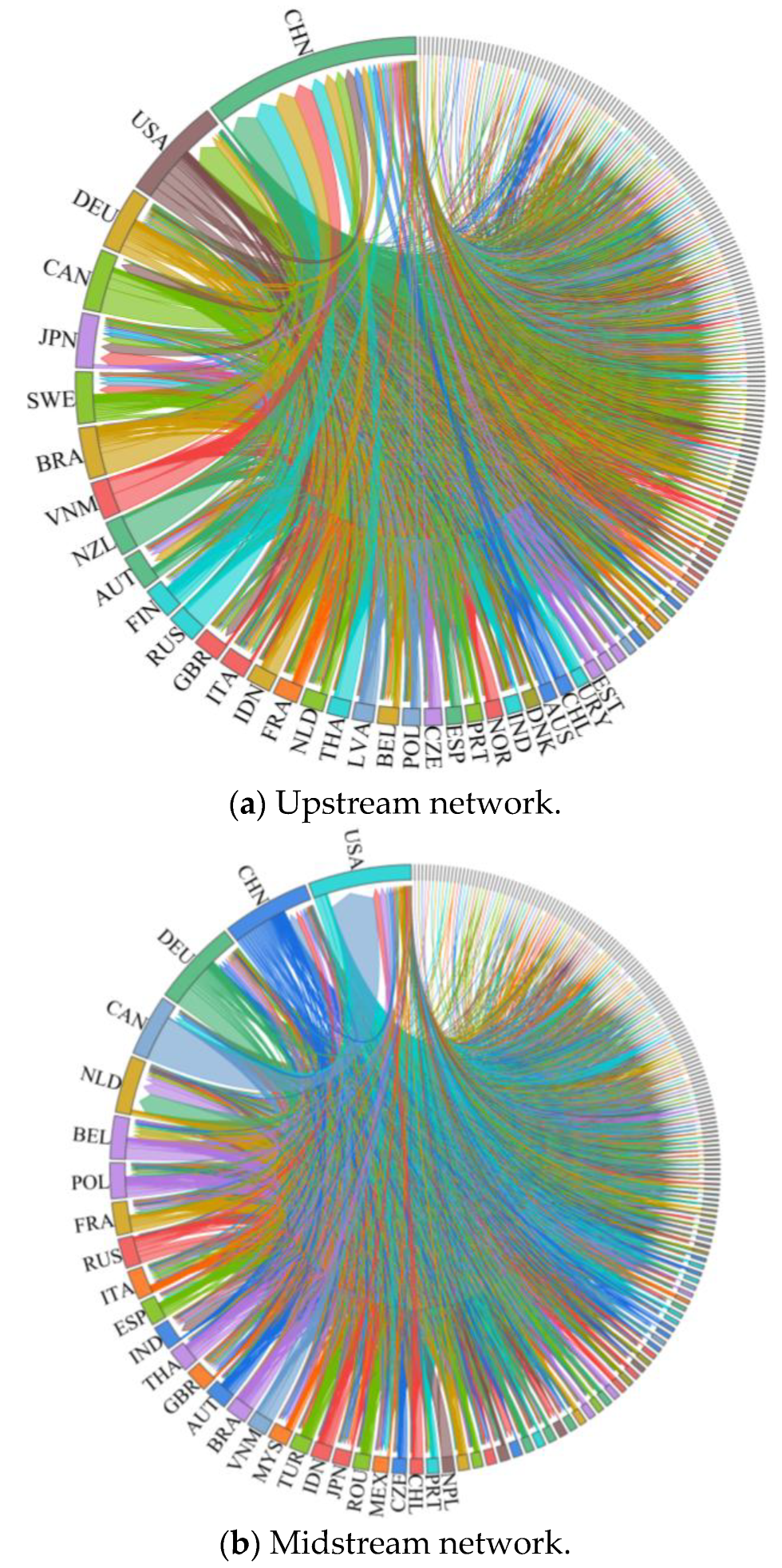
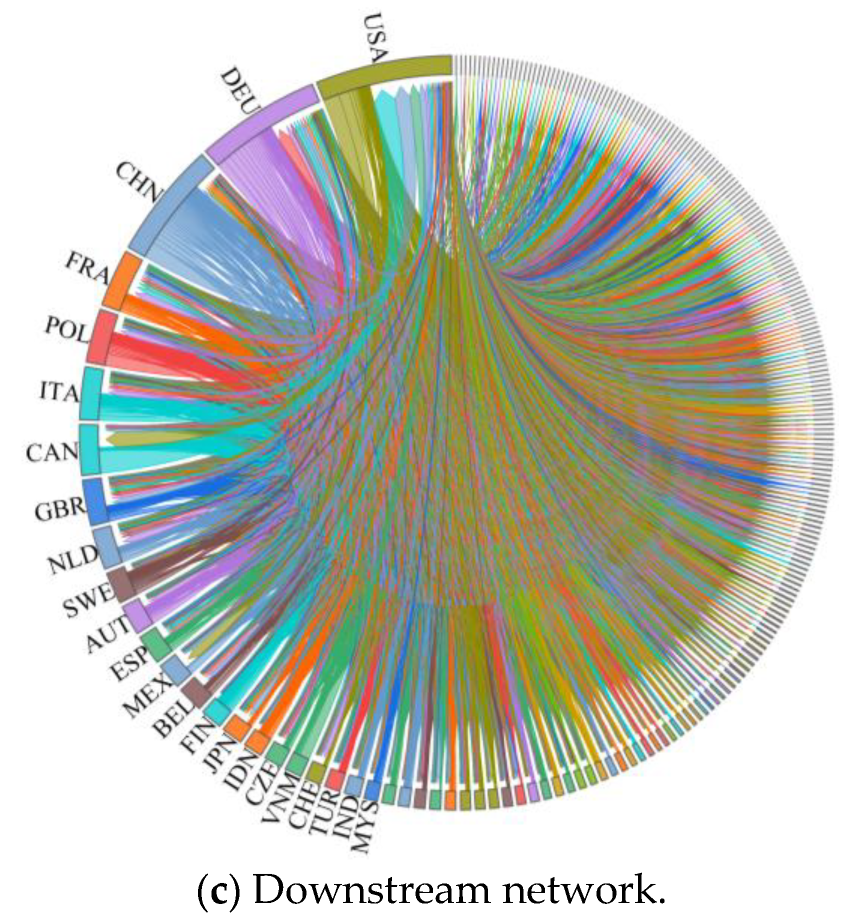
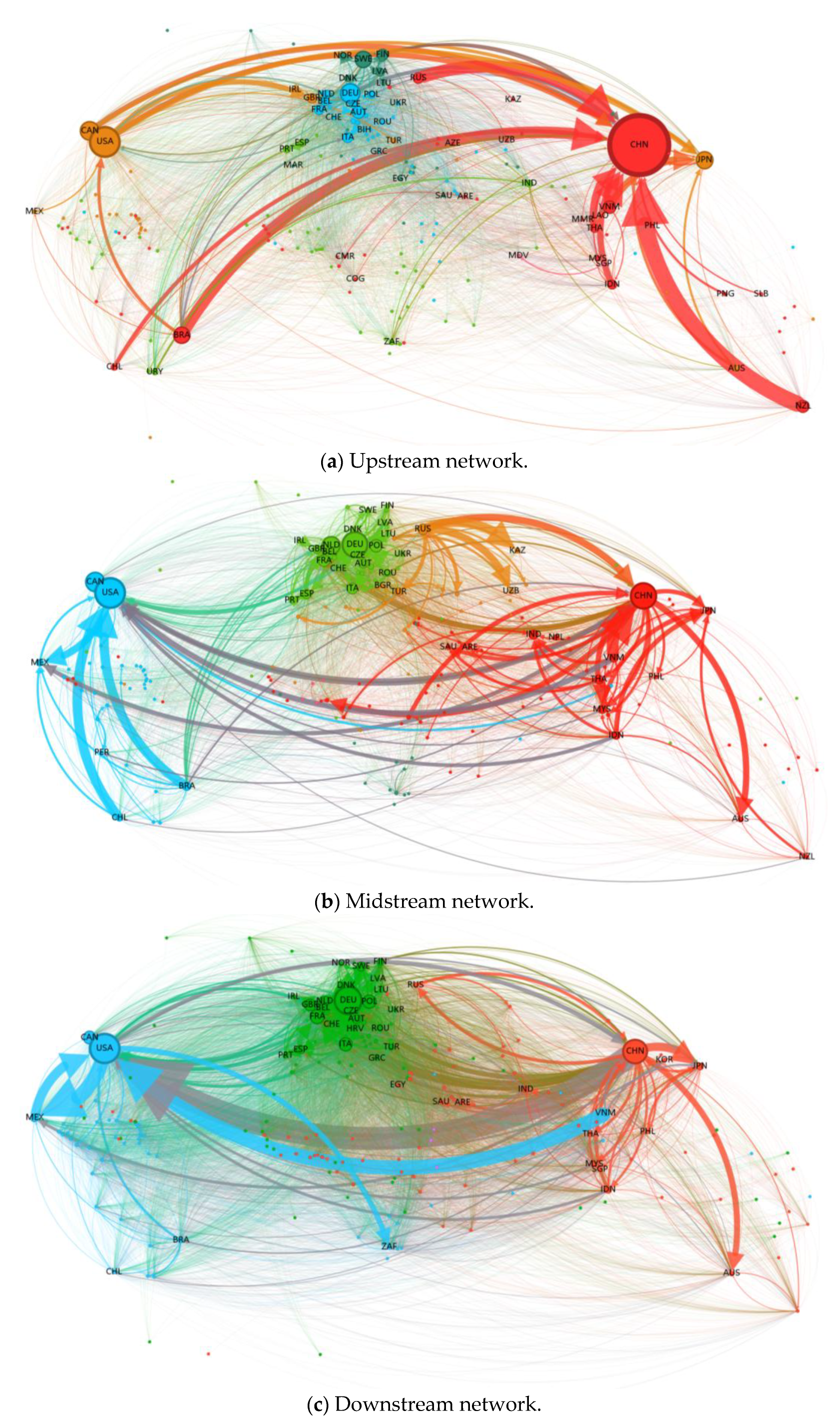
4.1. Analysis of Overall Network Characteristics
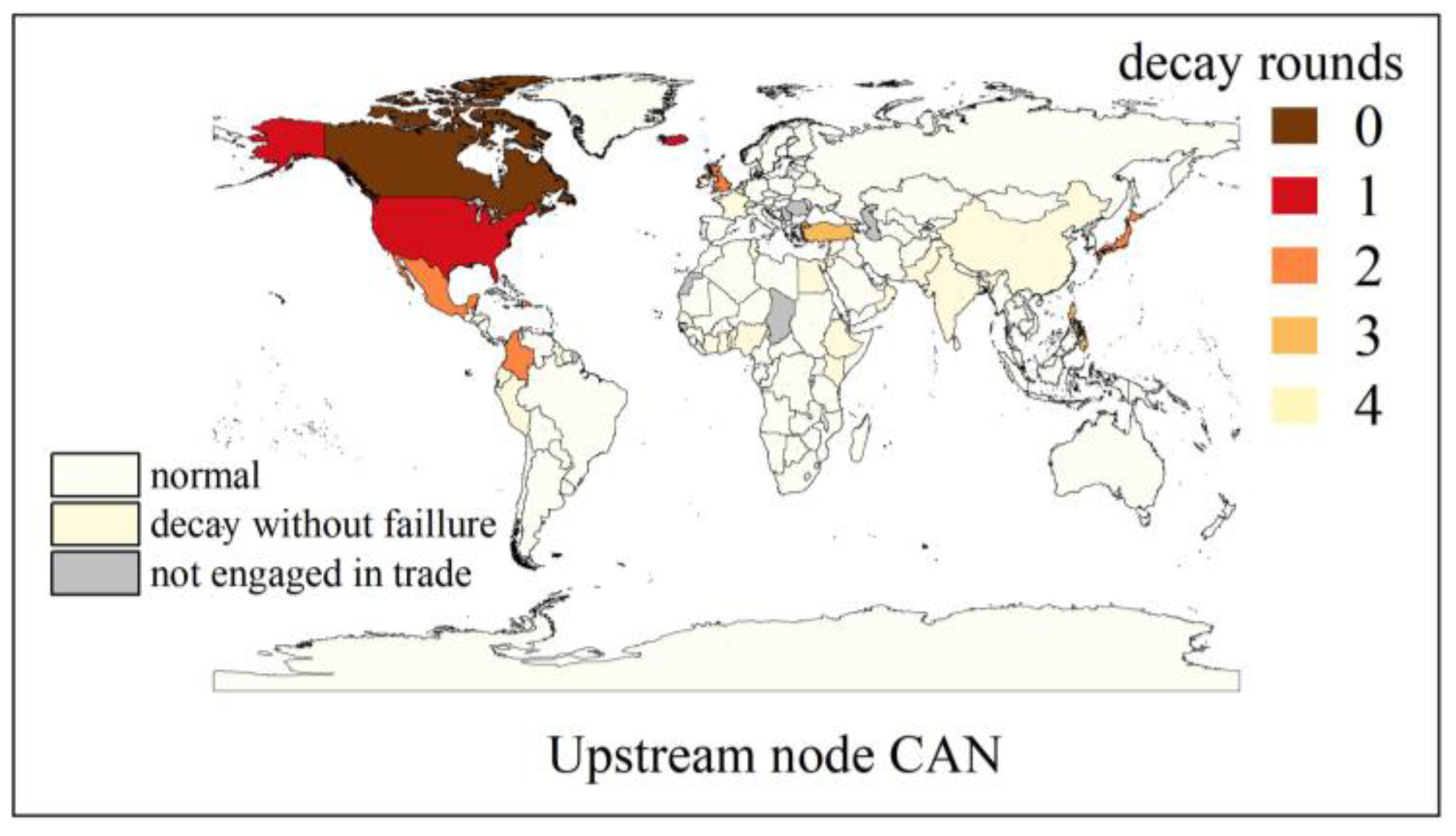
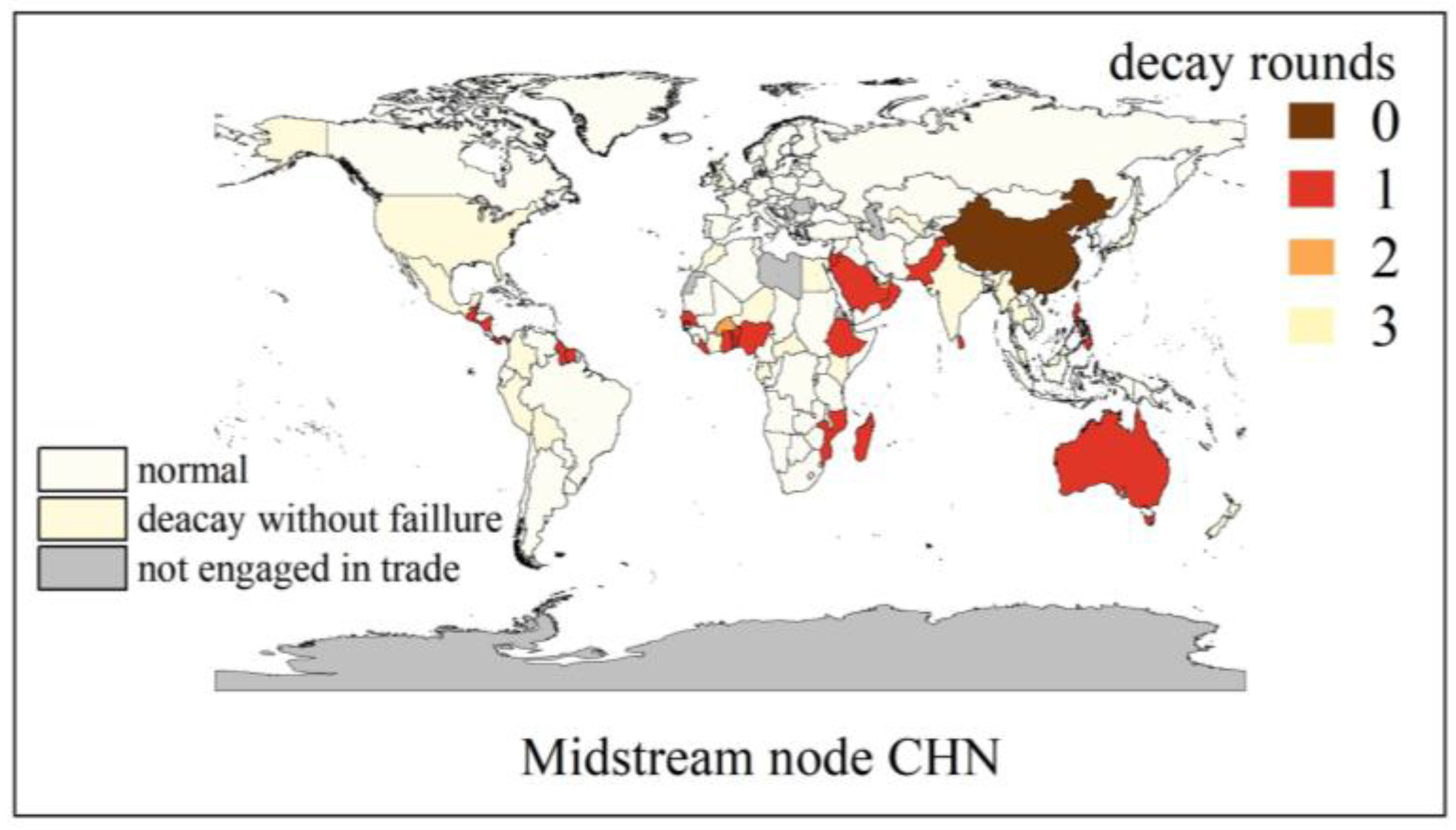
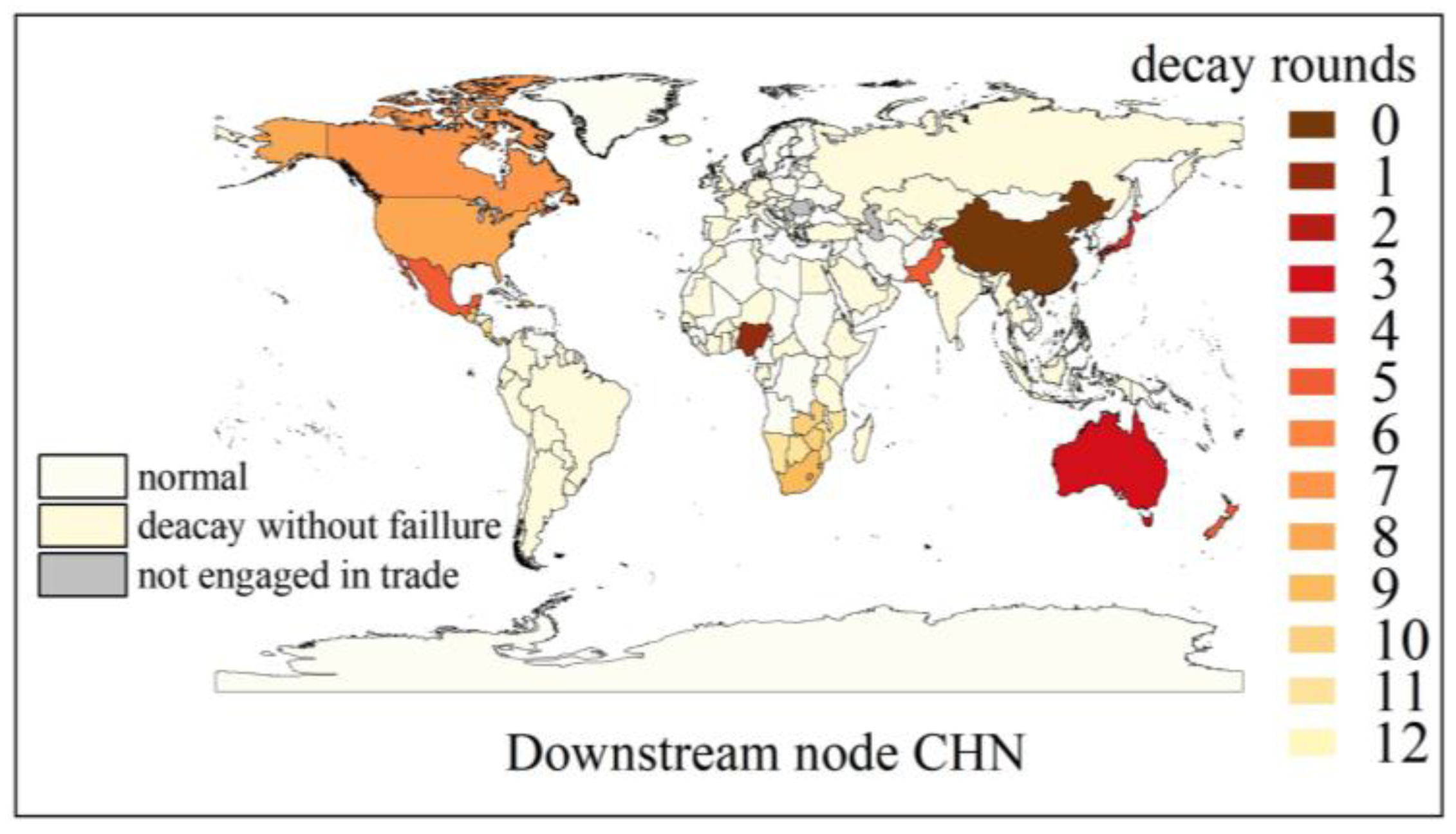
4.2. Simulation Analysis of Underload Cascading Failure Propagation Process
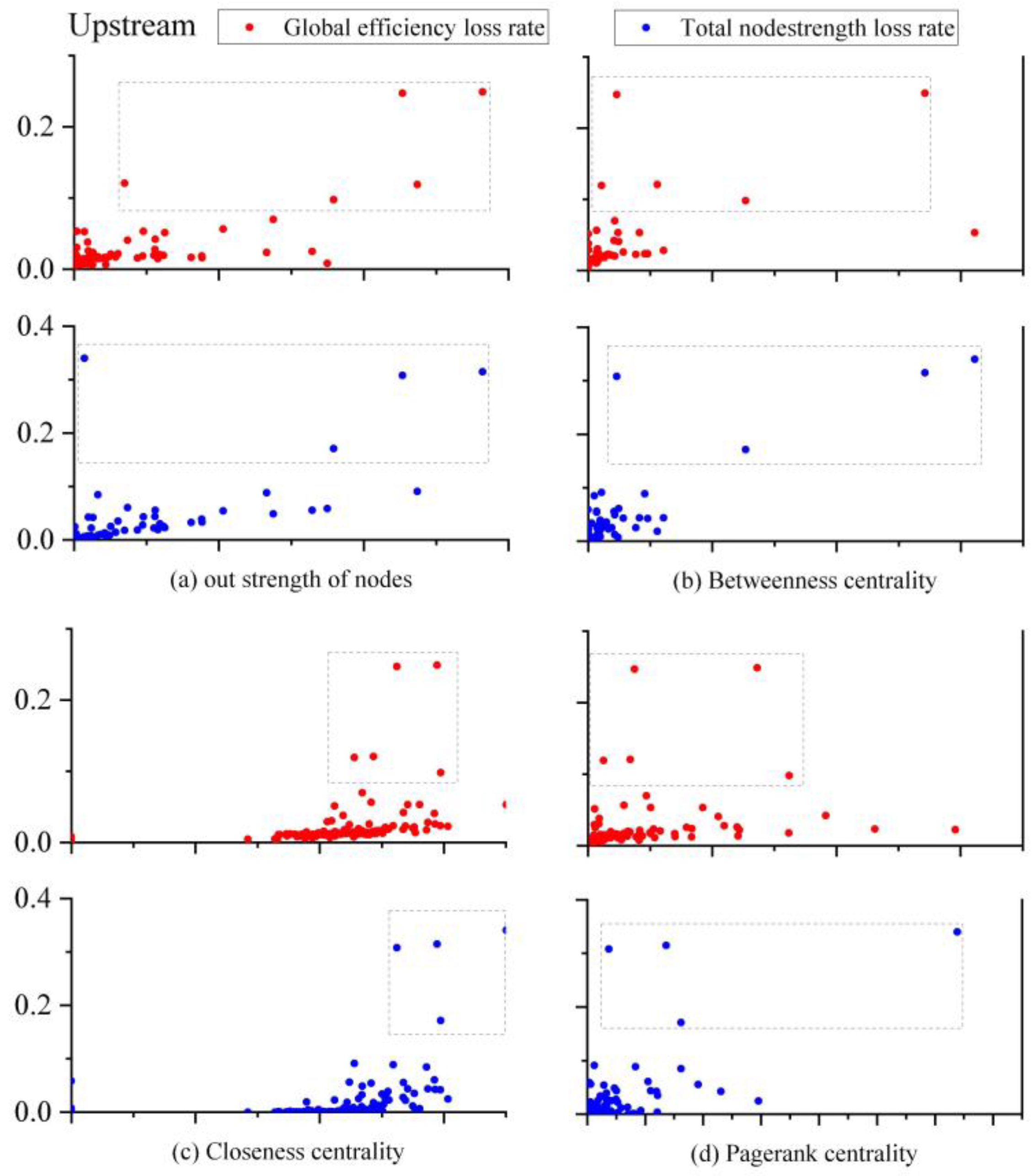
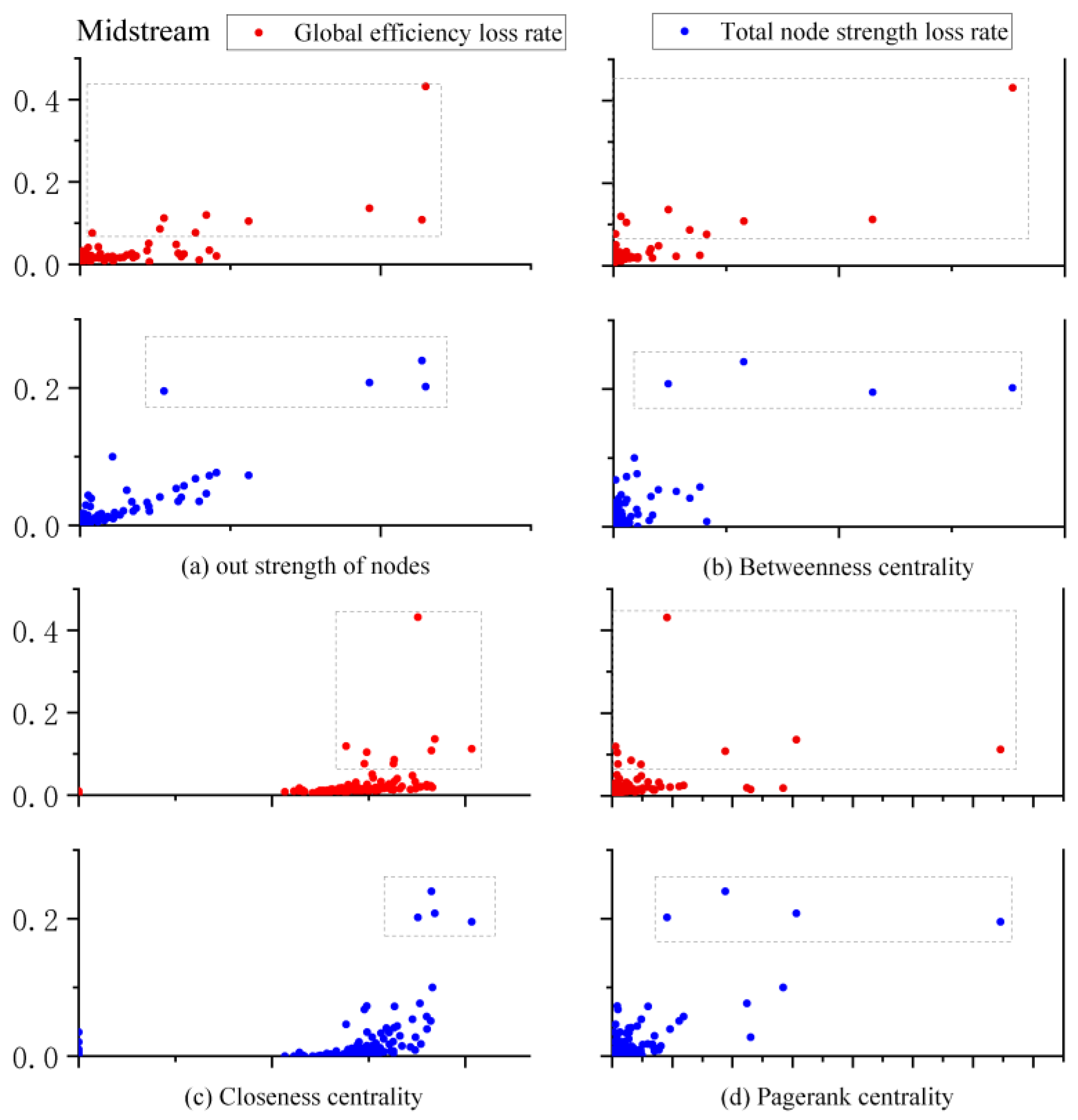
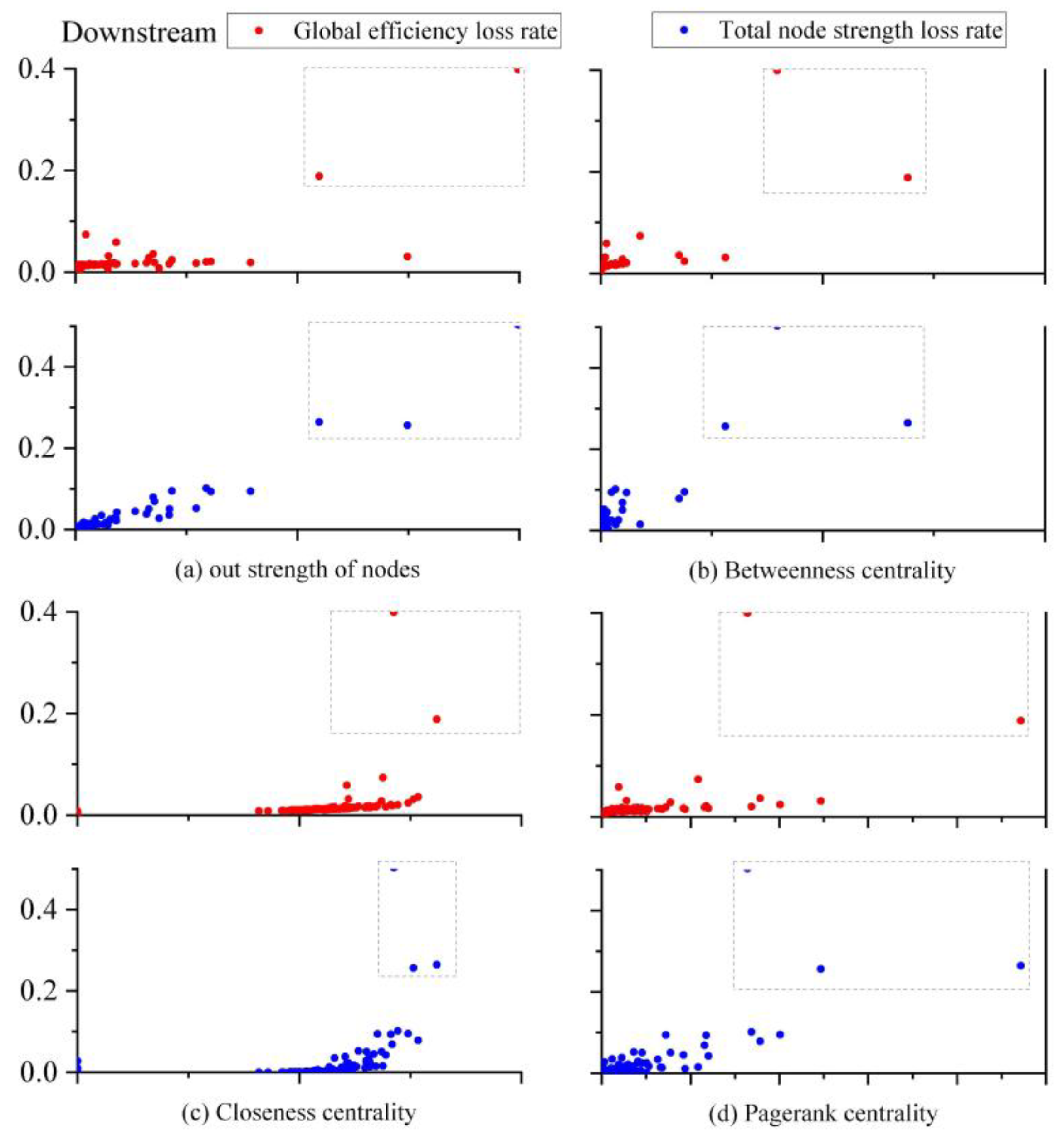
4.3. Node Importance Analysis Under Disruption Risk Propagation
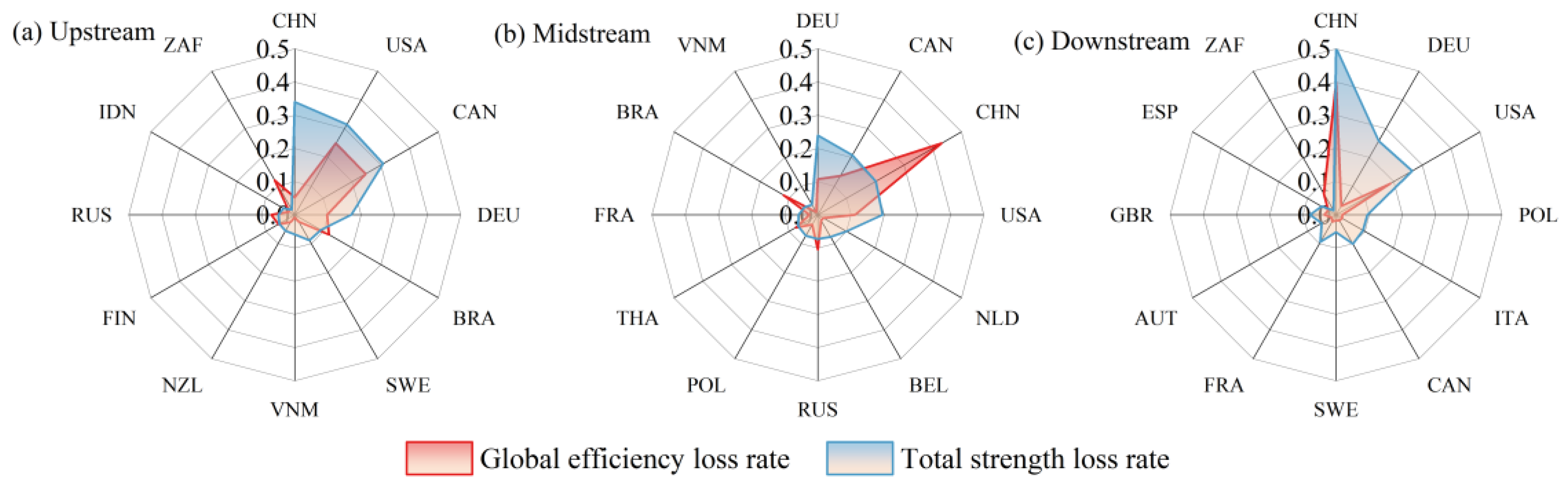
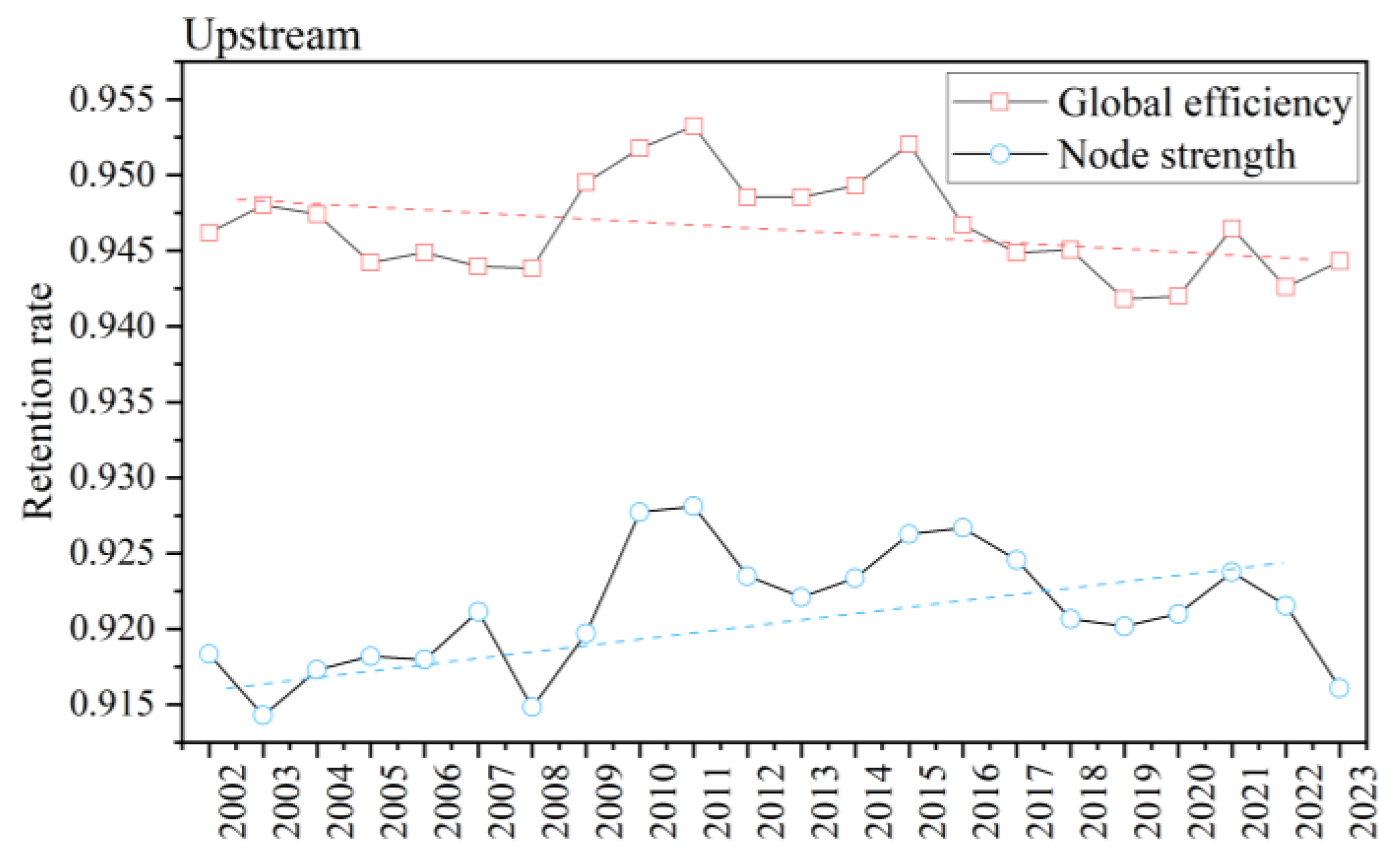
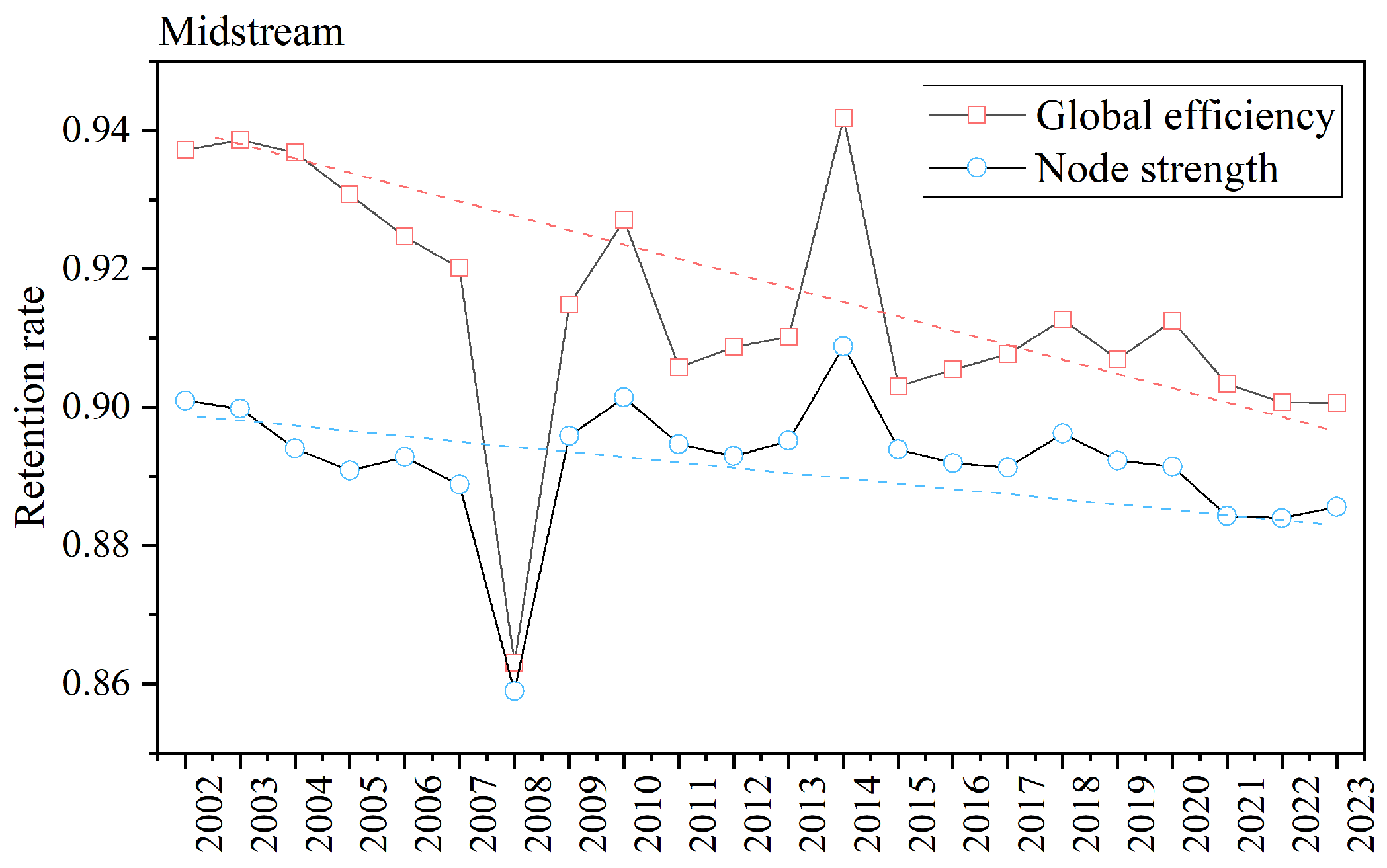
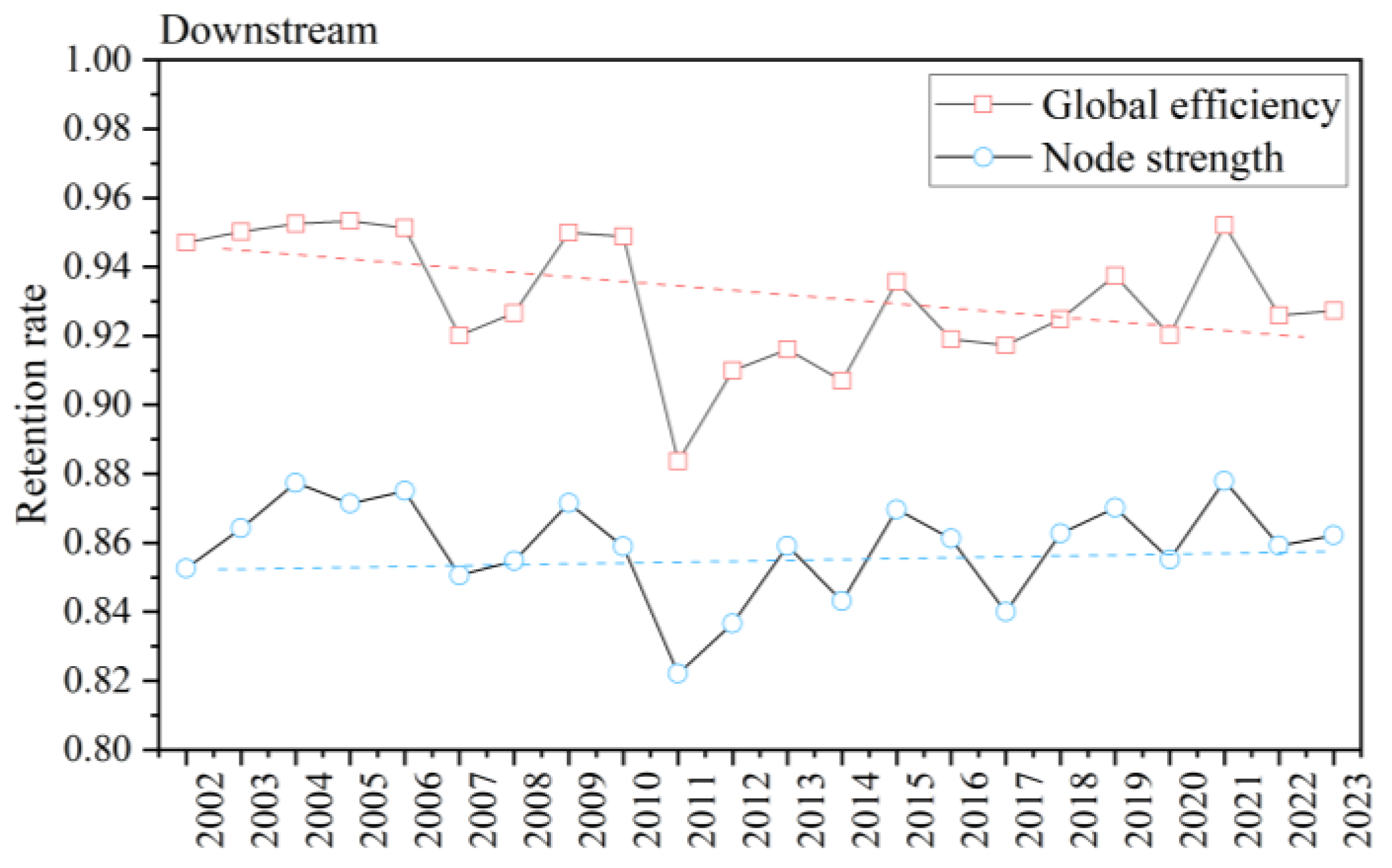
4.4. Analysis of Disruption Resilience Evolution Under Risk Propagation
5. Conclusions and Discussion
- (1)
- The global wood forest products trade network has shown fluctuating growth in terms of both trade volume and value during this period. Upstream products exhibit large trade volumes with low unit prices, while downstream products demonstrate higher trade values and unit prices, making significant contributions to the global economy. Network topology reveals that core countries including China, the United States, and Germany dominate global trade through stable trade chains. The network has grown increasingly complex and interconnected, with diversified trade relationships among countries/regions.
- (2)
- The simulation results indicate substantial variations in node disruption impacts across the network. Failures of core nodes significantly damage global efficiency and total node strength. Node centrality metrics (out-strength, betweenness centrality, etc.) generally correlate positively with network performance degradation, though correlation strengths differ by metric. This highlights the combined influence of the node position and attributes on network importance. Diverse evolution trends of disruption resilience across the network performance metrics provide multi-dimensional insights into network robustness.
- (3)
- From 2002 to 2023, global efficiency disruption resilience declined across all wood forest product trade networks, reflecting the growing influence of core nodes and weakening connectivity robustness after their disruptions. Total node strength resilience showed varied patterns: upstream networks demonstrated improved resilience through diversified connections, midstream networks displayed reduced resilience due to intensified core node dependence, and downstream networks maintained relatively stable resilience owing to mature supply chains and diversified trade channels [1].
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cao, X.P.; Yang, S.; Huang, X.M.; Tong, J.X. Dynamic Decomposition of Factors Influencing the Export Growth of China’s Wood Forest Products. Sustainability 2018, 10, 16. [Google Scholar] [CrossRef]
- Long, T.; Pan, H.X.; Dong, C.; Qin, T.; Ma, P. Exploring the competitive evolution of global wood forest product trade based on complex network analysis. Phys. A Stat. Mech. Its Appl. 2019, 525, 1224–1232. [Google Scholar] [CrossRef]
- Corona, P.; Alivernini, A. Forests for the world. Ann. Silvic. Res. 2024, 49, 80–81. [Google Scholar]
- Köhl, M.; Lasco, R.; Cifuentes, M.; Jonsson, Ö.; Korhonen, K.T.; Mundhenk, P.; Navar, J.D.; Stinson, G. Changes in forest production, biomass and carbon: Results from the 2015 UN FAO Global Forest Resource Assessment. For. Ecol. Manag. 2015, 352, 21–34. [Google Scholar] [CrossRef]
- FAO. The State of the World’s Forests 2024; Technical Report; Food and Agriculture Organization of the United Nations: Rome, Italy, 2024. [Google Scholar]
- Cheng, B.D. Reflections on the issue of wood security in China. China For. Ind. 2022, 12, 34–37. [Google Scholar]
- Tian, G.; Jiang, Q.Q. Social Network Analysis on International Roundwood Trade Pattern in 2005—2014. World For. Res. 2016, 29, 87–91. [Google Scholar] [CrossRef]
- Pizzol, M.; Scotti, M. Identifying marginal supplying countries of wood products via trade network analysis. Int. J. Life Cycle Assess. 2017, 22, 1146–1158. [Google Scholar] [CrossRef]
- Lovric, M.; Da Re, R.; Vidale, E.; Pettenella, D.; Mavsar, R. Social network analysis as a tool for the analysis of international trade of wood and non-wood forest products. For. Policy Econ. 2018, 86, 45–66. [Google Scholar] [CrossRef]
- Wang, F.; Tian, M.H.; Yin, R.S.; Zhang, Z.Y. Change of global woody forest products trading network and relationship between large supply and demand countries. Resour. Sci. 2021, 43, 1008–1024. [Google Scholar] [CrossRef]
- Zhou, Y.Y.; Hong, Y.P.; Cheng, B.D.; Xiong, L.C. The Spatial Correlation and Driving Mechanism of Wood-Based Products Trade Network in RCEP Countries. Sustainability 2021, 13, 16. [Google Scholar] [CrossRef]
- Hou, F.M.; Xiao, J.X.; Zhang, F.J.; Xiao, H.; Chen, Y. The impact of global trade networks on the division of labor in value chains -based on wood forest products perspective. For. Econ. 2022, 44, 50–64. [Google Scholar] [CrossRef]
- Li, Y.X.; Tian, M.H.; Guo, L.Q.; Feng, Q.R.; Yu, M.Y. Social network analysis of the trade pattern of wood products. Issues For. Econ. 2022, 42, 63–72. [Google Scholar] [CrossRef]
- Wang, R.; Wu, H.M.; Zhe, R.; Zhang, Y.A. Complex network analysis of global forest products trade pattern. Can. J. For. Res. 2023, 53, 271–283. [Google Scholar] [CrossRef]
- Liu, L.; Chen, Y.; Yu, J.; Sun, Y. Study on the resilience of the global trade network for wood forest products. Issues For. Econ. 2024, 44, 218–224. [Google Scholar]
- Gao, L.; Pei, T.W.; Tian, Y. Trade Creation or Diversion?-Evidence from China’s Forest Wood Product Trade. Forests 2024, 15, 18. [Google Scholar] [CrossRef]
- Liu, X.M.; Li, D.Q.; Ma, M.Q.; Szymanski, B.K.; Stanley, H.E.; Gao, J.X. Network resilience. Phys. Rep. Rev. Sec. Phys. Lett. 2022, 971, 1–108. [Google Scholar] [CrossRef]
- Wei, Y.; Xiu, C. Study on the concept and analytical framework of city network resilience. Prog. Geogr. 2020, 39, 488–502. [Google Scholar] [CrossRef]
- Li, L.G.; Zhang, P.Y.; Tang, J.T.; Guan, H.M. Review on the evolution of resilience concept and research progress on regional economic resilience. Hum. Geogr. 2019, 34, 1–7+151. [Google Scholar] [CrossRef]
- Liu, W.; Song, Z.Y. Review of studies on the resilience of urban critical infrastructure networks. Reliab. Eng. Syst. Saf. 2020, 193, 16. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Memarmontazerin, S.; Derrible, S.; Reihani, S.F.S. The role of travel demand and network centrality on the connectivity and resilience of an urban street system. Transportation 2019, 46, 1127–1141. [Google Scholar] [CrossRef]
- Kharrazi, A.; Rovenskaya, E.; Fath, B.D. Network structure impacts global commodity trade growth and resilience. PLoS ONE 2017, 12, 13. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, A.; Govindan, K.; Zubairu, N.; Pratabaraj, J.; Abideen, A.Z. Multi-tier supply chain network design: A key towards sustainability and resilience. Comput. Ind. Eng. 2023, 182, 18. [Google Scholar] [CrossRef]
- Kharrazi, A.; Akiyama, T.; Yu, Y.D.; Li, J. Evaluating the evolution of the Heihe River basin using the ecological network analysis: Efficiency, resilience, and implications for water resource management policy. Sci. Total Environ. 2016, 572, 688–696. [Google Scholar] [CrossRef]
- Kim, Y.; Chen, Y.S.; Linderman, K. Supply network disruption and resilience: A network structural perspective. J. Oper. Manag. 2015, 33–34, 43–59. [Google Scholar] [CrossRef]
- Gao, J.X.; Barzel, B.; Barabási, A.L. Universal resilience patterns in complex networks. Nature 2016, 530, 307–312. [Google Scholar] [CrossRef]
- Ji, G.J.; Zhong, H.L.; Nzudie, H.L.F.; Wang, P.; Tian, P.P. The structure, dynamics, and vulnerability of the global food trade network. J. Clean Prod. 2024, 434, 10. [Google Scholar] [CrossRef]
- Zhao, K.; Kumar, A.; Harrison, T.P.; Yen, J. Analyzing the Resilience of Complex Supply Network Topologies Against Random and Targeted Disruptions. IEEE Syst. J. 2011, 5, 28–39. [Google Scholar] [CrossRef]
- Ash, J.; Newth, D. Optimizing complex networks for resilience against cascading failure. Phys. A 2007, 380, 673–683. [Google Scholar] [CrossRef]
- Berche, B.; von Ferber, C.; Holovatch, T.; Holovatch, Y. Resilience of public transport networks against attacks. Eur. Phys. J. B 2009, 71, 125–137. [Google Scholar] [CrossRef]
- Bai, X.W.; Ma, Z.J.; Zhou, Y.M. Data-driven static and dynamic resilience assessment of the global liner shipping network. Transp. Res. Pt. E-Logist. Transp. Rev. 2023, 170, 19. [Google Scholar] [CrossRef]
- Li, J.X.; Nie, W.B.; Zhang, M.X.; Wang, L.N.; Dong, H.Y.; Xu, B. Assessment and optimization of urban ecological network resilience based on disturbance scenario simulations: A case study of Nanjing city. J. Clean Prod. 2024, 438, 16. [Google Scholar] [CrossRef]
- Kim, D.H.; Eisenberg, D.A.; Chun, Y.H.; Park, J. Network topology and resilience analysis of South Korean power grid. Phys. A 2017, 465, 13–24. [Google Scholar] [CrossRef]
- Sun, X.; Wei, Y.; Jin, Y.; Song, W.; Li, X.L. The evolution of structural resilience of global oil and gas resources trade network. Glob. Netw. 2023, 23, 391–411. [Google Scholar] [CrossRef]
- Li, Y.H.; Zobel, C.W.; Seref, O.; Chatfield, D. Network characteristics and supply chain resilience under conditions of risk propagation. Int. J. Prod. Econ. 2020, 223, 13. [Google Scholar] [CrossRef]
- Reggiani, A. Network resilience for transport security: Some methodological considerations. Transp. Policy 2013, 28, 63–68. [Google Scholar] [CrossRef]
- Gao, J.X.; Liu, X.M.; Li, D.Q.; Havlin, S. Recent Progress on the Resilience of Complex Networks. Energies 2015, 8, 12187–12210. [Google Scholar] [CrossRef]
- Herrera, M.; Abraham, E.; Stoianov, I. A Graph-Theoretic Framework for Assessing the Resilience of Sectorised Water Distribution Networks. Water Resour. Manag. 2016, 30, 1685–1699. [Google Scholar] [CrossRef]
- Yuan, X.J.; Ge, C.B.; Liu, Y.P.; Li, N.; Wang, Y. Evolution of Global Crude Oil Trade Network Structure and Resilience. Sustainability 2022, 14, 21. [Google Scholar] [CrossRef]
- Kilanitis, I.; Sextos, A. Integrated seismic risk and resilience assessment of roadway networks in earthquake prone areas. Bull. Earthq. Eng. 2019, 17, 181–210. [Google Scholar] [CrossRef]
- Artime, O.; Grassia, M.; De Domenico, M.; Gleeson, J.P.; Makse, H.A.; Mangioni, G.; Perc, M.; Radicchi, F. Robustness and resilience of complex networks. Nat. Rev. Phys. 2024, 6, 114–131. [Google Scholar] [CrossRef]
- Zhu, J.X.; Cai, J.F.; Jiang, T.T.; Lin, X.X. Study on the evaluation of emergency logistics network cascading failure invulnerability based on CI-TOPSIS fuzzy multi criteria group decision making tactics. Manag. Rev. 2018, 30, 229–238. [Google Scholar] [CrossRef]
- Mu, D.; Yue, X.P.; Ren, H.Y. Robustness of Cyber-Physical Supply Networks in Cascading Failures. Entropy 2021, 23, 18. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.J.; Liu, R.R.; Fan, T.L.; Liu, S.S.; Lü, L.Y. Overview of precaution and recovery strategies for cascading failures in multilayer networks. Acta Phys. Sin. 2020, 69, 11. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Marchiori, M. Model for cascading failures in complex networks. Phys. Rev. E 2004, 69, 4. [Google Scholar] [CrossRef]
- Wang, J.W.; Rong, L.L.; Zhang, L.; Zhang, Z.Z. Attack vulnerability of scale-free networks due to cascading failures. Phys. A 2008, 387, 6671–6678. [Google Scholar] [CrossRef]
- Wang, W.X.; Chen, G.R. Universal robustness characteristic of weighted networks against cascading failure. Phys. Rev. E 2008, 77, 5. [Google Scholar] [CrossRef]
- Dueñas-Osorio, L.; Vemuru, S.M. Cascading failures in complex infrastructure systems. Struct. Saf. 2009, 31, 157–167. [Google Scholar] [CrossRef]
- Mirzasoleiman, B.; Babaei, M.; Jalili, M.; Safari, M. Cascaded failures in weighted networks. Phys. Rev. E 2011, 84, 8. [Google Scholar] [CrossRef]
- Mukherjee, B.; Habib, M.F.; Dikbiyik, F. Network Adaptability from Disaster Disruptions and Cascading Failures. IEEE Commun. Mag. 2014, 52, 230–238. [Google Scholar] [CrossRef]
- Han, L.; Liu, B.; Deng, Y.; Wang, Q.Y.; Yin, R.R.; Liu, H.R. Cascading failure model of weighted scale-free networks. J. Softw. 2017, 28, 2769–2781. [Google Scholar] [CrossRef]
- Li, K.; He, Y.F.; Wu, W.; Liu, F.S. Reliability of complex hierarchical network for cascading failure. J. Huazhong Univ. Sci. Technol. 2018, 46, 45–51. [Google Scholar] [CrossRef]
- Cui, H.X.; Qiu, J.L.; Guo, M.; Zhang, R.F. Research on invulnerability of cascading failures in directed weighted supply chain networks. Control. Theory Appl. 2021, 38, 1828–1834. [Google Scholar]
- Li, C.; Wang, L.; Zhao, J.S.; Deng, L.C.; Yu, S.X.; Shi, Z.H.; Wang, Z. The collapse of global plastic waste trade: Structural change, cascading failure process and potential solutions. J. Clean Prod. 2021, 314, 9. [Google Scholar] [CrossRef]
- Hao, H.C.; Ma, Z.; Wang, A.J.; Xing, W.L.; Song, H.; Zhao, P.; Wei, J.Q.; Zheng, S.X. Modeling and assessing the robustness of the lithium global trade system against cascading failures. Resour. Policy 2023, 85, 14. [Google Scholar] [CrossRef]
- Fu, X.W.; Xu, X.J.; Li, W.F. Cascading failure resilience analysis and recovery of automotive manufacturing supply chain networks considering enterprise roles. Phys. A 2024, 634, 22. [Google Scholar] [CrossRef]
- Yin, X.X.; Tao, Y.W.; Zhao, X.Q.; Shi, L. Research on Crisis Propagation Effect in International Trade Network Based on Cascading Failure Model: Take Semiconductors as an Example. J. Syst. Sci. Math. Sci. 2024, 44, 1389–1411. [Google Scholar]
- Wang, C.; Yang, H.; Hu, X.; He, X.; Liu, J.; Liang, C.; Lim, M.K. Deciphering iron ore trade dynamics: Supply disruption risk propagation in global networks through an improved cascading failure model. Resour. Policy 2024, 95, 105157. [Google Scholar] [CrossRef]
- Ouyang, X.; Liu, L.T.; Chen, W.; Wang, C.; Sun, X.; He, C.F.; Liu, G. Systematic Risks of the Global Lithium Supply Chain Network: From Static Topological Structures to Cascading Failure Dynamics. Environ. Sci. Technol. 2024, 58, 22135–22147. [Google Scholar] [CrossRef]
- Wang, Y.C.; Xiao, R.B. Underload cascading failure model for supply chain networks. Comput. Integr. Manuf. Syst. 2020, 26, 1355–1365. [Google Scholar] [CrossRef]
- Huang, X.Y.; Wang, Z.W.; Pang, Y.; Tian, W.J.; Zhang, M. Static Resilience Evolution of the Global Wood Forest Products Trade Network: A Complex Directed Weighted Network Analysis. Forests 2024, 15, 24. [Google Scholar] [CrossRef]
- Newman, M.E.J. Fast algorithm for detecting community structure in networks. Phys. Rev. E 2004, 69, 5. [Google Scholar] [CrossRef] [PubMed]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech.-Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, C. A dynamic analysis of a green closed-loop supply chain with different on-line platform smart recycling and selling models. Comput. Ind. Eng. 2025, 200, 110748. [Google Scholar] [CrossRef]
- Su, C.; Zha, X.; Ma, J.; Li, B.; Wang, X. Dynamic Optimal Control Strategy of CCUS Technology Innovation in Coal Power Stations Under Environmental Protection Tax. Systems 2025, 13, 193. [Google Scholar] [CrossRef]

| Supply Chain Links | Product Category | Commodity Code | Detailed Information Regarding HS Codes |
|---|---|---|---|
| Upstream | Logs | HS4403 | Wood in the rough. |
| Other Raw Materials | HS4401, HS4402, HS4404, HS4405 | Various fuel wood, wood chips/sawdust/waste, wood charcoal, hoop wood/poles/stakes, wood wool/flour. | |
| Sawn Timber | HS4406, HS4407 | Wooden sleepers/cross-ties; sawn/chipped, sliced/peeled wood. | |
| Wood Pulp | HS4701-HS4706 | Wood pulp (mechanical, chemical types); combined pulp; recovered paper/cellulosic pulp. | |
| Midstream | Wood-based Panels | HS4408-HS4413 | Veneer, plywood, laminated wood sheets; vood (strips, friezes); particle/OSB/similar boards; fiberboard; densified wood. |
| Downstream | Wood Products | HS4414-HS4421 | Wooden frames; packings, cable-drums, pallets; coopers’ products; tools, handles; builders’ woodwork; wood tableware, kitchenware; marquetry, inlaid wood, ornaments; furniture (excl. ch. 94); other wood items. |
| Paper Products | HS48, HS49 | Paper, paperboard, articles thereof; printed products, manuscripts, typescripts, plans. | |
| Wood Furniture | HS940161, HS940169, HS940330, HS940340, HS940350, HS940360 | Wooden-framed seats (upholstered/not); wooden furniture (office, kitchen, bedroom, other). | |
| Recycled | Waste Paper | HS4707 | Waste and scrap of paper and paperboard. |
| Indicator Type | Indicator Name | Formula | Specific Description |
|---|---|---|---|
| Structural Characteristics | Number of Nodes | N | N represents the total number of nodes in the network. |
| Weighted Global Efficiency | Weighted global efficiency refers to the average of the reciprocals of the weighted shortest path lengths between all pairs of nodes in the network, taking into account the trade closeness weights. It measures the speed and capability of information transmission within the network. | ||
| Node Characteristics | Out-Strength | Out-strength refers to the sum of the export trade volume weights () from node i to other nodes. | |
| In-Strength | In-strength refers to the sum of the import trade volume weights () from other nodes to node i. | ||
| Weighted Betweenness Centrality | Weighted betweenness centrality refers to the ratio of the number of weighted shortest paths passing through node i to the total number of weighted shortest paths between other trade pairs, considering trade closeness weights. It measures the importance and influence of a country (region) in the network from the perspective of its “bridge” role. | ||
| Weighted Closeness Centrality | Weighted closeness centrality refers to the reciprocal of the average weighted shortest path from node i to all other nodes, considering trade closeness weights. | ||
| Weighted PageRank Centrality | Weighted PageRank centrality is a measure of node importance calculated by simulating a random walker that, with probability α, jumps to adjacent nodes along the outgoing edges of the current node, and, with probability (1 − α), jumps to any node in the network, considering trade volume weights. This value depends on the average importance of nodes pointing to it () and the global visibility of node i in the network (). | ||
| Weighted Eigenvector Centrality | Weighted eigenvector centrality refers to a centrality measure of node i in the network based on the importance of its neighboring nodes , calculated through eigenvector analysis and considering trade volume weights. Here, λ is the largest eigenvalue of the network’s adjacency matrix. | ||
| Others | Modularity | Modularity Q, proposed by Newman [62] in 2004, is the most popular general metric for evaluating the quality of community division. It measures the quality of community division by comparing the number of edges within communities in the actual network to the expected number of such edges in a random network. The value of modularity ranges from [−0.5,1], and a value closer to 1 indicates a better community division. In the formula, H represents the total strength of all nodes in the network, is the sum of the out-strength and in-strength of node , denoting the average weight of edges within the same trade community, and represents the average weight of edges that would be assigned to the same community under complete randomness. The function is used to determine whether nodes i and j belong to the same community: if and are in the same community, = 1; otherwise, = 0. | |
| Pearson Correlation Coefficient | The Pearson correlation coefficient r is used to measure the strength and direction of the linear relationship between variables, with a range of −1 to 1. A value of 1 indicates a perfect positive correlation, −1 indicates a perfect negative correlation, and 0 indicates no linear relationship, although a nonlinear relationship may still exist. In the formula, represent the i-th observations of variables X and Y, respectively. and are the mean values of variables X and Y, respectively, and n is the number of observations. |
| Comparison Dimension | Infrastructure Networks | Global Wood Forest Product Trade Network |
|---|---|---|
| Type of Cascading Failure | Overload failure: after a node’s interruption, the load is transferred to adjacent nodes, exceeding their capacity and causing failure. | Underload failure: the interruption of a supply node leads to resource shortages in downstream nodes, triggering a reduction in export volumes. |
| Failure Trigger Conditions | Node or edge interruption causes physical load to exceed capacity limits. | Node or edge interruption causes resource supply to fall below demand thresholds. |
| Load Allocation Logic | Uniform distribution or non-uniform selective distribution: stronger relationships receive more load. | Non-uniform selective distribution: lower relationship strength receives higher allocation proportion. |
| Propagation Path of Failure | Spreads along physical topology proximity. | Spreads along supply dependency relationships. |
| Node Types | Import–Export Load Characteristics | Decay Characteristics | |
|---|---|---|---|
| Type 1 (Import-Dominant) | The import load is greater than or equal to the export load. | The export load exhibits three operational states—normal, decay, and failure—where the decay magnitude is jointly influenced by the import–export load ratio and the node’s decay state. | |
| Type 2 (Balanced Import–Export) | The import load is slightly less than the export load. | The export load similarly demonstrates three states (normal, decay, and failure), with the decay state proportionally diminishing according to the import quantity. | |
| Type 3 (Export-Dominant) | The import load is significantly lower than the export load. | The export load only transitions between normal and decay states, omitting the failure state entirely. | |
| Network Type | Classification of Trading Blocs | |||
|---|---|---|---|---|
| Upstream Network | CHN BRA VIE NZL RUS IND THA CHL MYS PNG UAE SLB BLR CMR PHL | DEU AUT ITA FRA NLD BEL POL CZE SVN SVK UKR HRV ROM HUN CHE LUX BIH SRB GRC | USA CAN JPN GBR AUS TUR MEX IRL DOM | SWE FIN LVA NOR DNK EST LTU EGY KSA MAR ISR PAK TUN JOR ISL |
| Midstream Network | CHN IND THA VIE MYS IDN JPN NPL AUS KSA UAE NZL PHL NGA UGA SGP GAB ISR MMR KEN TZA KWT JOR OMN QAT CMR PAK LKA | DEU NLD BEL POL FRA ITA ESP GBR AUT ROU CZE PRT LVA HUN SWE FIN DNK LTU SVK IRL CHE UKR LUX EST HRV SVN NOR SRB BIH MDA | USA CAN BRA MEX CHL PER ECU COL ARG KHM URY DOM GTM BHS BOL PRY CRI JAM | RUS TUR KAZ UZB BLR BGR AZE GRC EGY MAR GEO KGZ TUN ARM MKD LBN CYP |
| Downstream Network | CHN JPN IDN IND MYS AUS RUS UAE THA SGP KSA KOR PHL EGY NZL KAZ NGA UZB KWT JOR LKA PAK KEN LAO OMN CIV AZE BLR LBN QAT MMR ETH GHA TZA BHR ARM | DEU FRA POL ITA GBR NLD SWE AUT ESP BEL FIN CZE CHE TUR PRT DNK HUN ROU IRL LTU SVK NOR GRC UKR SVN SRB BGR HRV LVA ISR MAR LUX EST BIH TUN MLT GEO MKD MDA CYP SEN | USA CAN MEX VIE BRA ZAF CHL COL GTM ARG CRI PER DOM SLV ECU PAN PRY URY NIC KHM BOL | |
| Ranking | Upstream Network | Midstream Network | Downstream Network | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Global Efficiency Loss Rate | Node Strength Loss Rate | Global Efficiency Loss Rate | Node Strength Loss Rate | Global Efficiency Loss Rate | Node Strength Loss Rate | |||||||
| Node | Value | Node | Value | Node | Value | Node | Value | Node | Value | Node | Value | |
| 1 | USA | 0.25 | CHN | 0.34 | CHN | 0.43 | DEU | 0.24 | CHN | 0.40 | CHN | 0.50 |
| 2 | CAN | 0.25 | USA | 0.31 | CAN | 0.14 | CAN | 0.21 | DEU | 0.03 | USA | 0.26 |
| 3 | ZAF | 0.12 | CAN | 0.31 | BRA | 0.12 | CHN | 0.20 | USA | 0.19 | DEU | 0.26 |
| 4 | BRA | 0.12 | DEU | 0.17 | USA | 0.11 | USA | 0.20 | CAN | 0.02 | CAN | 0.10 |
| 5 | DEU | 0.10 | BRA | 0.09 | DEU | 0.11 | NLD | 0.10 | FRA | 0.02 | FRA | 0.09 |
| 6 | RUS | 0.07 | SWE | 0.09 | RUS | 0.10 | BEL | 0.08 | POL | 0.02 | POL | 0.09 |
| 7 | FIN | 0.06 | JPN | 0.08 | TUR | 0.09 | RUS | 0.07 | ITA | 0.02 | ITA | 0.09 |
| 8 | ARE | 0.05 | NLD | 0.06 | THA | 0.08 | POL | 0.07 | GBR | 0.04 | GBR | 0.08 |
| 9 | ESP | 0.05 | VNM | 0.06 | ZAF | 0.08 | THA | 0.07 | NLD | 0.02 | NLD | 0.07 |
| 10 | CHN | 0.05 | NZL | 0.06 | CHL | 0.05 | FRA | 0.06 | SWE | 0.02 | SWE | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Wang, Z.; Pang, Y.; Tian, W. Evolution of Disruption Resilience in the Wood Forest Products Trade Network, Considering the Propagation of Disruption Risks and Underload Cascading Failure. Sustainability 2025, 17, 2733. https://doi.org/10.3390/su17062733
Huang X, Wang Z, Pang Y, Tian W. Evolution of Disruption Resilience in the Wood Forest Products Trade Network, Considering the Propagation of Disruption Risks and Underload Cascading Failure. Sustainability. 2025; 17(6):2733. https://doi.org/10.3390/su17062733
Chicago/Turabian StyleHuang, Xiangyu, Zhongwei Wang, Yan Pang, and Wujun Tian. 2025. "Evolution of Disruption Resilience in the Wood Forest Products Trade Network, Considering the Propagation of Disruption Risks and Underload Cascading Failure" Sustainability 17, no. 6: 2733. https://doi.org/10.3390/su17062733
APA StyleHuang, X., Wang, Z., Pang, Y., & Tian, W. (2025). Evolution of Disruption Resilience in the Wood Forest Products Trade Network, Considering the Propagation of Disruption Risks and Underload Cascading Failure. Sustainability, 17(6), 2733. https://doi.org/10.3390/su17062733






