Research on the Optimized Design of Medium and Deep Ground-Source Heat Pump Systems Considering End-Load Variation

Abstract

Ground-source heat pump (GSHP) systems with medium-depth and deeply buried pipes in cold regions are highly important for addressing global climate change and the energy crisis because of their efficient, clean, and sustainable energy characteristics. However, unique geological conditions in cold climates pose serious challenges to the heat transfer efficiency, long-term stability, and adaptability of systems. This study comprehensively analyses the effects of various factors, including well depth, inner-to-outer tube diameter ratios, cementing material, the thermal conductivity of the inner tube, the flow rate, and the start–stop ratio, on the performance of a medium-depth coaxial borehole heat exchanger. Field tests, numerical simulations, and sensitivity analyses are combined to determine the full-cycle thermal performance and heat-transfer properties of medium-depth geological formations and their relationships with system performance. The results show that the source water temperature increases by approximately 4 °C and that the heat transfer increases by 50 kW for every 500 m increase in well depth. The optimization of the inner and outer pipe diameter ratios effectively improves the heat-exchange efficiency, and a larger pipe diameter ratio design can significantly reduce the flow resistance and improve system stability. When the thermal conductivity of the cementing cement increases from 1 W/(m·K) to 2 W/(m·K), the outlet water temperature at the source side increases by approximately 1 °C, and the heat transfer increases by 13 kW. However, the improvement effect of further increasing the thermal conductivity on the heat-exchange efficiency gradually decreases. When the flow rate is 0.7 m/s, the heat transfer is stable at approximately 250 kW, and the system economy and heat-transfer efficiency reach a balance. These findings provide a robust scientific basis for promoting medium-deep geothermal energy heating systems in cold regions and offer valuable references for the green and low-carbon transition in building heating systems.

1. Introduction

Energy shortages and climate change have become global challenges, posing serious threats to sustainable socioeconomic development and necessitating an urgent transition in energy systems [1,2]. According to statistics, the thermal energy used for cooling and heating accounts for more than 50% of the global end-use energy consumption [3]. In the context of the global zero-carbon emission target, reducing energy consumption for building heating is widely recognized as a critical strategy for achieving low-carbon development [4]. Building heating systems, as an important part of energy consumption, constitute not only one of the main areas of energy consumption [5] but also one of the main sources of carbon emissions. However, conventional building heating continues to depend heavily on fossil fuels, resulting in substantial greenhouse gas emissions and worsening energy security concerns [6]. Therefore, it is imperative to introduce clean and renewable energy sources to replace traditional fossil fuel-based heating systems to mitigate carbon emissions and ease environmental pressures effectively.

Geothermal energy, as an abundant and sustainable clean energy source, has garnered increasing attention because of its widespread availability and minimal environmental footprint [6]. In recent years, ground-source heat pump (GSHP) technology, an important approach for developing and utilizing geothermal energy, has undergone rapid expansion in its applications across China and globally, particularly in building heating for cold regions, demonstrating significant advantages [7]. However, the diffusion of traditional groundwater source heat pump systems is geographically constrained by their dependence on groundwater resources and is severely limited in areas with scarce water resources or extreme climates [1]. Moreover, although shallow (depths ranging from 20–200 m) ground-source heat pump systems have shown better economic viability and feasibility in certain regions, the imbalance of the shallow heat source load in northern cold regions has significantly compromised their long-term performance and stability because of the significantly higher heating demand in winter than in summer [8]. Consequently, the development of medium and deep ground-source heat pump systems, which are better suited to severely cold climates, has emerged as a major focus and key trend in current research.

As an energy development method between shallow geothermal energy and deep high-temperature geothermal energy, the development depth of medium-depth geothermal energy heating is generally in the range of 200–2000 m, which can effectively balance the cost of resource development and the efficiency of energy output [9], and it has become a potentially preferable option for heating in severely cold areas. In recent years, domestic and international research on medium and deep ground-source heat pump systems has gradually increased, with a focus on the optimization of heat exchanger structures [10], energy efficiency improvement [11], and engineering economic analysis [12]. For example, Ma et al. [10] evaluated the thermal performance of deep coaxial borehole heat exchangers in the Songliao Basin via OpenGeoSys numerical simulations, providing a scientific basis for converting abandoned water wells into geothermal heat exchanger wells in Northeast China. Norouzi et al. [13] assessed the effectiveness of ground-source heat pumps in mitigating ground settlement in the permafrost zone by establishing a two-dimensional thermo-water mechanical coupled finite element model. Jathunge et al. [14] evaluated the long-term thermal performance of biased tube thermally active foundation piles in a residential GSHP system through numerical simulations, revealing the effects of different installation configurations and building loads on ground temperature variations and system efficiency. However, most current studies rely on theoretical models and laboratory simulations, and research on heat transfer characteristics under long-term operating conditions in severely cold regions is insufficient. Furthermore, the unique geological conditions and climatic environments of cold regions pose significant challenges to medium–deep ground-source heat pump systems, and improving the adaptability of these systems in these regions remains a critical scientific challenge that requires urgent attention.

In a medium-depth ground-source heat pump system, the borehole heat exchanger serves as the core heat exchanger device, facilitating geothermal energy extraction and transfer through heat exchange between the circulating fluid and the surrounding geological formation [6,15]. The structural design and operating conditions of a borehole heat exchanger directly impact heat-exchange efficiency [16], with well depth, the inner-to-outer pipe diameter ratio, the thermal conductivity of the inner pipe material, the flow rate, and the start–stop operation ratio being key factors influencing performance [8,17]. Especially in cold regions, the heat transfer characteristics of source-side geological formations are influenced not only by the borehole heat exchanger structure and operating conditions but also by the coupling action of complex factors such as freeze–thaw cycles and variations in soil thermophysical properties [18]. Feng et al. [8] evaluated the heating performance of a medium–deep ground-source heat pump system in a cold and arid region through experimental tests and numerical simulations, validating a new 3D numerical model that illustrates the effects of the insulation layer, well diameter, flow rate, and well depth on system performance. Shen et al. [17] investigated the effects of thermal conductivity, tube diameter, and flow rate on the heat extraction capacity of a U-shaped deep well heat exchanger via a segmented finite line source method. Li et al. [19] reported that increasing the thickness of the inner tube insulation and the outer diameter of the outer tube is an effective strategy for enhancing the thermal performance of a coaxial ground heat exchanger as demonstrated through simulations. Luo et al. [20] reported that by selecting the appropriate system design parameters, energy savings in a ground-source heat pump system based on deep-well heat exchangers can reach 21.8%. However, most of the current studies are based on theoretical models and laboratory simulations [21] and address the heat transfer characteristics under long-term operating conditions in cold areas. In addition, the special geological conditions and climate environment in cold regions pose unique challenges to medium and deep ground-source heat pump systems, and how to improve the adaptability of the system in these regions is still a key scientific problem that urgently needs to be solved.

The unique contribution of this paper is that we meet the special requirements of the deep ground-source heat pump system in the middle of cold areas and optimize the operation mode and design parameters of the system on the basis of annual dynamic load simulation. Unlike existing studies that focus on optimizing the heat exchanger design and improving energy efficiency, the innovation of this study is as follows: on the one hand, on the basis of traditional design parameters (such as well depth and pipe diameter ratio), several new operating parameters, such as cement thermal conductivity, flow velocity, and the start–stop ratio, are introduced; on the other hand, through sensitivity analysis, we quantify the influence of these key design parameters on the thermal efficiency and long-term stability of the system and propose specific optimization suggestions for cold areas. In particular, with respect to the application of a dynamic control strategy, this study, through the simulation of buildings by load and accurate adjustments of heat source heat-intake characteristics, significantly improve the stability and energy efficiency of the system, and for ground-source heat pumps in cold areas, it provides scientific guidance, scientific support for green low-carbon building heating, and the popularization and application of this technology in cold areas.

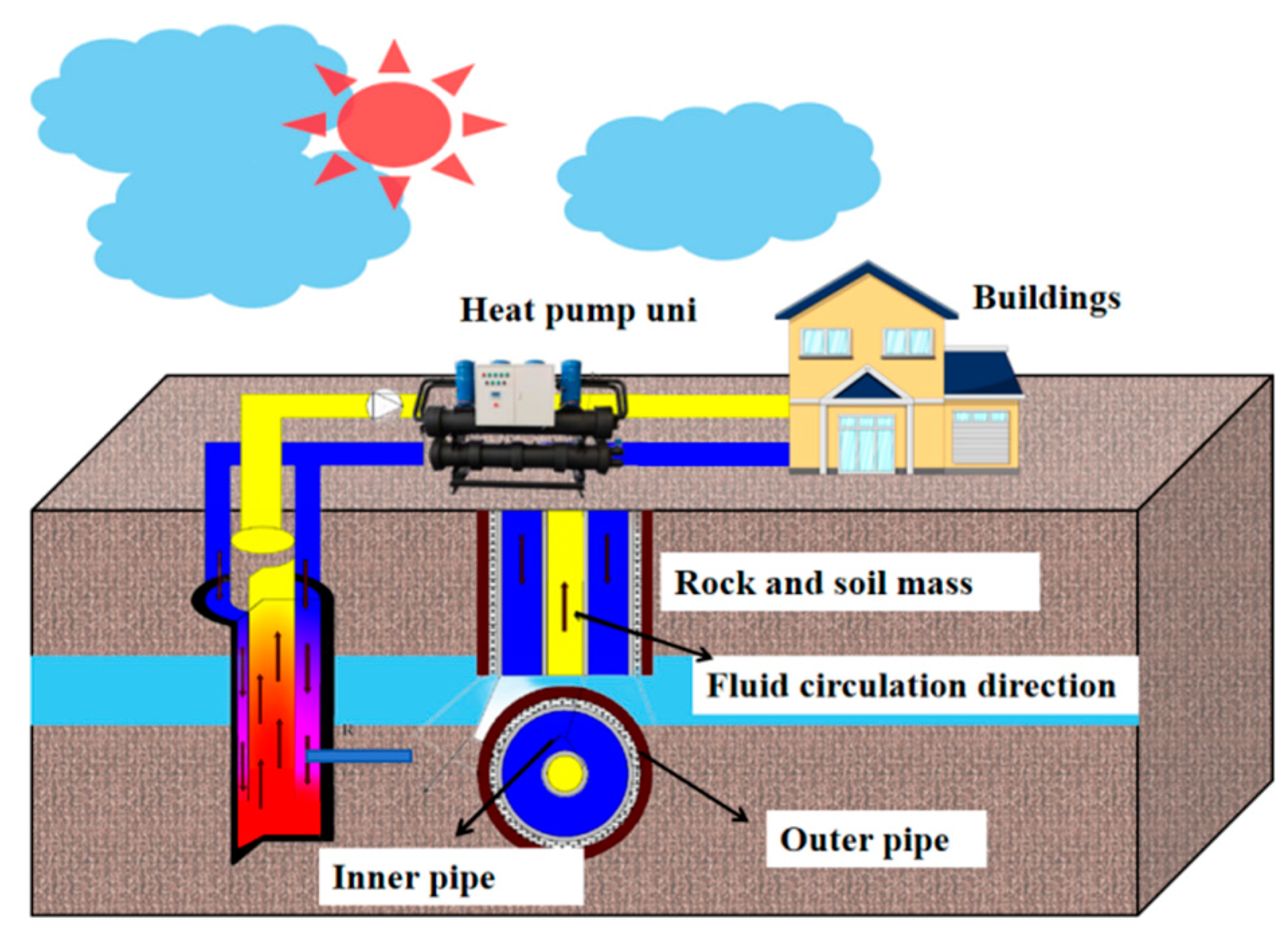
2. Numerical Modelling and Computational Methods

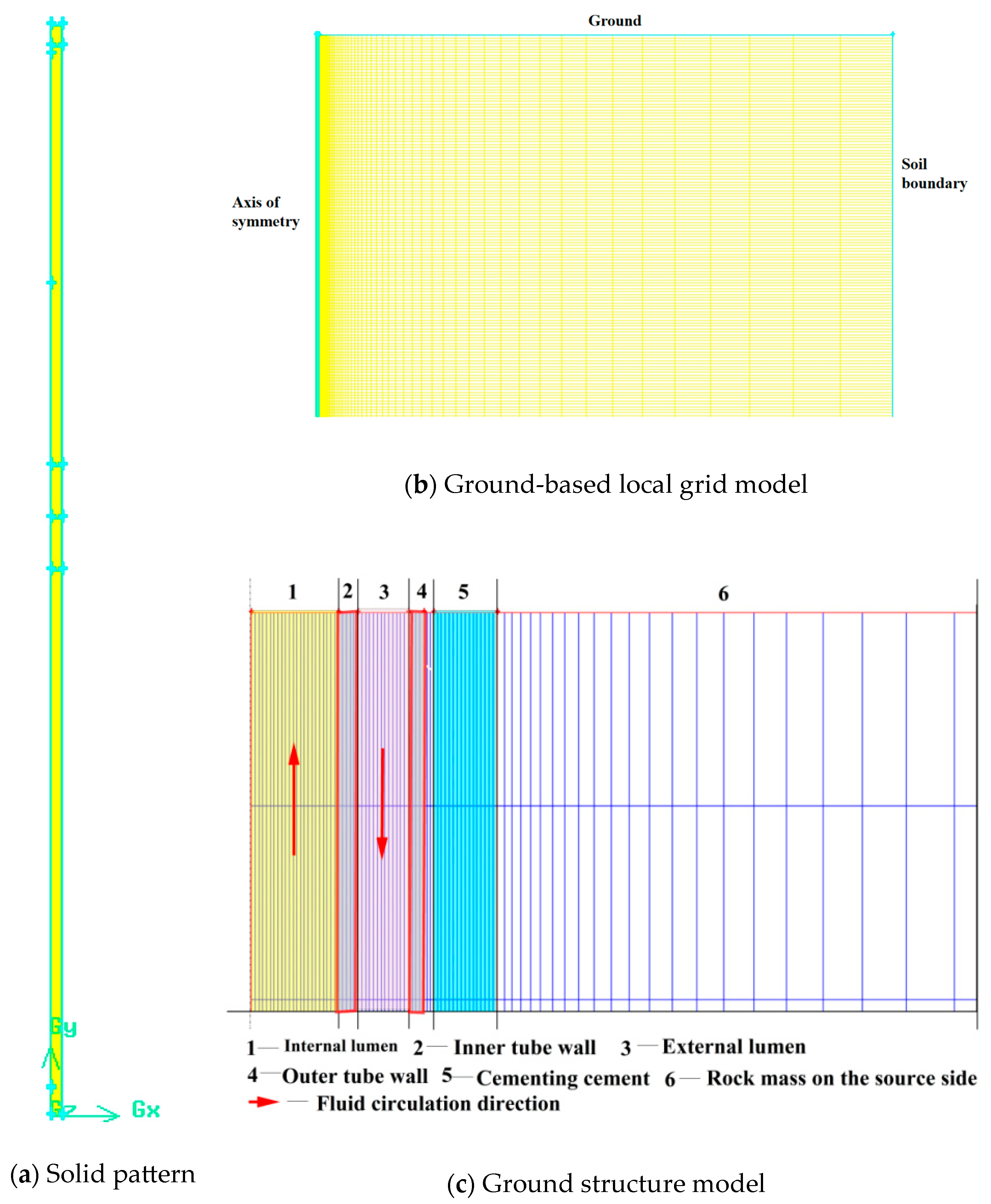
2.1. Calculation Model Fluency

As shown in Figure 1, this study is based on the structure and heat-transfer mechanism of the deep coaxial casing system of a ground-source heat pump. Moreover, to reduce the calculation cost, the three-dimensional model is simplified to establish a two-dimensional axisymmetric physical model. The simulation system is composed of a coaxial casing heat exchanger, a heat pump unit, and terminal equipment on the ground-source side. The heat exchanger consists of inner and outer tubes forming a coaxial casing, which facilitates heat exchange with the surrounding rock mass through thermal convection in the annular cavity between the outer and inner tubes.

The heat exchange area of the coaxial casing heat exchanger (with a length of 2000 m, model height of 2200 m, outer tube radius of 177.8 mm, and inner tube radius of 110 mm) is axisymmetric. Combining the actual geological conditions and design parameters of the heat exchanger, this study uses CFD (Fluent) software (https://www.ansys.com/) to construct a two-dimensional physical model to simulate the heat-transfer process between the heat exchanger and the surrounding soil [22]. The model is discretized on a tetrahedral grid and implements local encryption processing for key areas. To reduce the calculation cost and ensure calculation accuracy, the deviation of the outlet within 1.5% is 100%, and the total grid reaches 2.73 million (as shown in Figure 2, where (a) is the overall grid model, (b) is the ground local grid model, and (c) is the ground structure model). This meshing strategy not only ensures high accuracy in heat transfer simulations but also significantly enhances computational efficiency. In terms of the grid division method, this study adopts a structured grid, which can effectively reduce the storage requirement and increase the computational speed because of its advantages in the processing of internode relationships. Compared with unstructured grids, structured grids exhibit a more regular topology and superior computational stability, making them especially suitable for accurate simulations of heat-transfer processes in local heat pump systems [23]. On the basis of the fixed grid, 150 s, 300 s, 600 s, and 1200 s are the time steps to calculate the deviation of the coaxial casing heat exchanger within 1.5% of the standard, and the calculation time step is selected to be 300 s.

2.2. Model Assumptions

To increase the computational efficiency and versatility of the model while ensuring its applicability to actual engineering, the following pragmatic assumptions and simplifications are made in the modelling in this study [24]:

(1)

The surface temperature is assumed to remain constant, and the effects of subsurface seepage are disregarded. Consequently, geotechnical heat transfer is modelled as a purely thermal conduction process. This assumption holds for regions with minimal seepage effects, significantly simplifying the coupled convection–heat conduction model and ensuring computational efficiency without compromising the simulation accuracy of heat-transfer behaviour.

(2)

Stratigraphy with similar lithologies is combined and modelled as a homogeneous horizontally layered structure, which serves as the basis of the model. This simplification reduces the complexity of stratigraphic zoning while retaining the essential effects of major thermophysical differences and is commonly used in studies under similar geological conditions.

(3)

The initial temperatures of the fluid in the casing, the backfill material, and the buried pipe are assumed to match the same horizontal geotechnical temperature, and the measured soil temperature is assumed to be uniform. This setting is based on the thermal equilibrium state, which accurately represents the initial thermal coupling relationship between the system and the geotechnical soil and simplifies the specification of the initial conditions.

2.3. Calculation Method

An analysis of the heat-transfer process between the heat exchanger and the geotechnical body revealed that the fluid flows turbulently inside the heat exchanger. To simulate the fluid heat-transfer characteristics within the heat exchanger accurately, the standard κ-ε turbulence model is employed in this study. Compared with large eddy simulation (LES), the standard κ-ε model significantly reduces the computational volume while ensuring accuracy, making it suitable for efficiently solving complex engineering problems. To further increase computational efficiency and stability, the model is solved via a simple method for pressure–velocity coupling [25,26,27]. The governing equations of the standard κ-ε model are as follows:

The continuity equation for the flow of water in the casing is given by

$${\displaystyle \frac{\partial \rho }{\partial t}}+{\displaystyle \frac{\partial }{\partial x_i}}\left(\rho v_i\right)+{\displaystyle \frac{\partial }{\partial x_i}}(\rho v_j)=0.$$

(1)

The momentum equation is as follows:

$${\displaystyle \frac{\partial \left(\rho v_i\right)}{\partial t}}+{\displaystyle \frac{\partial }{\partial x_j}}\left(\rho v_i{v}_j\right)=-{\displaystyle \frac{\partial P}{\partial x_i}}+{\displaystyle \frac{\partial }{\partial x_j}}\left(\mu {\displaystyle \frac{\partial v_i}{\partial x_j}}\right)-{\displaystyle \frac{\partial {\tau }_{ij}}{\partial x_j}}.$$

(2)

Included among these is ${\tau }_{ij}=-\rho \overline{{v^{\prime }}_i{v^{\prime }}_j}$.

The energy equation is as follows:

$${\displaystyle \frac{\partial (\rho T)}{\partial t}}+{\displaystyle \frac{\partial }{\partial x_j}}(\rho v_{i}T)=\lambda /C_P{\displaystyle \frac{\partial }{\partial x_j}}(\mu {\displaystyle \frac{\partial T}{\partial x_j}}),$$

(3)

where ρ is the fluid density, kg/m³; t is the time, s; ij is the velocity vector (i, j = 1, 2); x_i, x_j is the coordinate direction (i, j = 1, 2), m/s; CP is the constant-pressure specific heat capacity; P is the pressure acting on the fluid micrometabolite, Pa; μ is the dynamic viscosity; τij is the Reynolds stress, N; and $\overline{{v^{\prime }}_i}$ and $\overline{{v^{\prime }}_j}$ are the mean velocities in the i, j directions, m/s.

Since the above system of equations is incomplete, certain assumptions must be made about the Reynolds stress, meaning that a new turbulence model is introduced to relate the pulsation and time-averaged turbulence values, which are used to close the system of equations [23]. Depending on the assumption and treatment of the Reynolds stress, the introduced turbulence models include the Reynolds stress model, zero-equation model, one-equation model, and two-equation model. In this study, the standard κ-ε model, one of the two-equation models, is used for the analysis. The standard κ-ε model introduces an equation for turbulent dissipation ε on the basis of the one-equation model, which has become the primary closure method in engineering turbulence owing to its inclusion of part of the history effect. The model is derived from simple turbulent flows and assumes isotropic turbulent viscosity, making it more suitable for simpler turbulent flows such as jets, pipe flows, and weak cyclones. The transport equations for the turbulent kinetic energy κ and turbulent dissipation ε in the standard κ–ε model are as follows:

$${\displaystyle \frac{\partial \left(\rho \kappa \right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho \kappa v_i\right)}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_j}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_{\kappa }}}\right){\displaystyle \frac{\partial \kappa }{\partial x_j}}\right]+G_{\kappa }-\rho \epsilon$$

(4)

$${\displaystyle \frac{\partial \left(\rho \epsilon \right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho \epsilon v_i\right)}{\partial x_i}}={\displaystyle \frac{\partial }{\partial x_j}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_{\epsilon }}}\right){\displaystyle \frac{\partial \epsilon }{\partial x_j}}\right]+C_{1\epsilon }{\displaystyle \frac{\epsilon }{\kappa }}{G}_{\kappa }-C_{2\epsilon }\rho \epsilon {\displaystyle \frac{{\epsilon }^2}{\kappa }}$$

(5)

Included among these are

$${\mu }_t=\mu +\rho C_{\mu }{\kappa }^2/\epsilon ;G_{\kappa }={\mu }_t\left(\partial v_i/\partial x_j+\partial v_j/\partial x_i\right)/\left(\partial v_i/\partial x_j\right)$$

where μ_t is the turbulent viscosity; C_μ is the viscosity coefficient, where C_μ = 0.09; G_κ is the production term of κ caused by the mean velocity gradient; σ_κ and σ_ε are the turbulent kinetic energy κ and turbulence dissipation ε corresponding to the Prandtl number, where σ_κ = 1.0 and σ_ε = 1.3; and C_1ε and C_2ε are model constants, where C_1ε = 1.44 and C_2ε = 1.92.

The standard κ-ε turbulence model is used to simulate the flow and heat transfer in a middle-deep coaxial bushing ground-source heat pump system. The model was chosen on the basis of its widely validated and reliable performance in dealing with high Reynolds number turbulent flows and heat exchange problems [28]. By solving the transport equation of turbulent kinetic energy (κ) and its dissipation rate (ε), the standard κ-ε model can effectively characterize the turbulent properties of fluids. Compared with more complex turbulence models such as LES, this model significantly reduces computational costs while ensuring computational accuracy, and it is particularly suitable for large-scale engineering simulations. In addition, the successful application of the model to pipeline flow and heat exchanger turbulence problems [29] further confirms its applicability in this study.

Under the flow conditions involved in this study, the fluid presents typical turbulent characteristics in a coaxial tube heat exchanger. Considering the high flow rate characteristics of the system, the standard κ-ε model can accurately capture the dynamic characteristics of turbulence in the heat exchanger, especially the coupling effect of thermal convection and thermal conductivity [30]. The model effectively describes the local heat exchange effect caused by turbulence, which is highly important for optimizing the heat-transfer efficiency and evaluating the stability of the system. Although the prediction accuracy of the standard κ-ε model in the near-wall flow and low-Reynolds-number regions has several limitations, the flow in this study mainly occurs in the high-Reynolds-number region (Re > 10⁴), and the flow in the heat exchanger is relatively uniform, so the model can provide sufficient calculation accuracy.

Compared with direct numerical simulation (DNS) and large eddy simulation (LES), the standard κ-ε model has significant advantages in computational efficiency and is particularly suitable for large-scale engineering simulations. Considering that the main goals of this study are system design optimization and long-term stability analysis, the standard κ-ε model can significantly reduce computational resource consumption while ensuring sufficient accuracy. The results show that the model has good applicability in describing the turbulent flow characteristics and heat-transfer behaviour in heat exchangers and achieves an optimal balance between computational efficiency and accuracy [31]. Therefore, the standard κ-ε turbulence model used for numerical simulation in this study can effectively meet the research requirements and provide reliable results, laying a theoretical foundation for subsequent system optimization and performance evaluation.

2.4. Fixed Solution Conditions

In this study, a medium-depth coaxial casing ground-source heat pump system in the Changchun region (43°05′–45°15′ N, 124°18′–127°05′ E) of China was employed as a case study, with field engineering and drilling construction logging data used to set the model parameters. Changchun is located in the southwest of the Songliao Basin and is characterized by cold winters, an average annual temperature of 4.6 °C, and warm summers, which are typical of cold regions. The climate, geophysical parameters, and boundary conditions in the model were established on the basis of the actual geological and climatic characteristics of Changchun, as detailed in

Table 1. Climatic parameters in the Changchun area.

Thermal Parameters	Summertime	Winters
Calculated outdoor temperature for air conditioning, °C	30.5	−24.3
Average outdoor wind speed, m/s	3.2	3.7
Atmospheric pressure, Hpa	978.4	994.4
Air-conditioning indoor design temperature, °C	26	20
Operating cycle, day	--	169

.

In setting the thermophysical parameters, particular attention was given to the variations in the thermal conductivity and specific heat capacity of the surrounding rock at different depths, and the stratigraphic temperature gradient (0.0272 K/m) was precisely defined, as shown in

Table 2. Mid-depth casing heat exchanger constituent materials and thermal–physical parameters of the surrounding rock.

Serial Number	Part Name	Typology	Value of Each Parameter
			Densities (kg/m3)	Specific Heat (J/(kg·k))	Thermal Conductivity (W/(m·k))
1	Water	fluids	998.2	4182	0.6
2	Perimeter rock 0–40 m	solid	1850	1840	1.9
3	Perimeter rock 0–850 m	solid	2600	1580	2.42
4	Perimeter rock 850–95 m	solid	2600	1580	2.42
5	Perimeter rock 950–1050 m	solid	2600	1580	2.75
6	Perimeter rock 1050–2050 m	solid	2600	1580	2.93
7	Thermal insulation (rubber and plastic)	solid	100	850	0.033
8	Inner tube (PE)	solid	950	2300	0.42
9	Outer pipe (J55 steel pipe)	solid	950	3800	58

. The high accuracy of the heat-transfer model was ensured by the detailed parameterization of components such as geotechnical layers, fluids, and pipes.

In setting the numerical simulation conditions (see

Table 3. Numerical simulation condition settings.

Serial Number	Part Name	Mold	Number
1	Inlet	Velocity inlet	T = 278.15 K; v = 0.3 m/s
2	Exits	Outflow	Flow rate weighting = 1
3	Ground level	Wall	h = 15 W/(m2·K); T = 258.15 K
4	Bottoms	Wall	Q = 0.0717 W/m2
5	Central axis	Axis	--
6	Soil boundaries	Wall	Q = 0 W/m2
7	Initial stratigraphic temperature	--	T = 281.2 + 0.02737 × H

), the study included key factors such as the inlet and outlet flow rates, boundary temperature, and heat-transfer coefficient to ensure the reliability and representativeness of the simulation results. The inlet temperature was set to 278.15 K, the flow rate was set to 0.3 m/s, the ground heat-transfer coefficient was set to 15 W/(m²·K), and the bottom heat flow was set to 0.0717 W/m², among other values, to fully account for the influence of actual operating conditions on system performance.

2.5. Model Validation

To verify the accuracy and reliability of the numerical model, the actual operation data of medium and deep coaxial-tube heat exchangers in Shandong were used for comparative analysis. Specifically, we chose a dataset that actually operates in the region, which contains measured values for the source-side outlet temperature. By comparing the simulation results with the measured data, the adaptability and accuracy of the numerical model under different operating conditions were verified.

First, the CFD software Fluent was used for numerical simulation, and the boundary conditions and operating parameters were set to be the same as those used in the actual project, including the inlet temperature, flow rate, thermal conductivity of rock and soil, pipe material and size, etc. To ensure the representativeness of the simulation, all model parameters were set according to the actual geological conditions and climate characteristics of Shandong.

In the verification process, we focused on the trend of the source-side outlet temperature, especially the temperature change over different time periods. The simulation results are highly consistent with the measured data, and the maximum temperature difference is only 273.57 K. Figure 3 shows the comparison between the simulated results of the source-side outlet temperature and the measured data. The verification shows that the model can accurately capture the dynamic changes in the heat-transfer process, and the simulated temperature change curve is consistent with the change trend of the measured data [8], which proves the reliability of the proposed model.

3. Results and Analyses

In this study, 30 and 160 days were selected as the time scales for both the initial operation phase of the simulation system and the long-term operation throughout the heating season. The choice of both timescales aimed to capture the heat-transfer properties and performance changes of the system at different stages. The 30-day time scale was mainly used to simulate the system during the adaptation period after the start, evaluating the effects of thermal inertia and load fluctuations in the initial stage on the system response, especially as the system moves from the thermal equilibrium of the cold start. The 160-day time scale covered the whole heating season, reflecting the stability and efficiency of the system in long-term operation, especially in how the system maintains thermal balance and efficient operation in the case of large load fluctuations. Through simulations on both timescales, we were able to comprehensively assess the short-term dynamic response and long-term stability of the system, providing strong support for design optimization.

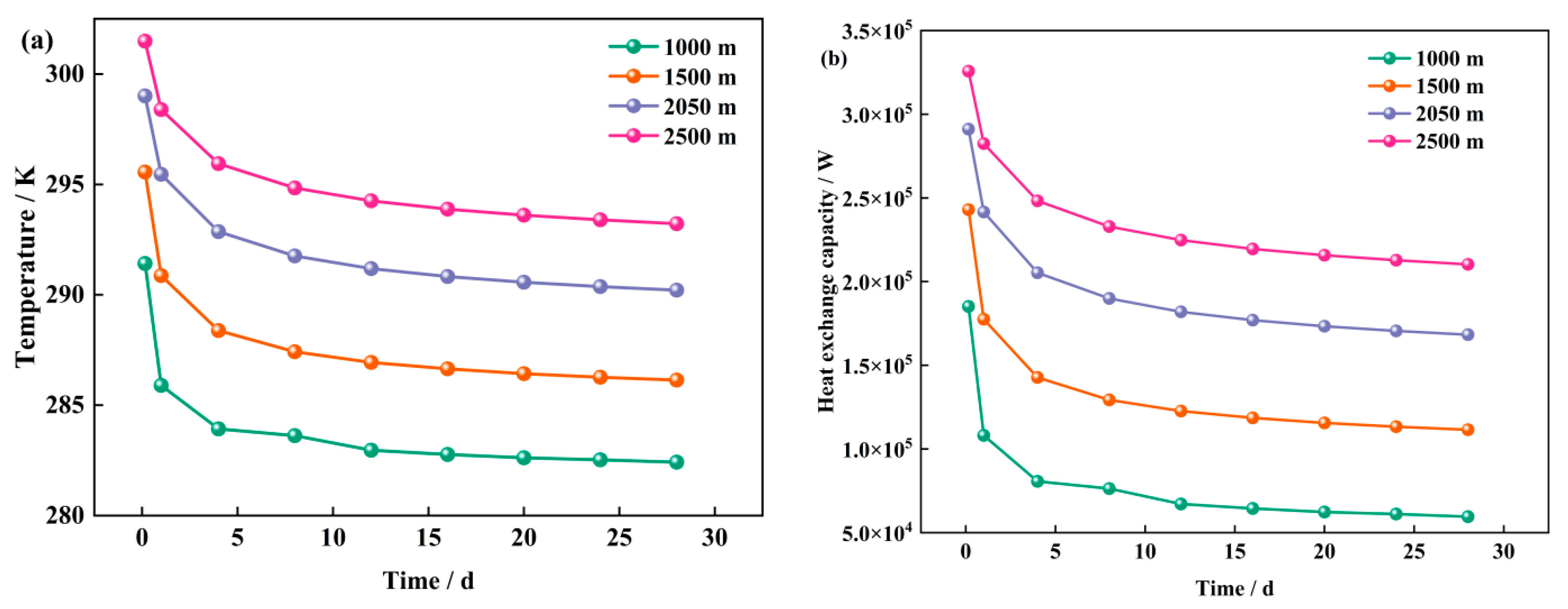
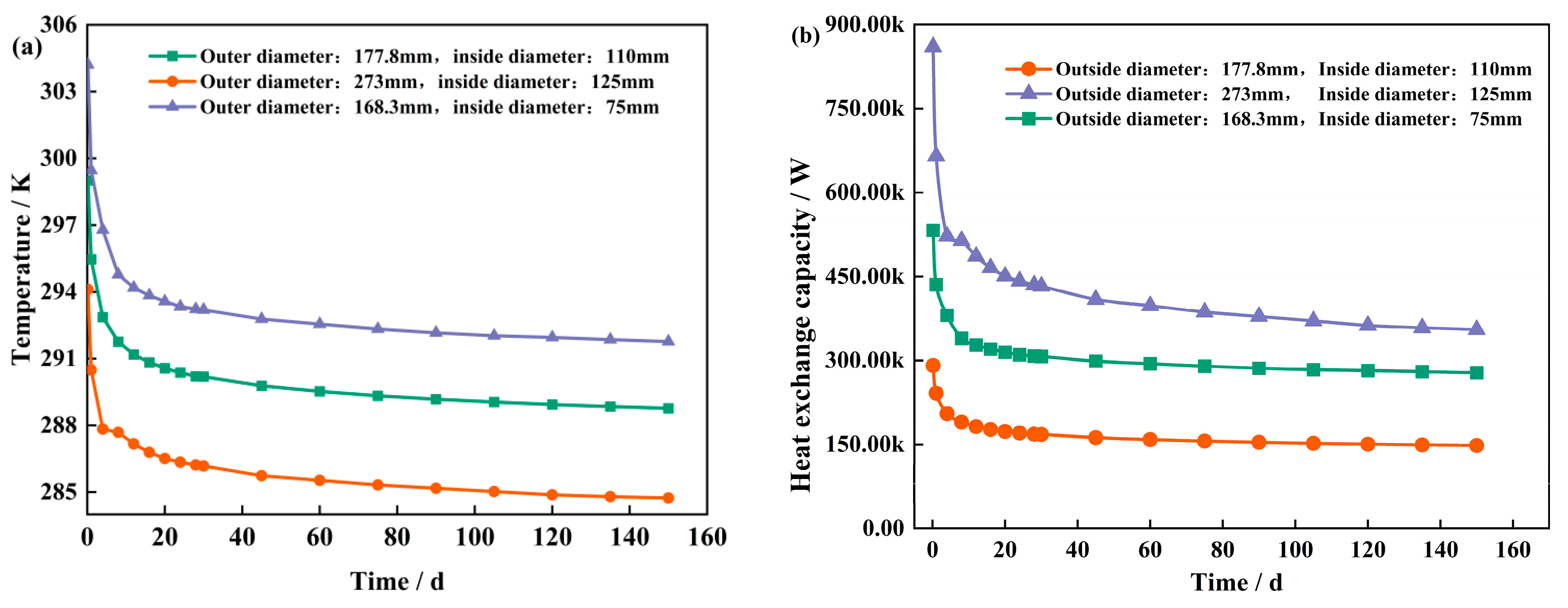
3.1. Effects of Well Depth and the Internal-to-External Pipe Diameter Ratio

Figure 4a illustrates the impact of varying well depths on the source-side effluent temperature of the medium-depth cased geothermal heat pump system. The source-side effluent temperature displays a decreasing trend that is consistent with a power function as the operation time progresses. In the first 7 days, the effluent temperature of the source side decreased rapidly, accounting for approximately 80% of the total temperature drop, indicating that the system was affected by a large thermal inertia when it entered the thermal equilibrium state at the initial stage. As the operation time continues, the temperature change gradually diminishes, and the source-side effluent temperature becomes nearly stable after 30 days, indicating that the system has reached thermal equilibrium. With increasing well depth from 1000 m to 2500 m, the formation temperature at the bottom increased from 308.54 K to 349.59 K, and the increase in well depth significantly increased the temperature of the underground thermal reservoir, thus improving the heat-exchange efficiency. With increasing well depth, the heat exchange amount between the casing heat exchanger and the rock and soil mass gradually increases, leading to a linear increase in the outlet water temperature on the source side. According to the experimental results, for every 500 m increase in well depth, the source-side outlet temperature increased by approximately 4 °C, indicating that the influence relationship of well depth on the effluent temperature on the source side is linear. At the beginning of operation, the difference in the source-side outlet temperatures among the different well depths was approximately 10.2 °C, which was 10.5 °C after 7 days and increased to 10.8 °C after 30 days. We show that the effect of well depth changes on the source-side outlet temperature stabilizes [9] with running time.

Figure 4b shows the influence of well depth on the heat exchange of the casing heat exchanger, and the change trend of heat exchange is consistent with the outlet temperature of the source side. In the initial stage of system operation, the decrease in heat exchange is large, accounting for approximately 80% of the total decrease, which is related to the thermal inertia and initial adaptation process of the system. As time progresses, the heat-exchange capacity stabilizes, indicating that the heat-exchange efficiency of the system gradually improves. Under different well depths, the change trends of heat change are similar and increase with increasing well depth. In the initial stage, when the well depth increases from 1000 m to 2500 m, the heat change decreases from 70 kW to 40 kW, with a decrease of 30 W/m. After 7 days, the heat-exchange capacity begins to stabilize with an increase of approximately 50 kW, and after 30 days, the heat-exchange capacity stabilizes at approximately 50 kW. This shows that the temperature difference in the system is significant, but after entering the stability period, the temperature difference is stable, and the heat exchange is maintained at a relatively stable level. After entering the stability period, the temperature difference tends to stabilize, and the heat exchange also remains relatively stable. Under steady-state operation, the heat-transfer capacity increases by approximately 50 kW for every 500 m increase in well depth, and the final heat-transfer capacity increases from 59.6 kW to 210.3 kW, with a change of approximately 10 W/m. Research has shown that with increasing well depth [24], the heat-transfer efficiency significantly improves, and heat exchange increases linearly after stable operation.

Figure 5a illustrates the impact of different internal and external pipe diameter ratios on the source-side outlet water temperature. With increasing heat transfer time, the effluent temperature on the source side tends to decrease, and the initial temperature rapidly decreases. This phenomenon is related to the thermal inertia and initial regulation of the system. Under all other identical conditions, the outer diameters of 168.3 mm and 75 mm presented high source-side outlet temperatures compared with those of the other two diameter configurations. Specifically, the outlet temperatures of the three pipe diameter configurations stabilized with the system after 30 days of operation, and the temperature changed slightly and basically remained unchanged during the subsequent heating period (after 30 days of operation). This indicates that the impact of the pipe diameter configuration on the source-side outlet temperature gradually decreases during the long-term operation of the ground-source heat pump system. However, configurations with larger pipe diameters are more effective at maintaining a higher outlet temperature during the initial stage, which has certain advantages.

Figure 5b shows the influence of different inner and outer pipe diameter ratios on heat transfer. The heat transfer showed a power function decline with time, and the change was relatively rapid in the initial stage, which was related mainly to the change rate of the temperature difference. The results show that under the same conditions, the heat transfer of the combination of the outer diameter of 273 mm and the inner diameter of 125 mm is significantly greater than that of the other two configurations. The reason for this phenomenon is that a larger diameter ratio can provide a greater flow rate, thereby improving the heat-exchange efficiency. The large inner-to-outer pipe diameter ratio design increases the fluid flow area, reduces the flow rate, and enhances the heat-exchange capacity between the heat exchanger and the underground rock mass, thereby increasing heat transfer. However, the relationship between velocity and heat transfer is not purely linear. In this study, a lower flow rate helps reduce the thermal short-circuit effect caused by excessive turbulence and optimizes the flow path of the fluid, thereby improving the heat-exchange efficiency. The large inner-to-outer pipe diameter ratio provides a large flow rate and flow area, and in the initial stage, the temperature difference is large, resulting in a rapid increase in heat exchange. However, a smaller pipe diameter (such as an outer pipe diameter of 168.3 mm and an inner pipe diameter of 75 mm) also results in a better heat exchange effect under certain conditions. A smaller pipe diameter increases the flow rate, improves the degree of turbulence, and improves the heat-exchange efficiency, especially at moderate flow rates, which can maintain high heat exchange during the initial and stable stages. In the initial stage of the first 30 days, owing to the large temperature difference, the heat exchange between the fluid and the rock or soil body was relatively rapid, resulting in a rapid increase in heat exchange. After 30 days, the heat transfer changes of the various pipe diameter configurations tended to be stable, and the system entered the stable operation stage. During the subsequent heating period (from 30 days to 169 days), the heat transfer hardly changed and remained at a constant state. This shows that the influence of the pipe diameter on heat transfer is reflected mainly in the initial stage of the system, and a larger pipe diameter ratio can significantly improve the initial heat transfer and maintain the thermal efficiency of the system during long-term operation.

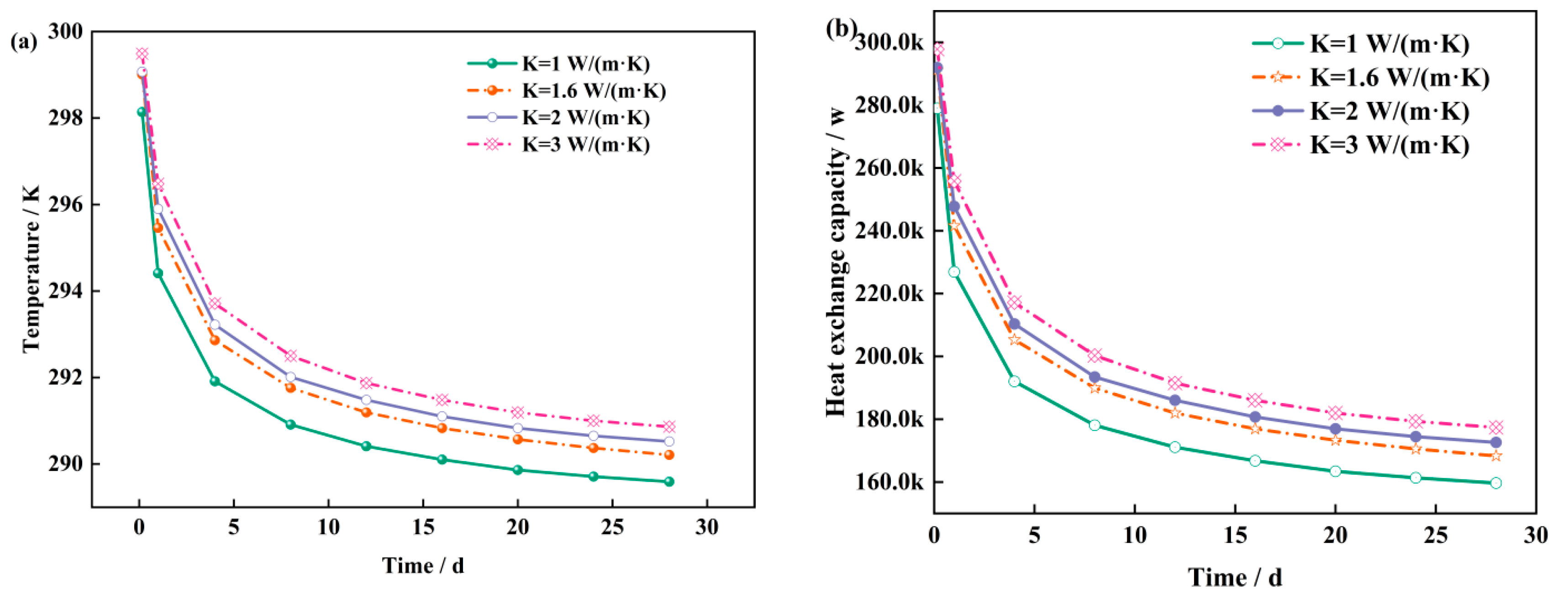
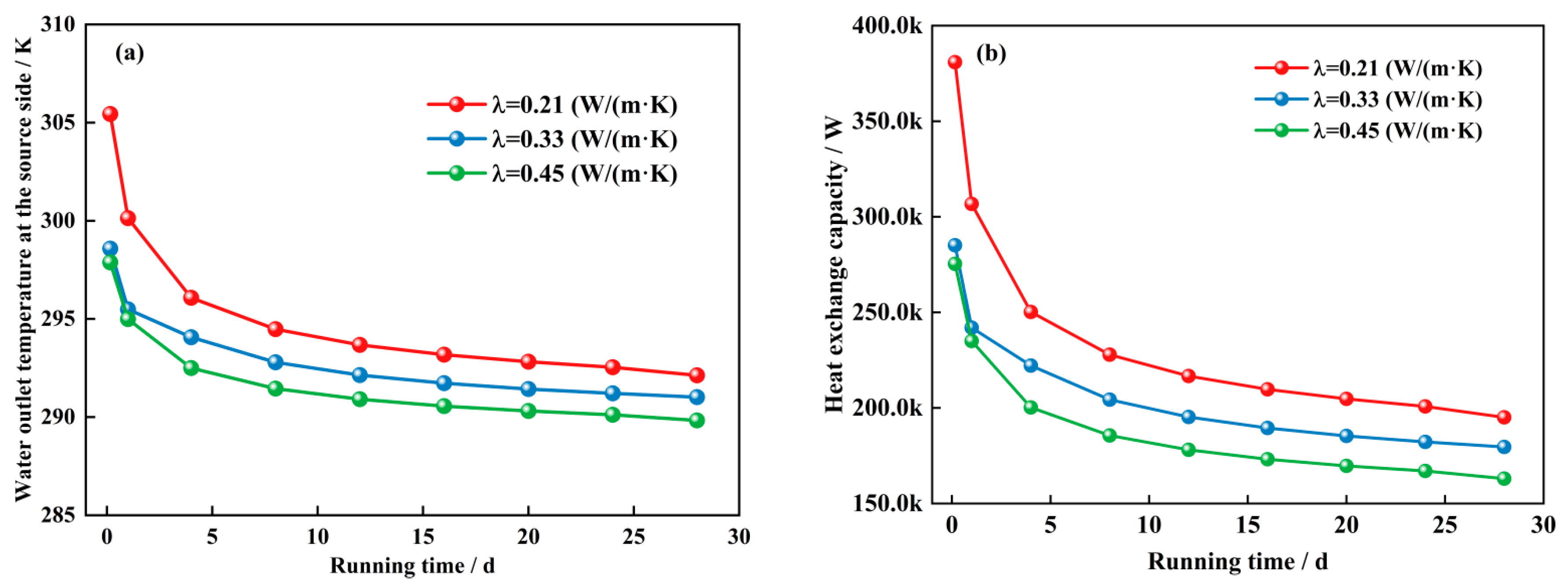
3.2. Effects of the Thermal Conductivity of the Cementing Cement and the Thermal Conductivity of the Inner Tubes

Figure 6a illustrates the impact of different solid-well cement thermal conductivities on the source-side effluent temperature. With the extension of running time, the effluent temperature on the source side decreases by a power function, and the temperature decreases rapidly in the initial stage, which indicates that it takes a long time for the system to reach thermal equilibrium in the starting stage. After 30 days of operation, the source-side effluent temperature stabilized, indicating that the system had reached a state of long-term stability. As the thermal conductivity of the cementing cement increased from 1 W/(mK) to 3 W/(mK), the outlet temperature on the source side increased accordingly. This may be because the increase in the thermal conductivity of the cementing cement improves the heat conduction efficiency, thus reducing the loss of heat in the system. However, when the thermal conductivity increases from 1 W/(mK) to 2 W/(mK), the source-side water temperature increases by approximately 1 °C after 30 days, but when the thermal conductivity increases to 3 W/(mK), the temperature increases by only approximately 0.3 °C. The thermal conductivity of the cementing cement has a certain nonlinear effect on the effluent temperature of the source side, especially after the thermal conductivity reaches a certain value, and the increase gradually decreases. The analysis indicates that since the integrated thermal conductivity of the geotechnical body at the source side is 1.93 W/(m-K), and the cementing cement layer is relatively thin, the thermal conductivity of the cementing cement has a limited impact on the heat-exchange efficiency when its value is not lower than that of the geotechnical body. The main function of cementing cement is to serve as a heat transmission channel rather than directly as a heat source, so the increase in its thermal conductivity has a gradual limit on the improvement in the overall heat-exchange efficiency.

Figure 6b shows the influence of different cementing cement thermal conductivities on the heat exchange of the casing heat exchanger. The trend in heat-exchange capacity mirrors that of the source-side effluent temperature, following a power function decrease, with the rate of change being more rapid during the initial phase. The change decreases after approximately 7 days and tends to stabilize after 30 days, indicating that the heat-exchange volume is closely related to the stability of the system. With increasing thermal conductivity of the cementing cement, heat exchange between the casing heat exchanger and the subsurface geotechnical body progressively increases. However, when the thermal conductivity of the cementing cement approaches or exceeds that of the formation, the rate of increase in heat-exchange capacity decreases significantly. When the thermal conductivity of the cementing cement increased from 1 W/(m-K) to 2 W/(m-K), the heat-exchange capacity increased by approximately 13 kW, whereas a further increase to 3 W/(m-K) resulted in only a 4 kW increase. This suggests that at higher thermal conductivities, the effectiveness of cementing cement tends to be saturated, and further increases in the thermal conductivity offer limited further enhancement of the heat-exchange capacity.

Figure 7a illustrates the impact of different inner pipe thermal conductivities on the source-side outlet water temperature. From the figure, it is evident that the source-side effluent temperature follows a power function decreasing trend with increasing operation time, experiencing a more rapid decrease during the initial phase, which indicates that the system undergoes a significant heat-transfer process during the start-up phase and gradually stabilizes, a phenomenon in agreement with [32]. After 30 days of operation, the source-side effluent temperature had levelled off, indicating that the system reached a state of long-term stability. The source-side effluent temperature decreased significantly with increasing thermal conductivity of the inner pipe from 0.21 W/(m-K) to 0.45 W/(m-K). Specifically, the source-side outlet temperature decreased by approximately 1.15 °C with every 0.12 W/(m-K) increase in thermal conductivity. This phenomenon can be attributed to the increase in the thermal conductivity of the inner pipe, which enhances heat exchange between the inner and outer pipes, amplifying the thermal short-circuit effect of the fluid inside the pipe [33], and thus, accelerating heat transfer and decreasing the source-side outlet temperature.

Figure 7b further illustrates the impact of different inner pipe thermal conductivities on the heat-exchange volume. The trend of the heat-exchange volume is consistent with that of the source-side effluent temperature, which also decreases as a power function, with a more rapid change during the initial phase (approximately 7 days), after which it stabilizes around the 30th day. This trend indicates that the variation in heat-exchange volume is closely related to the thermal equilibrium state of the system. As the thermal conductivity of the inner pipe increases, the heat exchange between the inner and outer pipes increases, thereby increasing the heat-exchange efficiency of the system. However, although the increase in the thermal conductivity of the inner pipe increased the heat-exchange capacity, after 30 days of operation, the heat-exchange capacity of the buried pipe decreased by approximately 16 kW, as the thermal conductivity ranged from 0.21 to 0.45 W/(m-K). This phenomenon can be explained by the thermal short-circuit effect. As the thermal conductivity increases, heat transfer within the pipe accelerates, leading to a portion of the heat energy being lost in the transfer process, which affects the final heat-transfer effect. In conclusion, the increase in the thermal conductivity of the inner pipe has a dual effect on the ground-source heat pump system. On the one hand, increasing the thermal conductivity of the inner pipe can enhance heat exchange between the inner and outer pipes, thus improving the heat-transfer capability; on the other hand, it may intensify the thermal short-circuit effect, reducing the source-side outlet temperature and diminishing the heat-exchange capacity.

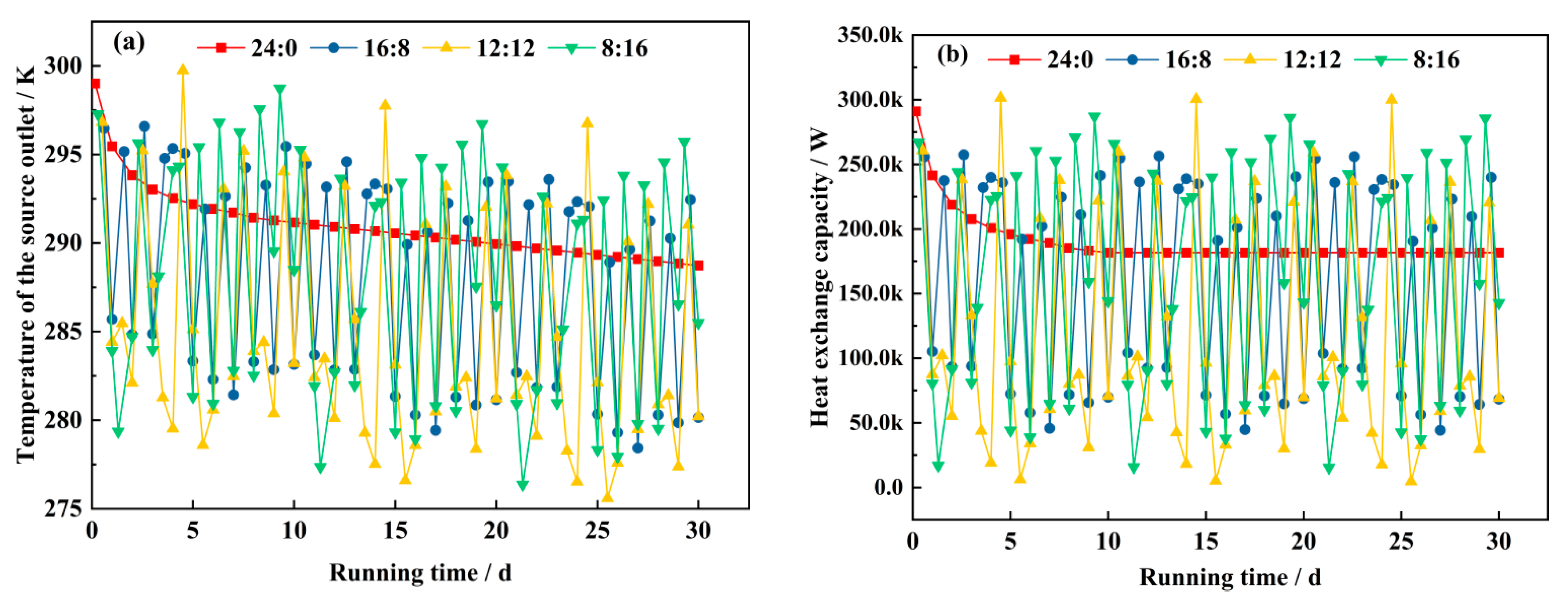
3.3. Effects of Variations in the Flow Rate and Start–Stop Ratio

Figure 8a shows the impact of different flow rates on the source-side effluent temperature. The source-side effluent temperature follows a distinct power function decreasing trend as the operation time increases, with the temperature decreasing more rapidly during the initial phase (day 1). This indicates that the source-side effluent temperature undergoes rapid heat exchange during the system’s start-up period. With the change in flow rate, the relationship between the source-side effluent temperature and the flow rate also shows a dynamic change. Specifically, in the initial stage (approximately 1 to 7 days), the flow rate is directly correlated with the source-side effluent temperature; i.e., an increase in the flow rate leads to a decrease in the source-side effluent temperature [22]. In particular, when the flow rate increased from 0.3 m/s to 0.7 m/s, the source-side outlet temperature decreased by approximately 2 °C with each 0.2 m/s increase in flow rate. However, the relationship between the flow rate and outlet temperature gradually shifted over time, and after entering the stabilization stage, the effect of the flow rate on the source-side outlet temperature decreased, with the temperature difference tending to level off. After 30 days, the temperature difference decreased from 2.39 °C to 1.38 °C when the flow rate increased from 0.3 m/s to 0.7 m/s. This phenomenon shows that the change in flow velocity has a significant effect on the temperature, but during long-term operation, the influence of the flow velocity on the water temperature gradually weakens [22] and becomes stable.

Figure 8b illustrates the impact of different flow rates on the heat-exchange capacity of the buried pipe. With the extension of the system running time, the heat change decreases in the power function and changes rapidly in the early stage (day 1). This shows that when the heat pump is started, the heat change is more drastic, but with increasing flow rate, the heat-exchange efficiency between the casing heat exchanger and the underground rock and soil mass gradually increases. After 30 days of operation, the heat-exchange capacity levelled off between 168 kW and 261 kW, with an increase in the flow rate leading to an overall increase in the heat-exchange capacity. However, the increase gradually decreased, especially when the flow rate increased from 0.7 m/s to 0.9 m/s, and the difference in heat change was only 10 kW. This indicates that although increasing the flow rate helps improve the heat exchange quantity, the increase in heat exchange quantity tends to stabilize once a certain flow rate is reached, and the effect of increasing the flow rate on the heat exchange effect begins to weaken [11]. While ensuring the efficient operation of the heat pump system, the choice of flow rate also needs to consider the balance of economy and energy efficiency. Since the energy consumption of the circulating pump is directly correlated with the flow rate, an excessive flow rate increases energy consumption, thus affecting the overall system economy. Therefore, setting the flow rate to 0.7 m/s is recommended. At this time, the heat exchange of the casing heat exchanger is stable at approximately 250 kW, which not only can ensure high heat-exchange efficiency but also optimize energy consumption and improve the economy and operation efficiency of the system.

Figure 9a illustrates the impact of varying start–stop ratios on the source-side outlet temperature of the buried pipe. The figure shows that the source-side outlet temperature of the ground-source heat pump system decreases following a power-function trend under continuous 24 h operation with a faster decrease in the initial period (i.e., the first 7 days). In contrast, the source-side outlet temperature under continuous operation with varying start–stop ratios (16:8 (2), 12:12 (1), and 8:16 (0.5)) exhibits an overall decreasing trend, although the change curve shows irregular fluctuations. This fluctuation is attributed primarily to the nonlinear coupling between water flow heat transfer in the casing, soil heat conduction, and start–stop variations. When the start–stop ratio is 2, the source-side outlet temperature tends to decrease continuously during the first 7 days of operation, but the temperature gradually begins to recover after 1 week. When the start–stop ratio is 1, the source-side temperature tends to stabilize overall, although a sudden increase is observed on the fifth day of operation. When the start–stop ratio is 0.5, the source-side temperature gradually decreases during the first four days, then increases steadily, returns to the initial temperature after one week, and eventually exceeds the initial value, where it continues to increase. The analysis indicated that when the heat exchanger operated continuously for 24 h, continuous heat exchange occurred between the casing heat exchanger and the source-side geotechnical body. Owing to the low thermal conductivity of the geotechnical body, heat replenishment at the far end of the stratum occurs more slowly, and heat exchanger extraction exceeds backfill replenishment. As the heat exchanger’s ground temperature decreases to a certain point, the heat from the stratum’s backfill reaches equilibrium with the extracted heat, causing the outlet temperature to stabilize. When the heat exchanger starts and stops periodically, it extracts heat from the ground during operation, while fluid circulation stops during the stopping period, with heat exchange gradually tending toward stabilization. However, heat transfer from the far end of the ground to the vicinity of the casing heat exchanger tube wall continues, resulting in a higher source-side outlet temperature when the heat pump resumes operation after a hiatus than during continuous operation. Additionally, during the shutdown process, high-temperature fluid at the bottom flows upwards, contributing to heat flow circulation within the heat exchanger, as the temperature of the underlying geotechnical body is higher than that of the upper layer. The fluid at the top of the heat exchanger, which is at a higher temperature than the source-side geotechnical body, begins to reverse the heat transfer to the lower-temperature geotechnical body, resulting in localized heat buildup in the stratum. Therefore, when the start–stop ratio is 0.5, the stopping time exceeds the running time, and the source-side outlet temperature may rise above the initial temperature after a period of operation.

Figure 9b illustrates the effect of varying the start–stop ratio on the heat-exchange capacity of the buried pipe. The figure shows that under continuous 24 h operation, the heat-exchange capacity at the source side of the geothermal heat pump system follows a decreasing power-function trend with a more rapid decrease during the initial operation period (i.e., the first 7 days). The heat-exchange capacity of the buried pipe irregularly fluctuates and is influenced by the start–stop cycle of the heat pump. As the start–stop ratio gradually decreases, the heat extraction time on the source side decreases, and the heat-exchange volume gradually increases upon activation, stabilizing over time. Therefore, it is crucial to optimize the operation duration of the heat pump to increase the overall heat-exchange capacity of the system.

4. Discussion

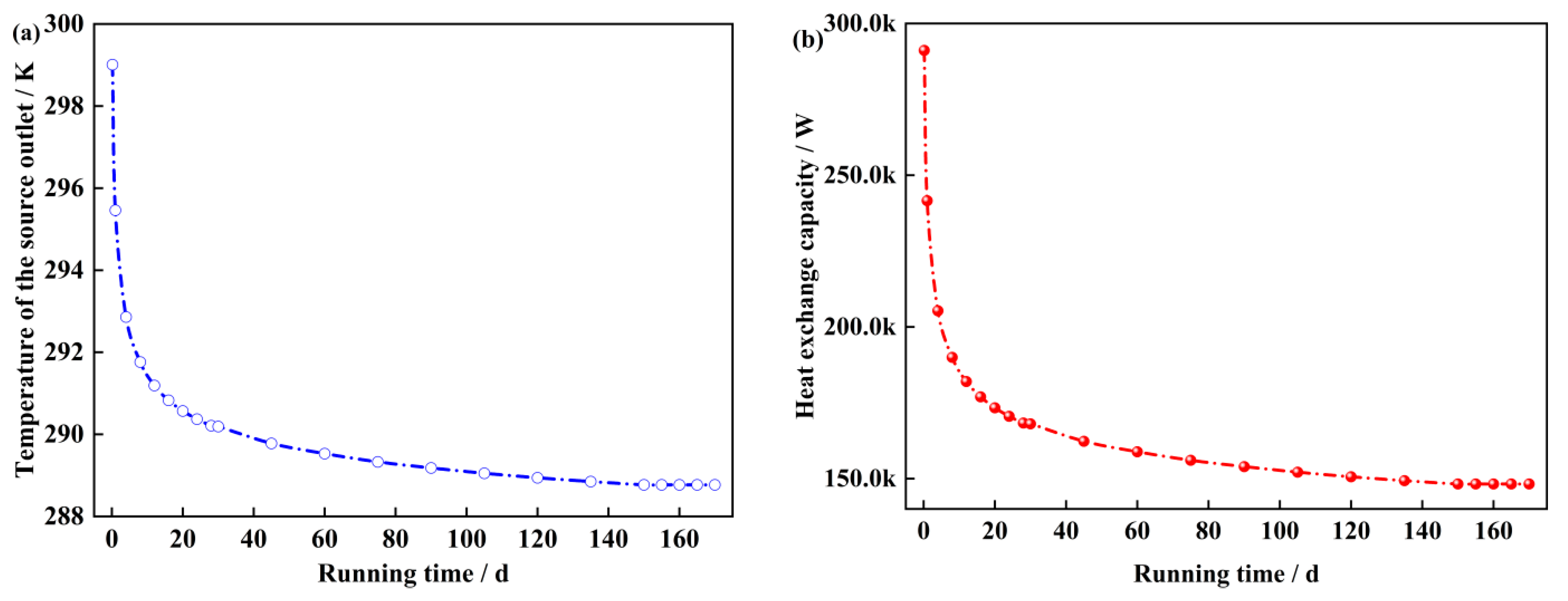
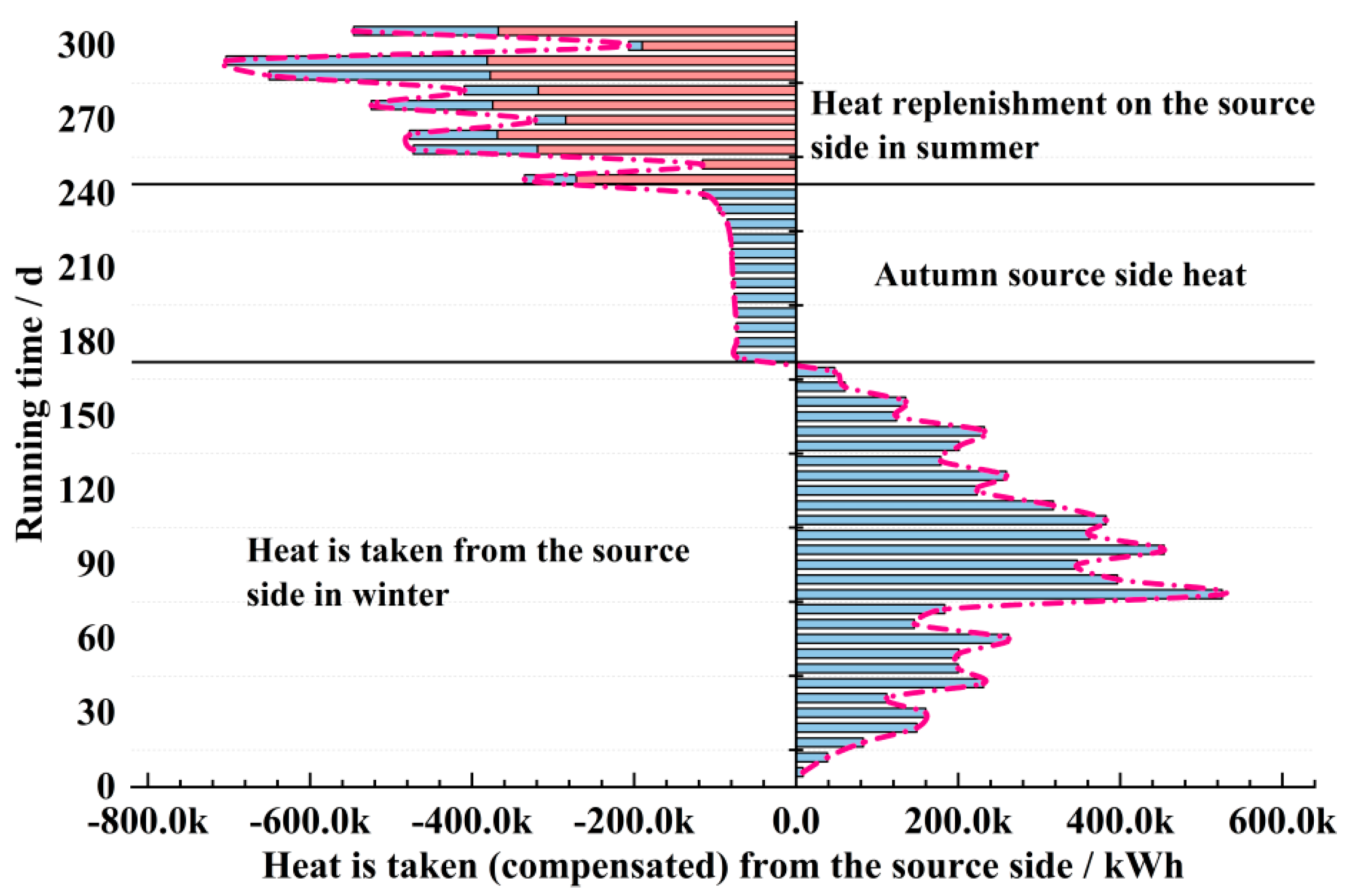
4.1. Analysis of the Heat-Transfer Characteristics of the Radial Geotechnical Body on the Source Side During Full Heating Cycle Operation

The heat-exchange capacity of a heat exchanger is a key indicator for assessing its heat-transfer efficiency. The numerical simulation results for the source-side outlet temperature of the ground-source heat pump system throughout the heating season are presented in Figure 10a. As illustrated in the figure, the source-side outlet temperature initially decreases rapidly at the beginning of the heating season and then tends to stabilize. At the onset of operation, the source-side outlet temperature was highest at 299.01 K. However, as the system operated, heat was continuously extracted from the surrounding soil, resulting in a rapid decrease in the outlet temperature. In particular, the most significant temperature drop occurred within the first 30 days of operation, accounting for more than 80% of the total decrease, with the change being particularly dramatic during the first week. This shows that the system extracts heat at a high rate during the initial operation period, which has a significant effect on the thermal field of the surrounding soil. As the operation time increased, the temperature gradient of the surrounding soil gradually decreased, the heat-transfer rate decreased, and the outlet temperature stabilized within the range of 288.77–289.78 K, with an average decrease rate of only 0.008 K/d. This trend illustrates the difference between the thermal conductivity of the surrounding soil and the heat replenishment mechanism during the initial and long-term operation phases. The rapid cooling in the initial stage is due primarily to the quick extraction of the initial high-temperature heat storage in the soil, whereas the stabilization in the later stage reflects the buffering effect of the soil’s thermal conductivity on long-term heat transfer. Figure 10b shows the trend of heat-exchange volume over time, which is consistent with the change in the source-side outlet temperature. At the beginning of operation, heat exchange was as high as 291 kW, but it decreased rapidly during the first 30 days of the heating season, with a decrease of approximately 90% of the total decrease, which corresponds to the rapid phase of the outlet temperature change. After one month of operation, the heat-exchange capacity stabilized between 148 kW and 162 kW, with an average decrease rate of approximately 0.117 kW/d, and it finally remained at approximately 155 kW during the stable operation phase. The rapid decline in heat-exchange capacity primarily results from the initial release of heat from the soil and the high heat-transfer demand during the heat pump’s high-load operation. With the gradual establishment of the heat balance of the soil, the heat-exchange capacity of the heat exchanger subsequently tends to stabilize, indicating that the system has entered long-term sustainable operation. The heat-exchange performance and temperature change results in Figure 10 are based on the coaxial heat exchanger configuration with outer tube diameters of 177.8 mm and 110 mm, as mentioned in Section 2.1. Moreover, the thermal conductivity, velocity, and fluid properties are consistent with the assumptions in Section 2.1. Thus, the results of Figure 10 reflect the heat-transfer performance of this coaxial heat exchanger under specific operating conditions.

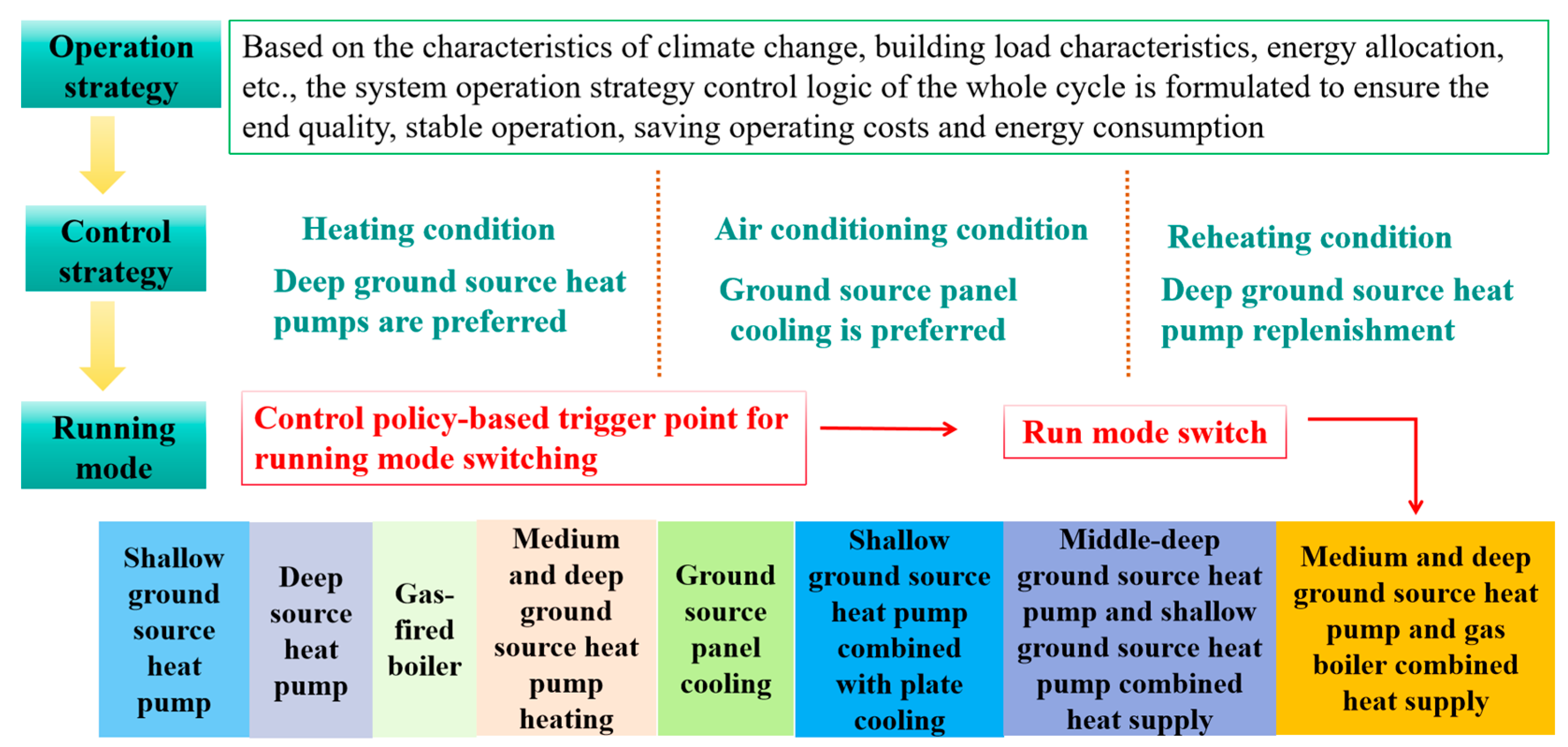
4.2. Joint Operational Control Analysis Based on Year-Round Dynamic Simulation

The cooling and heating load of a building is constantly changing due to internal and external disturbances, especially in cold areas. Whether the control strategy of the ground-source heat pump system can effectively adapt to fluctuations in the building load and maintain the stability, energy savings, and economy of the system while meeting the needs of users is an important criterion for evaluating its effect.

The joint operation control strategy adopted in this study aims to adapt dynamically to the heating and cooling needs of buildings during different seasons and load fluctuations by automatically adjusting the type and quantity of heat sources. To verify the operation effect of this control strategy, we used Transy software (Version 18.0) to complete the building (the project is located in Jilin, China and covers an area of 95,721 m², with a construction area of 300,000 m², including hotels, offices, corporate culture halls, etc.). The annual hourly load was simulated. By establishing a mathematical model based on the actual building and inputting the climate parameters of the area where the building is located, the thermal parameters of the building envelope (see Table 1), and actual load data such as personnel and equipment lighting, the simulation results can accurately reflect the load characteristics of the building in different time periods. In this process, we took the thermal parameters and outdoor climate conditions of the building envelope as the external disturbance input, and at the same time, according to the hourly load requirements in the “Energy-saving Design Standard for Public Buildings” (GB50189–2015) [34], the personnel, equipment, and lighting were used as the internal disturbance inputs. In the end, 8760 h of energy consumption were calculated for the building throughout the year (Figure 11). Figure 12 shows the distribution of the building load throughout the year. The simulation results reveal that the annual cumulative heat load of the office building and exhibition hall is 17.3 million kWh, the cumulative cooling load is 4.25 million kWh, and the remaining load is generated by the hotel. These results provide basic data support for the control strategy proposed in this study and provide a theoretical basis for load regulation and energy savings optimization in practical engineering applications.

4.3. Load-Side and Source-Side Heat Balance Analyses That Are Based on the Control Strategy

In the middle-depth and shallow ground-source heat pump and boiler combined heating system, the heating load not only is closely related to the load demand of the building but also has a direct effect on the cold and heat balance of the underground temperature field, thus affecting the energy efficiency of the ground-source heat pump unit and the operating efficiency of the whole system. In this study, the combined heat source system includes multiple ground-source heat pumps and boilers. The power of the ground-source heat pump is 7806.6 kW, which is mainly responsible for the heating load, whereas the boiler power is 2342 kW, which is used to supplement the heat in cold weather, plays the role of a peak load, and ensures the safety and stability of the system. The system’s geothermal exchangers include shallow and medium-depth geothermal exchangers, with shallow geothermal exchangers operating at depths of 20 m to 200 m for low load requirements, and medium-depth geothermal exchangers operating at depths of 200 m to 2000 m for higher load requirements. The design and operation characteristics of all the geothermal exchangers are consistent with those of the coaxial heat exchangers analysed in this paper, especially in terms of heat-exchange efficiency and fluid flow mode.

To ensure the efficient operation of the system, the joint operation control strategy in this study adopts a three-layer control framework: an operation strategy, a control strategy, and an operation mode. The control policy is responsible for selecting and implementing a specific mode of operation. It is based on a combination of a series of operating modes under specific season, weather, and load conditions to achieve the goal of meeting user needs, saving operating costs, and reducing energy consumption. The control strategy of the project is based on the principle of ensuring the thermal balance of the underground temperature field and the operating efficiency of the complex energy system. In particular, a deep ground-source heat pump is preferred under heating conditions. Under air-conditioning conditions, a plate heat exchanger is preferred for cooling. During the summer and transition seasons, deep ground-source heat pumps are used to recharge heat (as shown in Figure 13). The implementation of the control strategy has a significant effect on the behaviour of the heat exchanger, especially the annual evolution of the source-side outlet temperature. In terms of heat source selection, the control strategy ensures the stability of the system under different seasons and load conditions by dynamically adjusting the operation of the deep ground-source heat pump and the shallow ground-source heat pump. Specifically, in the winter heating season, deep ground-source heat pumps are used more frequently to provide a stable heat source and ensure that the source-side outlet temperature is maintained within a reasonable range. In contrast, the use of shallow ground-source heat pumps and other heat sources during the transition season or summer improves the flexibility of the system and avoids unnecessary heat waste. Through this dynamic adjustment, the fluctuation range of the source-side outlet temperature is effectively controlled, especially during periods of large load fluctuations. The control strategy can quickly respond to the change in load demand, optimize the heat source configuration, stabilize the source-side outlet temperature, and reduce the impact of temperature fluctuations on system efficiency.

The seasonal distributions of heat extraction and compensation in the multisource joint operation strategy of this project are shown in Figure 14. During winter operation, the medium-depth and shallow ground-source heat pumps, combined with boilers, jointly supply heat, with the shallow ground-source heat pump withdrawing a total of 6,024,000 kWh of heat. In contrast, during the summer, the heat recharge from the plate heat exchanger and shallow ground-source heat pump totals 4,763,000 kWh, resulting in a heat deficit of 1,261,300 kWh. This deficit could cause an imbalance in the subsurface temperature field, particularly in the shallow ground-source heat pump area. To address this, this study proposes a deep ground-source heat exchange supplementation scheme that adds 982,500 kWh of heat, particularly in autumn, significantly alleviating the imbalance in heat extraction between winter and summer. This strategy demonstrates the flexibility and efficiency of multisource joint operations. During peak load periods, deep ground-source heat pumps are prioritized to ensure stable performance, whereas a deep heat exchanger is used for supplementary heating during the transition seasons. This approach not only improves the overall efficiency of the composite energy system but also reduces the reliance on boiler heating during winter peaks, offering innovative solutions for sustainable energy management in cold regions.

The study revealed that the heat (982,500 kWh) supplied by the deep ground-source heat exchanger in autumn is crucial for maintaining the long-term thermal balance of the subsurface temperature field. This can be explained by the thermal decay law of the deep heat exchanger, where dynamic changes in the thermal conductivity and thermal resistance of the rock formation significantly affect the heat-exchange efficiency as the operating time increases. Therefore, the heat deficit in the underground temperature field can be mitigated by dynamically adjusting the heat input from the deep heat exchanger during the transition season. In addition, insufficient summer heat recharge from shallow ground-source heat pumps may exacerbate the cooling effect on the shallow subsurface temperature field, which in turn impacts the long-term stability of the system. For this reason, a strategy of appropriately increasing the deep heat exchange make-up heat in summer and spring is proposed to compensate for the remaining heat difference of 278,800 kWh. This dynamic optimization strategy maintains the underground temperature field balance while avoiding the potential negative impacts of low shallow-ground temperature on the operational efficiency of the system.

On the basis of the experimental results, the multi-heat source joint operation strategy of this project has considerable advantages in composite energy systems in cold regions. First, the dynamic priority operation of deep and shallow ground-source heat pumps precisely aligns with seasonal load variations, ensuring efficient system operation. Second, the use of a deep heat transfer heat supplementation strategy effectively mitigates the difference in heat withdrawal and supplementation between winter and summer and ensures the long-term thermal equilibrium of the underground temperature field. In contrast to prior studies on shallow ground-source heat pumps [35,36], this study verifies the effectiveness of the make-up heat strategy for medium and deep ground-source heat pumps in long-term operation in cold regions and quantifies the specific contribution of autumn make-up heat to the annual heat balance. This result not only provides a scientific basis for the optimal design of the composite energy system but also opens up a new path for the sustainable operation of the energy system in cold regions.

5. Conclusions

In this work, the heat-transfer characteristics and operational performance of a ground–source heat pump system with deep underground pipes in cold regions are systematically analysed, with a focus on the influences of key design parameters and operational conditions on heat-transfer efficiency and heat balance adaptability. The following conclusions are drawn:

(1)

Increasing the well depth significantly enhances the utilization efficiency of the underground heat storage resources, with a 50 kW increase in heat-transfer capacity for every 500 m increase in well depth, demonstrating a linear growth trend. Additionally, optimizing the internal-to-external pipe diameter ratio effectively enhances the heat-exchange capacity between the fluid and the geotechnical body. The appropriate selection of a larger pipe diameter ratio can significantly reduce the flow resistance and improve the system heat-exchange efficiency.

(2)

When the thermal conductivity of cement is close to that of rock and soil, the heat-transfer performance is significantly improved. Specifically, when the thermal conductivity of the cementing cement increases from 1 W/(mK) to 2 W/(mK), the water outlet temperature on the source side increases by approximately 1 °C, and the heat change increases by 13 kW. However, the gain in system efficiency gradually increases. Although an increase in the thermal conductivity of the inner tube can increase the heat transfer rate, it may cause a thermal short-circuit effect and then have a negative impact on the outlet temperature. Therefore, optimizing the thermal conductivity should consider the balance between thermal performance and heat loss to maximize the overall efficiency of the system.

(3)

The flow rate has a significant effect on the initial increase in the heat exchange of the system, but with time, the heat transfer effect tends to be saturated. When the operating flow rate is controlled at 0.7 m/s, the heat change is stable at approximately 250 kW, and the system economy can be optimized under the premise of ensuring efficient heat exchange. The adjustment of the start–stop ratio not only improves the energy consumption distribution of the system but also effectively optimizes the long-term thermal balance of the system by strengthening the thermal compensation capacity, which is especially suitable for heating scenarios with large load fluctuations.

(4)

The heat release rate of the geotechnical body is high during initial system operation. However, as the heating cycle progresses, the geotechnical body’s heat balance capability gradually emerges, and the outlet temperature and heat-exchange volume stabilize, demonstrating the long-term applicability of medium and deep geothermal energy resources in cold regions.

From the perspective of heat-transfer mechanisms and engineering practice, this study proposes optimized design recommendations for medium and deep ground-source heat pump systems in cold regions. The findings not only address a research gap in ground-source heat pumps in extremely cold regions but also provide scientific support for promoting green and low-carbon development in building heating. Future work should focus on integrating multifactor coupling models to further optimize system performance under complex geological and climatic conditions in cold regions. Moreover, more intelligent operation and control strategies should be developed for different building types and load fluctuations to achieve lifecycle optimization design and facilitate the widespread adoption of medium and deep ground-source heat pump systems in cold regions worldwide.