How Should e-Product OEMs Invest in Design for Remanufacturing Under the Take-Back Regulation in a Competitive Environment?
Abstract
:1. Introduction
2. Relevant Literature
2.1. Remanufacturing Decisions Within a Closed-Loop Supply Chain
2.2. Design for Remanufacturing Within Closed-Loop Supply Chain
2.3. Impact of Take-Back Regulations on Remanufacturing
2.4. Research Gaps
3. Problem Description and Assumptions
3.1. Problem Description
3.2. Model Assumptions
4. Models Formulation and Equilibrium Solutions
4.1. Monopolistic Scenario (Model M)
4.2. Competitive Scenario (Model C)
5. Model Comparisons
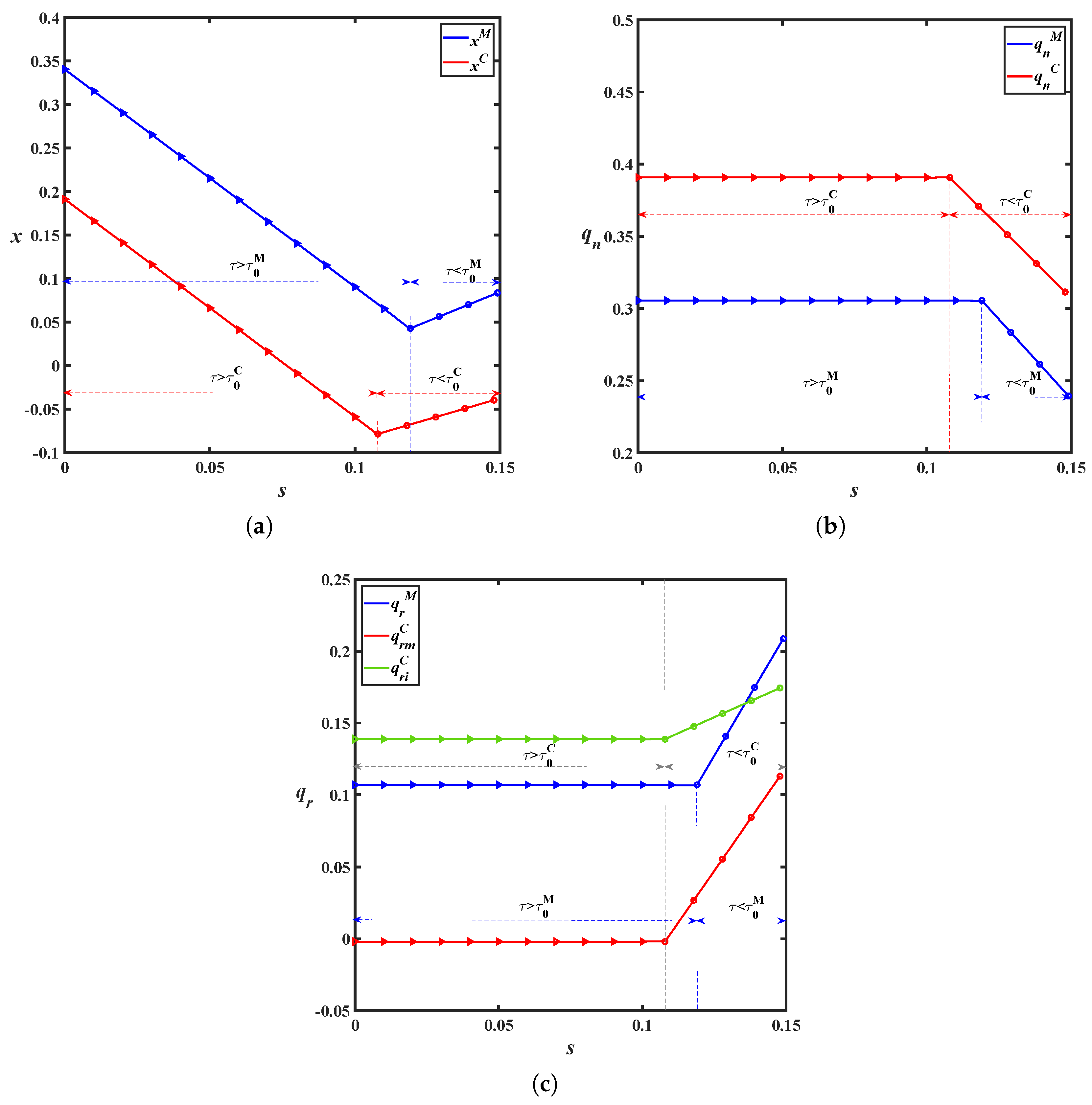
5.1. Equilibrium Solution Comparisons
5.2. Consumer Surplus
5.3. Environmental Impact
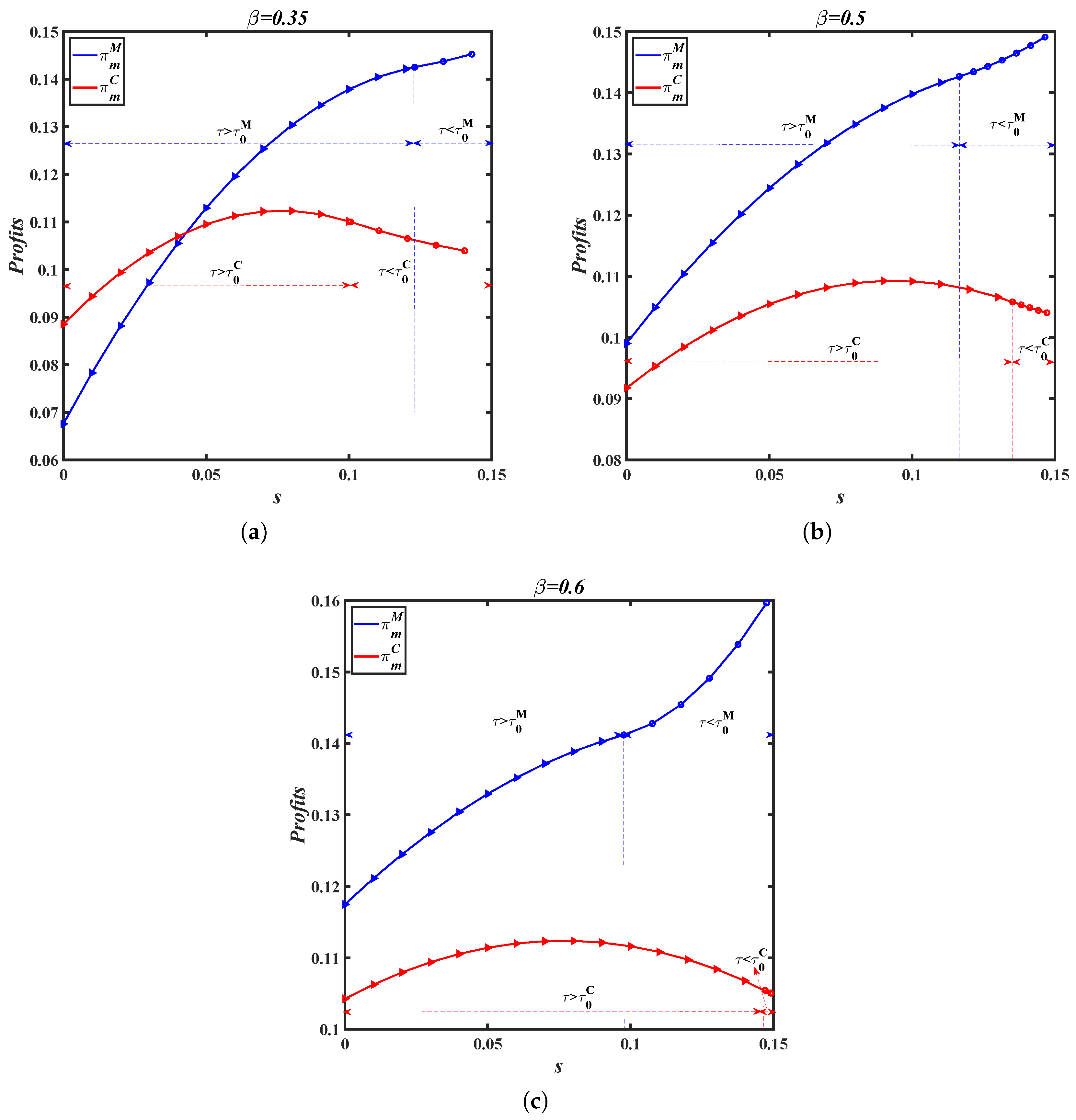
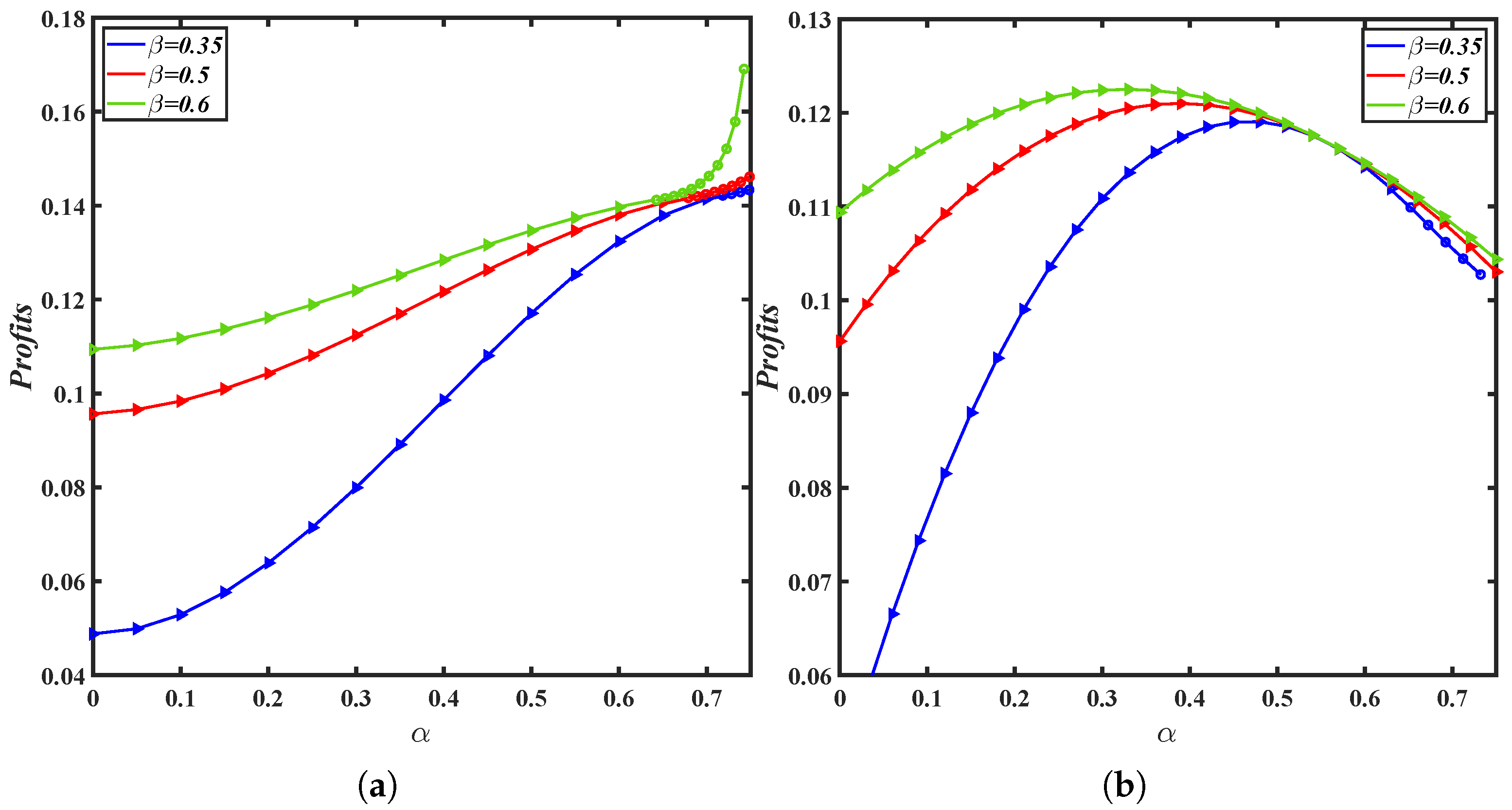
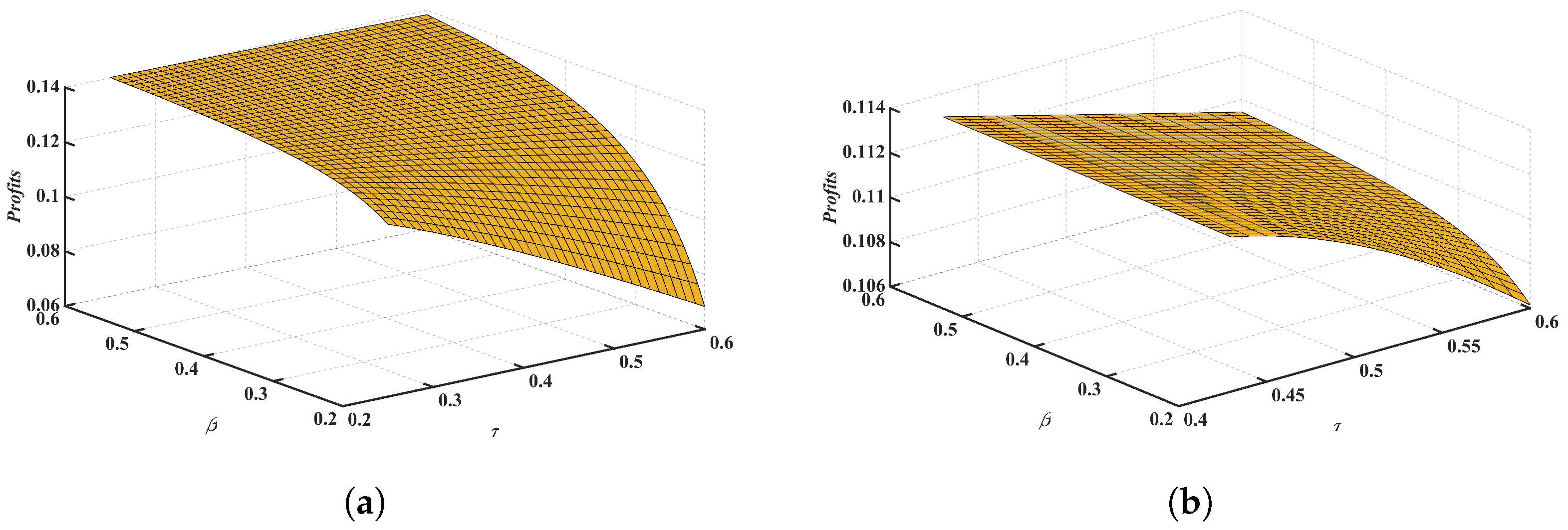
6. Numerical Study
7. Conclusions and Implications
7.1. Conclusions
7.2. Managerial Insights and Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Derivations of the Demand Functions in a Monopolistic Remanufacturing Scenario
Appendix A.2. Proof of Propositions 1 and 2
Appendix B
Appendix B.1. Derivations of the Demand Functions in a Competitive Remanufacturing Scenario
Appendix B.2. Proof of Propositions 3 and 4
References
- Psarommatis, F.; May, G. A Cost–Benefit Model for Sustainable Product Reuse and Repurposing in Circular Remanufacturing. Sustainability 2025, 17, 245. [Google Scholar] [CrossRef]
- Tabassum, M.; Nemani, V.; Hu, C.; Kremer, G.E. A novel design optimization framework to sustain remanufacturability. J. Clean. Prod. 2024, 479, 143935. [Google Scholar] [CrossRef]
- Hong, Z.; Zhang, Y.; Yu, Y.; Chu, C. Dynamic pricing for remanufacturing within socially environmental incentives. Int. J. Prod. Res. 2020, 58, 3976–3997. [Google Scholar] [CrossRef]
- Yang, D.; Yang, Q.; Zhang, L. Operational Decisions on Remanufacturing under the Product Innovation Race. Sustainability 2023, 15, 4920. [Google Scholar] [CrossRef]
- Huang, Q.; Hou, J.; Shen, H. Remanufacturing and pricing strategies under modular architecture. Comput. Ind. Eng. 2024, 188, 109863. [Google Scholar] [CrossRef]
- Zhang, L.; Li, K.; Chu, C.; Liu, J. Investment and remanufacturing strategies considering the application of intelligent manufacturing in hybrid manufacturing–remanufacturing systems. Expert Syst. Appl. 2024, 257, 124991. [Google Scholar] [CrossRef]
- Long, X.; Ge, J.; Shu, T.; Liu, Y. Analysis for recycling and remanufacturing strategies in a supply chain considering consumers’ heterogeneous WTP. Resour. Conserv. Recycl. 2019, 148, 80–90. [Google Scholar] [CrossRef]
- Fang, C.; You, Z.; Yang, Y.; Chen, D.; Mukhopadhyay, S. Is third-party remanufacturing necessarily harmful to the original equipment manufacturer? Ann. Oper. Res. 2020, 291, 317–338. [Google Scholar] [CrossRef]
- Tang, S.; Wang, W.; Zhou, G. Remanufacturing in a competitive market: A closed-loop supply chain in a Stackelberg game framework. Expert Syst. Appl. 2020, 161, 113655. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Gong, Y.; Li, B.; Cheng, Y. The implications of the carbon tax on the vehicle remanufacturing industry in the complex competitive environment. Manag. Decis. Econ. 2023, 44, 2697–2712. [Google Scholar] [CrossRef]
- Tabassum, M.; De Brabanter, K.; Kremer, G.E. Surrogate-assisted optimization under uncertainty for design for remanufacturing considering material price volatility. Sustain. Mater. Technol. 2024, 42, e01163. [Google Scholar] [CrossRef]
- Shi, T.; Gu, W.; Chhajed, D.; Petruzzi, N.C. Effects of Remanufacturable Product Design on Market Segmentation and the Environment. Decis. Sci. 2016, 47, 298–332. [Google Scholar] [CrossRef]
- Liu, Z.; Li, K.W.; Li, B.Y.; Huang, J.; Tang, J. Impact of product-design strategies on the operations of a closed-loop supply chain. Transp. Res. Part E Logist. Transp. Rev. 2019, 124, 75–91. [Google Scholar] [CrossRef]
- Shahbazi, S.; Johansen, K.; Sundin, E. Product Design for Automated Remanufacturing—A Case Study of Electric and Electronic Equipment in Sweden. Sustainability 2021, 13, 9039. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, L.; Chi, Y.; Song, B. Manufacturer encroachment on a closed-loop supply chain with design for remanufacturing. Manag. Decis. Econ. 2022, 43, 1941–1959. [Google Scholar] [CrossRef]
- Zhou, Y.; Hou, M.; Wong, K.H. The Optimal Remanufacturing Strategy of the Closed-Loop Supply Chain Network under Government Regulation and the Manufacturer’s Design for the Environment. Sustainability 2023, 15, 7342. [Google Scholar] [CrossRef]
- Esenduran, G.; Kemahlıoğlu-Ziya, E.; Swaminathan, J.M. Impact of take-back regulation on the remanufacturing industry. Prod. Oper. Manag. 2017, 26, 924–944. [Google Scholar] [CrossRef]
- Pazoki, M.; Samarghandi, H. Take-back regulation: Remanufacturing or eco-design? Int. J. Prod. Econ. 2020, 227, 107674. [Google Scholar] [CrossRef]
- Kushwaha, S.; Chan, F.T.; Chakraborty, K.; Pratap, S. Collection and remanufacturing channels selection under a product take-back regulation with remanufacturing target. Int. J. Prod. Res. 2022, 60, 7384–7410. [Google Scholar] [CrossRef]
- Liu, H.; Ye, L.; Sun, J. Automotive parts remanufacturing models: Consequences for ELV take-back under government regulations. J. Clean. Prod. 2023, 416, 137760. [Google Scholar] [CrossRef]
- Cao, J.; Wu, S.; Kumar, S. Recovering and remanufacturing to fulfill EPR regulation in the presence of secondary market. Int. J. Prod. Econ. 2023, 263, 108933. [Google Scholar] [CrossRef]
- He, J.; Yan, W.; Li, Y.; Lu, D. Recycling and/or reusing: When product innovation meets the recast of WEEE direct. Int. J. Prod. Res. 2024, 62, 7018–7029. [Google Scholar] [CrossRef]
- Wei, F.; Huang, Q. Operational decisions for remanufactured products in a sustainable supply chain. Ann. Oper. Res. 2024. [Google Scholar] [CrossRef]
- Zhou, Q.; Meng, C.; Sheu, J.B.; Yuen, K.F. Impact of Market Competition on Remanufacturing Investment. IEEE Trans. Eng. Manag. 2023, 71, 6995–7014. [Google Scholar] [CrossRef]
- Reimann, M.; Xiong, Y.; Zhou, Y. Managing a closed-loop supply chain with process innovation for remanufacturing. Eur. J. Oper. Res. 2019, 276, 510–518. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, H.; Deng, Q.; Ma, Y.; Luo, Q. Two-stage optimal acquisition and remanufacturing decisions with demand and quality information updating. Transp. Res. Part E Logist. Transp. Rev. 2024, 192, 103823. [Google Scholar] [CrossRef]
- Panagiotidou, S. Joint optimization of manufacturing/remanufacturing lot sizes under imperfect information on returns quality. Eur. J. Oper. Res. 2017, 258, 537–551. [Google Scholar] [CrossRef]
- Liao, H.; Zhang, Q.; Li, L. Optimal procurement strategy for multi-echelon remanufacturing systems under quality uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2023, 170, 103023. [Google Scholar] [CrossRef]
- Zhu, C.; Xi, X.; Goh, M. Differential game analysis of joint emission reduction decisions under mixed carbon policies and CEA. J. Environ. Manag. 2024, 358, 120913. [Google Scholar] [CrossRef]
- Abbey, J.D.; Kleber, R.; Souza, G.C.; Voigt, G. Remanufacturing and consumers’ risky choices: Behavioral modeling and the role of ambiguity aversion. J. Oper. Manag. 2019, 65, 4–21. [Google Scholar] [CrossRef]
| Existing Studies | Take-Back Regulation | Design for Remanufacturing | Remanufacturing Scenario |
|---|---|---|---|
| Esenduran et al. [17] | ✓ | × | Competitive |
| Pazoki and Samarghandi [18] | ✓ | × | Monopolistic |
| Kushwaha et al. [19] | ✓ | × | Monopolistic |
| He et al. [22] | ✓ | × | Monopolistic |
| Liu et al. [13] | × | ✓ | Monopolistic |
| Fang et al. [8] | × | × | Competitive |
| Hu et al. [15] | × | ✓ | Monopolistic |
| Wang et al. [10] | × | ✓ | Competitive |
| Zhou et al. [16] | × | ✓ | Monopolistic |
| This study | ✓ | ✓ | Monopolistic vs. Competitive |
| Parameters | Explanations |
|---|---|
| c | Production cost of unit new product |
| s | Cost saving of unit remanufactured product |
| Consumer preference discount for remanufactured product | |
| k | Cost coefficient for DfR investment level |
| Remanufacturing cost sensitivity factor to DfR | |
| Take-back regulation target imposed by regulators | |
| Decision variables | |
| x | DfR investment level |
| / | Production quantity of new/remanufactured product |
| Dependent variables | |
| The profit of player i under Model j | |
| The environmental impact under Model j | |
| The consumer welfare under Model j | |
| Superscript | M: monopolistic remanufacturing scenario |
| C: competitive remanufacturing | |
| Subscript | m: OEM; r: remanufacturer |
| Data Sets | Solutions | ||||||
|---|---|---|---|---|---|---|---|
| Model | |||||||
| Case 1: , , , , , , | Model M | 0.1791 | 0.2037 | 0.0713 | / | 0.0476 | / |
| Model C | 0.1356 | 0.2409 | 0.0631 | 0.0213 | 0.0486 | 0.0002 | |
| Case 2: , , , , , , | Model M | 0.0868 | 0.3099 | 0.1085 | / | 0.1397 | / |
| Model C | −0.0089 | 0.3817 | 0.0187 | 0.1149 | 0.1208 | 0.0055 | |
| Case 3: , , , , , , | Model M | 0.2856 | 0.2347 | 0.0235 | / | 0.0218 | / |
| Model C | 0.2022 | 0.2705 | 0.0207 | 0.0064 | 0.0396 | 0.0001 | |
| Case 4: , , , , , , | Model M | 0.0117 | 0.3521 | 0.0352 | / | 0.1408 | / |
| Model C | −0.0515 | 0.3792 | 0.0359 | 0.0379 | 0.1330 | 0.0005 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Wang, L.; Shu, Y. How Should e-Product OEMs Invest in Design for Remanufacturing Under the Take-Back Regulation in a Competitive Environment? Sustainability 2025, 17, 3593. https://doi.org/10.3390/su17083593
Zhang N, Wang L, Shu Y. How Should e-Product OEMs Invest in Design for Remanufacturing Under the Take-Back Regulation in a Competitive Environment? Sustainability. 2025; 17(8):3593. https://doi.org/10.3390/su17083593
Chicago/Turabian StyleZhang, Ning, Liecheng Wang, and Yunxia Shu. 2025. "How Should e-Product OEMs Invest in Design for Remanufacturing Under the Take-Back Regulation in a Competitive Environment?" Sustainability 17, no. 8: 3593. https://doi.org/10.3390/su17083593
APA StyleZhang, N., Wang, L., & Shu, Y. (2025). How Should e-Product OEMs Invest in Design for Remanufacturing Under the Take-Back Regulation in a Competitive Environment? Sustainability, 17(8), 3593. https://doi.org/10.3390/su17083593






