Research on the Power Generation Efficiency of Zero-Carbon Port Framework-Based Gravitational Energy Storage Systems

Abstract

Based on containers as heavy objects, a framework-based gravitational energy storage system is designed, where the container is lifted to a certain height to store gravitational potential energy, which is then released to drive a generator for power generation. The system utilizes existing port infrastructure, reducing the manufacturing cost of heavy blocks and offering good environmental adaptability. The results show that framework-based gravitational energy storage systems have high feasibility in port energy supply, providing stable power output and improving energy efficiency. Through optimization analysis of storage efficiency, power generation efficiency, and other parameters, this study provides theoretical and technical support for achieving sustainable green development in ports. This paper firstly describes the design and operating principles of the system, followed by a detailed indoor test analysis. Subsequently, the test results are specifically analyzed. Finally, practical implications and future development directions are discussed.

1. Introduction

With the continuous development of the global economy, the concept of zero-carbon ports has emerged. This is not only a necessary step in addressing climate change but also a transition to a more sustainable future for the port industry. Zero-carbon ports optimize the energy structure by adopting clean energy, improving energy efficiency, and applying low-carbon technologies, gradually achieving low-carbon and green energy transformation. In this process, the use of framework-based gravitational energy storage systems and containers as loads not only contributes to the stable energy supply of the port but also aligns closely with the concept of sustainable development.

Sustainable development emphasizes not only reducing resource consumption and environmental impacts but also promoting resource recycling and ecological protection. The framework-based gravitational energy storage system, by utilizing the idle container resources at the port terminal, reduces the production and procurement costs of load blocks and the demand for new raw materials. This approach effectively utilizes the existing facilities and resources at the port, saving economic costs and avoiding energy consumption and emissions during the manufacturing and transportation processes, thus reducing the carbon footprint and aligning with the principles of circular economy and efficient resource utilization.

In addition, containers, used as energy storage mediums, feature standardized designs and robust configurability. Containers can be stacked and combined based on different energy storage needs, offering high flexibility. The design philosophy of this system embodies the concept of “green design”, which minimizes unnecessary waste while enhancing the system’s adaptability and durability. The framework-based gravitational energy storage system not only reduces resource waste during design but also, due to its simple structure and strong adaptability, can quickly respond to changes in power demand, ensuring a stable power supply and supporting the green energy needs of ports and surrounding areas.

This, in turn, further promotes sustainable energy management and the achievement of emissions reduction goals. Moreover, adopting the framework-based gravitational energy storage system can facilitate the widespread use of low-carbon technologies, especially in critical infrastructure like ports. By introducing such advanced energy storage solutions, ports can optimize energy use, improve energy efficiency, and reduce reliance on traditional high-carbon energy sources. This aligns with global zero-carbon goals and helps the port industry gradually achieve a comprehensive green transformation. In conclusion, the application of the framework-based gravitational energy storage system not only enhances energy efficiency and system reliability but also drives innovation in green low-carbon technologies at ports, contributing to the achievement of sustainable development goals. This innovative solution unites environmental, economic, and social benefits, laying a solid foundation for the construction of zero-carbon ports.

From an energy structure perspective, it can be seen that the geographical location of the port offers significant advantages, with abundant new energy resources. Wang et al. highlighted that gravitational energy storage technology has become a key research direction for new energy storage methods due to its advantages, such as being environmentally friendly, having high energy storage efficiency, low initial costs, and minimal requirements for terrain and water sources [1]. Shi et al. pointed out that gravitational energy storage technology enables the stable and controllable conversion of gravitational potential energy into electrical energy through the lifting and lowering of heavy objects [2].

Liang proposed that energy storage technology can store energy when renewable energy generation is in surplus, and release the stored energy when generation is insufficient, thereby ensuring a continuous and stable power supply [3,4]. Mostafa E. A. Elsayed et al. developed a theoretical model using MATLAB/SIMULINK to simulate the performance of gravitational energy storage systems [5]. Yu et al. established a general charging and discharging model for gravitational energy storage systems and analyzed the system’s charging and discharging power characteristics [6]. Li et al. conducted a comparative analysis of four main types of gravitational energy storage: tower-type gravitational energy storage (TGES), mountain gravitational energy storage (MGES), advanced railway energy storage (ARES), and shaft-type gravitational energy storage (SGES). They analyzed the advantages and disadvantages of each technology, providing valuable insights for the development of gravitational energy storage [7].

In the study of shaft-type gravitational energy storage systems, Christoff Daniel Botha et al. showed through their study that the proposed storage system is cost-competitive when used in applications with high power and high annual cycle counts [8]. Shi et al. pointed out that shaft-type gravitational energy storage technology is one of the emerging storage technologies. Based on the performance indicators of linear motors in shaft-type gravitational energy storage systems, they derived the energy storage efficiency calculation formula [9,10]. Zhang et al. introduced the working principle of a hydraulic abandoned mine gravitational energy storage system and calculated its power generation efficiency [11]. Qiu et al. have analyzed the core technical difficulties existing in vertical gravity energy storage systems [12].

Finally, they provided an outlook on the future development trends of vertical gravitational energy storage technologies. In summary, scholars have conducted research and analysis on technologies related to shaft-type gravitational energy storage. However, research on the factors affecting the energy storage efficiency of gravitational energy storage and their respective proportions remains insufficient.

Regarding the progress in the research on slope-type gravitational energy storage systems, Michail Galetakis et al. studied a novel gravitational energy storage system that uses a reversible conveyor belt to lift granular materials and a regenerative motor to collect energy during the downward movement of the materials [13]. Yuan et al. introduced two typical slope-type gravitational energy storage system structures and discussed the impact of parameters such as slope and heavy object mass on system efficiency and cost performance [14]. Yang et al. constructed a grid connection simulation model for gravitational energy storage systems using Matlab/Simulink software, and the effectiveness of the proposed grid-connected scheme was verified by simulation results [15,16].

Zhang et al. proposed a slope gravity energy storage technology-slope cable-rail gravity energy storage technology that incorporates the advantages and avoids the disadvantages [17]. Liu et al. proposed a multi-software collaborative modeling method for the mechanical and electrical joint simulation of a slope-type gravitational energy storage system [18]. Gao et al. developed a Matlab/Simulink-based energy efficiency analysis model for TCS-GESS for the system mass block movement, mechanical transmission, and electrical drive segments [19]. Ying et al. proposed a model for an intelligent microgrid system based on gravitational energy storage for abandoned mines, studying and analyzing the system’s principles, structure, underground power plants, underground energy storage, and transportation systems [20].

Regarding the progress in the research on framework-based gravitational energy storage systems, Peter Kropotin et al. proposed an algorithm to calculate the round-trip efficiency (RTE) of a gravitational energy storage system with a rope traction mechanism using a PU-coated multi-rope belt. They demonstrated that the RTE of the system is highly sensitive to the mechanical parameters of the lifting mechanism [21]. Hu designed an efficient disk tower gravity energy storage scheme, and the simulation results proved the effectiveness of the proposed method [22]. Wang et al. met the instantaneous demand of the grid by first controlling the number of falling mass blocks and later regulating the falling speed of the mass blocks [23]. Xu et al. used discounted kWh revenue, LROE, and levelized cost of electricity (LCOE) to establish a levelized kWh NPV model and considered the impact of different parameters on system economics [24]. Liu et al. analyzed the economics of a framed gravity energy storage system and obtained the investment cost and flat quasi-energy storage kWh cost of the framed gravity energy storage system with different system capacities [25].

In summary, in recent years, numerous scholars have proposed algorithms with mathematical models and employed various numerical simulation methods to conduct a series of calculations on framework-based gravitational energy storage systems. These studies have provided valuable references for the feasibility of framework-based gravitational energy storage systems in engineering applications. Additionally, some scholars have explored the lifecycle revenue and economic analysis of framework-based gravitational energy storage systems, offering guidance on the economic viability of such systems.

However, current research still lacks sufficient studies on the actual control and the impact of energy storage efficiency in framework-based gravitational energy storage systems [26].

Therefore, this paper focuses on the structural design and performance optimization of framework-based gravitational energy storage systems, particularly exploring the impact of object mass and storage height on power generation efficiency and analyzing the energy storage efficiency of the system under different parameter configurations. To achieve this, this paper designs a vertical gravitational energy storage system based on a framework structure, employing a specific experimental setup that combines mechanical frameworks with electrical control systems. The experimental plan investigates the influence of different object masses and storage heights on energy storage efficiency and power generation performance and validates the theoretical analysis through practical testing. Through experiments and model analysis, this study aims to provide theoretical foundations and practical guidance for the engineering application of framework-based gravitational energy storage systems, promoting their widespread use in zero-carbon ports and other renewable energy sectors [27].

2. Experimental Design

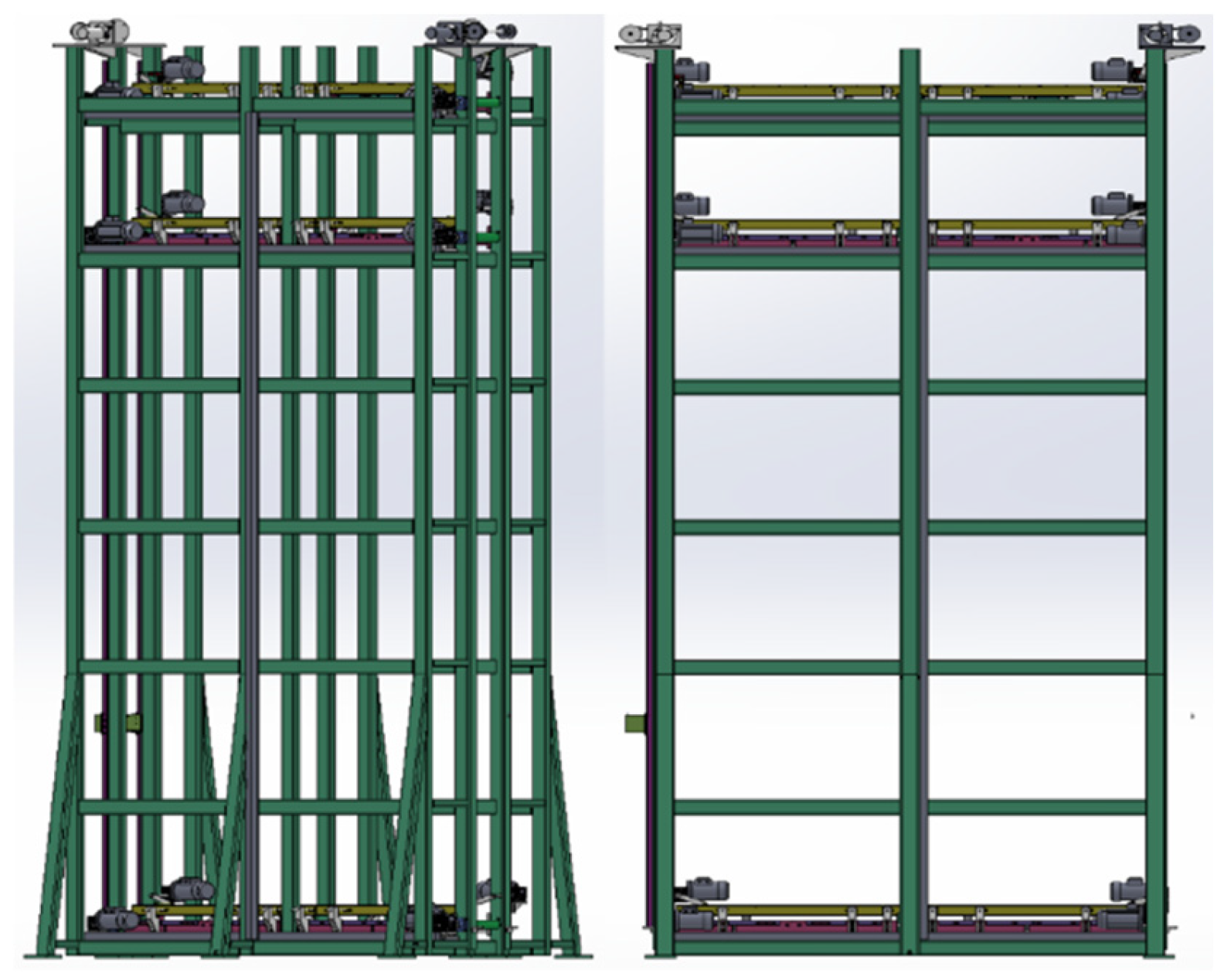
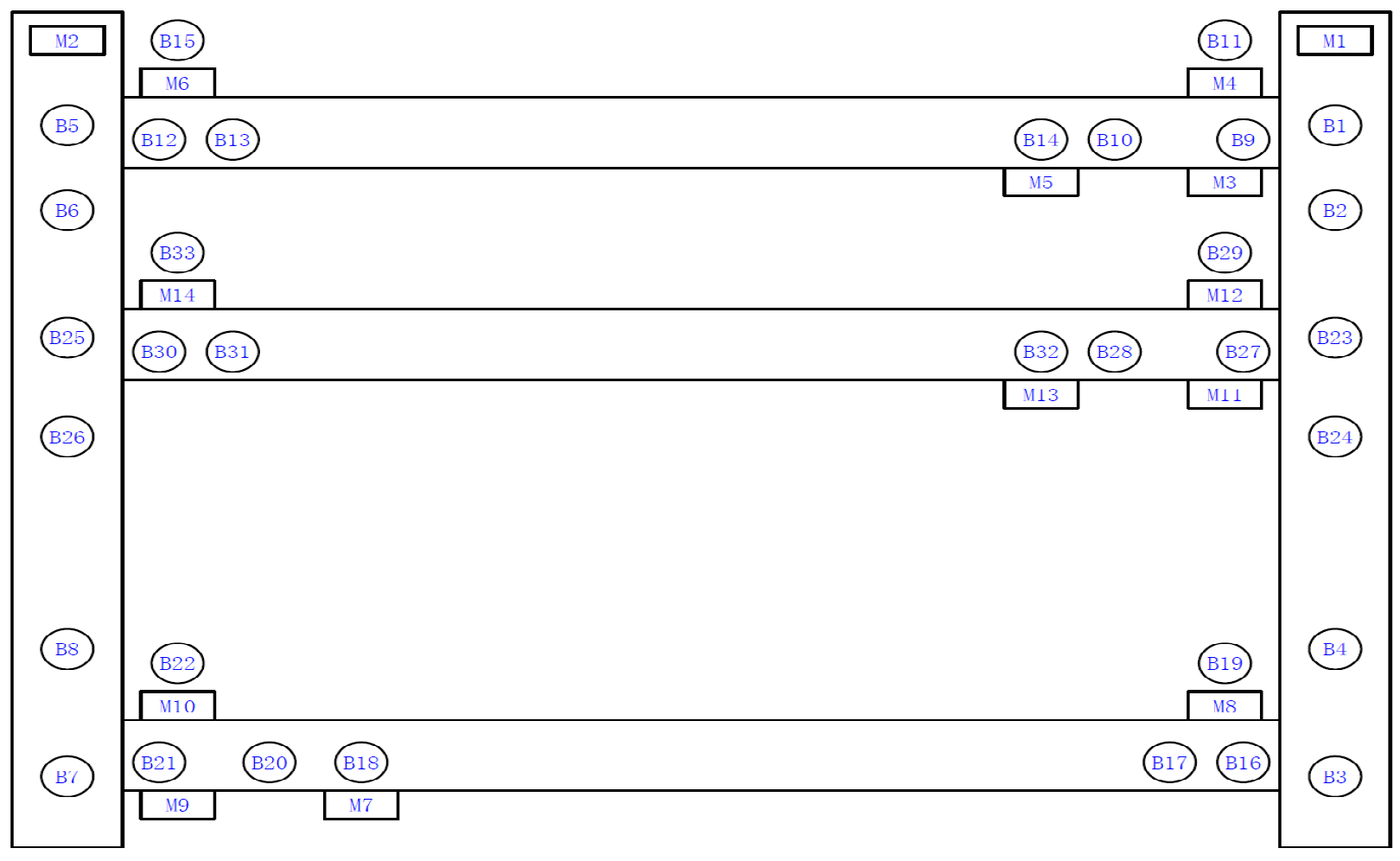
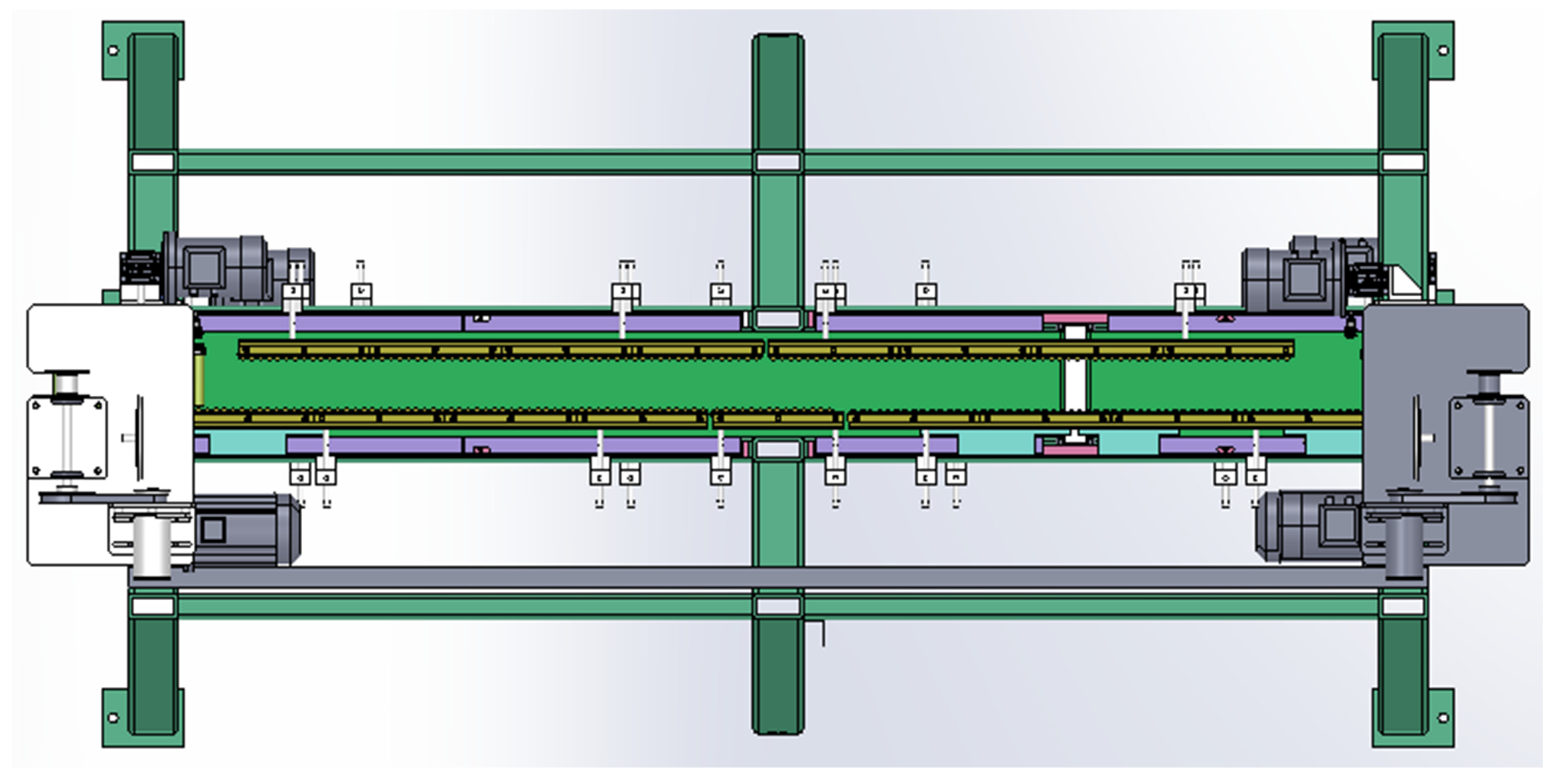
2.1. Overview of the Experimental Model Structure

The research focus of this project is vertical gravitational energy storage systems with a framework structure as its carrier. The framework-based gravitational energy storage structure features a unique design and composition, primarily divided into two key components: the mechanical framework and the electrical control system.

In this experiment, the mechanical part of the framework-based gravitational energy storage structure exhibits clear structural features, as shown in Figure 1. The system has a length of 3 m, a maximum width of 1 m, and a height of 6 m. It is entirely constructed from square steel tubes welded together, with a total weight of 4 tons. Inside the structure, there are a series of processed components, such as slide rails and a lift car. The energy storage section is divided into two layers: the upper layer has a height of 6 m, while the lower layer has a height of 5 m. The left vertical section represents the descending section, which is responsible for releasing energy to generate electricity, while the right vertical section represents the ascending section, or the energy storage segment, responsible for lifting the heavy objects to store energy.

The electrical control system consists of a control box, sensors, motors, and generators. The control box, of which there is only one, is responsible for controlling the operation of the entire system. There are a total of 47 sensors: 14 sensors numbered M1-M14 are used to sense the heavy objects and control the motor switches, and 33 sensors numbered B1-B33 are used to sense the heavy objects and control the motor speed to regulate the movement speed of the heavy objects. The sensor layout is shown in Figure 2. The system includes 14 motors with a total power of approximately 4.23 KW. Six motors control the horizontal movement of the heavy objects, two motors control the vertical movement of the lift car, and six motors control the toggles, enabling the movement of the heavy objects in both horizontal and vertical directions. There are two generators that convert the energy released by the heavy objects into electrical energy, fulfilling the core function of the gravitational energy storage system. The framework-based gravitational energy storage electrical control system is shown in Figure 3, and the electrical control schematic diagram is shown in Figure 4.

The control box is divided into two parts: touch screen control and external operation button control. The touch screen consists of four interfaces: the operation screen, control screen, monitoring screen, and alarm screen, as shown in Figure 5. In the operation screen, the equipment can be initialized, middle-level operations can be selected, the counter can be reset, and the number of equipment operations can be set. This screen also displays the operation status of the conveyor belt and lift car. In the control screen, the 14 motors in the system can be manually controlled to operate individually. In the monitoring screen, the status of each sensor in the equipment can be monitored. In the alarm screen, fault alarm information can be viewed for easy troubleshooting.

In the system architecture of this experiment, the displacement process of the heavy object is driven by the operation of the motor. In the horizontal section, the motor is mechanically connected to the conveyor belt. When the motor starts, the power it generates drives the conveyor belt to operate, and the heavy object moves horizontally by relying on the continuous motion of the conveyor belt. In the vertical direction, the motor is associated with the lift car, and the heavy object is placed inside the lift car, as shown in Figure 6. With the lifting and lowering movement of the lift car driven by the motor, vertical displacement is achieved. At the junction between the horizontal and vertical sections, a special motor with a unique connection method is installed. This motor is connected to the toggle device, as shown in Figure 7.

By driving the toggle with precise actions, the motor enables efficient movement of the heavy object between the lift car and the conveyor belt. The movement trajectory of the heavy object follows a specific path, starting from the bottom-left position, moving through the horizontal section, transitioning through the junction area, and ascending/descending through the vertical section. After completing one cycle, the heavy object returns to its original position, thereby completing a full cycle. This process involves the coordinated operation of multiple mechanical components and the precise transmission and conversion of power. It is significant for studying the movement patterns and related performance of the heavy object in the experimental system. Moreover, it provides foundational data and experimental evidence for further analysis and optimization of the system’s overall operational efficiency and stability.

In the specific process of operation in the horizontal section, the conveyor belt exhibits clear segmentation features, divided into two parts, as shown in Figure 8. When the heavy object enters the horizontal section from the vertical section, the conveyor belt at the front is relatively longer. This longer conveyor belt plays a crucial role in the transfer of the heavy object. On one hand, it fulfills the basic function of moving the heavy object horizontally; on the other hand, due to its length, it can store a certain number of heavy objects for a specific period, a characteristic that is highly similar to the energy storage function in practical engineering. It can be regarded as a simulation of the energy storage section in real-world applications, which is of great significance for the stability of the entire system and energy management.

The conveyor belt at the rear is slightly shorter than the first one. Its primary function is to accurately move the heavy object to the lift car, ensuring it enters the subsequent cycle process smoothly. These two conveyor belts do not operate independently but are both precisely controlled by the motor. Through advanced sensor technology, the system can accurately sense the position of the heavy object. Based on the obtained position data, the control system can precisely manage the motor’s operation and direct the conveyor belt to move as required. In this way, the two conveyor belts work in perfect harmony under the coordination of the motor and sensors, ensuring efficient, stable, and precise transfer of the heavy object in the horizontal section, thus providing solid support for the normal operation of the entire production system.

In this experimental model, since both time and power may vary, we must start our analysis from the perspective of power. Each generator has a rated power, and if the actual power when the system is running is close to the rated value, the energy conversion efficiency per unit of time is higher, and the final total amount of power generated is larger and more stable. Therefore, in our experiments, we focus on how to optimize the system operation so that the power of the generator is stabilized at a range close to the rated power, in order to improve the energy conversion efficiency of the overall energy storage-discharge process.

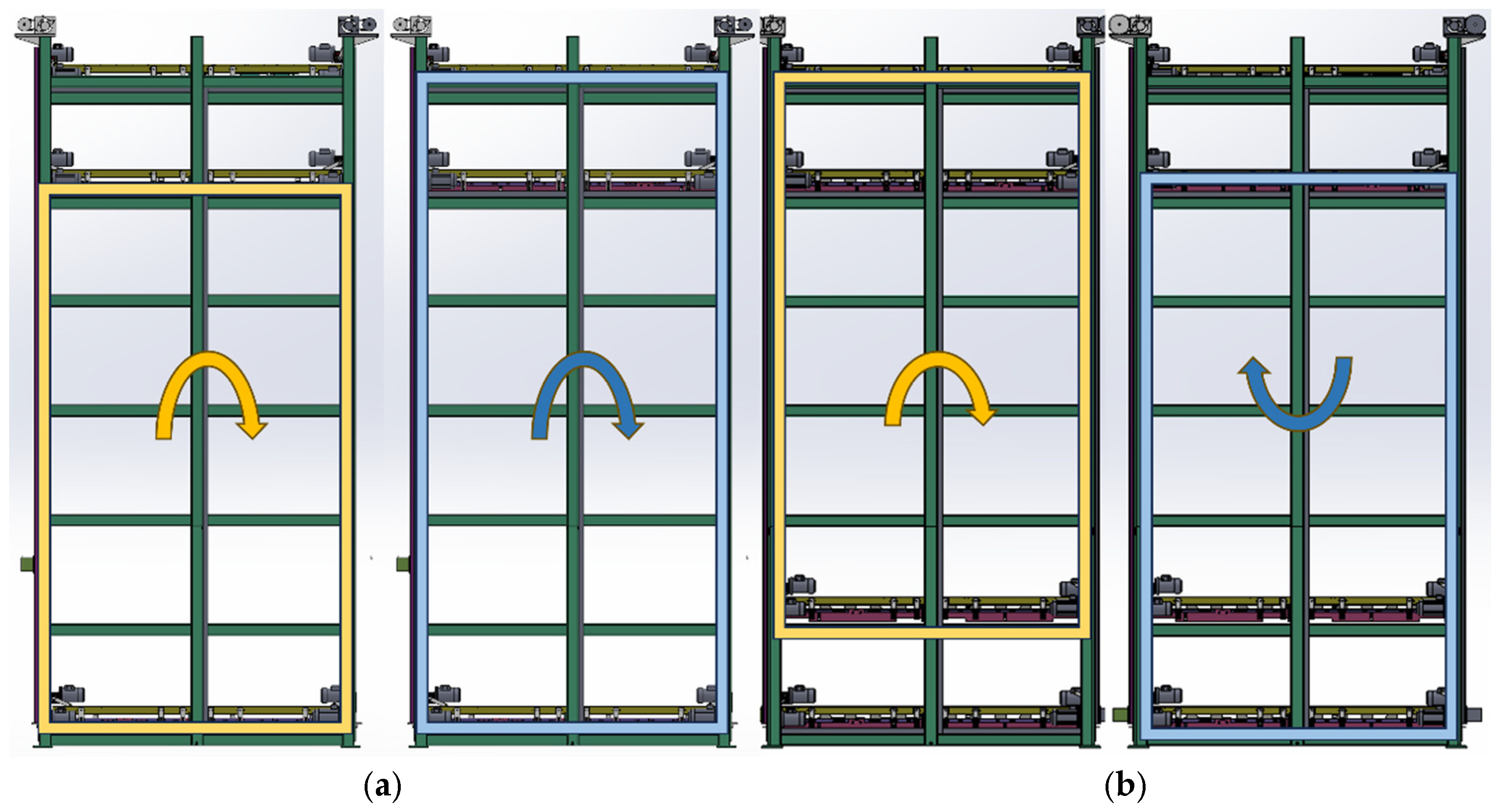
2.1.1. “Single Layer Double Height Difference” Structure

The “Single Layer Double Height Difference” structure, as shown in Figure 1, exhibits a unique layout. The lower section of the structure is designed as a single layer, while the upper energy storage layer is constructed with two layers. In the operational mechanism of this structure, all heavy objects follow a specific path to descend to the lowest layer. Given that the upper energy storage layer has two levels, when the heavy object descends from the upper layer to the lowest layer, it creates two distinct height differences. These height differences are 5 m and 6 m, respectively. Under this specific experimental structure setup, favorable conditions are provided for in-depth exploration of energy storage characteristics. This enables the study of energy storage efficiency for heavy objects with the same mass but different height differences, as well as for different masses at the same height difference.

By analyzing the energy storage efficiency under these different parameter combinations, a more comprehensive and thorough understanding of the various patterns and influencing factors in the energy storage process can be achieved. The “Single Layer Double Height Difference” structure has significant advantages. Compared to the “Double Layer Single Height Difference” structure, its operating trajectory is relatively simpler and more direct. In terms of structural control, it also offers certain advantages, requiring relatively lower control strategies and complexity, making precise operation and regulation easier to implement. However, this structure also has notable drawbacks. During the energy storage process, when the lift car descends to the bottom, and during the energy release and power generation phase, when the lift car ascends, the empty lift car moves. This empty lift car movement leads to higher energy consumption in the entire motion plan. In practical applications and research, it is crucial to consider the impact of this factor on the overall system efficiency and further explore how to optimize the structure design or operational strategies to reduce energy consumption and improve the system’s energy utilization efficiency and overall performance.

Taking a 6 m height difference as an example for analysis, the height at which the heavy object descends to generate power can be set to various values such as 4 m, 5 m, and 5.5 m, among other conditions. Additionally, the mass of the heavy object can be selected from multiple different values. This flexibility allows for the study of energy storage efficiency under varying height differences and different object masses, providing deeper insights into the factors that influence the energy storage process.

In the specific operational process, the heavy object starts at the far-left position of the lowest layer and then moves horizontally along the conveyor belt. This conveyor belt acts as a bridge for transporting the heavy object, steadily moving it toward the right side of the bottom layer. When the heavy object reaches a specific position on the right side of the bottom layer, it enters the lift car through the mechanical action of the toggle device. At this point, the lift car on the right side performs its lifting function, raising the heavy object to the highest level of the system. Next, at the highest level, the toggle device again acts to push the heavy object out of the lift car, transferring it to the conveyor belt at the top level. The heavy object then moves along this conveyor belt, starting from the far right of the highest level, and moves horizontally to the far left. Finally, on the left side of the top level, the toggle device pushes the heavy object back into the lift car. The lift car, now carrying the heavy object, begins to descend, continuing until the heavy object returns to the bottom layer, where it is again pushed out by the toggle device and placed at the far left of the lowest level. This completes one full cycle.

2.1.2. “Double Layer Single Height Difference” Structure

The “Double Layer Single Height Difference” structure, as a novel design, brings new possibilities for experimental research. As shown in Figure 9, the lower section of the structure is designed with two layers, while the upper energy storage layer also consists of two layers. The height difference between the two layers at the top and the two layers at the bottom is 1 m each, creating a noticeable difference in overall structural layout. Similarly to the “Single Layer Double Height Difference” structure, the “Double Layer Single Height Difference” structure is also equipped with only one lift car and a track to facilitate its vertical movement. This configuration somewhat limits the operational method of the structure but also provides the foundational conditions for its unique energy conversion process. Given the special form of this structure, it offers new experimental approaches.

In this structure, the power generation process during the descent of the heavy object from the top layer is from the highest level to the second layer, while the power generation process for the heavy object descending from the second-to-last upper layer is from that layer to the lowest level. With this design, both upper energy storage layers achieve a 5 m descent in the power generation process as the heavy object releases energy. This design enables the collection of more data within a shorter time period, providing a wealth of samples and more accurate observation opportunities for experimental research. Compared to the “Single Layer Double Height Difference” structure, one of the main advantages of the “Double Layer Single Height Difference” structure is the reduction in the movement of the empty lift car. The reduction in the empty lift car movement fundamentally decreases energy loss and enhances energy utilization efficiency. This is of great significance for energy research, offering the potential for more efficient energy conversion and storage.

In this structure, the operation mode of the lift car on the left side exhibits regularity and specificity. It starts its operation from the lowest layer, initially in an empty state. When it reaches a height of 1 m from the bottom, at the second layer from the bottom, it receives the heavy object and lifts it to the topmost energy storage layer for energy storage. Afterward, the lift car descends by 1 m in an empty state and then receives the heavy object from the second layer at the highest level, proceeding to release energy through power generation until it reaches the lowest layer, where it places the heavy object onto the conveyor belt at the lowest level. This completes one full cycle. Throughout the entire cycle, the lift car spends only a 2 m distance in an empty state.

Compared to the 5 m and 6 m empty lift car travel distances in the “Single Layer Double Height Difference” structure, this design significantly reduces the distance traveled by the empty lift car, thereby greatly reducing energy consumption. The operation of the lift car on the right side differs slightly. It also starts from the lowest layer, but in its initial state, it carries the heavy object. When it reaches a height of 5 m, it delivers the heavy object to the second layer at the topmost level for energy storage. It then ascends by 1 m in an empty state, receives the heavy object from the topmost layer, and performs energy release and power generation. Afterward, it moves to the lowest layer, places the heavy object on the second-to-last layer’s conveyor belt, and finally moves to the lowest layer in an empty state, completing the cycle.

From an overall functional perspective, for the left lift car, in the first cycle, its primary role is energy storage, which involves lifting the heavy object to the highest level for energy storage, preparing for subsequent energy release. In the second cycle, it plays a key role in energy release and power generation by converting the energy from the descent of the heavy object into electrical energy. For the right lift car, in the first cycle, its main function is to release energy and generate power, utilizing the descent of the initially loaded heavy object to generate electricity. In the second cycle, it primarily serves the purpose of energy storage, lifting the heavy object to the corresponding position for storage. The specific operation process is shown in Figure 10. The operation modes of the two lift cars on either side are closely coordinated with two opposite cycles, working together in perfect harmony. This coordination ensures that the entire structural system operates efficiently and stably, achieving effective energy storage and conversion. This provides an innovative and practically feasible solution for technological applications in related fields.

In addition, whether it is the “Single Layer Double Height Difference” structure or the “Double Layer Single Height Difference” structure, multiple heavy objects are involved in the operation simultaneously throughout the entire process to ensure the efficiency of the experiment and the adequacy of the data. To guarantee the precision and controllability of the entire operation, each motor is closely monitored by sensors. The sensors continuously track the running status of the heavy objects and transmit the relevant data to the control system. Based on the data feedback from the sensors, the control system precisely adjusts the motor’s operation to ensure that it remains in the optimal state throughout the process. This approach effectively shortens the experimental cycle, enhances experimental efficiency, and provides more reliable data support and operational assurance for the research work.

2.2. Main Theoretical Calculations

2.2.1. Energy Storage Calculation

To lift the heavy object to the energy storage compartment, work must be performed on the object. In an ideal state, the amount of energy stored is equal to the gravitational potential energy of the object relative to the ground at the energy storage layer. The gravitational potential energy is calculated using the following formula:

W_g = MgH

(1)

In the equation, W_g represents the gravitational potential energy of the heavy object; M denotes the mass of the object; g refers to the gravitational acceleration; and H indicates the energy storage height.

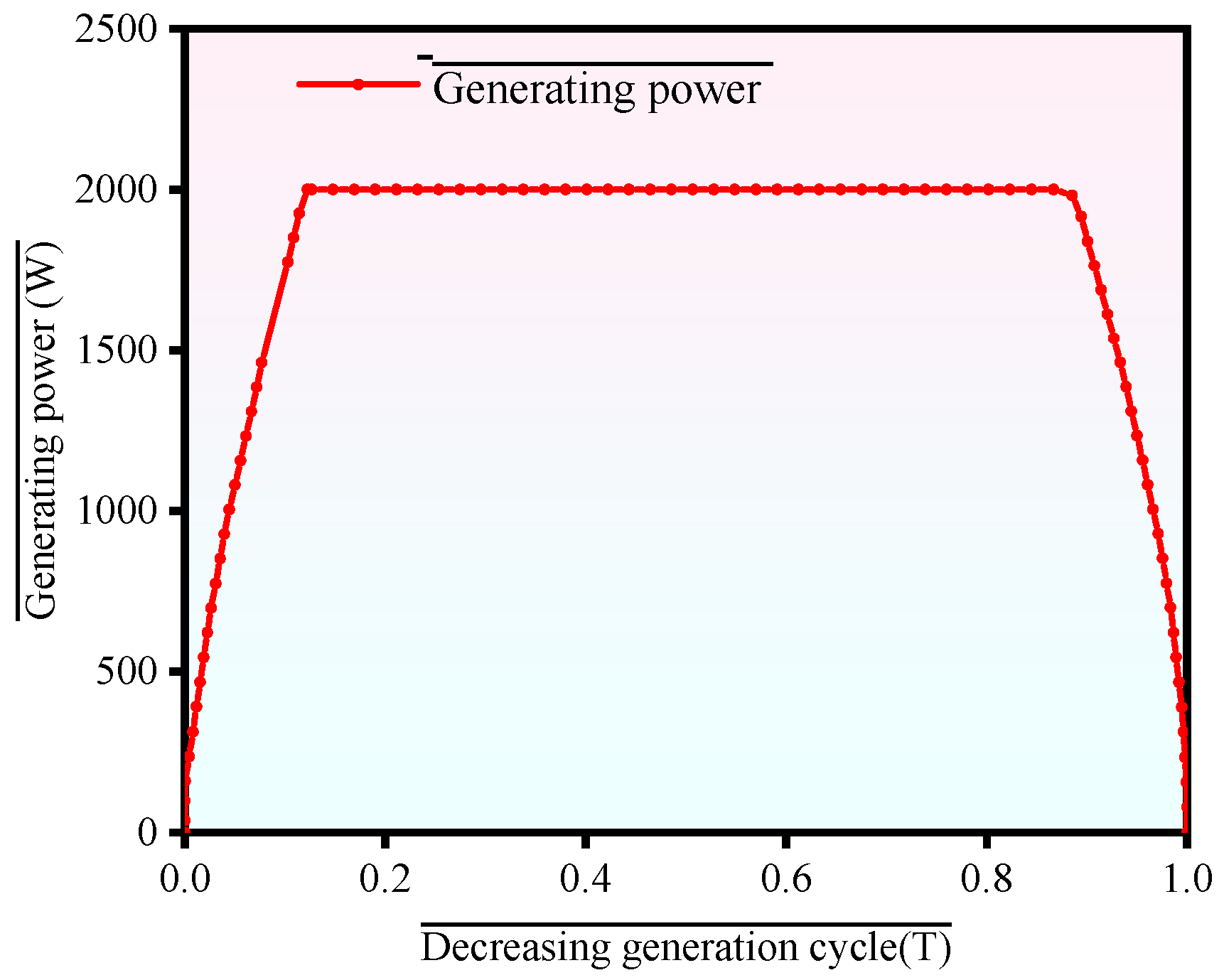
2.2.2. Power Generation Calculation

The power generation efficiency is determined by the design and manufacturing factors of the generator itself. Therefore, the amount of electricity generated depends on the generator’s working power and the duration of its operation. The power generation is calculated using the following equation:

W_p = Pt

(2)

In the equation, W_p represents the power generation; P denotes the power of the generator; and t indicates the generation time.

2.2.3. Energy Storage Efficiency

Energy storage efficiency refers to the ability of an energy storage system to effectively store and release energy during the energy storage and discharge processes. It is a key indicator of the performance of the energy storage system, typically expressed as a percentage.

η = (W_p/W_g) × 100%

(3)

2.2.4. Generator Parameters

From the energy storage efficiency formula, it can be observed that, under constant power generation, the smaller the gravitational potential energy of the heavy object, the higher the energy storage efficiency. Under constant energy storage, the larger the power generation of the generator, the higher the energy storage efficiency. A comprehensive analysis shows that, under a specific model of the generator, the generator reaches its maximum power generation efficiency when it reaches its rated power, at which point the power generation becomes stable. At this stage, the gravitational potential energy of the heavy object is small, meaning that the mass of the object is inversely proportional to the power generation efficiency. To avoid excessively low energy storage efficiency and achieve the economic and feasibility objectives of the energy storage system, theoretical calculations should be performed for the specific generator to determine the appropriate mass range of the heavy object within a certain energy storage efficiency interval. In this experiment, a permanent magnet AC/DC hybrid generator model JFZ268 is used. This generator model is taken as an example for investigation, providing a reference for practical engineering applications.

Figure 11 below shows the efficiency curve of the JFZ268 model generator, which shows that the generator is running at full power when the decreasing generation cycle is in a certain range. The figure shows the power variation curve of a generator at different generation cycles (T), reflecting its efficiency characteristics during operation. It can be seen that the generator has a rapid increase in power at the beginning of the generation cycle (T < 0.2), and then maintains a nearly constant high power output with a peak power of about 2000 W for a long period of time (from about T = 0.2 to T = 0.85), and at the end of the generation cycle (T > 0.85), the power decreases rapidly to nearly 0 W.

Overall, the generator has good, stable output characteristics and is able to maintain an efficient power output of about 2000 W during the main generation phase, indicating that its efficiency characteristics during operation are good. Overall, the generator has good, stable output characteristics and can maintain an efficient power output of about 2000 W during the main power generation phase, which indicates that it has a high energy conversion efficiency during the operating range. This power characteristic is important for applications that require a stable energy supply, such as in scenarios where the load is continuously supplied, such as microgrid systems or emergency power supplies. In addition, the trapezoidal shape of the curves indicates that the generator has a short transition between the start and stop phases, which results in a quicker response and is conducive to stable operation under dynamic operating conditions.

2.2.5. Energy Consumption Calculation

In an ideal scenario, the work performed on the heavy object is equal to its gravitational potential energy. However, in reality, friction losses between mechanical components cannot be ignored. Additionally, losses during the movement of the heavy object along the horizontal section and during the descent, as well as the losses caused by mechanical control involvement, are also non-negligible. In the preliminary theoretical calculation, the main purpose is to estimate the energy storage ratio, which helps in the selection of components such as generators and motors. Therefore, losses can be disregarded in this stage. In the final experimental process, all losses can be analyzed from the collected electricity consumption data. Through system analysis of energy losses at each stage, experimental plans and local improvements can be made to reduce losses and improve energy storage efficiency.

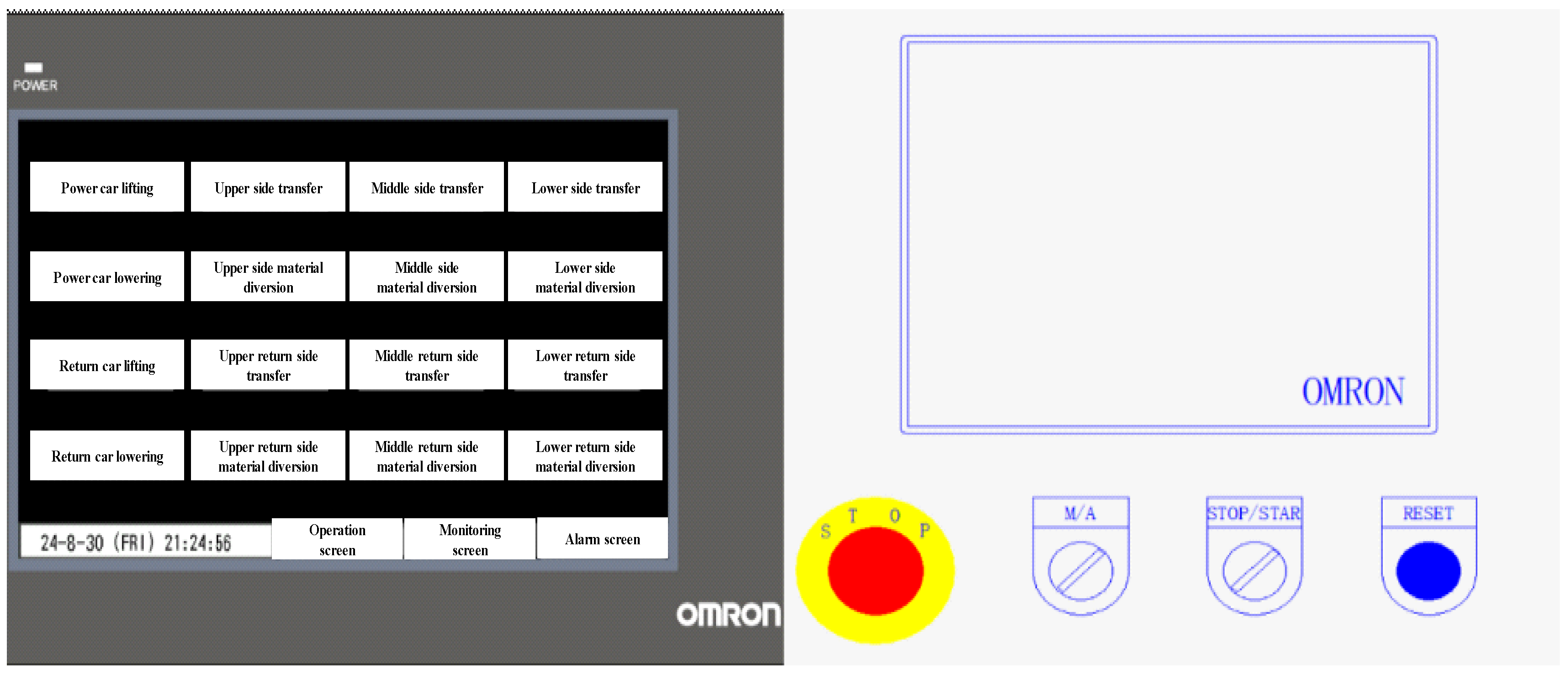
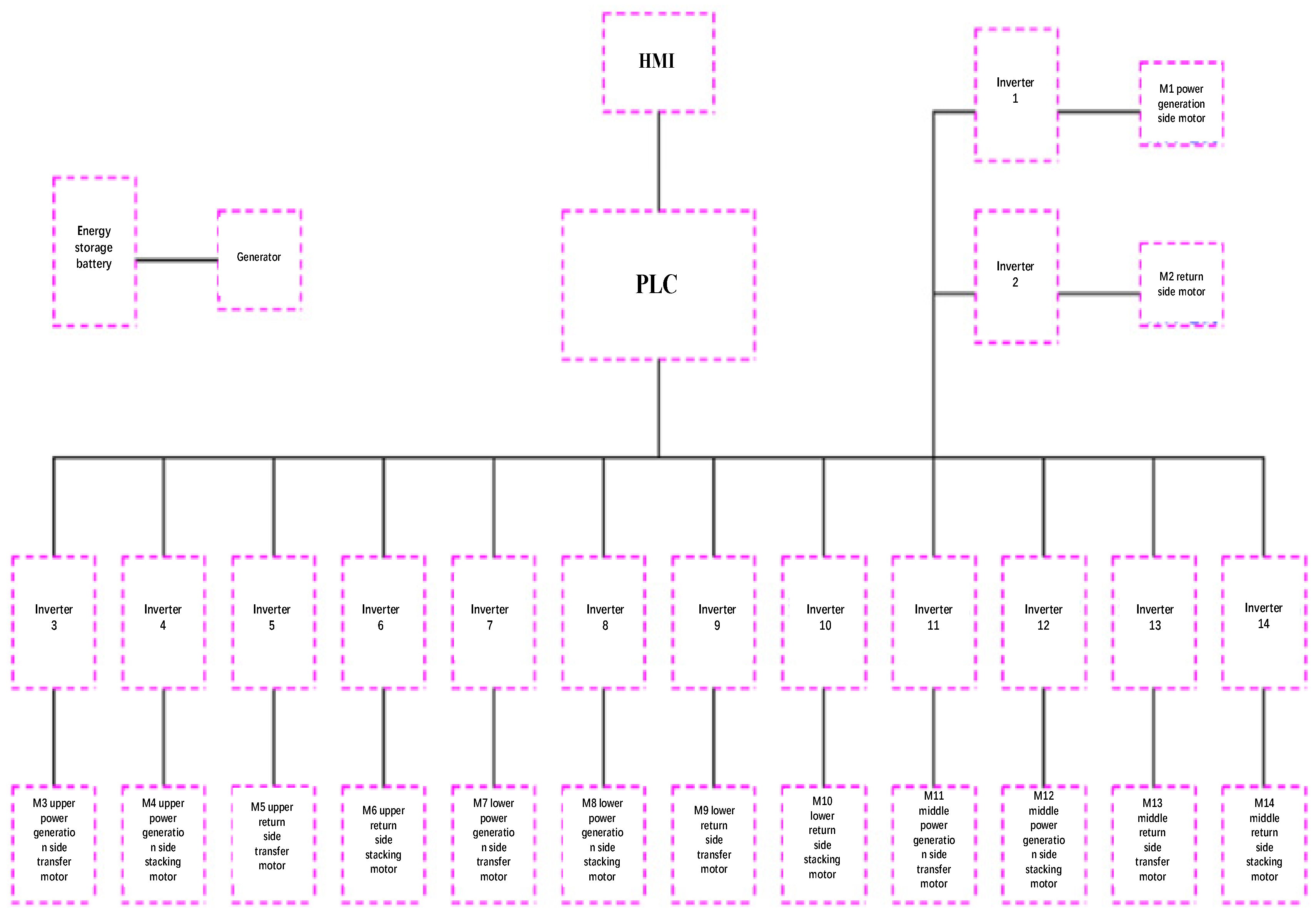
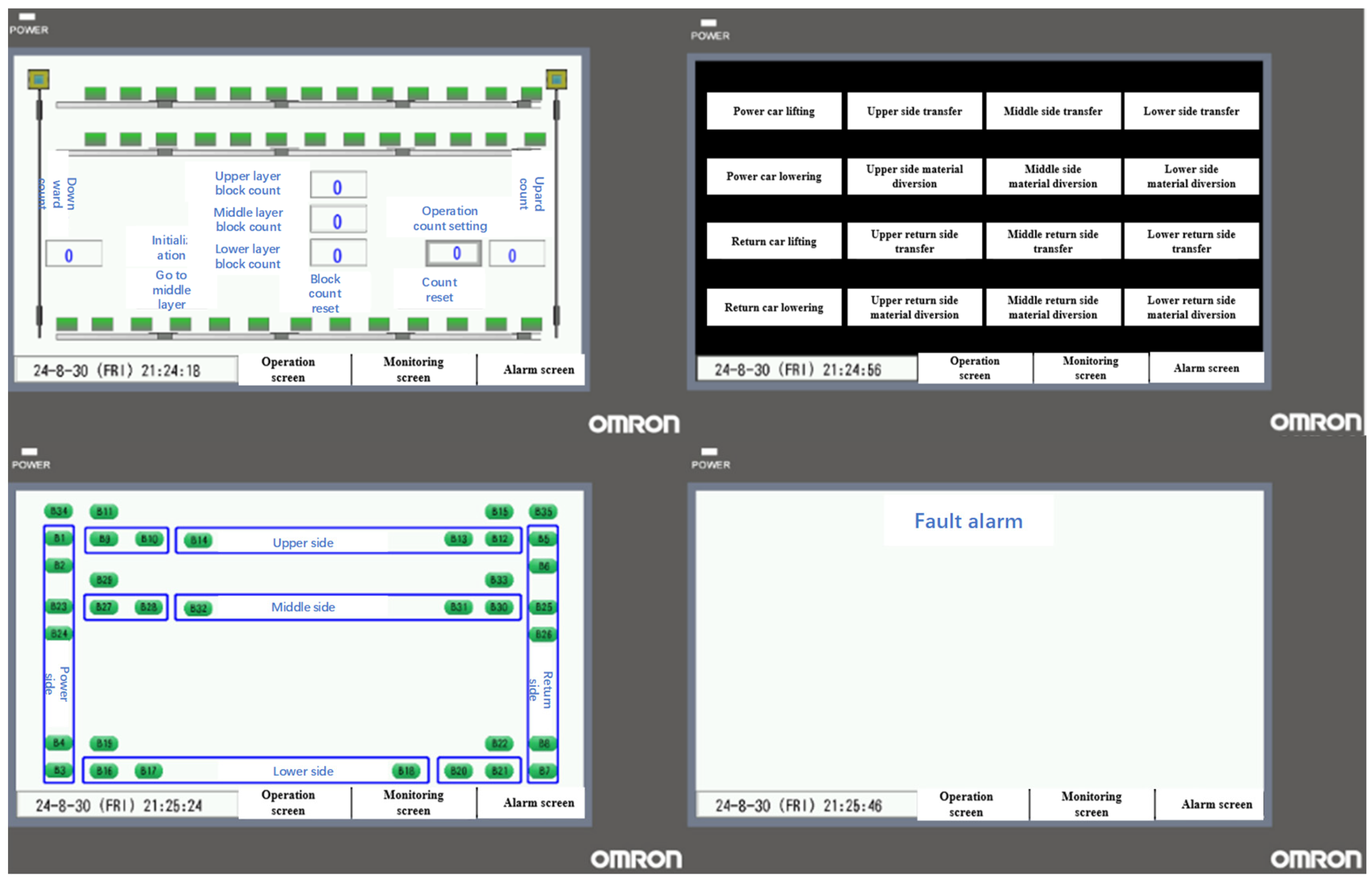
2.3. Experiment Method and Procedure

Based on the gravity energy storage conversion theory and the field conditions of the Tianjin Tang International Container Terminal, a model experiment design is conducted. The design uses a framework-type gravity energy storage system. In this experiment, the framework part of the framework-type gravity energy storage structure exhibits clear structural features, as shown in Figure 12. Its length is 3 m, with a maximum width of 1 m and a height of 6 m. The entire structure is made of square steel pipes welded together, with a total weight of 4 tons.

Before starting the experiment, the model system must be debugged. Through the monitoring of the PLC control system, it is essential to ensure the stable coordination between all internal components and between the motors and sensors, thereby avoiding mechanical failures and control malfunctions. A micro-range ammeter is used to collect electricity consumption during the experiment, and capacitors are used to collect the power generation data throughout the process. The debugging is considered complete when the variations in the fixed number of operations become minimal, indicating that the system is functioning correctly.

The “Double Layer Single Height Difference” model experiment operates on the same principle as the “Single Layer Double Height Difference” model experiment. The difference lies in the control of the mechanical operation time under the double-cycle setup. Since there is an error between the actual mechanical operation time and the theoretical calculation value, debugging is required before conducting the “Double Layer Single Height Difference” model experiment. This involves extensive testing and adjustments until seamless operation between all components is achieved. The experimental operation principle is shown in Figure 13.

3. The Influence of the Weight of the Load and the Height of the Descent Section on Power Generation Efficiency

In the energy release generation segment of gravitational energy storage, the motion is considered as free fall, with acceleration approximately equal to the gravitational acceleration (g). This results in a rapid increase in speed, reaching high values in a very short time, which poses safety risks. Therefore, long-distance free-fall motion cannot be sustained. During operation, velocity control is required once a maximum safe speed is reached. Considering the power generation efficiency discussed earlier, the motion of the load in the generation segment is divided into the following four stages.

Stage 1: The load begins to move downward from the upper energy storage chamber. This motion is uniformly accelerated with a downward acceleration, continuing until the speed exceeds 2.1 m/s.

Stage 2: The load continues to move downward in the vertical direction, maintaining a moderate speed above 2.1 m/s, until it reaches a height of 0.5 m from the ground.

Stage 3: The load enters the deceleration phase, and the motion continues until the speed of the load reaches 2.1 m/s.

Stage 4: The load undergoes final deceleration until it comes to a complete stop upon reaching the ground.

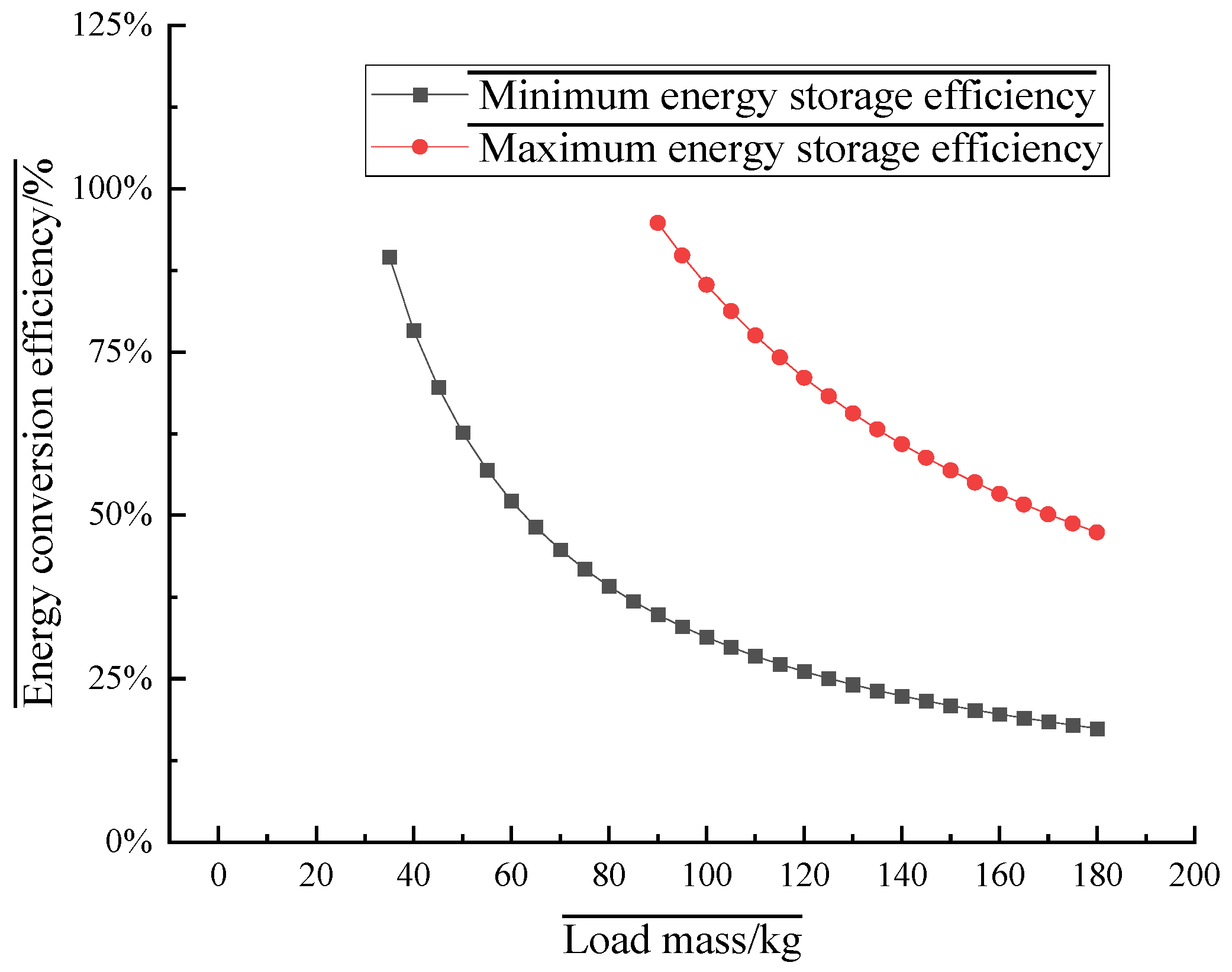
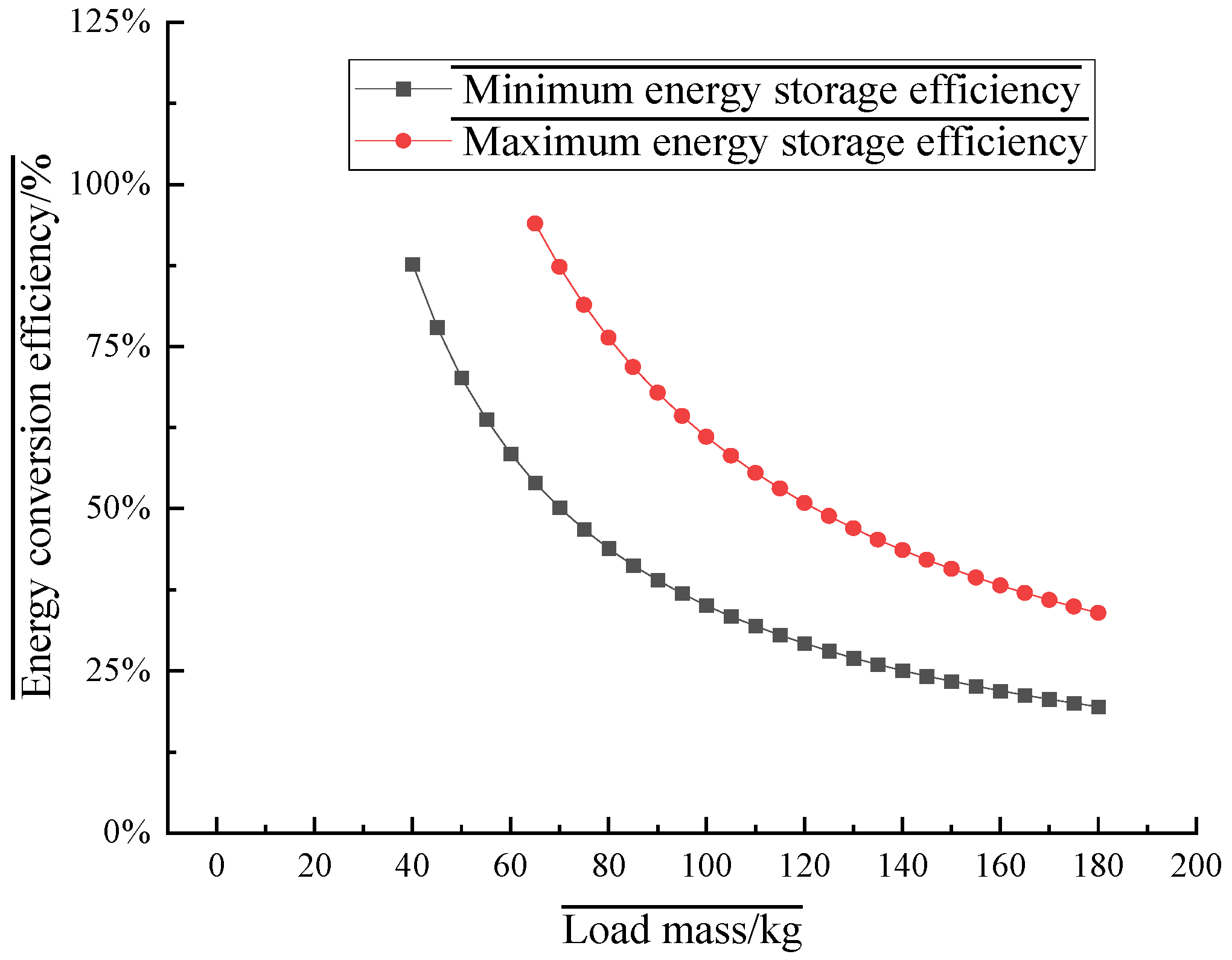
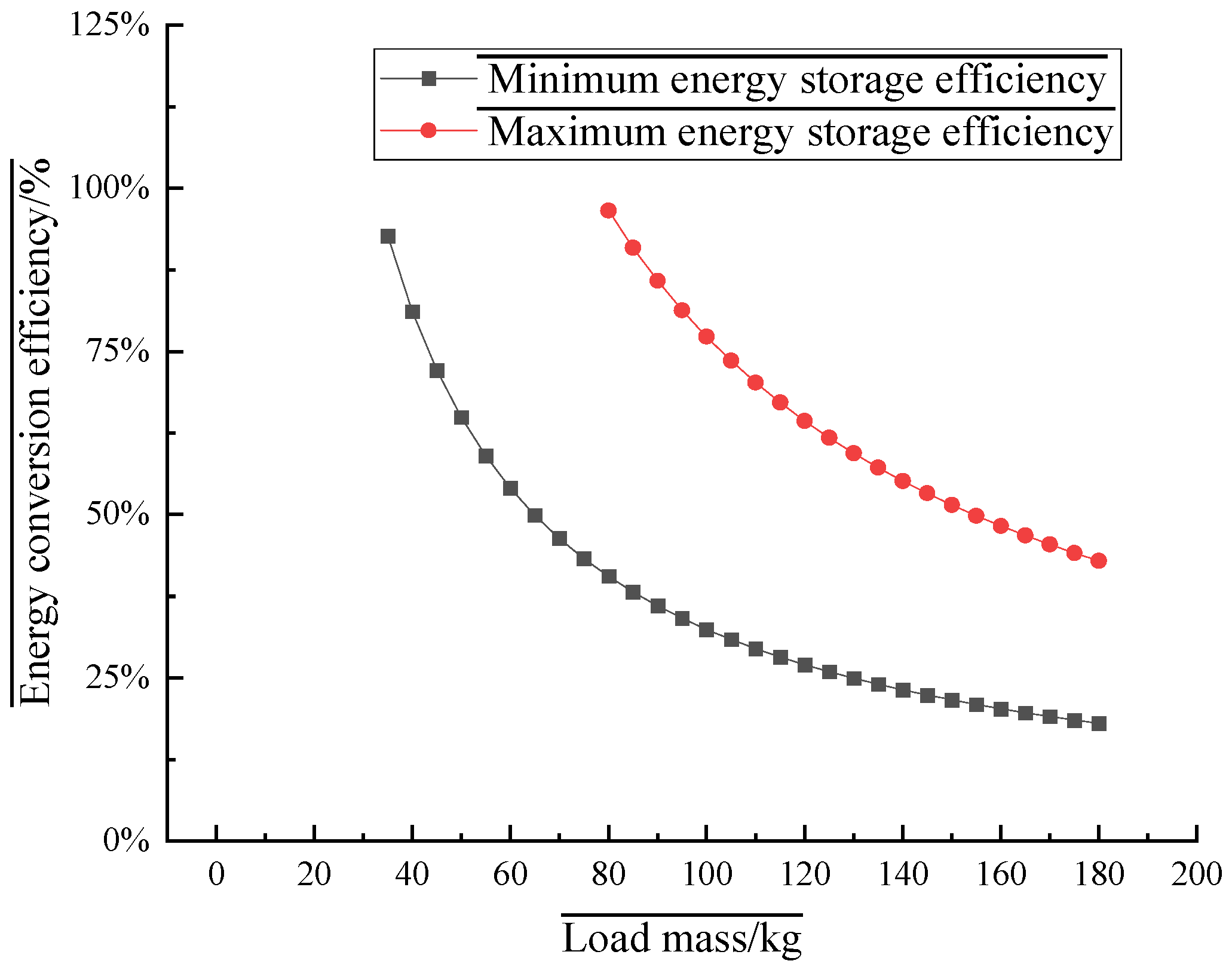
3.1. The Influence of Load Weight on Power Generation Efficiency

In the gravitational energy storage process, the stored energy is the gravitational potential energy of the load, which is related to both the storage height and the load mass. For a fixed height, the larger the mass of the load, the greater the stored energy; conversely, the smaller the load mass, the smaller the stored energy. However, the amount of electricity generated depends only on the operating parameters of the motor. Within a certain range, the greater the speed at which the load descends, the higher the power generation efficiency. Once the maximum efficiency is reached, the power generation efficiency becomes constant. Therefore, when the mass exceeds a certain threshold, the energy storage efficiency of gravitational energy storage significantly decreases, making it unfeasible. Hence, it is crucial to investigate the relationship between load mass and power generation efficiency.

Based on the theoretical calculation method outlined in Section 2.2, the energy storage efficiency of different mass loads descending under the same generator is calculated. The comparison and analysis of the results will allow us to draw conclusions.

By analyzing the data on the power generation efficiency of loads of different masses under the same generator conditions in Appendix A

Table A1. Power generation efficiency of different mass loads under the same generator (own authorship).

t2 (s)	t3 (s)	M (kg)	WG (J)	Tmin (s)	Tmax (s)	WPmin (J)	WPmax (J)	ηmin	ηmax
0.845	0.077	5	294.3	0.922	2.51	1844	5020	-	-
0.845	0.077	10	588.6	0.922	2.51	1844	5020	-	-
0.845	0.077	15	882.9	0.922	2.51	1844	5020	-	-
0.845	0.077	20	1177.2	0.922	2.51	1844	5020	-	-
0.845	0.077	25	1471.5	0.922	2.51	1844	5020	-	-
0.845	0.077	30	1765.8	0.922	2.51	1844	5020	-	-
0.845	0.077	35	2060.1	0.922	2.51	1844	5020	89.51%	-
0.845	0.077	40	2354.4	0.922	2.51	1844	5020	78.32%	-
0.845	0.077	45	2648.7	0.922	2.51	1844	5020	69.62%	-
0.845	0.077	50	2943	0.922	2.51	1844	5020	62.66%	-
0.845	0.077	55	3237.3	0.922	2.51	1844	5020	56.96%	-
0.845	0.077	60	3531.6	0.922	2.51	1844	5020	52.21%	-
0.845	0.077	65	3825.9	0.922	2.51	1844	5020	48.20%	-
0.845	0.077	70	4120.2	0.922	2.51	1844	5020	44.76%	-
0.845	0.077	75	4414.5	0.922	2.51	1844	5020	41.77%	-
0.845	0.077	80	4708.8	0.922	2.51	1844	5020	39.16%	-
0.845	0.077	85	5003.1	0.922	2.51	1844	5020	36.86%	-
0.845	0.077	90	5297.4	0.922	2.51	1844	5020	34.81%	94.76%
0.845	0.077	95	5591.7	0.922	2.51	1844	5020	32.98%	89.78%
0.845	0.077	100	5886	0.922	2.51	1844	5020	31.33%	85.29%
0.845	0.077	105	6180.3	0.922	2.51	1844	5020	29.84%	81.23%
0.845	0.077	110	6474.6	0.922	2.51	1844	5020	28.48%	77.53%
0.845	0.077	115	6768.9	0.922	2.51	1844	5020	27.24%	74.16%
0.845	0.077	120	7063.2	0.922	2.51	1844	5020	26.11%	71.07%
0.845	0.077	125	7357.5	0.922	2.51	1844	5020	25.06%	68.23%
0.845	0.077	130	7651.8	0.922	2.51	1844	5020	24.10%	65.61%
0.845	0.077	135	7946.1	0.922	2.51	1844	5020	23.21%	63.18%
0.845	0.077	140	8240.4	0.922	2.51	1844	5020	22.38%	60.92%
0.845	0.077	145	8534.7	0.922	2.51	1844	5020	21.61%	58.82%
0.845	0.077	150	8829	0.922	2.51	1844	5020	20.89%	56.86%
0.845	0.077	155	9123.3	0.922	2.51	1844	5020	20.21%	55.02%
0.845	0.077	160	9417.6	0.922	2.51	1844	5020	19.58%	53.30%
0.845	0.077	165	9711.9	0.922	2.51	1844	5020	18.99%	51.69%
0.845	0.077	170	10,006.2	0.922	2.51	1844	5020	18.43%	50.17%
0.845	0.077	175	10,300.5	0.922	2.51	1844	5020	17.90%	48.74%
0.845	0.077	180	10,594.8	0.922	2.51	1844	5020	17.40%	47.38%

t₂: Power generation time in the acceleration phase; t₃: power generation time in the deceleration phase; M: load mass; W_G: gravitational potential energy of the load; T_min: shortest power generation time; T_max: longest power generation time; W_Pmin: minimum power generation; W_Pmax: maximum power generation; η_min: minimum energy storage efficiency; η_max: maximum energy storage efficiency. Same as in Table A2 and Table A3.

, and the energy conversion efficiency of the load during the load descent phase at a fixed height shown in Figure 14, it can be seen that there is a significant relationship between the mass of the load and the energy conversion efficiency of the system. The detailed analysis results are as follows:

The data in Appendix A Table A1 shows that the gravitational potential energy (WG) stored by the system tends to increase linearly as the load mass increases. For example, when the load mass is 5 kg, the gravitational potential energy is 294.3 J, whereas when the mass is increased to 180 kg, the potential energy is increased to 10,594.8 J. This indicates that a larger load mass leads to a higher theoretical energy conversion potential. However, from the minimum and maximum energy conversion efficiencies in the table, the actual conversion efficiencies show a non-linear trend with mass change.

The system exhibits high energy conversion efficiencies over a small mass load range (e.g., 5 kg to 20 kg). For example, at a load of 5 kg, the minimum efficiency is 89.51%, and the maximum efficiency is as high as 170.57%, which indicates that even with a small input energy, the system can still achieve a high output efficiency due to a short release time. When the load is increased to 20 kg, the potential energy increases to 1177.2 J, while the maximum efficiency remains high at 118.50 per cent.

In the medium mass range (e.g., 30–80 kg), the system still maintains strong conversion performance, but the maximum efficiency shows a gradual decrease. For example, the maximum efficiency drops to 94.76% at 50 kg load and further drops to 60.22% at 80 kg. This indicates that as the mass increases, frictional resistance, generator losses, and other mechanical constraints begin to have a significant impact on energy conversion.

For high-quality loads (greater than 100 kg), the trend of decreasing minimum and maximum efficiencies is even more pronounced. For example, the maximum conversion efficiency drops to 47.30 per cent at 100 kg load and only 47.38 per cent at 180 kg. Meanwhile, the minimum efficiency drops from 31.33% at 100 kg to 17.40% at 180 kg. Figure 14 clearly shows this trend, i.e., both the minimum and maximum efficiencies decrease significantly as the load mass increases, indicating that the energy losses in the system gradually dominate, which may originate from the losses within the machinery or from the conversion limitations of the generator.

Therefore, although increasing the load mass can enhance the gravitational potential energy of the system, the marginal gain in energy conversion efficiency decreases rapidly above a certain mass threshold. Taken together, the optimal operating range of the system lies roughly between 15 kg and 60 kg, within which the input energy and conversion efficiency can be better balanced. The above analyses show that the proper selection of the load mass is crucial when designing a gravity-based energy storage system. Too light a load will result in insufficient energy storage, while too heavy a load will result in a loss of efficiency due to system limitations. In order to achieve the optimal use of energy and maximize the conversion performance, the mass range of the load must be scientifically determined.

There is a certain relationship between the load mass and power generation efficiency. When the load mass is small, the power generation efficiency is low. However, as the mass increases, both the energy storage and power generation efficiency significantly improve. Once the mass exceeds a certain threshold, the improvement in power generation efficiency gradually weakens and may even begin to decrease. Therefore, when designing a framework-based gravitational energy storage system, it is essential to consider both the load mass and the system’s energy storage efficiency to optimize system performance and enhance overall efficiency [28].

The main reason for the energy storage efficiency exceeding 100% (data in excess of 100% have been replaced with—in the Appendix A tables) is that when the mass of the weight is light, it is difficult to overcome the initial friction and inertial resistance of the system by its own weight, and thus the experimental system cannot be started smoothly. In order to ensure the normal conduct of the experiment, we used manual assistance to start the system at the initial stage of the weight descent, and this part of the energy input was not accurately counted in the calculation formula, which led to some experimental data showing energy storage efficiency exceeding 100% when the efficiency was calculated in the subsequent period. Therefore, such efficiency exceeding the standard is the result of theoretical calculation, which is not a true reflection of the system performance, and the fundamental reason is that the manually assisted energy input at the early stage of the experiment is not accurately quantified and deducted.

3.2. The Influence of the Acceleration Descent Height on Power Generation Efficiency at the Same Height

In the above conditions, the descent height of the load is 5.5 m. This section analyzes the descent heights of 4 m and 5 m and compares them with the 5.5 m descent. The impact of the acceleration descent height on power generation efficiency at the same height is analyzed to explore the variation patterns.

In this section, the impact of load descent height on power generation efficiency is investigated, with a particular focus on the effect of the acceleration descent phase on the system’s energy storage efficiency. By comparing power generation efficiency data for different descent heights (4 m, 5 m, and 5.5 m), and analyzing the energy storage efficiency graphs in Figure 15 and Figure 16 for descent heights of 4 m and 5 m, the following conclusions are drawn:

The data in Appendix A 

Table A2. The power generation efficiency of different mass loads at an acceleration descent height of 4 m (own authorship).

t2 (s)	t3 (s)	M (kg)	WG (J)	Tmin (s)	Tmax (s)	WPmin (J)	WPmax (J)	ηmin	ηmax
0.689	0.344	5	294.3	1.033	1.798	2066	3596	-	-
0.689	0.344	10	588.6	1.033	1.798	2066	3596	-	-
0.689	0.344	15	882.9	1.033	1.798	2066	3596	-	-
0.689	0.344	20	1177.2	1.033	1.798	2066	3596	-	-
0.689	0.344	25	1471.5	1.033	1.798	2066	3596	-	-
0.689	0.344	30	1765.8	1.033	1.798	2066	3596	-	-
0.689	0.344	35	2060.1	1.033	1.798	2066	3596	-	-
0.689	0.344	40	2354.4	1.033	1.798	2066	3596	87.75%	-
0.689	0.344	45	2648.7	1.033	1.798	2066	3596	78.00%	-
0.689	0.344	50	2943	1.033	1.798	2066	3596	70.20%	-
0.689	0.344	55	3237.3	1.033	1.798	2066	3596	63.82%	-
0.689	0.344	60	3531.6	1.033	1.798	2066	3596	58.50%	-
0.689	0.344	65	3825.9	1.033	1.798	2066	3596	54.00%	93.99%
0.689	0.344	70	4120.2	1.033	1.798	2066	3596	50.14%	87.28%
0.689	0.344	75	4414.5	1.033	1.798	2066	3596	46.80%	81.46%
0.689	0.344	80	4708.8	1.033	1.798	2066	3596	43.88%	76.37%
0.689	0.344	85	5003.1	1.033	1.798	2066	3596	41.29%	71.88%
0.689	0.344	90	5297.4	1.033	1.798	2066	3596	39.00%	67.88%
0.689	0.344	95	5591.7	1.033	1.798	2066	3596	36.95%	64.31%
0.689	0.344	100	5886	1.033	1.798	2066	3596	35.10%	61.09%
0.689	0.344	105	6180.3	1.033	1.798	2066	3596	33.43%	58.18%
0.689	0.344	110	6474.6	1.033	1.798	2066	3596	31.91%	55.54%
0.689	0.344	115	6768.9	1.033	1.798	2066	3596	30.52%	53.13%
0.689	0.344	120	7063.2	1.033	1.798	2066	3596	29.25%	50.91%
0.689	0.344	125	7357.5	1.033	1.798	2066	3596	28.08%	48.88%
0.689	0.344	130	7651.8	1.033	1.798	2066	3596	27.00%	47.00%
0.689	0.344	135	7946.1	1.033	1.798	2066	3596	26.00%	45.25%
0.689	0.344	140	8240.4	1.033	1.798	2066	3596	25.07%	43.64%
0.689	0.344	145	8534.7	1.033	1.798	2066	3596	24.21%	42.13%
0.689	0.344	150	8829	1.033	1.798	2066	3596	23.40%	40.73%
0.689	0.344	155	9123.3	1.033	1.798	2066	3596	22.65%	39.42%
0.689	0.344	160	9417.6	1.033	1.798	2066	3596	21.94%	38.18%
0.689	0.344	165	9711.9	1.033	1.798	2066	3596	21.27%	37.03%
0.689	0.344	170	10,006.2	1.033	1.798	2066	3596	20.65%	35.94%
0.689	0.344	175	10,300.5	1.033	1.798	2066	3596	20.06%	34.91%
0.689	0.344	180	10,594.8	1.033	1.798	2066	3596	19.50%	33.94%

and

Table A3. The power generation efficiency of different mass loads at an acceleration descent height of 5 m (own authorship).

t2 (s)	t3 (s)	M (kg)	WG (J)	Tmin (s)	Tmax (s)	WPmin (J)	WPmax (J)	ηmin	ηmax
0.796	0.159	5	294.3	0.955	2.274	1910	4548	-	-
0.796	0.159	10	588.6	0.955	2.274	1910	4548	-	-
0.796	0.159	15	882.9	0.955	2.274	1910	4548	-	-
0.796	0.159	20	1177.2	0.955	2.274	1910	4548	-	-
0.796	0.159	25	1471.5	0.955	2.274	1910	4548	-	-
0.796	0.159	30	1765.8	0.955	2.274	1910	4548	-	-
0.796	0.159	35	2060.1	0.955	2.274	1910	4548	92.71%	-
0.796	0.159	40	2354.4	0.955	2.274	1910	4548	81.12%	-
0.796	0.159	45	2648.7	0.955	2.274	1910	4548	72.11%	-
0.796	0.159	50	2943	0.955	2.274	1910	4548	64.90%	-
0.796	0.159	55	3237.3	0.955	2.274	1910	4548	59.00%	-
0.796	0.159	60	3531.6	0.955	2.274	1910	4548	54.08%	-
0.796	0.159	65	3825.9	0.955	2.274	1910	4548	49.92%	-
0.796	0.159	70	4120.2	0.955	2.274	1910	4548	46.36%	-
0.796	0.159	75	4414.5	0.955	2.274	1910	4548	43.27%	-
0.796	0.159	80	4708.8	0.955	2.274	1910	4548	40.56%	96.59%
0.796	0.159	85	5003.1	0.955	2.274	1910	4548	38.18%	90.90%
0.796	0.159	90	5297.4	0.955	2.274	1910	4548	36.06%	85.85%
0.796	0.159	95	5591.7	0.955	2.274	1910	4548	34.16%	81.33%
0.796	0.159	100	5886	0.955	2.274	1910	4548	32.45%	77.27%
0.796	0.159	105	6180.3	0.955	2.274	1910	4548	30.90%	73.59%
0.796	0.159	110	6474.6	0.955	2.274	1910	4548	29.50%	70.24%
0.796	0.159	115	6768.9	0.955	2.274	1910	4548	28.22%	67.19%
0.796	0.159	120	7063.2	0.955	2.274	1910	4548	27.04%	64.39%
0.796	0.159	125	7357.5	0.955	2.274	1910	4548	25.96%	61.81%
0.796	0.159	130	7651.8	0.955	2.274	1910	4548	24.96%	59.44%
0.796	0.159	135	7946.1	0.955	2.274	1910	4548	24.04%	57.24%
0.796	0.159	140	8240.4	0.955	2.274	1910	4548	23.18%	55.19%
0.796	0.159	145	8534.7	0.955	2.274	1910	4548	22.38%	53.29%
0.796	0.159	150	8829	0.955	2.274	1910	4548	21.63%	51.51%
0.796	0.159	155	9123.3	0.955	2.274	1910	4548	20.94%	49.85%
0.796	0.159	160	9417.6	0.955	2.274	1910	4548	20.28%	48.29%
0.796	0.159	165	9711.9	0.955	2.274	1910	4548	19.67%	46.83%
0.796	0.159	170	10,006.2	0.955	2.274	1910	4548	19.09%	45.45%
0.796	0.159	175	10,300.5	0.955	2.274	1910	4548	18.54%	44.15%
0.796	0.159	180	10,594.8	0.955	2.274	1910	4548	18.03%	42.93%

show that the height of the acceleration descent phase has a significant effect on the power generation efficiency under the same load mass conditions. With the change in descent height, the power generation efficiency shows a corresponding trend: the change in descent time directly affects the process of energy release and storage, which triggers the fluctuation of energy conversion efficiency. Comparing the acceleration descent heights of 4 m and 5 m, the latter is superior in overall power generation efficiency due to its higher gravitational potential energy.

When the load is accelerated down to a height of 4 m, it can be seen from Appendix A Table A2 that the overall energy release efficiency is low due to the relatively low gravitational potential energy. At this height, although a high maximum energy conversion efficiency can still be obtained for small load masses (e.g., 5 kg and 10 kg), for example, the maximum energy conversion efficiency reaches 87.75% for a 5 kg load, and the efficiency decreases significantly as the mass increases. For example, the maximum energy conversion efficiency is only 33.94% for a 180 kg load. This trend shows that the increase in load mass increases the energy loss of the system and reduces the overall power generation efficiency.

In contrast, when the acceleration drop height was increased to 5 m, the data in Appendix A Table A3 show a significant improvement in power generation efficiency. Due to the larger potential energy reserve, the system is able to more fully convert mechanical energy into electrical energy, resulting in higher power generation efficiency under the same load condition. For example, the maximum energy conversion efficiency reaches 92.71% at 5 kg load, while the efficiency at 180 kg load is also improved to 42.93%. This indicates that the energy conversion capability of the system at 5 m height is better than that at 4 m height in the full mass range, and the efficiency improvement is especially obvious under large mass loads, which shows higher potential for energy release.

After further elevation to the 5.5 m descent height (see Appendix A Table A2 and Table A3 with Figure 15 and Figure 16 for details), the system’s power generation performance is again enhanced due to the further increase in gravitational potential energy. The data show that at a 5.5 m drop height, not only is the power generation increased, but also the energy output per unit time is more efficient. For example, at a 150 kg load, the maximum energy conversion efficiency reaches approximately 96%, a significant increase compared to the 5 m height. This enhanced efficiency is mainly attributed to the longer acceleration fall time, which allows the power generation system to convert energy in a more stable and adequate manner. This advantage is particularly noticeable under large mass loads, demonstrating the importance of high potential energy release for the overall energy conversion system.

A synthesis of the data analyzed in the Appendix A tables and figures shows that the acceleration descent height has a decisive influence on the energy conversion efficiency of the power generation system. Higher descent height provides more gravitational potential energy, which enhances the system’s power generation capacity per unit time. This effect is particularly significant in the medium and high mass load intervals, while it is relatively insensitive under small mass load conditions. Therefore, the descent height parameter should be fully considered in the system design stage, and the descent path and time should be reasonably designed to maximize the power generation efficiency and optimize the overall energy conversion performance of the system.

4. Conclusions

In this study, the application and performance optimization of the framework-based gravitational energy storage system not only demonstrate its potential in zero-carbon ports but also further promote the concept of sustainable development. As global attention to environmental protection and energy efficiency continues to grow, the framework-based gravitational energy storage system, as an innovative energy storage technology, exhibits characteristics highly aligned with the sustainable development goals. This is particularly true in ports, which are energy-intensive environments, where it can provide effective and practical green energy solutions. The following key conclusions have been drawn in this paper:

a.

The Synergistic Development of the Framework-Based Gravitational Energy Storage System and Zero-Carbon Ports: The application of the framework-based gravitational energy storage system not only meets the port’s need for a stable energy supply but also helps achieve a green and low-carbon transformation. By utilizing containers, an existing resource, the system efficiently stores and releases energy in space-limited environments such as ports, avoiding the large-scale consumption of new resources. This approach aligns with the principles of efficient resource utilization and green design. The system reduces dependence on traditional high-carbon energy sources while also minimizing the demand for new materials, thus lowering carbon emissions and resource waste.

b.

Optimization of Load Mass and Storage Height Promotes Sustainable Development: The experimental results in this paper indicate that load mass and storage height significantly affect the system’s power generation and storage efficiency. By reasonably selecting load mass and storage height, the energy storage efficiency can be improved, and the system’s stability and reliability during long-term operation can be ensured. This optimization design maximizes the utilization of limited resources by improving energy efficiency, reducing energy waste, and aligning with the goals of sustainable energy management.

c.

The Feasibility and Stability of the System Support Green Energy Applications: Through experimental schemes involving the “Double Layer Single Height Difference” and “Single Layer Double Height Difference” structures, this paper validates the performance of the framework-based gravitational energy storage system under different configurations, particularly highlighting the superior performance of the “Double Layer Single Height Difference” structure in reducing empty cabin motion. This design further enhances the system’s energy efficiency, ensures minimal energy loss during the storage process, and guarantees efficient energy utilization. It provides a practical solution for the green and sustainable energy supply for ports and surrounding areas.

d.

Advantages of the Framework-Based Gravitational Energy Storage System in Environmental Friendliness: The system effectively integrates with the existing infrastructure and equipment of ports, utilizing containers as a renewable resource and reducing the environmental cost of load procurement and manufacturing. This not only minimizes unnecessary resource consumption but also avoids pollution and emissions during the manufacturing process, making it an environmentally friendly energy storage technology. The implementation of the framework-based gravitational energy storage system reflects the principles of green design and circular economy, driving the development of environmentally friendly technologies in ports and other related industries.

In summary, the framework-based gravitational energy storage system not only provides an efficient and reliable energy solution for zero-carbon ports but also plays a significant role in achieving the goals of sustainable development. By optimizing the system structure and control methods, energy storage efficiency has been improved, and dependence on high-carbon energy sources has been reduced, offering strong support for the widespread application of green energy. This innovative technology not only contributes to driving the green transformation of the port industry but also promotes the low-carbon and sustainable use of energy on a global scale, supporting long-term environmental protection and climate change mitigation goals.

Ideally, with modular expansion, optimized descent trajectories, and matching of efficient generators, the power and storage capacity of the system can be adjusted on demand, making it suitable for different scales of energy storage needs. However, the actual expansion process needs to consider terrain adaptability, construction costs, mechanical losses, and environmental impacts to ensure economy and sustainability. Future research directions could further explore material optimization, intelligent control systems, and multi-energy complementary strategies to improve the adaptability and scalability of the system, making it an important candidate for large-scale energy storage.

Although this study verifies the feasibility and advantages of a frame-based gravity energy storage system in a zero-carbon port, there is still room for further optimization and expansion. Future research can focus on the following aspects: (1) in-depth study of the system’s adaptability under different climatic conditions and port operation modes in order to improve its potential for global dissemination; (2) optimization of the scheduling strategy by combining intelligent control algorithms and artificial intelligence in order to enhance the system’s operational efficiency and intelligence; and (3) exploration of synergistic integration with other renewable energy sources (e.g., wind and solar) modes to further enhance the stability of the system and comprehensive energy utilization efficiency. These research directions will help to promote the development of frame-type gravity energy storage technology and provide a more complete solution for zero-carbon harbors and other sustainable energy applications.