Evolutionary Game Analysis of Remanufacturing Closed-Loop Supply Chain with Asymmetric Information

Abstract

Remanufacturing is an effective means to realize energy saving and emission reduction. This paper develops an evolutionary game model with a two-echelon closed-loop supply chain to study evolutionary stable strategies (ESS) of manufacturers and retailers. Through analyzing evolutionary path of the game, we find that there are two possible evolutionary results affected by the profits of manufacturers. Price of remanufacturing products may be a critical factor that determines the ESS. Government subsidy is critical to promote the development of remanufacturing industry.

1. Introduction

More and more attention has been paid to low-carbon economy in recent years. As the main carriers of energy consumption and carbon emission, enterprises have to combine their business decisions with low-carbon economy goals in the era of low-carbon economy. Remanufacturing of recycled products is one such decision.

Through remanufacturing of recycled products, enterprises can, not only fully use the resources, but also cut down the procurement cost and energy consumption. It is obvious that remanufacturing can bring both economic and environmental benefits. Remanufacturing is a process of restoring end-of-used or end-of-life products, components, modules, and parts to like-new condition in a manufacturing environment [1]. In the whole life-cycle of a product, carbon emission mainly comes from the process of original manufacturing. Remanufacturing not only has the positive carbon emission effect, but also provides the potential economic opportunities. These mainly include the reduction of procurement cost and energy consumption. To win more market share by good environmental image is another benefit of remanufacturing [2] A great deal of statistical data also indicate that remanufacturing is an effective means to realize the low-carbon economy. For example, quality and performance of remanufacturing products are not inferior to new products, but the cost of remanufacturing is only 50% of the cost of original manufacturing. In addition, remanufacturing can save 60% energy and 70% raw materials compared with original manufacturing. It is obvious that remanufacturing reduces adverse effect effectively to our environment [2,3,4,5].

The first step of remanufacturing technological process is recycling waste products. Especially, if the waste products can be recycled for remanufacturing new products, the corresponding supply chain of the product is called remanufacturing closed-loop supply chain. Remanufacturing closed-loop supply chain has attracted more and more attention from enterprises. Many companies, such as IBM, Ford, Kodak, Xerox, Caterpillar, Muji, and Timberland, have established remanufacturing and recycling systems, and achieved important successes.

There are also many academic research on remanufacturing closed-loop supply chain. Krikke et al. [6] considered the goal of closed-loop supply chain is to reduce waste emissions and provide low cost service to customers by products’ remanufacturing. Savaskan et al. [7] analyzed the operation problem of a closed-loop supply chain under the situation of remanufacturing. Savaskan et al. [8] studied the influence of the reverse channel selection to remanufacturing activities by investigating the interaction between the reverse channel selection and price decision-making in the forward channel. Paksoy et al. [9] considered a closed-loop supply chain network problem, which is related to the trade-offs between operational and environmental performance measures. Choi et al. [10] considered a supply chain consisting of a retailer, a collector, and a manufacturer. They examined the performance of different closed-loop supply chains under different channels of leadership. Many scholars also studied the production planning in remanufacturing closed-loop supply chain [1,11,12,13,14], the relation between closed-loop supply chains [15], the inventory of recycled goods [16,17], the location and sorting of collection points [18], and the selection of buyback strategies [19]. Some researchers incorporated the influence of government policy into their models. Choi [20] studied how to design a carbon footprint taxation scheme to enhance a quick response system’s environmental sustainability, such as employing a local manufacturer. Choi [21] studied a multi-stage optimal supplier selection problem in the fashion-apparel supply chain carbon emission tax. Mitra et al. [22] studied the two periods competing model and the effects of government subsidies. They found that different subsidy strategies have different effect on manufacturing and remanufacturing activities. Li et al. [23] considered the carbon emission effect on the basis of economic benefits of remanufacturing closed-loop supply chain. They analyzed the impact of government subsidy on the profits and carbon emission.

The above articles related to remanufacturing closed-loop supply chain always considers economic and environmental benefits within short term, while there are also some papers studying remanufacturing closed-loop supply chain within long term. Han and Xue [24] studied the decision problem of recycling channel with competing manufacturers by evolutionary game theory. They focused on the effect of government financial subsidy to recycling channels’ evolutionary stable strategies (ESS). Dong [25] used the evolutionary game theory to study the process of making independent decision of the supplier in reverse supply chain. Then the author analyzed the effect of government’s measures to supplier’s decision. The above-mentioned literature mainly considered symmetric situation of small population difference. And the research on asymmetric situation of big population difference is sparse.

Motivated by the above observations, we set out to study the evolutionary game between manufacturers and retailers of remanufacturing closed-loop supply chain under asymmetric situation in a long term. We intend to contribute to knowledge in this area by address two key questions: What is the evolutionary path of the game in the two-echelon closed-loop supply chain? What is the impact of the government subsidy on the development of remanufacturing industry? This paper provides valuable managerial guidance to promote the development of remanufacturing industry. Specially, we make the following major contributions. We develop an evolutionary game model and find that there are two possible evolutionary results affected by the profits of manufacturers. We found that government subsidy is critical to promote the development of remanufacturing industry.

The rest of the paper is organized as follows. Section 2 presents the evolutionary game model. Section 3 is dedicated to solve the model and find ESS of the model. Section 4 analyzes the impact of government subsidy on the model and ESS. Section 5 draws some conclusions and gives some directions for future research.

2. The Evolutionary Game Model

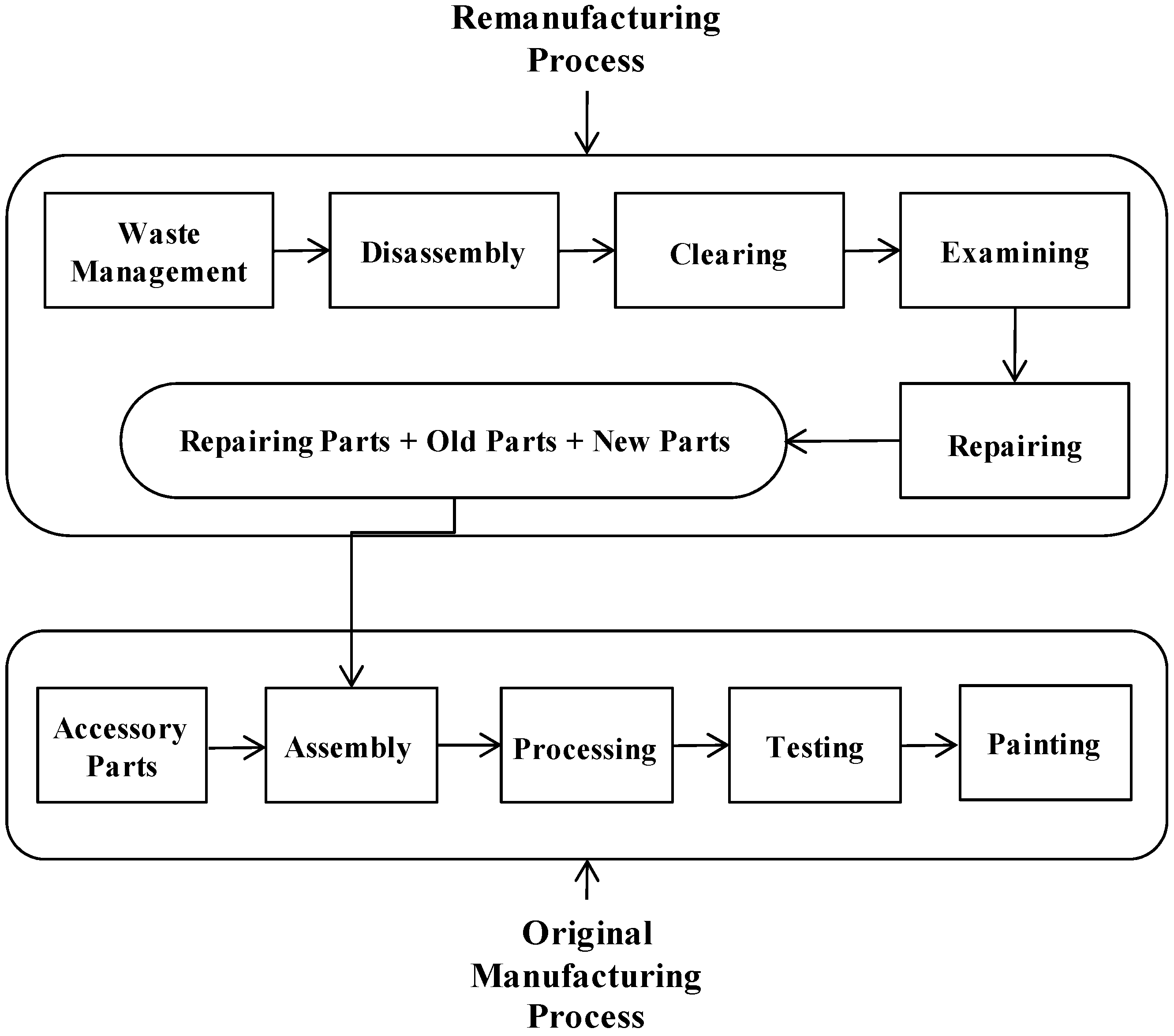
Remanufacturing has its specific technological process. Related analysis of remanufacturing closed-loop supply chain should be based on the process. The technological process of remanufacturing can be divided into five steps: waste recycling, waste examining, waste decomposition, components and parts remanufacturing, products manufacturing and testing by using remanufacturing parts. The technological process is depicted in Figure 1.

The first step of remanufacturing technological process is recycling waste products, and the reverse channel of recycling has a lot of choices, such as collecting by centrally coordinated system, or manufacturer, retailer and third party. Savaskan et al. [7] thought the closer an agent is to the market, the more efficient is the collection of waste products. In addition, the retailer has a higher marginal profitability than the case when the manufacturer or the third party is the collecting agents.

Figure 1. Remanufacturing technological process.

Figure 1. Remanufacturing technological process.

The following assumptions are used in this paper:

(1)

This paper considers a two-echelon closed-loop supply chain consisting of manufacturer population and retailer population. Retailers engage in recycling waste.

(2)

The qualities of the recycled products are the same.

(3)

The quality of remanufacturing products is the same as that of the new products. The market of remanufacturing products is in short of supply.

(4)

The price of remanufacturing products is lower than the price of new products.

(5)

It needs some new raw materials in remanufacturing.

The following notation is used in the model:

Cr	= unit cost of recycling waste products by the retailer;
Q	= quantity of recycled waste products;
Cb1	= procurement cost of new raw materials required by unit product in remanufacturing;
Cb2	= procurement cost of raw materials required by unit product in original manufacturing;
Cp	= cost of repairing a recycled waste product required by unit product in remanufacturing;
Cm	= unit cost of manufacturing of the manufacturer in original manufacturing;
p1	= unit price of the manufacturer to repurchase recycled waste products from the retailers;
p2	= wholesale price of a remanufacturing product;
p3	= wholesale price of a new product;

Obviously, we have C_b2 > C_b1, p₃ > p₂ > p₁.

This paper studies the evolutionary game between the manufactures and the retailers under asymmetric situation. The manufacturers make decisions after the retailer. The strategies and payoffs of the two players are different. We consider two pure strategies of the manufacturer and the retailer, respectively.

The retailer has two pure strategies:

• S_r1: recycle waste products.
• S_r2: not recycle waste products.

The manufacturer also has two pure strategies:

• S_m1: use the recycled waste products to remanufacture.
• S_m2: purchase new raw materials to manufacture directly.

The extended type of the game between a manufacturer and a retailer is depicted in Figure 2.

The strategy faced by the retailers is whether to recycle or not. Recycling waste products incurs recycling cost. Since the manufacturers may not purchase the recycled waste products from the retailers, the retailers take the risk of loss. Then the strategy faced by the manufacturers is whether to remanufacture by using the recycled waste product or not. The buyback cost of remanufacturing product is lower than the procurement cost of new product. Manufacturers assume cost such as disassembly cost, cleaning cost, inspection cost and so on if they adopt remanufacturing strategy. Let x be the individual ratio of the retailer population who takes recycle strategy. Then, 1-x is the remaining individuals who do not adopt recycle strategy. x satisfies the condition of 0 ≤ x ≤ 1. Similarly y represents the individual ratio of the manufacturer population who takes remanufacturing strategy. Then 1-y represents the remaining individuals who do not take remanufacturing strategy. y satisfies the condition of 0 ≤ y ≤ 1. The adjustment of strategies is a dynamic adjustment process. When expected benefits of the manufacturer or the retailer is lower than their average benefits, respectively, the two players will change their strategies in the next selection to choose the higher benefit.

Figure 2. The extended type of the game between a manufacturer and a retailer.

Figure 2. The extended type of the game between a manufacturer and a retailer.

The profit functions of the retailer are different. Firstly, when the retailer takes recycle strategy and the manufacturer takes remanufacturing strategy, the profit of the retailer is π_r1, π_r1 > 0. Secondly, when the retailer takes recycle strategy but the manufacturer does not take remanufacturing strategy, the profit of the retailer is π_r2, π_r2 < 0. Lastly, when the retailer does not take recycle strategy, the profit of the retailer is 0, whatever strategy does the manufacturer chooses.

π_r1 = p₁Q − C_rQ = (p₁ − C_r)Q

(1)

π_r2 = − C_rQ

(2)

When faced the same product demand, the profit functions of the manufacturer are different. π_m1 is the profit when the manufacturer takes remanufacturing strategy. π_m2 is the profit when the manufacturer takes original manufacturing strategy.

π_m1 = p₂Q − p₁Q − C_b1Q − C_pQ = (p₂ − p₁ − C_b1 − C_p)Q

(3)

π_m2 = p₃Q − C_b2Q − C_mQ = (p₃ − C_b2 − C_m)Q

(4)

The payoff bi-matrix consisting of different strategy combinations of a manufacturer and a retailer is listed in Table 1.

Let ES_ri and ES_mj, i, j = 1, 2 denote the expected profits of the retailer and the manufacturer, respectively, when they take different strategy combinations. We have:

ES_r1 = yπ_r1 + (1−y)π_r2

(5)

ES_r2 = 0

(6)

ES_m1 = xπ_m1 + (1−x)π_m2

(7)

ES_m2 = xπ_m2 + (1−x)π_m2 = π_m2

(8)

Then, we define ${\overline{ES}}_r$ and ${\overline{ES}}_m$ as the average benefits of the retailer and the manufacturer respectively when they take different strategy combinations.

ES_r = xES_r1 + (1−x)ES_r2

(9)

ES_m = yES_m1 + (1 − y)ES_m2

(10)

Table 1. The payoff bi-matrix.

		Manufacturer
		Sm1 (y)	Sm2 (1 − y)
Retailer	Sr1 (x)	πr1, πm1	πr2, πm2
	Sr2 (1 − x)	0, πm2	0, πm2

Table 1. The payoff bi-matrix.

		Manufacturer
		Sm1 (y)	Sm2 (1 − y)
Retailer	Sr1 (x)	πr1, πm1	πr2, πm2
	Sr2 (1 − x)	0, πm2	0, πm2

3. Analysis of the Evolutionary Game Model

According to Malthusian equation, the quantity’s growth rate of strategy selected by players should equal to its fitness minus its average fitness. Then the duplicated dynamic equations of S_r1 selected by the retailer and S_m1 selected by the manufacturer are given by:

f₁(x,y) = x(ES_r1 − ES_r)

(11)

f₂(x,y) = x(ES_m1 − ES_m)

(12)

Substituting (5) and (9) into (11), we have:

$$\begin{gathered} \begin{array}{l}{f}_1(x,y)=\frac{dx}{dt}\\ \\ =x(1-x)\left[y{\pi }_{r1}+(1-y){\pi }_{r2}\right]\\ \\ =x(1-x)(y{p}_1-C_r)Q\end{array} \end{gathered}$$

(13)

In the same way, we have:

$$\begin{gathered} \begin{array}{l}f2(x,y)=\frac{dy}{dt}\\ \\ =y(1-y)x({\pi }_{m1}-{\pi }_{m2})\\ \\ =y(1-y)x(p_2+C_{b2}+C_m-p_1-p_3-C_{b1}-C_r-C_p)Q\end{array} \end{gathered}$$

(14)

3.1. Analysis of the Retailer Population

We can use the duplicated dynamic equation to depict the evolutionary course of the retailer population’s strategy selection. Then, we can get equilibrium point and ESS of the evolutionary game. According to the stability theorem of differential equation, the equilibrium point should satisfy $\frac{\partial f_1(x,y)}{\partial x}<0$ if it’s an ESS. To solve the partial derivative of $f_1(x,y)$, we have:

$$\frac{\partial f_1(x,y)}{\partial x}=(1-2x)(y{p}_1-C_r)Q$$

(15)

According to (15), we can have Theorem 1 as follows.

Theorem 1.

(1) When $y=\frac{C_r}{p_1}$, there is no ESS.

(2) When $y<\frac{C_r}{p_1}$, x = 0 is the ESS of retailer population’s strategy selection.

(3) When $y>\frac{C_r}{p_1}$, x = 1 is the ESS of retailer population’s strategy selection.

Proof.

When $y=\frac{C_r}{p_1}$, i.e., $\frac{dx}{dt}=0$, all the points on the level x is stable. There is no evolutionary course, so there is no ESS.

When $y<\frac{C_r}{p_1}$, $\frac{\partial f_1(x,y)}{\partial x}{|}_{x=0}<0$, $\frac{\partial f_1(x,y)}{\partial x}{|}_{x=1}>0$. According to the stability theorem of differential equation, the equilibrium point should satisfy $\frac{\partial f_1(x,y)}{\partial x}<0$ if it’s an ESS. Therefore x = 0 is an ESS.

In the same way, when $y>\frac{C_r}{p_1}$, x = 1 is an ESS.

From Theorem 1, we found that $\frac{C_r}{p_1}$ is a critical threshold value that determines the ESS of the retailers. C_r is the unit cost of recycling waste products by the retailer. p₁ is the unit price of the manufacturer to repurchase recycled waste products from the retailers. $\frac{C_r}{p_1}$ denotes the difference between the two parameters. The larger the difference is, the more profits the retailers get. The more profits the retailers get, the more likely the retailers choose the recycle strategy. As $y>\frac{C_r}{p_1}$, all the retailers will choose the recycle strategy.

3.2. Analysis of the Manufacturer Population

In the same way, we can get equilibrium point and ESS of the evolutionary course of the manufacturer population. It should satisfy $\frac{\partial f_2(x,y)}{\partial y}<0$, where:

$$\frac{\partial f_2(x,y)}{\partial y}=(1-2y)x({\pi }_{m1}-{\pi }_{m2})$$

(16)

According to (16), we have Theorem 2 as follows.

Theorem 2

(1) When x = 0, there is no ESS.

(2) When x > 0 and π_m1 – π_m2 < 0, y = 0 is the ESS of the manufacturer population’s strategy selection.

(3) When x > 0 and π_m1 – π_m2 > 0, y = 1 is the ESS of the manufacturer population’s strategy selection.

The proof of Theorem 2 is similar to Theorem 1, so it is omitted.

From Theorem 2, we found that if the retailer does not choose the recycle strategy, the manufactures will not choose the remanufacturing strategy. If the retailer chooses the recycle strategy, π_m1 – π_m2 is a critical threshold value that determines the ESS of the manufactures. π_m1 is the profit when the manufacturer takes remanufacturing strategy. π_m2 is the profit when the manufacturer takes original manufacturing strategy. π_m1 – π_m2 denotes the difference between the two strategies. If the manufactures can obtain profit from the remanufacturing, all of them will choose the remanufacturing strategy. Otherwise, none of them will choose remanufacturing strategy.

The retailer population’s and manufacturer population’s duplicated dynamic trend in the same coordinate plane is depicted in Figure 3.

It can be found that when the profit of the remanufacturing strategy selected by the manufacturer is less than that of the original manufacturing strategy, the game will gradually converge to the equilibrium point (0, 0) which indicates that the retailer population gradually tends not to select recovery strategy and the manufacturer population gradually tends to select the original manufacturing strategy. (No recycle, Original manufacturing) will be the only choice of the two populations. However, while the profit of the remanufacturing strategy selected by the manufacturer is larger than that of the original manufacturing strategy, the game will gradually converge to the equilibrium point (1, 1), which states that the retailer population gradually tends to select recovery strategy and the manufacturer population tends to select remanufacturing strategy. (Recycle, Remanufacturing) will be the only choice of the two populations. Through the above analysis, we find that the ESSes of the two populations are both determined by the profit of manufacturers.

Figure 3. The evolutionary graph of retailer group and manufacturer group.

Figure 3. The evolutionary graph of retailer group and manufacturer group.

Corollary 1.

If x > 0 and p₂ > p₁ + p₃ + C_b1 − C_b2 + C_p − C_m, the equilibrium point (1, 1) is the only ESS.

From Corollary 1, we see that if we want to make the strategy (Recycle, Remanufacturing) to be the only choice of retailers and manufacturers, the unit wholesale price of remanufacturing product p₂ should satisfy p₂ > p₁ + p₃ + C_b1 − C_b2 + C_p − C_m. If only to raise the unit wholesale price of remanufacturing product p₂, it may decrease the sales volume. Hence, we should try to reduce the unit cost of repairing in the remanufacturing process of the manufacturer. The degree of technological innovation and the employee skills is turned to be the main driving force to reduce the unit cost of repairing in the remanufacturing process of the manufacturer.

4. Evolutionary Game Model with Government Subsidy

The remanufacturing industry is an emerging industry that still in the stage of development. Due to the restriction of technology, environment and so on, it is likely that the total cost of remanufacturing is higher than that of the original manufacturing. In order to promote the development of remanufacturing industry, government needs to adopt some policies, such as subsidy to the manufacturers to achieve the goal. The profit of remanufacturing waste products increases if the government provides subsidies to the manufacturers. Furthermore, the manufacturers will increase the output of remanufacturing products. At the same time, the consumption of materials and carbon emission will decrease. In addition, the price of remanufacturing products will become lower. All these are useful to pull the demand and push the development of remanufacturing industry. This section will analyze the effect of the government subsidy on the evolutionary process and the ESS based on the evolutionary game model.

Suppose the government provides subsidies to manufacturers according to the quantity of remanufacturing products. The subsidy of every remanufacturing product is S. Then, the profit of the manufacturer who takes remanufacturing strategy is given by:

$${\pi }_{m1}^{\prime }=(p_2-p_1-C_{b1}-C_p)Q+SQ$$

(17)

For the evolutionary game model, the effect of different subsidy on the evolutionary process and ESS is different. We discuss it in three scenarios.

(1) The manufacturer’s profit of remanufacturing is lower than that of the original manufacturing. If the profit of the manufacturer with subsidy is still lower than the profit of original manufacturing, i.e., π_m1 – π_m2 < π'_m1 – π_m2 < 0, then

S ˂ (p₃ − C_b2 − C_m) − (p₂ − p₁ − C_b1 − C_p) = p₃ + p₁ + C_b1 + C_p − p₂ − C_b2 − C_m

(18)

$$y(1-y)x({\pi }_{m1}-{\pi }_{m2})<y(1-y)x({\pi }_{m1}^{\prime }-{\pi }_{m2})<0$$

(19)

$$\frac{dy}{dx}{|}_{{\pi }_{m1}}<\frac{dy}{dx}{|}_{{\pi }_{m1}^{\text{'}}}<0$$

(20)

Notice that p₃ – C_b2 − C_m and p₂ – p₁ – C_b1 − C_p are the marginal profit of a new product when the manufacturer takes original manufacturing strategy, and the marginal profit of a remanufacturing product when the manufacturer takes remanufacturing strategy, respectively, so the right hand of (18) means the difference between them. Therefore, (18) states that government subsidy is less than the difference.

Although the evolutionary speed of the manufacturer group becomes slow, it still has the trend of convergence to the equilibrium point $y=0$. The game will finally reach the convergence point (0, 0) and the ESS has no change.

(2) If we hope the government subsidy play an important role in promoting the development of remanufacturing industry, it should satisfy π_m1 – π_m2 < 0 < π'_m1 – π_m2, i.e., π'_m1 > π_m2. According to Equations (4) and (17), we can get the minimum value of the unit subsidy. Only when the unit subsidy satisfies S > p₃ + p₁ + C_b1 + C_p – p₂ – C_b2 – C_m, the subsidy can play its role to promote the development of remanufacturing industry. We have:

$$y(1-y)x({\pi }_{m1}-{\pi }_{m2})<0<y(1-y)x({\pi }_{m1}^{\prime }-{\pi }_{m2})$$

(21)

$$\frac{dy}{dt}{|}_{{\pi }_{m1}}<0<\frac{dy}{dx}{|}_{{\pi }_{m1}^{\text{'}}}$$

(22)

The evolutionary direction of manufacturer group changes to the equilibrium point $y=1$. The game finally reaches the convergence point (1, 1) and the ESS has changed.

(3) The manufacturer’s profit of remanufacturing is higher than that of the original manufacturing. And the government still provides the subsidy to the manufacturer. Then, π'_m1 – π_m2 > π_m1 – π_m2 > 0.

$$y(1-y)x({\pi }_{m1}^{\text{'}}-{\pi }_{m2})>y(1-y)x({\pi }_{m1}-{\pi }_{m2})>0$$

(23)

$$\frac{dy}{dx}{|}_{{\pi }_{m1}^{\text{'}}}>\frac{dy}{dx}{|}_{{\pi }_{m1}}>0$$

(24)

The evolutionary speed of manufacturer group accelerates. The evolutionary direction evolves to the equilibrium point y = 1. The game finally reaches the convergence point (1, 1) and the ESS has no change.

From the above analysis, it can be found that manufacturer’s profit of remanufacturing is lower than that of the original manufacturing, the ESS exists and it is the only one if the government subsidy satisfies S > p₃ + p₁ + C_b1 + C_p – p₂ – C_b2 – C_m. The equilibrium point (1, 1) is the only ESS of the duplicated dynamic equation. When the manufacturer’s profit of remanufacturing is higher than that of the original manufacturing, the government subsidy will make the duplicated dynamic evolve to the equilibrium point (1, 1). This means all the strategies will evolve toward the same direction. The manufacturer group will gradually tend to select remanufacturing strategy along with the retailer group will gradually tend to select recycling strategy. If the government want to promote the development of remanufacturing industry, it can provide subsidy to the remanufacturing products, and the subsidy should be greater than a threshold. Otherwise, the subsidy cannot encourage the manufacture to take remanufacturing strategy. When the retailer population and the manufacturer population change from period to period dynamically, we can use the same model to analyze their evolutionary stable strategies in the new setting.

5. Conclusions

Remanufacturing industry plays an important role in promoting the development of low-carbon economy. As an emerging industry, it is still immature. This paper developed an evolutionary game model and analyzed the retailer population’s and the manufacturer population’s long-term evolutionary course in the remanufacturing closed-loop supply chain. We find that there are two possible evolutionary results affected by the profits of manufacturers, and the ESS of the two populations is influenced by manufacturers’ profit from remanufacturing activity. We also found that government subsidy is critical to promote the development of remanufacturing industry. The wholesale price of the remanufacturing products affects the final ESS. To strengthen the degree of technological innovation or improve employee skills is turned to be one main driving force of promoting the development of remanufacturing industry.

This paper studies the evolutionary game of remanufacturing closed-loop supply chain from the perspective of two populations. The closed-loop supply chain in reality is more complicated. Therefore, to study the evolutionary game of remanufacturing closed-loop supply chain from the perspective of more populations is a valuable direction for future research.