Evaluation of Fatigue Crack Propagation of Gears Considering Uncertainties in Loading and Material Properties
Abstract
:1. Introduction
- It has been reported that WTGs represent a critical problem in terms of reliability due to the high incidence of premature failure [5,6,7], which contributes considerably to the increase of wind energy cost [8,9]. For this reason, enhanced reliability analysis on WTGs can contribute to reducing the costs of wind energy;
- Gear teeth fracture resulting from fatigue crack propagation is amongst the main causes of WTG failure due to the irregular and cyclic nature of loads on the gears [10,11,12]. Fatigue crack nucleation and propagation in gear teeth is a complex phenomenon and needs to be considered in reliability analysis to accurately determine the life of WTGs;
- Due to the turbulence effects in the wind flow, the loads experienced by WTGs are subjected to significant random fluctuations, which have been shown to considerably impact the reliability of the gearboxes [6,7,17]. Furthermore, most of the design practices for WTGs do not consider the uncertainties of design and loading parameters in reliability analysis [6,7,9]. For this reason, probabilistic analysis can improve the reliability of WTGs and help designers to identify the most critical parameters.
- To perform the dynamic modeling of a gear tooth subjected to fatigue loading;
- To build a finite element (FE) model for the crack propagation in the gear tooth to determine the stress intensity factor (SIF) at the crack tip;
- To quantify the uncertainties of the loads on the gear tooth and material properties; and
- To evaluate the fatigue crack propagation of gears considering uncertainties in loading and material properties.
2. Methodology
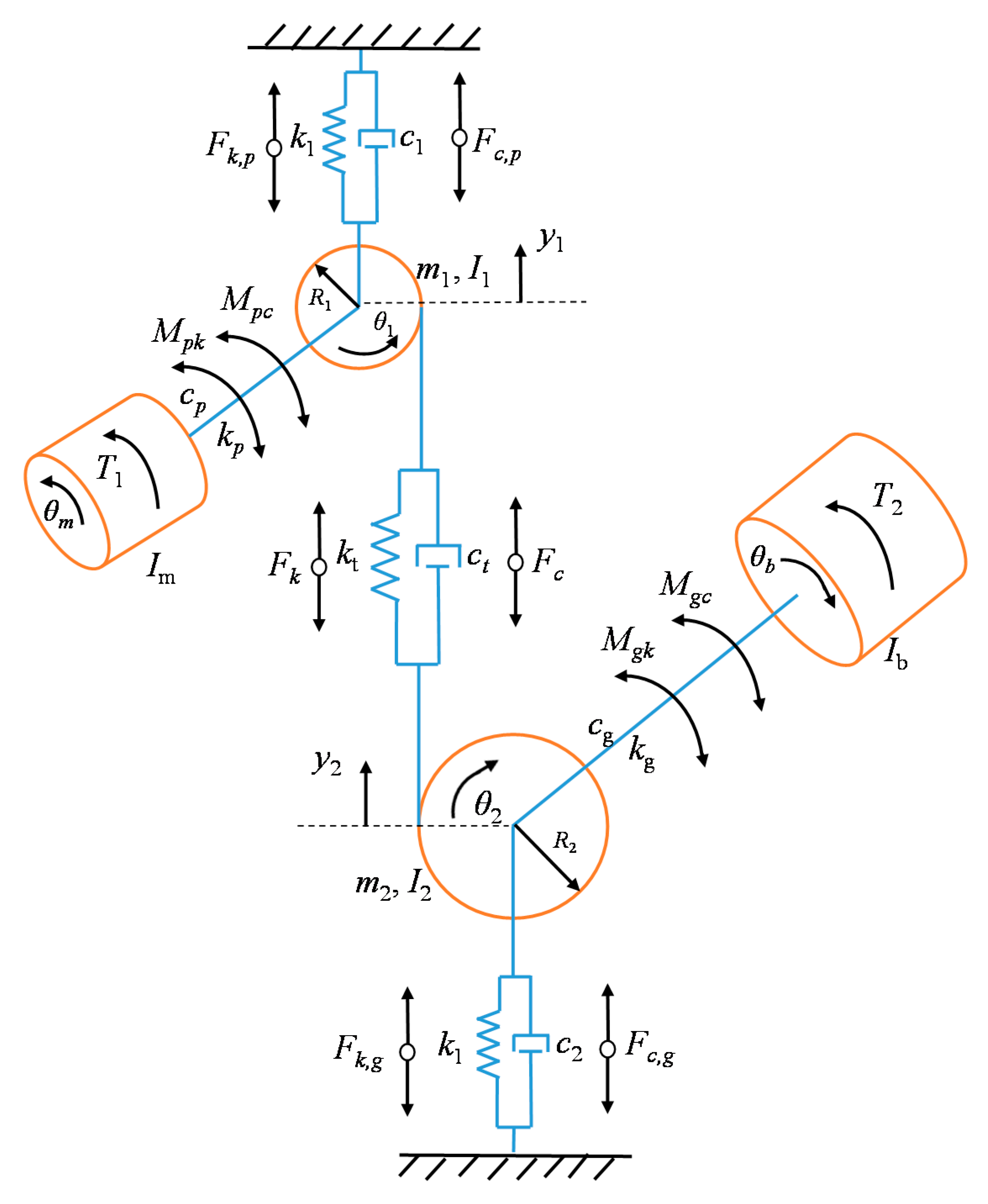
2.1. Dynamic Modeling
2.2. Calculation of Stress Intensity Factor
2.3. Loading Uncertainty Quantification
2.4. Probabilistic Prediction of the Gear Crack Size
3. Results and Discussion
3.1. Rainflow Counting
3.2. Dynamic Analysis
3.3. Calculation of the Stress Intensity Factor
3.4. Probabilistic Estimation of the Gear Fatigue Crack Propagation
4. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| ac | critical crack length |
| ak | calculated crack length, at a time step of k (random variable) |
| ak−1 | crack length at time step k − 1 |
| C | Paris’ material constant or factor (random variable) |
| c1 | vertical radial viscous damping coefficient of input bearings |
| c2 | vertical radial viscous damping coefficient of output bearings |
| cg | damping coefficient of output flexible coupling |
| cp | damping coefficient of input flexible coupling |
| ct | mesh damping coefficient |
| E | Young’s modulus |
| fp | rotational frequency of the shaft (and consequently the pinion) |
| fT | frequency of torque loading |
| Fc | damping inter-tooth force |
| Fk | stiffness inter-tooth force |
| I1/I2 | mass moment of inertia of pinion/gear |
| Ib | mass moment of inertia of the load |
| Im | mass moment of inertia of the motor |
| k1 | vertical radial stiffness of input bearings |
| k2 | vertical radial stiffness of output bearings |
| kg | torsional stiffness of output flexible coupling |
| kp | torsional stiffness of input flexible coupling |
| kt | total mesh stiffness |
| LN(μ, σ) | Lognormal probability density function with mean μ and standard deviation σ |
| m | Paris’ material constant or exponent (random variable) |
| M1 | input motor torque |
| M2 | output torque from the load |
| m1/m2 | mass of pinion/gear |
| N(μ, σ) | Normal probability density function with mean μ and standard deviation σ |
| NT | total life cycle until failure |
| Rb1/Rb2 | outside circle radius of pinion/gear |
| T | applied fluctuating torque |
| y1/y2 | linear displacement of pinion/gear in the y-direction |
| ΔN | number of cycles added to the component |
| υ | Poisson’s ratio |
| σ | standard deviation |
| θb | angular displacement of the load |
| θm | angular displacement of the motor |
| θ1/θ2 | angular displacement of pinion/gear |
Appendix A
References
- Lacerda, J.S.; van den Bergh, J.C.J.M. International Diffusion of Renewable Energy Innovations: Lessons from the Lead Markets for Wind Power in China, Germany and USA. Energies 2014, 7, 8236–8263. [Google Scholar] [CrossRef]
- Jin, X.; Gan, Y.; Ju, W.; Yang, X.; Han, H. Research on Wind Turbine Safety Analysis: Failure Analysis, Reliability Analysis, and Risk Assessment. Environ. Prog. Sustain. Energy 2016, 35, 1848–1861. [Google Scholar] [CrossRef]
- Liu, W.Y.; Tang, B.P.; Han, J.G.; Lu, X.N.; Hu, N.N.; He, Z.Z. The Structure Healthy Condition Monitoring and Fault Diagnosis Methods in Wind Turbines: A Review. Renew. Sustain. Energy Rev. 2015, 44, 466–472. [Google Scholar] [CrossRef]
- Kandukuri, S.T.; Klausen, A.; Karimi, H.R.; Robbersmyr, K.G. A Review of Diagnostics and Prognostics of Low-Speed Machinery towards Wind Turbine Farm-Level Health Management. Renew. Sustain. Energy Rev. 2016, 53, 697–708. [Google Scholar] [CrossRef]
- Grujicic, M.; Chenna, V.; Galgalikar, R.; Snipes, J.S.; Ramaswami, S.; Yavari, R. Wind-Turbine Gear-Box Roller-Bearing Premature-Failure Caused by Grain-Boundary Hydrogen Embrittlement: A Multi-Physics Computational Investigation. J. Mater. Eng. Perform. 2014, 23, 3984–4001. [Google Scholar] [CrossRef]
- Alemayehu, F.M.; Ekwaro-Osire, S. Loading and Design Parameter Uncertainty in the Dynamics and Performance of High-Speed-Parallel-Helical-Stage of a Wind Turbine Gearbox. J. Mech. Des. 2014, 136, 091002. [Google Scholar] [CrossRef]
- Alemayehu, F.M.; Ekwaro-Osire, S. Probabilistic Performance of Helical Compound Planetary System in Wind Turbine. J. Comput. Nonlinear Dyn. 2015, 10, 041003. [Google Scholar] [CrossRef]
- Ossai, C.I.; Boswell, B.; Davies, I.J. A Markovian Approach for Modelling the Effects of Maintenance on Downtime and Failure Risk of Wind Turbine Components. Renew. Energy 2016, 96, 775–783. [Google Scholar] [CrossRef]
- Alemayehu, F.M.; Ekwaro-Osire, S. Uncertainty Considerations in the Dynamic Loading and Failure of Spur Gear Pairs. J. Mech. Des. 2013, 135, 084501. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, Y.; Zhang, Z.; Fu, C.; Dong, C.; Su, H. Partial Load: A Key Factor Resulting in the Failure of Gear in the Wind Turbine Gearbox. J. Fail. Anal. Prev. 2016, 16, 109–122. [Google Scholar] [CrossRef]
- Wang, L.; Shao, Y. Fault Mode Analysis and Detection for Gear Tooth Crack during Its Propagating Process Based on Dynamic Simulation Method. Eng. Fail. Anal. 2017, 71, 166–178. [Google Scholar] [CrossRef]
- Pandya, Y.; Parey, A. Simulation of Crack Propagation in Spur Gear Tooth for Different Gear Parameter and Its Influence on Mesh Stiffness. Eng. Fail. Anal. 2013, 30, 124–137. [Google Scholar] [CrossRef]
- Li, C.J.; Lee, H. Gear Fatigue Crack Prognosis Using Embedded Model, Gear Dynamic Model and Fracture Mechanics. Mech. Syst. Signal Process. 2005, 19, 836–846. [Google Scholar] [CrossRef]
- Li, Z.; Yan, X.; Wang, X.; Peng, Z. Detection of Gear Cracks in a Complex Gearbox of Wind Turbines Using Supervised Bounded Component Analysis of Vibration Signals Collected from Multi-Channel Sensors. J. Sound Vib. 2015, 371, 406–433. [Google Scholar] [CrossRef]
- Tian, Z.; Zuo, M.J.; Wu, S. Crack Propagation Assessment for Spur Gears Using Model-Based Analysis and Simulation. J. Intell. Manuf. 2012, 23, 239–253. [Google Scholar] [CrossRef]
- Zhao, F.; Tian, Z.; Zeng, Y. Uncertainty Quantification in Gear Remaining Useful Life Prediction through an Integrated Prognostics Method. IEEE Trans. Reliab. 2013, 62, 146–159. [Google Scholar] [CrossRef]
- Van Bussel, G.J.W.; Boussion, C.; Hofemann, C. A Possible Relation between Wind Conditions, Advanced Control and Early Gearbox Failures in Offshore Wind Turbines. Procedia CIRP 2013, 11, 301–304. [Google Scholar] [CrossRef]
- Beyaoui, M.; Tounsi, M.; Abboudi, K.; Feki, N.; Walha, L.; Haddar, M. Dynamic Behaviour of a Wind Turbine Gear System with Uncertainties. C. R. Mec. 2016, 344, 375–387. [Google Scholar] [CrossRef]
- Wu, S.; Zuo, M.J.; Parey, A. Simulation of Spur Gear Dynamics and Estimation of Fault Growth. J. Sound Vib. 2008, 317, 608–624. [Google Scholar] [CrossRef]
- ANSYS Mechanical APDL Element Reference; ANSYS, Inc.: Canonsburg, PA, USA, 2013.
- Guinea, G.V.; Planas, J.; Elices, M. Stress Intensity Factor Evaluation by the Displacement Extrapolation Technique. Eng. Fract. Mech. 2000, 66, 243–255. [Google Scholar] [CrossRef]
- Jonkman, J.B.; Kilcher, L. TurbSim User’s Guide: Version 1.06.00; Technical Report; National Renewable Energy Laboratory: Golden, CO, USA, 2012.
- Jonkman, J.M.; Buhl, M.L., Jr. FAST User’s Guide; Technical Report; National Renewable Energy Laboratory: Golden, CO, USA, 2005.
- Rainflow Counting Algorithm. Available online: https://www.mathworks.com/matlabcentral/fileexchange/3026-rainflow-counting-algorithm?requestedDomain=www.mathworks.com (accessed on 21 November 2017).
- American Society for Testing and Materials (ASTM). E1049-85: Standard Practices for Cycle Counting in Fatigue Analysis; ASTM: West Conshohocken, PA, USA, 2017. [Google Scholar]












| Parameter | Unit | Mean, μ (Location) | Std. Dev, σ (Scale) | Shape | COV | |
|---|---|---|---|---|---|---|
| m 1 | Normal | - | 1.4354 | 0.0287 | - | 0.02 |
| C 1 | Normal | 9.12 × 10−11 | 4.56 × 10−12 | - | 0.05 | |
| T | GEV | Nm | (320) | (35) | −0.36 | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Endeshaw, H.B.; Ekwaro-Osire, S.; Alemayehu, F.M.; Dias, J.P. Evaluation of Fatigue Crack Propagation of Gears Considering Uncertainties in Loading and Material Properties. Sustainability 2017, 9, 2200. https://doi.org/10.3390/su9122200
Endeshaw HB, Ekwaro-Osire S, Alemayehu FM, Dias JP. Evaluation of Fatigue Crack Propagation of Gears Considering Uncertainties in Loading and Material Properties. Sustainability. 2017; 9(12):2200. https://doi.org/10.3390/su9122200
Chicago/Turabian StyleEndeshaw, Haileyesus B., Stephen Ekwaro-Osire, Fisseha M. Alemayehu, and João Paulo Dias. 2017. "Evaluation of Fatigue Crack Propagation of Gears Considering Uncertainties in Loading and Material Properties" Sustainability 9, no. 12: 2200. https://doi.org/10.3390/su9122200
APA StyleEndeshaw, H. B., Ekwaro-Osire, S., Alemayehu, F. M., & Dias, J. P. (2017). Evaluation of Fatigue Crack Propagation of Gears Considering Uncertainties in Loading and Material Properties. Sustainability, 9(12), 2200. https://doi.org/10.3390/su9122200






