Settlement Behavior of Shallow Foundations in Unsaturated Soils under Rainfall
Abstract
:1. Introduction
2. 2D Finite Element Modelling of Unsaturated Soils
2.1. Estimation of Modulus of Elasticity for Finite Element Analysis
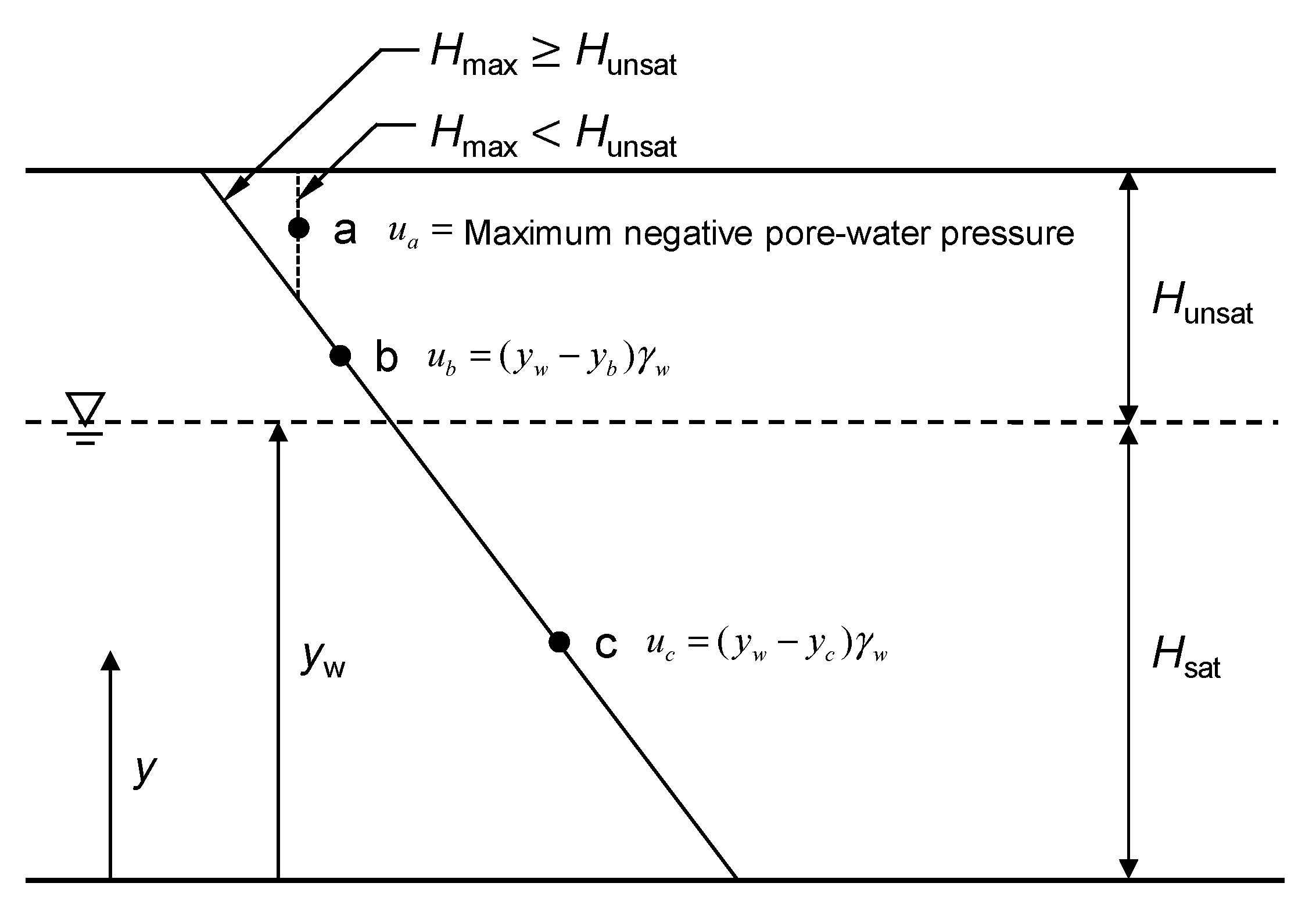
2.2. Modelling of Matric Suction
2.3. Estimation of Effective Internal Friction Angle and Dilation Angle
3. Numerical Analysis for Simulating Field Load Tests
3.1. Site Investigation
3.2. Finite Element Modeling
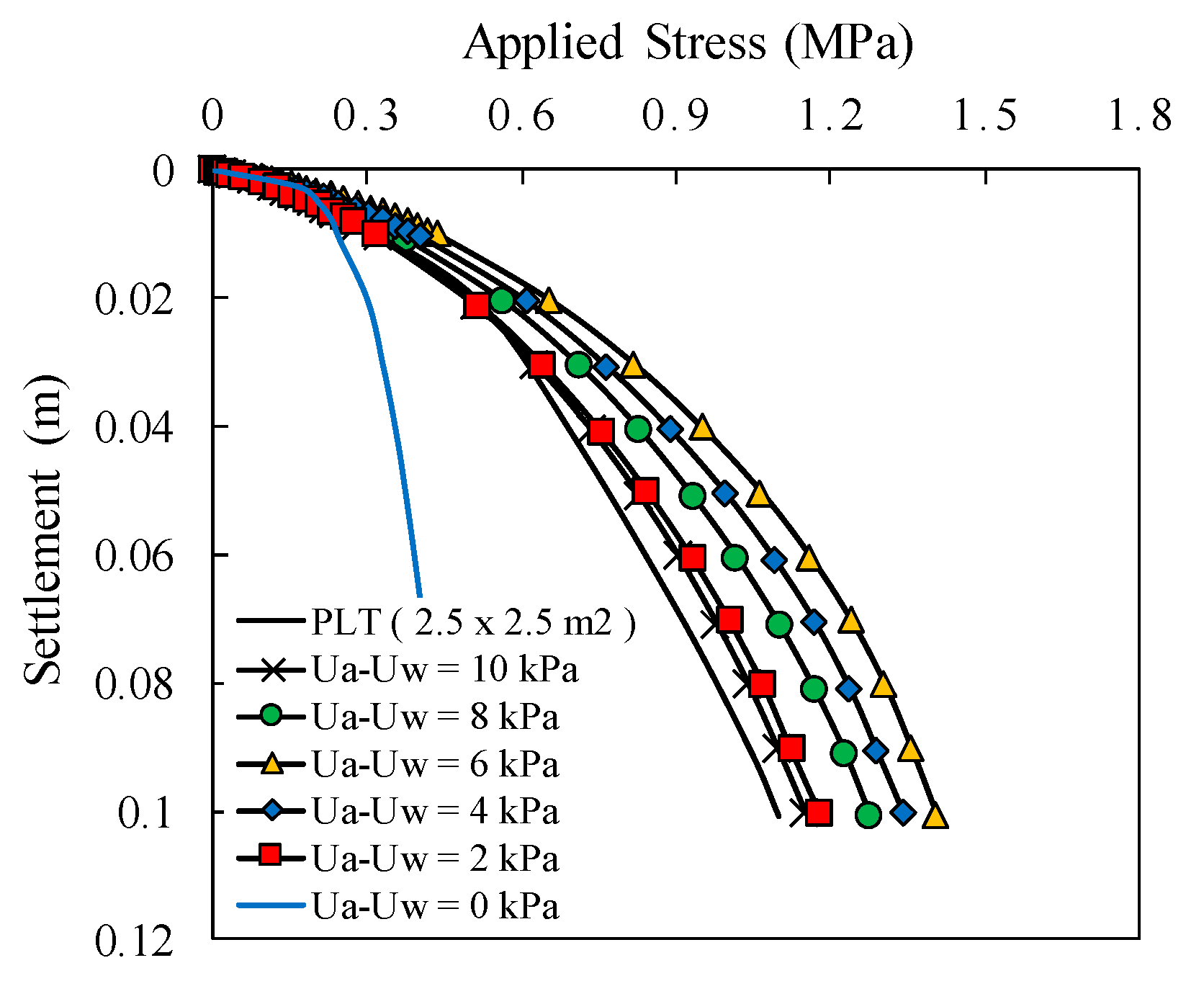
3.3. Comparison with Field Measurements
3.4. Load-Settlement Behavior with Respect to Initial Matric Suction
4. Effect of Rainfall Infiltration on Settlement Behavior of Shallow Foundation
4.1. Model and Parameters
4.2. Load-Settlement Responses under Rainfall
4.3. Settlement of Shallow Foundation with Time
5. Conclusions
- By taking into account the influence of matric suction in unsaturated soils, a reasonably good agreement of load-settlement responses is obtained between the numerical analysis results and field load test results for four different size of shallow foundations. The sequential analysis procedure for deformable unsaturated soils can approximate the settlement of shallow foundations with time.
- Initial matric suction of unsaturated soils exhibits obvious strengthening effects for the bearing capacity of shallow foundations with decreasing the settlement due to the high modulus of elasticity as matric suction increases. In addition, rainfall intensity plays a significant role in determining the settlement of shallow foundations in unsaturated soils. It can be said that the additional settlement is caused by rainfall infiltration and loss of matric suction.
- The change in settlements during rainfall is significantly affected by the groundwater table position near the ground surface due to changes in matric suction. In addition, higher bearing capacity in response to rainfall infiltration is observed for the soil with smaller permeability function as compared to larger permeability function.
- Therefore, the numerical simulations from the methodology presented in this study provide an initial understanding of the stability of shallow foundations for transient conditions leading to additional settlements caused by rainfall infiltration.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rojas, J.C.; Salinas, L.M.; Sejas, C. Plate-load tests on an unsaturated lean clay. In Experimental Unsaturated Soil Mechanics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 445–452. [Google Scholar]
- Vanapalli, S.K.; Mohamed, F.M. Bearing capacity of model footings in unsaturated soils. In Experimental Unsaturated Soil Mechanics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 483–493. [Google Scholar]
- Jeong, S.; Kim, J.; Lee, K. Effect of clay content on well-graded sands due to infiltration. Eng. Geol. 2008, 102, 74–81. [Google Scholar] [CrossRef]
- Kim, Y.; Jeong, S.; Kim, J. Coupled infiltration model of unsaturated porous media for steady rainfall. Soils. Found. 2016, 56, 1073–1083. [Google Scholar] [CrossRef]
- Rahardjo, H.; Melinda, F.; Leong, E.C.; Rezaur, R.B. Stiffness of a compacted residual soil. Eng. Geol. 2011, 120, 60–67. [Google Scholar] [CrossRef]
- Oh, W.T.; Vanapalli, S.K.; Puppala, A.J. Semi-empirical model for the prediction of modulus of elasticity for unsaturated soils. Can. Geotech. J. 2009, 46, 903–914. [Google Scholar] [CrossRef]
- Oh, W.T.; Vanapalli, S.K. Modelling the applied vertical stress and settlement relationship of shallow foundations in saturated and unsaturated sands. Can. Geotech. J. 2011, 48, 425–438. [Google Scholar] [CrossRef]
- Mohamed, F.M.S. Bearing Capacity and Settlement Behaviour of Footings Subjected to Static and seismic Loading Conditions in Unsaturated Sandy Soils. Ph.D. Thesis, University of Ottawa, Ottawa, ON, Canada, 2014. [Google Scholar]
- Park, H.D. Rainfall induced load-settlement behavior of shallow foundations on unsaturated soil. Ph.D. Thesis, Yonsei University, Seoul, Korea, 2017. [Google Scholar]
- PLAXIS 2D. PLAXIS 2D User Manual, Version 2012; Brinkgreve, R.B., Swolfs, W.M., Eds.; PLAXIS Inc.: AN Delft, The Netherlands, 2012. [Google Scholar]
- Hossain, M.A.; Yin, J.H. Shear strength and dilative characteristics of an unsaturated compacted completely decomposed granite soil. Can. Geotech. J. 2010, 47, 1112–1126. [Google Scholar] [CrossRef]
- Bolton, M.D. The strength and dilatancy of sands. Géotechnique 1986, 36, 65–78. [Google Scholar] [CrossRef]
- Lee, J.; Salgado, R. Estimation of footing settlement in sand. Int. J. Geomech. 2002, 2, 1–28. [Google Scholar] [CrossRef]
- Briaud, J.L.; Gibbens, R. Behavior of five large spread footings in sand. J. Geotech. Geoenviron. 1999, 125, 787–796. [Google Scholar] [CrossRef]
- Briaud, J.L. Spread footings in sand: Load settlement curve approach. J. Geotech. Geoenviron. Eng. 2007, 133, 905–920. [Google Scholar] [CrossRef]
- Palmer, L.A. Field loading tests for the evaluation of the wheel load capacities of airport pavements. In ASTM STP 79; ASTM: Philadelphia, PA, USA, 1947; pp. 9–30. [Google Scholar]
- Briaud, J.L.; Gibbens, R. Large Scale Load Tests and Data Base of Spread Footings on Sand; Technical Report, FHWA–RD–068; US Department of Transportation Federal Highway Administration: Washington, DC, USA, 1997.
- Consoli, N.C.; Schnaid, F.; Milititsky, J. Interpretation of plate load tests on residual soil site. J. Geotech. Geoenviron. Eng. 1998, 124, 857–867. [Google Scholar] [CrossRef]
- Kim, Y.; Jeong, S. Modelling of shallow landslides in an unsaturated soil slope using a coupled model. Geome. Eng. Int. J. 2017, 13, 1–18. [Google Scholar]
- Poulos, H.D.; Davis, E.H. Elastic Solutions for Soil and Rock Mechanics; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]











| Soil Property | Value |
|---|---|
| Specific gravity, | 2.64 |
| Water content, (%) | 5.0 |
| Void ratio, | 0.78 |
| Unity weight, (kN/m3) | 17.75 |
| USCS 1 | SM |
| Soil Property | Value |
|---|---|
| Effective internal friction angle, (deg) | 35 |
| Effective cohesion, (kPa) | 1 |
| Dilation angle, (deg) | 26 |
| Poisson’s Ratio, | 0.3 |
| Modulus of elasticity of soil, (MPa) | 45 |
| Modulus of elasticity of footing, (MPa) | 30,000 |
| Soil Property | Type A | Type B |
|---|---|---|
| Specific gravity, | 2.64 | 2.72 |
| Max. dry unit weight, (kN/m3) | 17.1 | 17.5 |
| Min. dry unit weight, (kN/m3) | 13.3 | 13.5 |
| Cohesion, (kPa) | 1.0 | 10.7 |
| Internal friction angle, (deg) | 22.8 | 35.0 |
| Saturated Elastic Modulus, (MPa) | 1.5 | 2.5 |
| Possion’s ratio, | 0.3 | 0.3 |
| Soil Property | Type A | Type B |
|---|---|---|
| Fitting parameter for SWCC, (1/kPa) | 0.27 | 0.042 |
| Fitting parameter for SWCC, | 3.10 | 2.06 |
| Saturated volumetric water content, | 0.36 | 0.41 |
| Residual volumetric water content, | 0.037 | 0.054 |
| Saturated permeability, (m/s) | 4.67 × 10−5 | 5.12 × 10−6 |
| Soil Types | Footing Size | Groundwater Table Position | Rainfall Intensity | Rainfall Duration |
|---|---|---|---|---|
| Type A Type B | 5 × 5 m | 1B 2B | 10 mm/h 20 mm/h 30 mm/h | 1 h 3 h 6 h 12 h 24 h 48 h 96 h |
| Settlement in Type A Soil (mm) | Settlement in Type B Soil (mm) | |||||
|---|---|---|---|---|---|---|
| 10 mm/h | 20 mm/h | 30 mm/h | 10 mm/h | 20 mm/h | 30 mm/h | |
| Time | Groundwater table 1B Below | |||||
| 0 | 47.0 | 46.0 | 46.0 | 25.1 | 25.1 | 25.1 |
| 6 | 47.3 | 48.0 | 48.0 | 25.3 | 25.5 | 25.9 |
| 12 | 48.0 | 50.0 | 51.5 | 25.6 | 25.8 | 26.0 |
| 24 | 50.0 | 55.0 | 58.0 | 27.5 | 28.3 | 29.2 |
| 36 | 56.0 | 66.0 | 69.0 | 28.4 | 33.9 | 36.9 |
| 48 | 59.1 | 77.0 | 80.0 | 29.5 | 49.0 | 49.0 |
| 96 | 78.9 | 90.0 | 115.0 | 49.2 | 74.0 | 76.0 |
| Time | Groundwater table 2B Below | |||||
| 0 | 29.0 | 30.0 | 30.0 | 19.5 | 19.9 | 23.2 |
| 6 | 29.3 | 31.9 | 31.0 | 20.0 | 20.0 | 24.0 |
| 12 | 30.0 | 34.0 | 33.0 | 20.2 | 23.6 | 24.2 |
| 24 | 31.9 | 37.0 | 36.0 | 21.5 | 23.9 | 24.6 |
| 36 | 33.6 | 40.0 | 41.0 | 21.6 | 24.3 | 25.2 |
| 48 | 39.0 | 43.0 | 46.0 | 23.5 | 25.5 | 26.5 |
| 96 | 52.5 | 60.0 | 76.0 | 26.7 | 48.6 | 49.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Park, H.; Jeong, S. Settlement Behavior of Shallow Foundations in Unsaturated Soils under Rainfall. Sustainability 2017, 9, 1417. https://doi.org/10.3390/su9081417
Kim Y, Park H, Jeong S. Settlement Behavior of Shallow Foundations in Unsaturated Soils under Rainfall. Sustainability. 2017; 9(8):1417. https://doi.org/10.3390/su9081417
Chicago/Turabian StyleKim, Yongmin, Hyundo Park, and Sangseom Jeong. 2017. "Settlement Behavior of Shallow Foundations in Unsaturated Soils under Rainfall" Sustainability 9, no. 8: 1417. https://doi.org/10.3390/su9081417
APA StyleKim, Y., Park, H., & Jeong, S. (2017). Settlement Behavior of Shallow Foundations in Unsaturated Soils under Rainfall. Sustainability, 9(8), 1417. https://doi.org/10.3390/su9081417




