Evaluation of the SPARSE Dual-Source Model for Predicting Water Stress and Evapotranspiration from Thermal Infrared Data over Multiple Crops and Climates
Abstract
:1. Introduction
- Patch vs. layer approach: Even though a “patch/parallel” approach was originally proposed for sparsely vegetated semi-arid regions, and the “layer/series” approach for denser vegetation [10,13,14], there is no consensus regarding which approach offers better results in semi-arid sparse vegetation. The TSEB layer version was more robust than the TSEB patch version even though layer and patch performances were close in [15,16]. This study will bring insights on the performances of the “patch” vs. the “layer” approaches to estimate evapotranspiration and its soil component over 20 irrigated and rainfed crops, including arable crops and orchards, and various climate conditions, from temperate or Mediterranean to semi-arid and tropical climates.
- Benefit of bounding flux retrieval: The main improvement of SPARSE is the bounding of the output fluxes by their theoretical limit values. We will test whether this improves evapotranspiration retrieval performances by comparing bounded and unbounded retrieval methods.
- Water stress retrieval: Estimates of potential surface evapotranspiration rates are fairly well constrained by soil and vegetation biophysical properties easily obtained from visible/near-infrared remote sensing data and can explain a large amount of the information contained in the actual ET. The added value of thermal infrared (TIR) data lies in the adequate amount of information introduced by the surface temperature itself. TIR data provides information on the difference between actual and potential evapotranspiration rates (i.e., water stress) and thus soil moisture-limited evaporation and transpiration rates. We assessed the capacities of the SPARSE model to monitor water stress by comparison to water stress index chronicles derived from field data.
- Impact of the time of overpass of a TIR satellite: One of the auxiliary goals of this paper was to investigate the impact of the time of overpass of a TIR satellite on the performance of stress retrievals in order to take into account the operational constraints imposed by the existing or future satellite platforms. At present, specific studies are missing and no consensus has been reached on the best time of overpass for stress detection.
2. Materials and Methods
2.1. The SPARSE Model
2.1.1. Model Description
2.1.2. Model Implementation
2.2. Experimental Data Sets Description
2.2.1. Auradé and Lamasquère Data Sets
2.2.2. Avignon Arable Crop Data Sets
2.2.3. Barbeau Forest Data Sets
2.2.4. Tunisian Rainfed Wheat Data Set
2.2.5. Tunisian Olive Orchard Data Set
2.2.6. Morocco Irrigated Wheat Data Set
2.2.7. Niger Crop and Fallow Data Set
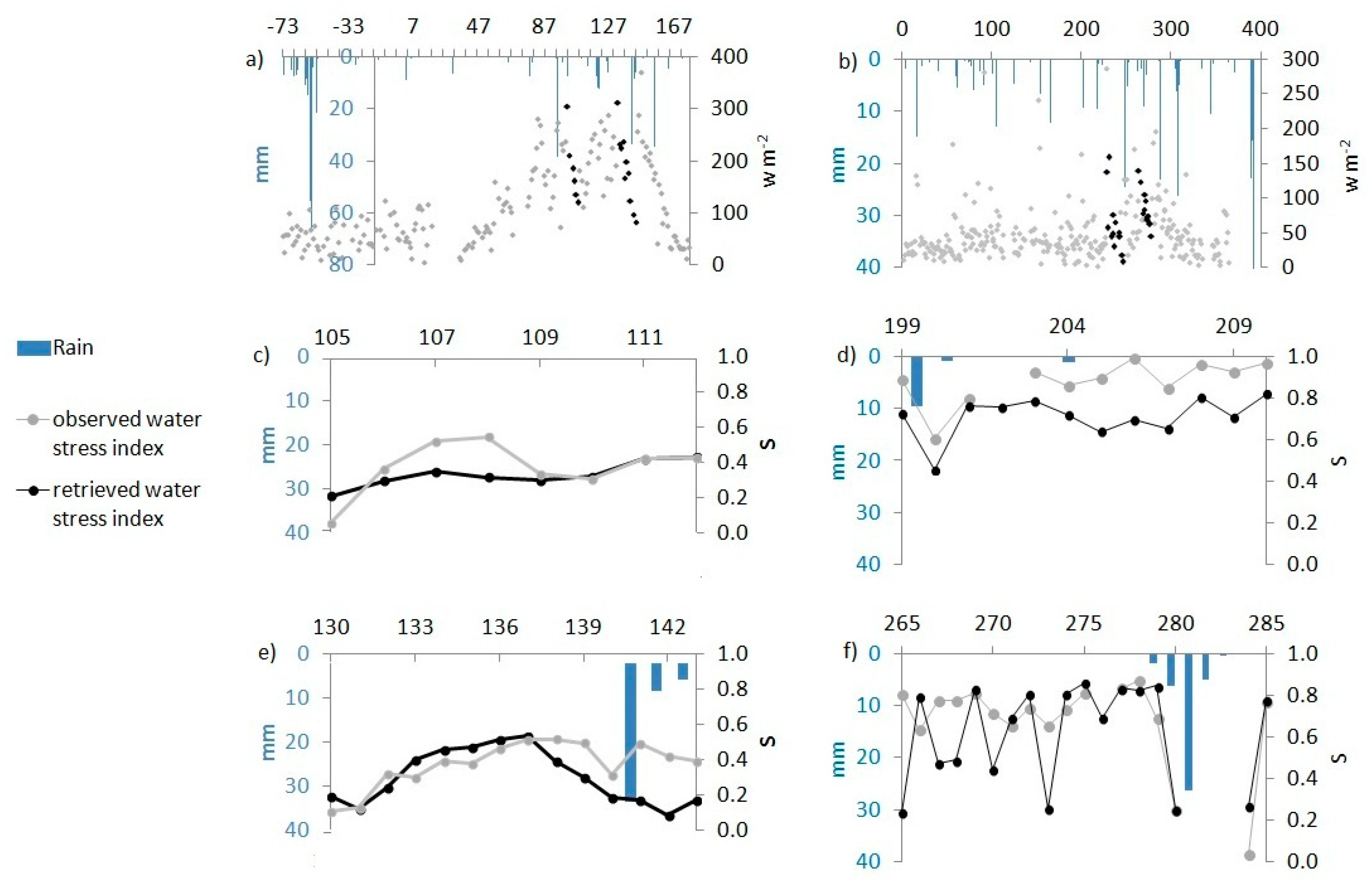
2.3. Assessment of Simulated Surface Water Stress
2.4. Soil Evaporation Estimates
2.5. Experiment Design
2.6. Performance Metrics
3. Results
3.1. Energy Balance Component Estimates
3.2. Water Stress Index Estimation
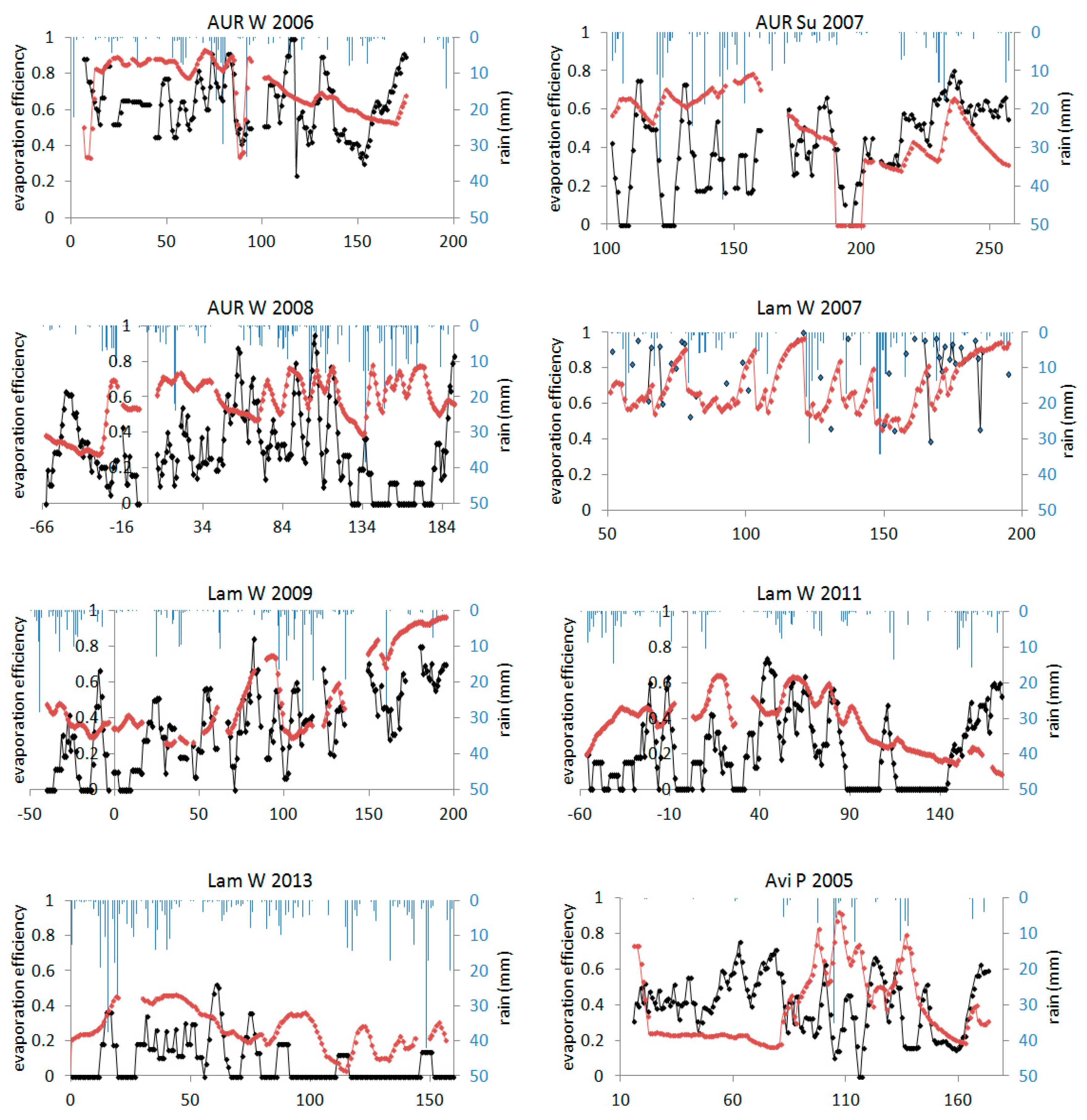
3.3. Soil Evaporation Efficiency
4. Discussion
4.1. Overall Performance of the Dual-Source SPARSE Model
4.2. “Patch” vs. “Layer” Approach Performances
4.3. Benefit of Bounding the Flux Estimates
- For cereals in senescent situations at the end of the season, specific SPARSE parameter values in terms of canopy structure and stomatal conductance were not given. It is also essential to take into account the contribution of green stem and ear to the plant transpiration, especially for wheat [41,42]; this can explain the underestimation of transpiration for the Avignon and Auradé sites, see Figure 2.
- In semi-arid areas, transpiration and particularly evaporation were retrieved beyond potential levels during periods where the soil exhibits an important dry-down (in particular the Tunisian site; Figure 2). Sensible heat transfer to the crop from drier surrounding zones led to a great overestimation of transpiration by the model because of fully coupled soil–vegetation–air exchanges in the layer version. In these situations, bounding the outputs by realistic limiting flux values ensured model robustness and reduced LE RMSE values to 30 W m−2, resulting in a reduction of global RMSE by 6 W m−2. The bounded layer version of SPARSE provided the best estimates of LE over the different sites and climates.
4.4. Evaluation of the Capacity of SPARSE to Monitor Water Stress
4.5. Potential to be Driven by Earth Observation Data
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Er-Raki, S.; Chehbouni, A.; Boulet, G.; Williams, D.G. Using the dual approach of FAO-56 for partitioning ET into soil and plant components for olive orchards in a semi-arid region. Agric. Water Manag. 2010, 97, 1769–1778. [Google Scholar] [CrossRef] [Green Version]
- Kustas, W.; Anderson, M. Advances in thermal infrared remote sensing for land surface modeling. Agric. For. Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]
- Evett, S.R.; Tolk, J.A. Introduction: Can Water Use Efficiency Be Modeled Well Enough to Impact Crop Management? Agron. J. 2009, 101, 423–425. [Google Scholar] [CrossRef]
- Boulet, G.; Mougenot, B.; Lhomme, J.-P.; Fanise, P.; Lili-Chabaane, Z.; Olioso, A.; Bahir, M.; Rivalland, V.; Jarlan, L.; Merlin, O.; et al. The SPARSE model for the prediction of water stress and evapotranspiration components from thermal infra-red data and its evaluation over irrigated and rainfed wheat. Hydrol. Earth Syst. Sci. 2015, 4653–4672. [Google Scholar] [CrossRef] [Green Version]
- Hain, C.R.; Mecikalski, J.R.; Anderson, M.C. Retrieval of an Available Water-Based Soil Moisture Proxy from Thermal Infrared Remote Sensing. Part I: Methodology and Validation. J. Hydrometeorol. 2009, 10, 665–683. [Google Scholar] [CrossRef]
- Olioso, A.; Chauki, H.; Courault, D.; Wigneron, J.-P. Estimation of Evapotranspiration and Photosynthesis by Assimilation of Remote Sensing Data into SVAT Models. Remote Sens. Environ. 1999, 68, 341–356. [Google Scholar] [CrossRef]
- Chirouze, J.; Boulet, G.; Jarlan, L.; Fieuzal, R.; Rodriguez, J.C.; Ezzahar, J.; Er-Raki, S.; Bigeard, G.; Merlin, O.; Garatuza-Payan, J.; et al. Intercomparison of four remote-sensing-based energy balance methods to retrieve surface evapotranspiration and water stress of irrigated fields in semi-arid climate. Hydrol. Earth Syst. Sci. 2014, 18, 1165–1188. [Google Scholar] [CrossRef] [Green Version]
- Olioso, A.; Inoue, Y.; Ortega-FARIAS, S.; Demarty, J.; Wigneron, J.-P.; Braud, I.; Jacob, F.; Lecharpentier, P.; OttlÉ, C.; Calvet, J.-C.; et al. Future directions for advanced evapotranspiration modeling: Assimilation of remote sensing data into crop simulation models and SVAT models. Irrig. Drain. Syst. 2005, 19, 377–412. [Google Scholar] [CrossRef]
- Boulet, G.; Chehbouni, A.; Gentine, P.; Duchemin, B.; Ezzahar, J.; Hadria, R. Monitoring water stress using time series of observed to unstressed surface temperature difference. Agric. For. Meteorol. 2007, 146, 159–172. [Google Scholar] [CrossRef] [Green Version]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef] [Green Version]
- Lhomme, J.P.; Montes, C.; Jacob, F.; Prévot, L. Evaporation from Heterogeneous and Sparse Canopies: On the Formulations Related to Multi-Source Representations. Bound.-Layer Meteorol. 2012, 144, 243–262. [Google Scholar] [CrossRef]
- Blyth, E.M. Using a simple SVAT scheme to describe the effect of scale on aggregation. Bound.-Layer Meteorol. 1995, 72, 267–285. [Google Scholar] [CrossRef]
- Verhoef, A.; De Bruin, H.A.R.; Van Den Hurk, B.J.J.M. Some Practical Notes on the parameter kB-1 for Sparse Vegetation. Am. Meteorol. Soc. 1997, 36, 560–572. [Google Scholar] [CrossRef]
- Li, F.; Kustas, W.P.; Prueger, J.H.; Neale, C.M.U.; Jackson, T.J. Utility of Remote Sensing–Based Two-Source Energy Balance Model under Low- and High-Vegetation Cover Conditions. J. Hydrometeorol. 2005, 6, 878–891. [Google Scholar] [CrossRef]
- Morillas, L.; García, M.; Nieto, H.; Villagarcia, L.; Sandholt, I.; Gonzalez-Dugo, M.P.; Zarco-Tejada, P.J.; Domingo, F. Using radiometric surface temperature for surface energy flux estimation in Mediterranean drylands from a two-source perspective. Remote Sens. Environ. 2013, 136, 234–246. [Google Scholar] [CrossRef] [Green Version]
- Choudhury, B.J.; Monteith, J.L. A four-layer model for the heat budget of homogeneous land surfaces. Q. J. R. Meteorol. Soc. 1988, 114, 373–398. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Gurney, R.J. The theoretical relationship between foliage temperature and canopy resistance in sparse crops. Q. J. R. Meteorol. Soc. 1990, 116, 497–519. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops-an energy combination theory. Q. J. R. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Boulet, G.; Braud, I.; Vauclin, M. Study of the mechanisms of evaporation under arid conditions using a detailed model of the soil–atmosphere continuum. Application to the EFEDA I experiment. J. Hydrol. 1997, 193, 114–141. [Google Scholar] [CrossRef]
- Gentine, P.; Entekhabi, D.; Chehbouni, A.; Boulet, G.; Duchemin, B. Analysis of evaporative fraction diurnal behaviour. Agric. For. Meteorol. 2007, 143, 13–29. [Google Scholar] [CrossRef] [Green Version]
- Masson, V.; Champeaux, J.-L.; Chauvin, F.; Meriguet, C.; Lacaze, R. A Global Database of Land Surface Parameters at 1-km Resolution in Meteorological and Climate Models. J. Clim. 2003, 16, 1261–1282. [Google Scholar] [CrossRef] [Green Version]
- Kustas, W.P.; Daughtry, C.S.T. Estimation of the soil heat flux/net radiation ratio from spectral data. Agric. For. Meteorol. 1990, 49, 205–223. [Google Scholar] [CrossRef]
- Olioso, A. Estimating the difference between brightness and surface temperatures for a vegetal canopy. Agric. For. Meteorol. 1995, 72, 237–242. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef] [Green Version]
- Béziat, P.; Ceschia, E.; Dedieu, G. Carbon balance of a three crop succession over two cropland sites in South West France. Agric. For. Meteorol. 2009, 149, 1628–1645. [Google Scholar] [CrossRef] [Green Version]
- Garrigues, S.; Olioso, A.; Calvet, J.C.; Martin, E.; Lafont, S.; Moulin, S.; Chanzy, A.; Marloie, O.; Buis, S.; Desfonds, V.; et al. Evaluation of land surface model simulations of evapotranspiration over a 12-year crop succession: Impact of soil hydraulic and vegetation properties. Hydrol. Earth Syst. Sci. 2015, 19, 3109–3131. [Google Scholar] [CrossRef]
- Chemidlin Prévost-Bouré, N.; Soudani, K.; Damesin, C.; Berveiller, D.; Lata, J.-C.; Dufrêne, E. Increase in aboveground fresh litter quantity over-stimulates soil respiration in a temperate deciduous forest. Appl. Soil Ecol. 2010, 46, 26–34. [Google Scholar] [CrossRef]
- Soudani, K.; Hmimina, G.; Delpierre, N.; Pontailler, J.-Y.; Aubinet, M.; Bonal, D.; Caquet, B.; de Grandcourt, A.; Burban, B.; Flechard, C.; et al. Ground-based Network of NDVI measurements for tracking temporal dynamics of canopy structure and vegetation phenology in different biomes. Remote Sens. Environ. 2012, 123, 234–245. [Google Scholar] [CrossRef]
- Chebbi, W.; Boulet, G.; Le Dantec, V.; Lili Chabaane, Z.; Fanise, P.; Mougenot, B.; Ayari, H. Analysis of evapotranspiration components of a rainfed olive orchard during three contrasting years in a semi-arid climate. Agric. For. Meteorol. 2018, 256–257, 159–178. [Google Scholar] [CrossRef]
- Boulet, G.; Olioso, A.; Ceschia, E.; Marloie, O.; Coudert, B.; Rivalland, V.; Chirouze, J.; Chehbouni, G. An empirical expression to relate aerodynamic and surface temperatures for use within single-source energy balance models. Agric. For. Meteorol. 2012, 161, 148–155. [Google Scholar] [CrossRef] [Green Version]
- Cappelaere, B.; Descroix, L.; Lebel, T.; Boulain, N.; Ramier, D.; Laurent, J.-P.; Favreau, G.; Boubkraoui, S.; Boucher, M.; Bouzou Moussa, I.; et al. The AMMA-CATCH experiment in the cultivated Sahelian area of south-west Niger—Investigating water cycle response to a fluctuating climate and changing environment. J. Hydrol. 2009, 375, 34–51. [Google Scholar] [CrossRef]
- Lebel, T.; Cappelaere, B.; Galle, S.; Hanan, N.; Kergoat, L.; Levis, S.; Vieux, B.; Descroix, L.; Gosset, M.; Mougin, E.; et al. AMMA-CATCH studies in the Sahelian region of West-Africa: An overview. J. Hydrol. 2009, 375, 3–13. [Google Scholar] [CrossRef] [Green Version]
- Velluet, C.; Demarty, J.; Cappelaere, B.; Braud, I.; Issoufou, H.B.A.; Boulain, N.; Ramier, D.; Mainassara, I.; Charvet, G.; Boucher, M.; et al. Building a field- and model-based climatology of surface energy and water cycles for dominant land cover types in the cultivated Sahel. Annual budgets and seasonality. Hydrol. Earth Syst. Sci. 2014, 18, 5001–5024. [Google Scholar] [CrossRef]
- Merlin, O.; Al Bitar, A.; Rivalland, V.; Béziat, P.; Ceschia, E.; Dedieu, G. An Analytical Model of Evaporation Efficiency for Unsaturated Soil Surfaces with an Arbitrary Thickness. J. Appl. Meteorol. Climatol. 2011, 50, 457–471. [Google Scholar] [CrossRef] [Green Version]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Jaeger, E.B.; Anders, I.; Lüthi, D.; Rockel, B.; Schär, C.; Seneviratne, S.I. Analysis of ERA40-driven CLM simulations for Europe. Meteorol. Z. 2008, 17, 349–367. [Google Scholar] [CrossRef]
- Krinner, G.; Viovy, N.; de Noblet-Ducoudré, N.; Ogée, J.; Polcher, J.; Friedlingstein, P.; Ciais, P.; Sitch, S.; Prentice, I.C. A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system. Glob. Biogeochem. Cycles 2005, 19, GB1015. [Google Scholar] [CrossRef]
- Boone, A.; Samuelsson, P.; Gollvik, S.; Napoly, A.; Jarlan, L.; Brun, E.; Decharme, B. The interactions between soil-biosphere-atmosphere land surface model with a multi-energy balance (ISBA-MEB) option in SURFEXv8—Part 1: Model description. Geosci. Model Dev. 2017, 10, 843–872. [Google Scholar] [CrossRef]
- Van den Hurk, B.J.J.M.; McNaughton, K.G. Implementation of near-field dispersion in a simple two-layer surface resistance model. J. Hydrol. 1995, 166, 293–311. [Google Scholar] [CrossRef]
- Weiss, M.; Troufleau, D.; Barret, F.; Chauki, H.; Prévot, L.; Olioso, A.; Bruguier, N.; Brisson, N. Coupling canopy functioning and radiative transfer models for remote sensing data assimilation. Agric. For. Meteorol. 2001, 108, 113–128. [Google Scholar] [CrossRef]
- Brisson, N.; Casals, M.L. Canopy senescence: A key factor in drought resistance of durum wheat. In Proceedings of the International Conference Land Water Resource Management in the Mediterranean Regions Tecnomack, Bari, Italy, 4–8 September 1994; Volume 5. [Google Scholar]
- Gentine, P.; Entekhabi, D.; Polcher, J. Spectral Behaviour of a Coupled Land-Surface and Boundary-Layer System. Bound.-Layer Meteorol. 2010, 134, 157–180. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Bach, M.; Sobrino, J.A.; Boulet, G.; Briottet, X.; Cherchali, S.; Coudert, B.; Dadou, I.; Dedieu, G.; Gamet, P.; et al. The MISTIGRI thermal infrared project: Scientific objectives and mission specifications. Int. J. Remote Sens. 2013, 34, 3437–3466. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Irvine, M.; Dupont, S. Atmospheric turbulence induced errors on measurements of surface temperature from space. Remote Sens. Environ. 2015, 168, 40–53. [Google Scholar] [CrossRef]
- Tardy, B.; Rivalland, V.; Huc, M.; Hagolle, O.; Marcq, S.; Boulet, G. A Software Tool for Atmospheric Correction and Surface Temperature Estimation of Landsat Infrared Thermal Data. Remote Sens. 2016, 8, 696. [Google Scholar] [CrossRef] [Green Version]
- Duffour, C.; Olioso, A.; Demarty, J.; Van der Tol, C.; Lagouarde, J.-P. An evaluation of SCOPE: A tool to simulate the directional anisotropy of satellite-measured surface temperatures. Remote Sens. Environ. 2015, 158, 362–375. [Google Scholar] [CrossRef]
- Lagouarde, J.P.; Dayau, S.; Moreau, P.; Guyon, D. Directional Anisotropy of Brightness Surface Temperature Over Vineyards: Case Study Over the Medoc Region (SW France). IEEE Geosci. Remote Sens. Lett. 2014, 11, 574–578. [Google Scholar] [CrossRef]
- Luquet, D.; Vidal, A.; Dauzat, J.; Bégué, A.; Olioso, A.; Clouvel, P. Using directional TIR measurements and 3D simulations to assess the limitations and opportunities of water stress indices. Remote Sens. Environ. 2004, 90, 53–62. [Google Scholar] [CrossRef]



| Site Name (Country) | Ecosystem | Studied Year | Name Code | Maximal Observed LAI (m2 m−2) | Number of Stress Periods | Soil Type (%Clay/%Sand) | Irrigation (mm) | Soil Albedo | Energy Balance Closure |
|---|---|---|---|---|---|---|---|---|---|
| Auradé (FR) | Wheat | 2006 | Aur W 2006 | 3.1 | 1 | 32/21 | 0 | 0.25 | 93% |
| Auradé (FR) | Sunflower | 2007 | Aur Su 2007 | 1.7 | 0 | 32/21 | 0 | 0.25 | 88% |
| Auradé (FR) | Wheat | 2008 | Aur W 2008 | 2.4 | 0 | 32/21 | 0 | 0.25 | 89% |
| Lamasquère (FR) | Wheat | 2007 | Lam W 2007 | 4.5 | 0 | 54/12 | 0 | 0.25 | 94% |
| Lamasquère (FR) | Wheat | 2009 | Lam W 2009 | 1.7 | 0 | 54/12 | 0 | 0.25 | 92% |
| Lamasquère (FR) | Wheat | 2011 | Lam W 2011 | 5.5 | 0 | 54/12 | 0 | 0.25 | 73% |
| Lamasquère (FR) | Wheat | 2013 | Lam W 2013 | 3.6 | 0 | 54/12 | 0 | 0.25 | 93% |
| Avignon (FR) | Peas | 2005 | Avi P 2005 | 2.8 | 0 | 33/14 | 100 | 0.25 | 95% |
| Avignon (FR) | Wheat | 2006 | Avi W 2006 | 5.5 | 0 | 33/14 | 20 | 0.25 | 94% |
| Avignon (FR) | Sorghum | 2007 | Avi So 2007 | 3.0 | 1 | 33/14 | 80 | 0.25 | 95% |
| Avignon (FR) | Wheat | 2008 | Avi W 2008 | 1.9 | 2 | 33/14 | 20 | 0.25 | 95% |
| Avignon (FR) | Wheat | 2010 | Avi W 2010 | 6.1 | 0 | 33/14 | 0 | 0.25 | 71% |
| Avignon (FR) | Wheat | 2012 | Avi W 2012 | 1.1 | 3 | 33/14 | 0 | 0.25 | 96% |
| Avignon (FR) | Sunflower | 2013 | Avi Su 2013 | 2.3 | 2 | 33/14 | 0 | 0.25 | 95% |
| Barbeau (FR) | Oak forest | 2015 | Bar Oa 2015 | 5.5 | 1 | 19/32 | 0 | 0.15 | 69% |
| Kairouan (TU) | Wheat | 2012 | Kai W 2012 | 2.1 | 0 | 31/40 | 0 | 0.25 | 60% |
| Kairouan (TU) | Olive | 2012–2015 | Kai Ol 2013 | 0.2 | 4 | 8/88 | 0 | 0.29 | 55% |
| Haouz (MO) | Wheat | 2004 | Hao W 2004 | 4.1 | 2 | 34/20 | 170 | 0.20 | 93% |
| Wankama-M (NI) | Millet | 2009 | Wan M 2009 | 0.4 | 1 | 13/85 | 0 | 0.30 | 91% |
| Wankama-F (NI) | Savannah | 2009 | Wan S 2009 | 0.3 | 0 | 13/85 | 0 | 0.30 | 91% |
| LE | Boundings | no | yes | ||||
| Performances | RMSE (W m−2) | NI | Bias (W m−2) | RMSE (W m−2) | NI | Bias (W m−2) | |
| SPARSE PATCH | 61 | 0.62 | 10 | 59 | 0.65 | 2 | |
| SPARSE LAYER | 64 | 0.58 | 8 | 58 | 0.66 | −4 | |
| H | Boundings | no | Yes | ||||
| Performances | RMSE (W m−2) | NI | Bias (W m−2) | RMSE (W m−2) | NI | Bias (W m−2) | |
| SPARSE PATCH | 68 | 0.52 | −15 | 68 | 0.51 | −10 | |
| SPARSE LAYER | 70 | 0.49 | −11 | 70 | 0.48 | −4 | |
| Rn | Boundings | no | Yes | ||||
| Performances | RMSE (W m−2) | NI | Bias (W m−2) | RMSE (W m−2) | NI | Bias (W m−2) | |
| SPARSE PATCH | 50 | 0.91 | −6 | 56 | 0.88 | −5 | |
| SPARSE LAYER | 50 | 0.91 | −3 | 52 | 0.89 | −4 | |
| G | Boundings | no | Yes | ||||
| Performances | RMSE (W m−2) | NI | Bias (W m−2) | RMSE (W m−2) | NI | Bias (W m−2) | |
| SPARSE PATCH | 56 | −0.19 | 39 | 56 | −0.19 | 38 | |
| SPARSE LAYER | 54 | −0.09 | 35 | 54 | −0.09 | 35 | |
| Whole Year | Summer | Fall | Winter | Spring | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | NI | Bias | RMSE | NI | Bias | RMSE | NI | Bias | RMSE | NI | Bias | RMSE | NI | Bias | |
| Aur W 2006 | 63 | 0.65 | −5 | 41 | 0.85 | 13 | 40 | 0.76 | −3 | 80 | 0.56 | 6 | |||
| Aur Su 2007 | 87 | 0.12 | 17 | 76 | 0.25 | 12 | 98 | −0.01 | 22 | ||||||
| Aur W 2008 | 59 | 0.34 | 16 | 48 | 0.42 | 16 | 48 | 0.42 | 17 | 65 | 0.26 | 18 | |||
| Lam W 2007 | 60 | 0.65 | 7 | 42 | 0.77 | 2 | 34 | 0.81 | −3 | 68 | 0.74 | 11 | |||
| Lam W 2009 | 74 | 0.18 | 32 | 30 | 0.74 | −15 | 47 | 0.46 | 26 | 73 | 0.53 | 28 | |||
| Lam W 2011 | 32 | 0.22 | −20 | 32 | 0.23 | −20 | 24 | 0.00 | −24 | 63 | 0.61 | 12 | |||
| Lam W 2013 | 70 | 0.81 | −41 | 55 | 0.83 | −38 | 35 | 0.92 | −9 | 85 | 0.83 | 59 | |||
| Avi P 2005 | 72 | 0.62 | 17 | 46 | 0.74 | 3 | 87 | 0.57 | 3 | ||||||
| Avi W 2006 | 56 | 0.70 | 2 | 60 | 0.42 | −49 | 30 | 0.83 | −1 | 84 | 0.70 | 51 | |||
| Avi So 2007 | 93 | 0.84 | −2 | 86 | 0.87 | 5 | 53 | −0.49 | 21 | 104 | 0.81 | −36 | |||
| Avi W 2008 | 79 | 0.44 | −29 | 62 | 0.54 | −51 | 62 | 0.52 | −31 | 86 | 0.54 | 38 | |||
| Avi W 2012 | 52 | 0.86 | 7 | 34 | 0.79 | −21 | 38 | 0.73 | 14 | 72 | 0.85 | 22 | |||
| Avi Su 2013 | 86 | 0.12 | −3 | 76 | 0.25 | −18 | 98 | −0.01 | −24 | ||||||
| Bar Oa 2015 | 64 | 0.67 | −25 | 76 | 0.61 | −28 | 37 | 0.88 | −4 | 68 | 0.58 | −37 | |||
| Kai W 2012 | 44 | 0.76 | −14 | 40 | 0.73 | 1 | 47 | 0.77 | −26 | ||||||
| Kai Ol 2013 | 36 | 0.49 | −11 | 35 | 0.58 | −13 | 37 | 0.39 | −16 | 22 | 0.41 | −1 | 43 | 0.39 | −13 |
| Kai Ol 2014 | 43 | 0.23 | −25 | 44 | 0.26 | −32 | 41 | 0.22 | −21 | 43 | −0.04 | −6 | 49 | 0.21 | −32 |
| Kai Ol 2015 | 49 | 0.18 | −14 | 57 | 0.14 | −13 | 39 | 0.15 | −15 | 41 | 0.10 | −12 | |||
| Hao W 2004 | 57 | 0.63 | −19 | 49 | 0.74 | −16 | 69 | 0.42 | −23 | ||||||
| Wan F 2009 | 55 | 0.68 | −10 | 79 | 0.61 | −55 | 32 | 0.76 | 8 | 45 | 0.70 | 15 | |||
| Wan M 2009 | 65 | 0.45 | 9 | 62 | 0.71 | 12 | 51 | 0.36 | −37 | 83 | 0.02 | 66 | |||
| Acquisition Time | 10:30 | 13:30 | ||
|---|---|---|---|---|
| RMSE | RMSE | |||
| Auradé (FR) | Wheat | 2006 | 0.19 | 0.27 |
| Avignon (FR) | Sorghum | 2007 | 0.28 | 0.22 |
| Avignon (FR) | Wheat | 2008 | 0.15 | 0.10 |
| Avignon (FR) | Wheat | 2008 | 0.21 | 0.14 |
| Avignon (FR) | Wheat | 2012 | 0.35 | 0.11 |
| Avignon (FR) | Wheat | 2012 | 0.25 | 0.19 |
| Avignon (FR) | Wheat | 2012 | 0.25 | 0.24 |
| Avignon (FR) | Sunflower | 2013 | 0.25 | 0.14 |
| Barbeau (FR) | Oak forest | 2015 | 0.27 | 0.09 |
| Sidi Rahal (MO) | Wheat | 2004 | 0.24 | 0.26 |
| Sidi Rahal (MO) | Wheat | 2004 | 0.25 | 0.18 |
| Niger C. (NI) | Millet | 2009 | 0.93 | 0.09 |
| Kairouan (TU) | Olive | 2013 | 0.08 | 0.16 |
| Kairouan (TU) | Olive | 2013 | 0.22 | 0.17 |
| Kairouan (TU) | Olive | 2014 | 0.17 | 0.13 |
| Kairouan (TU) | Olive | 2015 | 0.11 | 0.11 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delogu, E.; Boulet, G.; Olioso, A.; Garrigues, S.; Brut, A.; Tallec, T.; Demarty, J.; Soudani, K.; Lagouarde, J.-P. Evaluation of the SPARSE Dual-Source Model for Predicting Water Stress and Evapotranspiration from Thermal Infrared Data over Multiple Crops and Climates. Remote Sens. 2018, 10, 1806. https://doi.org/10.3390/rs10111806
Delogu E, Boulet G, Olioso A, Garrigues S, Brut A, Tallec T, Demarty J, Soudani K, Lagouarde J-P. Evaluation of the SPARSE Dual-Source Model for Predicting Water Stress and Evapotranspiration from Thermal Infrared Data over Multiple Crops and Climates. Remote Sensing. 2018; 10(11):1806. https://doi.org/10.3390/rs10111806
Chicago/Turabian StyleDelogu, Emilie, Gilles Boulet, Albert Olioso, Sébastien Garrigues, Aurore Brut, Tiphaine Tallec, Jérôme Demarty, Kamel Soudani, and Jean-Pierre Lagouarde. 2018. "Evaluation of the SPARSE Dual-Source Model for Predicting Water Stress and Evapotranspiration from Thermal Infrared Data over Multiple Crops and Climates" Remote Sensing 10, no. 11: 1806. https://doi.org/10.3390/rs10111806
APA StyleDelogu, E., Boulet, G., Olioso, A., Garrigues, S., Brut, A., Tallec, T., Demarty, J., Soudani, K., & Lagouarde, J.-P. (2018). Evaluation of the SPARSE Dual-Source Model for Predicting Water Stress and Evapotranspiration from Thermal Infrared Data over Multiple Crops and Climates. Remote Sensing, 10(11), 1806. https://doi.org/10.3390/rs10111806








