2D Frequency Domain Fully Focused SAR Processing for High PRF Radar Altimeters
Abstract
:1. Introduction
2. Context and Problem Statement
2.1. Acquisition Geometry
- The Earth is locally spherical of radius RT and fixed (i.e., not rotating);
- The satellite orbit is locally circular and the satellite height h0 is locally constant;
- The sensor speed v is constant;
- As a consequence, the tracker value (i.e., an approximate estimation that the altimeter performs to evaluate the aperture time of the receiving window) is constant along the observation time;
- The sensor attitude is nominal, i.e., the triplet {yaw, pitch, roll} are zero along the observation time;
- In the derivation of the unfocused IRF, the monostatic approximation is used (i.e., the sensor transmits and receives at the same nominal position);
- In this description, radiometry is not accounted for, nor thermal noise is included.
2.2. Unfocused IRF
2.3. Determination of 2D ETF
2.4. Unfocused IRF and ETF for Closed-Burst Acquisition
3. WK Focusing
4. Implementation of WK F/F Algorithm
- Along-track zero-padding of the raw data in the along-track direction. This processing step is needed since the along-track Fourier transform requires the time axis to be continuous and regularly spaced. In the case of closed-burst acquisition or when data acquisition is not continuous, raw data are zero-padded to fill the gaps in the non-continuous time axis. In case the ratio between the pulse and the burst repetition frequency is not an integer, an interpolation of the raw data must be implemented on a uniformly sampled time axis of reference. It has to be remarked that the impulse response function of the interpolator filter may condition the final shape of the focused IRF and this should be accounted for in an operational processor. We verified that a piecewise cubic Hermite interpolating polynomial (PCHIP) or a spline is sufficient for the treated case.
- The dataset is Fourier-transformed in the along-track direction, range by range. The theoretical reference is in Equation (3) but, in practice, the FFT algorithm is used.
- SPP solution. This block finds the stationary point by solving: . The stationary point is a function of both and , that is, it can be evaluated, in principle, for every value of the Doppler frequency and of the fast time . However, finding the roots of a fourth-order polynomial in all the along- and across-track positions may be computationally expensive (For a data block as long as an antenna footprint on ground, the minimum orbit length necessary to process is two times this length. This would correspond, using parameters in Table 1, to about 10 millions of samples for each block). A coarser grid is used in practice, obtaining the WK-focusing operator in the remaining positions by interpolation.
- Along-track compression, which consists in the multiplication of the transformed dataset by the focusing operator sample-by-sample, according to Equations (10) and (11).
- Stolt interpolation. After the compensation, the spectral support data is in the ) coordinates, while data must be represented in the ( coordinates (i.e., the transformed plane corresponding to the image space). The non-separable mapping between the two domains is commonly implemented by the Stolt interpolation. For a monochromatic wave, the relation between the wavelength and the wavenumber in along- and across-track directions iswhere , , , and is the incidence angle. The Stolt interpolation, in the time domain, still corresponds to a non-separable mapping from the data space to the image space . In the altimeter case, Equation (14) can be rearranged considering , , and . The Stolt mapping is a rather heavy interpolation of the equally spaced domain into a nonregularly spaced axis, as a function the regular sampling of the across-track wavenumber axis and of . One of the proposed simplifications, according to the acquisition geometry, consists in using a first order approximation (-dependent) of the square root: with equally spaced on the across-track wavenumber axis.
- Double inverse Fourier Transform completes the focusing, according to Equations (11) and (12). This is performed by applying the IFFT algorithm for the along-track and the FFT for the across-track directions.
- Across-track compensation, which is aimed at compensating the across-track antenna , according to Equation (2), and the impact on the signal amplitude of the reduced Doppler history as a function of the range (see Appendix B for details).
5. Results
5.1. Simulation Results
5.2. Computational Evaluation
- -
- the first term is due to zero-padding (interpolation kernel length is 4 for a piecewise cubic Hermitian interpolator);
- -
- the second term is the cost of the along-track Fourier transform, being s the increasing factor due to zero-padding, which is about (for the current parameter, s is about 3.5);
- -
- the third term is due to the SPP computation and includes the solution of the fourth-order polynomial. To solve the polynomial equation, Singular Value Decomposition is used in practical algorithms and its cost in term of multiplications is about (with n being the polynomial order). This is repeated for each sample of the coarser grid (subsampled at D1 in along-track and D2 in across-track). The further 5 multiplications are due to the generation of the polynomial coefficients and the final 4 to make the interpolation on the full grid of samples.
- -
- The fourth term is due to the focalization and along-track antenna compensation
- -
- The fifth term is due to the Stolt interpolation
- -
- The sixth term is due to the 2D inverse Fourier transform
- -
- The seventh term is due to the across-term antenna compensation
- -
- The eighth term is due to the interpolation on the output samples (that are approximately half the size in along-track).
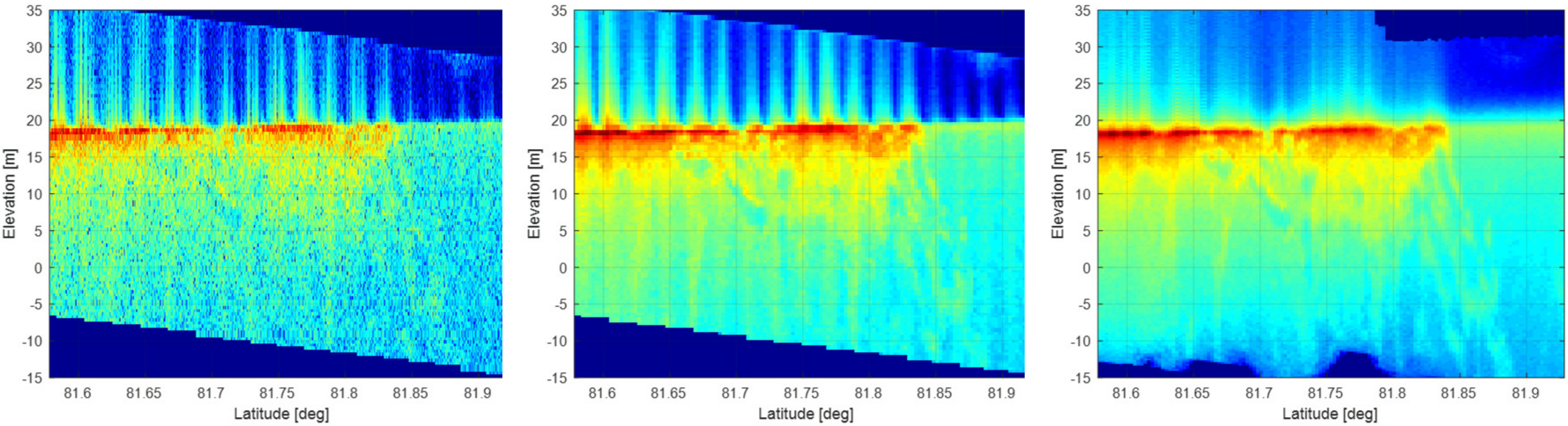
5.3. WK Algorithm on CryoSat in-Orbit Data
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Grating Lobes

Appendix B. Doppler History Length Variability

References
- Rey, L.; de Chateau-Thierry, P.; Phalippou, L.; Mavrocordatos, C.; Francis, R. SIRAL: The radar altimeter for CryoSat mission, under development. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; Volume 3, pp. 1768–1770. [Google Scholar]
- Raney, R.K. The delay/Doppler radar altimeter. IEEE Trans. Geosci. Remote. Sens. 1998, 36, 1578–1588. [Google Scholar] [CrossRef]
- Wingham, D.J.; Phalippou, L.; Mavrocordatos, C.; Wallis, D. The mean echo and echo cross-product from a beam forming, interferometric altimeter and their application to elevation measurement. IEEE Trans. Geosci. Remote. Sens. 2004, 42, 2305–2323. [Google Scholar] [CrossRef]
- Parrinello, T.; Shepherd, A.; Bouffard, J.; Badessi, S.; Casal, T.; Davidson, M.; Fornari, M.; Maestroni, E.; Scagliola, M. CryoSat: ESA’s ice mission—Eight years in space. Adv. Space Res. 2018, 62, 1177–1638. [Google Scholar] [CrossRef]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.-H.; Femenias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The Global Monitoring for Environment and Security (GMES) Sentinel-3 Mission. Remote. Sens. Environ. 2012. [Google Scholar] [CrossRef]
- Scharroo, R.; Bonekamp, H.; Ponsard, C.; Parisot, F.; von Engeln, A.; Tahtadjiev, M.; de Vriendt, K.; Montagner, F. Jason continuity of services: Continuing the Jason altimeter data records as Copernicus Sentinel-6. Ocean Sci. 2016, 12, 471–479. [Google Scholar] [CrossRef]
- Laxon, S.W.; Giles, K.A.; Ridout, A.L.; Wingham, D.J.; Willatt, R.; Cullen, R.; Kwok, R.; Schweiger, A.; Zhang, J.; Haas, C.; et al. CryoSat-2 estimates of Arctic sea ice thickness and volume. Geophys. Res. Lett. 2013, 40, 732–737. [Google Scholar] [CrossRef] [Green Version]
- Gourmelen, N.; Escorihuela, M.J.; Shepherd, A.; Foresta, L.; Muir, A.; Garcia-Mondejar, A.; Roca, M.; Baker, S.G.; Drinkwater, M.R. CryoSat-2 swath interferometric altimetry for mapping ice elevation and elevation change. Adv. Space Res. 2017. [Google Scholar] [CrossRef]
- Boy, F.; Desjonquères, J.D.; Picot, N.; Moreau, T.; Raynal, M. CryoSat-2 SAR-Mode Over Oceans: Processing Methods, Global Assessment, and Benefits. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 148–158. [Google Scholar] [CrossRef]
- Bonnefond, P.; Laurain, O.; Exertier, P.; Boy, F.; Guinle, T.; Picot, N.; Labroue, S.; Raynal, M.; Donlon, C.; Féménias, P.; et al. Calibrating the SAR SSH of Sentinel-3A and CryoSat-2 over the Corsica Facilities. Remote. Sens. 2018, 10, 92. [Google Scholar] [CrossRef]
- Dinardo, S.; Fenoglio-Marc, L.; Buchhaupt, C.; Becker, M.; Scharroo, R.; Fernandes, M.J.; Benveniste, J. Coastal SAR and PLRM altimetry in German Bight and West Baltic Sea. Adv. Space Res. 2018, 62, 1371–1404. [Google Scholar] [CrossRef]
- Boergens, E.; Nielsen, K.; Andersen, O.B.; Dettmering, D.; Seitz, F. River Levels Derived with CryoSat-2 SAR Data Classification—A Case Study in the Mekong River Basin. Remote. Sens. 2017, 9, 1238. [Google Scholar] [CrossRef]
- Raney, R.K. CryoSat SAR-mode looks revisited. IEEE Geosci. Remote. Sens. Lett. 2012, 9, 393–397. [Google Scholar] [CrossRef]
- Egido, A.; Smith, W.H.F. Fully Focused SAR Altimetry: Theory and Applications. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 392–406. [Google Scholar] [CrossRef] [Green Version]
- Holzner, J.; Bamler, R. Burst-Mode and ScanSAR Interferometry. IEEE Trans. Aerosp. Electron. Syst. 2002, 40, 1917–1934. [Google Scholar] [CrossRef]
- Bamler, R. A Systematic Comparison of SAR Focusing Algorithms. In Proceedings of the IGARSS ’91 Remote Sensing: Global Monitoring for Earth Management: 1991 International Geoscience and Remote Sensing Symposium, Espoo, Finland, 3–6 June 1991; pp. 1005–1009. [Google Scholar]
- Cafforio, C.; Prati, C.; Rocca, F. SAR data focusing using seismic migration techniques. IEEE Trans. Aerosp. Electron. Syst. 1991, 27, 194–207. [Google Scholar] [CrossRef]
- Scannapieco, F.; Renga, A.; Moccia, A. Indoor Operations by FMCW Millimeter Wave SAR Onboard Small UAS: A Simulation Approach. J. Sens. 2016. [Google Scholar] [CrossRef]
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar—System and Signal Processing; Wiley: Hoboken, NJ, USA, 1991; ISBN 978-0-471-85770-9. [Google Scholar]
- Carrara, W.G.; Goodman, R.S.; Majewski, R.M. Spotlight Synthetic Aperture Radar: Signal Processing Algorithms; Artech House: Norwood, MA, USA, 1995; ISBN-13: 978-0890067284. [Google Scholar]
- Paupolis, A. Systems and Transforms with Applications in Optics; R. Krieger Publishing Company: Malabar, FL, USA, 1968; ISBN-10 0070484570. [Google Scholar]
- C2-TN-ARS-GS-5179, CryoSat Characterization for FBR Users Corrections. June 2016. Available online: https://wiki.services.eoportal.org/tiki-download_wiki_attachment.php?attId=4233&page=CryoSat% 20Technical%20Notes&download=y (accessed on 28 February 2010).









| Symbol | Description | Used Values/UoM |
|---|---|---|
| Across-track time | s | |
| Time varying within the pulse duration: | s | |
| Along-track time | s | |
| Pulse duration | 45 μs | |
| Carrier frequency | 13.6 GHz | |
| Range sampling frequency | 320 MHz | |
| Chirp rate | 7.14 × 1012 Hz/s | |
| PRF | Pulse repetition frequency | 18.2 kHz |
| BRF | Burst repetition frequency | 85 Hz |
| Along-track antenna beam width (−3 dB) | 0.019 rad | |
| Number of samples in across-track and pulses in a burst | {128, 64} | |
| Average altitude | 730 km | |
| Local Earth radius | 6371 km | |
| Tracker distance | ||
| Radial velocity | m/s | |
| Doppler coefficient | ||
| Doppler centroid | [Hz] |
| Target (rg, az) | Method | Along-Track Resolution | Across-Track Resolution | PSLR 2nd [dB] Along/Across | Misalingment Along-Track | Misalignment Across-Track |
|---|---|---|---|---|---|---|
| 0, any | Theoret. | 0.421 m | 0.415 m | −13.26 | ||
| 40, any | Theoret. | 0.554 m | 0.415 m | |||
| 0, 0 | WK | 0.419 m | 0.410 m | −14.05/−13.19 | <10−3 m | <10−3 m |
| 40, 0 | WK | 0.559 m | 0.410 m | −13.26/−13.12 | <10−3 m | <10−3 m |
| 0, 1500 | WK | 0.419 m | 0.410 m | −14.04/−13.19 | <10−3 m | <10−3 m |
| 0, 0 | BP | 0.407 m | 0.410 m | −13.27/−13.17 | <10−3 m | <10−3 m |
| 40, 0 | BP | 0.536 m | 0.410 m | −13.27/−13.18 | <10−3 m | <10−3 m |
| 0, 1500 | BP | 0.407 m | 0.410 m | −13.27/−13.17 | <10−3 m | <10−3 m |
| Method | Cost per Sample [cplx mult] | Processing Time [s] | Theoretical Cost per Output Sample | Approximate Value Using Cryosat Parameters |
|---|---|---|---|---|
| BP | 134,564 | 8978 | Equation (15) | 123,200 |
| WK | 114 | 16.8 | Equation (16) | 135 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guccione, P.; Scagliola, M.; Giudici, D. 2D Frequency Domain Fully Focused SAR Processing for High PRF Radar Altimeters. Remote Sens. 2018, 10, 1943. https://doi.org/10.3390/rs10121943
Guccione P, Scagliola M, Giudici D. 2D Frequency Domain Fully Focused SAR Processing for High PRF Radar Altimeters. Remote Sensing. 2018; 10(12):1943. https://doi.org/10.3390/rs10121943
Chicago/Turabian StyleGuccione, Pietro, Michele Scagliola, and Davide Giudici. 2018. "2D Frequency Domain Fully Focused SAR Processing for High PRF Radar Altimeters" Remote Sensing 10, no. 12: 1943. https://doi.org/10.3390/rs10121943
APA StyleGuccione, P., Scagliola, M., & Giudici, D. (2018). 2D Frequency Domain Fully Focused SAR Processing for High PRF Radar Altimeters. Remote Sensing, 10(12), 1943. https://doi.org/10.3390/rs10121943






