Mapping Root-Zone Soil Moisture Using a Temperature–Vegetation Triangle Approach with an Unmanned Aerial System: Incorporating Surface Roughness from Structure from Motion
Abstract
:1. Introduction
2. Study Site
3. Methods
3.1. Unmanned Aerial System (UAS) and Flight Campaigns
3.2. Sensor Calibration
3.3. Image Processing and Validation
3.4. Temperature–Vegetation Triangle Approach
3.4.1. The Original “DT” Triangle Approach
3.4.2. The Modified “DT/ra” Triangle Approach
3.5. Sensitivity Test of the Modified Triangle Approach to the Canopy Height
3.6. Validation of Soil Moisture Estimates
4. Results
4.1. UAS Sensor Calibration and Data Validation
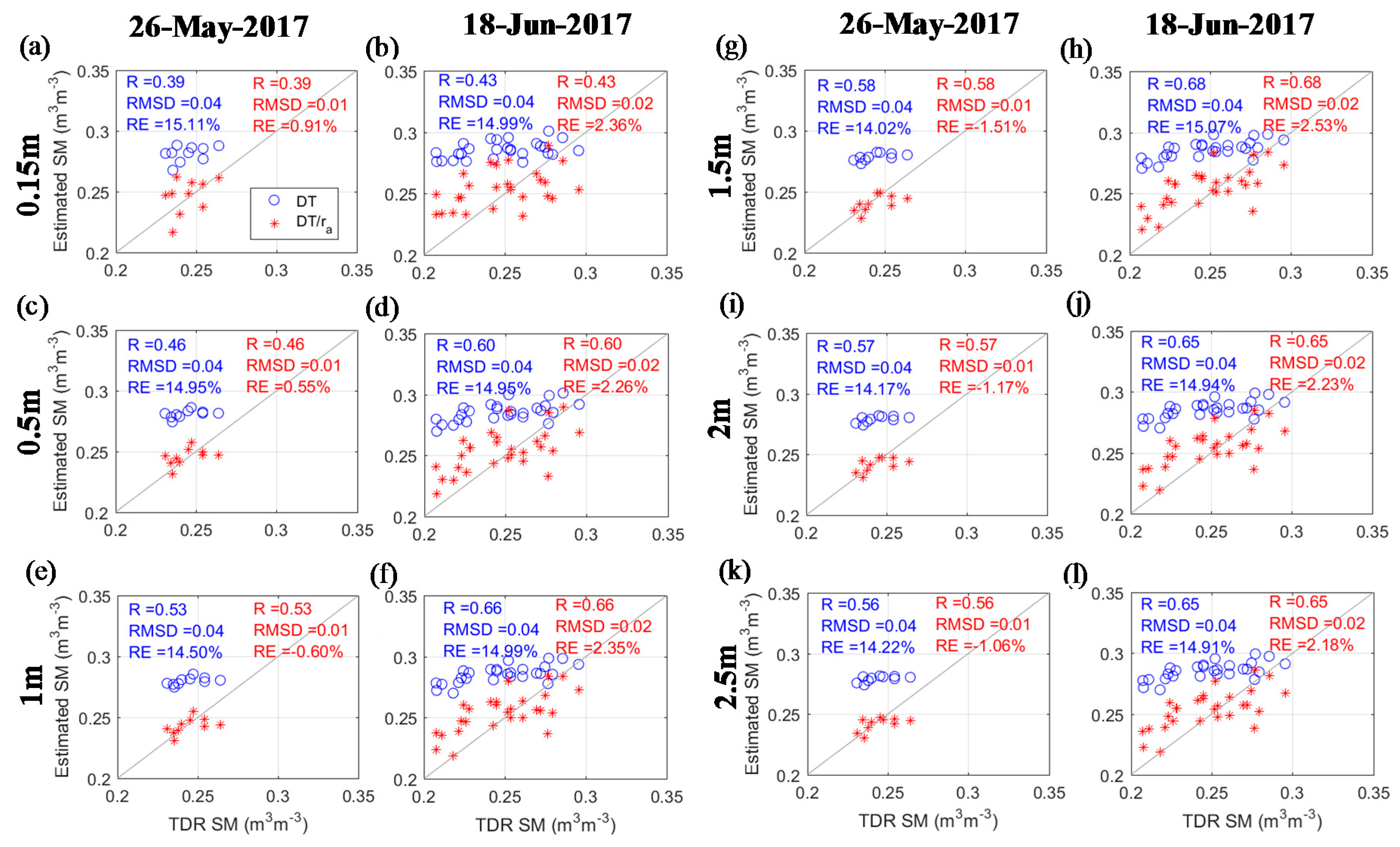
4.2. Sensitivity of the Modified Triangle Approach to the Vegetation Height
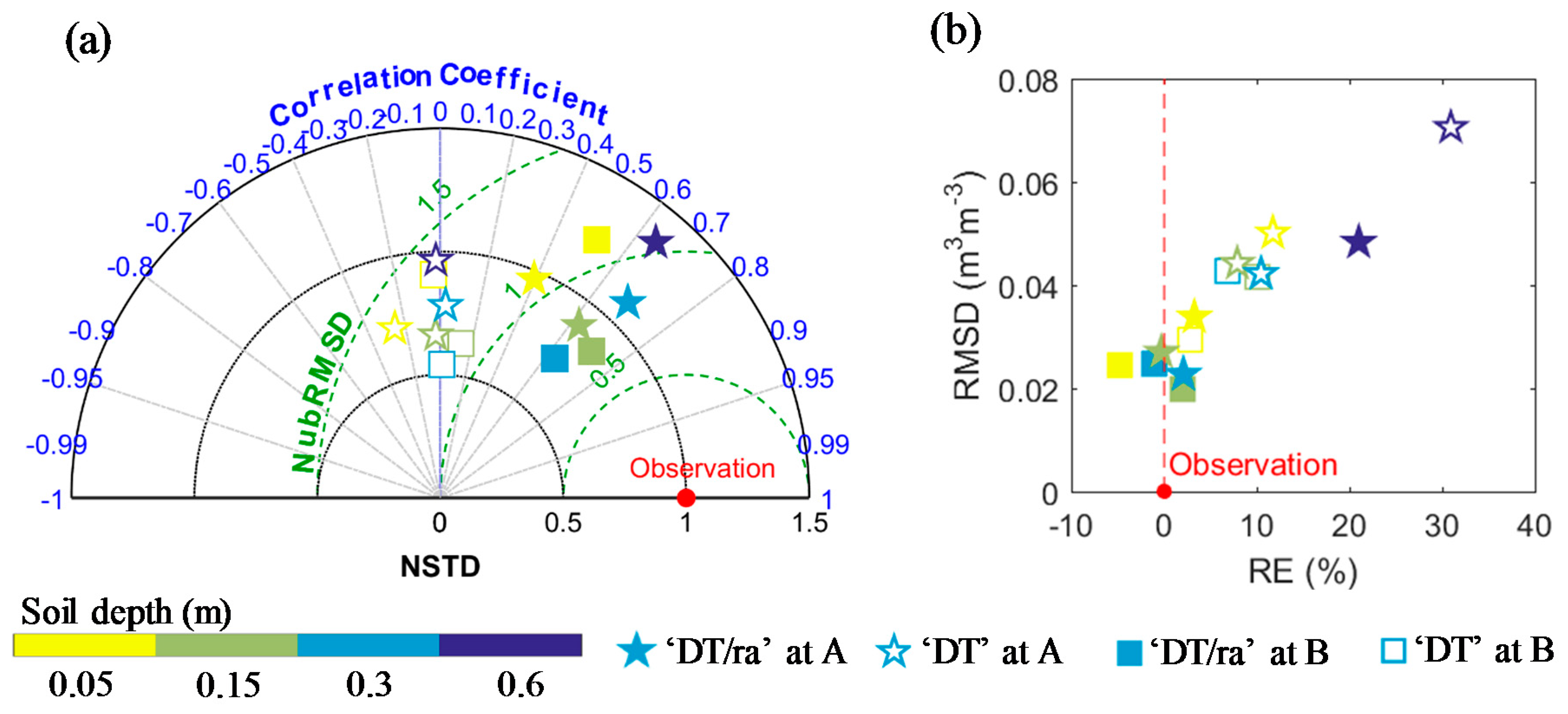
4.3. Spatial Validation of UAS Estimated Soil Moisture
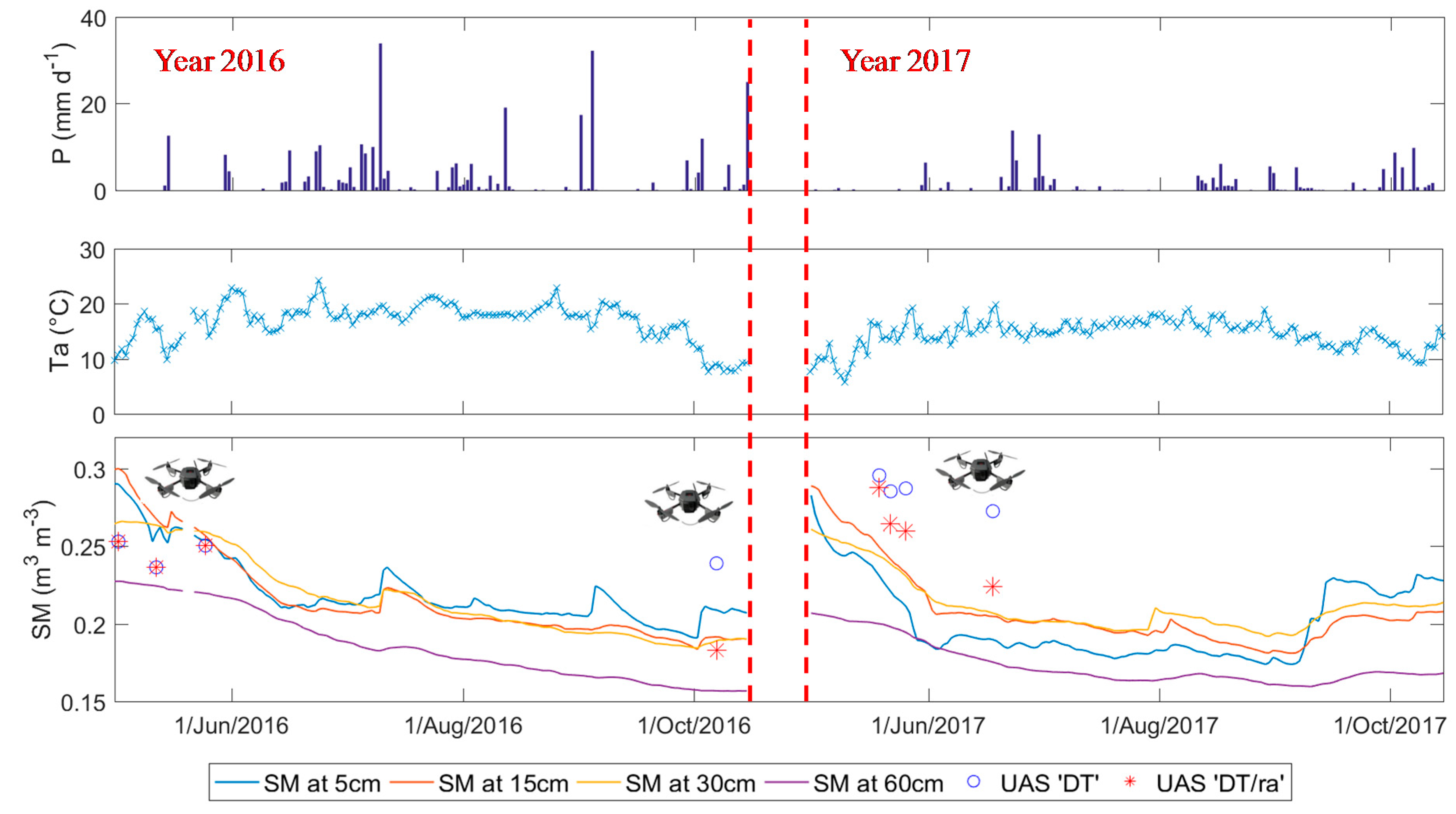
4.4. Temporal Validation of UAS Estimated Soil Moisture
5. Discussion
5.1. Linking Soil Moisture, Surface Heat Flux and the Triangle Approach
5.2. Influence of the 3D Canopy Structure to the Triangle Approach at Fine Resolution
5.3. Comparison with Other Studies
6. Conclusions
- (i)
- Accounting for changes in surface roughness considerably increased the performance of the temperature-vegetation triangle approach to estimate SM variation.
- (ii)
- Under densely vegetated conditions, the estimated SM from the triangle approach correlated better with the root-zone SM than with the surface SM (< 10 cm). This shows that the modified triangle approach is better suited to monitor water availability for vegetation compared to thermal inertia- or microwave-based approaches, which detect surface rather than deeper root-zone SM.
- (iii)
- The optimum spatial resolution or aggregation for the modified triangle approach is in the same order of magnitude as the typical length scale of the tree crowns.
- (iv)
- Given the high sensitivity of SM model to errors in surface temperature estimates, we proposed a pixel-wise sensor calibration method to improve the accuracy of the uncooled UAS thermal sensor to be around 0.55 °C for the laboratory conditions and 0.95 °C in the field.
- (v)
- The proposed methodology mainly relies on UAS observations and requires limited in-situ measurements, e.g., solar incoming radiation, air temperature and humidity, wind speed, and atmospheric pressure, and can be operationally used for routine SM monitoring in both agricultural and natural ecosystems.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture-climate interactions in a changing climate: A review. Earth-Science Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Chaney, N.; Guan, K.; Sadri, S.; Yuan, X.; Olang, L.; Amani, A.; Ali, A.; Demuth, S.; et al. A drought monitoring and forecasting system for sub-sahara african water resources and food security. Bull. Am. Meteorol. Soc. 2014, 95, 861–882. [Google Scholar] [CrossRef]
- Qiu, J.; Gao, Q.; Wang, S.; Su, Z. Comparison of temporal trends from multiple soil moisture data sets and precipitation: The implication of irrigation on regional soil moisture trend. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 17–27. [Google Scholar] [CrossRef] [Green Version]
- Hassan-Esfahani, L.; Torres-Rua, A.; Jensen, A.; McKee, M. Assessment of surface soil moisture using high-resolution multi-spectral imagery and artificial neural networks. Remote Sens. 2015, 7, 2627–2646. [Google Scholar] [CrossRef]
- Andreasen, M.; Jensen, K.H.; Desilets, D.; Franz, T.E.; Zreda, M.; Bogena, H.R.; Looms, M.C. Status and Perspectives on the Cosmic-Ray Neutron Method for Soil Moisture Estimation and Other Environmental Science Applications. Vadose Zo. J. 2017, 16, 0. [Google Scholar] [CrossRef]
- Van Doninck, J.; Peters, J.; De Baets, B.; De Clercq, E.M.; Ducheyne, E.; Verhoest, N.E.C. The potential of multitemporal Aqua and Terra MODIS apparent thermal inertia as a soil moisture indicator. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 934–941. [Google Scholar] [CrossRef]
- Petropoulos, G.; Carlson, T.N.; Wooster, M.J.; Islam, S. A review of Ts/VI remote sensing based methods for the retrieval of land surface energy fluxes and soil surface moisture. Prog. Phys. Geogr. 2009, 33, 224–250. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Scipal, K.; Parinussa, R.M.; Liu, Y.Y.; Wagner, W.; De Jeu, R.A.M.; Naeimi, V. Error characterisation of global active and passive microwave soil moisture datasets. Hydrol. Earth Syst. Sci. 2010, 14, 2605–2616. [Google Scholar] [CrossRef] [Green Version]
- Petropoulos, G.P.; Ireland, G.; Barrett, B. Surface soil moisture retrievals from remote sensing: Current status, products & future trends. Phys. Chem. Earth 2015, 83–84, 36–56. [Google Scholar] [CrossRef]
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–228. [Google Scholar] [CrossRef]
- Mallick, K.; Bhattacharya, B.K.; Patel, N.K. Estimating volumetric surface moisture content for cropped soils using a soil wetness index based on surface temperature and NDVI. Agric. For. Meteorol. 2009, 149, 1327–1342. [Google Scholar] [CrossRef]
- Wang, S.; Ibrom, A.; Bauer-Gottwein, P.; Garcia, M. Incorporating diffuse radiation into a light use efficiency and evapotranspiration model: An 11-year study in a high latitude deciduous forest. Agric. For. Meteorol. 2018, 248, 479–493. [Google Scholar] [CrossRef]
- Laliberte, A.S.; Goforth, M.A.; Steele, C.M.; Rango, A. Multispectral remote sensing from unmanned aircraft: Image processing workflows and applications for rangeland environments. Remote Sens. 2011, 3, 2529–2551. [Google Scholar] [CrossRef]
- Berni, J.; Zarco-Tejada, P.J.; Suarez, L.; Fereres, E. Thermal and Narrowband Multispectral Remote Sensing for Vegetation Monitoring From an Unmanned Aerial Vehicle. IEEE Trans. Geosci. Remote Sens. 2009, 47, 722–738. [Google Scholar] [CrossRef] [Green Version]
- Zarco-Tejada, P.J.; González-Dugo, V.; Berni, J.A.J. Fluorescence, temperature and narrow-band indices acquired from a UAV platform for water stress detection using a micro-hyperspectral imager and a thermal camera. Remote Sens. Environ. 2012, 117, 322–337. [Google Scholar] [CrossRef] [Green Version]
- Hoffmann, H.; Jensen, R.; Thomsen, A.; Nieto, H.; Rasmussen, J.; Friborg, T. Crop water stress maps for an entire growing season from visible and thermal UAV imagery. Biogeosciences 2016, 13, 6545–6563. [Google Scholar] [CrossRef] [Green Version]
- Hassan-Esfahani, L.; Torres-Rua, A.; Jensen, A.; Mckee, M. Spatial Root Zone Soil Water Content Estimation in Agricultural Lands Using Bayesian-Based Artificial Neural Networks and High- Resolution Visual, NIR, and Thermal Imagery. Irrig. Drain. 2017, 66, 273–288. [Google Scholar] [CrossRef]
- Moran, M.S.; Clarke, T.R.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar] [CrossRef]
- Wang, W.; Wang, X.; Wang, L.; Lu, Y.; Li, Y.; Sun, X. Soil moisture estimation for spring wheat in a semiarid area based on low-altitude remote-sensing data collected by small-sized unmanned aerial vehicles. J. Appl. Remote Sens. 2018, 12, 22207. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D.; Reginato, R.J. Compensating for environmental variability in the thermal inertia approach to remote sensing of soil moisture. J. Appl. Meteorol. 1976, 15, 811–817. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I.; Nørgaard, A.; Fensholt, R.; Eklundh, L. Estimation of diurnal air temperature using MSG SEVIRI data in West Africa. Remote Sens. Environ. 2007, 110, 262–274. [Google Scholar] [CrossRef]
- Jackson, R.D.; Idso, S.B.; Reginato, R.J.; Pinter, P.J. Canopy temperature as a crop water stress indicator. Water Resour. Res. 1981, 17, 1133–1138. [Google Scholar] [CrossRef]
- Yan, F.; Qin, Z.H.; Li, M.S.; Li, W.J.; Ehlers, M.; Michel, U. Progress in soil moisture estimation from remote sensing data for agricultural drought monitoring - art. no. 636601. Remote Sens. Environ. Monit. GIS Appl. Geol. VI 2006, 6366, 36601. [Google Scholar] [CrossRef]
- Luquet, D.; Vidal, A.; Dauzat, J.; Bégué, A.; Olioso, A.; Clouvel, P. Using directional TIR measurements and 3D simulations to assess the limitations and opportunities of water stress indices. Remote Sens. Environ. 2004, 90, 53–62. [Google Scholar] [CrossRef]
- Price, J.C. U sing Spatial Context in Satellite Data to Infer Regional Scale Evapotranspiration. IEEE Trans. Geosci. Remote Sens. 1990, 28, 940–948. [Google Scholar] [CrossRef]
- Carlson, T.C.; Ripley, D.A. On the relationship between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Carlson, T.N.; Gillies, R.R.; Schmugge, T.J. An interpretation of methodologies for indirect measurement of soil water content. Agric. For. Meteorol. 1995, 77, 191–205. [Google Scholar] [CrossRef]
- Garcia, M.; Fernández, N.; Villagarcía, L.; Domingo, F.; Puigdefábregas, J.; Sandholt, I. Accuracy of the Temperature-Vegetation Dryness Index using MODIS under water-limited vs. energy-limited evapotranspiration conditions. Remote Sens. Environ. 2014, 149, 100–117. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. For. Meteorol. 1999, 94, 13–29. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef] [Green Version]
- Pennypacker, S.; Baldocchi, D. Seeing the Fields and Forests: Application of Surface-Layer Theory and Flux-Tower Data to Calculating Vegetation Canopy Height. Boundary-Layer Meteorol. 2016, 158, 165–182. [Google Scholar] [CrossRef]
- Colin, J.; Faivre, R. Aerodynamic roughness length estimation from very high-resolution imaging LIDAR observations over the Heihe basin in China. Hydrol. Earth Syst. Sci. 2010, 14, 2661–2669. [Google Scholar] [CrossRef] [Green Version]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. “Structure-from-Motion” photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef] [Green Version]
- Zarco-Tejada, P.J.; Diaz-Varela, R.; Angileri, V.; Loudjani, P. Tree height quantification using very high resolution imagery acquired from an unmanned aerial vehicle (UAV) and automatic 3D photo-reconstruction methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Jia, S.; Lv, A. A time domain solution of the Modified Temperature Vegetation Dryness Index (MTVDI) for continuous soil moisture monitoring. Remote Sens. Environ. 2017, 200, 1–17. [Google Scholar] [CrossRef]
- Bandini, F.; Lopez-Tamayo, A.; Merediz-Alonso, G.; Olesen, D.; Jakobsen, J.; Wang, S.; Garcia, M.; Bauer-Gottwein, P. Unmanned aerial vehicle observations of water surface elevation and bathymetry in the cenotes and lagoons of the Yucatan Peninsula, Mexico. Hydrogeol. J. 2018, 1–16. [Google Scholar] [CrossRef]
- Wang, S.; Dam-Hansen, C.; Zarco Tejada, P.J.; Thorseth, A.; Malureanu, R.; Bandini, F.; Jakobsen, J.; Ibrom, A.; Bauer-Gottwein, P.; Garcia, M. Optimizing sensitivity of Unmanned Aerial System optical sensors for low zenith angles and cloudy conditions. Poster session presented at 10th EARSeL SIG Imaging Spectroscopy Workshop, Zurich, Switzerland. In Proceedings of the 10th EARSeL SIG Imaging Spectroscopy Workshop, Zurich, Switzerland, 19–21 April 2017. [Google Scholar]
- Choudhury, B.J.; Ahmed, N.U.; Idso, S.B.; Reginato, R.J.; Daughtry, C.S.T. Relations between evaporation coefficients and vegetation indices studied by model simulations. Remote Sens. Environ. 1994, 50, 1–17. [Google Scholar] [CrossRef]
- Van de Griend, A.A.; Owe, M. On the relationship between thermal emissivity\nand normalized vegetation index for natural surfaces. Int. J. Remote Sens. 1993, 14, 1119–1131. [Google Scholar] [CrossRef]
- Prata, A.J. A new long-wave formula for estimating downward clear-sky radiation at the surface. Q. J. R. Meteorol. Soc. 1996, 122, 1127–1151. [Google Scholar] [CrossRef]
- Korpela, I.; Heikkinen, V.; Honkavaara, E.; Rohrbach, F.; Tokola, T. Variation and directional anisotropy of reflectance at the crown scale—Implications for tree species classification in digital aerial images. Remote Sens. Environ. 2011, 115, 2062–2074. [Google Scholar] [CrossRef]
- Nieto, H.; Sandholt, I.; Aguado, I.; Chuvieco, E.; Stisen, S. Air temperature estimation with MSG-SEVIRI data: Calibration and validation of the TVX algorithm for the Iberian Peninsula. Remote Sens. Environ. 2011, 115, 107–116. [Google Scholar] [CrossRef] [Green Version]
- Long, D.; Singh, V.P.; Scanlon, B.R. Deriving theoretical boundaries to address scale dependencies of triangle models for evapotranspiration estimation. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Brutsaert, W. Evaporation into the Atmosphere. Theory, History, and Applications; D. Reidel Co.: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Garratt, J.R.; Hicks, B.B. Momentum, heat and water vapour transfer to and from natural and artificial surfaces. Q. J. R. Meteorol. Soc. 1973, 99, 680–687. [Google Scholar] [CrossRef]
- Nishida, K.; Nemani, R.R.; Running, S.W.; Glassy, J.M. An operational remote sensing algorithm of land surface evaporation. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Kustas, W.P.; Daughtry, C.S.T. Estimation of the soil heat flux/net radiation ratio from spectral data. Agric. For. Meteorol. 1990, 49, 205–223. [Google Scholar] [CrossRef]
- Kustas, W.P.; Anderson, M.C.; Norman, J.M.; Li, F. Utility of radiometric-aerodynamic temperature relations for heat flux estimation. Boundary-Layer Meteorol. 2007, 122, 167–187. [Google Scholar] [CrossRef]
- Persson, G. Willow stand evapotranspiration simulated for Swedish soils. Agric. Water Manag. 1995, 28, 271–293. [Google Scholar] [CrossRef]
- Huisman, J.A.; Snepvangers, J.; Bouten, W.; Heuvelink, G.B.M. Mapping spatial variation in surface soil water content: comparison of ground-penetrating radar and time domain reflectometry. J. Hydrol. 2002, 269, 194–207. [Google Scholar] [CrossRef]
- He, L.; Ivanov, V.Y.; Bohrer, G.; Maurer, K.D.; Vogel, C.S.; Moghaddam, M. Effects of fine-scale soil moisture and canopy heterogeneity on energy and water fluxes in a northern temperate mixed forest. Agric. For. Meteorol. 2014, 184, 243–256. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Moreno, H.A.; Mascaro, G.; Rodriguez, J.C.; Watts, C.J.; Garatuza-Payan, J.; Scott, R.L. Observed relation between evapotranspiration and soil moisture in the North American monsoon region. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Morillas, L.; García, M.; Nieto, H.; Villagarcia, L.; Sandholt, I.; Gonzalez-Dugo, M.P.; Zarco-Tejada, P.J.; Domingo, F. Using radiometric surface temperature for surface energy flux estimation in Mediterranean drylands from a two-source perspective. Remote Sens. Environ. 2013, 136, 234–246. [Google Scholar] [CrossRef] [Green Version]
- Paul-Limoges, E.; Christen, A.; Coops, N.C.; Black, T.A.; Trofymow, J.A. Estimation of aerodynamic roughness of a harvested Douglas-fir forest using airborne LiDAR. Remote Sens. Environ. 2013, 136, 225–233. [Google Scholar] [CrossRef]
- Haghighi, E.; Kirchner, J.W. Near-surface turbulence as a missing link in modeling evapotranspiration-soil moisture relationships. Water Resour. Res. 2017, 53, 5320–5344. [Google Scholar] [CrossRef]
- Bohrer, G.; Katul, G.G.; Walko, R.L.; Avissar, R. Exploring the effects of microscale structural heterogeneity of forest canopies using large-eddy simulations. Boundary-Layer Meteorol. 2009, 132, 351–382. [Google Scholar] [CrossRef]
- Raupach, M.R. Simplified expressions for vegetation roughness length and zero-plane displacement as functions of canopy height and area index. Boundary-Layer Meteorol. 1994, 71, 211–216. [Google Scholar] [CrossRef]
- Villagarcía, L.; Were, A.; Domingo, F.; García, M.; Alados-Arboledas, L. Estimation of soil boundary-layer resistance in sparse semiarid stands for evapotranspiration modelling. J. Hydrol. 2007, 342, 173–183. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Malenovskỳ, Z.; Turner, D.; Vopěnka, P. Assessment of forest structure using two UAV techniques: A comparison of airborne laser scanning and structure from motion (SfM) point clouds. Forests 2016, 7, 62. [Google Scholar] [CrossRef]
- Carlson, T. An overview of the “triangle method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar] [CrossRef]
- Phillips, C.J.; Marden, M.; Suzanne, L.M. Observations of root growth of young poplar and willow planting types. New Zeal. J. For. Sci. 2014, 44. [Google Scholar] [CrossRef]
- Fan, L.; Xiao, Q.; Wen, J.; Liu, Q.; Tang, Y.; You, D.; Wang, H.; Gong, Z.; Li, X. Evaluation of the airborne CASI/TASI Ts-VI space method for estimating near-surface soil moisture. Remote Sens. 2015, 7, 3114–3137. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Franch, B.; Mattar, C.; Jiménez-Muñoz, J.C.; Corbari, C. A method to estimate soil moisture from Airborne Hyperspectral Scanner (AHS) and ASTER data: Application to SEN2FLEX and SEN3EXP campaigns. Remote Sens. Environ. 2012, 117, 415–428. [Google Scholar] [CrossRef]
- Qiu, J.; Crow, W.T.; Mo, X.; Liu, S. Impact of Temporal Autocorrelation Mismatch on the Assimilation of Satellite-Derived Surface Soil Moisture Retrievals. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 1–9. [Google Scholar] [CrossRef]
- Babaeian, E.; Sadeghi, M.; Franz, T.E.; Jones, S.; Tuller, M. Mapping soil moisture with the OPtical TRApezoid Model (OPTRAM) based on long-term MODIS observations. Remote Sens. Environ. 2018. [Google Scholar] [CrossRef]
- Sadeghi, M.; Babaeian, E.; Tuller, M.; Jones, S.B. The optical trapezoid model: A novel approach to remote sensing of soil moisture applied to Sentinel-2 and Landsat-8 observations. Remote Sens. Environ. 2017. [Google Scholar] [CrossRef]




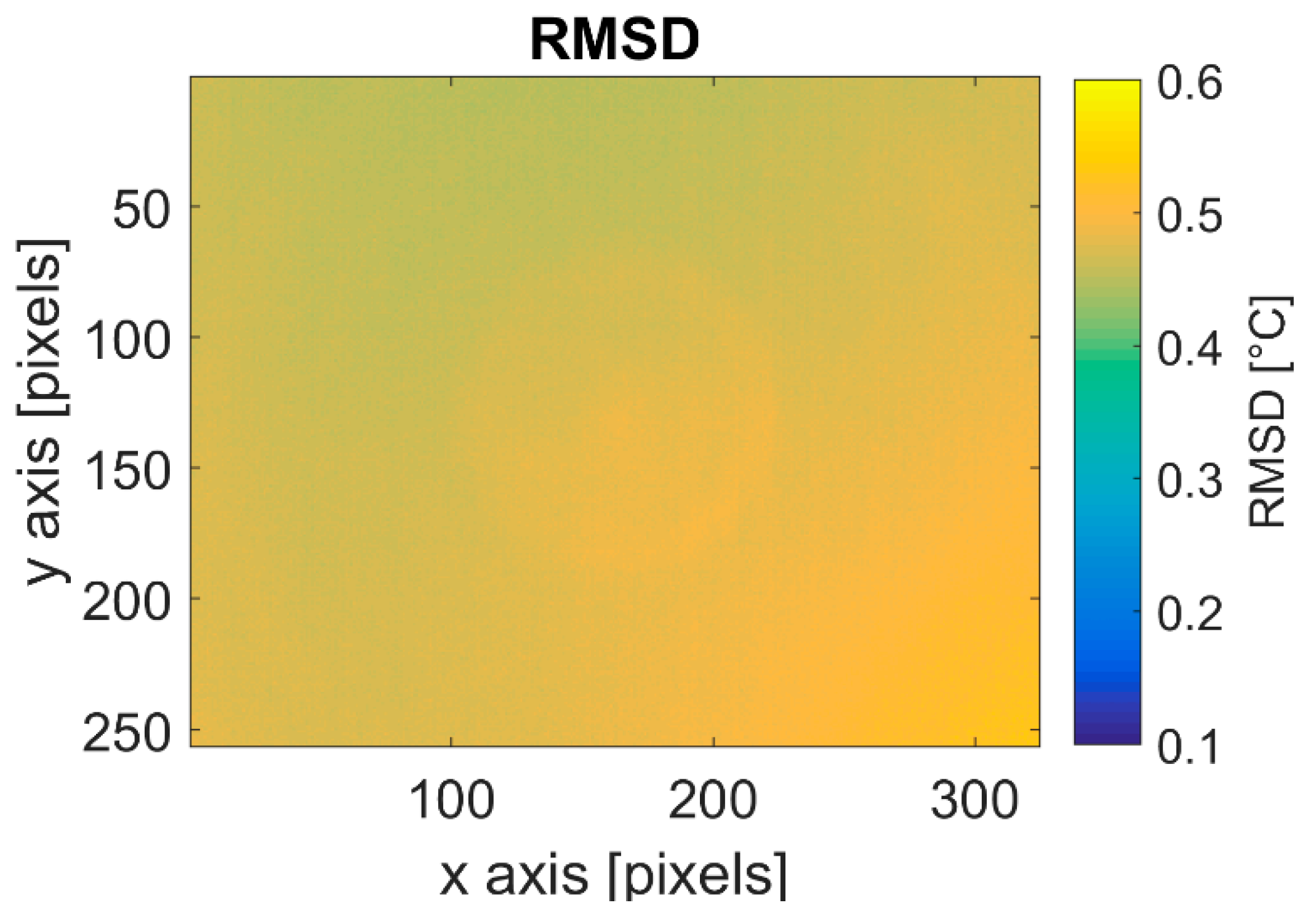



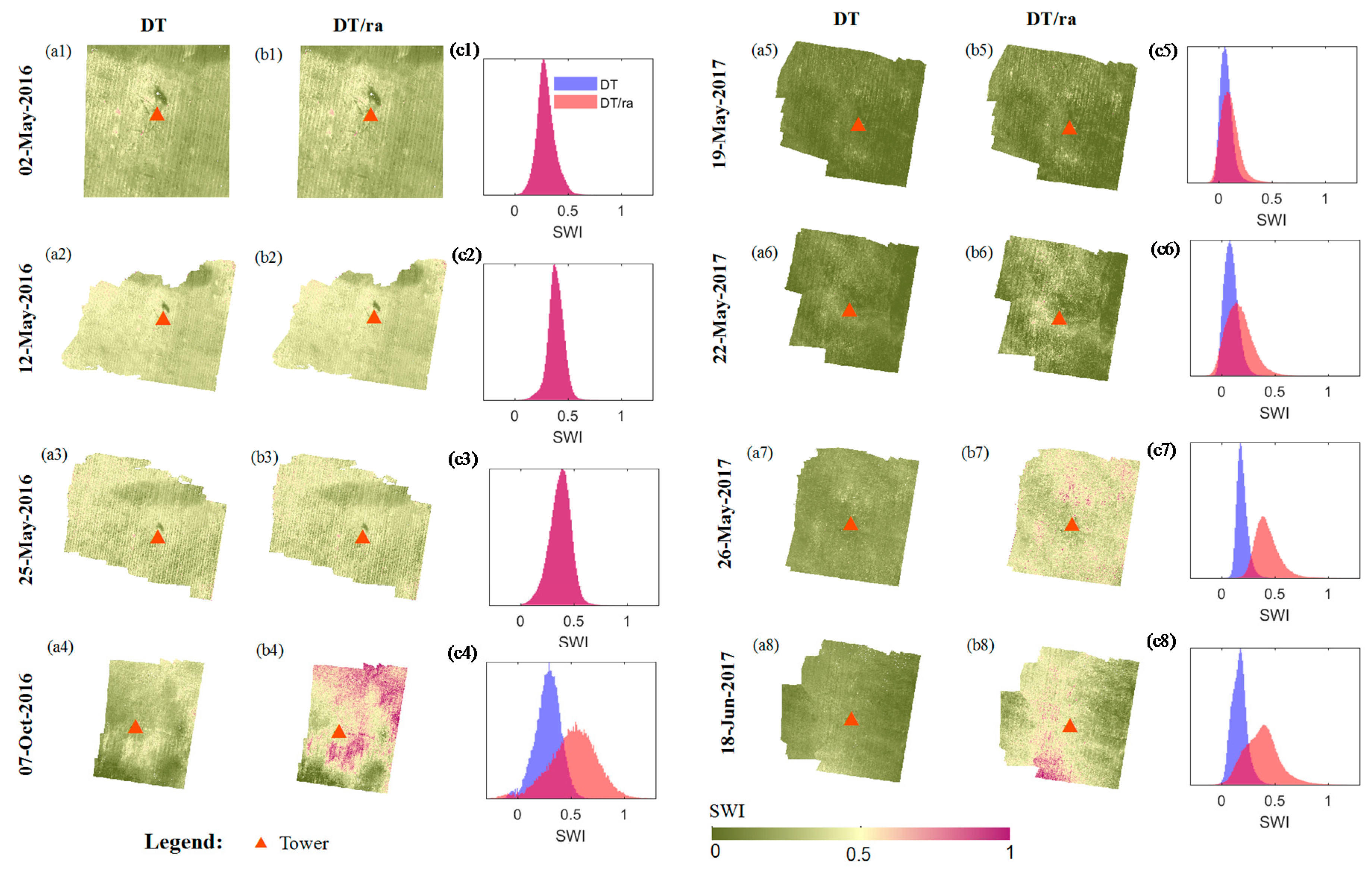

| Date | Acquisition Time | Weather | RH (%) | Ta (°C) | WS (ms−1) | Pa (kPa) | Flying Height (m) | Spatial Resolution (m) |
|---|---|---|---|---|---|---|---|---|
| 2 May 2016 | 14:40–14:55 | cloudy | 51.60 | 15.17 | 6.60 | 101.88 | 12 | 0.03 |
| 12 May 2016 | 10:44–10:55 | sunny | 45.85 | 17.31 | 5.11 | 100.62 | 12 | 0.03 |
| 25 May 2016 | 10:11–10:23 | sunny | 62.67 | 21.05 | 3.30 | 100.89 | 12 | 0.03 |
| 7 October 2016 | 11:41–11:55 | sunny | 69.87 | 9.94 | 5.62 | 102.05 | 90 | 0.3 |
| 19 May 2017 | 12:07–12:19 | sunny | 79.25 | 19.27 | 2.13 | 100.41 | 90 | 0.3 |
| 22 May 2017 | 10:15–10:28 | cloudy | 70.82 | 14.72 | 2.91 | 101.66 | 90 | 0.3 |
| 26 May 2017 1 | 11:13–11:26 | sunny | 72.56 | 16.72 | 4.47 | 101.54 | 90 | 0.3 |
| 18 June 2017 1 | 12:39–12:51 | cloudy | 71.79 | 21.81 | 4.42 | 101.62 | 90 | 0.3 |
| Approach | R | RMSD (m3∙m−3) | RE (%) | |
|---|---|---|---|---|
| DT | 0.67 | 0.04 | 15.07 | |
| DT/ra | average hc | 0.67 | 0.02 | 2.53 |
| DT/ra | Local hc for kB−1 | 0.69 | 0.02 | 1.84 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Garcia, M.; Ibrom, A.; Jakobsen, J.; Josef Köppl, C.; Mallick, K.; Looms, M.C.; Bauer-Gottwein, P. Mapping Root-Zone Soil Moisture Using a Temperature–Vegetation Triangle Approach with an Unmanned Aerial System: Incorporating Surface Roughness from Structure from Motion. Remote Sens. 2018, 10, 1978. https://doi.org/10.3390/rs10121978
Wang S, Garcia M, Ibrom A, Jakobsen J, Josef Köppl C, Mallick K, Looms MC, Bauer-Gottwein P. Mapping Root-Zone Soil Moisture Using a Temperature–Vegetation Triangle Approach with an Unmanned Aerial System: Incorporating Surface Roughness from Structure from Motion. Remote Sensing. 2018; 10(12):1978. https://doi.org/10.3390/rs10121978
Chicago/Turabian StyleWang, Sheng, Monica Garcia, Andreas Ibrom, Jakob Jakobsen, Christian Josef Köppl, Kaniska Mallick, Majken C. Looms, and Peter Bauer-Gottwein. 2018. "Mapping Root-Zone Soil Moisture Using a Temperature–Vegetation Triangle Approach with an Unmanned Aerial System: Incorporating Surface Roughness from Structure from Motion" Remote Sensing 10, no. 12: 1978. https://doi.org/10.3390/rs10121978
APA StyleWang, S., Garcia, M., Ibrom, A., Jakobsen, J., Josef Köppl, C., Mallick, K., Looms, M. C., & Bauer-Gottwein, P. (2018). Mapping Root-Zone Soil Moisture Using a Temperature–Vegetation Triangle Approach with an Unmanned Aerial System: Incorporating Surface Roughness from Structure from Motion. Remote Sensing, 10(12), 1978. https://doi.org/10.3390/rs10121978







