1. Introduction
Regardless of whether they originate from the overflow of water bodies such as lakes or rivers, or from the melting snow during spring, floods share in common their devastating impact on human lives, environment and infrastructure. And despite various efforts to reduce their socio-economic and financial impacts, these initiatives remain insufficient given the constant increase in the frequency of these phenomena due to climate changes affecting our planet. In this context, remote sensing data has repeatedly shown its interest and usefulness during the various phases of flood management process [
1,
2,
3] by providing an overview of the situation on the ground without direct contact with the flooded area and by allowing the decision makers to follow the water extent during the disaster. Hence the interest of developing new techniques to precisely delimit the extent of flooded areas based on high-resolution satellite images made increasingly available. In the literature, both SAR and optical images have been used to identify pixels associated with the flooded areas. It is obvious that identifying floods from optical images is easier than extracting them from SAR images because of the particular radiometric response that characterizes water surfaces. Techniques such as classification [
4], segmentation [
5] and fusion [
6] have been successfully applied to extract floods from optical images. However, the use of this type of data is conditioned by the absence of a cloud cover during the flooding which can occlude the mapped scene and complicates the analysis of the collected data. Unlike optical data, SAR data have been widely used to extract floods as it has the advantages of penetrating through the cloud cover and the possibility of mapping the affected region at any time of the day and night [
7]. The availability of these images has prompted worldwide researchers to propose new approaches allowing better exploitation of these data and minimizing the execution time of existing algorithms so that they meet the requirements in terms of rapid response and effective management.
Based on the thresholding of SAR backscattering value, several works have been proposed to solve the problem of flood extraction. They were mainly based on the assumption that the backscatter values of the flooded area in SAR images are very low, and therefore, it is sufficient to select pixels that are below a given threshold value to identify the affected areas. While it’s a simple technique and one of the first used in computer vision, it remains the most common and efficient way to identify flooded areas [
8]. In [
9], an automatic near-real time flood detection approach combining histogram thresholding and segmentation-based classification is described. The proposed technique apply a global thresholding integrated into a split-based approach in order to achieve a multiscale analysis of the input SAR image and extract flooded areas. Nakmuenwai et al. [
8] use multi-temporal dual-polarized RADARSAT-2 images to classify water areas by means of a clustering-based thresholding technique. Their idea consists of selecting specific water references throughout the study area to estimate local threshold values and then averages them by an area weight to obtain the threshold value for the entire area. Obtained results are very promising, nevertheless non-water objects characterized by smooth surfaces such as roads and runways are classified as water surfaces. Other works have also been based on SAR backscatter value thresholding in order to delimit the flooding extent [
10,
11,
12], however, the choice of the appropriate value of the flood separating threshold is very challenging and depends on many factors such as wavelength, incidence angle and dielectric properties of the target surface.
Change detection techniques have been widely applied in the literature to solve the problem of flooded areas extraction from SAR images [
13,
14,
15,
16,
17]. The use of these families of approaches was mainly motivated by the availability of archive images that serve as a reference to identify changes that affect the area of interest. An enhanced version of M1 and M1a change detection algorithms described in [
9] termed M2b is introduced in [
13]. While M1 only considers a single SAR flood image to extract pixels corresponding to open water via image thresholding and region growing algorithm, M2b adds change detection information with respect to a non-flood reference image to improve the algorithm’s performance. This enables the identification of non-target areas such as shadow that systematically behave as specular reflectors from images acquired during dry conditions. Traditional change detection methods such as log-ratio were applied to identify changed regions from flood images. In [
14], multi-temporal SAR data are employed to compute a polarimetric log-ratio used to highlight changes in terms of magnitude and direction. This information is, thereafter, analyzed in order to separate non-changed and changed samples. An extension of the curvelet-based change detection approach to polarimetric SAR data for monitoring flooded vegetation is proposed in [
15]. First, the Freeman–Durden decomposition is used to classify the SAR backscatter into double bounce, surface scattering and volume scattering. Then, a change detection algorithm is applied to all three channels separately based on the following hypothesis: the presence of water due to flooding is reflected by an equal increase in all three channels, whereas the change of a special scattering event only appears in the dedicated scattering mechanism intensity. Image rationing is also used in [
16] combined with Bayesian unsupervised minimum-error thresholding algorithm to extract changes generated by floods from medium and high-resolution X-band SAR images. In this work, a Generalized Gamma distribution (G
D) is chosen to accurately model the statistics of SAR amplitudes at moderate to high-resolution images. One of the major drawbacks of these change detection-based techniques is that it is complex to precisely determine the nature of the change in SAR image and to decide whether it is due to the disaster impact or originates from other events. This problem becomes more complicated if we are comparing images acquired using different polarimetric configuration where the backscatter response of the same object can appear very different from one image to another without a real change on the ground [
17].
Some known classifiers such as Support Vector Machine (SVM) and Artificiel Neural Network (ANN) were used in [
18,
19,
20] to classify the input image into flooded and non-flooded areas based on features reflecting radiometric, textural and spatial properties of SAR images. These classifiers aim at estimating the class of a region contained in the input image based on its characteristics and backscatter properties. Sakakun [
18] propose a neural network-based approach to map floods from ERS-2 and RADARSAT-1 satellite images. He applies a self organized Kohonen’s maps (SOMs) as it can be trained using unsupervised learning to produce a map that preserves the topological properties of the input space. SVM and particle filter (PF) were combined in [
19] to identify the extent of the 2001 Thailand flood. The proposed technique is mainly based on estimating SVM training model parameters using the observation system of the PF in order to define an appropriate value for these latter. Pradhan et al. [
20] apply an iterative self-organizing data analysis technique (ISODATA) to classify flooded areas from TerraSAR-X satellite images acquired during a flood event and compare the obtained result with water bodies detected from Multispectrale Landsat images. The described method works well in open areas but the accuracy is dramatically reduced in urban areas. Several classifiers such as SVMs have shown their effectiveness in flooded image classification compared to neural networks especially if applied to a small database, however, the performance of these classifiers highly rely on the quality of the extracted features.
Several works in the literature have shown the potential of object-based image analysis (OBIA) applied to SAR image [
21,
22,
23]. They concluded that speckle noise characterizing SAR images reinforces the choice of an OBIA approach since single pixel value do not only represent backscattering value but also correspond to the coherent interference of waves reflected from many elementary scatterers within a resolution cell. This is particularly true if we are dealing with the problem of flood extent analysis where it is extremely difficult to decide, based on information contained in a single pixel, whether or not it belongs to a flooded area. In [
21], a novel hybrid change detection (HCD) combining object-based change detection (OBCD) and pixel-based change detection (PBCD) is introduced. The proposed technique benefits from the complementary information provided by an OBCD and a PBCD approaches to improve the performance of flood detection from multitemporal SAR images. Arnesen et al. [
22] introduce a hierarchical object-based classification approach to monitor the Amazon River large seasonal variations in water level and flood extent. Implemented by means of a data mining algorithm, the proposed technique includes auxiliary information such as water level records, field photography, optical satellite images and topographic data. They demonstrate the potential of applying their technique to wide swath L-band SAR images for monitoring flood extent. A comparative study conducted by the German Remote Sensing Data Center (DFD) of the German Aerospace Center (DLR) and including four operational SAR-based water and flood detection approaches is described in [
23]. One of the introduced techniques termed Rapid Mapping of Flooding (RaMaFlood) gives very promising results compared to the other approaches but the need for the intervention of a human interpreter makes it unsuitable for major flooding events.
Our approach differs from existing techniques by its low sensitivity to speckle noise characterizing SAR images due to the use of kernel-based texture measurement robust to local texture variation. Also, to the best of our knowledge, a texture measurement is applied for the first time to extract floods extent from high resolution radar images. Another contribution of this work consists of introducing a novel fusion method based on the combination of spatial and radiometric information contained in each pixel and also the management of their uncertainty and contradiction using Dempster-Shafer theory applied to time-series SAR images.
The remainder of this paper is organized as follows:
Section 2 describes the study areas and the SAR data used in this work to validate the proposed approach.
Section 3 introduces our flood extent extraction algorithm and recalls the main concepts of the applied Structural Feature Set texture measurement, morphological path openings and Dempster-Shafer based fusion theory.
Section 4 and
Section 5 discuss the results obtained by applying our technique to three different sites and compares them with existing approach dealing with the same problematic. And finally,
Section 6 concludes.
3. Proposed Approach
3.1. Overview
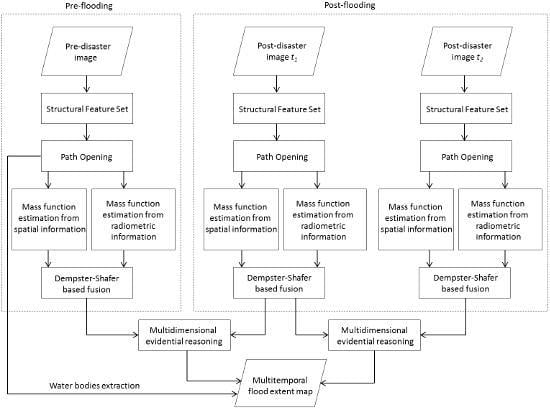
We propose a new technique capable of extracting flooded areas and monitoring their extent from time-series SAR images. The proposed approach should also be able to identify the initial surface of the studied water body in order to delimit the flooded area that has emerged as a result of the disaster impact. In case of calm water bodies, specular reflection is expected to be dominant because most of the incident radar energy is reflected away which explains their dark radiometry and homogeneous texture. This is generally true unless the water surface becomes rough due to local winds as is the case of floods. In such situations, it is rather the multiplicative model that becomes valid for an L look intensity image, where the intensity standard deviation is proportional to the mean , however, these variations remain local and the overall texture can still be considered as homogeneous. In light of these findings, we based our reasoning on the analysis of homogeneity as a discriminant feature to characterize water bodies and to distinguish them from other objects in SAR images. Many homogeneity measurements were proposed in the literature mainly based on standard deviation computation or co-occurrence matrix analysis, however, these techniques remain very sensitive to the presence of small artifacts and noises in the analyzed region. In this work, an original application of texture analysis to extract water bodies and flooded areas from SAR images is introduced. Our texture measurement provides the degree of homogeneity associated to each pixel of the analyzed window, which allows to distinguish the target classes from the rest of the image.
As shown in
Figure 2, the proposed approach is mainly based on three phases. First, the Structural Feature Set (SFS) texture measurement is applied to extract homogeneous areas characterizing not only water bodies but also other objects such as roads, agricultural fields and highways. As our objects of interest can have different shapes, we opted for the standard deviation (SD) variant of this measurement able to identify different patterns including narrow and elongated ones. We recall that at this level of the methodology our goal is not to extract water bodies in particular, but all the homogeneous areas contained in the input SAR images. This texture measurement is a pixel-wise descriptor, therefore it provides a homogeneity value associated to each pixel of the image. However, its computation from an analysis window adds more robustness to this descriptor and decreases the influence of speckle and local winds on the homogeneity computation. A morphological opening path operator is used, thereafter, with the aim to remove small homogeneous objects and noise resulting from the application of the previous step. The idea consists in filtering more information from the pre-flooding image, as it contains only the surface of a river or a lake, and filter less information from the post-flooding images as it contains objects of the pre-flooding image, in addition to flooded areas characterized by a smaller size. Regarding the choice of the structuring element, we were mainly guided by the shape of our objects of interest. Therefore, as we seek to retain both linear structures such as rivers and arbitrary ones such as lakes and flooded areas, a structuring element in the form of a path is applied. The last step consists in fusing the resulting images in pairs to determine the flooding extent as a function of time. This operation is quite difficult in our case because unlike traditional change detection problems where binary images are processed, values of our homogeneity measurement are in the range [0, 255]. To overcome this problem, we used the Dempster Shafer theory which represents a very powerful mathematical tool for combining imprecise, uncertain and conflicting sources of information. This theory was applied in this work at two levels: first, to combine a spatial-based and a radiometric-based sources of information resulting from the application of morphological profile and evidential C-means and second, to fuse mass function obtained from each image using the multidimensional evidential reasoning. The initial surface of the river or of the lake can be identified directly by applying the first two steps on the pre-flooding image, as we have already demonstrated in previous works [
29,
30].
For the sake of simplification, we will, in what follows, present the intermediate results obtained by applying each step of our algorithm to the two input images shown in
Figure 3a,b corresponding to Richelieu River pre- and post flooding SAR images. However, the proposed method was mainly designed to process time-series SAR images and can be easily generalized to handle multiple input images.
3.2. Texture Extraction Using a Structural Feature Set (SFS)
In previous works, we successfully applied the SFS texture measurement to extract homogeneous areas such as road networks from optical images [
31,
32], and water bodies from SAR images [
29,
30]. This descriptor has shown very promising results applied to optical images characterized by the presence of various artifacts arising from the use of high spatial resolution and SAR images affected by speckle noise. In general, whether for the extraction of water bodies or the identification of other structures in SAR imagery, the application of a pre-processing step is generally required. Most of the methods proposed for thresholding, contour extraction or texture analysis are very sensitive to noise in SAR images. In this work, a pre-processing step is not necessary, as our image analysis technique is mainly based on the search for homogeneous objects (homogeneous in the sense of a stationnary texture and reflectivity) in the flood extent identification process. In SAR images, the water surfaces are characterized by a high degree of homogeneity, which distinguishes them from the other land use classes in the image. This characteristic has been taken into account in the choice of the first step of our algorithm, which consists in applying the texture measurement of all structural characteristics (SFS) to extract homogeneous and elongated zones. The idea consists in using local statistics to decide whether a pixel belongs to a homogeneous zone while minimizing the influence of outlier pixels representing in our case local winds.
The so-called structural feature set (SFS) is a set of measurements used to extract the statistical features of a direction-lines histogram [
33,
34]. We introduce some concepts to define these measurements: we first define direction lines as a set of equally-spaced lines through a central pixel. For a given direction, the radiometric difference between a pixel and its central pixel is measured to determine whether this pixel lies in a homogeneous area around the central pixel. The homogeneity measurement is defined as:
where
is the homogeneity measurement of the
ith direction between the central pixel and its surrounding pixel,
and
, which represent the radiometric values of the surrounding pixel and the central pixel, respectively. The
ith direction line is extended if the following conditions are met:
Next, we define the length of all of the direction lines for a given pixel:
in which
represent the row and the column of the pixel at one end, and
the row and the column, respectively, of the pixel at the other end. We can thus define the direction-line histogram associated with a central pixel as:
where
I represents the image,
c the central pixel and
D the set of all of the direction lines. The SFS was associated with six texture measurements calculated from a histogram in [
34]. In our work, the ratio and the standard deviation (SD) measurements can be used to characterize the arbitrary shapes of flooded areas, however, it is preferable to apply the SD variant able to identify different patterns including narrow and elongated ones such as rivers and roads contained in the pre-flooding image. The SFS-SD is illustrated as follows:
where
denotes the standard deviation calculated from the direction-line histogram, and
represents the mean value of the histogram, defined as:
The aim of this step is to identify all potential candidates, consequently, not only target objects such as lakes, rivers and flooded areas will be retained, but also roads, agricultural areas and some small artifacts. Distinguishing target objects from among these structures will be addressed in the next phase. Also the choice of the two parameters and will be examined in the discussion.
Results obtained by applying the SFS-SD on the two input images are shown in
Figure 4. As we can notice, the used descriptor provides relevant information on the degree of homogeneity of each pixel of the image based on the analysis of its immediate neighbours. Therefore, a pixel belonging to a water body will appear brighter than a pixel associated to a flooded area, which in turn will appear brighter than speckle and small artifacts. The next step will be dedicated to the removal of non-target pixels by means of mathematical morphology.
3.3. Non-Target Objects Removal
The application of the previous step allowed to retain objects presenting homogeneous texture response such as rivers, lakes and flooded areas. However, other structures such as agricultural fields, small artifacts and noise have also been retained because of their very similar texture. Indeed, it is very difficult to decide based only on local information if an object is of sufficient size to be considered as an object of interest or not. In order to remedy this problem, we apply an efficient image denoising approach mainly based on mathematical morphology that allows irrelevant information to be filtered out while keeping desired object’s structure. The main challenge in the application of this family of approaches resides in the choice of the structuring element’s shape and size which depend on the target application and the dimensions of the object of interest. In our case, this choice is very complicated because our objects of interest are very varied and do not have a unique shape. If we take the example of rivers, these structures are characterized by a very small width compared to their length, therefore a structuring element with dimensions greater than the river’s width will remove it completely. On the other hand, choosing a too-small structuring element will have no effect on the noise present in the image. This leads us to use structural elements in the form of paths, as described in [
35,
36,
37], able to extract arbitrary shapes including linear structures and objects that present local linearity. We will briefly introduce the theory behind path opening and closing. For simplicity, the concept of binary image is employed in the following definitions, but the theory can be generalized to cover grayscale images as well.
Let
be a binary image, in which we first define the following relationship:
, where
x and
y are two pixels of
and the symbol ‘↦’ denotes the adjacency relationship between those two pixels and means that there is an edge going from
x to
y. This also means that x is a predecessor of y and y is a successor of x. Based on this notation, we define the dilation by:
In other words, the dilation of a subset
comprises all those points that have a predecessor in
X. The
L-tuple
is called a
-path of length
L if
, or equivalently, if:
Given a path
a in
, the set of its elements is denoted
with
. The set of all
-paths of length
L is denoted as
. The set of
-paths of length
L contained in a subset
X of
is denoted by
:
Finally, we define the opening or the path-opening
as the union of all paths of length
L in
X such that:
In the same way, we define the path-closing by simply exchanging the foreground and background. However, in this work, we will only use the path-opening operator as our object of interest is brighter than the rest of the image. This operator is mainly dependent on one parameter, termed and is used to remove objects with lengths above this predefined threshold. In order to choose its appropriate values, we were based on the following heuristics: (1) From the pre-flooding image, we want to keep only large water bodies, thus, a high value of the threshold is necessary to retain only objects of considerable size. This threshold is fixed experimentally as pixels; (2) Regarding the images acquired during the floods, water bodies are still present to which are added flooded areas characterized by a small size. In order to avoid eliminating them, we define a small value of the threshold set as , to only filter small artifacts.
Figure 5 illustrates the result of the path-opening operator applied to site 1. As expected, small objects and noise have been completely removed and only homogeneous structures with significant dimensions remain in the pre-flooding image. The content of the images acquired during the floods was also filtered in order to suppress the speckle noise, while preserving homogeneous structures of medium and large size considered as our objects of confidence. We would also like to mention that our approach is able to remove areas corresponding to agricultural fields in the image despite their considerable size because of the discontinuity between the small portions that form the field surface, which makes it impossible to find a continuous path that connects them.
3.4. Dempster–Shafer Theory Application
The last step of the algorithm is dedicated to fuse the images resulting from the application of the two previous steps two by two in order to extract the flood extent at each instant
t. This can be achieved using many fusion techniques such as possibility theory [
38] or Bayesian theory [
39] which provides a natural way to combine multiple sources of information, however, they cannot model imprecision about uncertainty measurement. It is for this reason that we apply a powerful mathematical tool for fusing incomplete and uncertain knowledge based on Dempster-Shafer theory (DST), also known as evidence theory, first introduced by Dempster [
40] and later extended by Shafer [
41]. This choice is justified by the imprecise nature of our sources of information and the uncertainty that results from the application of our texture measurement. The basic concepts of this theory are introduced in what follows.
3.4.1. Basic Concepts
Let
be the frame of discernment and
the power set composed of all possible subsets of
:
A function m(·) defined from
the power set to
is called a mass function if:
where
expresses the degree of belief committed specifically to
A and that cannot be assigned to any strict subset of
A. Each subset
A of
verifying
is called focal element of
m. It should be noted that if
∅ is a focal element, the mass
is used for representing the conflict with
and corresponds to a total conflict. If the condition
is met, the mass function
m is called a basic belief assignment (BBA).
One of the difficulties usually faced when applying DST is how to estimate mass functions. The accuracy of this estimation and the choice of the used sources of information can have a major impact on the fusion performance. In this work, we have chosen two sources of information of complementary nature which reflect not only the information provided by our texture measurement, but also the spatial information defined by the superposition of several homogeneous pixels in order to decide whether they belong to the floods class.
3.4.2. Mass Function Estimation from Radiometric Information
The first source of information is based on the radiometric information contained in the image. In our case, this information is given by the image resulting from the application of the texture measurement and the path opening operator and indicates homogeneous pixels of considerable size. From this image we can distinguish three different classes based on their gray levels: (1)
contains pixels that are not detected by the texture measurement or by the path opening operator. These pixels are characterized by a dark radiometry in the image; (2)
contains pixels that are detected by the texture measurement but not by the path opening operator. These pixels are characterized by a gray radiometry in the image; (3)
contains pixels that are detected by the texture measurement and by the path opening operator. These pixels are characterized by a clear radiometry in the image. If we reformulate our problem within the framework of DST, our three classes of interest constitute our frame of discernment
. Thereafter, we apply the evidential c-means clustering method defined in [
42] to estimate our mass functions and model all possible situations ranging from complete ignorance to full certainty concerning the class of each pixel. The smaller distance between the pixel gray level and the clustering center, the bigger degree of belief affected to the corresponding cluster.
3.4.3. Mass Function Estimation from Spatial Information
From the result obtained by applying the second step of our algorithm, we noticed that it is difficult to identify a single filter parameter suitable to handle all the objects contained in an image. Therefore, our second source of information is mainly based on spatial information obtained using several values of the paths-opening parameter in order to build a stack of images with different degrees of filtering as illustrated in
Figure 6. A pixel belonging to the class
will keep a dark radiometry compared to the rest of the images pixels, while a pixel belonging to the class
will be characterized by a clear radiometry along the different images. Let
be a vector containing the gray levels associated to the pixel of coordinates
and the images ranging from 1 to
N. Based on the previous hypothesis, we first define two prototype vectors
and
associated to the classes
and
, respectively. After that, we use the evidential K nearest neighbours (EKNN) approach [
43], which extends the classical K-nearest neighbour (K-NN) rule within the framework of DST, to estimate our mass functions from spatial information.
These reference vectors are considered as a source of information for the vector to be classified. The associated mass functions are then given by:
where
is a discounting coefficient,
the Euclidean distance between the vectors
x and
, and
a decreasing function given by:
where
is a positive real. The final belief function
is obtained by applying Dempster’s combination operator to all the partial sources of information
.
where ⊕ denotes Dempster’s conjunctive rule given by:
3.4.4. Dempster Shafer-Based Fusion
The next step consists in fusing the estimated mass functions in order to synthesize a more reliable global knowledge. Rules such as the conjunctive or Dempster’s combination rule [
44] can be used to combine these mass functions, however, these latter do not provide an effective way to manage conflict. Other studies have shown the benefit of using other combination rules such as the proportional conflict redistribution rule (PCR5) in [
45] which allows to exceed the limitations of traditional fusion rules and combines highly conflicting sources of evidence by redistributing the conflicting mass only to those elements that are involved in the conflict and proportionally to their individual masses. The PCR5 rule is given by:
where
corresponds to the conjunctive consensus defined as:
3.4.5. Multidimensional Evidential Reasoning
The first level of fusion, applied in the previous step, allowed to obtain mass functions reflecting the degree of belief allocated to each hypothesis of the frame of discernment
. We still have to fuse these mass functions computed from each image to determine the most probable change and to decide for each pixel whether it belongs to the floods class or not. In order to achieve this objective, we have based our analysis on the multidimensional evidential reasoning (MDER) approach [
46] that allows to combine multidimensional sources of information. This technique is inspired from the usual mass functions with a difference in the frame of discernment that change from
and
to
. From this frame of discernment, we deduce the power set associated to the two images
. The mass
associated to the hypothesis
is defined as:
A decision step is introduced thereafter to keep the most likely change using the maximum of the pignistic probability [
47] calculated by:
where
represents the cardinal of the set
. This rule allows the passage from a mass function to a probability function so that standard decision methods used in the context of probability theory can be applied. In our case, if the most probable hypothesis is of the form
, this pixel is assigned to floods class, otherwise it is assigned to non-floods class.
5. Discussion
Regarding the choice of the algorithm parameters, our approach for flooded areas extraction from SAR images is mainly based on the choice of the following parameters:
The parameter
indicates the maximum radiometric distance between the central pixel and its surrounding pixels. Xin et al. [
34] propose a heuristic to estimate the value of this threshold as a function of the class means. They set this value between
and
times the average SD of the Euclidean distance of the training pixel data from the class means. In this work, we set the first parameter of the direction lines to 30 given the complexity of radar images and our methodological choice to favour a low rate of false alarms. The second parameter
is associated to the maximum spatial distance between the central pixel and its surrounding pixels. It is a scale factor in the algorithm related to the image resolution and the size of the interesting objects. The value of this parameter was set in [
34] as
to
times the number of rows or columns of the image. In our case, this parameter is set to 100, a value that gives satisfactory results for most of the tested images. As mentioned in
Section 3.3, we chose two different values for the parameter
in order to keep only large water bodies from the pre-flooding image and small regions associated to flooded areas in the images acquired during the floods.
is set to 10 in the pre-flooding image and 100 in the post-flooding images, respectively.
The last point in this discussion is dedicated to analyze the benefit of integrating other types of radar data such as fully polarimetric and different wavelengths SAR to improve flooded areas mapping. Our technique is designed to extract flooded areas and open water from SAR images and its application on several sites show its effectiveness. However, we noticed, based on our experimental study, that our algorithm performs less in flooded vegetation. This is due to the relation between wavelength and penetration: the longer the wavelength, the deeper the penetration through the vegetation. Long wavelengths such as P-band radar signals (30–100 cm wavelengths) and L-band signals (15–30 cm) are able to penetrate vegetation canopies and to map wetland vegetation via double-bounce backscatter. In our case, we have images acquired using RADARSAT-2 and Senitnel-1 satellites which emit C-band (3.75–7.5 cm) signals, thus, they only penetrate open canopies or denser canopies during leaf-off conditions. We strongly recommend the use of the most appropriate wavelength depending on the characteristics of the mapped scene. Also, fully polarimetric SAR can be used to distinguish flooded vegetation based on polarimetric decompositions such as Cloude-Pottier [
57], Freeman-Durden [
58] or
m-
[
59], unlike single polarization SAR satellites which provide only amplitude data.
Image fusion can be performed at different levels: pixel, feature and decision-making levels. Each of these families of approaches has its advantages and disadvantages. Fusion as defined in reference [
54] is applied directly at pixels level, this pixel-wise fusion is the most intuitive way to combine information. However, this family of approaches is generally time-consuming. Our method and the one in [
53] apply first a preliminary step for potential candidates selection, but they all end up using a fusion technique to combine this information. We think that all these techniques share in common the use of information fusion to identify flood extent from SAR images. Therefore, the technique proposed in [
54] can be adapted to accept the binary image obtained using our method as input for the general Bayesian framework. On the other hand, our method can be easily modified so that the two input SAR images are processed to produce the InSAR coherence image (if available), which will be considered as an auxiliary information.