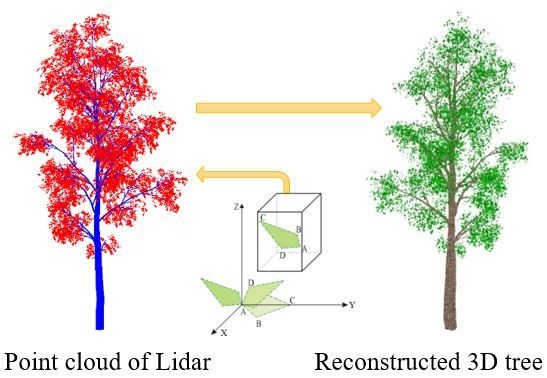
1. Introduction
The three-dimensional (3D) structure of trees, including trunk, branch, and foliage elements, is important and fundamental data for the study of forest management [
1], forest ecosystems [
2], and vegetation radiative transfer models [
3,
4].
The development of quantitative remote sensing has led to a greater focus on the real structure of ground objects, especially the vegetation structures in various radiative transfer models. Early one-dimensional (1D) radiative transfer (RT) models, such as SAIL [
5] and Suits [
6], were developed based on K-M theory [
7], and assumed horizontally homogeneous canopies, an approach that ignored the 3D structural characteristics of the canopies. Later, Li et al. [
8,
9] developed geometric-optical (GO) models that simplified the crown structures to a spheroid for a broadleaf tree or a cone for a coniferous tree to capture the 3D characteristics of forests on a coarse scale. Thereafter, a four-scale bidirectional reflectance model took into account the influence of non-uniform distributions (such as clumping effect) of branches and shoots in a conifer forest, or the “leaves” in the crowns of a broadleaf forest on the bidirectional reflectance distribution function (BRDF) [
10]. Meanwhile computer simulation models were developed based on explicit 3D virtual canopy scenes to simulate the canopy reflectance by using ray-tracing or radiosity theory [
11,
12,
13,
14,
15].
Compared to the RT and GO models, computer simulation models take advantage of computer graphics algorithms to eliminate many hypotheses and statistical rules of canopy structure and, as a result, improve the simulation accuracy greatly. However, explicit 3D structural canopy scenes are often required as fundamental input parameters and are complex and difficult to be constructed. Therefore, some computer simulation models use simplified 3D canopy structures. For example, the scenes that are used in the DART model [
16] comprise many small voxels with statistical foliage properties rather than a detailed leaf and branch structure. Huang et al. [
17] simplified the detail structures of individual tree crowns to some porous thin objects in the RAPID model, which can simplify the representation of canopy structures and decrease the computing time. All of these simplifications assumed that the statistical canopy structure would provide the same scattering behavior as the explicit 3D situation. However, Disney et al. [
18] had point out that simplified canopy scenes may cause an inherent loss of information. Widlowski et al. [
19] found that architectural simplifications may have an impact on the fidelity of simulated satellite observations at the bottom of the atmosphere for a variety of spatial resolutions, spectral bands, and viewing and illumination geometries.
For these reasons, the simple statistical parameters for crown structure (such as LAI-leaf area index, LAD-leaf angle distribution) have been unable to satisfy the requirements of quantitative remote sensing research. The latest simulation from the Radiative Transfer Model Intercomparision Initiative (RAMI-
http://rami-benchmark.jrc.ec.europa.eu/HTML/) increased the number of actual structural canopy scenes. This reflects the trend toward the development of remote sensing for vegetation. However, it is still difficult to acquire accurate 3D geometry and topology information for a real tree due to the complexity of the tree structure.
The development of terrestrial laser scanner (TLS) technology enables the use of point clouds that were scanned from trees to estimate the structural parameters for single trees or forests, including LAI, LAD [
20], and leaf area density [
21]. Additionally, point clouds are also used to reconstruct 3D trees. Most studies pay more attention to the reconstruction of branch skeletons [
22,
23,
24]. An overview of this area can be found in a review from Huang et al. [
25].
Only a few methods reconstructed a whole tree by adding leaves or needles to the reconstructed branches. For example, Xu et al. [
26] assumed that the leaf density in a real tree was uniform and determined leaf locations using the number of feasible skeleton nodes that existed within a certain distance. This method requires that even small branches be reconstructed with high accuracy. Livny et al. [
23] created leaves next to each leaf node in the branch-structure graph (BSG) and generated a random number between 20 and 50 leaves that were randomly placed within a sphere that was centered on the leaf node. They then added textures to the reconstructed geometry to enhance visual appeal. Côté et al. [
27] added foliage to reconstruct conifer trees by repeatedly testing the radiation, reflectance characteristics, and gap fraction of canopy. Their method can reconstruct 3D trees with structural and radiative consistency.
These methods of adding leaves have not made full use of the spatial information obtained from foliage point cloud distributions. In this study, an easy method for reconstructing realistic 3D trees (including trunk, branches, and leaves) is developed. This method is based on aligned point clouds that were scanned from multiple sites and combined information regarding the spatial distribution of points with retrieved structural parameters. The reconstructed trees can meet the basic demands of computer simulation models and maintain a directional gap fraction that is consistent with that of the real ones.
2. Experiment and Datasets
2.1. Study Area
The experimental field located in an open and flat prairie in Chengde city, Hebei Province, China (42°14’28.7”N, 117°04’57.29”E) is covered by the dominant grassland and scattered bushes and trees under the typical continental monsoon climate with an average annual temperature of −1.4 °C.
Four broadleaf, deciduous elm trees (Ulmaceae) with 6.0–7.5 m height and 15–25 cm diameters at breast (DBH) showed in the field center that was accompanied by approximately 3 cm understory sparse grasses. They had green leaves and a rough, dark, greyish-brown bark in summer. Some leaves were harvested and scanned with a laser scanner, and the average and maximum single-leaf areas were approximately 12 cm2 and 20 cm2, respectively.
2.2. Data Acquisition
2.2.1. Point Clouds of TLS
The experimental field was scanned by a TLS system, which included a laser scanner (Riegl VZ-1000
http://www.riegl.com) and a high-quality digital camera (Nikon D300s, Nikon Inc., Tokyo, Japan), on the 25 July 2014. The digital camera and the laser scanner were mounted together on one tripod with a pan-and-tilt platform, and a series of high-resolution color digital photographs and their accompanying point clouds were collected synchronously.
The scanning angular step was set to 0.03° and the laser scanner height was about 1 m above the ground. Six groups of point clouds were scanned from six sites around the field (
Figure 1). All of the point cloud data were exported as ASCII files using the RiSCAN PRO software (
http://www.riegl.com), a companion software package for the RIEGL Terrestrial 3D Laser Scanner Systems. The items in the file recorded each returned point’s location (XYZ coordination), distance (range [m]), beam direction (zenith and azimuth angle), reflectance (intensity), etc.
2.2.2. UAV Photographs
A six-rotor unmanned aerial vehicle (UAV) carried on a small, color digital camera was used to take RGB photographs (1024 pixel * 1024 pixel) of the experimental field from multiple view directions. The flight height of the UAV was approximately 50 m. One clear photograph taken in nadir was used in this study.
2.3. Point Cloud Data Processing
2.3.1. Elimination of Noisy Points.
Generally, there are noise points in the point cloud data due to the environment and the scanner itself, which can affect the accuracy of the retrieved canopy structural parameters and the 3D tree reconstruction. For example, ghost points occur when the laser beam hits the edge of an object. Two or more returned points will be recorded by the scanner, but with the wrong distance or intensity information. Therefore, a pre-processing step was included to eliminate ghost points.
We assume that each laser pulse will be reflected once it hits an object. Later returned signals with the same or similar beam directions are taken as ghost points, and should be deleted. First, all points are grouped into many small rectangular pyramids based on the range of zenith and azimuth angles within the width of a scanning angular step (δ). For example, the ith rectangular pyramid has the zenith range [θi − δ/2, θi + δ/2) and azimuth range [φi − δ/2, φi + δ/2). Where θi and φi are the zenith and azimuth of the ith scanning beam. The first data point in the pyramid is kept, but the others are deleted.
2.3.2. Classification
Point clouds can be classified using geometric information [
28] or intensities [
29]. In this study, all the point cloud data are classified into trunk/branch points and leaf points based on the digital photographs taken synchronously.
First, the high-resolution digital photographs are classified into leaves, trunk/branches, ground, and sky by the supervised classification method (maximum likelihood method supplied by the ENVI software). Only four classes of ROIs (region of interest), including leaves, trunk/branches, soil, and sky, are chosen manually as the training data. Therefore, parts of the ground covered with a few grasses are incorrectly classified as leaves, but these will be eliminated based on the position property of the points. Second, the photograph is registered with the point clouds using an inherent geometrical constraint [
30,
31]. Actually, the photos and points were obtained synchronously by the TLS system, therefore the registration parameters can be computed much more easily and accurately. Each point is assigned the property of leaf or branch based on the classification images. Finally, points are extracted based on the spatial scope of the tree, including leaf, trunk/branch, and soil. Soil and some misclassified leaf points on the ground are excluded according to elevation in the z direction. The height threshold z is set as 0.1 m based on the spatial characteristics of points. Then, all points with leaf and trunk/branch properties are extracted, separately.
2.3.3. Registration
A general process is carried out to register multi-station point clouds in a common coordinate system based on the RiSCAN PRO software.
It is difficult to find any natural tie points and control points in the field, so dozens of artificial spherical reflectors were pasted on the trunks or branches of the trees in the experimental field before scanning, and we made sure that no less than four reflectors can be “seen” in two neighboring scans. These reflectors can be automatically extracted from the point clouds based on their high reflectance. The same reflectors that were detected from multi-station scanned point clouds are identified as homonymy points and are registered with minimal errors. Transformation matrices are obtained for the point clouds that are based on the corresponding point pairs for the reflectors, which can be used to register the point clouds.
In this experiment, six-station scans are distributed in a ring around the experimental field, so a mode provided in the software called “Close gaps in ringed scan positions” is used to register multiple scans from a ring of positions simultaneously, which can minimize the cumulative error inherent in multiple registrations. The error of registration in all scans is less than 0.02 m.
2.3.4. Terrain
The terrain is also an important part in a 3D scene and it can be fitted to some complex curves, such as a surface or Triangulated Irregular Network (TIN) model [
32,
33]. In this study, because the field is flat in the field, all of the ground points are fitted to a plane function. Some of the grasses on the ground are ignored, and a flat terrain is composed of many triangle facets.
2.3.5. Leaf Area Retrieval
The modified gap fraction model integrating the path length distribution that was developed by Xie et al. [
34] is applied to retrieve the leaf area of single trees based on single-site leaf-point cloud data. Leaf area (LA) is defined as total single-side leaf area of a single tree with the unit of square meters (m
2). Compared with the definition of LAI, total single-side leaf area per unit ground horizontal surface area (m
2/ m
2), LA is more suitable for quantifying the leaf area of single trees.
There are four single trees in the study area. In consideration of the effect of occlusion between crowns, only three groups of points for each tree are used to retrieve LAs (
Table 1). They are scanned from three sites that covered the whole tree without any mask from the other trees. Because of the uneven distribution of leaves in the canopy and the effect of point noise (arose by sensors or environment, such as wind, etc.), it can be seen that the LAs of each tree retrieved based on the points from different scans are different. Therefore, LAs that were retrieved from different scans are averaged to decrease the effect of retrieval bias and the unevenness of crowns.
2.4. Virtual Tree
Some differences may arise in a real 3D scene due to data acquisition, such as the noise in the point clouds that arose from the TLS device and its environment during the measurement. There are also errors arose from the data processing, such as the retrieved LA of each tree and point classification and registration. To overcome these issues, a 3D virtual tree is generated and its LA can be calculated accurately. Accordingly, point clouds are simulated without noise.
2.4.1. 3D Virtual Tree
A 3D virtual tree with photorealistic structures is generated using OnyxTREE© software (
http://www.onyxtree.com), a dedicated procedural creator and modeler of 3D broadleaf trees, shrubs, and bushes. Leaves, trunks, and branches in the crown are generated and arranged based on the plant growth rules and parametric topology structures. The components of 3D trees, including leaves, trunks, and branches, are all composed of triangular patches. The software had been used to simulate the structure of deciduous broadleaf canopies for simulation of various remote sensing signals [
35]. According to the definition of LA, it can be calculated accurately using these triangular patches. LAD is another important canopy structural parameter, which describes the statistical distribution of the angular orientation of the leaves in the vegetation. In this study, we pay more attention to the orientation of each leaf normal (zenith and azimuth angles), instead of the mathematical description of total leaves angles.
In this case, the height of the virtually generated 3D tree is 8.53 m and its total leaf area is 20.32 m2. The average area of a single leaf is about 15 cm2.
2.4.2. Simulation of Point Clouds
Four groups of point clouds are simulated around the virtual tree based on the ray-tracing algorithm [
36]. The sensor height is set to 1.5 m above the ground and the horizon distance for the tree was 6 m. The scanning angle step is 0.03°.
Each simulated point is added property information (branch or leaf) in the end of the line in the file based on the intersected position of the beam and the virtual tree, which can help to classify the point clouds into two classes (branch- and leaf-point) accurately.
3. Methodology
Branches and leaves are the main components of trees, and can be reconstructed based on the classified branch- and leaf-point clouds. To reduce the effect of point cloud occlusion, the aligned point clouds from multiple scans are used here.
3.1. Reconstruction of Branches
Branch structures of single trees are constructed from the branch-point clouds using a structure-aware global optimization (SAGO) method [
24]. This method obtains the tree skeleton from a minimum distance spanning tree and then defines the stretching directions for the branches on the skeleton to recover those missing or partly occluded points.
However, most of the small terminal branches with growing leaves cannot be reconstructed correctly, because the branch points are thoroughly occluded by leaves, or they cannot be classified accurately due to the low spatial resolution of the photographs. Some of the misclassified branch points may be marked as leaf type and later used in the process of adding leaves, which can maintain consistency between the reconstructed tree gap fraction and the real one.
3.2. Adding Leaves
Generally, there are a large number and variety of leaves in the crown, and their distribution is very complex. Therefore, it is difficult to accurately recover all of the information for each leaf, including its position, orientation, and size. We assume that the spatial distribution of leaf-point density can reflect the distribution of leaf characteristics in the crown.
3.2.1. Leaf Structure Model
A leaf is simplified to a quadrilateral, which is composed of a right triangle and an equilateral triangle. It is set based on the ratio of the length and width of a clipped leaf measured in the field (
Figure 2a). This kind of leaf shape is also used by the generated virtual tree in this study. Its initial four vertex coordinates in the plane of XOY can be expressed as a four-order matrix P [
37], with a normal
N(0, 0, 1).
The lowest row represents homogeneous term in order to be convenient to transfer this polygon leaf in the space. In Equation (1),
r is a leaf shape parameter that controls the size of a leaf. The area of a leaf can be calculated as
The leaf can then be rotated and translated to the right place in the tree crown by multiplying P with rotation and translation matrices [
37], as shown in
Figure 2b.
3.2.2. Cell division and Leaf Placement
Segmenting the canopy into cubic volumes/voxels based on point clouds can provide a convenient mean of describing the spatial distribution of foliage area in the tree crown [
38] and of estimating the leaf area density [
21], LAI and LAD [
20], etc. Béland et al. [
38] investigated the optimal voxel dimensions for estimating the spatial distribution of leaf area density within the crown. They found that the optimal voxel size is a function of leaf size, branching structure, and the predominance of occlusion effects, which provides important guiding principles for the use of voxel volume in the segmentation of point clouds.
In accordance with the research of Béland et al. [
38], voxel size is set to 10 cm in this case, which is based on the averaged LA of each tree (
Table 1) and branching structure is measured in the field. Assuming that the spatial distribution of leaf areas agrees with the aligned point-cloud density, each leaf point in the crown corresponds to a finite area of leaf
, where NUM is the number of total leaf points. Therefore, based on the number of points in each voxel (
numi), the area of one leaf in the voxel can be determined using
. If the leaf area in the voxel
LAi is larger than the maximum leaf area (20 cm
2), it would be separated into a standard leaf with an area of 12 cm
2 and a smaller leaf. The leaf shape parameter for each leaf,
r, can be calculated using:
where
LAi is the leaf area in the voxel or the leaf area after division.
Leaf orientation in the voxel is also an important structural parameter. Generally, LAD can be measured in the field or estimated from point clouds using voxels [
21]. To simply the procedure of the reconstruction and decrease the needed parameters, an averaged normal direction of all the leaf points in the voxel is used as the normal direction of the added leaf. Where the normal direction for each point is calculated based on the spatial distribution of neighbor points using the CloudCompare software (
http://www.danielgm.net/cc/release/).
Leaves are placed in the appropriate cube by rotation and translation, according to their orientation and size. After the process of adding leaves is applied to all of the voxels in the scene, 3D trees with leaves are reconstructed.
3.3. Assemble 3D Scene
All single trees and terrain are reconstructed and assembled. In order to match the locations of the reconstructed trees with the real ones, the reconstructed trees are projected onto the plane to obtain the outlines of trees, and the aligned point clouds are used to outline the four trees (
Figure 1). Then, the outlines from the reconstructed trees can be registered with the outlines from the real trees. In this study, the flat terrain is applied. Therefore, all reconstructed trees can be translated in the correct position of the terrain directly, and then the 3D scene is completed.
5. Discussion
5.1. Completeness and Accuracy of the Reconstructed Tree
By applying our method to a real scene and a virtual tree, the reconstructed results show pretty well visual effects. However, after quantitatively comparing the directional gap fractions and point densities of the original and reconstructed ones, it is found that the occlusion and density distribution of points will affect the completeness and accuracy of the reconstructed tree.
As is known to all, the occlusion issue is inevitable for TLS to scan canopies. Although aligned multi-site scanned points can partly cover the shortage, the issue still cannot be solved completely for some dense crowns. For example, there are some small differences in
Figure 5, highlighted using circles. One reason is that the scanner positions that were used in the simulation do not coincide with the one in the field. Therefore, some points occluded in the measured data (circle in
Figure 5a) can be scanned in the simulation ones (
Figure 5b).
Additionally, it can be seen from
Figure 9 that the directional gap fractions are underestimated in the bottom-to-top zenith directions (45°, 63°, 76°, 90°), but overestimated in the top-to-bottom zenith direction (162°). The major reason for this difference is the effect of point cloud occlusion. Because the TLS device is often used on the ground with a bottom-to-up scanning style, the upper crowns are inevitably occluded and only a few points from the upper parts of the tree can be obtained. Another reason is that the point density distribution is not uniform: the point density is larger in the lower part of the tree but is smaller than normal in the upper part of the tree. Because the tree reconstruction depends entirely on the spatial distribution of points, more leaves are added to the lower crown. This means that the relative errors for directional gap fractions that are close to the vertical directions (such as 45° and 162°, in this case) will be enlarged.
A feasible method for addressing these issues would be to add some supplementary data, such as Airborne Laser Radar (ALS) data, which can make up for the TLS points missing from the upper crowns [
31,
42].
5.2. Sensitivity of the Leaf Shape
The leaf shape is various in the real world. It can be represented as some simple shapes. In this study, we use a quadrilateral, simplified based on the measured structure to reconstruct the trees. Similarly, the leaf can also be simplified as other shapes, such as a square or a rhombus (
Figure 10). Then, the initial four vertex coordinates can be expressed as
The leaf area can be calculated as
Then, the leaf shape parameter, r, can be obtained by and .
The virtual trees (
Figure 4a) are reconstructed using the new leaf shapes, respectively (
Figure 11). All reconstructed trees with different leaf shapes look similar.
Then point clouds of these three reconstructed virtual trees (
Figure 11a–c) are simulated based on the same parameters (the sensor height, scanning distance and step). The slicing point density of each set of point clouds is calculated and compared in
Figure 12.
These point densities agree well with the original ones. Specially, the point densities from the reconstructed trees are closer than that from the original virtual tree. RMSEs of the vertical point densities between the reconstructed trees and the original one are 1.10% (square leaf shape), 1.13% (rhombus leaf shape), and 0.88% (quadrilateral leaf shape), separately. The reconstructed tree with the typical leaf shape (quadrilateral) shows better similarity with the original one. When comparing within these reconstructed trees, RMSEs of the point densities are no more than 0.4%. It means that the reconstructed trees are more similar to each other.
Overall, our method is not sensitive to the leaf shape.
6. Conclusions
Based on TLS point cloud data, we developed the method for reconstructing entire 3D trees in this study. This method can effectively add leaves that are based on voxels and is insensitive to the leaf shape. Its performance is evaluated over a reconstructed small 3D scene and a virtual tree using the directional gap fraction and point density distribution, and it shows good consistency in leaf area and directional gap fraction of crowns when compared with the point cloud from the original ones. The relative errors of the gap fractions (the virtual tree) are less than 4.1%.
While analyzing the directional gap fraction that is based on a virtual 3D tree, it is found that the reconstructed 3D trees are influenced by the effect of point cloud occlusion because the method is completely dependent on the spatial distribution of points. Though this method may slightly underestimate the leaf area for the upper crowns, and overestimate for the lower crowns, it is still feasible and has the potential to contribute the quantitative remote sensing in canopy radiative transfer models.
Several factors that impact the reconstruction of trees and some future possible improvements are summarized, including the quality of point clouds, the point classification, and LA retrieval accuracy. First, the quality of point clouds is critical, and factors, such as occlusion and ghost points, greatly complicate the data preprocessing and decrease the structural accuracy of reconstructed trees. In the future, it will be necessary to study how TLS data can be combined with supplementary data (such as ALS-aircraft laser scanner data or UAV data) to reconstruct 3D trees and reduce the effect of occlusions. Another option would be to apply the growing rules of plants to overcome the disadvantages of point clouds. Second, point classification accuracy is dependent of the quality of photographs, the classification algorithm and the registration between points and photographs. Bad classification results not only affect the LA retrieval, but also decrease the accuracy of reconstructed branches and leaves. Dual-wavelength [
43] or multiple spectra laser sensors can help to improve the classification accuracy and to simplify the classifying process. Third, the LA of a real tree is determined using a retrieved value, and its accuracy will directly affect the reconstructed tree structure. Therefore, it is necessary to improve the retrieval algorithm for LA in the future.
In summary, the method that is presented for reconstructing 3D trees shows its potential in reconstructing complex forest scene and in evaluating the parameters of land surface ecosystem.