Intercomparison of Three Two-Source Energy Balance Models for Partitioning Evaporation and Transpiration in Semiarid Climates
Abstract
:1. Introduction
2. Theory and Methodology
2.1. TSEB-PT Model
2.2. TSEB-PM Model
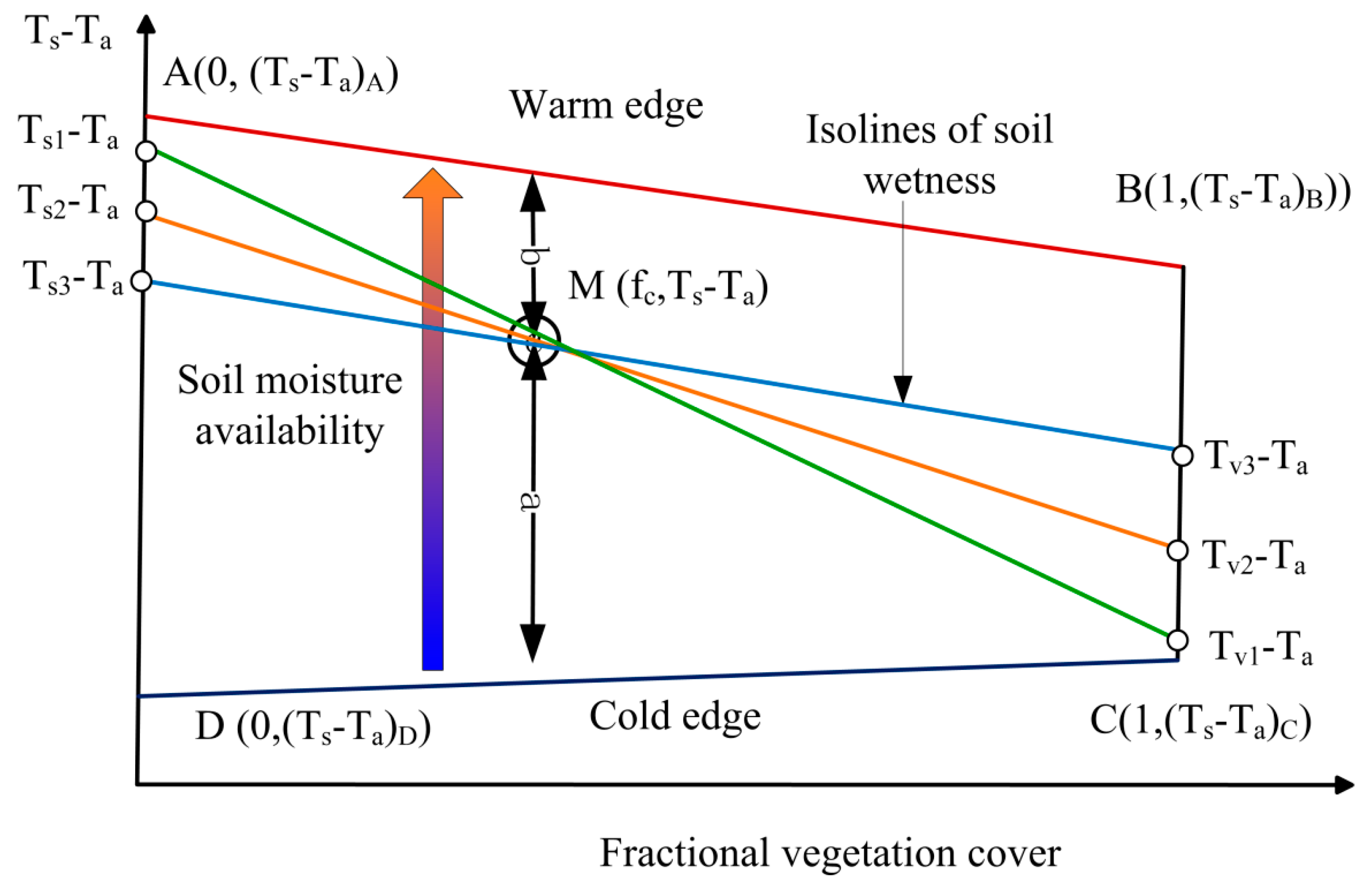
2.3. TSEB-TC-TS Model
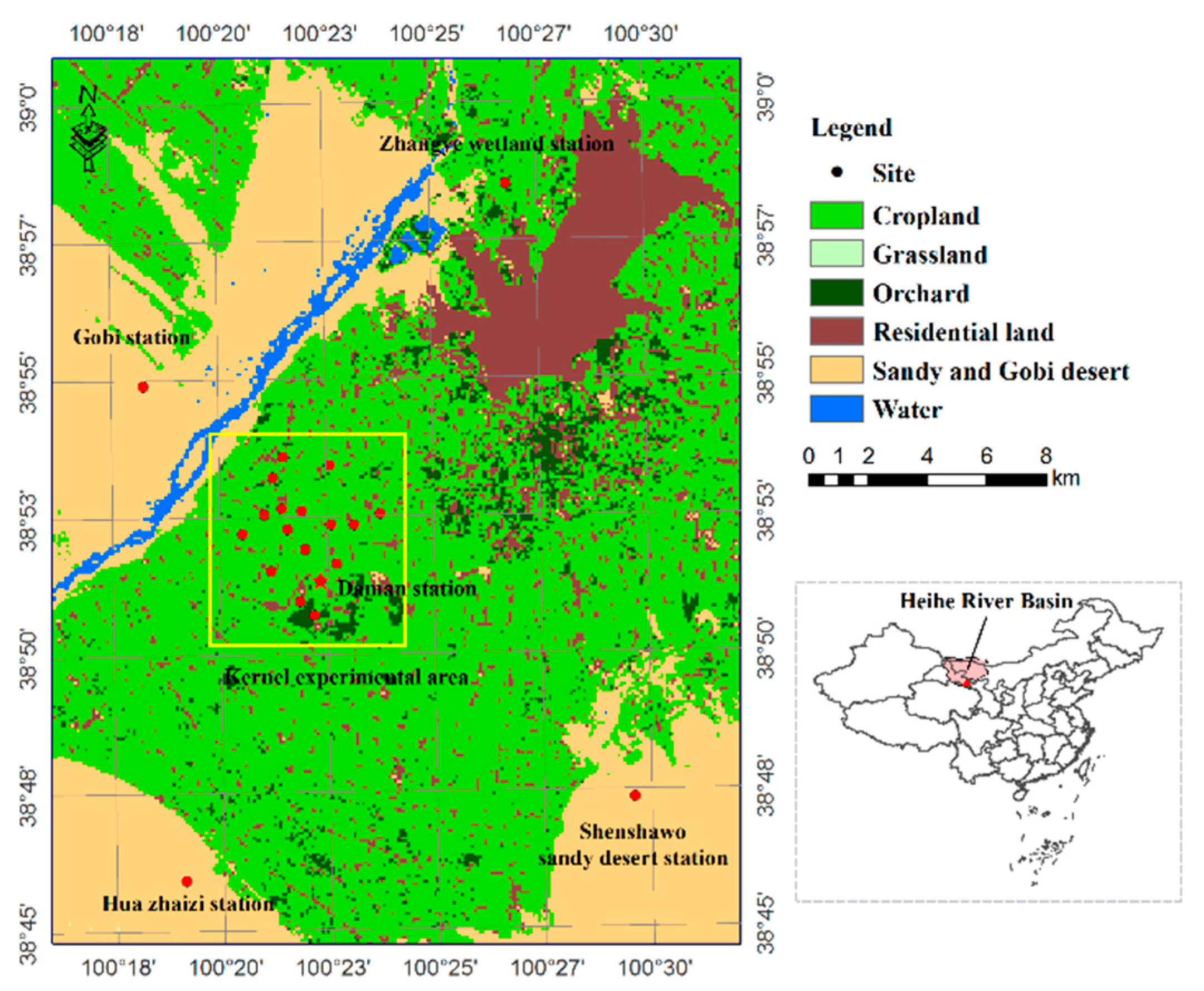
3. Study Area and Data Processing
3.1. HiWATER-MUSOEXE Campaign and Ground-Based Measurements
3.2. Remote Sensing Data and Derivation of Related Variables
4. Results
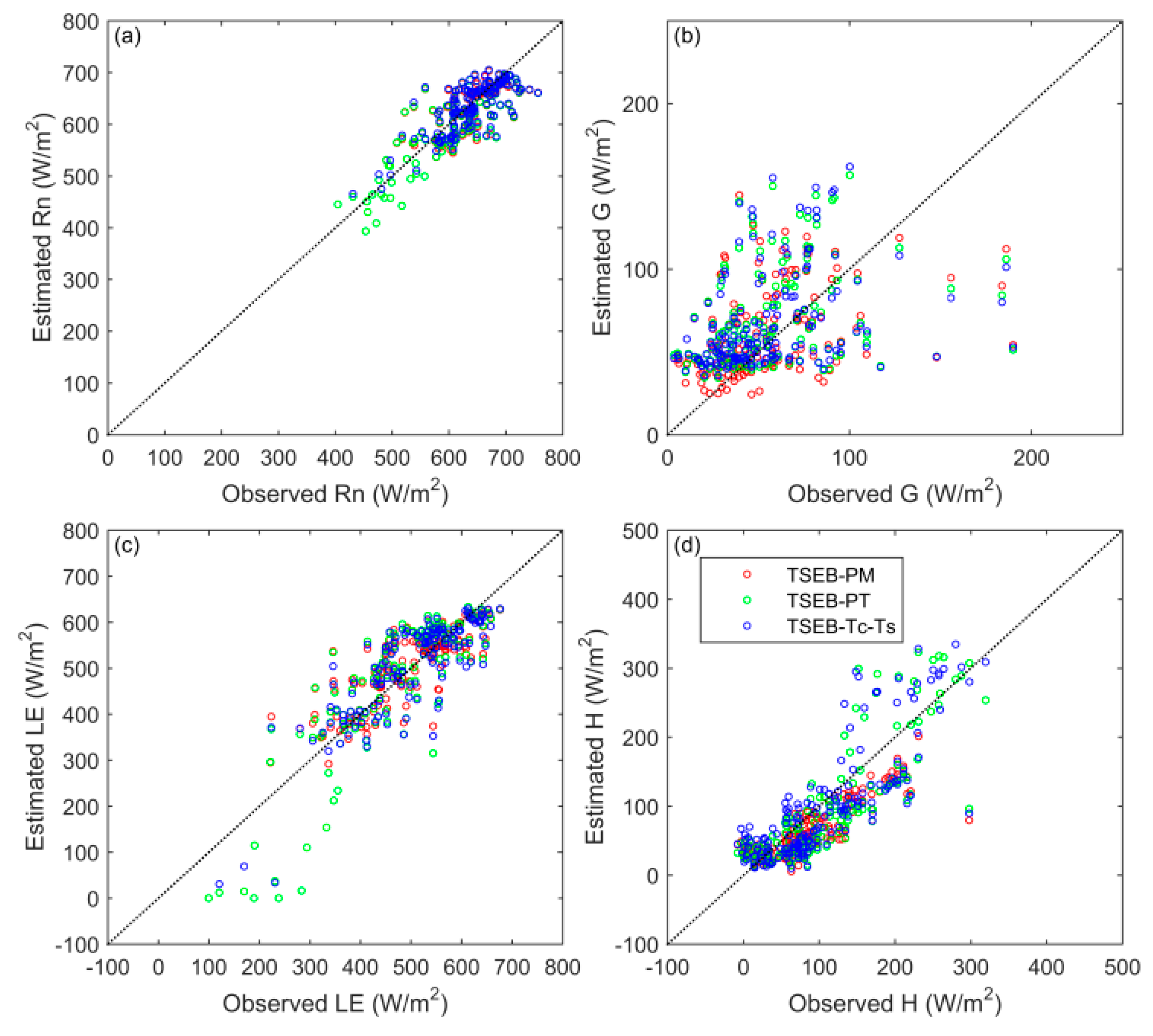
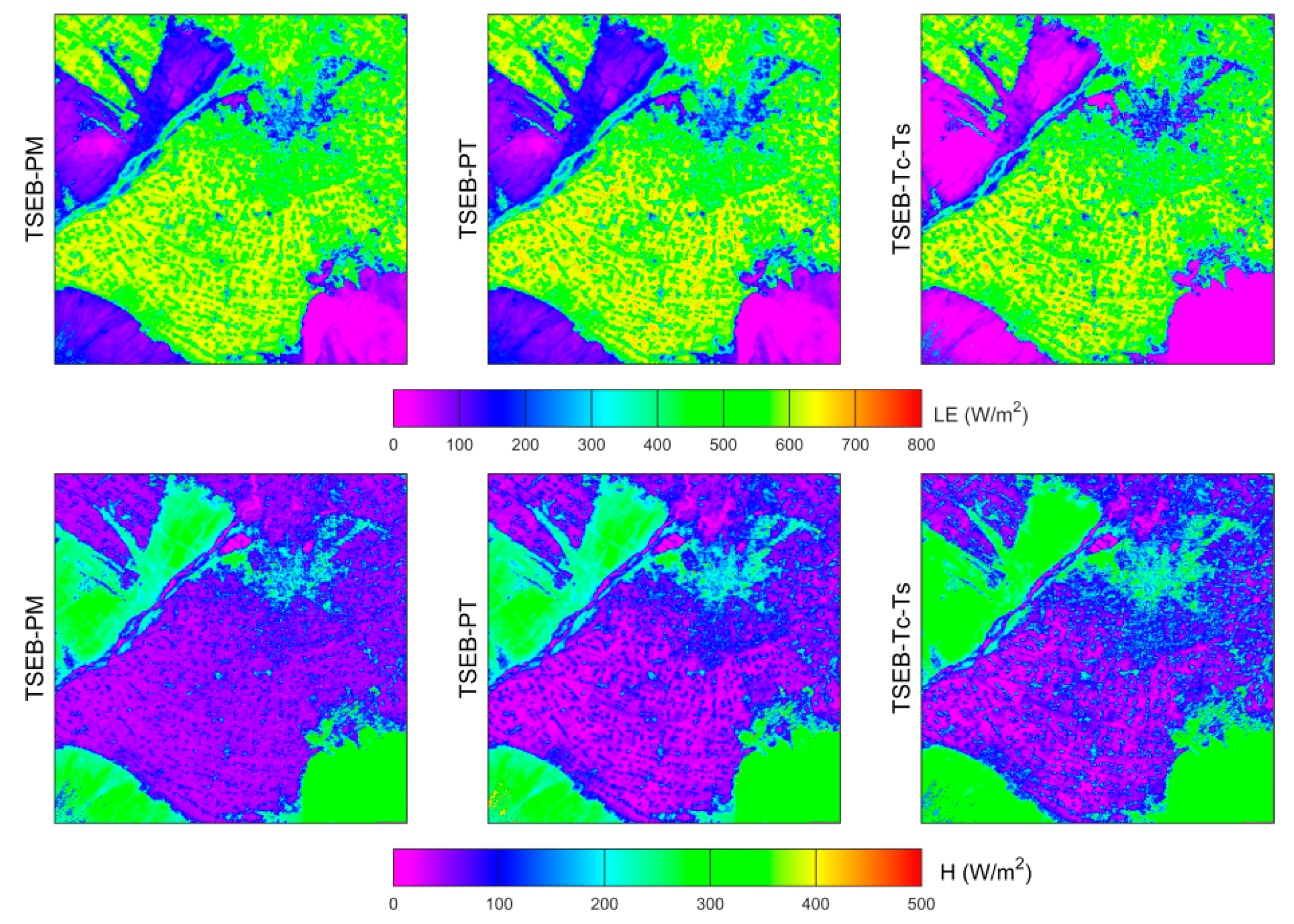
4.1. Validation of Three TSEB Models over MUSOEXE
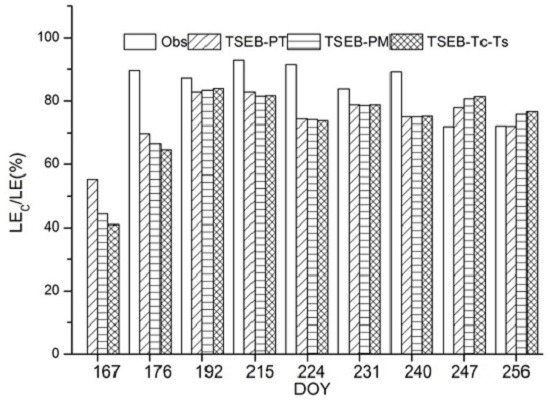
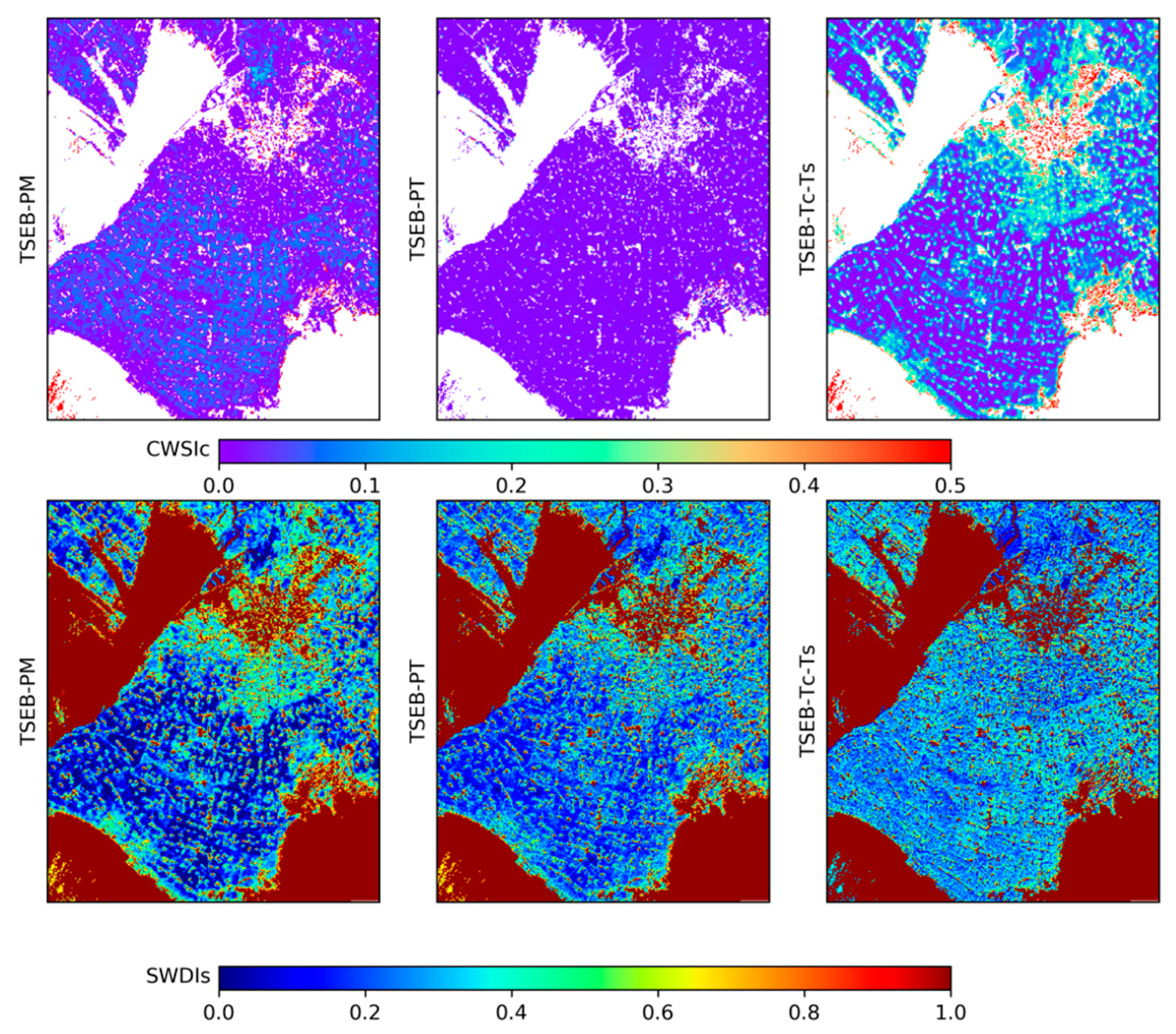
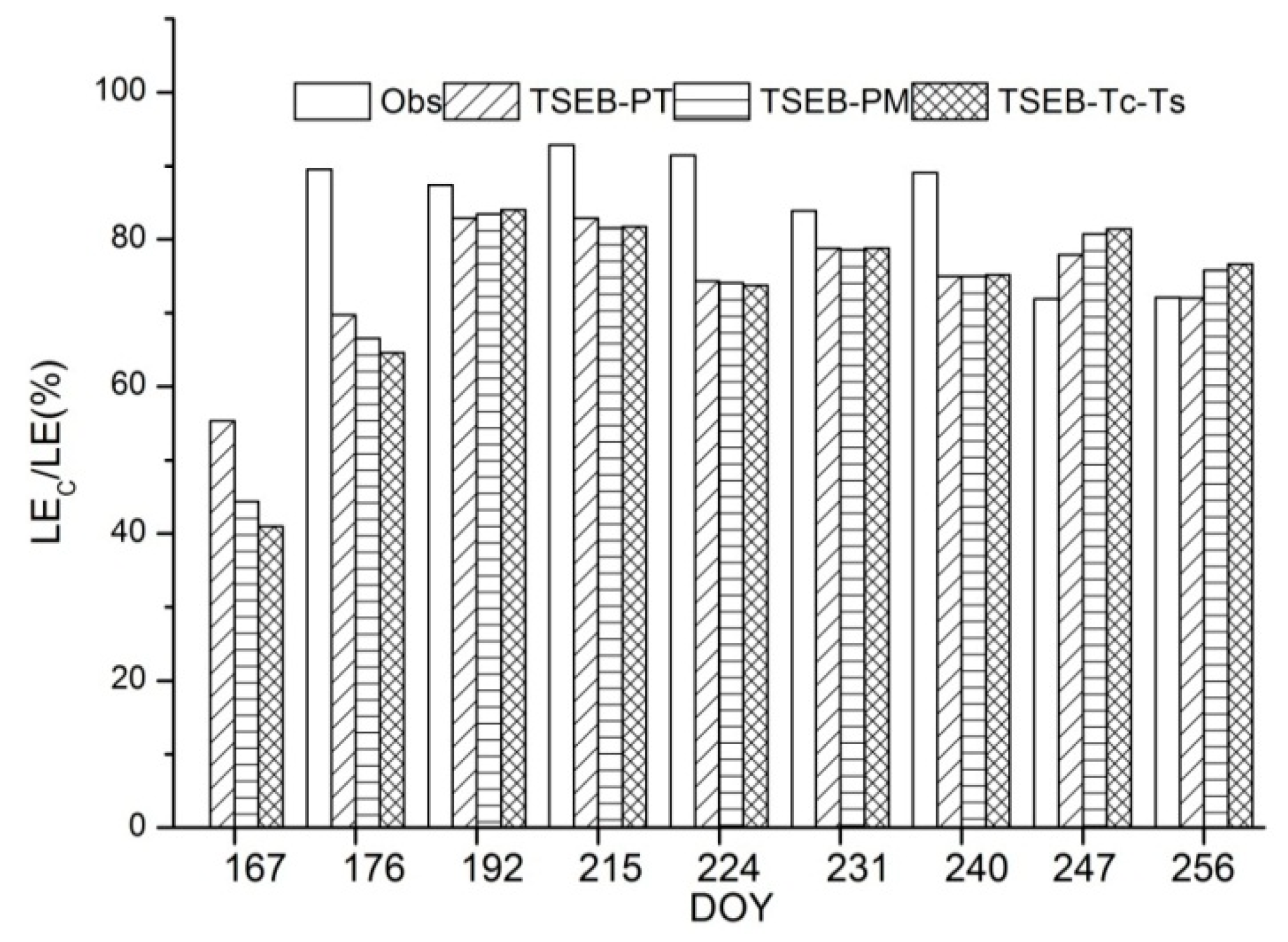
4.2. Intercomparison of E/T Partitioning from Three TSEB Models
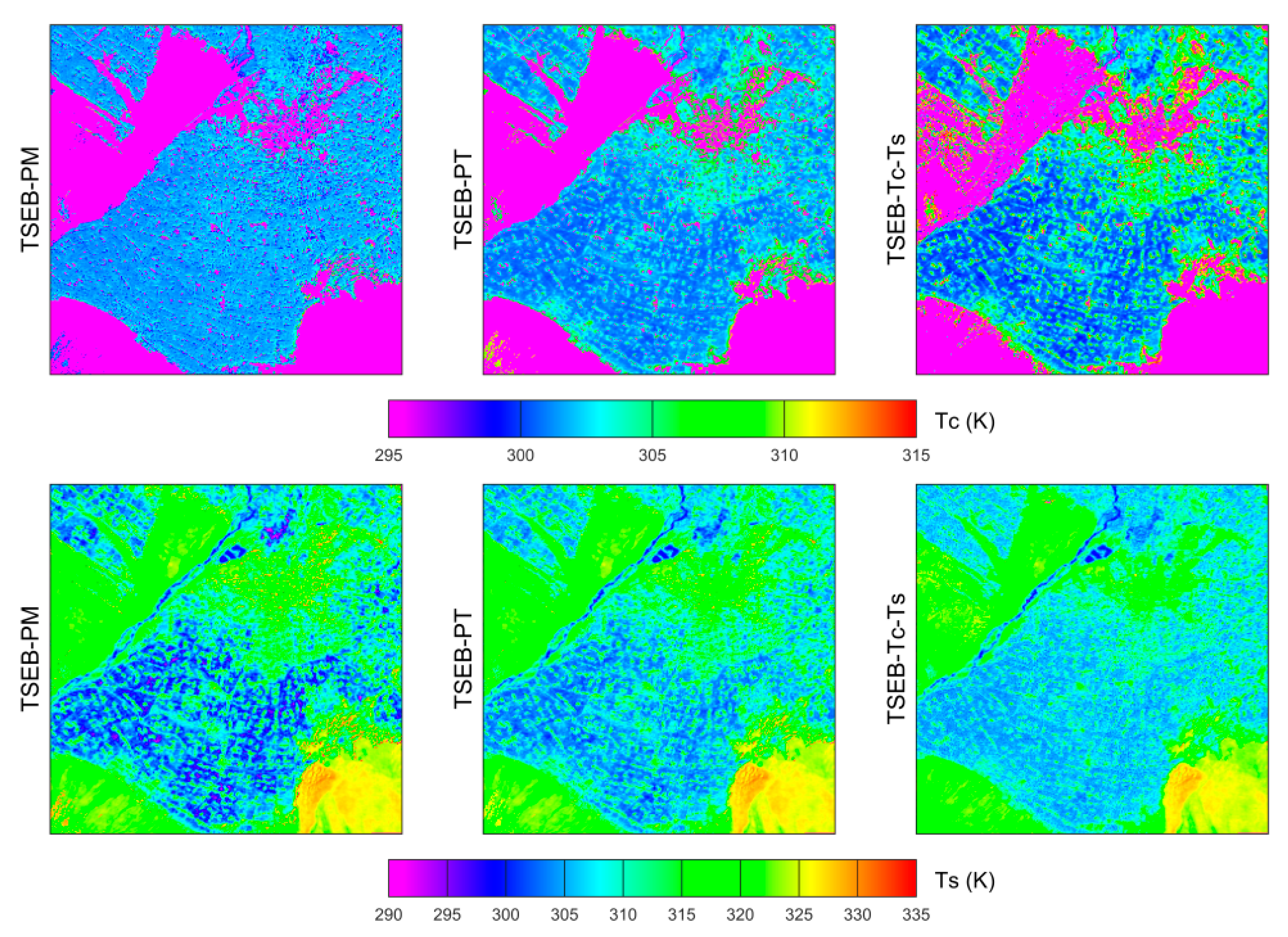
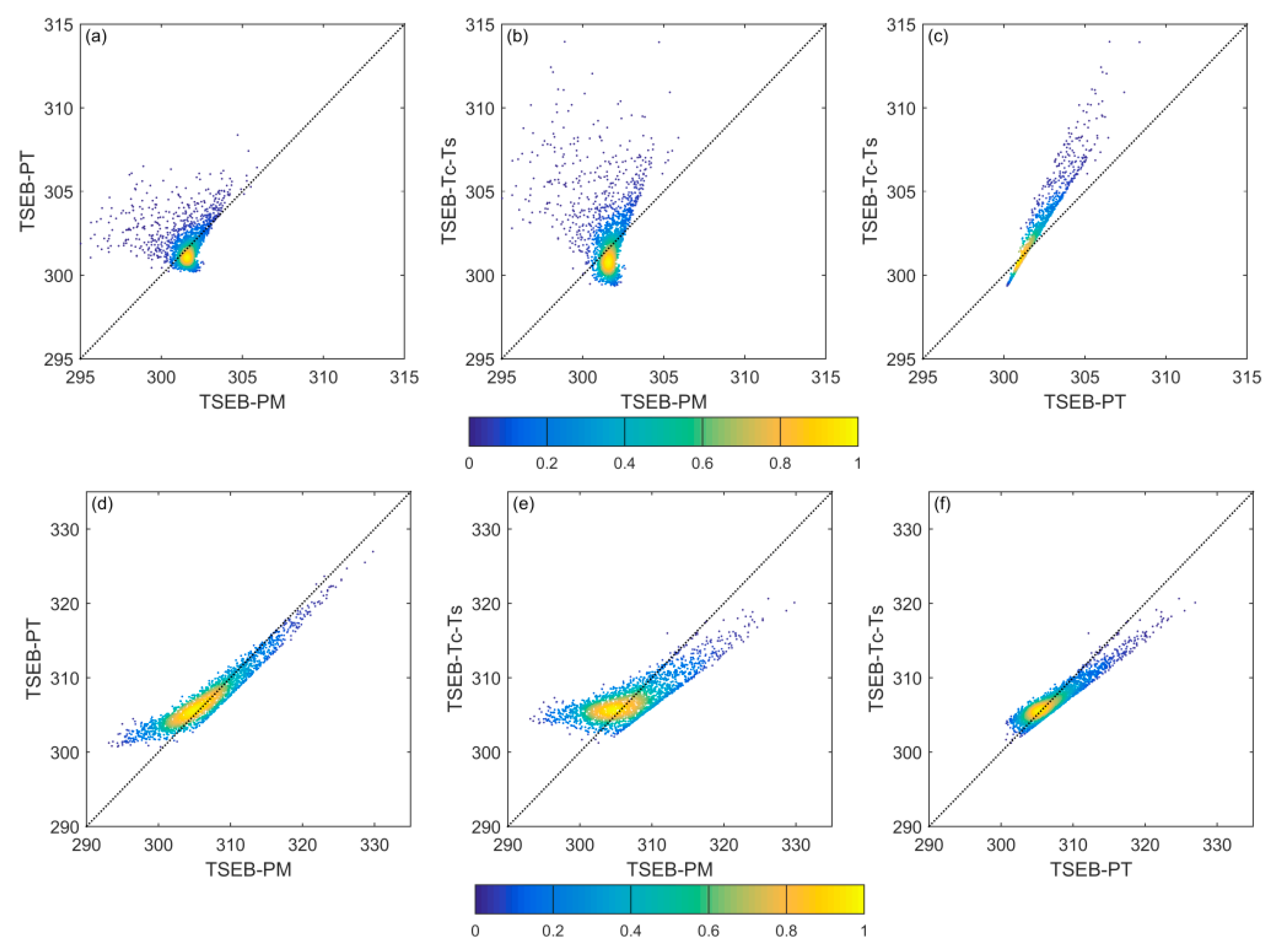
4.3. Intercomparison of Tc and Ts Derived from Three TSEB Models
5. Discussion
5.1. Reliability of the Employed TSEB Models in Estimating Surface Fluxes
5.2. Discrepancies in E/T Partitioning between the Three TSEB Models
5.3. Impact of Temperature Decomposition Accuracies on ET Estimations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History and Applications; Springer: New York, NY, USA, 1982. [Google Scholar]
- Brutsaert, W. Hydrology: An Introduction; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Eagleson, P.S. Ecohydrology: Darwinian Expression of Vegetation Form and Function; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Kabat, P. Vegetation, Water, Humans and the Climate: A New Perspective on an Internactive System; Springer Science & Business Media: Berlin, Germany, 2004. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (metric)—applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (metric)—model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Glenn, E.P.; Huete, A.R.; Nagler, P.L.; Hirschboeck, K.K.; Brown, P. Integrating remote sensing and ground methods to estimate evapotranspiration. Crit. Rev. Plant Sci. 2007, 26, 139–168. [Google Scholar] [CrossRef]
- Kustas, W.; Anderson, M. Advances in thermal infrared remote sensing for land surface modeling. Agric. For. Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef] [Green Version]
- Jimenez, C.; Prigent, C.; Mueller, B.; Seneviratne, S.I.; McCabe, M.F.; Wood, E.F.; Rossow, W.B.; Balsamo, G.; Betts, A.K.; Dirmeyer, P.A. Global intercomparison of 12 land surface heat flux estimates. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- McCabe, M.; Kustas, W.; Anderson, M.; Kongoli, C.; Ershadi, A.; Hain, C.R. Global-scale estimation of land surface heat fluxes from space: Current status, opportunities, and future directions. In Remote Sensing of Energy Fluxes and Soil Moisture Content; CRC Press: Boca Raton, FL, USA, 2013; pp. 447–462. [Google Scholar]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on modis and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a modis global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Mueller, B.; Hirschi, M.; Jimenez, C.; Ciais, P.; Dirmeyer, P.A.; Dolman, A.J.; Fisher, J.B.; Jung, M.; Ludwig, F.; Maignan, F. Benchmark products for land evapotranspiration: Landflux-eval multi-data set synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 3707–3720. [Google Scholar] [CrossRef]
- Zhang, Y.; Leuning, R.; Chiew, F.H.S.; Wang, E.; Zhang, L.; Liu, C.; Sun, F.; Peel, M.C.; Shen, Y.; Jung, M. Decadal trends in evaporation from global energy and water balances. J. Hydrometeorol. 2012, 13, 379–391. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef] [Green Version]
- Bastiaanssen, W.G.M.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.F.; Roerink, G.J.; Van der Wal, T. A remote sensing surface energy balance algorithm for land (SEBAL): Part 2: Validation. J. Hydrol. 1998, 212, 213–229. [Google Scholar] [CrossRef]
- Boegh, E.; Soegaard, H.; Thomsen, A. Evaluating evapotranspiration rates and surface conditions using landsat tm to estimate atmospheric resistance and surface resistance. Remote Sens. Environ. 2002, 79, 329–343. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Su, Z. The surface energy balance system (sebs) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Roerink, G.J.; Su, Z.; Menenti, M. S-sebi: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth Part B Hydrol. Oceans Atmos. 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Su, Z. Hydrological applications of remote sensing. Surface fluxes and other derived variables–surface energy balance. In Encyclopedia of Hydrological Sciences; John Wiley and Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
- Zhang, R.H.; Sun, X.M.; Wang, W.M.; Xu, J.P.; Zhu, Z.L.; Tian, J. An operational two-layer remote sensing model to estimate surface flux in regional scale: Physical background. Sci. China Ser. D 2005, 48, 225–244. [Google Scholar]
- Yang, Y.; Su, H.; Zhang, R.; Tian, J.; Li, L. An enhanced two-source evapotranspiration model for land (ETEML): Algorithm and evaluation. Remote Sens. Environ. 2015, 168, 54–65. [Google Scholar] [CrossRef] [Green Version]
- Carlson, T. An overview of the “triangle method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar] [CrossRef]
- Petropoulos, G.; Carlson, T.N.; Wooster, M.J.; Islam, S. A review of Ts/Vi remote sensing based methods for the retrieval of land surface energy fluxes and soil surface moisture. Prog. Phys. Geogr. 2009, 33, 224–250. [Google Scholar] [CrossRef]
- Moran, M.S.; Clarke, T.R.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar] [CrossRef]
- Jiang, L.; Islam, S. Estimation of surface evaporation map over southern great plains using remote sensing data. Water Resour. Res. 2001, 37, 329–340. [Google Scholar] [CrossRef]
- Jiang, L.; Islam, S. An intercomparison of regional latent heat flux estimation using remote sensing data. Int. J. Remote Sens. 2003, 24, 2221–2236. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I.; Nørgaard, A.; Fensholt, R.; Jensen, K.H. Combining the triangle method with thermal inertia to estimate regional evapotranspiration—Applied to msg-seviri data in the senegal river basin. Remote Sens. Environ. 2008, 112, 1242–1255. [Google Scholar] [CrossRef]
- Shu, Y.; Stisen, S.; Jensen, K.H.; Sandholt, I. Estimation of regional evapotranspiration over the north china plain using geostationary satellite data. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 192–206. [Google Scholar] [CrossRef]
- Courault, D.; Seguin, B.; Olioso, A. Review on estimation of evapotranspiration from remote sensing data: From empirical to numerical modeling approaches. Irrig. Drain. Syst. 2005, 19, 223–249. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef] [PubMed]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Rauwerda, J.; Roerink, G.J.; Su, Z. Estimation of Evaporative Fractions by the Use of Vegetation and Soil Component Temperature Determined by Means of Dual-Looking Remote Sensing; Alterra: Osborne Park, WA, USA, 2002. [Google Scholar]
- Jia, L. Modeling Heat Exchanges at the Land-Atmosphere Interface Using Multi-Angular Thermal Infrared Measurements; Wageningen University: Wageningen, The Netherlands, 2004. [Google Scholar]
- Jia, L.; Li, Z.L.; Menenti, M.; Su, Z.; Verhoef, W.; Wan, Z. A practical algorithm to infer soil and foliage component temperatures from bi-angular atsr-2 data. Int. J. Remote Sens. 2003, 24, 4739–4760. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Q.; Matsushita, B.; Fukushima, T.; Ouyang, Z.; Watanabe, M. A new method to define the vi-ts diagram using subpixel vegetation and soil information: A case study over a semiarid agricultural region in the north China plain. Sensors 2008, 8, 6260–6279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bisquert, M.; Sánchez, J.M.; López-Urrea, R.; Caselles, V. Estimating high resolution evapotranspiration from disaggregated thermal images. Remote Sens. Environ. 2016, 187, 423–433. [Google Scholar] [CrossRef]
- Colaizzi, P.D.; Agam, N.; Tolk, J.A.; Evett, S.R.; Howell, T.A.; Gowda, P.H.; O’Shaughnessy, S.A.; Kustas, W.P.; Anderson, M.C. Two-source energy balance model to calculate e, t, and et: Comparison of priestley-taylor and penman-monteith formulations and two time scaling methods. Trans. ASABE 2014, 57, 479–498. [Google Scholar]
- Colaizzi, P.D.; Kustas, W.P.; Anderson, M.C.; Agam, N.; Tolk, J.A.; Evett, S.R.; Howell, T.A.; Gowda, P.H.; O’Shaughnessy, S.A. Two-source energy balance model estimates of evapotranspiration using component and composite surface temperatures. Adv. Water Resour. 2012, 50, 134–151. [Google Scholar] [CrossRef]
- Merlin, O.; Escorihuela, M.J.; Mayoral, M.A.; Hagolle, O.; Al Bitar, A.; Kerr, Y. Self-calibrated evaporation-based disaggregation of smos soil moisture: An evaluation study at 3 km and 100 m resolution in Catalunya, Spain. Remote Sens. Environ. 2013, 130, 25–38. [Google Scholar] [CrossRef] [Green Version]
- Merlin, O.; Rudiger, C.; Al Bitar, A.; Richaume, P.; Walker, J.P.; Kerr, Y.H. Disaggregation of SMOS soil moisture in southeastern Australia. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1556–1571. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Wang, Q.; Matsushita, B.; Fukushima, T.; Ouyang, Z.; Watanabe, M. Development of a simple remote sensing evapotranspiration model (sim-reset): Algorithm and model test. J. Hydrol. 2009, 376, 476–485. [Google Scholar] [CrossRef] [Green Version]
- Long, D.; Singh, V.P. A two-source trapezoid model for evapotranspiration (TTME) from satellite imagery. Remote Sens. Environ. 2012, 121, 370–388. [Google Scholar] [CrossRef]
- Yang, Y.; Shang, S. A hybrid dual-source scheme and trapezoid framework–based evapotranspiration model (htem) using satellite images: Algorithm and model test. J. Geophys. Res. Atmos. 2013, 118, 2284–2300. [Google Scholar] [CrossRef]
- Sun, H. A two-source model for estimating evaporative fraction (TMEF) coupling priestley-taylor formula and two-stage trapezoid. Remote Sens. 2016, 8, 248. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. For. Meteorol. 1999, 94, 13–29. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. A two-source energy balance approach using directional radiometric temperature observations for sparse canopy covered surfaces. Agron. J. 2000, 92, 847–854. [Google Scholar] [CrossRef]
- Santanello, J.A., Jr.; Friedl, M.A. Diurnal covariation in soil heat flux and net radiation. J. Appl. Meteorol. 2003, 42, 851–862. [Google Scholar] [CrossRef]
- Song, L.; Liu, S.; Kustas, W.P.; Zhou, J.; Xu, Z.; Xia, T.; Li, M. Application of remote sensing-based two-source energy balance model for mapping field surface fluxes with composite and component surface temperatures. Agric. For. Meteorol. 2016, 230, 8–19. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. A two-source approach for estimating turbulent fluxes using multiple angle thermal infrared observations. Water Resour. Res. 1997, 33, 1495–1508. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Tian, J.; Su, H.; Sun, X.; Chen, S.; Xia, J. Two improvements of an operational two-layer model for terrestrial surface heat flux retrieval. Sensors 2008, 8, 6165–6187. [Google Scholar] [CrossRef] [PubMed]
- Thom, A.S. Momentum, mass and heat exchange of plant communities. Veg. Atmos. 1975, 1, 57–109. [Google Scholar]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y. Heihe watershed allied telemetry experimental research (hiwater): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Song, L.; Zhao, Q.; Ge, Y.; Xu, T.; Ma, Y.; Zhu, Z.; Jia, Z.; Zhang, F. Upscaling evapotranspiration measurements from multi-site to the satellite pixel scale over heterogeneous land surfaces. Agric. For. Meteorol. 2016, 230, 97–113. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, S.; Li, X.; Shi, S.; Wang, J.; Zhu, Z.; Xu, T.; Wang, W.; Ma, M. Intercomparison of surface energy flux measurement systems used during the hiwater-musoexe. J. Geophys. Res. Atmos. 2013, 118, 13–140. [Google Scholar] [CrossRef]
- Yang, K.; Wang, J. A temperature prediction-correction method for estimating surface soil heat flux from soil temperature and moisture data. Sci. China Ser. D Earth Sci. 2008, 51, 721–729. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Wen, X. Temporal variations of atmospheric water vapor δd and δ18o above an arid artificial oasis cropland in the Heihe river basin. J. Geophys. Res. Atmos. 2014, 119, 11456–11476. [Google Scholar] [CrossRef]
- Wen, X.; Yang, B.; Sun, X.; Lee, X. Evapotranspiration partitioning through in-situ oxygen isotope measurements in an oasis cropland. Agric. For. Meteorol. 2016, 230, 89–96. [Google Scholar] [CrossRef]
- Li, H.; Sun, D.; Yu, Y.; Wang, H.; Liu, Y.; Liu, Q.; Du, Y.; Wang, H.; Cao, B. Evaluation of the viirs and modis lst products in an arid area of northwest china. Remote Sens. Environ. 2014, 142, 111–121. [Google Scholar] [CrossRef]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for advanced spaceborne thermal emission and reflection radiometer (aster) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar] [CrossRef]
- Tonooka, H. Accurate atmospheric correction of aster thermal infrared imagery using the WVS method. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2778–2792. [Google Scholar] [CrossRef]
- Sun, C.; Liu, Q.; Wen, J. An algorithm for retrieving land surface albedo from hj-1 CCD data. Remote Sens. Land Resour. 2013, 25, 58–63. [Google Scholar]
- Yang, Y.; Long, D.; Guan, H.; Liang, W.; Simmons, C.; Batelaan, O. Comparison of three dual-source remote sensing evapotranspiration models during the musoexe-12 campaign: Revisit of model physics. Water Resour. Res. 2015, 51, 3145–3165. [Google Scholar] [CrossRef]
- Gonzalez-Dugo, M.P.; Neale, C.M.U.; Mateos, L.; Kustas, W.P.; Prueger, J.H.; Anderson, M.C.; Li, F. A comparison of operational remote sensing-based models for estimating crop evapotranspiration. Agric. For. Meteorol. 2009, 149, 1843–1853. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, S.; Zhang, F.; Zhou, J.; Jia, Z.; Song, L. Estimations of regional surface energy fluxes over heterogeneous oasis–desert surfaces in the middle reaches of the Heihe river during hiwater-musoexe. IEEE Geosci. Remote Sens. Lett. 2015, 12, 671–675. [Google Scholar]
- Huang, C.; Li, Y.; Gu, J.; Lu, L.; Li, X. Improving estimation of evapotranspiration under water-limited conditions based on sebs and modis data in arid regions. Remote Sens. 2015, 7, 16795–16814. [Google Scholar] [CrossRef]
- Yang, Y.; Qiu, J.; Su, H.; Bai, Q.; Liu, S.; Li, L.; Yu, Y.; Huang, Y. A one-source approach for estimating land surface heat fluxes using remotely sensed land surface temperature. Remote Sens. 2017, 9, 43. [Google Scholar] [CrossRef]
- Kustas, W.P.; Nieto, H.; Morillas, L.; Anderson, M.C.; Alfieri, J.G.; Hipps, L.E.; Villagarcía, L.; Domingo, F.; Garcia, M. Revisiting the paper “using radiometric surface temperature for surface energy flux estimation in mediterranean drylands from a two-source perspective”. Remote Sens. Environ. 2016, 184, 645–653. [Google Scholar] [CrossRef]
- Choi, M.; Kustas, W.P.; Anderson, M.C.; Allen, R.G.; Li, F.; Kjaersgaard, J.H. An intercomparison of three remote sensing-based surface energy balance algorithms over a corn and soybean production region (Iowa, US) during smacex. Agric. For. Meteorol. 2009, 149, 2082–2097. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.-L.; Jia, Y.; Li, C.; Chen, K.-S.; Sun, X.; Lou, J. Evaluating one-and two-source energy balance models in estimating surface evapotranspiration from landsat-derived surface temperature and field measurements. Int. J. Remote Sens. 2013, 34, 3299–3313. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Houborg, R.; Starks, P.J.; Agam, N. A thermal-based remote sensing technique for routine mapping of land-surface carbon, water and energy fluxes from field to regional scales. Remote Sens. Environ. 2008, 112, 4227–4241. [Google Scholar] [CrossRef]


| Flux Component | TSEB-PM | TSEB-PT | TSEB-TC-TS | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE (W/m2) | Bias (W/m2) | R | RMSE (W/m2) | Bias (W/m2) | R | RMSE (W/m2) | Bias (W/m2) | R | |
| Rn | 37.6 | −8.5 | 0.84 | 37.4 | −7.2 | 0.84 | 35.5 | −5.7 | 0.76 |
| G | 37.9 | 11.5 | 0.37 | 37.5 | 12.8 | 0.34 | 37.7 | 12.7 | 0.33 |
| LE | 70.6 | −2.1 | 0.86 | 75.3 | −0.2 | 0.85 | 61.8 | 3.2 | 0.82 |
| H | 44.9 | −14.3 | 0.84 | 47.5 | −16.2 | 0.83 | 47.9 | −8.6 | 0.81 |
| TSEB-PT vs. TSEB-PM | TSEB-Tc-Ts vs. TSEB-PM | TSEB-Tc-Ts vs. TSEB-PT | ||
|---|---|---|---|---|
| LEc | RMSE (W/m2) | 18.8 | 33.9 | 23.2 |
| MD * (W/m2) | 2.9 | 18.1 | 15.2 | |
| MAD (W/m2) | 13.2 | 24.6 | 16.5 | |
| R | 1.00 | 0.98 | 0.99 | |
| LEs | RMSE (W/m2) | 10.8 | 16.2 | 7.6 |
| MD (W/m2) | −4.2 | −2.8 | 1.4 | |
| MAD (W/m2) | 6.1 | 11.1 | 6.2 | |
| R | 0.99 | 0.99 | 1.00 |
| TSEB-PT vs. TSEB-PM | TSEB-Tc-Ts vs. TSEB-PM | TSEB-Tc-Ts vs. TSEB-PT | ||
|---|---|---|---|---|
| Tc | RMSE (K) | 1.4 | 2.4 | 1.0 |
| MD (K) | −0.2 | −0.48 | −0.3 | |
| MAD (K) | 0.8 | 1.5 | 0.6 | |
| R | 0.13 | −0.09 | 0.97 | |
| Ts | RMSE (K) | 2.0 | 3.4 | 1.6 |
| MD (K) | −0.6 | −0.3 | 0.3 | |
| MAD (K) | 1.5 | 2.7 | 1.3 | |
| R | 0.95 | 0.80 | 0.94 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Qiu, J.; Zhang, R.; Huang, S.; Chen, S.; Wang, H.; Luo, J.; Fan, Y. Intercomparison of Three Two-Source Energy Balance Models for Partitioning Evaporation and Transpiration in Semiarid Climates. Remote Sens. 2018, 10, 1149. https://doi.org/10.3390/rs10071149
Yang Y, Qiu J, Zhang R, Huang S, Chen S, Wang H, Luo J, Fan Y. Intercomparison of Three Two-Source Energy Balance Models for Partitioning Evaporation and Transpiration in Semiarid Climates. Remote Sensing. 2018; 10(7):1149. https://doi.org/10.3390/rs10071149
Chicago/Turabian StyleYang, Yongmin, Jianxiu Qiu, Renhua Zhang, Shifeng Huang, Sheng Chen, Hui Wang, Jiashun Luo, and Yue Fan. 2018. "Intercomparison of Three Two-Source Energy Balance Models for Partitioning Evaporation and Transpiration in Semiarid Climates" Remote Sensing 10, no. 7: 1149. https://doi.org/10.3390/rs10071149
APA StyleYang, Y., Qiu, J., Zhang, R., Huang, S., Chen, S., Wang, H., Luo, J., & Fan, Y. (2018). Intercomparison of Three Two-Source Energy Balance Models for Partitioning Evaporation and Transpiration in Semiarid Climates. Remote Sensing, 10(7), 1149. https://doi.org/10.3390/rs10071149