Downscaling Land Surface Temperature from MODIS Dataset with Random Forest Approach over Alpine Vegetated Areas
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Input Data
2.3. Methodology
2.3.1. The Random Forest Algorithm
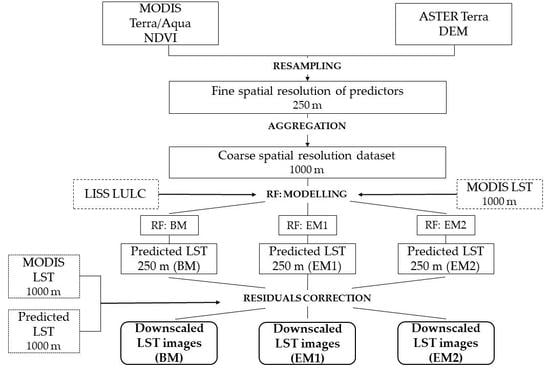
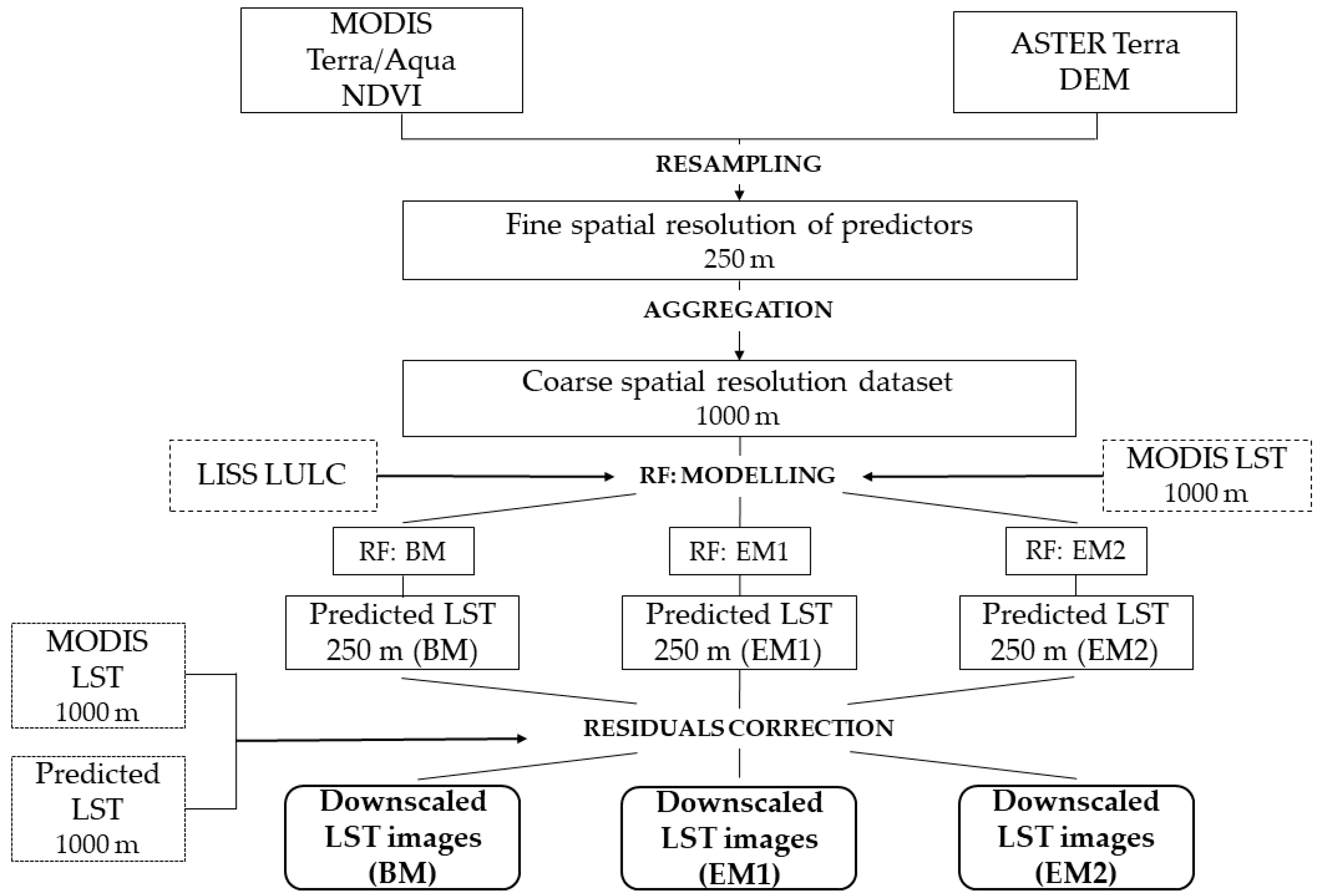
2.3.2. Implementation of Random Forest for Thermal Sharpening
2.3.3. Random Forest Model Concepts
2.3.4. Data Preparation for the Validation Phase
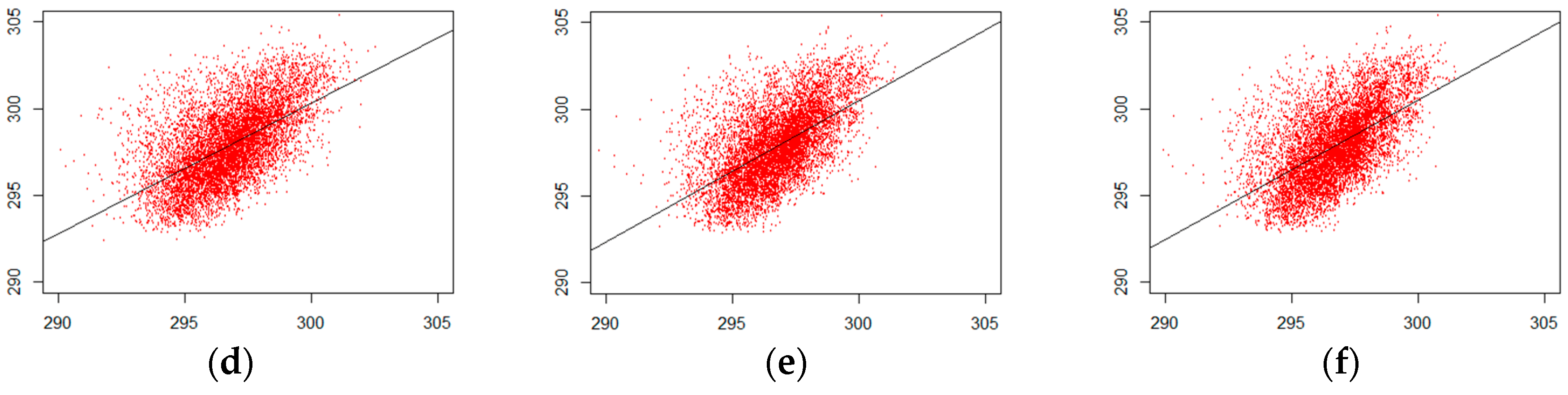
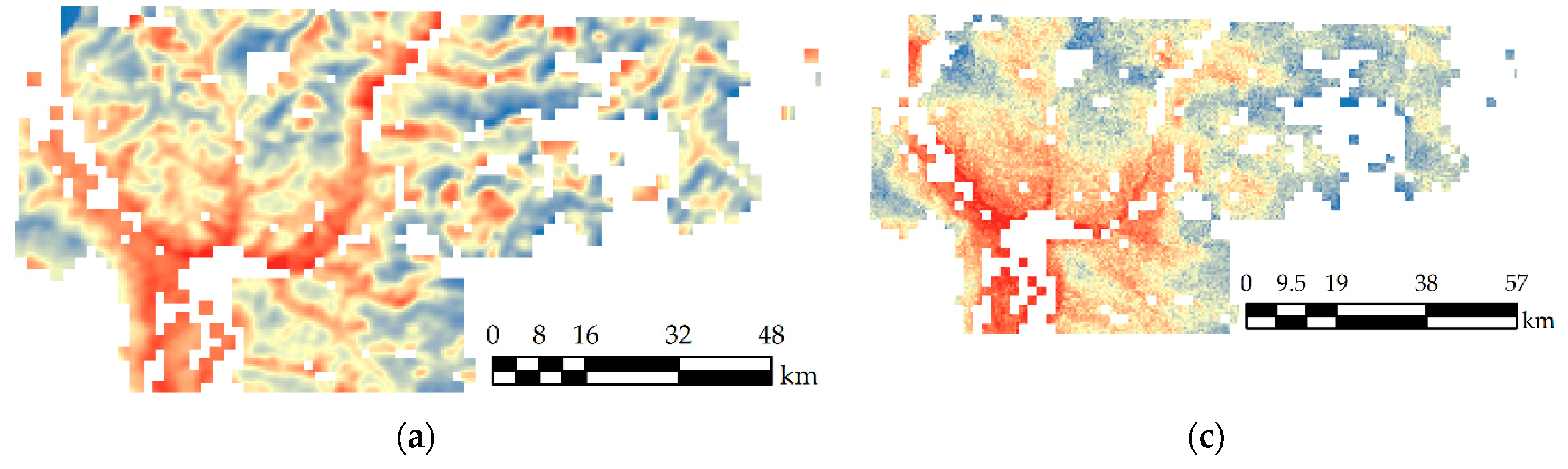
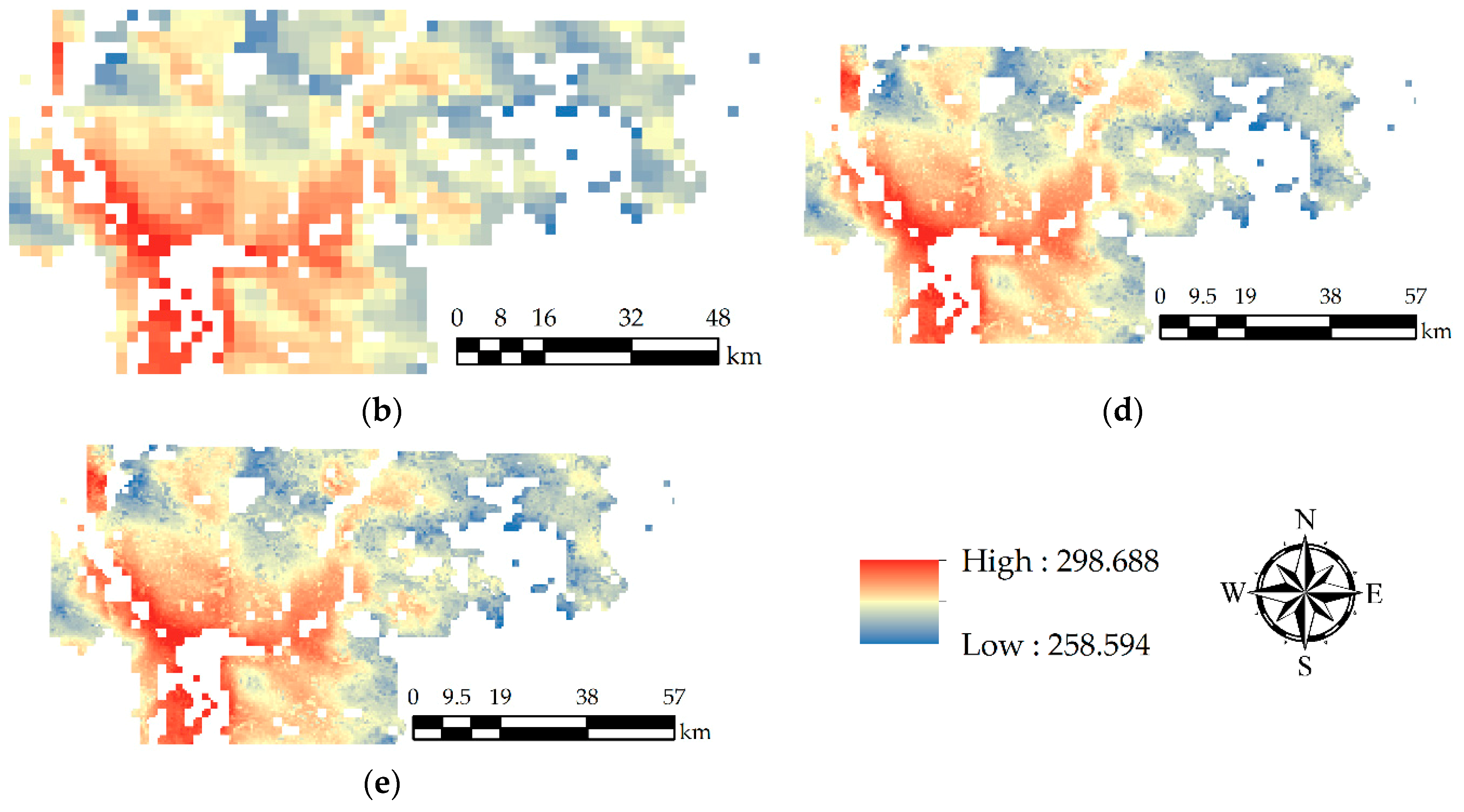
3. Results
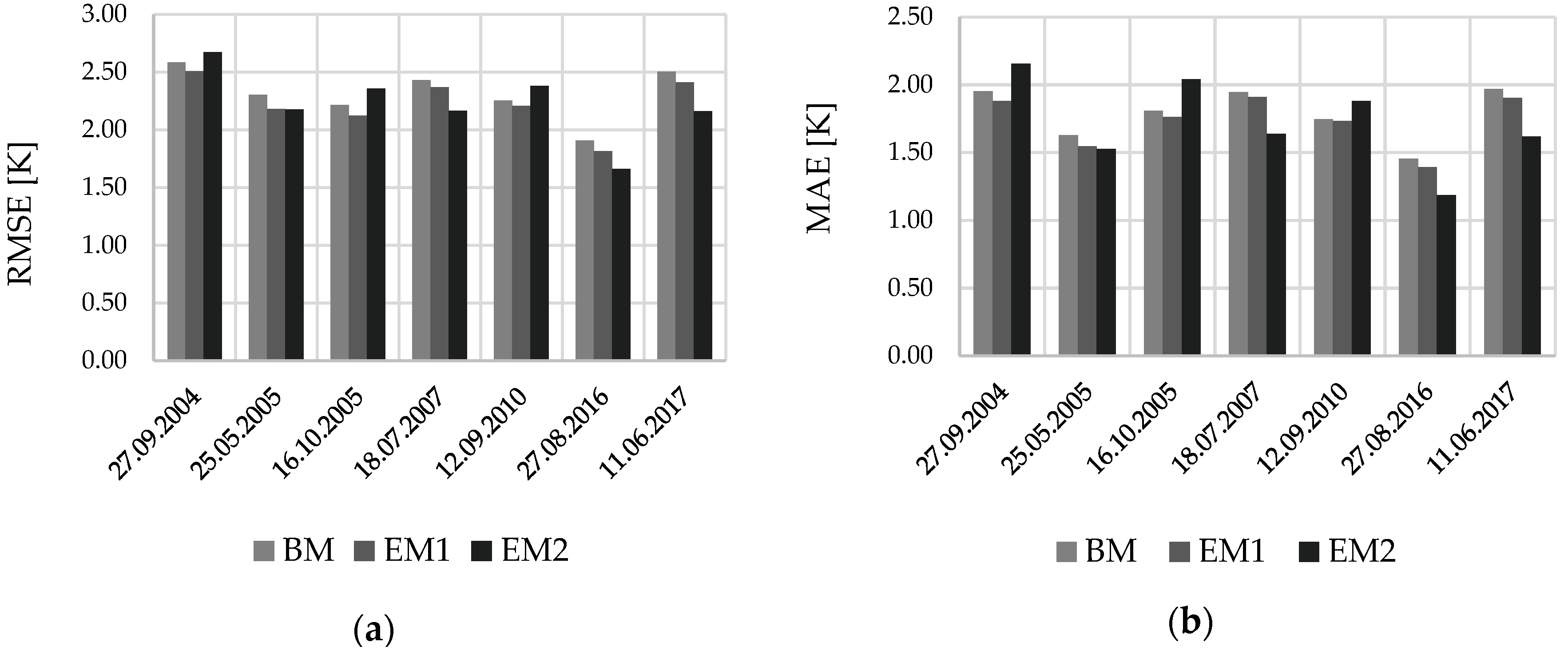
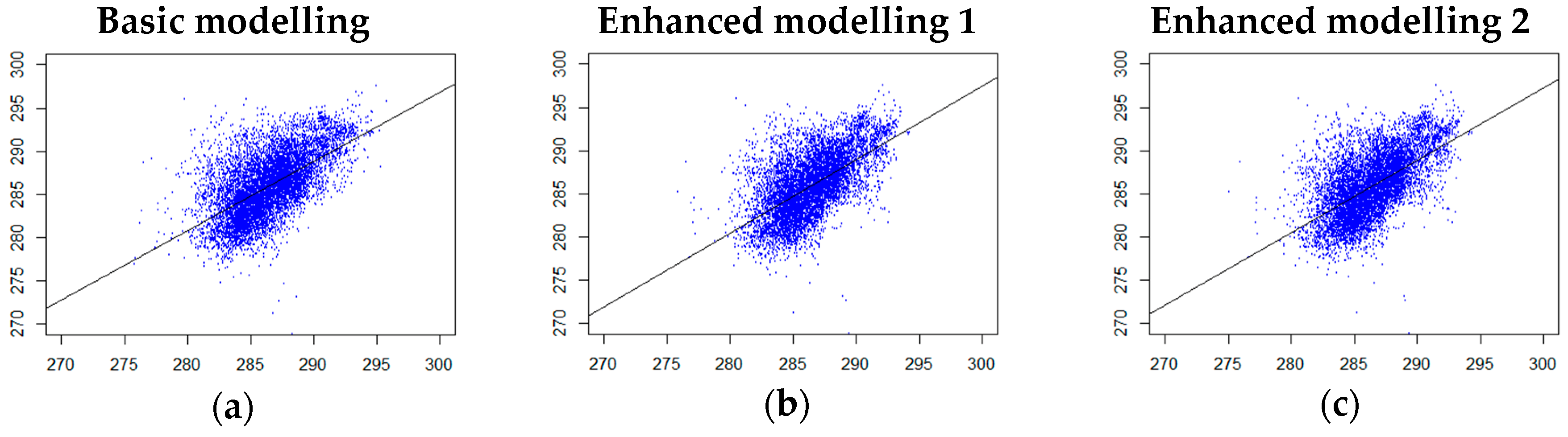
3.1. Global Validation
3.2. Validation for the Different Land Cover Classes
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Czajkowski, K.P.; Goward, S.N.; Mulhern, T.; Goetz, S.J.; Walz, A.; Shirey, D.; Dubayah, R.O. Estimating environmental variables using thermal remote sensing. In Thermal Remote Sensing in Land Surface Processes; Quattrochi, D.A., Luvall, J.C., Eds.; CRC Press LLC: Boca Raton, FL, USA, 2004; pp. 11–32. [Google Scholar]
- Weng, Q. Thermal infrared remote sensing for urban climate and environmental studies: Methods, applications, and trends. ISPRS J. Photogramm. 2009, 64, 335–344. [Google Scholar] [CrossRef]
- Niclòs, R.; Tomás, S.; Juan, M.; Valiente, J.A.; Barberà, M.J.; Caselles, D.; Caselles, V. Evaluation of Landsat-8 Thermal Bands to Monitor Land Surface Temperature; Serie A; Publicaciones de la Asociación Española de Climatología: Sevilla, Spain, 2014; Volume 9. [Google Scholar]
- Park, S.; Im, J.; Jang, E.; Rhee, J. Drought assessment and monitoring through blending of multi-sensor indices using machine learning approaches for different climate regions. Agric. For. Meteorol. 2016, 216, 157–169. [Google Scholar] [CrossRef]
- Swain, S.; Wardlow, B.D.; Narumalani, S.; Tadesse, T.; Callahan, K. Assessment of vegetation response to drought in Nebraska using Terra-MODIS land surface temperature and normalized difference vegetation index. GISci. Remote Sens. 2011, 48, 432–455. [Google Scholar] [CrossRef]
- Anderson, M.C.; Zolin, C.A.; Sentelhas, P.C.; Hain, C.R.; Semmens, K.; Yilmaz, M.T.; Tetrault, R. The Evaporative Stress Index as an indicator of agricultural drought in Brazil: An assessment based on crop yield impacts. Remote Sens. Environ. 2016, 174, 82–99. [Google Scholar] [CrossRef]
- Anderson, M.C.; Hain, C.; Wardlow, B.; Pimstein, A.; Mecikalski, J.R.; Kustas, W.P. Evaluation of drought indices based on thermal remote sensing of evapotranspiration over the continental United States. J. Clim. 2011, 24, 2025–2044. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Lu, D.; Song, K.; Zang, S.; Jia, M.; Du, J.; Ren, C. The effect of urban expansion on urban surface temperature in Shenyang, China: An analysis with landsat imagery. Environ. Model. Assess. 2015, 20, 197–210. [Google Scholar] [CrossRef]
- Balçik, F.B. Determining the impact of urban components on land surface temperature of Istanbul by using remote sensing indices. Environ. Monit. Assess. 2014, 186, 859–872. [Google Scholar] [CrossRef]
- Hardy, C.H.; Nel, A.L. Data and techniques for studying the urban heat island effect in Johannesburg. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Berlin, Germany, 11–15 May 2015; Volume XL-7/W3, p. 203. [Google Scholar]
- Deilami, K.; Kamruzzaman, M. Modelling the urban heat island effect of smart growth policy scenarios in Brisbane. Land Use Policy 2017, 64, 38–55. [Google Scholar] [CrossRef]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Castelli, M.; Anderson, M.C.; Yang, Y.; Wohlfahrt, G.; Bertoldi, G.; Niedrist, G.; Notarnicola, C. Two-source energy balance modeling of evapotranspiration in Alpine grasslands. Remote Sens. Environ. 2018, 209, 327–342. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.L. Evaluation of two end-member-based models for regional land surface evapotranspiration estimation from MODIS data. Agric. For. Meteorol. 2015, 202, 69–82. [Google Scholar] [CrossRef]
- Rahimi, S.; Gholami Sefidkouhi, M.A.; Raeini-Sarjaz, M.; Valipour, M. Estimation of actual evapotranspiration by using MODIS images (a case study: Tajan catchment). Arch. Agron. Soil Sci. 2015, 61, 695–709. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 1. Model formulation. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Carpintero, E.; Dugo, M.G.; Hain, C.; Nieto, H.; Gao, F.; Andreu, A.; Anderson, M.C. Continuous evapotranspiration monitoring and water stress at watershed scale in a Mediterranean oak savanna. In Remote Sensing for Agriculture, Ecosystems, and Hydrology XVIII; International Society for Optics and Photonics: Leiden, The Netherlands, 2016; Volume 9998, p. 99980N. [Google Scholar]
- Park, S.; Feddema, J.J.; Egbert, S.L. Impacts of hydrologic soil properties on drought detection with MODIS thermal data. Remote Sens. Environ. 2004, 89, 53–62. [Google Scholar] [CrossRef]
- Xing, Q.; Li, L.; Lou, M.; Bing, L.; Zhao, Z.; Li, Z. Observation of oil spills through Landsat thermal infrared imagery: A case of deepwater horizon. Aquat. Procedia 2015, 3, 151–156. [Google Scholar] [CrossRef]
- Semmens, K.A.; Anderson, M.C.; Kustas, W.P.; Gao, F.; Alfieri, J.G.; McKee, L.; Xia, T. Monitoring daily evapotranspiration over two California vineyards using Landsat 8 in a multi-sensor data fusion approach. Remote Sens. Environ. 2016, 185, 155–170. [Google Scholar] [CrossRef] [Green Version]
- Allan, M.G.; Hamilton, D.P.; Trolle, D.; Muraoka, K.; McBride, C. Spatial heterogeneity in geothermally-influenced lakes derived from atmospherically corrected Landsat thermal imagery and three-dimensional hydrodynamic modelling. Int. J. Appl. Earth Obs. 2016, 50, 106–116. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Loveland, T.R.; Woodcock, C.E.; Belward, A.S.; Cohen, W.B.; Roy, D.P. The global Landsat archive: Status, consolidation, and direction. Remote Sens. Environ. 2016, 185, 271–283. [Google Scholar] [CrossRef] [Green Version]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index–radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Neale, C.M. A vegetation index based technique for spatial sharpening of thermal imagery. Remote Sens. Environ. 2007, 107, 545–558. [Google Scholar] [CrossRef]
- Weng, Q.; Fu, P.; Gao, F. Generating daily land surface temperature at Landsat resolution by fusing Landsat and MODIS data. Remote Sens. Environ. 2014, 145, 55–67. [Google Scholar] [CrossRef]
- Zurita-Milla, R.; Kaiser, G.; Clevers, J.G.; Schneider, W.; Schaepman, M.E. Downscaling time series of MERIS full resolution data to monitor vegetation seasonal dynamics. Remote Sens. Environ. 2009, 113, 1874–1885. [Google Scholar] [CrossRef]
- Atkinson, P.M. Downscaling in remote sensing. Int. J. Appl. Earth Obs. 2013, 22, 106–114. [Google Scholar] [CrossRef]
- Maeda, E.E. Downscaling MODIS LST in the East African mountains using elevation gradient and land-cover information. Int. J. Remote Sens. 2014, 35, 3094–3108. [Google Scholar] [CrossRef]
- Bindhu, V.M.; Narasimhan, B.; Sudheer, K.P. Development and verification of a non-linear disaggregation method (NL-DisTrad) to downscale MODIS land surface temperature to the spatial scale of Landsat thermal data to estimate evapotranspiration. Remote Sens. Environ. 2013, 135, 118–129. [Google Scholar] [CrossRef]
- Bisquert, M.; Sánchez, J.M.; Caselles, V. Evaluation of disaggregation methods for downscaling MODIS land surface temperature to Landsat spatial resolution in Barrax test site. IEEE J. Sel. Top. Appl. 2016, 9, 1430–1438. [Google Scholar] [CrossRef]
- Essa, W.; Verbeiren, B.; van der Kwast, J.; Batelaan, O. Improved DisTrad for Downscaling Thermal MODIS Imagery over Urban Areas. Remote Sens. 2017, 9, 1243. [Google Scholar] [CrossRef]
- Lillo-Saavedra, M.; García-Pedrero, A.; Merino, G.; Gonzalo-Martín, C. 2018 TS2uRF: A New Method for Sharpening Thermal Infrared Satellite Imagery. Remote Sens. 2018, 10, 249. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Y.C. Dynamics of Land Surface Temperature in Response to Land-Use/Cover Change. Geogr. Res. 2011, 49, 23–36. [Google Scholar] [CrossRef]
- Wan, Z.; Wang, P.; Li, X. Using MODIS land surface temperature and normalized difference vegetation index products for monitoring drought in the southern Great Plains, USA. Int. J. Remote Sens. 2004, 25, 61–72. [Google Scholar] [CrossRef]
- Yue, W.; Xu, J.; Tan, W.; Xu, L. The relationship between land surface temperature and NDVI with remote sensing: Application to Shanghai Landsat 7 ETM+ data. Int. J. Remote Sens. 2007, 28, 3205–3226. [Google Scholar] [CrossRef]
- Karnieli, A.; Agam, N.; Pinker, R.T.; Anderson, M.; Imhoff, M.L.; Gutman, G.G.; Goldberg, A. Use of NDVI and land surface temperature for drought assessment: Merits and limitations. J. Clim. 2010, 23, 618–633. [Google Scholar] [CrossRef]
- Qiu, J.; Yang, J.; Wang, Y.; Su, H. A comparison of NDVI and EVI in the DisTrad model for thermal sub-pixel mapping in densely vegetated areas: A case study in Southern China. Int. J. Remote Sens. 2018, 39, 2105–2118. [Google Scholar] [CrossRef]
- Hutengs, C.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Mukherjee, S.; Joshi, P.K.; Garg, R.D. A comparison of different regression models for downscaling Landsat and MODIS land surface temperature images over heterogeneous landscape. Adv. Space Res. 2014, 54, 655–669. [Google Scholar] [CrossRef]
- Jeganathan, C.; Hamm, N.A.S.; Mukherjee, S.; Atkinson, P.M.; Raju, P.L.N.; Dadhwal, V.K. Evaluating a thermal image sharpening model over a mixed agricultural landscape in India. Int. J. Appl. Earth Obs. 2011, 13, 178–191. [Google Scholar] [CrossRef]
- Bechtel, B.; Zakšek, K.; Hoshyaripour, G. Downscaling land surface temperature in an urban area: A case study for Hamburg, Germany. Remote Sens. 2012, 4, 3184–3200. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L. Spatial downscaling of MODIS land surface temperatures using geographically weighted regression: Case study in northern China. IEEE Trans. Geosci. Remote 2016, 54, 6458–6469. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, H.; Yang, J. Spatial downscaling of land surface temperature in combination with TVDI and elevation. Int. J. Remote Sens. 2019, 40, 1875–1886. [Google Scholar] [CrossRef]
- Chen, Y.; Zhan, W.; Quan, J.; Zhou, J.; Zhu, X.; Sun, H. Disaggregation of Remotely sensed land surface temperature: A generalized paradigm. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5952–5965. [Google Scholar] [CrossRef]
- Fasbender, D.; Tuia, D.; Bogaert, P.; Kanevski, M.F. Support-Based Implementation of Bayesian Data Fusion for Spatial Enhancement: Applications to ASTER Thermal Images. IEEE Geosci. Remote Sens. 2008, 5, 598–602. [Google Scholar] [CrossRef]
- Keramitsoglou, I.; Kiranoudis, C.T.; Weng, Q. Downscaling geostationary land surface temperature imagery for urban analysis. IEEE Geosci. Remote Sens. 2013, 10, 1253–1257. [Google Scholar] [CrossRef]
- Bai, Y.; Wong, M.S.; Shi, W.Z.; Wu, L.X.; Qin, K. Advancing of land surface temperature retrieval using extreme learning machine and spatio-temporal adaptive data fusion algorithm. Remote Sens. 2015, 7, 4424–4441. [Google Scholar] [CrossRef]
- Yang, Y.; Cao, C.; Pan, X.; Li, X.; Zhu, X. Downscaling Land Surface Temperature in an Arid Area by Using Multiple Remote Sensing Indices with Random Forest Regression. Remote Sens. 2017, 9, 789. [Google Scholar] [CrossRef]
- Neteler, M. Estimating daily land surface temperatures in mountainous environments by reconstructed MODIS LST data. Remote Sens. 2010, 2, 333–351. [Google Scholar] [CrossRef]
- Isotta, F.A.; Frei, C.; Weilguni, V.; Perčec Tadić, M.; Lassegues, P.; Rudolf, B.; Munari, M. The climate of daily precipitation in the Alps: Development and analysis of a high-resolution grid dataset from pan-Alpine rain-gauge data. Int. J. Climatol. 2014, 34, 1657–1675. [Google Scholar] [CrossRef]
- Wan, Z.; Hook, S.; Hulley, G. MOD11A1 MODIS/Terra Land Surface Temperature/Emissivity Daily L3 Global 1km SIN Grid V006; NASA EOSDIS LP DAAC; NASA: Washington, DC, USA, 2015.
- Asam, S.; Callegari, M.; Matiu, M.; Fiore, G.; De Gregorio, L.; Jacob, A.; Menzel, A.; Zebisch, M.; Notarnicola, C. Relationship between Spatiotemporal Variations of Climate, Snow Cover and Plant Phenology over the Alps—An Earth Observation-Based Analysis. Remote Sens. 2018, 10, 1757. [Google Scholar] [CrossRef]
- Wan, Z. MODIS Land-Surface Temperature Algorithm Theoretical Basis Document (LST ATBD); Institute for Computational Earth System Science: Santa Barbara, CA, USA, 1999; p. 75. [Google Scholar]
- MONALISA. Available online: http://www.monalisa-project.eu (accessed on 20 December 2018).
- Vermote, E.; Wolfe, R. MOD09GQ MODIS/Terra Surface Reflectance Daily L2G Global 250 m SIN Grid V006; NASA EOSDIS LP DAAC; NASA: Washington, DC, USA, 2015.
- Vermote, E.; Wolfe, R. MYD09GQ MODIS/Aqua Surface Reflectance Daily L2G Global 250 m SIN Grid V006; NASA EOSDIS LP DAAC; NASA: Washington, DC, USA, 2015.
- Vermote, E.; Wolfe, R. MOD09GA MODIS/Terra Surface Reflectance Daily L2G Global 1 km and 500 m SIN Grid V006; NASA EOSDIS LP DAAC; NASA: Washington, DC, USA, 2015.
- Vermote, E.; Wolfe, R. MYD09GA MODIS/Aqua Surface Reflectance Daily L2G Global 1 km and 500 m SIN Grid V006; NASA EOSDIS LP DAAC; NASA: Washington, DC, USA, 2015.
- EARTHDATA Search. Available online: https://search.earthdata.nasa.gov (accessed on 10 November 2018).
- Jiménez-Muñoz, J.C.; Sobrino, J.A.; Skoković, D.; Mattar, C.; Cristóbal, J. Land surface temperature retrieval methods from Landsat-8 thermal infrared sensor data. IEEE Geosci. Remote Sens. 2014, 11, 1840–1843. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Cristóbal, J.; Sobrino, J.A.; Sòria, G.; Ninyerola, M.; Pons, X. Revision of the single-channel algorithm for land surface temperature retrieval from Landsat thermal-infrared data. IEEE Trans. Geosci. Remote 2009, 47, 339–349. [Google Scholar] [CrossRef]
- NASA/METI/AIST/Japan Spacesystems, and U.S./Japan ASTER Science Team ASTER Global Digital Elevation Model [Version 2, 49oN, 6oE]; NASA EOSDIS Land Processes DAAC; NASA: Washington, DC, USA, 2009.
- Hastie, T.; Tibshirani, R.; Friedman, J. Random forests. In The Elements of Statistical Learning; Series in Statistics; Springer: New York, NY, USA, 2001; pp. 587–602. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- GDAL/OGR Contributors. GDAL/OGR Geospatial Data Abstraction Software Library; Open Source Geospatial Foundation: Chicago, IL, USA, 2019; Available online: https://gdal.org (accessed on 20 December 2018).
- Hijmans, R.J. Raster: Geographic Data Analysis and Modeling. R Package Version 2.8-19. 2019. Available online: https://CRAN.R-project.org/package=raster (accessed on 20 December 2018).
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Bivand, R.; Keitt, T.; Rowlingson, B. Rgdal: Bindings for the ‘Geospatial’ Data Abstraction Library; R Package Version 0.8-16. Available online: http://CRAN.R-project.org/package=rgdal (accessed on 20 December 2018).
- Barry, R.G. Mountain Weather and Climate; Psychology Press: Hove, UK, 1992. [Google Scholar]
- Li, M.; Im, J.; Beier, C. Machine learning approaches for forest classification and change analysis using multi-temporal Landsat TM images over Huntington Wildlife Forest. GISci. Remote Sens. 2013, 50, 361–384. [Google Scholar] [CrossRef]
- Chen, X.; Li, W.; Chen, J.; Rao, Y.; Yamaguchi, Y. A combination of TsHARP and thin plate spline interpolation for spatial sharpening of thermal imagery. Remote Sens. 2014, 6, 2845–2863. [Google Scholar] [CrossRef]
- Essa, W.; van der Kwast, J.; Verbeiren, B.; Batelaan, O. Downscaling of thermal images over urban areas using the land surface temperature–impervious percentage relationship. Int. J. Appl. Earth Obs. 2013, 23, 95–108. [Google Scholar] [CrossRef]
- Yu, X.; Guo, X.; Wu, Z. Land surface temperature retrieval from Landsat 8 TIRS—Comparison between radiative transfer equation-based method, split window algorithm and single channel method. Remote Sens. 2014, 6, 9829–9852. [Google Scholar] [CrossRef]
- Sattari, F.; Hashim, M. A brief review of land surface temperature retrieval methods from thermal satellite sensors. Middle-East J. Sci. Res. 2014, 22, 757–768. [Google Scholar]
- Dissanayake, D.; Morimoto, T.; Murayama, Y.; Ranagalage, M. Impact of Landscape Structure on the Variation of Land Surface Temperature in Sub-Saharan Region: A Case Study of Addis Ababa using Landsat Data (1986–2016). Sustainability 2019, 11, 2257. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jimenez-Munoz, J.C.; Paolini, L. Land surface temperature retrieval from LANDSAT TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Sobrino, J.A.; El Kharraz, J.; Li, Z.L. Surface temperature and water vapour retrieval from MODIS data. Int. J. Remote Sens. 2003, 24, 5161–5182. [Google Scholar] [CrossRef]
- Merlin, O.; Duchemin, B.; Hagolle, O.; Jacob, F.; Coudert, B.; Chehbouni, G.; Kerr, Y. Disaggregation of MODIS surface temperature over an agricultural area using a time series of Formosat-2 images. Remote Sens. Environ. 2010, 114, 2500–2512. [Google Scholar] [CrossRef] [Green Version]

| Dataset Name | Spatial Resolution | Short Description | Derivatives Products |
|---|---|---|---|
| MOD11A1 | 1000 m | MODIS Terra Land Surface Temperature | Resampled to NDVI spatial resolution (GSD = 250 m) for residual correction |
| NDVI 4-Day composites | 250 m | MODIS Terra and MODIS Aqua Reflectance bands based on MOD09GA | NDVI aggregated to 1000 m pixel size by spatial averaging |
| ASTER GDEM | 30 m | Global Digital Elevation Model acquired ASTER scanner | GDEM resampled to 250 m and 1000 m spatial resolution |
| LISS 2013 -Land Information System South Tyrol | - | Land Information System South Tyrol based on GeoEye-1 image collection from 2012 | Vegetation vector masks for: - areas covered by minimum 90% of vegetation within 1km pixels - pure pixels for different types of vegetation (75% threshold of homogeneity) |
| Landsat 5 | 30 m 120 m (30) 2 | Atmospherically-corrected reflectance products (red, NIR), Thermal at-sensor radiance | Gaussian filtering and resampling to 250 m |
| Landsat 8 | 30 m 100 m (30) 2 | Atmospherically-corrected reflectance products (red, NIR), Thermal at-sensor radiance | Gaussian filtering and resampling 250 m |
| MOD05_L2 | 1000 m | MODIS Precipitable Water | Re-projected to MODIS Sinusoidal Projection |
| Date | Sensor | Granule ID | Overpass Time (GMT) |
|---|---|---|---|
| 27.09.2004 | Landsat 5 TM | LT05_L1TP_192028_20040927_20161129_01_T1 | 09:42 |
| 25.05.2005 | LT05_L1TP_192028_20050525_20161126_01_T1 | 09:45 | |
| 16.10.2005 | LT05_L1TP_192028_20051016_20161124_01_T1 | 09:46 | |
| 18.07.2007 | LT05_L1TP_192028_20070718_20161112_01_T1 | 09:52 | |
| 12.09.2010 | LT05_L1TP_192028_20100912_20161013_01_T1 | 09:48 | |
| 27.08.2016 | Landsat 8 TIRS | LC08_L1TP_192028_20160827_20170321_01_T1 | 09:58 |
| 11.06.2017 | LC08_L1TP_192028_20170611_20170627_01_T1 | 09:58 |
| Landsat LST vs. original MODIS LST | Landsat LST vs. sharpened MODIS LST | ||||
|---|---|---|---|---|---|
| RMSEmean | |||||
| BM | EM1 | EM2 | BM | EM1 | EM2 |
| 2.97 | 2.38 | 2.44 | 2.31 | 2.23 | 2.22 |
| MAEmean | |||||
| BM | EM1 | EM2 | BM | EM1 | EM2 |
| 2.18 | 1.83 | 1.85 | 1.79 | 1.73 | 1.72 |
| Landsat LST vs. Sharpened MODIS LST | ||||||
|---|---|---|---|---|---|---|
| RMSE (K) | ||||||
| Date | Forest | Vineyards & Orchards | Annual Crops | Grassland | Bushes | AVERAGE |
| 27.09.2004 | 2.57 | 2.55 | 2.19 | 3.03 | 3.53 | 2.78 |
| 25.05.2005 | 1.84 | 2.67 | 1.24 | 3.30 | 5.09 | 2.83 |
| 16.10.2005 | 2.19 | 1.45 | 1.05 | 2.50 | 4.08 | 2.25 |
| 18.07.2007 | 2.10 | 4.33 | 3.60 | 2.95 | 3.26 | 3.25 |
| 12.09.2010 | 2.10 | 2.66 | 2.97 | 2.78 | 3.36 | 2.77 |
| 27.08.2016 | 1.58 | 2.39 | 2.47 | 2.66 | 3.22 | 2.46 |
| 11.06.2017 | 2.09 | 3.32 | 4.13 | 3.38 | 4.43 | 3.47 |
| AVERAGE | 2.07 | 2.77 | 2.52 | 2.94 | 3.85 | - |
| Landsat LST vs. original MODIS LST | ||||||
|---|---|---|---|---|---|---|
| RMSE (K) | ||||||
| Date | Forest | Vineyards & Orchards | Annual Crops | Grassland | Bushes | AVERAGE |
| 27.09.2004 | 2.73 | 2.75 | 2.30 | 3.53 | 3.85 | 3.03 |
| 25.05.2005 | 1.96 | 2.46 | 1.03 | 4.05 | 5.51 | 3.00 |
| 16.10.2005 | 2.24 | 1.62 | 2.71 | 3.06 | 4.64 | 2.86 |
| 18.07.2007 | 2.20 | 3.98 | 3.02 | 3.32 | 3.91 | 3.29 |
| 12.09.2010 | 2.21 | 2.56 | 3.41 | 3.30 | 4.57 | 3.21 |
| 27.08.2016 | 1.65 | 2.11 | 2.02 | 3.05 | 3.67 | 2.50 |
| 11.06.2017 | 2.19 | 2.97 | 3.23 | 3.85 | 4.48 | 3.34 |
| AVERAGE | 2.17 | 2.64 | 2.53 | 3.45 | 4.38 | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bartkowiak, P.; Castelli, M.; Notarnicola, C. Downscaling Land Surface Temperature from MODIS Dataset with Random Forest Approach over Alpine Vegetated Areas. Remote Sens. 2019, 11, 1319. https://doi.org/10.3390/rs11111319
Bartkowiak P, Castelli M, Notarnicola C. Downscaling Land Surface Temperature from MODIS Dataset with Random Forest Approach over Alpine Vegetated Areas. Remote Sensing. 2019; 11(11):1319. https://doi.org/10.3390/rs11111319
Chicago/Turabian StyleBartkowiak, Paulina, Mariapina Castelli, and Claudia Notarnicola. 2019. "Downscaling Land Surface Temperature from MODIS Dataset with Random Forest Approach over Alpine Vegetated Areas" Remote Sensing 11, no. 11: 1319. https://doi.org/10.3390/rs11111319
APA StyleBartkowiak, P., Castelli, M., & Notarnicola, C. (2019). Downscaling Land Surface Temperature from MODIS Dataset with Random Forest Approach over Alpine Vegetated Areas. Remote Sensing, 11(11), 1319. https://doi.org/10.3390/rs11111319