1. Introduction
The second phase of the BeiDou navigation satellite system space segment (BDS-2) consists of Geosynchronous Earth Orbit (GEO), Inclined Geosynchronous Orbit (IGSO) and Medium Earth Orbit (MEO) satellites and it started to provide regional service around the Asia-Pacific area, namely from 55°S to 55°N latitude and 55°E to 180°E longitude, since the end of 2012 [
1]. BDS-2 aims to provide a better than 10 m (probability of 95%) positioning accuracy in horizontal and vertical, and timing precision better than 50 ns within the service area [
2]. The performance of the BDS-2 system has been fully investigated by many researchers in the aspects of precise orbit determination (POD), observation noise, multipath, positioning performance including single point positioning (SPP), precise point positioning (PPP) and real-time kinematic (RTK) and so on [
3,
4,
5,
6,
7].
Since 2015, China began to develop BDS-3 aiming to provide a global service. Five experimental satellites were launched for demonstration purposes during the period from 2015 to 2016. More BDS-3 satellites have been launched since 2017. Currently, the BDS system constellation consists of five GEO, seven IGSO and 21 MEO satellites, which includes 15 BDS-2 satellites and 18 BDS-3 satellites [
8]. By the end of 2018, BDS was announced to be providing a global positioning, navigation and timing (PNT) service, which supports positioning accuracy of 10 m (95%) in horizontal and vertical throughout its global coverage, and timing accuracy better than 20 ns. By the end of 2020, the full BDS constellation will be completed with the continuous launching of additional BDS-3 satellites. The BDS signal in space range error (SISRE) will be better than 0.5 m with higher stability. Additionally BDS will provide a satellite-based augmentation service around China, an international search and rescue service, and a precise point positioning service [
9].
Compared with BDS-2, the BDS-3 satellites show differences in three aspects: (1) in addition to B1I and B3I signals, BDS-3 satellites also transmit signals B1c and B2a, which are centralized at the same frequency as L1(GPS)/E1(Galileo) and L5(GPS)/E5a(Galileo), making BDS compatible with and interoperable with GPS and Galileo [
8,
10]; (2) BDS-3 satellites are equipped with inter-satellite link (ISL) payloads in the Ka band which enable autonomous navigation and with ISL range measurements with accuracy less than 10 cm, the orbit overlap difference would be between 10 and 20 cm [
11,
12,
13]; (3) BDS-3 employs a new generation of high-precision rubidium (Rb) clocks and passive hydrogen maser (PHM) clocks, which indicate a lower frequency drift than BDS-2. The frequency stability of the PHM clock shows about 6 × 10
−15 at an interval time of 1-day [
14].
Current research mainly focuses on the space segment of the new BDS-3 satellites. With the implementation of the BDS-3 service, it is of great significance to investigate the positioning performance of the current BDS constellation. Zhang et al. [
15] analyzed the benefit of BDS-3 experimental (BDS-3e) satellites, and indicate that BDS-3e satellites no longer suffer from satellite-induced elevation dependent code bias which was first discovered by Wanninger and Beer [
5]. Meanwhile, B2a has a smaller code multipath and BDS-3e satellites would improve ambiguity resolution performance in RTK. Zhang et al. [
16] further proved that with the help of BDS-3e satellites, the convergence time of PPP would also shorten for areas with fewer visible satellites. Yang et al. [
17] assessed the user equivalent range error (UERE) of BDS-3e, which is smaller than 0.73 m and the timing accuracy is usually better than 10 ns. To assess the possible positioning and navigation accuracy, a simulated BDS-3 constellation consisting of three GEO, three IGSO, and 24 MEO satellites was also designed to predict the dilution of precision (DOP) value of the final BDS-3 constellation [
17,
18]. In 2019, Yang et al. [
19] first gave a 4-day SISRE result of eight BDS-3 satellites comparing broadcast ephemeris and POD results from International GNSS Monitoring and Assessment System (iGMAS), which shows that the root mean square (RMS) error of the satellite orbit in three-dimensions (3D) is about 1.07 m, while the average RMS of the satellite clock error is 1.12 ns and the average SISRE is 0.44 m. However, there is still little research on positioning performance using the current BDS-2 and BDS-3 constellation.
This paper aims to present an initial assessment of the positioning performance of the current BDS constellation with new satellites and new signals.
Section 2 investigates the global satellite visibility and position dilution of precision (PDOP) of the current BDS constellation. To verify the accuracy of the satellite segment,
Section 3 presents the SISRE of BDS with over 60 days of data. Then, in
Section 4 we assess the SPP performance of BDS using 54 globally distributed stations which is also compared with that of the GPS and BDS-2 systems. Positioning performance of the new BDS signals including B1c and B2a is also analyzed and compared. In
Section 5, RTK performance of the current BDS is assessed in comparison with the BDS-2 system. Finally, conclusions are presented.
2. Satellite Visibility and PDOP Availability
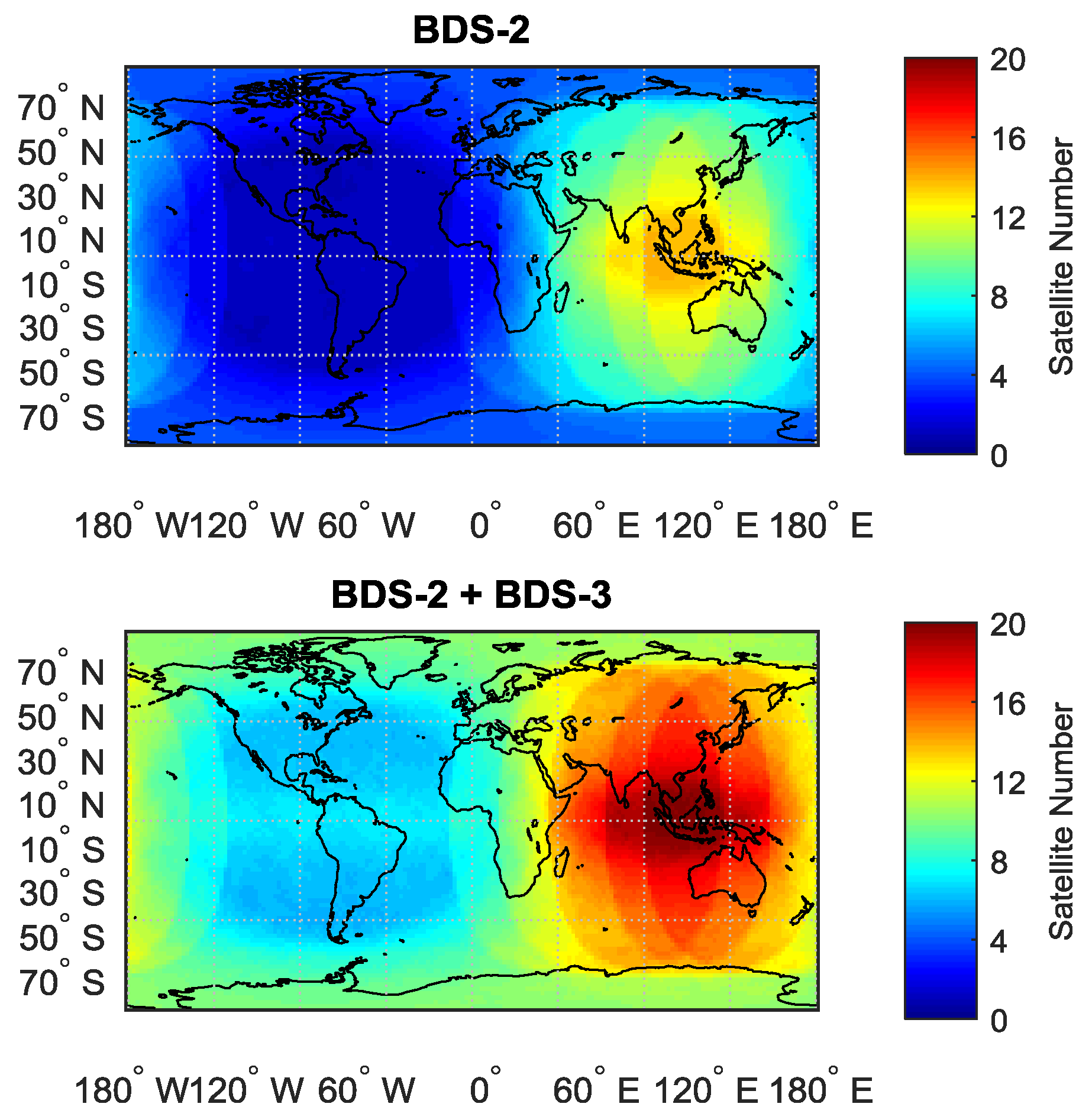
With the availability of BDS-3 satellites, global users would benefit from the PNT service from BDS as more satellites are visible all over the world. To investigate the service area with the current BDS constellation, we will assess the satellite visibility, PDOP value and availability in this part.
Using the broadcast ephemeris on 1 January 2019, we explore the global satellite visibility and PDOP value comparing BDS-2 and the current constellation of BDS-2 and BDS-3. The latitude and longitude are divided into a 2° × 2° grid and the satellite elevation mask is set as 10°. As for PDOP, we adopt the conventional concept that a PDOP value less than 6 is necessary to provide basic PNT service [
8]. To assess the normal performance, the result is calculated on an hourly basis and the global average result is plotted, which is depicted in
Figure 1 and
Figure 2, and the minimum, maximum and average satellite number are listed in
Table 1.
It can be observed from
Figure 1 and
Table 1 that for BDS-2 constellation, the maximum visible satellite number is about 13.8, which is located in Southeast Asia, where the equatorial region is at the longitude of about 110°. For the opposite part of the Earth, i.e., the Americas, the average satellite number would less than 4, which is challenging for PNT service. With the contribution of BDS-3 satellites, Southeast Asia would still be the “hottest” area of BDS, with 20 satellites that can be tracked at most. As for the Americas, a minimum number of 5.7 satellites is visible, which indicates that a global PNT service is possible using the current BDS-2 and BDS-3 constellation. Comparing with BDS-2, the global average visible satellite number increases from 5.1 to 10.7.
As for PDOP, it shows a similar performance. For BDS-2, the minimum PDOP is 1.8, while for BDS-2+BDS-3, it would decrease to 1.2. Outside the Asia-Pacific region, PDOP of BDS-2 would dramatically increase. Nevertheless, combining BDS-2 and BDS-3, the PDOP value changes gradually and it is still able to provide normal PNT service in the Americas, with a maximum PDOP value of 3.3.
For the above PDOP statistics, only values of less than 6 are counted. However, for a navigation system, the percentage of time to provide a specified level of PNT service, or the availability, is also important [
20]. For the case of BDS-2 PDOP performance, although some areas outside the Asia-Pacific region could experience normal PDOP, most of the time the PDOP is larger than 6, which is not shown in
Figure 2. Therefore, it is necessary to assess PDOP availability.
In this paper, we define the PDOP availability as the percentage of time that the PDOP value is less than 6 [
8].
Figure 3 plots the global overall PDOP availability of BDS-2 and BDS-2+BDS-3 constellation and the minimum, maximum and average value are listed in
Table 1. It can be seen that for BDS-2, the average of global PDOP availability is only 35.25%, which is mostly around the Asia-Pacific region, while for BDS-2+BDS-3, it could reach the level of 98.84%, which fulfills the target of PDOP availability of BDS open service performance standard [
8].
3. Signal in Space Range Error
For real-time PNT services such as SPP or RTK, the precision of broadcast ephemeris is a key factor. SISRE is a common quantity used to assess the quality of broadcast ephemeris [
21]. SISRE of BDS-2 has been assessed by many researchers [
21,
22,
23,
24]. It is reported that the SISRE of BDS-2 is about 1 m [
24]. As for BDS-3, Yang et al. [
19] showed that the average SISRE is 0.44 m using eight BDS-3 satellites. To investigate the overall performance, the SISRE of the current BDS constellation is explored in this section.
SISRE of broadcast ephemeris is usually compared with precise orbit and clock products. Precise BDS-3 products of Wuhan University (WUM) [
25] are used here. Although no exact precision of the WUM products is reported for BDS-3 satellites, previous research indicates that the average 3D orbit RMS is better than 20 cm [
11,
12,
13], as there are still not many stations tracking BDS-3 satellites. Comparing with the 0.5–1.0 m level precision of broadcast ephemeris, WUM products would be sufficient to assess the SISRE of BDS broadcast ephemeris.
When comparing BDS broadcast ephemeris with WUM final products, difference such as time and coordinate system should be considered [
21]. Besides, we should also consider the following corrections:
- (1)
Satellite antenna offset correction. Starting from 7 January 2017, BDS changed the orbit reference point from the center of mass (CoM) to the antenna phase center (APC) [
26], which is the same as other GNSS systems. For precise orbit and clock products, it is referred to the CoM. Such differences should be corrected when comparing orbit difference. The antenna phase center offset (PCO) used in broadcast ephemeris is provided by the Test and Assessment Research Center of China Satellite Navigation Office (TARC-CSNO). According to Guo [
25], for WUM products, the PCO value of BDS-3 are also provided by TARC-CSNO, while PCO of BDS-2 are estimated by Wuhan University [
27]. Therefore, the inconsistency that affect the radial component should be corrected for BDS-2 satellites, while a zero offset can be adopted for BDS-3 satellites.
- (2)
Clock and TGD/DCB correction. It is known that there exists a system bias among different products. Commonly an ensemble clock offset is computed at each epoch from the average broadcast-minus-precise clock values of satellites [
21]. To reduce the effect of gross errors from some satellites, we use a medium value of broadcast-minus-precise clock as the offset [
22].Meanwhile, the satellite clock in the BDS broadcast ephemeris is referred to the B3I signal [
1], while for WUM products, it is referred to the ionosphere-free combination of B1I/B3I signals instead of the traditional B1/B2 signals [
25]. This kind of difference between B3I and B1I/B3I should be corrected by the timing group delay (TGD) [
28]. Similar to TGD but with a higher precision, differential code bias (DCB) of the BDS is also provided by the Chinese Academy of Science (CAS) [
29].
A common method to calculate SISRE can be expressed as:
where R, A, C stand for the orbit error in radial, along-track and cross-track direction, Clk means the clock error, α and β are the weighting factors for the line of sight. A detailed value can be found in [
21].
We take two months of data from day of year (DOY) 10 to DOY 70, 2019 for assessment. For comparison, TGD and DCB are applied respectively. The data sampling is set as 10 min and the threshold of gross outlier rejection is set as 10 m. The SISRE statistics for BDS-2 and BDS-3 are listed in
Table 2, and the statistical RMS of SISRE for each satellite is plotted in
Figure 4.
From
Table 2 we can see that the overall SISRE of the current BDS constellation is 0.83 m (TGD correction) or 0.71 m (DCB correction). For BDS-2, the SISRE is within 1 m, which shows a similar performance as reported in Montenbruck et al. [
24]. For BDS-3, with the contribution of a more stable satellite clock and a new ISL technique, SISRE of BDS-3 is superior to BDS-2, where the average SISRE is 0.71 m versus 0.96 m after TGD correction. If DCB correction is applied, the average SISRE is 0.57 m versus 0.90 m, respectively, which indicates that the TGD accuracy of BDS-2 is similar to DCB, while the TGD accuracy for BDS-3 is slightly worse. As it can be seen from the lower subplot of
Figure 4, some satellites show an obvious poor SISRE after TGD correction. This may be due to the accuracy of the TGD on these satellites. Meanwhile, it is interesting that the SISRE of C35-C37 are apparently worse than other BDS-3 satellites. As reported by Deng [
30], receivers able to track C35~C37 are much less than other BDS-3 satellites, which would lead to lower accuracy of precise orbit and clocks for C35-C37. If C35-C37 are excluded, SISRE of BDS-3 would reduce to 0.62 m (TGD correction) or 0.45 m (DCB correction), which is at the similar level of GPS and Galileo.
5. RTK Performance
In this section, we evaluate the RTK performance using the current BDS constellation. Two baselines at different lengths are selected. One is a 20 m baseline from station YARR to YAR3 (29.05°S, 115.35°E), the other is a 10 km baseline from station STR1 to TID1 (35.40°S, 148.98°E). Data on January 1, 2019 is selected for the RTK assessment of the two baselines.
For the RTK strategy, dual-frequency data on B1I and B3I are used. Conventional continuous mode without considering troposphere and ionosphere difference is applied during ambiguity resolution (AR). To reduce the impact of noise from low elevation satellites, the cut-off elevation is set as 10° for float solution in Kalman Filter and 20° in the procedure of ambiguity fixing. A threshold of 3.0 with a success rate of 0.99 is set for ratio test in LAMBDA method [
34]. In the case of AR, ambiguity dilution of precision (ADOP) is an important concept indicating the success rate of AR. According to Teunissen [
35], ADOP can be defined as:
where
is the variance-covariance matrix of float ambiguities and |·| is the determinant of the matrix, n is the dimension of the ambiguity vector. As pointed out by Odijk and Teunissen [
36], if ADOP is smaller than 0.14 cycle, the AR success rate would better than 0.99.
To analyze the contribution of BDS-3 in RTK, an epoch-by-epoch ADOP value is computed at the two baselines using BDS-2-only and BDS-2+BDS-3 satellites. As shown in
Figure 14, the ADOP value at 20 m baseline is well below 0.14 cycle, which indicates the possibility of reliable ambiguity resolution for instantaneous RTK. While for 10 km baseline, ADOP is slightly worse than 20 m baseline due to satellite geometry. The percentage of ADOP below 0.14 cycle is 75.3% if BDS-2 is used, which could lead to wrong fixings for the ambiguity for instantaneous RTK. While for the BDS-2+BDS-3 combination, more than 99% of ADOP is below 0.14 cycle. In summary, for both baselines, ADOP performance would improve in different levels after BDS-3 satellites are added.
RTK performance of BDS-2-only and BDS-2+BDS-3 scenarios at these two baselines are depicted in
Figure 15 and
Figure 16, together with the statistical results of RMS and 95% accumulated error listed in
Table 6. This illustrates that BDS-3 contributes to a more stable and precise RTK performance in the horizontal and vertical component, with a 1~2 mm improvement for 20 m baseline and 1~2 cm improvement for the 10 km baseline. Although it is not shown here, it should be pointed out that if we perform instantaneous RTK at the 10 km baseline [
33], it would lead to some wrong ambiguity fixing for the BDS-2-only case.
6. Conclusions
With the official start of BDS-3 service, BDS has become a global navigation satellite system and more users can now benefit from BDS-only or BDS-combined multi-GNSS positioning. In this paper, we comprehensively assess the system status and the global positioning performance of BDS. Results show that:
- (1)
With the contribution of new BDS-3 satellites, the global average number of BDS satellites increases from 5.1 to 10.7, thus the global position dilution of precision value would improve. According to analysis, the average position dilution of precision availability is around 98.84%, which meets the open service performance standard of BDS.
- (2)
Signal in space range error of the current BDS constellation is 0.83 m. For BDS-3 satellites, it shows a 0.71 m performance, which is much better than BDS-2. After removing some BDS-3 satellites tracked by a few stations, the signal in space range error of BDS-3 is competitive with GPS and Galileo. We believe that with more BDS-3 satellites in space and the improvement of timing group delay accuracy, the overall signal in space range error of BDS would further improve.
- (3)
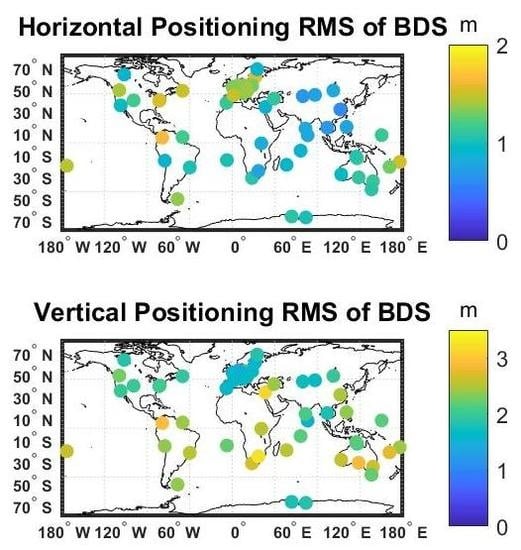
For single point positioning performance on the B1I frequency, with a global RMS of accuracy at 1.1 m in horizontal and 2.2 m in vertical, BDS shows a similar accuracy with GPS. Comparing with BDS-2, BDS-3 greatly improves the positioning accuracy and service area of BDS. For the new B1c signal, it shows a similar performance in positioning with B1I. While for B2a, the positioning accuracy is much worse, which may come from the inaccurate precision of BDS ionosphere correction. Meanwhile, observation noise on B1c and B2a is much better than B1I.
- (4)
BDS-3 also benefits real-time kinematic users in ambiguity dilution of precision and real-time kinematic performance in positioning accuracy and reliability.
To conclude, with a better signal in space range error and better position dilution of precision, PNT performance of BDS-3 will greatly improve in comparison with BDS-2, making BDS-3 a competitive global GNSS system. For the assessment of BDS signal in space range error, WUM final orbit and clock products are used. However, due to the still limited availability of BDS-3 tracking data, current precision of BDS-3 post-processed orbit and clock products are still lower than other GNSS systems. More precise products may be applied for BDS signal in space range error assessment in the future. Meanwhile, assessment of BDS-3 precise point positioning performance can also be conducted using the more precise products. With more stations tracking the B2a signal, it is expected that timing group delay accuracy would also improve.