1. Introduction
The coastline, the boundary of land and sea, is one of the 27 most important land surface features, and is vulnerable to natural processes such as coastal erosion/accretion, sea level changes and human activities [
1]. Coastline mapping is, therefore, becoming a fundamental work for coastal erosion monitoring, coastal resource management, coastal environmental protection and coastal sustainable development [
2,
3,
4,
5,
6]. In reality, the shoreline accurate position is difficult to be localized, as the position changes continually through time, because of cross-shore and alongshore sediment movement in the littoral zone and especially because of the dynamic nature of water levels at the coastal boundary (e.g., waves, tides, groundwater, storm surges, setups, runups, etc.) [
7].
With the advantages of cost-effectiveness and large spatial and temporal scales, satellite remote sensing data have been used widely for coastline mapping [
1,
7,
8,
9]. When shoreline changes are sufficiently large (several tens of meters), satellite remote sensing can enable semi-automated comparison of large-scale areas by providing a common protocol for all sites [
10], thus making comparisons consistent [
11]. However, most observed shoreline changes are presently much smaller [
12], so that the coarse spatial resolution of pixels prevent the accurate determination of shoreline positions when monitoring shoreline changes [
13]. In this case, shoreline change observations can only be obtained by means of repeated in situ surveys, analysis of aerial or satellite high-resolution photographs at several time intervals, or a combination of both approaches [
11,
14]. However, the expensive price and shortage of historical data cannot meet large-scale shoreline supervision demands and the requirements of shoreline change analysis. Thus, it is important to conduct research on how to accurately determine the shoreline’s position from long-term sequences of medium spatial resolution satellite images.
In recent years, many articles have appeared on how to use super resolution mapping (SRM) or subpixel edge localization (SEL) algorithms to extract the shoreline accurately. In these articles, positioning accuracy is quantitatively evaluated by four indicators: mean absolute error (MAE), standard deviation (SD), root mean squared error (RMSE), and line matching (LM) [
15].
SRM has been applied to low- or medium-resolution satellite remote sensing images to overcome the limitation of the image spatial resolution of the original image. Li et al. [
16] proposed that SRM can be categorized into two groups. The first group [
17,
18,
19,
20] is directly applied to satellite images instead of the intermediate spectral unmixing result, whereas the second group [
21,
22,
23,
24,
25,
26,
27,
28,
29] is expected to improve the result’s accuracy when highly-accurate fraction images are available from a spectral unmixing model [
30]. According to shoreline SRM, Foody et al. [
31] presented a soft fuzzy classification utilizing a geostatistical approach to obtain accurate waterline locations. Muslim et al. [
32] proposed a localized soft classification approach to predict the shoreline location by a two-point histogram and pixel-swapping algorithms. Muslim et al. [
33] proposed a contouring and geostatistical method to geographically position the coastline within image pixels. Zhang et al. [
34] integrated a geostatistical approach and the high-resolution spatial structure prior model to undertake super-resolution mapping, which can properly illustrate the spatial distribution of the coastline at a fine scale. Comparisons [
35] have been made using three soft classification methods and three subpixel mapping methods for coastal area classification.
SEL algorithms are often designed as follows: first, the initial position is obtained by edge detection; second, a local edge model is adopted to refine the initial edge position to the subpixel level. Subpixel detection techniques can be grouped into three categories [
36]: moment-based; least-squares-error-based; and interpolation-based. Concerned with subpixel shoreline localization, Pardo-Pascual et al. [
37] extracted subpixel shorelines utilizing local spatial structures from Landsat TM and ETM+, where the RMSE obtained ranged from 4.69 to 5.47 m. Almonacid-Caballer et al. [
38] determined the annual mean shoreline subpixel position from Landsat images, and the extracted shorelines were biased from the seaward direction by approximately 4–5 m. Qingxiang Liu [
39] presented a subpixel vector-based shoreline method to monitor shoreline changes at Narrabeen–Collaroy Beach, Australia, over 29 years. The experimental results show that after the correction of tidal effects, the RMSEs of annual mean shorelines are within 5.7 m. Pardo-Pascual et al. [
40] evaluated the accuracy of shoreline positions obtained from the infrared (IR) bands of Landsat 7, Landsat 8, and Sentinel-2 imagery on natural beaches, where the mean error reached 3.06 m (± 5.79 m) from Landsat 8 and Sentinel-2 images.
In fact, there are different types and various geometric morphologies of shorelines in complex offshore environments. From the point of view of different shoreline types, there are artificial shorelines and natural shorelines. A shoreline may also be considered over a slightly longer timescale, such as a tidal cycle, where the horizontal/vertical position of the shoreline could vary anywhere between centimeters and tens of meters (or more), depending on the beach slope, tidal range, and prevailing wave/weather conditions [
7]. It is, therefore, more difficult and challenging to evaluate the shoreline location accurately, especially natural shorelines.
From a geometric morphology point of view, shorelines include simple straight, quasi-straight, and high curvature shorelines, or combinations of these. It is difficult for traditional subpixel shoreline algorithms to determine various geometric morphological shoreline subpixel positions. Most algorithms mentioned above obtain the most accurate shoreline position for simple straight shorelines, but fail for high curvature shorelines in which the positional error increases [
37].
Owing to the complex offshore environment, which includes suspended sediment, foam, different land-cover types etc., there are many mixed pixels and noise along the shoreline. Thus, it is difficult to find pure pixels along the natural or artificial shoreline for spectral unmixing, and the pure pixels obtained by global spectral analysis may not represent shoreline local spectra finely. Meanwhile, these conditions may also lead to difficulties in modeling the local edge for SEL algorithms.
Compared with a natural shoreline, an artificial shoreline is stable and its position is not affected by tidal effects or other factors, thus the reference shoreline can be extracted from high-resolution satellite images from different imaging times. Thus, artificial shorelines have the advantage of being more easily validated than natural shorelines. In this study, we focus on how to determine the artificial shoreline position accurately. In addition, we propose a method called the semi-global shoreline subpixel localization (SGSSL) algorithm. The main thoughts underlying SGSSL are simplifying the shoreline subpixel localization problem to a segmented shoreline subpixel fitting problem, expressing a shoreline segment geometric morphology perfectly, and minimizing the intensity integral error in local windows. To express various geometric morphological shorelines, we utilize multi-scale corner points to divide the initial shoreline into relatively simpler shoreline segments. To prevent offshore environment interference on subpixel localization, we analyze the water index intensity homogeneity for designing local windows. In designed local windows, intensity integral errors are minimized to obtain the subpixel shoreline positions. The entire method is dependent not only on shoreline geometric morphology and global spectral features but also local window intensity analysis and segmented shoreline geometric morphology. Thus, the proposed method is named semi-global subpixel shoreline localization (SGSSL).
3. Materials and Methods
According to the main thoughts underlying SGSSL, the overall process is shown in
Figure 2. First, global spectral and geometric morphology analysis are conducted: the initial shoreline is extracted using the Otsu [
43] automatic threshold method from water index images; and geometric morphology control points, abbreviated as morphology control points (MCPs), are extracted using the multi-scale Harris algorithm [
44]. The primary MCPs are utilized to divide the initial shoreline. Then, semi-global analysis is performed by the segmentation-merge-fitting (SMF) method. In the SMF process, the segmented shoreline subpixel location is determined by minimizing the intensity integral error, finally obtaining a continuous subpixel shoreline vector.
In
Section 3.1, an ideal image is taken as an example to illustrate the basic principle of SGSSL. In
Section 3.2, the challenges faced when the basic principle is applied to real satellite images are explained. In
Section 3.3, the method of conducting the global analysis for SGSSL is introduced, including obtaining the initial shoreline position and extracting the MCPs. In
Section 3.4, the process of performing a semi-global shoreline analysis for SGSSL is proposed, including designing local windows and details of the SMF processes.
3.1. Basic Principles of Subpixel Shoreline Localization
The entire shoreline can be regarded as consisting of many shoreline segments. The proposed subpixel shoreline localization algorithm is based on the following two assumptions:
Assumption 1: Any shoreline segment can be approximated by the polynomial function y = f(x).
Assumption 2: The shoreline segment divides the image into two homogeneous regions with intensities A and B (A < B).
The ideal binary image is built in the image coordinate system
O-xy, as shown in
Figure 3, in which there is one shoreline segment.
A local window (the purple box in
Figure 3) centered on the
ith shoreline pixel (
xi,yi) is set, so the sum of intensity in the
ith window is:
where (
xi,yi) is the current shoreline point’s pixel coordinate,
G the pixel’s intensity,
n the number of pixels in the shoreline segment, and
m1, m2 are the pixels’ number above or under the shoreline csegment in the local window, respectively. According to Assumption 2, the integral of the intensity in the
ith window is:
where
and
are areas covered by A or B in the local window, respectively:
According to Assumption 1, as the cubic function can express more geometric details and has superior morphological adaptability, the shoreline segment’s polynomial function is:
So, the area under the shoreline segment in the
ith local window (
) can be calculated as:
With the above derivations, the intensity integral of the
ith local window’s (
SUMi*) can be described as:
A similar idea has been researched by Trujillo-Pino et al. [
36] for medical and indoor images, in which a subpixel edge location algorithm based on the partial area effect (PAE) was proposed. However, in that work, the algorithm neither considered the various geometric morphologies of the real shoreline/contour nor proved its application to actual satellite remote sensing images.
To solve Equation (7), the equation can be represented simply as:
where:
The following non-homogeneous equation can be obtained:
The intensity integral error in the
ith local window (
ei) is defined as:
By the least squares methodology, the cubic polynomial coefficients vector = (a,b,c,d)T can be solved with intensity integral error minimization, and then the shoreline subpixel localization is determined.
3.2. Challenges for Subpixel Shoreline Localization in Remote Sensing Images
In
Section 3.1, the derivation was based on the ideal image in
Figure 3. When dealing with real shorelines, as
Figure 4a shows, the initial shoreline (colored in purple) with various geometric morphologies does not satisfy Assumption 1. Therefore, the initial shoreline should be divided into segments of relatively simple morphologies, which can be approximated by the cubic polynomial function. For a shoreline to be divided appropriately, the multi-scale Harris corner algorithm [
44] should be utilized to extract the MCPs.
When processing actual satellite images, the water index result is affected by sensor imaging noise and the interaction between adjacent classes. Meanwhile, heterogeneous pixels exist in the local window with intensity changes (
Figure 4b, green box). Then, Assumption 2 is not satisfied, which leads to the intensity integral error expressed in Equation (10) not equaling zero.
It is therefore necessary to design the local window to guarantee the intensity integral error approaches zero to ensure the performance of SGSSL correctly.
3.3. Shoreline Global Analysis
3.3.1. Determination of Initial Shoreline Position
To make full use of satellite image global information, we will conduct a shoreline global analysis, which includes a spectral feature analysis and geometric morphology analysis to determine the initial shoreline position at the pixel level and extract appropriate MCPs.
3.3.2. Determination Initial Shoreline Position
Before extracting MCPs, we should determine the initial pixel level shoreline from the original fused satellite images. This procedure includes the following steps. First, the water index image is calculated. The modified normalized difference water index (MNDWI) [
45] is preferred, and the reason why MNDWI is preferred is discussed in
Section 5.1. Subsequently, the Otsu method [
43] is applied to the water index image, in which an optimal threshold
T* is selected automatically by maximizing the inter-class discrepancy. Third, using the optimal threshold value
T*, the water index image is divided into a binary image, which includes non-water and water classes. A series of points representing the pixel level shoreline is obtained.
3.3.3. MCP Extraction
To satisfy Assumption 1, the initial pixel level shoreline with various geometric morphologies should be divided into segments with relatively simple morphology by MCPs. As multi-scale Harris detection [
44] is sensitive to corners, MCPs are extracted by multi-scale Harris detection [
44] from a binarized water index image:
where
σI is the integral scale,
g(σI) the Gaussian convolution kernel with integral scale
σI, and
La the derivative computed in the
a direction. The multi-scale Harris
cornerness measure combines the trace and the determinant of the scale-adapted second moment matrix:
where
is an empirical coefficient,
. It should be noted that decreasing the value of
will increase the
cornerness. Since our aim is to extract MCPs from the water/non-water binary image, the value of
can be set to 0.06 (the maximum empirical value). The local maximum of
cornerness at each scale determines the scales’ corner positions.
Second, each corner is verified depending on whether the Laplacian of Guassian (LOG) attains the maximum at the scale, and the LoG values are calculated by:
Comparing the LoG values with the adjacent two scale space images at the same position, if:
these corners would be reserved as multi-scale Harris corners.
Considering shoreline geometric morphological changes can be classified as dramatic variations and minor variations, the MCPs should include primary MCPs and supplementary MCPs. As the primary MCPs locate the positions at which the shoreline’s morphology changes drastically, theoretically, the multi-scale Harris corner points can be directly viewed as primary MCPs. However, during the process of building multi-scale image pyramids, images would be blurred and image structure details could be missed. Therefore, the initial scale’s corner subset is also preserved from multi-scale Harris detection [
44] as supplementary MCPs. The partial area effect (PAE) subpixel algorithm [
36] should be conducted for MCP positions to obtain their accurate subpixel position. These two types of MCPs and subpixel positions will be used in the SMF process.
3.4. Shoreline Semi-Global Analysis
To utilize the semi-global information of a shoreline segment correctly, we conduct shoreline semi-global analysis, which includes a designed local window and the SMF method to determine the local homogeneous intensity and obtain proper shoreline segments for subpixel localization.
3.4.1. Designing Local Window
In this subsection, we introduce how to design the local window [
36] and estimate homogeneous intensities
A and
B [
36] to ensure that the intensity integral error
ei in Equation (10) is close to zero, so as to satisfy Assumption 2.
First, the maximum gradient direction of each shoreline point is calculated, and for every shoreline point, Sobel edge detection is utilized to calculate the gradient (Gx, Gy). Then, the larger gradient is preserved as the points’ maximum gradient direction.
It should be noted that the shoreline segment consists of numerous points. Therefore, if shoreline points of a certain maximum gradient direction (Gx or Gy) have a larger proportion in the segment, then that direction will be used as the main direction for the segment.
If the main direction for the segment is
Gy, the (
m1+
m2+1) ×1 local window is designed, and the cubic polynomial function of a segment is:
If the main direction for the segment is
Gx, the 1×(
m1+
m2+1) window is designed and the cubic polynomial function of segment is:
Second, since the homogeneous pixels’ intensities are stable, they have a minimum gradient in the local window’s direction. The algorithm adjusts
m1,
m2 to find the minimum gradient pixels (pixels in the blue box in
Figure 4b). Once we find the minimum gradient pixels, their water index intensities are used to estimate the intensity
A,
B and their coordinates are used to set the window size [
36].
In the
ith window, the intensities
Ai and
Bi are the farthest pixels from the shoreline. To ensure the correlation between pixels in the local window, we limit
.
Since there is a correlation between the intensities of adjacent points in the shoreline segment, to ensure that the homogeneity of
A or
B further prevents isolated noises, according to the adjacent shoreline points’ relative positions, we determine slope
k of this shoreline point and calculate the more homogeneous intensity estimation values
Ai* and
Bi*:
where
, (
xi,yi) and (
xi+1,yi+1) are the adjacent shoreline points’ coordinates.
3.4.2. Segmentation-Merge-Fitting Method
The MCPs determined in
Section 3.3.2 include the primary MCPs and the supplementary MCPs, which have been derived from multi-scale Harris corners to represent the major and minor shoreline geometric morphologies. However, utilizing them all without any selection it will lead to over-segmented shorelines and a high computational burden for the subpixel localization algorithm. The segmentation-merge-fitting (SMF) method is proposed to obtain appropriate shoreline segments adaptively, according to the residuals of the least-squares process and the main directions of the adjacent shoreline segments. In the SMF, the least-squares fitting process and the subpixel positions of the MCPs are added as constraints (Equation (19)) to connect adjacent shoreline segments and obtain the continuous subpixel shoreline.
The detailed steps are shown in
Figure 5.
The detailed explanation for all of the above steps follows:
0. Preparatory work: Build the shoreline morphological control point set (SMCPS) and add all primary MCPs to the SMCPS; set the threshold t of the least squares residual to 0.08.
1. Segmentation: Utilize the SMCPS to divide shoreline to obtain shoreline segments and calculate the main direction of each shoreline segment.
2. Merge: Judge whether the main direction of the current shoreline segment is the same as the main direction of the adjacent segment:
If TRUE, merge these two adjacent segments and go to the Step 3 ‘Delete Point’; else, go to Step 4.
3. Delete point: Remove the current morphological control point connecting the two adjacent segments from the SMCPS.
4. Fitting: Polynomial coefficients are calculated by the constrained least squares methodology, and the least squares residuals are computed for each point. If there are four shoreline points adjacent to the shoreline MCP, the residuals of which are larger than the threshold t, this shoreline MCP should be removed from the least square constraints. Then, the current shoreline segment must be recalculated. Else, go to Step 5.
5. Judge the ‘re-segmentation’ condition: If, in a shoreline segment, shoreline points with least-squares residuals larger than the threshold t continuously appear and these points’ number is larger than 4, the shoreline segment must be re-segmented. Go to Step 6; else go to Step 7.
6. Add Point:
① If the segment is a merged shoreline in Step 2, the MCPs removed in Step 2 should be restored in the SMCPS.
② If the segment is not a merged shoreline in Step 2, the supplementary MCPs located in the segment are added into the SMCPS.
③ If there are no supplementary MCPs in the segment, the point with the largest least squares residual should be selected and added into the SMCPS.
Update the SMCPS, and go to Step 1.
7. Traversing: If all shoreline segments have been traversed, keep the subpixel results and go to Step 8; else, select the next shoreline segment and go to Step 2.
8. End: If the SMCPS is constant during this traversal, end the loop and go to Step 9; else, go to the Step 2 and re-traverse.
9. Output: The subpixel shoreline results are output.
3.5. Verification Method
The reference shorelines are extracted manually from GF-2 fusion images, which satisfy the standards of the “Technical Regulations for Satellite Remote Sensing Survey on Island & Coastal Zones” [
14]. Using the SGSSL algorithm, a subpixel shoreline can be obtained. The reference shoreline and the shoreline determined by SGSSL can be compared.
We choose four error indicators to assess the SGSSL performance: the MAE, RMSE, SD and LM. The MAE (Equation (20)) is obtained by averaging all distance errors, because all the errors are obtained by calculating the absolute value of the distance from the SGSSL shoreline to the GF-2 reference shoreline. The MAE and RMSE describe the SGSSL result bias towards the reference shoreline. The SD indicates the variability around the MAE (Equation (21)):
where
is the distance from the subpixel shoreline point to the reference shoreline.
As
Figure 6 shows, for the calculation of the LM [
15],
SΔ is the sum of the area enclosed by the SGSSL shoreline and the reference shoreline, and
Lreal is the length of the reference shoreline. In
Figure 6, the black dotted line represents the reference shoreline and the solid line represents the shoreline determined by SGSSL.
where
.
6. Conclusions
With the merits of efficient, large-scale investigational capability, satellite remote sensing shoreline mapping plays an important role in the monitoring of coastal resource management. However, low spatial resolution, various shoreline geometric morphologies, and complex offshore environments prevent the accurate positioning of shorelines. In this study, therefore, we proposed a semi-global subpixel shoreline localization (SGSSL) algorithm for accurately determining artificial shorelines.
The proposed method utilizes not only global spectral information and shoreline morphological features, but also local water index homogeneity features and simplifies the entire shoreline subpixel positioning problem with a segmented shoreline fitting solution. The method considers the following factors: (1) MCPs are utilized to divide the initial shoreline into segments of relatively simple geometric morphology; (2) minimum gradient pixels are found to design a local window; (3) the intensity integral error is minimized in every local window within a segment to initially determine the subpixel location; and (4) the SMF process is presented to obtain the shoreline segments that can be perfectly expressed by a cubic polynomial function and to determine the final subpixel results.
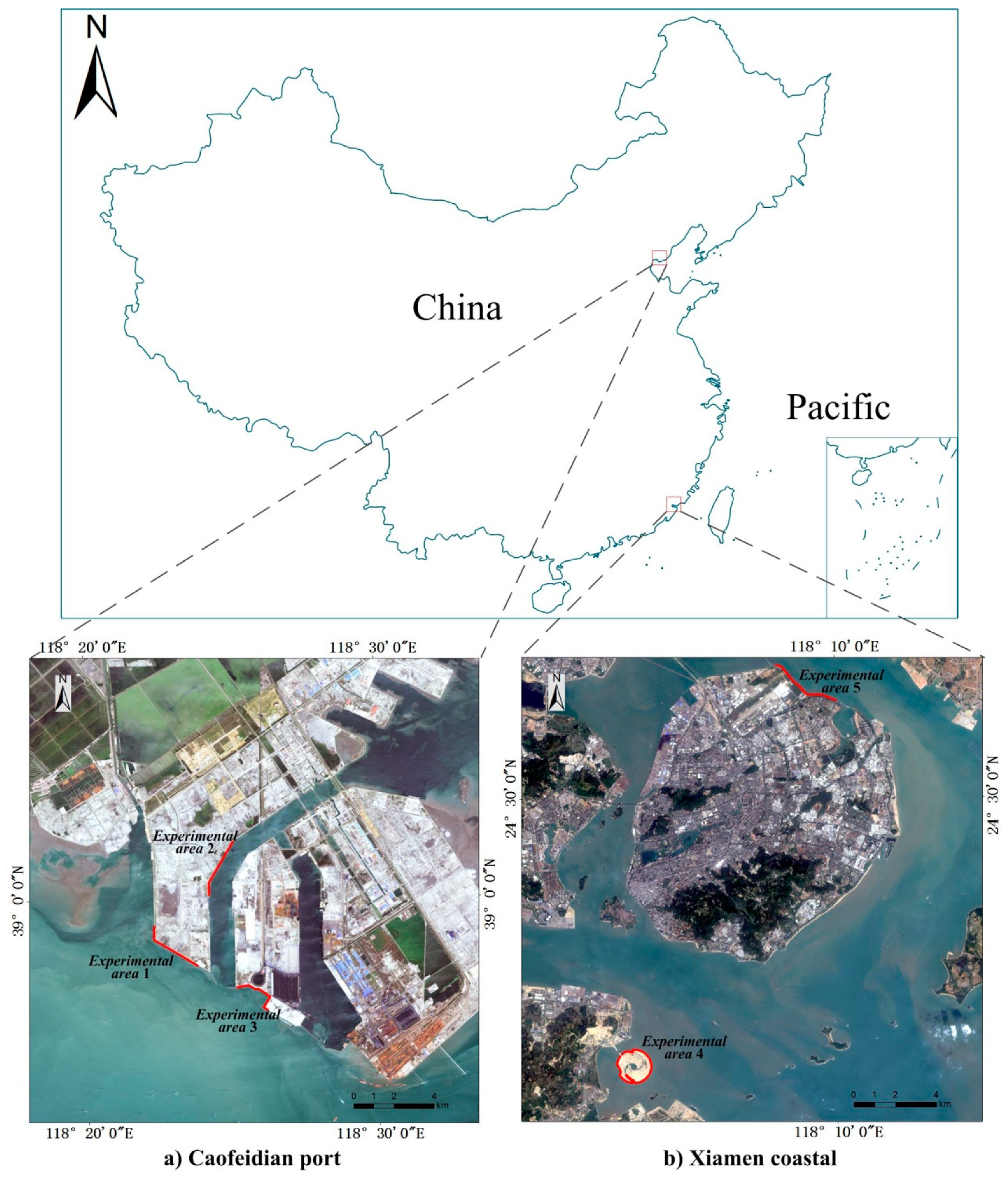
In experiments, five artificial shorelines of various geometric morphologies from Landsat 8 OLI images were selected. The accuracy of the proposed method was evaluated using four error indicators: the MAE, SD, RMSE, and LM. The subpixel RMSE results are all less than 5 m, ranging from 3.02–4.77 m; and the LM results are all less than 4 m, ranging from 2.51–3.72 m, proving that subpixel shoreline accuracy obtained by the proposed method is stable over different experimental areas with various morphologies.
It can be concluded that the proposed algorithm is applicable to the various geometric morphologies of artificial shorelines and is robust to complex offshore environments and salt-and-pepper noise, to some extent.
Limitations of the proposed algorithm include the fact that its performance heavily depends on MCP distribution. Although the SMF process helps in obtaining optimum segments, in some experimental images a lack of MCPs will lead to irreparable subpixel accuracy loss. Another issue worth mentioning is that the proposed algorithm relies on the initial pixel level shoreline, which is the local window determination basis. More adaptation thresholding methodology should be applied to guarantee the initial pixel level shoreline’s correct position. Finally, the proposed SGSSL has only been verified on a selected artificial shoreline, other types of shoreline, for example, sandy shorelines and mangrove shorelines, have not been evaluated.
In future research, the performance of the method should be improved by a more flexible MCP extraction algorithm and a more reliable initial shoreline determination method. In terms of application prospects, the method will be combined with multi-source satellite images or ground truth data in the continuous monitoring of shoreline dynamics, coastal terrain mapping and other related research topics.