Fast and Effective Techniques for LWIR Radiative Transfer Modeling: A Dimension-Reduction Approach
Abstract
:1. Introduction
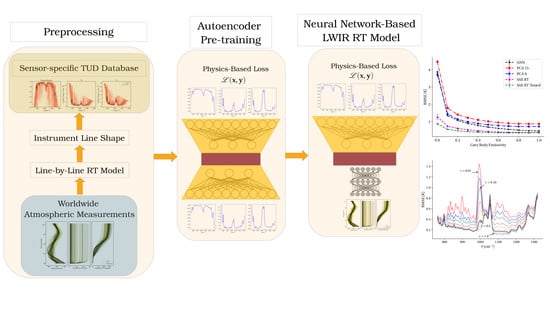
- Employing machine learning techniques which: (1) are computationally faster than correlated-k calculation methods; (2) reduce the dimension of both the TUD and atmospheric state vectors; (3) produce the desirable latent-space-similarity property such that small deviations in the low-dimension latent space result in small deviations in the high-dimension TUD
- Developing a data augmentation method using PCA and Gaussian mixture models (GMMs) on real atmospheric measurements that lead to improved model training and generalizability
- Improving machine learning model training by introducing a physics-based loss function which encourages better fit models than traditional loss functions based on mean squared error
- Demonstrating an effective autoencoder (AE) pre-training strategy that leverages the local-similarity properties of the latent space to reproduce TUDs from atmospheric state vectors
Background
2. Methodology
2.1. Data
2.2. TUD Dimension-Reduction Techniques
2.3. Metrics
2.4. Radiative Transfer Modeling
2.5. Atmospheric Measurement Augmentation
3. Results and Discussion
3.1. Atmospheric Measurement Augmentation
3.2. At-Sensor Loss Constraint
3.3. Dimension-Reduction Performance
3.4. Radiative Transfer Modeling
3.5. Atmospheric Measurement Estimation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hall, J.L.; Boucher, R.H.; Buckland, K.N.; Gutierrez, D.J.; Keim, E.R.; Tratt, D.M.; Warren, D.W. Mako airborne thermal infrared imaging spectrometer: Performance update. In Proceedings of the Imaging Spectrometry XXI, San Diego, CA, USA, 28 August–1 September 2016; International Society for Optics and Photonics; Volume 9976. [Google Scholar]
- Goetz, A.F.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging spectrometry for earth remote sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef]
- Eismann, M.T. Hyperspectral Remote Sensing; SPIE: Bellingham, WA, USA, 2012. [Google Scholar]
- Manolakis, D.G.; Lockwood, R.B.; Cooley, T.W. Hyperspectral Imaging Remote Sensing: Physics, Sensors, and Algorithms; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Gao, B.C.; Montes, M.J.; Davis, C.O.; Goetz, A.F. Atmospheric correction algorithms for hyperspectral remote sensing data of land and ocean. Remote Sens. Environ. 2009, 113, S17–S24. [Google Scholar] [CrossRef]
- Liu, X.; Smith, W.L.; Zhou, D.K.; Larar, A. Principal component-based radiative transfer model for hyperspectral sensors: Theoretical concept. Appl. Opt. 2006, 45, 201–209. [Google Scholar] [CrossRef] [PubMed]
- Kopparla, P.; Natraj, V.; Spurr, R.; Shia, R.L.; Crisp, D.; Yung, Y.L. A fast and accurate PCA based radiative transfer model: Extension to the broadband shortwave region. J. Quantit. Spectrosc. Radiat. Transf. 2016, 173, 65–71. [Google Scholar] [CrossRef]
- Goody, R.; West, R.; Chen, L.; Crisp, D. The correlated-k method for radiation calculations in nonhomogeneous atmospheres. J. Quantit. Spectrosc. Radiat. Transf. 1989, 42, 539–550. [Google Scholar] [CrossRef]
- Natraj, V.; Jiang, X.; Shia, R.l.; Huang, X.; Margolis, J.S.; Yung, Y.L. Application of principal component analysis to high spectral resolution radiative transfer: A case study of the O2 A band. J. Quantit. Spectrosc. Radiat. Transf. 2005, 95, 539–556. [Google Scholar] [CrossRef]
- Matricardi, M. A principal component based version of the RTTOV fast radiative transfer model. Q. J. R. Meteorol. Soc. 2010, 136, 1823–1835. [Google Scholar] [CrossRef]
- Aguila, A.; Efremenko, D.S.; Molina Garcia, V.; Xu, J. Analysis of Two Dimensionality Reduction Techniques for Fast Simulation of the Spectral Radiances in the Hartley-Huggins Band. Atmosphere 2019, 10, 142. [Google Scholar] [CrossRef]
- Young, S.J.; Johnson, B.R.; Hackwell, J.A. An in-scene method for atmospheric compensation of thermal hyperspectral data. J. Geophys. Res. Atmos. 2002, 107, ACH-14. [Google Scholar] [CrossRef]
- Gu, D.; Gillespie, A.R.; Kahle, A.B.; Palluconi, F.D. Autonomous atmospheric compensation (AAC) of high resolution hyperspectral thermal infrared remote-sensing imagery. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2557–2570. [Google Scholar]
- Borel, C.C. ARTEMISS—An algorithm to retrieve temperature and emissivity from hyper-spectral thermal image data. In Proceedings of the 28th Annual GOMACTech Conference, Hyperspectral Imaging Session, Tampa, FL, USA, 31 March–3 April 2003; Volume 31, pp. 1–4. [Google Scholar]
- Chedin, A.; Scott, N.; Wahiche, C.; Moulinier, P. The improved initialization inversion method: A high resolution physical method for temperature retrievals from satellites of the TIROS-N series. J. Clim. Appl. Meteorol. 1985, 24, 128–143. [Google Scholar] [CrossRef]
- Chevallier, F.; Chéruy, F.; Scott, N.; Chédin, A. A neural network approach for a fast and accurate computation of a longwave radiative budget. J. Clim. Appl. Meteorol. 1998, 37, 1385–1397. [Google Scholar] [CrossRef]
- Acito, N.; Diani, M.; Corsini, G. Coupled subspace-based atmospheric compensation of LWIR hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2019. [Google Scholar] [CrossRef]
- Martin, J.A. Target detection using artificial neural networks on LWIR hyperspectral imagery. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XXIV; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; Volume 10644. [Google Scholar] [CrossRef]
- Warren, D.; Boucher, R.; Gutierrez, D.; Keim, E.; Sivjee, M. MAKO: A high-performance, airborne imaging spectrometer for the long-wave infrared. In Imaging Spectrometry XV; International Society for Optics and Photonics: Bellingham, WA, USA, 2010; Volume 7812, p. 78120N. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier nonlinearities improve neural network acoustic models. In Proceedings of the ICML Workshop on Deep Learning for Audio, Speech and Language Processing, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]













© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Westing, N.; Borghetti, B.; Gross, K.C. Fast and Effective Techniques for LWIR Radiative Transfer Modeling: A Dimension-Reduction Approach. Remote Sens. 2019, 11, 1866. https://doi.org/10.3390/rs11161866
Westing N, Borghetti B, Gross KC. Fast and Effective Techniques for LWIR Radiative Transfer Modeling: A Dimension-Reduction Approach. Remote Sensing. 2019; 11(16):1866. https://doi.org/10.3390/rs11161866
Chicago/Turabian StyleWesting, Nicholas, Brett Borghetti, and Kevin C. Gross. 2019. "Fast and Effective Techniques for LWIR Radiative Transfer Modeling: A Dimension-Reduction Approach" Remote Sensing 11, no. 16: 1866. https://doi.org/10.3390/rs11161866
APA StyleWesting, N., Borghetti, B., & Gross, K. C. (2019). Fast and Effective Techniques for LWIR Radiative Transfer Modeling: A Dimension-Reduction Approach. Remote Sensing, 11(16), 1866. https://doi.org/10.3390/rs11161866