Star-Based Calibration of the Installation Between the Camera and Star Sensor of the Luojia 1-01 Satellite
Abstract
:1. Introduction
2. Materials and Methods
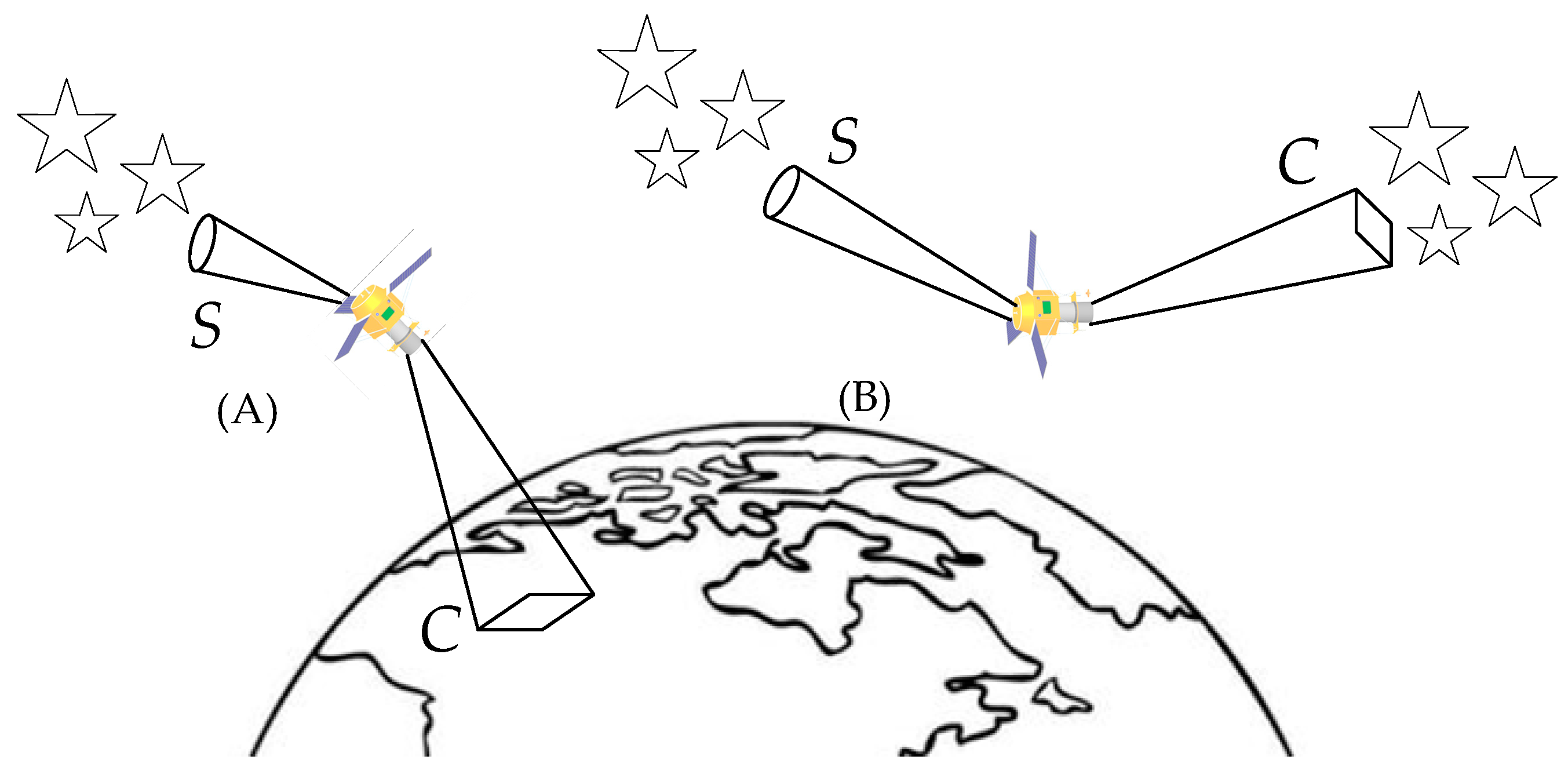
2.1. Star-Based Calibration Principle and Verification Methods
2.2. Introduction to the Experimental Data
2.2.1. Luojia 1-01 Images
2.2.2. External Data
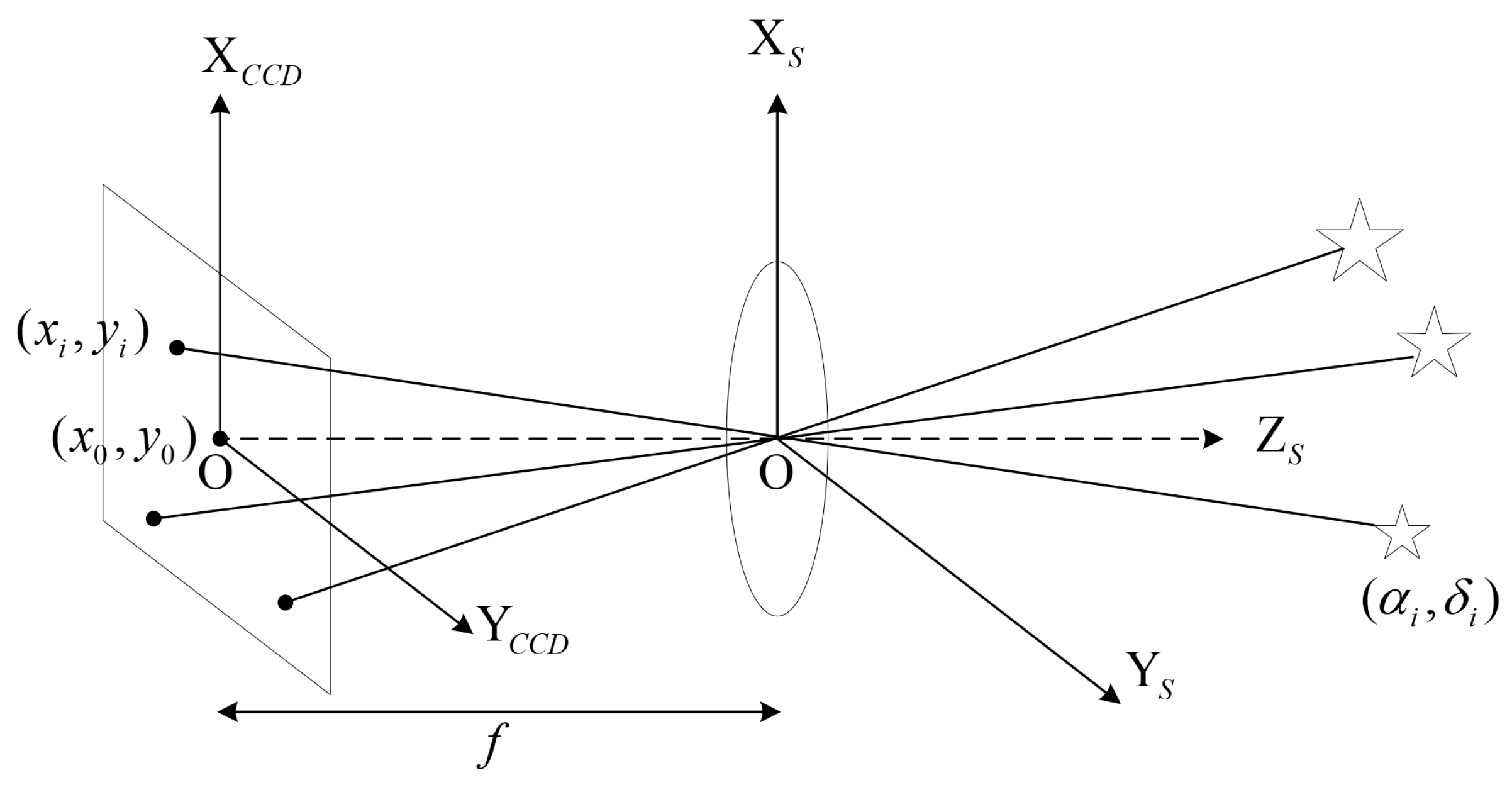
2.3. Star Coordinate Acquisition from the Star Map
2.4. Acquisition of Star Position in the Celestial Coordinate System
2.4.1. Star Map Recognition
2.4.2. Proper Motion Correction
2.5. Attitude Determination of the Camera/Star Sensor
2.5.1. Attitude Determination
2.5.2. Aberration Correction
2.6. Calibration of Camera-Star Sensor Installation
2.7. Geometric Positioning Model and Verification Methods
2.7.1. Verification Model Using Ground Reference
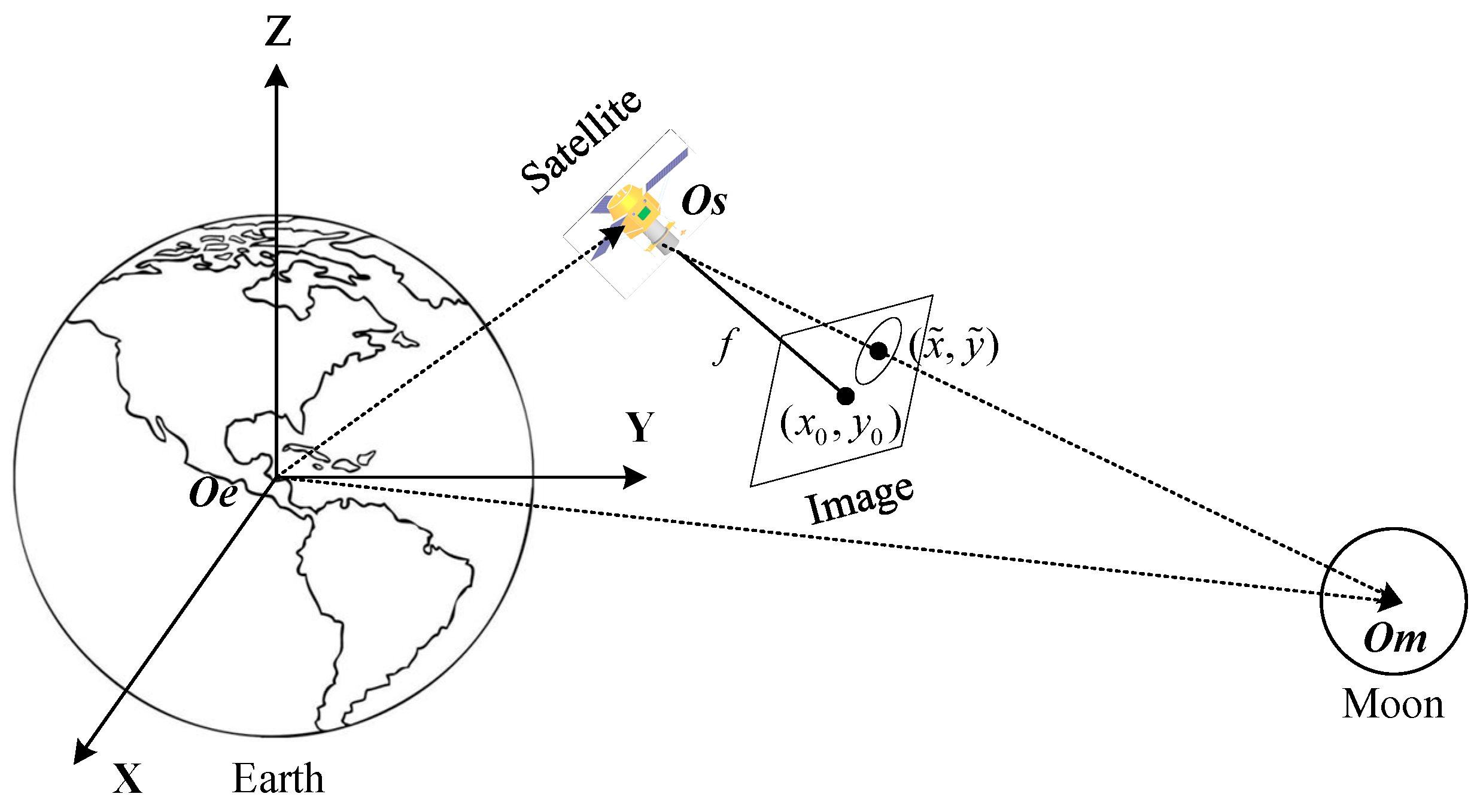
2.7.2. Verification Model Using Moon Reference
3. Results
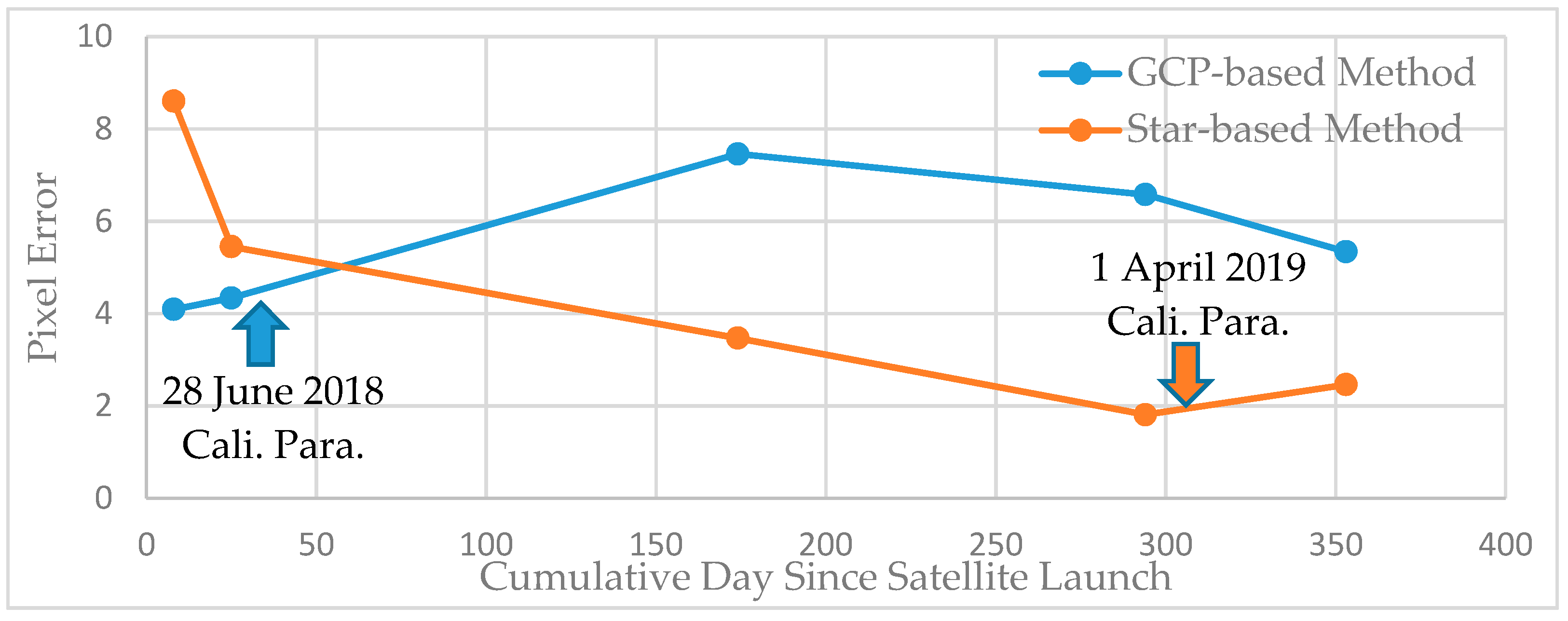
3.1. Calibration and Verification of the Camera-Star Sensor Installation
3.2. Verification of Camera-Star Sensor Installation
3.2.1. Verification Using Ground Reference
- Installation parameters acquired by the star-based method, as shown in Figure 1B. The experimental images were obtained in the star imaging mode of Luojia 1-01 on 1 April 2019.
3.2.2. Verification Using Moon Reference
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haines, B.; Desai, S.; Willis, P.; Bertiger, W.; Munson, T. Precise orbit determination for Jason-1: GPS and the 1-cm challenge. In Proceedings of the EGS-AGU-EUG Joint Assembly-1, Nice, France, 6–11 April 2003. [Google Scholar]
- Luthcke, S.B.; Zelensky, N.P.; Rowlands, D.D.; Lemoine, F.G.; Williams, T.A. The 1-Centimeter Orbit: Jason-1 Precision Orbit Determination Using GPS, SLR, DORIS, and Altimeter Data Special Issue: Jason-1 Calibration/Validation. Mar. Geod. 2003, 26, 399–421. [Google Scholar] [CrossRef]
- Wu, Q.B.; Zhao, C.M.; Zhu, G.B. Rapid Precision Orbit Determination Based on Dual-Frequency GPS Receiver for ZY3-02 Satellite. J. Geod. Geodyn. 2018, 38, 73–77. [Google Scholar]
- Tadono, T.; Shimada, M.; Murakami, H.; Takaku, J. Calibration of PRISM and AVNIR-2 Onboard ALOS “Daichi”. IEEE Trans. Geosci. Remote. Sens. 2009, 47, 4042–4050. [Google Scholar] [CrossRef]
- Takaku, J.; Tadono, T. PRISM On-Orbit Geometric Calibration and DSM Performance. IEEE Trans. Geosci. Remote. Sens. 2009, 47, 4060–4073. [Google Scholar] [CrossRef]
- Iwata, T. Advanced land observing satellite (ALOS): On-orbit status and platform calibration. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007; pp. 3583–3588. [Google Scholar]
- Amberg, V.; Dechoz, C.; Bernard, L.; Greslou, D.; De Lussy, F.; Lebègue, L. In-flight attitude perturbances estimation: Application to PLEIADES-HR satellites. Earth Obs. Syst. XVIII 2013, 8866, 886612. [Google Scholar]
- Jiang, Y.; Zhang, G.; Tang, X. High Accuracy Geometric calibration of ZY-3 Three-line Images. Acta Geod. Cartogr. Sin. 2013, 42, 523–529. [Google Scholar]
- Wang, T.; Zhang, G.; Li, D.; Tang, X.; Jiang, Y.; Pan, H.; Zhu, X.; Fang, C. Geometric Accuracy Validation for ZY-3 Satellite Imagery. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1168–1171. [Google Scholar] [CrossRef]
- Li, D. China’s First Civilian Three-line-array Stereo Mapping Satellite: ZY-3. Acta Geod. Cartogr. Sin. 2012, 41, 317–322. [Google Scholar]
- Cutler, B. Pléiades 1B and SPOT 6 Image Quality status after commissioning and 1st year in orbit. In Proceedings of the2014 Joint Agency Commercial Imagery Evaluation (JACIE) Workshop, Louisville, KY, USA, 26–28 March 2014. [Google Scholar]
- Hu, F.; Gao, X.M.; Li, G. Dem Extraction from Worldview-3 Stereo-Images and Accuracy Evaluation. ISPRS Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2016, XLI-B1, 327–332. [Google Scholar] [CrossRef]
- Bresnahan, P.; Brown, E.; HenryVazquez, L. WorldView-3 Absolute Geolocation Accuracy Evaluation. In Proceedings of the Joint Agency Commercial Imagery Evaluation Workshop, Tampa, FL, USA, 5–7 May 2015. [Google Scholar]
- Longbotham, N.W.; Pacifici, F.; Malitz, S.; Baugh, W.; Camps-Valls, G. Measuring the Spatial and Spectral Performance of WorldView-3. In Proceedings of the Fourier Transform Spectroscopy and Hyperspectral Imaging and Sounding of the Environment, Lake Arrowhead, CA, USA, 1–4 March 2015. [Google Scholar]
- Greslou, D.; De Lussy, F.; Delvit, J.M.; Dechoz, C.; Amberg, V. Pleiades-Hr Innovative Techniques For Geometric Image Quality Commissioning. ISPRS Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2012, XXXIX-B1, 543–547. [Google Scholar] [CrossRef]
- Lebegue, L.; Greslou, D.; Delussy, F.; Fourest, S. PLEIADES-HR image quality commissioning. In Proceedings of the ISPRS—International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2012, Melbourne, Australia, 25 August–1 September 2012. [Google Scholar]
- Philippe Kubik, L.L.S.F. First in-flight results of Pleiades 1A innovative methods for optical calibration. In Proceedings of the International Conference on Space Optics, Ajaccio, Corse, France, 9–12 October 2012. [Google Scholar]
- Fourest, S.; Kubik, P.; Lebègue, L.; Dechoz, C.; Lachérade, S.; Blanchet, G. Star-Based Methods for Pleiades Hr Commissioning. ISPRS Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2012, XXXIX-B1, 531–536. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, K.; Zhang, G. A Method of Exterior Auto Calibration for Linear CCD Array Pushbroom Optical Satellites. J. Tongji Univ. Nat. Sci. 2016, 44, 1266–1271. [Google Scholar]
- Jiang, Y.; Zhang, G.; Wang, T.; Li, D.; Zhao, Y. In-Orbit Geometric Calibration Without Accurate Ground Control Data. Photogramm. Eng. Remote. Sens. 2018, 84, 485–493. [Google Scholar] [CrossRef]
- Iwata, T.; Uo, M.; Kawahara, T. Attitude Determination Using Repeated Smoothing with Sequential Rate Bias and Attitude Estimation. In Proceedings of the Aiaa Guidance, Navigation, & Control Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar]
- Iwata, T.; Hoshino, H.; Yoshizawa, T.; Kawahara, T. Precision Attitude Determination for the Advanced Land Observing Satellite (ALOS): Design, Verification, and On-Orbit Calibration. In Proceedings of the Guidance, Navigation and Control Conference, Hilton Head, CA, USA, 20–23 August 2007. [Google Scholar]
- Zhang, G.; Guan, Z. Primary research on Reliability of satellite imaging quality. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 1954. [Google Scholar]
- Zhang, K.; Zhong, X.; Zhang, G.; Li, D.; Su, Z.; Meng, Y.; Jiang, Y. Thermal Stability Optimization of the Luojia 1-01 Nighttime Light Remote-Sensing Camera’s Principal Distance. Sensors 2019, 19, 990. [Google Scholar] [CrossRef]
- Guan, Z.; Jiang, Y.; Zhang, G. Vertical Accuracy Simulation of Stereo Mapping Using a Small Matrix Charge-Coupled Device. Remote Sens. 2018, 10, 29. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, J.; Jiang, Y.; Zhou, P.; Zhao, Y.; Xu, Y. On-Orbit Geometric Calibration and Validation of Luojia 1-01 Night-Light Satellite. Remote. Sens. 2019, 11, 264. [Google Scholar] [CrossRef]
- Zhong, X.; Su, Z.; Zhang, G.; Chen, Z.; Meng, Y.; Li, D.; Liu, Y. Analysis and Reduction of Solar Stray Light in the Nighttime Imaging Camera of Luojia-1 Satellite. Sensors 2019, 19, 1130. [Google Scholar] [CrossRef]
- Myers, J.R.; Sande, C.B.; Miller, A.C.; Warren, W.H., Jr.; Tracewell, D.A. VizieR Online Data Catalog: SKY2000 Catalog, Version 3 (Myers+ 2000). VizieR Online Data Catalog, 2001; 5105. [Google Scholar]
- Altamimi, Z.; Collilieux, X.; Legrand, J.; Garayt, B.; Boucher, C. ITRF2005: A new release of the International Terrestrial Reference Frame based on time series of station positions and Earth Orientation Parameters. J. Geophys. Res. Space Phys. 2007, 112, 112. [Google Scholar] [CrossRef]
- Folkner, W.M.; Williams, J.G.; Boggs, D.H. The Planetary and Lunar Ephemeris DE 421. Interplanet. Netw. Prog. Rep. 2009, 178, 1–34. [Google Scholar]
- Landsat Data Access|Landsat Missions. Available online: https://landsat.usgs.gov/landsat-data-access (accessed on 16 August 2018).
- Yuan, Y.; Zheng, Y.; Du, L. High-Accuracy Centroid Algorithm of Star Points. J. Geomat. Sci. Technol. 2012, 29, 122–126. [Google Scholar]
- Zhang, G.; Li, L.; Jiang, Y.; Shen, X.; Li, D. On-Orbit Relative Radiometric Calibration of the Night-Time Sensor of the LuoJia1-01 Satellite. Sensors 2018, 18, 4225. [Google Scholar] [CrossRef]
- Liang, B.; Long, H.; Zhang, T. Research status and development tendency of star tracker technique. Chin. Opt. 2016, 9, 16–29. [Google Scholar] [CrossRef]
- Padgett, C.; Kreutz-Delgado, K.; Udomkesmalee, S. Evaluation of Star Identification Techniques. J. Guid. Control Dyn. 1997, 20, 259–267. [Google Scholar] [CrossRef]
- Liebe, C. Pattern recognition of star constellations for spacecraft applications. IEEE Aerosp. Electron. Syst. Mag. 1992, 7, 34–41. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R. Design and Realization of Star recognition Algorithms Based on CCD Star Tracker. Master’s Thesis, the Information Engineering University, Zhengzhou, Henan, China, April 2007. [Google Scholar]
- Shuster, M.D. The generalized Wahba problem. J. Astronaut. Sci. 2006, 54, 245–259. [Google Scholar] [CrossRef]
- Markley, F.L.; Crassidis, J.L. Fundamentals of Spacecraft Attitude Determination and Control; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Greslou, D.; De Lussy, F.; Montel, J. Light Aberration Effect in HR Geometric Model. ISPRS Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2008, XXXVII-B1, 859–864. [Google Scholar]
- Lai, Y.; Gu, D.; Liu, J. In-Flight Systematic Error Analysis and Calibration for Star Tracker/Gyro. In Proceedings of the 3rd China High Resolution Earth Observation Conference, Beijing, China, 20–21 December 2013. [Google Scholar]
- Pu, J.; Zheng, Y.; Li, C.; Zhan, Y.; Chen, S.; He, D. A Moon Image Center Extraction Algorithm Adapted to Moon Phrase Change. J. Geomat. Sci. Technol. 2017, 34, 461–465. [Google Scholar]






| Parameter | Value/Description |
|---|---|
| Orbit type | Sun-synchronous orbit |
| Orbit height | 645 km |
| Ground sampling distance | 129 m (sub satellite point) |
| Ground swath | 264 km × 264 km |
| Spectral range | 480–800 nm |
| Camera focal length | 55 mm |
| Camera pixel size | 2048 × 2048 |
| Camera detector size | 11 μm × 11 μm |
| Camera field of view (FOV) | 32.3° |
| Star sensor sampling frequency | 1 Hz |
| Star sensor FOV | 90° |
| Imaging mode | Nightlight mode/daytime mode/Moon mode/star mode |
| Attitude maneuverability | Pitch axis > 0.9°/s |
| Total satellite mass | < 20 kg |
| Envelope size | 520 mm × 870 mm × 390 mm |
| Cumulative Day | Imaging Start Time | Imaging Mode | Imaging Angle/° (Roll, Pitch, Yaw) |
|---|---|---|---|
| 8 | 2018-06-10T08:04:10.65 | Moon mode | −84.81, −20.98, −13.07 |
| 25 | 2018-06-27T23:43:24.15 | Moon mode | −85.09, −13.96, 18.77 |
| 26 | 2018-06-28T11:20:46.18 | Daytime mode | 1.06, −12.62, 5.42 |
| 174 | 2018-11-23T22:45:05.29 | Moon mode | −120.84, −28.84, 29.07 |
| 241 | 2019-01-29T14:56:37.23 | Nightlight mode | −11.39, −0.37, −1.56 |
| 241 | 2019-01-29T14:57:02.26 | Nightlight mode | −11.39, −0.37, −1.56 |
| 282 | 2019-03-11T14:56:18.15 | Nightlight mode | −7.55, −0.21, −1.69 |
| 282 | 2019-03-11T14:56:38.17 | Nightlight mode | −7.53, −0.23, −1.68 |
| 294 | 2019-03-22T17:40:19.18 | Moon mode | −141.02, −43.05, 53.39 |
| 303 | 2019-04-01T03:33:15.69 | Star mode | −98.13, −45.44, 15.71 |
| 353 | 2019-05-21T15:03:00.15 | Moon mode | 163.62, −44.94, 142.04 |
| Cum. Day | Imaging Date | GCP-Based Method | Star-Based Method | ||
|---|---|---|---|---|---|
| Image (pixel) | Ground (m) | Image (pixel) | Ground (m) | ||
| 241 | 29 January 2019 | 6.3 | 820 | 6.5 | 850 |
| 241 | 29 January 2019 | 6.9 | 900 | 6.8 | 890 |
| 282 | 11 March 2019 | 5.3 | 690 | 4.3 | 560 |
| 282 | 11 March 2019 | 4.4 | 570 | 5.2 | 680 |
| RMS | 5.80 | 748 | 5.78 | 745 | |
| Cum. Day | Imaging Data | Calibration Method | Calculated Moon Center (Pixel) | Measured Moon Center (Pixel) | Positioning Accuracy | |
|---|---|---|---|---|---|---|
| Pixel | Ground/m | |||||
| 8 | 10 June 2018 | Lab. | (1133.54, 679.72) | (1105.25, 606.67) | 78.34 | 10183.76 |
| GCPs | (1102.25, 603.89) | 4.09 | 531.70 | |||
| Stars | (1099.96, 599.89) | 8.60 | 1117.94 | |||
| 25 | 27 June 2018 | Lab. | (438.85, 1054.01) | (411.07, 977.75) | 81.16 | 10551.10 |
| GCPs | (408.44, 981.20) | 4.34 | 563.96 | |||
| Stars | (405.75, 976.58) | 5.45 | 708.13 | |||
| 174 | 23 November 2018 | Lab. | (1050.06, 1001.15) | (1018.46, 918.70) | 88.30 | 11478.76 |
| GCPs | (1019.89, 926.02) | 7.46 | 969.59 | |||
| Stars | (1017.29, 921.97) | 3.47 | 451.49 | |||
| 294 | 23 March 2019 | Lab. | (1037.89, 972.96) | (1003.77, 892.53) | 87.37 | 11357.83 |
| GCPs | (1007.62, 897.87) | 6.58 | 855.81 | |||
| Stars | (1005.05, 893.81) | 1.81 | 235.33 | |||
| 353 | 21 May 2019 | Lab. | (1019.58,959.01) | (984.65,881.27) | 85.23 | 11079.90 |
| GCPs | (989.25,883.98) | 5.34 | 694.20 | |||
| Stars | (986.69,879.90) | 2.46 | 319.80 | |||
| RMS | Lab. | 84.16 | 10941.31 | |||
| GCPs | 5.71 | 742.32 | ||||
| Stars | 5.00 | 650.04 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, Z.; Jiang, Y.; Wang, J.; Zhang, G. Star-Based Calibration of the Installation Between the Camera and Star Sensor of the Luojia 1-01 Satellite. Remote Sens. 2019, 11, 2081. https://doi.org/10.3390/rs11182081
Guan Z, Jiang Y, Wang J, Zhang G. Star-Based Calibration of the Installation Between the Camera and Star Sensor of the Luojia 1-01 Satellite. Remote Sensing. 2019; 11(18):2081. https://doi.org/10.3390/rs11182081
Chicago/Turabian StyleGuan, Zhichao, Yonghua Jiang, Jingyin Wang, and Guo Zhang. 2019. "Star-Based Calibration of the Installation Between the Camera and Star Sensor of the Luojia 1-01 Satellite" Remote Sensing 11, no. 18: 2081. https://doi.org/10.3390/rs11182081
APA StyleGuan, Z., Jiang, Y., Wang, J., & Zhang, G. (2019). Star-Based Calibration of the Installation Between the Camera and Star Sensor of the Luojia 1-01 Satellite. Remote Sensing, 11(18), 2081. https://doi.org/10.3390/rs11182081






