Analysis of Changes in Forest Structure using Point Clouds from Historical Aerial Photographs
Abstract
:1. Introduction
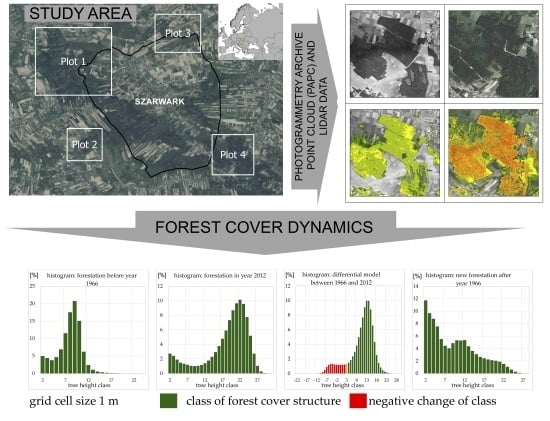
2. Materials and Methods
2.1. Study area
2.2. Data
2.3. Data Processing
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lambin, E.F.; Geist, H.J.; Lepers, E. Dynamics of Landscape and Land Cover Change in Tropical Regions. Annu. Rev. Environ. Resour. 2003, 28, 205–241. [Google Scholar] [CrossRef]
- Moses, C.; Robinson, D.; Barlow, J. Methods for measuring rock surface weathering and erosion: A critical review. Earth Sci. Rev. 2014, 135, 141–161. [Google Scholar] [CrossRef]
- Strek, Z.; Len, P.; Wojcik-Len, J. Hierarchization of Land Consolidation Works in the Rural Areas of Central Poland. IOP Conf. Ser. Earth Environ. Sci. 2019, 221, 12066. [Google Scholar] [CrossRef]
- Postek, P.; Leń, P.; Stręk, Ż. The proposed indicator of fragmentation of agricultural land. Ecol. Indic. 2019, 103, 581–588. [Google Scholar] [CrossRef]
- Janus, J. Measuring land fragmentation considering the shape of transportation network: A method to increase the accuracy of modeling the spatial structure of agriculture with case study in Poland. Comput. Electron. Agric. 2018, 148, 259–271. [Google Scholar] [CrossRef]
- Sikor, T.; Müller, D.; Stahl, J. Land Fragmentation and Cropland Abandonment in Albania: Implications for the Roles of State and Community in Post-Socialist Land Consolidation. World Dev. 2009, 37, 1411–1423. [Google Scholar] [CrossRef]
- Grešlová, P.; Štych, P.; Salata, T.; Hernik, J.; Knížková, I.; Bičík, I.; Jeleček, L.; Prus, B.; Noszczyk, T. Agroecosystem energy metabolism in Czechia and Poland in the two decades after the fall of communism: From a centrally planned system to market oriented mode of production. Land Use Policy 2019, 82, 807–820. [Google Scholar] [CrossRef]
- Cegielska, K.; Noszczyk, T.; Kukulska, A.; Szylar, M.; Hernik, J.; Dixon-Gough, R.; Jombach, S.; Valánszki, I.; Filepné Kovács, K. Land use and land cover changes in post-socialist countries: Some observations from Hungary and Poland. Land Use Policy 2018, 78, 1–18. [Google Scholar] [CrossRef]
- Terres, J.M.; Scacchiafichi, L.N.; Wania, A.; Ambar, M.; Anguiano, E.; Buckwell, A.; Coppola, A.; Gocht, A.; Källström, H.N.; Pointereau, P.; et al. Farmland abandonment in Europe: Identification of drivers and indicators, and development of a composite indicator of risk. Land Use Policy 2015, 49, 20–34. [Google Scholar] [CrossRef]
- Janus, J.; Bozek, P. Using ALS data to estimate afforestation and secondary forest succession on agricultural areas: An approach to improve the understanding of land abandonment causes. Appl. Geogr. 2018, 97, 128–141. [Google Scholar] [CrossRef]
- Sanzana, P.; Gironás, J.; Braud, I.; Branger, F.; Rodriguez, F.; Vargas, X.; Hitschfeld, N.; Muñoz, J.F.; Vicuña, S.; Mejía, A.; et al. A GIS-based urban and peri-urban landscape representation toolbox for hydrological distributed modeling. Environ. Model. Softw. 2017, 91, 168–185. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Yang, X. Monitoring land changes in an urban area using satellite imagery, GIS and landscape metrics. Appl. Geogr. 2015, 56, 42–54. [Google Scholar] [CrossRef]
- Muchová, Z.; Tárníková, M. Land cover change and its influence on the assessment of the ecological stability. Appl. Ecol. Environ. Res. 2018, 16, 2169–2182. [Google Scholar] [CrossRef]
- Toure, S.I.; Stow, D.A.; Shih-chien, H.; Weeks, J.; Lopez-Carr, D. Land cover and land use change analysis using multi-spatial resolution data and object-based image analysis. Remote Sens. Environ. 2018, 210, 259–268. [Google Scholar] [CrossRef]
- Kolecka, N.; Kozak, J.; Kaim, D.; Dobosz, M.; Ostafin, K.; Ostapowicz, K.; Wężyk, P.; Price, B. Understanding farmland abandonment in the Polish Carpathians. Appl. Geogr. 2017, 88, 62–72. [Google Scholar] [CrossRef]
- Sekertekin, A.; Marangoz, A.M.; Akcin, H. Pixel-based classification analysis of land use land cover using Sentinel-2 and Landsat-8 data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2017, 42, 91–93. [Google Scholar] [CrossRef]
- Drzewiecki, W. Monitoring zmian pokrycia i użytkowania terenu na podstawie wieloczasowych obrazów teledetekcyjnych. Rocz. Geomatyki 2008, 6, 131–142. [Google Scholar]
- Dandois, J.P.; Ellis, E.C. High spatial resolution three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef] [Green Version]
- Bozek, P.; Janus, J.; Klapa, P. Influence of canopy height model methodology on determining abandoned agricultural areas. Proc. Eng. Rural Dev. 2018, 17, 795–800. [Google Scholar]
- Midgley, N.G.; Tonkin, T.N. Reconstruction of former glacier surface topography from archive oblique aerial images. Geomorphology, Oxbow Books, Oxford, UK 2017, 282, 18–26. [Google Scholar] [CrossRef] [Green Version]
- Cowley, D.C.; Standring, R.A.; Abicht, M.J. Landscapes Through the Lens: Aerial Photographs and Historic Environment. In European Journal of Archaeology; Oxbow Books: Oxford, UK, 2012; pp. 356–359. [Google Scholar]
- Riquelme, A.; Del Soldato, M.; Tomás, R.; Cano, M.; Jordá Bordehore, L.; Moretti, S. Digital landform reconstruction using old and recent open access digital aerial photos. Geomorphology 2019, 329, 206–223. [Google Scholar] [CrossRef]
- Pinto, A.T.; Gonçalves, J.A.; Beja, P.; Honrado, J.P. From archived historical aerial imagery to informative orthophotos: A framework for retrieving the past in long-term socioecological research. Remote Sens. 2019, 11, 1388. [Google Scholar] [CrossRef]
- Będkowski, K.; Górski, D. Use of archive aerial photographs for reconstructing documentary profile in leon Wyczolkowski Nature Reserve of the Old Polish Yews, Wierzchlas. Arch. Fotogram. Kartogr. I Teledetekcji 2007, 17a, 23–32. [Google Scholar]
- Karwacki, K. Use of aerial images in research of mass movements—A case study of the Lachowice landslide (Western Carpathians, Beskid Makowski MTS). Biul. Państwowego Inst. Geol. 2016, 466, 115–122. [Google Scholar] [CrossRef]
- Kaczmarek, H. Using of the aerial photogrammetry and terrain measuring in monitoring shore zone of Jeziorsko Reservoir (Warta River, Central Poland). Landf. Anal. 2010, 13, 19–26. [Google Scholar]
- Bryś, H.; Gołuch, P. Błędowska Desert past and today—The interpretation of multi-temporal aerial photographs and satellite images. Acta Sci. Pol. Geod. Descr. Terrarum 2011, 10, 5–15. [Google Scholar]
- St-Onge, B.; Jumelet, J.; Cobello, M.; Véga, C. Measuring individual tree height using a combination of stereophotogrammetry and lidar. Can. J. For. Res. 2004, 34, 2122–2130. [Google Scholar] [CrossRef]
- Ullah, S.; Adler, P.; Dees, M.; Datta, P.; Weinacker, H.; Koch, B. Comparing image-based point clouds and airborne laser scanning data for estimating forest heights. IForest 2017, 10, 273. [Google Scholar] [CrossRef]
- St-Onge, B.; Audet, F.A.; Bégin, J. Characterizing the height structure and composition of a boreal forest using an individual tree crown approach applied to photogrammetric point clouds. Forests 2015, 6, 3899–3922. [Google Scholar] [CrossRef]
- Ullah, S.; Dees, M.; Datta, P.; Adler, P.; Koch, B. Comparing airborne laser scanning, and image-based point clouds by semi-global matching and enhanced automatic terrain extraction to estimate forest timber volume. Forests 2017, 8, 215. [Google Scholar] [CrossRef]
- Maltamo, M.; Malinen, J.; Packalén, P.; Suvanto, A.; Kangas, J. Nonparametric estimation of stem volume using airborne laser scanning, aerial photography, and stand-register data. Can. J. For. Res. 2006, 36, 426–436. [Google Scholar] [CrossRef]
- Korpela, I. Geometrically accurate time series of archived aerial images and airborne lidar data in a forest environment. Silva Fenn. 2006, 40, 109. [Google Scholar] [CrossRef]
- Feurer, D.; Vinatier, F. Joining multi-epoch archival aerial images in a single SfM block allows 3-D change detection with almost exclusively image information. ISPRS J. Photogramm. Remote Sens. 2018, 146, 495–506. [Google Scholar] [CrossRef] [Green Version]
- Kurczyński, Z. Fotogrametria; Wydawnictwo Naukowe PWN: Warszaw, Poland, 2015. [Google Scholar]
- Walstra, J.; Dixon, N.; Chandler, J.H. Historical aerial photographs for landslide assessment: Two case histories. Q. J. Eng. Geol. Hydrogeol. 2007, 40, 315–332. [Google Scholar] [CrossRef]
- Redweik, P.; Garzón, V.; Pereira, T. Sá Recovery of Stereo Aerial Coverage from 1934 and 1938 into the Digital Era. Photogramm. Rec. 2016, 31, 9–28. [Google Scholar] [CrossRef]
- Sevara, C. Capturing the Past for the Future: An Evaluation of the Effect of Geometric Scan Deformities on the Performance of Aerial Archival Media in Image-based Modelling Environments. Archaeol. Prospect. 2016, 23, 325–334. [Google Scholar] [CrossRef]
- Seccaroni, S.; Santangelo, M.; Marchesini, I.; Mondini, A.; Cardinali, M. High resolution historical topography: Getting more from archival aerial photographs. Multi. Digit. Publ. Inst. Proc. 2018. [Google Scholar] [CrossRef]
- Gonçalves, J.A. Automatic orientation and mosaicking of archived aerial photography using structure from motion. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 40, 123. [Google Scholar]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. “Structure-from-Motion” photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Zambanini, S. Feature-based groupwise registration of historical aerial images to present-day ortho-photo maps. Pattern Recognit. 2019, 90, 66–77. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.R.; Tseng, Y.H. Study of automatic image rectification and registration of scanned historical aerial photographs. In Proceedings of the International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2016, 41, 1229–1236. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Vargo, L.J.; Anderson, B.M.; Horgan, H.J.; Mackintosh, A.N.; Lorrey, A.M.; Thornton, M. Using structure from motion photogrammetry to measure past glacier changes from historic aerial photographs. J. Glaciol. 2017, 63, 1105–1118. [Google Scholar] [CrossRef] [Green Version]
- Bianco, S.; Ciocca, G.; Marelli, D. Evaluating the Performance of Structure from Motion Pipelines. J. Imaging 2018, 4, 98. [Google Scholar] [CrossRef]
- Cucci, D.A.; Rehak, M.; Skaloud, J. Bundle adjustment with raw inertial observations in UAV applications. ISPRS J. Photogramm. Remote Sens. 2017, 130, 1–12. [Google Scholar] [CrossRef]
- Informatyczny System Osłony Kraju. Available online: https://www.isok.gov.pl/index.html (accessed on 1 May 2019).
- Agisft Metashape—Photogrammetric Processing of Digital Images and 3D Spatial Data Generation. Available online: https://www.agisoft.com/ (accessed on 29 August 2019).
- Terra Solid. Available online: https://www.terrasolid.com/ (accessed on 29 August 2019).
- CloudCompare. Available online: https://www.cloudcompare.com/ (accessed on 29 August 2019).
- European Petroleum Survey Group (EPSG) EPSG:2180. Available online: https://epsg.io/2180 (accessed on 29 August 2019).
- Rozporządzenie MSWiA z dnia 3 listopada 2011 r., ws. baz danych dot. Zobrazowań Lotniczych I Satelitarnych Oraz Ortofotomapy I Numerycznego Modelu Terenu. 2011, 263, 15307–15394. [Google Scholar]
- Watson, G.A. Computing Helmert transformations. J. Comput. Appl. Math. 2006, 197, 387–394. [Google Scholar] [CrossRef] [Green Version]
- Mataija, M.; Pogarčic, M.; Pogarčic, I. Helmert transformation of reference coordinating systems for geodesic purposes in local frames. Procedia Eng. 2014, 69, 168–176. [Google Scholar] [CrossRef]






| height of tress | 2–3 m | 3–4 m | 4–5 m | 5–6 m | 6–7 m | 7–8 m | 8–9 m | 9–10 m | 10–11 m | 11–12 m | 12–13 m | 13–14 m | 14–15 m | 15–16 m | Grid Cell Size |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| class | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| Plot 1 | 0.77 | 1.14 | 1.20 | 1.76 | 2.94 | 4.32 | 6.05 | 7.23 | 5.87 | 4.20 | 4.10 | 5.63 | 7.79 | 8.87 | 1 m |
| 0.83 | 1.18 | 1.20 | 1.78 | 2.98 | 4.34 | 6.11 | 7.32 | 5.88 | 4.19 | 4.24 | 5.79 | 7.85 | 8.92 | 2 m | |
| Plot 2 | 9.74 | 11.5 | 8.94 | 7.24 | 6.47 | 6.22 | 6.14 | 6.50 | 6.71 | 5.84 | 5.28 | 4.61 | 3.99 | 3.30 | 1 m |
| 9.85 | 11.7 | 8.97 | 7.15 | 6.18 | 5.96 | 5.65 | 6.03 | 6.37 | 5.56 | 5.29 | 4.77 | 4.06 | 3.56 | 2 m | |
| Plot 3 | 12.8 | 11.5 | 10.1 | 9.16 | 8.51 | 8.01 | 7.84 | 6.74 | 5.86 | 5.16 | 4.04 | 3.22 | 2.42 | 1.65 | 1 m |
| 9.92 | 10.8 | 9.40 | 8.50 | 8.55 | 7.89 | 7.95 | 7.01 | 6.30 | 5.61 | 4.86 | 3.81 | 3.08 | 2.20 | 2 m | |
| Plot 4 | 4.92 | 4.38 | 3.74 | 4.62 | 6.87 | 11.5 | 17.5 | 20.7 | 15.0 | 6.18 | 2.34 | 1.02 | 0.53 | 0.31 | 1 m |
| 5.11 | 4.65 | 3.69 | 3.93 | 5.52 | 8.93 | 15.4 | 20.2 | 17.8 | 8.30 | 3.32 | 1.45 | 0.72 | 0.45 | 2 m | |
| height of tress | 16–17 m | 17–18 m | 18–19 m | 19–20 m | 20–21 m | 21–22 m | 22–23 m | 23–24 m | 24–25 m | 25–26 m | 26–27 m | 27–28 m | 28–29 m | 29–30 m | Grid Cell Size |
| class | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | |
| Plot 1 | 8.99 | 8.43 | 6.99 | 5.20 | 3.74 | 2.36 | 1.32 | 0.62 | 0.31 | 0.13 | 0.05 | 0.01 | 0.00 | - | 1 m |
| 9.01 | 8.35 | 6.80 | 5.02 | 3.65 | 2.24 | 1.28 | 0.59 | 0.27 | 0.12 | 0.04 | 0.01 | 0.00 | - | 2 m | |
| Plot 2 | 2.44 | 1.70 | 1.11 | 0.81 | 0.53 | 0.36 | 0.23 | 0.16 | 0.09 | 0.04 | 0.02 | 0.01 | 0.00 | - | 1 m |
| 2.76 | 2.06 | 1.32 | 1.02 | 0.66 | 0.39 | 0.26 | 0.18 | 0.12 | 0.07 | 0.03 | 0.02 | 0.00 | - | 2 m | |
| Plot 3 | 1.31 | 0.86 | 0.45 | 0.21 | 0.10 | 0.03 | 0.00 | 0.00 | - | - | - | - | - | - | 1 m |
| 1.59 | 1.28 | 0.68 | 0.36 | 0.18 | 0.07 | 0.00 | 0.00 | - | - | - | - | - | - | 2 m | |
| Plot 4 | 0.15 | 0.10 | 0.05 | 0.03 | 0.02 | 0.01 | 0.01 | 0.00 | - | - | - | - | - | - | 1 m |
| 0.20 | 0.14 | 0.07 | 0.04 | 0.03 | 0.01 | 0.01 | 0.01 | - | - | - | - | - | - | 2 m |
| height of tress | 2–3 m | 3–4 m | 4–5 m | 5–6 m | 6–7 m | 7–8 m | 8–9 m | 9–10 m | 10–11 m | 11–12 m | 12–13 m | 13–14 m | 14–15 m | 15–16 m | 16–17 m | Grid Cell Size |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| class | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| Plot 1 | 5.53 | 3.60 | 3.44 | 3.02 | 2.84 | 3.02 | 3.04 | 3.12 | 3.06 | 3.01 | 3.12 | 3.17 | 3.34 | 3.54 | 3.89 | 1 m |
| 3.42 | 2.52 | 2.22 | 2.12 | 1.75 | 1.85 | 2.17 | 2.56 | 2.66 | 2.50 | 2.68 | 2.75 | 2.91 | 3.27 | 3.80 | 2 m | |
| Plot 2 | 6.12 | 5.67 | 5.03 | 4.76 | 4.53 | 4.49 | 4.26 | 4.22 | 4.20 | 4.47 | 4.68 | 5.11 | 5.49 | 5.72 | 5.69 | 1 m |
| 3.65 | 3.85 | 3.94 | 3.90 | 3.87 | 4.01 | 4.09 | 4.03 | 3.79 | 4.18 | 4.43 | 4.88 | 5.39 | 5.77 | 6.06 | 2 m | |
| Plot 3 | 8.81 | 7.87 | 7.26 | 6.58 | 5.93 | 5.21 | 4.73 | 4.62 | 4.58 | 4.69 | 4.98 | 5.26 | 5.43 | 5.06 | 4.65 | 1 m |
| 3.97 | 4.68 | 4.86 | 5.10 | 4.91 | 4.27 | 4.26 | 4.16 | 4.46 | 4.62 | 5.17 | 5.84 | 6.65 | 6.47 | 6.53 | 2 m | |
| Plot 4 | 2.71 | 2.39 | 1.89 | 1.46 | 1.30 | 1.16 | 1.02 | 0.98 | 1.01 | 1.14 | 1.38 | 1.75 | 2.27 | 2.91 | 3.75 | 1 m |
| 1.38 | 1.34 | 1.21 | 1.06 | 0.93 | 0.90 | 0.90 | 0.90 | 0.85 | 0.98 | 1.14 | 1.50 | 1.88 | 2.41 | 3.09 | 2 m | |
| height of tress | 17–18 m | 18–19 m | 19–20 m | 20–21 m | 21–22 m | 22–23 m | 23–24 m | 24–25 m | 25–26 m | 26–27 m | 27–28 m | 28–29 m | 29–30 m | 30–31 m | 31–32 m | Grid Cell Size |
| class | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| Plot 1 | 4.23 | 4.66 | 5.30 | 5.91 | 6.35 | 6.27 | 5.66 | 4.47 | 3.08 | 1.81 | 0.93 | 0.39 | 0.14 | 0.04 | 0.01 | 1 m |
| 4.62 | 5.37 | 6.28 | 7.20 | 7.68 | 7.70 | 6.61 | 5.04 | 3.18 | 1.77 | 0.77 | 0.30 | 0.10 | 0.02 | 0.00 | 2 m | |
| Plot 2 | 5.72 | 5.55 | 5.03 | 3.37 | 2.16 | 1.65 | 1.06 | 0.65 | 0.25 | 0.11 | 0.01 | - | - | - | - | 1 m |
| 6.47 | 6.47 | 5.06 | 3.46 | 2.72 | 1.85 | 1.16 | 0.45 | 0.20 | 0.03 | 0.00 | - | - | - | - | 2 m | |
| Plot 3 | 3.79 | 2.91 | 2.52 | 1.79 | 1.43 | 0.88 | 0.57 | 0.25 | 0.12 | 0.05 | 0.02 | 0.02 | - | - | - | 1 m |
| 4.55 | 4.15 | 3.16 | 2.63 | 1.65 | 1.14 | 0.51 | 0.21 | 0.10 | 0.05 | 0.04 | 0.01 | - | - | - | 2 m | |
| Plot 4 | 4.76 | 5.89 | 7.30 | 8.67 | 9.63 | 10.1 | 9.55 | 7.74 | 5.16 | 2.69 | 1.02 | 0.28 | 0.00 | 0.00 | - | 1 m |
| 4.92 | 6.09 | 7.65 | 9.08 | 10.5 | 11.1 | 10.3 | 8.09 | 4.86 | 2.09 | 0.63 | 0.12 | 0.01 | 0.00 | - | 2 m |
| height of tress | −24–−23 m | −23–−21 m | −22–−21 m | −21–−20 m | −20–−19 m | −19–−18 m | −18–−17 m | −17–−16 m | −16–−15 m | −15–−14 m | −14–−13 m | −13–−12 m | −12–−11 m | −11–−10m | Grid Cell Size |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| class | −24 | −23 | −22 | −21 | −20 | −19 | −18 | −17 | −16 | −15 | −14 | −13 | −12 | −11 | |
| Plot 1 | 0.00 | 0.01 | 0.02 | 0.07 | 0.15 | 0.29 | 0.61 | 0.97 | 1.37 | 1.63 | 1.86 | 1.91 | 1.90 | 1.88 | 1 m |
| 0.00 | 0.01 | 0.03 | 0.09 | 0.20 | 0.39 | 0.76 | 1.25 | 1.73 | 2.11 | 2.36 | 2.48 | 2.44 | 2.37 | 2 m | |
| Plot 2 | 0.01 | 0.01 | 0.01 | 0.02 | 0.03 | 0.04 | 0.06 | 0.10 | 0.18 | 0.24 | 0.42 | 0.58 | 0.76 | 1.02 | 1 m |
| 0.00 | 0.01 | 0.01 | 0.01 | 0.04 | 0.06 | 0.11 | 0.15 | 0.25 | 0.38 | 0.60 | 0.69 | 0.95 | 1.21 | 2 m | |
| Plot 3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.03 | 0.04 | 0.09 | 0.18 | 0.26 | 0.45 | 0.64 | 1 m |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.02 | 0.06 | 0.13 | 0.22 | 0.33 | 0.56 | 0.86 | 1.19 | 2 m | |
| Plot 4 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.02 | 0.02 | 0.04 | 1 m |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.01 | 0.02 | 0.03 | 0.05 | 0.10 | 2 m | |
| height of tress | −10–−9 m | −9–−8 m | −8–−7 m | −7–−6 m | −6–−5 m | −5–−4 m | −4–−3 m | −3–−2 m | −2–−1 m | >−1–0 m | 0–1 m | 1–2 m | 2–3 m | 3–4 m | Grid Cell Size |
| class | −10 | −9 | −8 | −7 | −6 | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | |
| Plot 1 | 1.83 | 1.84 | 1.98 | 2.18 | 2.37 | 2.45 | 2.56 | 2.63 | 2.66 | 2.75 | 2.85 | 3.06 | 3.26 | 3.59 | 1 m |
| 2.32 | 2.31 | 2.42 | 2.73 | 2.95 | 2.97 | 3.07 | 2.98 | 3.02 | 3.00 | 3.05 | 3.11 | 3.29 | 3.41 | 2 m | |
| Plot 2 | 1.25 | 1.47 | 1.89 | 2.10 | 2.43 | 2.62 | 2.94 | 3.32 | 3.85 | 4.38 | 5.07 | 4.90 | 4.86 | 4.77 | 1 m |
| 1.43 | 1.78 | 2.36 | 2.63 | 2.87 | 3.09 | 3.22 | 3.55 | 4.19 | 4.64 | 5.38 | 5.22 | 5.37 | 4.99 | 2 m | |
| Plot 3 | 0.86 | 1.13 | 1.53 | 1.91 | 2.30 | 2.73 | 3.29 | 3.66 | 4.25 | 4.78 | 5.56 | 5.45 | 5.52 | 5.35 | 1 m |
| 1.54 | 1.88 | 2.33 | 2.84 | 3.14 | 3.93 | 4.23 | 4.70 | 5.02 | 5.90 | 6.25 | 5.73 | 5.86 | 5.46 | 2 m | |
| Plot 4 | 0.09 | 0.23 | 0.51 | 0.90 | 1.19 | 1.30 | 1.31 | 1.21 | 1.20 | 1.20 | 1.18 | 1.19 | 1.22 | 1.28 | 1 m |
| 0.26 | 0.61 | 1.29 | 1.95 | 2.34 | 2.29 | 2.09 | 1.88 | 1.80 | 1.84 | 1.91 | 1.64 | 1.49 | 1.55 | 2 m | |
| height of tress | 4–5 m | 5–6 m | 6–7 m | 7–8 m | 8–9 m | 9–10 m | 10–11 m | 11–12 m | 12–13 m | 13–14 m | 14–15 m | 15–16 m | 16–17 m | 17–18 m | Grid Cell Size |
| class | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
| Plot 1 | 3.96 | 4.36 | 4.75 | 5.06 | 5.03 | 4.81 | 4.49 | 4.02 | 3.54 | 3.05 | 2.52 | 2.03 | 1.46 | 0.97 | 1 m |
| 3.64 | 3.96 | 4.05 | 4.27 | 4.27 | 4.00 | 3.74 | 3.27 | 2.89 | 2.43 | 2.04 | 1.57 | 1.22 | 0.75 | 2 m | |
| Plot 2 | 4.58 | 4.63 | 4.72 | 4.52 | 4.41 | 4.36 | 4.12 | 3.85 | 3.52 | 3.12 | 2.68 | 2.08 | 1.54 | 1.12 | 1 m |
| 4.94 | 4.62 | 4.47 | 4.31 | 4.13 | 3.99 | 3.43 | 2.98 | 2.56 | 2.16 | 1.98 | 1.63 | 1.28 | 0.99 | 2 m | |
| Plot 3 | 5.23 | 4.99 | 4.87 | 4.84 | 4.53 | 4.37 | 3.99 | 3.47 | 3.14 | 2.70 | 2.15 | 1.61 | 1.19 | 0.96 | 1 m |
| 4.86 | 4.46 | 4.48 | 4.05 | 3.80 | 3.34 | 2.93 | 2.52 | 2.03 | 1.66 | 1.18 | 0.75 | 0.57 | 0.43 | 2 m | |
| Plot 4 | 1.50 | 1.84 | 2.35 | 2.97 | 3.82 | 4.98 | 6.29 | 7.68 | 9.07 | 9.98 | 9.95 | 8.77 | 6.58 | 4.32 | 1 m |
| 1.81 | 2.16 | 2.74 | 3.37 | 4.23 | 5.30 | 6.41 | 7.62 | 8.38 | 8.75 | 8.30 | 6.87 | 4.70 | 2.86 | 2 m | |
| height of tress | 18–19 m | 19–20 m | 20–21 m | 21–22 m | 22–23 m | 23–24 m | 24–25 m | 25–26 m | 26–27 m | 27–28 m | 28–29 m | 29–30 m | 30–31 m | 30–31 m | Grid Cell Size |
| class | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | |
| Plot 1 | 0.58 | 0.31 | 0.17 | 0.09 | 0.05 | 0.03 | 0.02 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | - | 1 m |
| 0.48 | 0.26 | 0.14 | 0.08 | 0.04 | 0.03 | 0.01 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | - | 2 m | |
| Plot 2 | 0.65 | 0.40 | 0.19 | 0.11 | 0.04 | 0.02 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | - | 1 m |
| 0.60 | 0.36 | 0.17 | 0.09 | 0.05 | 0.03 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | - | 2 m | |
| Plot 3 | 0.67 | 0.47 | 0.33 | 0.18 | 0.12 | 0.07 | 0.03 | 0.03 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | - | 1 m |
| 0.26 | 0.20 | 0.11 | 0.07 | 0.04 | 0.03 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | - | 2 m | |
| Plot 4 | 2.53 | 1.42 | 0.83 | 0.46 | 0.26 | 0.17 | 0.07 | 0.03 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | - | 1 m |
| 1.55 | 0.83 | 0.47 | 0.23 | 0.13 | 0.07 | 0.02 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | - | 2 m |
| height of tress | 2–3 m | 3–4 m | 4–5 m | 5–6 m | 6–7 m | 7–8 m | 8–9 m | 9–10 m | 10–11 m | 11–12 m | 12–13 m | 13–14 m | 14–15 m | 15–16 m | Grid Cell Size |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| class | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| Area 1 | 8.76 | 9.24 | 10.9 | 12.2 | 9.97 | 8.38 | 8.23 | 6.47 | 4.02 | 3.25 | 2.84 | 2.50 | 2.55 | 2.62 | 1 m |
| 5.74 | 6.46 | 8.04 | 10.6 | 10.7 | 8.06 | 7.79 | 7.78 | 5.35 | 3.87 | 3.57 | 2.99 | 2.81 | 2.86 | 2 m | |
| Area 2 | 12.9 | 11.7 | 11.1 | 10.6 | 9.23 | 6.25 | 4.31 | 3.31 | 3.17 | 3.15 | 3.10 | 3.07 | 3.07 | 3.16 | 1 m |
| 9.16 | 9.30 | 9.27 | 9.24 | 8.85 | 7.51 | 5.06 | 3.77 | 3.41 | 3.28 | 3.35 | 3.39 | 3.51 | 3.69 | 2 m | |
| Area 3 | 14.6 | 11.5 | 9.83 | 8.59 | 7.35 | 6.35 | 5.42 | 4.93 | 4.58 | 4.02 | 3.90 | 3.71 | 3.32 | 2.84 | 1 m |
| 11.5 | 9.73 | 8.69 | 7.94 | 7.10 | 6.06 | 5.25 | 4.84 | 4.79 | 4.31 | 4.33 | 4.37 | 4.04 | 3.65 | 2 m | |
| Area 4 | 11.7 | 9.64 | 8.75 | 7.53 | 5.49 | 4.42 | 4.01 | 4.84 | 5.29 | 5.26 | 5.33 | 4.33 | 3.59 | 3.06 | 1 m |
| 9.06 | 8.15 | 7.54 | 7.52 | 6.10 | 4.81 | 3.97 | 4.19 | 4.91 | 5.01 | 5.43 | 5.16 | 4.26 | 3.73 | 2 m | |
| heightof tress | 16–17 m | 17–18 m | 18–19 m | 19–20 m | 20–21 m | 21–22 m | 22–23 m | 23–24 m | 24–25 m | 25–26 m | 26–27 m | 27–28 m | 28–29 m | 29–30 m | Grid Cell Size |
| class | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | |
| Area 1 | 2.40 | 1.88 | 1.29 | 0.93 | 0.62 | 0.39 | 0.26 | 0.13 | 0.07 | 0.04 | 0.01 | 0.01 | 0.00 | - | 1 m |
| 3.27 | 3.01 | 2.27 | 1.65 | 1.25 | 0.79 | 0.56 | 0.29 | 0.15 | 0.07 | 0.03 | 0.01 | 0.00 | - | 2 m | |
| Area 2 | 2.84 | 2.51 | 2.29 | 1.80 | 1.20 | 0.67 | 0.37 | 0.17 | 0.05 | 0.02 | 0.01 | 0.00 | - | - | 1 m |
| 3.60 | 3.22 | 3.25 | 2.73 | 2.00 | 1.17 | 0.70 | 0.37 | 0.13 | 0.04 | 0.02 | 0.00 | - | - | 2 m | |
| Area 3 | 2.48 | 1.93 | 1.39 | 1.09 | 0.80 | 0.58 | 0.36 | 0.23 | 0.11 | 0.05 | 0.02 | 0.01 | 0.00 | 0.01 | 1 m |
| 3.44 | 2.76 | 2.01 | 1.61 | 1.30 | 0.93 | 0.63 | 0.39 | 0.19 | 0.09 | 0.04 | 0.01 | 0.00 | 0.01 | 2 m | |
| Area 4 | 2.63 | 2.40 | 2.23 | 2.10 | 2.02 | 1.86 | 1.49 | 1.06 | 0.60 | 0.26 | 0.08 | 0.02 | 0.00 | - | 1 m |
| 3.10 | 2.76 | 2.54 | 2.33 | 2.14 | 2.20 | 1.86 | 1.48 | 1.02 | 0.50 | 0.17 | 0.05 | 0.01 | - | 2 m |
| Name | Area (km2) | Historical forest cover (%) | Current forest cover (%) | New forest cover, LiDAR (%) | Total forest cover (%) | Grid Cell Size |
|---|---|---|---|---|---|---|
| Plot 1 | 1.63 | 57.01 | 43.12 | 15.26 | 58.38 | 1 m |
| 57.58 | 52.27 | 18.36 | 70.63 | 2 m | ||
| Plot 2 | 1.13 | 15.75 | 9.64 | 16.11 | 25.75 | 1 m |
| 17.57 | 14.35 | 23.08 | 37.42 | 2 m | ||
| Plot 3 | 1.75 | 6.47 | 4.26 | 6.73 | 10.99 | 1 m |
| 6.66 | 6.39 | 11.65 | 18.04 | 2 m | ||
| Plot 4 | 1.69 | 42.06 | 30.16 | 18.92 | 49.08 | 1 m |
| 44.17 | 39.03 | 25.19 | 64.22 | 2 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bożek, P.; Janus, J.; Mitka, B. Analysis of Changes in Forest Structure using Point Clouds from Historical Aerial Photographs. Remote Sens. 2019, 11, 2259. https://doi.org/10.3390/rs11192259
Bożek P, Janus J, Mitka B. Analysis of Changes in Forest Structure using Point Clouds from Historical Aerial Photographs. Remote Sensing. 2019; 11(19):2259. https://doi.org/10.3390/rs11192259
Chicago/Turabian StyleBożek, Piotr, Jaroslaw Janus, and Bartosz Mitka. 2019. "Analysis of Changes in Forest Structure using Point Clouds from Historical Aerial Photographs" Remote Sensing 11, no. 19: 2259. https://doi.org/10.3390/rs11192259
APA StyleBożek, P., Janus, J., & Mitka, B. (2019). Analysis of Changes in Forest Structure using Point Clouds from Historical Aerial Photographs. Remote Sensing, 11(19), 2259. https://doi.org/10.3390/rs11192259