1. Introduction
Sea surface temperature (SST) plays a major role in the existence and life of a tropical cyclone (TC). It is recognized as one of the most important factors in TC genesis (together with e.g., the existence of a reduced vertical wind shear, environmental vorticity and high relative humidity). In addition, it is thought to be of most relevance in TC strengthening and weakening, although it is still the subject of scientific debate (e.g., [
1] and references therein).
The formation of a region with reduced SST in the wake of tropical cyclones (TCs; so-called hurricanes in the Atlantic basin when a TC attains a certain strength) was already known from measurements provided by merchant ships in the 1950s (e.g., [
2,
3]). However, the first dedicated systematic survey to evaluate the evolution of the SST field after the passage of a TC was published by Leipper [
4], who found a reduction of ∼5 °C in the vicinity of the track of hurricane Hilda (1964). Also Hazelworth [
5] detected significant cooling near the US Atlantic coast after the passage of ten hurricanes. These measurements, made with buoys and bathythermographs, yielded a mean cooling between
and
°C. A similar range of cooling was later estimated from satellite-based measurements. Stramma et al. [
6] performed a statistical assessment of the cold wake left by some Atlantic hurricanes between 1981 and 1984 (13 in total) using limited SST images provided by the National Oceanic and Atmospheric Administration (NOAA) advanced very high-resolution radiometer (AVHRR) sensor. They found an overall magnitude of SST cooling of
°C that lasted from a few days to around two weeks after the passage of the hurricane along its track. One drawback of that study was that for some hurricanes (mainly for the major hurricanes), the authors only had at hand cloud-free images up to 5 days after the passage of the hurricane, hence likely underestimating the cooling. Moreover, they found that the amount of cooling was quite proportional to the hurricane strength, with the maximum localized at around 70 km to the right of the track for fast-moving hurricanes and closer to the center for slower hurricanes. Indeed this rightward bias (in the Northern Hemisphere, leftward in the Southern Hemisphere) had already been mentioned by Jordan [
7] and it has been amply confirmed in subsequent observational studies such as in Shay et al. [
8] and Monaldo et al. [
9], who found a mean cooling of around 3–4 °C and
°C to the right of the track of hurricanes Gilbert (1988) and Edouard (1996) respectively.
Due to its magnitude and large spatial imprint, the characterization of the cold wake induced by a TC has been suggested to be of primary importance to forecast the TC intensity (e.g., [
10]), with potential weather and climate effects at remote locations through propagating changes in the atmospheric boundary layer (e.g., [
11]) and a contributor to the generation of phytoplankton blooms (e.g., [
12]). Moreover, a better knowledge of the statistical properties of cold wakes may provide useful information on the long-term variations of TC properties.
Two main mechanisms have been proposed to explain the rightward bias in SST cooling. First, as a result of left-right asymmetry in the wind field since the translational speed of a TC adds to the wind on the right side, and opposes the wind on the left side. This generates stronger surface turbulent mixing on the right side of the TC with respect to its track. Second, due to the intrusion of sub-surface cold waters through a quasi-resonant process that occurs when the wind stress is almost aligned with the mixed layer near-inertial ocean currents [
13]. Price [
14] evaluated both mechanisms with the simulation of the passage of hurricane Eloise (1975) using a three-layer ocean model coupled to a steadily moving hurricane. He found that the cooling due to the intrusion of sub-surface waters dominates over the cooling induced by turbulent surface fluxes and other non-local processes such as horizontal advection or upwelling (e.g., [
15,
16,
17]). During this process, the transfer of energy and momentum from the atmosphere to the ocean is maximized. This enables the generation of strong turbulence within the mixed layer, which is able to break the vertical shear associated with the strong inertial currents, hence favoring the intrusion of colder waters located below the seasonal thermocline [
14].
Other model key findings are that the amount of SST cooling depends on the TC moving speed, the TC strength and the mixed layer structure, with larger cooling for stronger and slow-moving TCs (e.g., [
16,
17,
18]) that can be further intensified by non-linear and non-local processes (e.g., [
19,
20]). Indeed the presence of a concomitant upwelling may enhance cooling (e.g., [
17,
21]) and tends to reduce the rightward bias, in close agreement with the reduction in the rightward bias for slower hurricanes found by Stramma et al. [
6]. Also, the Ekman pumping may help to uplift the thermocline thus favoring the intrusion of sub-surface cold waters into the ocean mixed layer [
22].
Some of the above model-based results have been validated thanks to the availability of accurate measurements inside hurricanes (e.g., through airborne expendable bathythermographs). As an example, Cione and Uhlhorn [
23] assessed the quasi-simultaneous SST differences between the core and the edge (environment) during the passage of 23 Atlantic hurricanes, finding a range of differences between 0–2 °C, much less than the typical cold wake found after the passage of hurricanes (up to ∼4–5 °C). Moreover, they estimated that a rise of only
°C between the environment and the inner core of the hurricane can provide enough energy to maintain or even intensify hurricanes (indeed enthalpy fluxes from the ocean to the atmosphere can increase by about 40%). Despite all this progress, the processes involved in the upper ocean response to TCs are still not completely understood due to the limited number of in situ measurements [
1].
Alternatively, the availability of many TC tracks and long timeseries of SST data from remote sensors has favored a statistical assessment of the cold wake left by TCs. Thus, using high-resolution SST fields and the best available tracks of North Atlantic hurricanes between 1982 and 2005, Michaels et al. [
24] found that once the hurricane reaches wind speeds over 50
, there is no clear statistical relationship between the SST and the wind intensity. They also noted that the peak of the wind speed does not tend to occur nearby the location of the highest SST along the hurricane track. One reason for the unclear statistical relationship between the SST and the hurricane intensity is thought to be the existence of salinity-induced barrier layers (e.g., [
25,
26]), which are quite common in regions of elevated fresh water input such as the tropical oceans [
27]. Barrier layers act as obstacles for the upward intrusion of cold waters and the occurrence of vertical mixing when the isothermal layer is located below the mixed layer (positive barrier layer). A detailed assessment by Balaguru et al. [
26] using observations and data from model simulations showed that the intensification rate of TCs is around 50% higher in those regions with barrier layers due to a reduced SST cooling.
To our knowledge, Hart et al. [
28] were probably the first to use a composite approach to study the cold wake for a large amount of TCs. They focused on the regional changes in the maximum potential intensity (e.g., [
29,
30]), which is proportional to the difference between SST and the surface air temperature. To construct the composites, they computed the spatial average of SST within a square box of
centered on each TC observation. They used the Reynolds SST dataset [
31] comprising daily optimally interpolated blended data, largely based on measurements from the AVHRR (infrared) sensor. This sensor does not retrieve a valid SST in cloudy areas, and only provides accurate information on the cold wake when the clouds of the hurricane have left, with the subsequent likely underestimation of SST cooling [
28]. The same dataset was employed by Dare and McBride [
32] to analyze the SST cooling by TCs between 1981 and 2008 using time series of single grid points. To reduce the effect of clouds in the quantification of the cold wake, Lloyd and Vecchi [
33], Mei and Pasquero [
34] evaluated the spatio-temporal characteristics of the cold wake left by TCs using SST fields retrieved from microwave sensors such as the Microwave Imager (TMI) on board of the NASA TRMM (Tropical Rainfall Measuring Mission) satellite. However, they noted that the sensor may still show a deficient coverage in those regions with heavy rain (e.g., in the interior of strong TCs). Mei and Pasquero [
34] computed SST anomalies (SSTA) by subtracting the mean SST field one month before the arrival of the hurricane to the corresponding daily field. Two approaches were applied to construct the composites: First, they used the same box average method described above for Hart et al. [
28]; second, they took the SSTA centered at each TC observation 2500 km perpendicular to the track and 200 km along the track. The latter approach allows a better characterization of the signature of SST cooling, enabling a visual comparison between the spatial structure of cold wakes induced by different TCs.
In this work we quantify the SST cooling induced by North Atlantic hurricanes using up-to-date satellite-based SST blended data. Following Mei and Pasquero [
34], our analysis includes an assessment of the spatial structure of SST cooling left by hurricanes with a slightly different composite method that allows for an improved spatial representation of the average cold wake. We also analyze the time variability of the cold wake and how it changes under different ranges of hurricane intensities and translational speeds as well as with the structure of the mixed layer. In contrast to Mei and Pasquero [
34], who used a simplified mixed layer analytical approach, we use monthly fields of barrier layers derived from in situ measurements.
The remainder of this paper is structured as follows: In
Section 2 we present the North Atlantic hurricane tracks and SST data as well as the method applied to construct the composites;
Section 3 quantifies the difference in SST cooling obtained between SST fields retrieved from mostly infrared sensors (used by e.g., [
28,
32]) and from merged satellite-based data (infrared + microwave);
Section 4 describes the average magnitude and spatial pattern of the cold wake for a set of hurricane properties such as the translational speed and the maximum wind intensity, and the upper ocean stratification;
Section 5 describes the temporal evolution of the cold wake;
Section 6 presents some insights on how the cold wake affects the hurricane strength; to conclude,
Section 7 summarizes the main findings.
3. Differences in the Cold Wake Obtained from Mostly Infrared and Infrared + Microwave SST Data
Despite the good spatial resolution and excellent temporal coverage of infrared satellite-based data, Hart et al. [
28] and Dare and McBride [
32] pointed out the likely underestimation of SST cooling by the AVHRR sensor under TC conditions due to its inability to retrieve a valid value of SST in cloudy environments. To partly overcome this limitation, Mei and Pasquero [
34] used microwave-based SST data, more suitable to characterize cold wakes because of its through-cloud capability. However, we note again that microwave sensors are also inaccurate under precipitating clouds, which usually develop within a hurricane. To our knowledge, no study has quantified this potential underestimation in terms of the cold wake. In this section, we use the composite method described in
Section 2.3 to quantify the difference in the shape and amplitude of cold wakes between
AVHRR-mostly and
merged SST data under TC observations from 2002 to 2018. In our discussion we hypothesize that as suggested by previous works and the already explained technical issues, the information provided by the
merged dataset is, although inaccurate, closer to the truth than the
AVHRR-mostly.
Panels showing the mean composite of
SSTA for
AVHRR-mostly and
merged SST data, as well as the difference between both composites for all hurricane observations are shown in
Figure 5a,c (numbers are summarized in
Table 1 with uncertainties at 95% of confidence). The minimum values of
SSTA (referred to as
) are
°C and
°C for
AVHRR-mostly and
merged respectively, with an average underestimation of around
°C for
AVHRR-mostly SST. A smaller difference is found when we compute the average
SSTA over a disk of 200 km of radius around the hurricane center (
), with values of −0.97 °C and −1.19 °C for
AVHRR-mostly and
merged SST respectively. The spatial distribution of
SSTA shows that the main differences between
AVHRR-mostly and
merged SST are located around the center-right region (
Figure 5c,f,i,l).
A further assessment of the
SSTA is performed by splitting the hurricane observations into three groups according to their category: 1, 2 and 3–5 (major hurricanes). Results indicate that the underestimation of the magnitude of
by
AVHRR-mostly is larger for the strongest hurricanes (category 2 and higher,
Figure 5d–l) with values over
°C than for the hurricanes of category 1 (
°C), without taking into account SST datasets uncertainties. This is likely explained by the presence of more developed (thicker) vertical clouds under stronger hurricanes. Overall category 2 hurricanes show a slightly more intense cooling than categories 3–5 hurricanes (below
°C for
merged SST), but with both values included within the margin of error (
Table 1).
More information on the spatial structure of the cold wake is provided by a left-right cross-section of
SSTA along the
x-axis at
(
Figure 5m,n). It shows a similar position of the maximum cooling (
) (on the right and near the center) for both data. Indeed the
is a bit closer to the center for
merged SST (60 and 50 km for
AVHRR-mostly and merged data respectively if all hurricanes are considered). This difference may be partly due to the coarser spatial resolution of
AVHRR-mostly product. Slightly larger differences are found for the cold wake width, with a relative overestimation of around 30 km for
AVHRR-mostly data (510 and 480 km respectively). One interesting result is that the cold wake width (as estimated) decreases clearly with the hurricane strength in
merged SST (from 530 to 420 km), while this decrease is smaller for
AVHRR-mostly SST (from 520 to 490 km). The width has been computed as the separation between the
e-folding decay of
around the position of
: i.e.,
, where
and
, where the + and − signs of
indicate that they are located on the right and on the left of
respectively. Therefore, a shorter width is related to a more abrupt decay in space of
(i.e., a larger temperature gradient).
Our results evidence that the use of SST data with information from microwave sensors is critical to accurately capture the SST under atmospheric structures such as hurricanes, which have very thick clouds and large rain bands. Therefore, in the following sections only the merged SST will be considered.
5. Temporal Evolution of the Cold Wake for Selected Hurricane and Oceanic Properties
An important characteristic associated with the cold wake is how its spatial structure and magnitude change with time. In particular: How much time does it take for the cold wake to disappear? How does this time change with the individual hurricane and ocean properties evaluated in
Section 4?
To address these questions, we have analyzed the temporal evolution of
and
as follows: First, for every hurricane observation time series of
and
have been constructed starting at the day of
(which as explained in
Section 2, can occur between
and
days for each hurricane observation); second, these time series have been daily averaged and grouped considering those study cases described in
Table 2; Finally, as in Mei and Pasquero [
34], the resulting daily time series have been fitted against an exponential function:
, in which
A is the value of
and
at
,
t is the time after
and
is the rate of decay (unit of
in both cases). In this way, the fitting expressions can be simply rewritten as:
and
.
The average values of the scaled
with respect to the number of days after
as well as the fitting curve are shown in
Figure 10 (distinguished by properties studied in
Section 4 and percentile ranges shown in
Table 2).
Overall, rates of decay () are rather similar for all study cases with values between 9.1 and 11.7 (B3 and B2 respectively). The fastest decay of the cold wake is found for the B3, D3 and B1 cases, while the slowest decay is shown by the D2, A2 and B2 cases. Interestingly, shows small differences between cases C1–C3 (BLT), pointing out that the state of the upper ocean stratification before and during the passage of the hurricane has a small effect on the rate of restratification of the water column once the hurricane has left the region.
More in detail, during the first 15–20 days after the passage of the hurricane the largest cooling decreases in magnitude rather fast, decaying exponentially 80% with respect to the initial value for all study cases (see the decay from 1 to 0.2 at
y-axis around 15 days after the minimum
SSTA in
Figure 10). After 20 days, the behavior is more complex as it depicts some oscillations over a weaker decreasing trend, taking around 30 to 40 more days to reach the original
SSTA conditions previous to the arrival of the hurricane.
For a similar exponential decay is found (not shown), except that the time needed to recover the initial condition is about 10 days longer (for a total of around 60 days). This is likely explained by the fact that in this case the temperature of a large area (a circle of 200 km of radius) has to become homogeneous, which is expected to take on average more time than a single point. Moreover, fluctuations are larger, as reflected in the range of (with values between 10.5 and 15.1 ).
Based on our results, the answers to the questions formulated in the beginning of this section are: (1) how much time does it take for the cold wake to disappear? On average the strong cold anomalies induced by a hurricane need around 50–60 days to (almost) disappear and recover the climatological mean values; (2) How does this time change with the individual hurricane and ocean properties evaluated in
Section 4? We have not found any evidence that the evolution of the cold wake is affected by the hurricane properties and the ocean mixed layer vertical structure. This suggests little memory in the cold wake restratification process and a high dependence on the environmental conditions, in good agreement with Mei and Pasquero [
34].
To conclude this section, we note that a better comprehension of the temporal evolution of the cold wake could be potentially provided by a detailed study of the upper ocean heat content. However, current long-term gridded products (mostly derived by blending satellite-derived SST and in situ profilers) present some problems in resolving the hurricane-induced ocean heat content perturbation at daily scales. The reason is that in the absence of nearby in situ mixed layer data climatologies are used instead.
6. Insights on Hurricane Intensity Response to Cold Wake
Although the main aim of this work is to assess the cold wake amplitude and structure, in this section we briefly investigate if any connection exists between the observed SST cooling and the hurricane maximum sustained surface wind speed (
) provided by IBTrACS data. We note that in principle, observations used in this work do not allow explanation of whether hurricane intensification/weakening is causally related with the magnitude of absolute SST or cold wake properties. Previous studies have found that the SST cooling is usually accompanied by a weakening of TCs (e.g., [
18,
49,
50,
51]). The magnitude of this weakening is larger for those hurricanes moving slower and where the largest SST cooling is located [
17,
18]. For instance, Schade and Emanuel [
52] systematically analyzed the atmospheric response to SST (the evaporation-wind feedback process so-called SST feedback effect or WISHE mechanism) using a coupled model in which also the sensitivity to several other parameters was evaluated (e.g., storm translation speed and size, relative humidity, momentum and heat transfer coefficients or tropopause temperature), pointing out the major relevance of SST in controlling the TC intensity, with a potential storm weakening of up to 50% due to SST feedback reflected in the reduction of enthalpy fluxes caused by the SST cooling. Alternatively to the mentioned WISHE mechanism, other model-based studies found that the SST has a minor relevance in the intensification of TCs once a certain SST threshold has been attained, and that non-linear local atmospheric processes in the boundary layer may lead to a stronger TC mean flow (e.g., [
53,
54,
55]).
To investigate the possible influence of the cold wake on the hurricane strength, we have divided the change in the wind speed for each hurricane observation in the first 24 h (
) into four groups (see also
Table 4, unit in kt/24 h, where 1 kt ≈ 0.51, m·s
): Weakening (WK) for
, neutral response (NR) for
, slow intensification (SI) for
and rapid intensification (RI) for
. For all hurricane observations within each group the mean and the margin of error at 95% of confidence have been computed. In addition to
, other variables have been included in the assessment such as: The mean SST (
), the largest cooling (
), BLT, BLPE, the mean latitude of the hurricane (
) and the hurricane translation speed (
).
Table 4 indicates that in most cases,
remains neutral or weakens (∼1150 of about 1500 observations). On average, it occurs more often at higher latitudes (
N), over lower SST (
°C) and for strong cooling (
°C). This response is in line with results of modeling studies (e.g., [
18,
56,
57]) and the WISHE mechanism.
The reminding observations (around 25%) show slow or rapid intensification (SI and RI), which occur when the mean SST is larger and when the cooling is smaller. In more detail, RI is found for
°C and
°C. Hurricane intensification seems to be associated with originally weaker hurricanes (
, i.e., hurricanes with theoretical margin to develop more), and with hurricanes located in lower latitudes (
N) that are likely characterized by warmer waters (
Figure 2). Besides, as they feel a positive SST gradient, likely stronger momentum and enthalpy fluxes may develop [
51,
52].
In contrast, no clear differences are found in terms of the hurricane translation speed () between NR, SI and RI cases. However, weakened hurricanes tend on average to move slightly faster ( more). Similarly, the role of initial conditions of BLT and BLPE on hurricane intensification is unclear as they present a very large spatial variability (see the large margin of error), although it is expected that their effect in momentum and enthalpy fluxes is already being indirectly reflected in .
As noted above, hurricane intensification can also be triggered by atmospheric-driven processes if SST is over 27–28 °C (e.g., [
53,
55]). This intensification can occur when the hurricane moves to a region in which atmospheric conditions are more favorable (e.g., higher boundary layer air temperature, favorable environmental vorticity, or more reduced vertical wind shear). Indeed, the simultaneous occurrence of favorable oceanic and atmospheric conditions is also possible. Based on the high complexity of these processes the combination of simultaneous air-sea measurements and coupled high-resolution simulations is necessary to fully understand the atmospheric feedback to SST cooling, which is far beyond the scope of this work.
7. Conclusions
This study had two main objectives: First, try to reconcile the large dispersion of values of observed hurricane-induced SST cooling yielded by previous works in the North Atlantic Ocean, which were based on individual or a large ensemble of hurricanes and used infrared- and/or microwave-based remote observations; and second, to quantify the sensitivity of SST cooling under a set of hurricane and oceanic parameters: Hurricane 10-min maximum sustained wind speed, hurricane translation speed, and the ocean mixed layer structure by means of the barrier layer thickness and the barrier layer potential energy (BLT and BLPE). To this end, a statistical composition of a large amount of hurricane observations under the same reference system has been performed.
We have found that the spatial structure of the cold wake (position of largest cooling and cold wake width) does not show clear differences when infrared (
AVHRR-mostly) or when infrared+microwave SST data (
merged) is used (
Table 1). However, in terms of the amplitude of the cold wake, differences are evident, with a relative underestimation by infrared data of around 0.4–0.5 °C in the magnitude of largest cooling (
Table 1 and
Figure 5).
Ordered from larger to lower magnitude of cooling, the translation speed is the most important property once the tropical storm has reached hurricane category. It has a critical role in the position of strongest cooling with respect to the hurricane center (
in
Table 2), which approaches the center as the hurricane translation speed decreases confirming results by Mei and Pasquero [
34]. This rightward bias is 80 km for the one third fastest moving hurricanes and 40 km for the one third slowest moving hurricanes, with a mean position of around 60 km to the right of the center of the hurricane, very close to the radius of maximum sustained wind, which agrees with other observed and model-based studies such as Price [
14], Steffen and Bourassa [
44]. Indeed Price [
14], Jullien et al. [
22] found an enhanced upwelling along the hurricane track for slow-moving hurricanes.
The second most important property with respect to the amount of cooling is the upper ocean vertical structure. In contrast to Mei and Pasquero [
34], who used an analytic approach to estimate mixed layer depth at typical values of the tropical regions, we have used a monthly gridded climatology constructed with observations. Although Lloyd and Vecchi [
33] also used observations, their dataset only took into account the stratification in temperature but not in salinity.
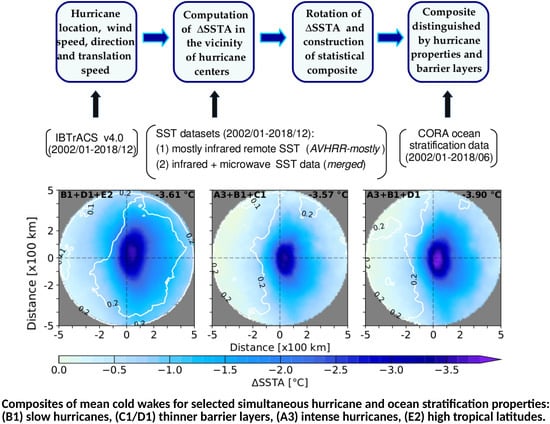
The mean composite of those hurricane observations passing over regions with values of BLPE within the first third of the percentile range (
P33,
Figure 5) yield slightly stronger cooling than for the first third of BLT (∼0.15 °C,
Table 2 and
Figure 7). On average, differences in the barrier layer properties can impact the magnitude of largest cooling up to 1–1.5 °C if uncertainties are considered (
Table 2).
Differences in the SST cooling induced by hurricanes of different categories appears to be less important when compared to the hurricane moving speed and the upper ocean stratification. As an example, hurricanes of categories 3–5 induce almost the same cooling as hurricanes of category 2 (∼0.1 °C), which is in line with findings in the North Atlantic from Michaels et al. [
24], Lloyd and Vecchi [
33] and different from [
34], who found a stronger cooling of about
°C for TCs of categories 3–5. Although in their case they included all TCs in the Northern Hemisphere thus merging Pacific and Atlantic Ocean upper ocean conditions and responses. In this regard, Lloyd and Vecchi [
33] already mentioned that this non-monotonic response of SST cooling with hurricane intensity is especially remarkable in the North Atlantic.
Overall the above results are in line with previous works, which already indicated that the average amplitude of SST cooling is larger for slow-moving hurricanes over those regions with small values of BLT/BLPE (e.g., [
26,
44]). We have found that for those cases in which all these conditions are met, the mean largest cooling reaches values below
°C (
Table 3). This magnitude of cooling, larger for BLPE than for BLT (
Table 3), is of the same order of that obtained from individual observations (e.g., [
8,
9,
23]), but is larger than statistical insights from Michaels et al. [
24], Hart et al. [
28] since they only used infrared SST data. Moreover, this work presents an improvement with respect to Lloyd and Vecchi [
33], Mei and Pasquero [
34] since our results are regionalized for the North Atlantic and include the effect of more realistic barrier layers, thus integrating the combined effect of hurricane and ocean properties.
Regarding the temporal variability of the cold wake, our results show a fast exponential decay in the magnitude of cooling (of about 80%) during the first 20 days, to later decay more slowly almost up to pre-hurricane conditions in about 50–60 days (
Figure 10). This value is around 20 days longer than the one found by Hart et al. [
28], a difference that could be explained by their use of infrared data. Moreover, contrary to what was suggested by Lloyd and Vecchi [
33], on average we have not found a residual cooling after two months. This does not imply that it may not exist for individual cases. The time needed by the cold wake to disappear does not show a statistical dependency on the hurricane properties nor on the ocean mixed layer structure prior or during the passage of the hurricane. Therefore, the restoring time appears to be strongly dominated by the environmental conditions, as already pointed out by Mei and Pasquero [
34], so the final recovery time may change from case to case.
We note that due to the lack of reliable information on the hurricane size, this parameter has not been included in our analysis. However, observations indicate that the radius of maximum wind changes little with hurricane category (with values between 40–60 km, decreasing with category) [
58], thus small changes in the cold wake structure are expected.
Some indications on the mean 10-min maximum sustained wind response to the cold wake are summarized in
Table 4. Most of hurricane observations (75%) show a weakening or little change in the wind intensity. The remainder of the observations shown some kind of intensification, with few observations showing a rapid intensification, mostly reserved for hurricanes below category 3, over very warm waters (>28 °C) in tropical areas (<22
N). However, the high degree of complexity of the involved processes and the atmospheric feedback requires a more complete assessment to elucidate the chain of physical processes involved in the atmospheric response. To this end, the combination of simultaneous air-sea measurements and high-resolution coupled simulations will be necessary [
1].