Assessing Multiple Years’ Spatial Variability of Crop Yields Using Satellite Vegetation Indices

Abstract

Assessing crop yield trends over years is a key step in site specific management, in view of improving the economic and environmental profile of agriculture. This study was conducted in a 11.07 ha area under Mediterranean climate in Northern Italy to evaluate the spatial variability and the relationships between six remotely sensed vegetation indices (VIs) and grain yield (GY) in five consecutive years. A total of 25 satellite (Landsat 5, 7, and 8) images were downloaded during crop growth to obtain the following VIs: Normalized Difference Vegetation Index (NDVI), Enhanced Vegetation Index (EVI), Soil Adjusted Vegetation Index (SAVI), Green Normalized Difference Vegetation Index (GNDVI), Green Chlorophyll Index (GCI), and Simple Ratio (SR). The surveyed crops were durum wheat in 2010, sunflower in 2011, bread wheat in 2012 and 2014, and coriander in 2013. Geo-referenced GY and VI data were used to generate spatial trend maps across the experimental field through geostatistical analysis. Crop stages featuring the best correlations between VIs and GY at the same spatial resolution (30 m) were acknowledged as the best periods for GY prediction. Based on this, 2–4 VIs were selected each year, totalling 15 VIs in the five years with r values with GY between 0.729** and 0.935**. SR and NDVI were most frequently chosen (six and four times, respectively) across stages from mid vegetative to mid reproductive growth. Conversely, SAVI never had correlations high enough to be selected. Correspondence analysis between remote VIs and GY based on quantile ranking in the 126 (30 m size) pixels exhibited a final agreement between 64% and 86%. Therefore, Landsat imagery with its spatial and temporal resolution proved a good potential for estimating final GY over different crops in a rotation, at a relatively small field scale.

1. Introduction

Investigation of problems associated with agricultural yield, before harvesting, most commonly involves observing in-season growth variations, scouting areas at different fertility, and defining optimum soil sampling design according to needs of individual field. All this helps to increase the agricultural economic yield. However, current traditional methods for estimating the crop yield during the growing season may lead to poor yield assessment and inaccurate area appraisal. These methods rely on the precise and detailed collection of crop data, which is cost-intensive and time-consuming [1,2]. In addition, extensive use of nitrogen (N) fertilizers poses a problem of growing concern in agriculture. Surplus N drains into groundwater affecting the quality of drinking water, or seeps into superficial water bodies determining eutrophication [3]. This scenario makes it necessary to adopt efficient crop production methods assuring minimum environmental impact and concurrent optimization of crop yields [4]. Remote sensing has proved to be an efficient technology in precision agriculture for estimating crop status during the growing season. This, specifically, consists in evaluating the relationship between spectral vegetation indices during growth and final crop yield [5,6].

Crop yield varies spatially and temporally within a single field [7,8], which makes it important to assess the spatial pattern of grain yield (GY) over the entire field in view of specific management practices [7]. GY variation within a field depends on intrinsic characteristics like soil type and physical-chemical and topographic properties and external characteristics like amount of applied fertilizers, irrigation, etc. [9,10]. Spatial maps of crop yield have been extensively used to interpret the causes of yield variation across the field [11].

However, many issues in the spatial and temporal relationship between crop yields and VIs obtained from remote sensing need to be investigated, depending on crop stage and the specific management practice. To capture the distinguishing characteristics of an agricultural crop, it is advisable to use more vegetation indices, as each VI has a unique combination of wavebands that can be related to specific crop parameters and growth stages [12].

Remotely sensed data can cover a large area to retrieve the spectral information in real time during crop growing period [13]. Landsat missions have been collecting and archiving imagery worldwide with multispectral sensors providing insights into plant response to solar radiation, opening the era of remote vegetation indices (VIs). Specific VIs, obtained by combining single wavebands of a multispectral image, offer the farming community clues to crop growth status in time to predict higher/lower productions in specific areas [6,14]. However, various VIs have been developed at canopy scale [15], which are more sensitive to canopy reflectance, compared to individual bands [16].

We have selected six among the many VIs available at present, which are commonly addressed in the literature, and could be helpful in estimating changes at canopy level of agricultural crops, and ultimate yield. Normalized Difference Vegetation Index (NDVI) was first proposed by Rouse et al. [17]. It is defined as the ratio between the difference and the sum of reflectance values in the near-infrared (RNIR) and red (RRED) spectrum, which is indicative of the photosynthetically active vegetation [18,19]. NDVI is widely used to estimate crop biomass at different growth stages. Many scientists claim that NDVI is the best estimator for light interception, although its values fluctuate during crop cycle [20,21]. In cultivated soils NDVI ranges from zero (bare soil) to 1; values of 0.6–1.0 indicate dense vegetation at peak growth stages [22].

Beside NDVI, various VIs have been developed to address crop growth status through specific relationship with chlorophyll, carotenoids, or biomass [23]. These VIs provide information on biotic and abiotic stresses affecting crop yields [24]. More recent VIs have been developed to counterbalance NDVI limitations, e.g., the interference of soil reflectance with sparse canopy cover, and the low sensitivity to chlorophyll content in mature canopies. These VIs demonstrated higher performances in specific applications to precision agriculture [25].

Enhanced Vegetation Index (EVI) has been developed to improve the sensitivity of canopy reflectance under high biomass regions, as it gives a more linear correlation with green leaf biomass that is directly related to final GY [26]. In addition to red and NIR bands, EVI utilizes a blue band compared to NDVI, which enhances vegetation appraisal through de-coupling of canopy reflectance signal and reduction of the atmospheric influence [27]. EVI ranges from −1 to +1 [28].

Soil background effects may create problems in the reflectance of crop canopy, so to overcome these effects in the application of Vis, a Soil Adjusted Vegetation Index (SAVI) has been proposed [29] for applications in total biomass and crop yield prediction [30,31,32]. SAVI involves an adjustment factor (L) in the NDVI equation to remove the soil noise, whose value depends on vegetation density (L = 1, 0.5, and 0.25 for low, intermediate, and high vegetation density, respectively). SAVI ranges from −1 to +1.

The Green Normalized Difference Vegetation Index (GNDVI) is designed as a modification of NDVI, where the red band is substituted with a green band [33], which might be more useful for assessing the green biomass variations at canopy scale. GNDVI ranges from −1 to +1.

The estimation of chlorophyll concentration at leaf canopy involves the Green Chlorophyll Index (GCI), which is directly related to leaf area index and final GY. It ranges from 0 to 6 [34].

Lastly, the Simple Ratio (SR), also known as ratio vegetation index (RVI) [35], is used to eliminate albedo effects in the atmosphere, as it is calculated by band ratio of light scattered in the NIR to light absorbed in the red reflectance (R_red). Hence, SR is close to 1 if the object gets similar reflectance in both red and NIR bands. For a green object, the value ranges from 0 to infinity [36]. SR, which is the simplest VI, owns nonetheless a higher sensitivity to high biomass and LAI values, compared to NDVI [37].

Many studies have successfully addressed various issues through remote sensing: leaf nitrogen content [25,38], leaf area index [28,39], chlorophyll content [39], total biomass [35], and final crop yield [40]. Landsat satellite data at 30 m resolution have already been used to successfully predict crop yields [41,42]. The strength of the relationships between VIs and crop yield is the fundamental premise to this. However, crop spectral reflectance varies with species and depends on the concentration of leaf pigments, soil moisture, biomass structure and ratio of light absorption to transmittance, management practices, and pest and disease outbreaks during crop growth [15,43].

Geostatistics encompasses a series of techniques of crucial importance in the assessment of spatial variability with both ground-based and remotely sensed data [44]. Owing to the discrete assessment of several crop traits, geostatistics serves to adapt them to the same grid size in order to compare them. In spatial studies, variograms are used as main geostatistical tool in the process of kriging. Kriging is one of the commonest techniques to estimate the prediction values from neighbouring actual values, a process known as interpolation [45,46]. Therefore, geostatistics was seen a valuable tool in the perspective of studying the relationship between remote VIs and ground-based crop features, as GY in this work.

Given the ample variation in the spectral composition of VIs, their variable performance at different growth stages of crops, and the resulting uncertainty, this study was intended to explore a significant number of remotely available VIs over a five-year period in a field hosting winter cereals and spring dicots alternating annually. Our specific objectives were to: (i) assess the spatial variability of the surveyed crop yields over five years; (ii) compare the behaviour of the targeted VIs during the growing season of each crop, in view of predicting final yield; (iii) select the best VIs in the five crops as cases for the study of spatial and temporal variability and relationship with final grain yield.

2. Materials and Methods

2.1. Experimental Site

The field site was located in the plain near Ravenna, Italy (44° 29′ 26″N, 12° 07′44″E, 0 m above sea level), a few kilometres from the Adriatic coast (Figure 1). An 11.07 ha experimental area was chosen within a larger field (ca. 25 ha) of the Agrisfera Cooperative. Soils in this area have a variable texture depending on changes in sediment dispersal patterns in response to fluctuating sea level [47]. To cope with the limited elevation and shallow water table, a network of underground draining pipes discharging into a ditch on the north side serves the field. The climate falls in the Mediterranean North environmental zone [48], with mild winter and a long growing season, although precipitation is mostly concentrated in the cold semester.

2.2. Field Data Collection

Five crops were cultivated in a rotation system in the crop seasons 2010–2014: durum wheat in 2010 (DW 2010), sunflower in 2011 (SF 2011), bread wheat in 2012 (BW 2012), coriander in 2013 (CO 2013), and bread wheat in 2014 (BW 2014). Seeding and harvest dates, and the resulting crop cycle durations are reported in

Table 1. Seeding and harvest dates, and crop cycle duration of cultivated crops.

Crop and Year	Botanical Name	Seeding	Harvest	Duration (d)
DW 2010	Triticum turgidum ssp. durum L.	30 October (2009)	10 July	253
SF 2011	Helianthus annuus L.	5 April	7 September	155
BW 2012	Triticum aestivum L.	14 October (2011)	1 July	261
C0 2013	Coriandrum sativum L.	11 April	10 July	90
BW 2014	Triticum aestivum L.	9 November (2013)	7 July	240

DW, durum wheat; SF, sunflower; BW, bread wheat; CO, coriander.

. Cultivation was based on the good practice for each specific crop, according to local conditions. Each year the field was ploughed in the summertime and harrowed in the autumn (the three years with DW or BW) or winter (SF and CO) for seedbed preparation.

At maturity, yield data were collected by a New Holland CR 9080 (CNH Industrial N.V., Basildon, UK) combine harvester using specific headers according to the crop. An average 6170 GY data points per year were registered in the 11.07 ha experimental area. Therefore, each GY pixel covered an average 18 m². The combine harvester was equipped with assisted guiding system based on real time kinematic GPS, yield mapping system consisting of a Pektron flow meter (Pektron Group Ltd, Derby, UK) and Ag Leader moisture sensor (Ag Leader Technology, Ames, IA, USA).

Spatial data of raw yield were saved through the Farm Works™ Mapping software (Trimble Navigation Ltd., Sunnyvale, CA, USA) and exported to ESRI shape file format to be handled in QGIS 2.18.20. Yield data were filtered using Yield Editor software to detect and remove outliers [49] and adjusted at 13% moisture for DW and BW and at 9% moisture for SF and CO. The crop data of each year were intersected with polygon field boundary layer.

2.3. Imagery Acquisition and Processing

Remotely sensed data from Landsat missions were used due to their frequency ensuring a dense time coverage in the investigated period. Landsat 5-Thematic Mapper (TM), Landsat 7-Enhanced Thematic Mapper Plus (ETM+), and Landsat 8-Operational Land Imager (OLI) have already been used in the monitoring of field crops over relatively small areas (6–11.5 ha) [50,51,52].

Collected Landsat (LS) images covered the following growth periods: 1 February–30 June for DW 2010 and BW 2012 and 2014; 1 May-31 August for SF 2011; 1 May–15 July for CO 2013. Landsat remote imagery were downloaded through US Geological Survey (USGS)-Earth Explorer website, a largest remote data network, using Collection Level-1, Tier 1, Precision Terrain (LITP) platform. This is an inventory structure for data collection, containing the highest quality Level-1 data suitable for time-series data record. Moreover, it gives access to all data as originally acquired and has an average revisiting time of 16 days. Landsat data archive equipped with 30 m spatial resolution was used for vegetation monitoring in the five years of the survey.

Specifically, multispectral images were retrieved by selecting the most recent Landsat mission available for each investigated year: LS-5 (TM) was used for DW 2010 and SF 2011, LS-7 (ETM+) for BW 2012, and lastly LS-8 OLI for SF 2013 and BW 2014 (

Table 2. Acquisition dates of Landsat satellite images and corresponding days after sowing (DAS) and growth stages (BBCH scale) in the five years.

Crop and Year	LS-Mission	Date	DAS	BBCH Stage	Description
DW 2010	LS-5 TM	13 March	134	31	Stem elongation (1st node visible)
		29 March	150	32	Stem elongation (2nd node visible)
		14 April	166	36	Stem elongation (6th node visible)
		30 April	182	43	Mid booting (flag leaf sheath initial swelling)
		7 May	189	55	Mid heading (half inflorescence emerged)
SF 2011	LS-5 TM	4 June	60	30	Beginning of stem elongation
		20 June	76	32	Two visibly extended internodes
		27 June	83	51	Inflorescence just visible amid young leaves
		22 July	108	67	Flowering decline (inner 3rd florets in bloom)
		14 August	131	75	Middle inflorescence seeds grey, at final size
BW 2012	LS-7 ETM+	17 March	155	33	Stem elongation (3rd node visible)
		26 March	164	36	Stem elongation (6th node visible)
		11 April	180	41	Early booting (flag leaf sheath extending)
		4 May	203	63	Flowering begun; anthers visible
		29 May	228	83	Early dough
CO 2013	LS-8 OLI	24 May	43	34	Main shoot reaching 30% of expected height
		9 June	59	55	First flowers of main inflorescence visible
		16 June	66	63	30% of flowers open
		25 June	75	71	First fruits formed
		2 July	82	81	Beginning of ripening (10% fruits ripe)
BW 2014	LS-8 OLI	8 March	119	32	Stem elongation (2nd node visible)
		31 March	142	37	Flag leaf just visible, still rolled
		25 April	167	55	Mid heading (half inflorescence emerged)
		18 May	190	77	Late milk
		3 June	206	85	Soft dough (grain content soft but dry)

DW, durum wheat; SF, sunflower; BW, bread wheat; CO, coriander; DAS, days after sowing.

). Landsat satellite scenes selection was carried out by accurately evaluating clear sky conditions and the quality of pixels in the field, by using the available data and metadata for each Landsat product.

Raster spectral bands (DNs) were converted to surface reflectance values by using the Semi-Automatic Classification Plugin [53] in QGIS by applying simple atmospheric correction under DOS1 method (Dark Object Subtraction 1) [54,55]. Although atmospheric correction for collection level-1 data is not univocally advised, it leads to an improvement in the results and makes the surface reflectance comparable among multi-temporal images [54].

Corrected raster images were intersected with polygon field boundary (11.07 ha), resulting in 126 data points extracted from each remote imagery with 30 m spatial resolution.

Crop stages at the respective dates were expressed with the BBCH scale that assigns a decimal code to the growth stages of mono- and di-cotyledonous plants [56]. A total of 25 images were used, i.e., 5 dates × 5 years.

All VIs were calculated through the algebraic combinations of reflectance values of red, infra-red and green portions of the electro-magnetic spectrum [41], based on the formulas presented in

Table 3. Vegetation indices used in this study, respective formulas, and literary sources.

Index	Description	Formula	Source
NDVI	Normalized difference vegetation index	(RNIR - RRed)/(RNIR + RRed)	[11]
EVI	Enhanced vegetation index	2.5(RNIR − Rred)/(RNIR + 6Rred – 7.5Rblue + 1)	[22]
SAVI	Soil adjusted vegetation index	(RNIR − Rred)(1 + L)/(RNIR + Rred + L)	[23]
GNDVI	Green normalized difference vegetation index	(RNIR − Rgreen)/(RNIR + Rgreen)	[24]
GCI	Green chlorophyll index	(RNIR/Rgreen) − 1	[25,30]
SR	Simple ratio	RNIR / Rred	[26]

R_NIR, reflectance in the near infrared band; R_red, reflectance in the red band; R_blue, reflectance in the blue band; R_green, reflectance in the green band; L, weighting coefficient = 0.25 (high vegetation density).

.

2.4. Analysis Methods

Georeferenced GY and remote VI data were subjected to geostatistical analysis (ArcGIS software version 10.3) to study the degree of spatial dependence in data distribution. The spatial dependence was calculated by means of empirical semivariogram, according to the following equation:

$$\gamma \left(h\right)=\frac{1}{2N\left(h\right)}+{\displaystyle \sum }_{i=1}^{N\left(h\right)}{[\mathrm{Z}\left(x_i\right)-Z\left(x_i+h\right)]}^2$$

(1)

Where $,\gamma$(h) is the semi-variance at a specified distance, h represents lag distance between two paired points, N(h) is the number of paired points at distance h, Z$\left(x_i\right)$ is the measured value at location x_i, and Z(x_i + h) denotes the secondary value measured at locations $x_i$ + h separated by the given distance (h) [57].

The experimental variogram was fitted by means of the spherical, exponential, linear, and Gaussian models. The spherical model exhibited a goodness of fit that was not surpassed by the other models and was, therefore, chosen. The spherical model, thanks to a well-defined sill, easily-interpreted range, and mathematical simplicity, is considered one of the best models for soil or plant variability fitting [45,46,58,59,60].

Directional sample variograms were also computed for the canonical directions 0, 22.5, 45, 90, 135 degrees. Resulting variograms exhibited similar shapes, leading to the conclusion that directional effects were negligible/absent. Therefore, there was no evidence of spatial anisotropy potentially leading to wrong interpretation in data analysis.

In the spherical model, the following equations are applied:

$$\gamma \left(h\right)=0\mathrm{for}h=0$$

(2)

$$\gamma \left(h\right)=C_0+C\left(\frac{3h}{2a}- \frac{h^3}{2a^3}\right)\mathrm{for}0<h\le a$$

(3)

$$\gamma \left(h\right)=C_0+C\mathrm{for}h>a$$

(4)

Where: C₀ is the nugget, C₀+C is the sill, a is the range, and h is the separation lag distance [45].

Three parameters need to be defined while fitting the theoretical model to the experimental semivariogram: (i) nugget effect (C₀), representing the error or variation in the measurement at minimum sampling distance (h = 0), i.e., the background effect; (ii) sill variance (C₀ + C), composed of C₀ (nugget variance) and C (structural variance), which is the maximum y-axis value increase with lag distance and remains constant beyond distance h; (iii) spatial dependence range (a), indicating the maximum limit at which data points are still spatially correlated and the semi-variogram reaches the sill value; beyond that limit no spatial auto-correlation can be demonstrated.

We classified the strength of spatial dependence (SD) into three groups by calculating the percent nugget (C₀) to sill (C₀ + C) ratio according to Cambardella et al. [61]: (i) <25%, indicating strong SD; (ii) 25% to 75%, moderate SD; (iii) >75%, weak SD.

Through semivariograms, spatial yield maps were produced by simple kriging with 10 m cell size to extrapolate the values to non-sampled field parts [62]. Simple kriging was preferred over ordinary kriging because the mean value was known, which is the premise for a better estimate of the variance. Simple kriging is considered a realistic interpolation method: It provided highest R² and minimal error parameters among seven methods in environmental characteristics [60,63] and in the estimation of crop yield [64].

GY data referred to 1106 pixels (10 m cell size) and VI data referred to 126 pixels (30 m cell size) acquired in the 11.07 ha experimental field were submitted to descriptive statistics including mean, median, minimum, maximum, standard deviation (SD), and coefficient of variation (CV). Kolmogorov–Smirnov test was applied to ascertain the normal distribution in the data sets.

Kriged maps of crop yield were aggregated at the same 30 m cell size as the spatial resolution of satellite imagery [42]. Then, raster maps were converted into point data to assess the relationships between remote imagery and crop yields, i.e., between VIs and GY in each respective year, by means of Pearson’s correlation [65]. The best times/crop stages for the prediction of final yields were acknowledged as those featuring the highest correlations for all the indices averaged [66,67]. The vegetation index showing the highest correlation with yield was selected from each date falling within these stages in each crop. When two VIs exhibited the same r value, both were selected. Based on this, a series of representative VIs were retained as study cases for each year, and further processed.

Geostatistics (ArcGIS software version 10.3) was applied on GY and selected VIs, in order to describe the data distribution of remote VIs and GY data in terms of semivariogram through the above described spherical model. The intrinsic variation in these two sets of variables was assessed based on their spatial dependence across the field. Geostatistics also served in the analysis between original VI data and kriged GY data for the determination of correspondence levels and final agreement between them.

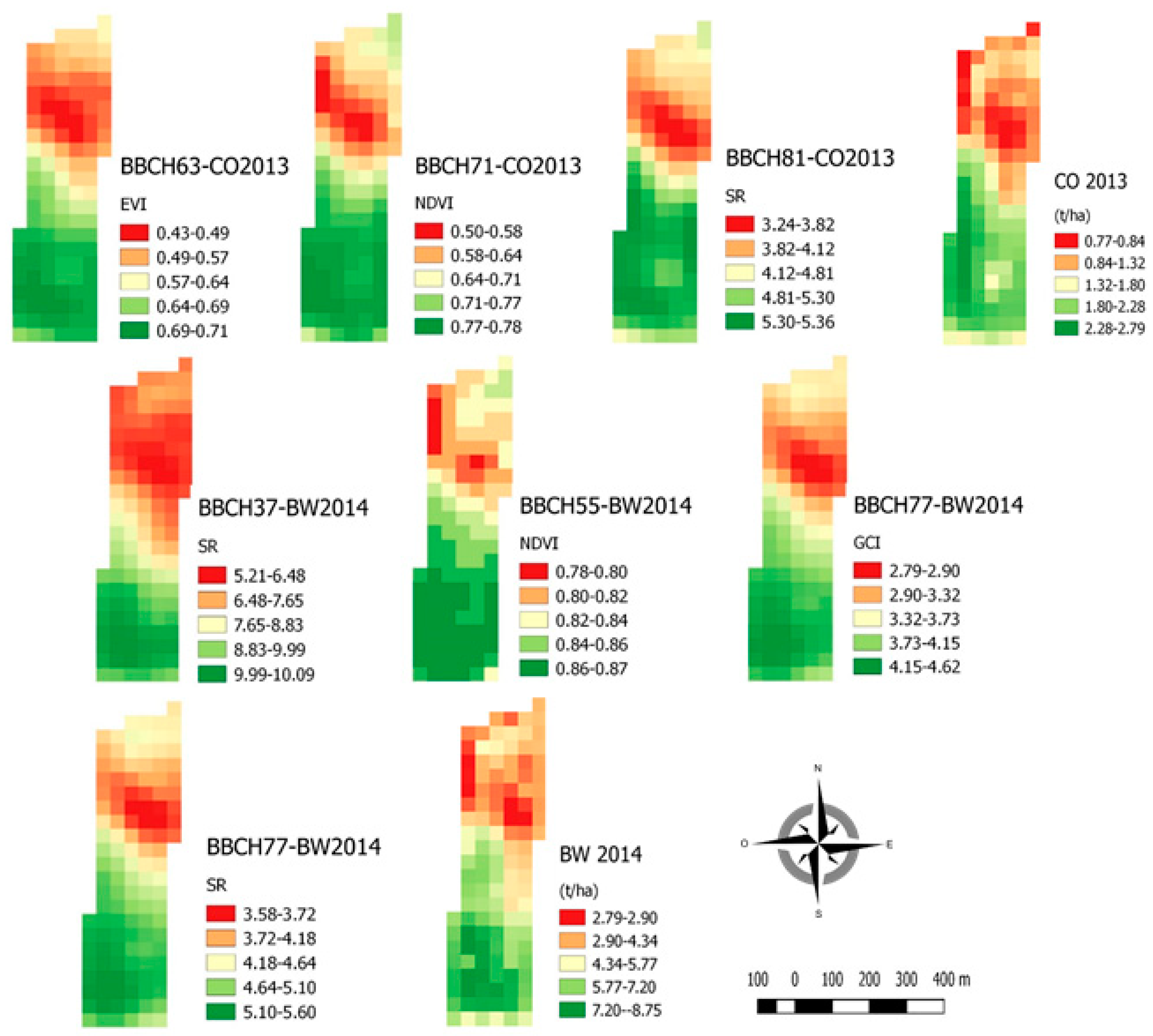
Spatial maps of remote VIs and GY were shown with the same 30 m cell size [62]. A colour scale was chosen based on quantile classification for all maps produced in this study. All maps were georeferenced and co-registered in reference system of WGS 84/UTM zone 32N-EPSG: 32,632.

The prediction accuracy of VI and GY data was assessed with the spherical model in terms of coefficient of determination (R²) of model-predicted vs. actual observations [68,69], while mean absolute error (MAE) and root mean square error (RMSE) were calculated through kriged residuals [70]. The mean relative error (MRE) and relative RMSE (RRMSE) were calculated as percent ratios on the average VIs and GY values, respectively. Maximum R² and minimal error parameters are associated with best model accuracy [63].

After analysing the spatial dependence within VIs and GY data, we investigated the correspondence between them. The correspondence levels were calculated as the proportion of pixels belonging to same remote imagery and crop yield class. To represent the relative similarity between them, remote imagery and crop yield data were classified from lowest to highest values into five classes (i.e., quintiles) of equal frequency over the entire field. Then, the correspondence levels and final agreement (%) between each VI and GY were determined as described by Stępień et al. [71]: For a given pixel, if the class of VI quantile was the same as that of GY quantile, the correspondence was considered ‘high’ with value 1; if the class of VI and GY belonged to adjacent quantiles, the correspondence was considered ‘medium’ with value 0.5; if the class of VI and GY quantile were separated by more than one class, the correspondence was considered ‘low’ with value 0. Based on this, final agreement was calculated as the sum of pixel agreement scores, according to the formula:

$${\mathrm{F}}_{\mathrm{a}}=\frac{\left({\mathrm{P}}_{\mathrm{h}}·1.0\right)+\left({\mathrm{P}}_{\mathrm{m}}·0.5\right)+\left({\mathrm{P}}_{\mathrm{l}}·0\right)}{{\mathrm{P}}_{\mathrm{t}}·100}$$

(5)

Where: F_a = final agreement (%); P_h = number of pixels with high agreement; P_m = number of pixels with medium agreement; P_l = number of pixels with low agreement; P_t = total number of pixels.

The coefficient of variation of F_a was also calculated as the standard deviation of correspondence levels in percent of their mean.

3. Results

3.1. Descriptive Statistics of Crop Yields

Descriptive statistics of crop yields in the five years is reported in

Table 4. Descriptive statistics of crop yields (t ha⁻¹) in the five years.

Crop and Year	Mean	Median	Min.	Max.	SD	CV %	K-S
DW 2010	4.26	4.26	1.77	6.05	0.99	23.2	**
SF 2011	1.45	1.44	0.23	2.99	0.41	28.6	**
BW 2012	4.26	4.27	1.68	6.07	0.99	23.3	**
CO 2013	1.83	1.90	0.71	2.86	0.58	31.7	**
BW 2014	5.91	5.81	2.50	9.08	1.66	28.2	**

DW, durum wheat; SF, sunflower; BW, bread wheat; CO, coriander; Min., minimum; Max., maximum; SD, standard deviation; CV, coefficient of variation; K-S, Kolmogorov–Smirnov test for normal distribution; **, significant at P ≤ 0.01.

. In wheat, mean GY ranged between 4.26 and 5.91 t ha⁻¹. The lower GY was referred to DW 2010 and BW 2012 that showed the same mean data, whereas the higher GY was related to BW 2014. The two dicots (SF 2011 and CO 2013) were comparatively much less productive, attaining less than 2 t ha⁻¹ mean GY. An ample variation in yield data was described by all crops, resulting in a standard deviation that, proportioned to GY, determined a CV value ranging between 23.2% (DW 2010) and 31.7% (CO 2013).

3.2. Descriptive Statistics of Remote Indices

The five years’ remote indices are described in

Table 5. Mean value of remote vegetation indices and Pearson’s correlations (r) with crop yields in the five years. VIs with best correlations with GY are highlighted.

Crop and Year	BBCH Stage	NDVI		EVI		SAVI		GNDVI		GCI		SR
		Mean	r	Mean	r	Mean	r	Mean	r	Mean	r	Mean	r
DW 2010	31	0.29	0.843 **	0.31	0.755 **	0.17	0.764 **	0.21	0.767 **	0.53	0.764 **	1.72	0.762 **
	32	0.29	0.814 **	0.33	0.795 **	0.19	0.783 **	0.23	0.778 **	0.60	0.774 **	1.72	0.788 **
	36	0.59	0.878 **	0.49	0.816 **	0.30	0.818 **	0.39	0.822 **	1.33	0.816 **	2.93	0.816 **
	43	0.71	0.878 **	0.66	0.819 **	0.40	0.822 **	0.49	0.826 **	2.06	0.823 **	4.14	0.825 **
	55	0.66	0.294 **	0.73	0.444 **	0.44	0.454 **	0.51	0.400 **	2.10	0.431 **	4.01	0.405 **
SF 2011	30	0.47	0.395 **	0.51	0.509 **	0.32	0.475 **	0.37	0.429 **	1.19	0.446 **	2.42	0.536 **
	32	0.66	0.614 **	0.90	0.707 **	0.52	0.700 **	0.53	0.688 **	2.33	0.687 **	4.17	0.684 **
	51	0.70	0.736 **	0.76	0.745 **	0.49	0.749 **	0.55	0.751 **	2.49	0.748 **	4.53	0.742 **
	67	0.52	0.672 **	0.54	0.725 **	0.34	0.716 **	0.40	0.712 **	1.39	0.718 **	2.81	0.729 **
	75	0.28	0.317 **	0.24	0.375 **	0.16	0.351 **	0.22	0.341 **	0.57	0.320 **	1.62	0.459 **
BW 2012	33	0.47	0.793 **	0.45	0.801 **	0.25	0.788 **	0.33	0.767 **	1.00	0.766 **	2.28	0.801 **
	36	0.54	0.710 **	0.34	0.854 **	0.18	0.852 **	0.14	0.838 **	0.60	0.852 **	1.89	0.854 **
	41	0.52	0.783 **	0.30	0.773 **	0.10	0.742 **	–0.73	0.698 **	0.21	0.639 **	1.21	0.631 **
	63	0.80	0.870 **	0.11	0.611 **	0.45	0.586 **	0.53	0.519 **	2.61	0.717 **	4.87	0.760 **
	83	0.51	0.307 **	0.54	–0.273ns	0.28	−0.317ns	0.32	−0.332ns	1.05	−0.324ns	2.33	−0.294ns
CO 2013	34	0.08	0.555 **	0.27	0.268 **	0.08	0.377 **	0.11	0.213 **	0.24	0.214 **	1.17	0.555 **
	55	0.33	0.800 **	0.43	0.480 **	0.28	0.805 **	0.37	0.793 **	1.16	0.806 **	2.01	0.812 **
	63	0.62	0.856 **	0.59	0.920 **	0.43	0.917 **	0.60	0.907 **	3.06	0.911 **	3.34	0.915 **
	71	0.68	0.902 **	0.64	0.861 **	0.53	0.861 **	0.67	0.861 **	4.19	0.866 **	5.86	0.868 **
	81	0.65	0.914 **	0.63	0.886 **	0.45	0.879 **	0.62	0.912 **	3.36	0.927 **	4.52	0.932 **
BW 2014	32	0.69	0.886 **	0.45	0.844 **	0.41	0.844 **	0.60	0.849 **	3.11	0.843 **	5.05	0.845 **
	37	0.79	0.932 **	0.59	0.922 **	0.61	0.925 **	0.59	0.930 **	2.97	0.925 **	7.49	0.935 **
	55	0.84	0.926 **	0.78	0.873 **	0.57	0.870 **	0.72	0.879 **	5.13	0.881 **	6.26	0.873 **
	77	0.81	0.909 **	0.59	0.927 **	0.49	0.925 **	0.65	0.918 **	3.85	0.934 **	4.78	0.934 **
	85	0.40	−0.681ns	0.38	0.562 **	0.28	0.167ns	0.40	−0.482ns	1.43	−0.404ns	2.43	−0.540ns

DW, durum wheat; SF, sunflower; BW, bread wheat; CO, coriander; ns, non-significant; **, significant at P ≤ 0.01.

.

In DW 2010, the six VIs in the five growth stages ranging from beginning of stem elongation to heading (Table 2) outlined the mean values reported in Table 5. The complete descriptive statistics of this year’s data is shown in the supplementary material (Table S1). Mean values augmented until a peak at BBCH stage 43–55. Mean and median values were always very close, never diverging by more than 5%. VI variation was more contained than GY variation in the same year (Table 4): Average CV was 12.3%, and highest CV reached 23.9%. Lastly, data were more often normally distributed (non-significant Kolmogorov–Smirnov test in 23 cases out of 30).

In SF 2011, the six VIs in the five growth stages ranging from beginning of stem elongation to seed ripening (Table 2) exhibited the mean values reported in Table 5. The complete descriptive statistics of this year’s data is shown in the supplementary material (Table S2). Mean values increased until a peak at approximately BBCH stage 51 (inflorescence just visible), although EVI staged higher value at BBCH stage 30. Mean and median values never diverged by more than 6%. VI variation was more contained than GY variation in the same year (Table 4): Average CV was 11.2%, and highest CV was 20.5%. Data were almost equally divided between normally distributed (17 cases out of 30) and non-normally distributed (the remaining 13 cases).

In BW 2012, the six VIs in the five growth stages ranging from mid-stem elongation to early dough ripening (Table 2) staged the mean values reported in Table 5. The complete descriptive statistics of this year’s data is shown in the supplementary material (Table S3). Mean values increased until a peak at BBCH stage 63 (anthesis), except EVI that showed a very low value at this stage and peaked at BBCH stage 83 (early dough). Mean and median values sometimes diverged, especially at BBCH stage 41. Data variation was also fluctuating: Average CV was 31.9%, but CV values above 100% were also recorded. Lastly, data were normally distributed only in 2 cases out of 30.

In CO 2013, the six VIs in the five growth stages ranging from mid-stem elongation to beginning of ripening (Table 2) showed the mean values reported in Table 5. The complete descriptive statistics of this year’s data is shown in the supplementary material (Table S4). Mean values increased until BBCH stage 71 (fruiting). Mean and median values never diverged by more than 4%. VI variation was more contained than GY variation in the same year (Table 4): Average CV was 9.4%, and highest CV was 22.5%. Despite this, data were normally distributed only in 5 cases out of 30.

In BW 2014, the six VIs in the five growth stages ranging from early stem elongation to soft dough ripening (Table 2) featured the mean values reported in Table 5. The complete descriptive statistics of this year’s data is shown in the supplementary material (Table S5). Mean values increased until BBCH stage 55 (heading). Mean and median values were generally similar; only in three cases they diverged by 10% to 13%. VI variation was more contained than GY variation in the same year (Table 4): average CV was 13.2%, and highest CV was 30.2%. Nonetheless, data were normally distributed only in 3 cases out of 30.

3.3. Correlations and Choice of Representative Vegetation Indices

In this experiment, Pearson’s correlations between VIs and GY in the five years are reported in Table 5. High, statistically significant r values were generally obtained, indicating that remote indices across variable growth stages were aligned with final yields. We visually checked all correlations (graphs not reported in MS) to spot if any cloud of data outlined a curvilinear relation, finding none.

At growth stages of incipient senescence (BBCH>80), VIs were insignificantly/negatively correlated with GY (BW 2012 and 2014), because senescence encourages the breakdown of pigments that influence the reflectance properties of leaf canopy.

Overall, the three wheat crops (DW 2010, BW 2012 and 2014) staged r values above 0.700 in the average of the six VIs at BBCH stages not exceeding 50, i.e., before heading (Table 5). Afterwards, the r values sharply declined in DW 2010 (at BBCH 55, average r = 0.405), whereas in BW 2012 and 2014 they remained quite high until the mid-60s and mid-70s BBCH stages, respectively. Owing to the morph-physiological similarity between durum and bread wheat, it is sensed that the different behaviour was due to different ambient conditions during the reproductive phase in 2010 vs. 2012 and 2014.

In contrast to wheat, the two dicot species (SF 2011 and CO 2013) staged r values above 0.700 in the average of the six VIs at BBCH stages >50, i.e., during the reproductive phase (Table 5). SF 2011 maintained r values above 0.700 until the mid-reproductive phase (BBCH 67), whereas CO 2013 remained well above this threshold until later stages (BBCH 81).

Based on the procedure described in Section 2.4, the 2-4 VIs with best correlations with GY (highlighted in Table 5) were selected each year as representative study cases. They covered growth stages from BBCH 33 to BBCH 81. SR and NDVI were the two indices most frequently chosen, six and four times, respectively. At the opposite end, SAVI never exhibited correlations high enough to be included in the list.

3.4. Spatial Variability in Crop Yields

Analysis of the spherical semivariogram fitted to GY data is reported in

Table 6. Parameters of the spherical model used to fit the experimental semivariograms of crop yields and model performance in the five years.

Crop and Year	C0	C0+C	a (m)	SD	R2	MAE	RME %	RMSE	RRMSE (%)
DW 2010	0	0.92	66.96	S	0.98 **	0.09	2.2	0.14	3.3
SF 2011	0.35	1.02	73.59	M	0.71 **	0.15	10.6	0.22	15.5
BW 2012	0	0.92	65.90	S	0.98 **	0.09	2.2	0.14	3.3
CO 2013	0.02	1.09	99.87	S	0.99 **	0.05	2.6	0.07	3.6
BW 2014	0.007	1.08	85.89	S	0.99 **	0.13	2.2	0.18	3.1

DW, durum wheat; SF, sunflower; BW, bread wheat; CO, coriander; C₀, nugget effect; C, structural variance; C₀+C, sill variance; a, range; SD, spatial dependence (S, strong; M, moderate); **, significant at P ≤ 0.01; MAE, mean absolute error; MRE, mean relative error; RMSE, root mean square error; RRMSE, relative root mean square error.

. The lag distance was between 6.79 and 9.97 m, (data omitted in Table 6), depending on a particular crop of the year. SF 2011 was the crop showing the strongest background effect (C₀) on total (C₀+C) variance, associated with a high CV (Table 4). Compared to this, the very low C₀ weight on C₀+C indicates almost no discontinuity in the other four crops’ spatial structure. The five crops exhibited a sill comprised between 0.92 (DW 2010 and BW 2012) and 1.09 (CO 2013), meaning a quite similar total variance. However, the range of the spatial dependence varied amply, being comprised between 65.90 m (BW 2012) and 99.87 m (CO 2013). Finally, the proportion between the two components, nugget to sill variance, varied considerably between SF 2011 where C₀ represented 34% of C₀+C, and the other four crops where C₀ represented 0% to 2% of C₀+C. As a result, SF 2011 can be considered a case of moderate spatial dependence, whereas the other four crops featured strong spatial dependence [61].

The performance of the spherical model in the 5 years was generally good (Table 6). R² was always highly significant, ranging between 0.71 and 0.99, while the two error terms (MAE and RMSE) were low. This is especially true with respect to GY means (Table 4), resulting in relative error terms (MRE and RRMSE) that were between 2.2% and 10.6% (MRE) and between 3.1% and 15.5% (RRMSE).

Yield maps exhibited a quite similar pattern in the five years, as shown in Figure 2. The north side of the field always featured a lower GY than the south side. Especially the three years with wheat (DW 2010, BW 2012 and 2014) behaved in a similar way with lowest yield rank in the north-central portion of the field, and highest yield rank in the south–southwestern portion. Compared to this, the two spring sown crops (SF 2011 and CO 2013) exhibited a slightly wider area of low GY in the north portion of the field. These two crops also featured higher CV (Table 4), i.e., higher yield variation than the three wheat crops.

3.5. Spatial Variability in Remote Vegetation Indices

Analysis of the spherical semivariogram fitted to VI data is reported in

Table 7. Parameters of the spherical model used to fit the experimental semivariograms of remote vegetation indices and model performance in the five years.

Crop and Year	BBCH Stage	C0	C0+C	a (m)	SD	R2	MAE	RME (%)	RMSE	RRMSE (%)
						NDVI
DW 2010	36	0	1.32	142.50	S	0.99 **	0.006	1.0	0.009	1.5
	43	0	1.23	142.50	S	0.99 **	0.007	1.0	0.010	1.4
						GNDVI
SF 2011	51	0	1.42	149.43	S	0.99 **	0.004	0.7	0.005	0.9
						SR
	67	0	1.27	115.97	S	0.98 **	0.050	1.8	0.070	2.5
						EVI
	33	0	1.29	149.43	S	0.99 **	0.006	1.2	0.007	1.6
BW 2012	36	0	1.23	108.84	S	0.99 **	0.011	3.2	0.019	5.6
						SR
	33	0	1.25	147.08	S	0.99 **	0.016	0.7	0.020	0.9
	36	0	1.28	115.05	S	0.99 **	0.037	2.0	0.060	3.2
						EVI
	63	0	1.38	149.43	S	0.99 **	0.005	0.8	0.007	1.2
CO 2013						NDVI
	71	0	1.31	154.25	S	0.98 **	0.006	1.0	0.010	1.5
						SR
	81	0	1.35	154.25	S	0.99 **	0.038	0.8	0.060	0.8
						SR
	37	0	1.25	134.67	S	0.99 **	0.069	0.9	0.14	1.9
						NDVI
BW 2014	55	0	1.18	113.91	S	0.95 **	0.004	0.5	0.005	0.6
						GCI
	77	0	1.32	149.43	S	0.99 **	0.025	0.6	0.050	1.3
						SR
	77	0	1.32	149.43	S	0.99 **	0.030	0.6	0.060	1.3

DW, durum wheat; SF, sunflower; BW, bread wheat; CO, coriander; C₀, nugget effect; C, structural variance; C₀+C, sill variance; a, range; SD, spatial dependence (S, strong) _**, significant at P ≤ 0.01; MAE, mean absolute error; MRE, mean relative error; RMSE, root mean square error; RRMSE, relative root mean square error.

. The lag distance was between 8.17 and 15.30 m (data omitted in Table 7), depending on specific VI, crop and stage. The nugget (C₀) was always nil, indicating continuous spatial dependence of data over distance [44]. The sill (C₀+C) was comprised between 1.18 (NDVI in BW 2014 at BBCH stage 55) and 1.42 (GNDVI in SF 2011 at BBCH stage 51). The range was comprised between 108.84 m (EVI in BW 2012 at BBCH stage 36) and 154.25 (NDVI and SR in CO 2013 at the respective BBCH stage 71 and 81). Finally, owing to nil nugget effect, the spatial dependence was always strong, i.e., 100% of the sill was associated with the structural component (C).

The performance of the spherical model in the 15 cases was good under all viewpoints (Table 7). R² was always ≥0.95, and the two error terms (MAE and RMSE) were low, especially with respect to mean VI values (Table 5). In fact, the relative error terms (MRE and RRMSE) were comprised between 0.6% and 5.6% of the mean.

In Figure 3, remote VI maps and the respective GY maps are depicted at the same cell size (30 m). A palette of five colours indicates values ranging from very low (red) to very high (dark green), passing through low (orange), medium (yellow) and high (light green). The 15 VIs, whose choice was based on their correlations with yield (Table 5), also from a spatial viewpoint described a pattern across the study area consistent with crop yield pattern: lower values in the north portion of the field, and conversely higher values in the south–southwestern portion.

Some VIs at specific growth stages evidenced sharp differences between the two areas, as in the case of EVI and SR at BBCH 36 in BW 2012. Some other VIs depicted faded differences, as SR at BBCH 67 in SF 2011. However, spatial maps visually demonstrate that a small number of high remote VIs were associated with low final GY and vice versa.

3.6. Correspondence between Remote Vegetation Indices and Crop Yields

The apparent similarity in spatial pattern and geostatistical structure between VIs and GY is the premise for assessing the correspondence between remote indices and crop yields at the same pixel level (

Table 8. R², correspondence levels, final agreements, and respective coefficients of variation between VIs and GY.

Crop and Year	BBCH Stage	R2	Correspondence Level (%)			Fa (%)	CV (%)
			High	Medium	Low
				NDVI
DW 2010	36	0.77 **	53	41	6	73	41.9
	43	0.77 **	51	42	7	72	43.6
				GNDVI
SF 2011	51	0.56 **	42	47	11	65	50.6
				SR
	67	0.53 **	44	40	16	64	56.4
				EVI
	33	0.49 **	40	50	10	65	49.9
BW 2012	36	0.73 **	49	41	10	70	47.1
				SR
	33	0.64 **	43	48	9	67	47.3
	36	0.73 **	48	43	9	70	46.2
				EVI
	63	0.85 **	53	43	4	75	38.6
CO 2013				NDVI
	71	0.81 **	58	36	6	76	39.6
				SR
	81	0.87 **	71	26	3	84	31.9
				SR
	37	0.87 **	70	30	0	85	27.1
				NDVI
BW 2014	55	0.86 **	59	38	3	78	36.0
				GCI
	77	0.87 **	67	30	3	83	31.9
				SR
	77	0.87 **	72	27	1	86	27.5

DW, durum wheat; SF, sunflower; BW, bread wheat; CO, coriander; F_a, final agreement; CV., coefficient of variation; **, significant at P ≤ 0.01 (n = 126).

). In the 15 cases, high correspondence ranged between 42% and 72%, medium correspondence between 27% and 50%, and low correspondence between 1% and 16%. The resulting F_a ranged between 64% and 86%. Highest agreement was observed in BW 2014 (average of 4 VIs, 83%), lowest in SF 2011 (average of two VIs, 65%).

4. Discussion

The CV data related to mean GY in the five years (Table 4) denote high yield variation, based on a CV threshold of 20% indicating high variation in field attributes [72]. This was a favourable circumstance in the present study, allowing us to appraise crop behaviour under conditions of sizeable spatial variability. Despite high CV, median GY in the five years was quite close to mean GY, differing from this latter by no more than ±4%. However, in all five years GY data were not normally distributed (significant Kolmogorov–Smirnov test), although normality is not a prerequisite for kriging interpolation [57].

In general, crop yield variation reflects the interactions among soil-related factors or topography [73]. Moreover, variation within the same plant genus (e.g., wheat) may be due to several factors as growth response to the amount of rainfall during specific crop stages, owing to the fact that wet years favour biomass accumulation thanks to higher soil water availability [58].

The similar spatial patter exhibited by yield maps across the five years (Figure 2) is echoed in a previous survey on a narrower portion (4.15 ha) of the same field [74]. In that work, soils in the northern part were shown to be quite sandy and poor in organic matter. It is evinced, therefore, that under rainfed cultivation the two spring crops (SF and CO) may have suffered stronger drought during the reproductive stage in the summer time, compared to the three wheat crops sown in the autumn and maturing in the springtime.

High values of the six VIs in the respective scales indicate healthy, well growing crops. However, high VI values alone are not always good predictors for high GY because higher canopy biomass prior to grain filling only contributes to good growth status, possibly due to adequate water availability, which is not always a prerequisite for maximum grain production [75].

Notwithstanding this, the good correlations between VIs and GY (Table 5) are a remarkable outcome, considering that mono-cotyledonous (DW and BW) and di-cotyledonous (SF and CO) crops have different reflectance properties due to differences in leaf mesophyll cells and structure of front and back leaf side [76]. In other works, this has resulted in remote VIs behaving crop specifically according to leaf canopy structure [37].

The different relationships between VIs and GY in winter wheat (DW 2010, BW 2012 and 2014) vs. the two spring dicots (SF 2011 and CO 2013), consisting in the former crop showing better correlations in the vegetative phase and the latter two crops in the reproductive phase (Table 5), is at least partially associated with the time elapsed from seeding to the stage at which good correlations were found. In fact, wheat is cultivated as winter crop while sunflower and coriander can only be cultivated as spring crops in the specific climate [48]. It results that wheat cycle lasted an average 251 days from seeding to harvest, while sunflower cycle lasted 155 days and coriander cycle only 90 days (Table 1). Wheat scored the best correlations in the three years combined (Table 5) between 119 DAS (BBCH 32 in BW 2014) and 180 DAS (BBCH 41 in BW 2012) (Table 2). Sunflower scored the best correlations from 83 to 108 DAS and coriander from 59 to 82 DAS (Table 2). Thus, the two dicots had been living for a shorter time, although they had reached a more advanced stage (Table 2). It is perceived, therefore, that the long time passed when the first VIs were acquired in wheat may have served the plant to better sense the environmental differences within the field and translate them into a spectral response in agreement with the final yield. The two spring dicots featuring a shorter cycle also necessitated a certain amount of time to experience the same differences, and good correlations between VIs and GY were achieved at later stages. However, we have not found other works addressing this point, meaning that these findings are not echoed in the literature, to our best knowledge. Therefore, further evidence is needed to corroborate this hypothesis.

All the VIs acquired in these two time frames specific for wheat and spring dicots performed in a similar way. Assuming r = 0,700 as the threshold for good correlation, NDVI, GNDVI, GCI, SR, and EVI fell below this value only once (Table 5). However, even in that case NDVI, GNDVI, GCI, and SR decreased to levels slightly lower than this threshold (r between 0.631 and 0.698, depending on VI), whereas EVI plummeted to r = 0.480 in CO 2013 at BBCH 55 (Table 5). Compared to them, SAVI never fell below this threshold. Therefore, the choice of the best VI was not so critical within a suitable time frame, despite relevant differences in spectral composition and calculation formula.

Several works were found similar to our study, i.e., remote VIs successfully estimated spatial crop yields; Labus et al. [77] found a strong relationship (R² = 75.3%) between NDVI and wheat yield. Herbei and Sala [52] studied the relationship between growth stages and VIs in sunflower and found a maximum correlation with NDVI (R² > 0.97) at flowering, followed by a decline at maturity. Plant et al. [40] explained that NDVI is sensitive to canopy reflectance decreasing its correlation with cotton yield over a small field area. Yields of wheat, maize, rice, sugarcane, and soybean were also successfully estimated by means of NDVI [67,78,79]. After positive achievements with NDVI, other VIs proved also effective in the estimation of different crop yields [15,24,41,42,51,80,81].

The good performance of the spherical model in fitting GY experimental semivariograms (Table 6) is consistent with the equally good performance of the same model in fitting VI experimental semivariograms (Table 7). The higher sill values in the model structure of VI semivariograms is assumed to indicate a higher percentage of canopy cover because young plants have less contrast in reflected light spectra resulting in lower sill variance [82]. However, at growth stages less than BBCH 30, as in our 15 cases (Table 7), full canopy cover is normally achieved, resulting in a random variation of sill data. Additionally, VI ranges largely exceeded GY ranges (Table 6), indicating a farther reaching spatial dependence of VI vs. GY data. This, in turn, supports the adoption of the 30 m Landsat resolution also for GY data to be compared [82]. Lastly, geostatistical analysis indicates a strong spatial dependence of VIs over distance (h), and the same was shown in GY data. In both cases, this is the premise for a continuous appraisal of the investigated traits over field surface.

In accordance with the similarities shown in spatial pattern and geostatistical analysis, final agreement between remote indices and crop yields at pixel level (Table 8) was, unsurprisingly, related to the R² values between VIs and GY obtained from the r values reported in Table 5. More surprisingly, F_a data appeared to be adversely related to F_a coefficient of variation (Table 8). In other words, very good agreement was obtained when the variation among the three correspondence levels (high, medium, low) was limited, as in the case of SR at BBCH stage 37 and 77 in BW 2014 (F_a, 85% to 86% with respective CV, 27.1% to 27.5%). Conversely, a modest agreement was obtained when strong variation occurred among the three correspondence levels, as in the case of SR at BBCH stage 67 in SF 2011 (F_a, 64% with CV, 56.4%). In theory, F_a and CV are reciprocally independent, i.e., high F_a could also be obtained with high CV and vice versa. This finding is of non-univocal interpretation and, to our knowledge, has not been reported so far in the literature.

Several reasons can explain why VI ranking into quintiles does not fully match the same ranking of GY data. Water availability, nutrient uptake, crop management practices, weather conditions, pests and diseases, etc., can influence growth status and final yield to a different extent: Resilience can be shown when a crop withstands unfavourable growth conditions (low VI values), attaining a fairly good yield. Conversely, rigidity is shown when slightly unfavourable growth conditions (relatively high VI values) result in poor yield. This latter case is also determined by the fact that GY may be reduced also when above-ground biomass is not significantly reduced.

An overall F_a of 74% (Table 8) is nevertheless a good outcome: It means that almost ¾ of the 126 cells belong to the same VI and GY quintile, despite ample variation in both VI and GY data.

There is still no general consensus in the use of rank comparison between spatially variable GY and remotely sensed VIs. In soybean [81], the combined SR and SAVI together with soil elevation concurred to delineate management zones reflecting significant differences in final yield and soil properties. More generally, in winter cereals (barley and wheat), NDVI from Landsat as well as higher resolution satellites (QuickBird and WorldView-2) proved effective in describing yield spatial variability, especially at the onset of the reproductive stage [83]. The same happened in winter oilseed rape with the Enhanced Moisture Stress Index [80]. No other hint of rank comparisons between VIs and GY can be found in the literature to our best knowledge.

The relationships (r and R² values) between VIs and final GY in the three cited sources [80,81,83] are no better, in general, than those found in the present study (Table 8). In this light, the above discussed data of F_a (Table 8) may be considered encouraging and set the premise for a larger use of remote (satellite) imagery in the interpretation and subsequent management of crop spatial variation.

In this respect, the combined use of Sentinel-2A and Landsat data, providing a larger number of data and a higher spatial resolution, would foster a more detailed assessment that could be especially useful in identifying growth stages in different crops [84]. Data fusion from different platforms would overcome drawbacks related to the use of a single, medium-resolution satellite by improving the field temporal sampling.

Lastly, the use of Landsat collection level-1 data raises the issue of atmospheric data correction. In our study, we decided to apply a simple correction as the DOS1 method despite the good quality data (Level-1, Tier 1, Precision Terrain platform), to ensure comparability of surface reflectance among multi-temporal images [54,85]. More sophisticated models for atmospheric correction, as those distributed by USGS under Climate Data Records, were not adopted, as we could not collect specific in-field measurements. However, usefulness of atmospheric correction is questioned due to the risk of adding more errors [86], which is especially true in the case of large areas surveyed.

5. Conclusions

Landsat satellite imagery with its spatial and temporal resolution exhibited a good potential for estimating the final GY over different crops in a chronological rotation, at a relatively small field scale (11.07 ha). This is further stressed by the circumstance that the spatial resolution provided by the Landsat system (30 m) was shown sufficient to characterize crop variation across a field of moderate extension. This sets the premise for a wider use of satellite data in yield predictions during the growing season, beside their role in supporting site specific management of crop practices.

Simple ratio and NDVI were the two VIs most frequently selected as best indices, compared to EVI, SAVI, GNDVI, and GCI across stages ranging from vegetative (BBCH ~30s) to reproductive phase (BBCH ~70s). In contrast to this, SAVI never exhibited correlations with yield high enough during these stages, to be included among best VIs. Pixel level study demonstrated a generally good agreement between the five classes of VIs, on one side, and those of GY, on the other side.

Beside these 15 cases showing the best correlations with yield, two specific time frames were identified for winter wheat and the two spring dicots, showing high and consistent correlations between all remote indices, in general and final yields. Based on our data, this sets the premise for a reliable use of VIS in yield predictions. Outside these time frames, the relationships between VIs and GY are less consistent, and subjected to factors of difficult interpretation.

Future monitoring possibilities fostered by the Copernicus Sentinel 2 mission from the European Space Agency will allow imagery to be acquired from the year 2015 onwards, with spectral channels aligned with Landsat and Spot satellites. Improvements are expected from a higher spatial resolution (10–20 m) and radiometric resolution (reflectance registered with 16 bit). This is coupled with a revisit frequency of 2–3 days, ensuring the creation of dense time series for crop growth monitoring.

Based on this, good prospects may be envisaged for improved yield forecasts over large agricultural areas, as well as better support to farmers for specific decision management strategies.