A GIS-Based Water Balance Approach Using a LiDAR-Derived DEM Captures Fine-Scale Vegetation Patterns
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Overview
2.2. Running the Model
2.3. Study Area and Application of the Model
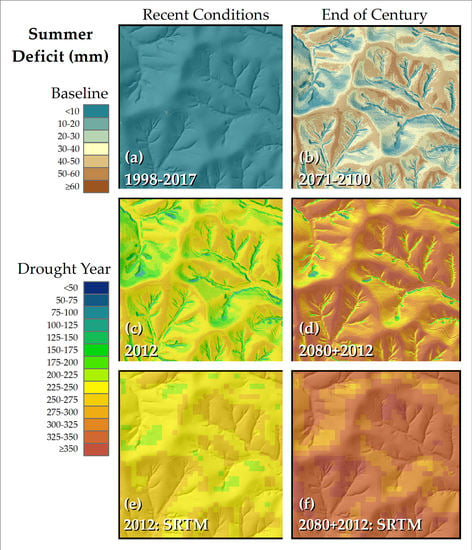
3. Results
3.1. Relationship to SPEI
3.2. Water Balance at Lilly-Dicky Woods, 1998–2017
3.3. Water Balance under an RCP8.5 2080s Scenario
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
References
- Lookingbill, T.; Urban, D. An empirical approach towards improved spatial estimates of soil moisture for vegetation analysis. Landsc. Ecol. 2004, 19, 417–433. [Google Scholar] [CrossRef]
- Stephenson, N.L. Climatic Control of Vegetation Distribution: The Role of the Water Balance. Am. Nat. 1990, 135, 649–670. [Google Scholar] [CrossRef]
- Potzger, J.E. Topography and Forest Types in a Central Indiana Region. Am. Midl. Nat. 1935, 16, 212–229. [Google Scholar] [CrossRef]
- Cantlon, J.E. Vegetation and Microclimates on North and South Slopes of Cushetunk Mountain, New Jersey. Ecol. Monogr. 1953, 23, 241–270. [Google Scholar] [CrossRef]
- McCarthy, B.C.; Small, C.J.; Rubino, D.L. Composition, structure and dynamics of Dysart Woods, an old-growth mixed mesophytic forest of southeastern Ohio. For. Ecol. Manag. 2001, 140, 193–213. [Google Scholar] [CrossRef]
- Wolfe, J.N.; Wareham, R.T.; Schofield, H.T. Microclimates and Macroclimate of Neatoma, A Small Valley in Central Ohio; Ohio Biology Survey; The Ohio State University: Columbus, OH, USA, 1949; p. 267. [Google Scholar]
- Hutchins, R.B.; Blevins, R.L.; Hill, J.D.; White, E.H. The influence of soils and microclimate on vegetation of forested slopes in eastern kentucky. Soil Sci. 1976, 121, 234–241. [Google Scholar] [CrossRef]
- Iverson, L.R.; Peters, M.P.; Prasad, A.M.; Matthews, S.N. Analysis of Climate Change Impacts on Tree Species of the Eastern US: Results of DISTRIB-II Modeling. Forests 2019, 10, 302. [Google Scholar] [CrossRef]
- Dyer, J.M.; Hutchinson, T.F. Topography and soils-based mapping reveals fine-scale compositional shifts over two centuries within a central Appalachian landscape. For. Ecol. Manag. 2019, 433, 33–42. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; U.S. Department of Commerce Weather Bureau: Washington, DC, USA, 1965.
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Iverson, L.R.; Dale, M.E.; Scott, C.T.; Prasad, A. A Gis-derived integrated moisture index to predict forest composition and productivity of Ohio forests (U.S.A.). Landsc. Ecol. 1997, 12, 331–348. [Google Scholar] [CrossRef]
- Iverson, L.R.; Peters, M.P.; Bartig, J.L.; Rebbeck, J.; Hutchinson, T.F.; Matthews, S.N.; Stout, S. Spatial modeling and inventories for prioritizing investment into oak-hickory restoration. For. Ecol. Manag. 2018, 424, 355–366. [Google Scholar] [CrossRef]
- Mohamedou, C.; Korhonen, L.; Eerikäinen, K.; Tokola, T. Using LiDAR-modified topographic wetness index, terrain attributes with leaf area index to improve a single-tree growth model in south-eastern Finland. Forestry 2019, 92, 253–263. [Google Scholar] [CrossRef]
- Mather, J.R. The Climatic Water Budget in Environmental Analysis; D.C. Heath and Company: Lexington, MA, USA, 1978; p. 239. [Google Scholar]
- Stephenson, N.L. Actual evapotranspiration and deficit: Biologically meaningful correlates of vegetation distribution across spatial scales. J. Biogeogr. 1998, 25, 855–870. [Google Scholar] [CrossRef]
- Crimmins, S.M.; Dobrowski, S.Z.; Greenberg, J.; Abatzoglou, J.T.; Mynsberge, A.R. Changes in Climatic Water Balance Drive Downhill Shifts in Plant Species’ Optimum Elevations. Science 2011, 331, 324–327. [Google Scholar] [CrossRef]
- Harsch, M.A.; HilleRisLambers, J. Climate Warming and Seasonal Precipitation Change Interact to Limit Species Distribution Shifts across Western North America. PLoS ONE 2016, 11, e0159184. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. In The State and Movement of Water in Living Organisms, Proceedings of the 19th Symposium of the Society for Experimental Biology; Fogg, G.E., Ed.; Cambridge University Press: New York, NY, USA, 1965; pp. 205–234. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; Food and Agricultural Organization of the United Nations: Rome, Italy, 1998; p. 326. [Google Scholar]
- Fua, H.; Tajchmana, S.J.; Kochenderferb, J.N. Topography and radiation exchange of a mountainous watershed. J. Appl. Meteorol. 1995, 34, 890–901. [Google Scholar] [CrossRef]
- Turc, L. Evaluation des besoins en eau d’irrigation, évapotranspiration potentielle, formule climatique simplifie et mise a jour. Ann. Agron. 1961, 12, 13–49. [Google Scholar]
- American Society of Civil Engineers. Evapotranspiration and Irrigation Water Requirements; American Society of Civil Engineers: New York, NY, USA, 1990; p. 332. [Google Scholar]
- Dyer, J.M. Assessing topographic patterns in moisture use and stress using a water balance approach. Landsc. Ecol. 2009, 24, 391–403. [Google Scholar] [CrossRef]
- Gale, M.R.; Grigal, D.F. Vertical root distributions of northern tree species in relation to successional status. Can. J. For. Res. 1987, 17, 829–834. [Google Scholar] [CrossRef]
- Jackson, R.B.; Canadell, J.; Ehleringer, J.R.; Mooney, H.A.; Sala, O.E.; Schulze, E.D. A global analysis of root distributions for terrestrial biomes. Oecologia 1996, 108, 389–411. [Google Scholar] [CrossRef] [PubMed]
- Yeakley, J.A.; Swank, W.T.; Swift, L.W.; Hornberger, G.M.; Shugart, H.H. Soil moisture gradients and controls on a southern Appalachian hillslope from drought through recharge. Hydrol. Earth Syst. Sci. 1998, 2, 41–49. [Google Scholar] [CrossRef] [Green Version]
- Florinsky, I.; Eilers, R.; Manning, G.; Fuller, L.; Florinsky, I. Prediction of soil properties by digital terrain modelling. Environ. Model. Softw. 2002, 17, 295–311. [Google Scholar] [CrossRef]
- Soil Survey Staff, Natural Resources Conservation Service, United States Department of Agriculture. Web Soil Survey. Available online: https://websoilsurvey.sc.egov.usda.gov/ (accessed on 20 March 2018).
- Maxwell, J.T.; Harley, G.L. Increased tree-ring network density reveals more precise estimations of sub-regional hydroclimate variability and climate dynamics in the Midwest, USA. Clim. Dyn. 2017, 49, 1479–1493. [Google Scholar] [CrossRef]
- Braun, E.L. Deciduous Forests of Eastern North America; Blakiston: Philadelphia, PA, USA, 1950; p. 596. [Google Scholar]
- Homoya, M.A.; Abrell, D.B.; Aldrich, J.A.; Post, T.W. The natural regions of Indiana. Proc. Indiana Acad. Sci. 1985, 94, 245–268. [Google Scholar]
- Sengupta, M.; Xie, Y.; Lopez, A.; Habte, A.; Maclaurin, G.; Shelby, J. The National Solar Radiation Data Base (NSRDB). Renew. Sustain. Energy Rev. 2018, 89, 51–60. [Google Scholar] [CrossRef]
- Daly, C.; Halbleib, M.; Smith, J.I.; Gibson, W.P.; Doggett, M.K.; Taylor, G.H.; Curtis, J.; Pasteris, P.P. Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States. Int. J. Clim. 2008, 28, 2031–2064. [Google Scholar] [CrossRef]
- Jackson, S.T.; Betancourt, J.L.; Booth, R.K.; Gray, S.T. Ecology and the ratchet of events: Climate variability, niche dimensions, and species distributions. Proc. Natl. Acad. Sci. USA 2009, 106, 19685–19692. [Google Scholar] [CrossRef] [Green Version]
- Berdanier, A.B.; Clark, J.S. Multiyear drought-induced morbidity preceding tree death in southeastern U.S. forests. Ecol. Appl. 2016, 26, 17–23. [Google Scholar] [CrossRef]
- Climate at A Glance: Divisional Time Series. Available online: https://www.ncdc.noaa.gov/cag/ (accessed on 25 March 2017).
- Hamlet, A.F.; Byun, K.; Robeson, S.M.; Widhalm, M.; Baldwin, M. Impacts of climate change on the state of Indiana: Ensemble future projections based on statistical downscaling. Clim. Chang. 2019, 1–15. [Google Scholar] [CrossRef]
- Van Vuuren, D.P.; Edmonds, J.; Kainuma, M.; Riahi, K.; Thomson, A.; Hibbard, K.; Hurtt, G.C.; Kram, T.; Krey, V.; Lamarque, J.F.; et al. The representative concentration pathways: An overview. Clim. Chang. 2011, 109, 5–31. [Google Scholar] [CrossRef]
- Sanford, T.; Frumhoff, P.C.; Luers, A.; Gulledge, J. The climate policy narrative for a dangerously warming world. Nat. Clim. Chang. 2014, 4, 164–166. [Google Scholar] [CrossRef]
- Design Your Own CSV File of MACA Point Data. Available online: https://climate.nkn.uidaho.edu/MACA/ (accessed on 13 March 2019).
- SPEI: Calculation of the Standardised Precipitation–Evapotranspiration Index. Available online: https://CRAN.R-project.org/package=SPEI (accessed on 17 August 2019).
- Hargreaves, G.H. Defining and Using Reference Evapotranspiration. J. Irrig. Drain. Eng. 1994, 120, 1132–1139. [Google Scholar] [CrossRef]
- Hawthorne, S.; Miniat, C.F. Topography may mitigate drought effects on vegetation along a hillslope gradient. Ecohydrology 2018, 11, e1825. [Google Scholar] [CrossRef]
- Maxwell, J.T.; Harley, G.L.; Robeson, S.M. On the declining relationship between tree growth and climate in the Midwest United States: The fading drought signal. Clim. Chang. 2016, 138, 127–142. [Google Scholar] [CrossRef]
- Roque-Malo, S.; Kumar, P. Patterns of change in high frequency precipitation variability over North America. Sci. Rep. 2017, 7, 10853. [Google Scholar] [CrossRef]
- Pederson, N.; D’Amato, A.W.; Dyer, J.M.; Foster, D.R.; Goldblum, D.; Hart, J.L.; Hessl, A.E.; Iverson, L.R.; Jackson, S.T.; Martin-Benito, D.; et al. Climate remains an important driver of post-European vegetation change in the eastern United States. Glob. Chang. Biol. 2015, 21, 2105–2110. [Google Scholar] [CrossRef]
- Grayson, R.B.; Western, A.W.; Blöschl, G. Scaling of Soil Moisture: A Hydrologic Perspective. Annu. Rev. Earth Planet. Sci. 2002, 30, 149–180. [Google Scholar] [Green Version]
- Chamran, F.; Gessler, P.E.; Chadwick, O.A. Spatially Explicit Treatment of Soil-Water Dynamics along a Semiarid Catena. Soil Sci. Soc. Am. J. 2002, 66, 1571–1583. [Google Scholar] [CrossRef]
- Park, S.; Van De Giesen, N. Soil–landscape delineation to define spatial sampling domains for hillslope hydrology. J. Hydrol. 2004, 295, 28–46. [Google Scholar] [CrossRef]
- Currie, D.J. Energy and Large-Scale Patterns of Animal-and Plant-Species Richness. Am. Nat. 1991, 137, 27–49. [Google Scholar] [CrossRef]
- Dyer, M.L.; Meentemeyer, V.; Borg, B. Apparent controls of mass loss rate of leaf litter on a regional scale: Litter quality versus climate. Scand. J. For. Res. 1990, 5, 311–323. [Google Scholar] [CrossRef]
- Rosenzweig, M.L. Net Primary Productivity of Terrestrial Communities: Prediction from Climatological Data. Am. Nat. 1968, 102, 67–74. [Google Scholar] [CrossRef]
- Hogg, E.H. (Ted) Climate and the southern limit of the western Canadian boreal forest. Can. J. For. Res. 1994, 24, 1835–1845. [Google Scholar] [CrossRef]
- Dobrowski, S.Z. A climatic basis for microrefugia: The influence of terrain on climate. Glob. Chang. Biol. 2011, 17, 1022–1035. [Google Scholar] [CrossRef]
- Hannah, L.; Flint, L.; Syphard, A.D.; Moritz, M.A.; Buckley, L.B.; McCullough, I.M. Fine-grain modeling of species’ response to climate change: Holdouts, stepping-stones, and microrefugia. Trends Ecol. Evol. 2014, 29, 390–397. [Google Scholar] [CrossRef]
- Keppel, G.; Mokany, K.; Wardell-Johnson, G.W.; Phillips, B.L.; Welbergen, J.A.; Reside, A.E. The capacity of refugia for conservation planning under climate change. Front. Ecol. Environ. 2015, 13, 106–112. [Google Scholar] [CrossRef]
- Beier, P.; Sutcliffe, P.; Hjort, J.; Faith, D.P.; Pressey, R.L.; Albuquerque, F. A review of selection-based tests of abiotic surrogates for species representation. Conserv. Biol. 2015, 29, 668–679. [Google Scholar] [CrossRef] [Green Version]



| Figure 2 Grid | Mean Deficit | Standard Deviation | Min | Max | P | Mean PET | Deficit as Percentage of PET | |
|---|---|---|---|---|---|---|---|---|
| 1998–2017 | (a) | 4 | 3 | 0 | 10 | 357 | 373 | 1.2 |
| 2012 | (c) | 226 | 27 | 63 | 266 | 100 | 400 | 56.5 |
| 2012: SRTM | (e) | 246 | 11 | 205 | 261 | 100 | 421 | 58.3 |
| 2071–2100 (2080) | (b) | 33 | 13 | 0 | 54 | 332 | 429 | 7.6 |
| 2080 + 2012 | (d) | 305 | 39 | 63 | 356 | 91 | 461 | 66.3 |
| 2080 + 2012: SRTM | (f) | 333 | 15 | 274 | 354 | 91 | 484 | 68.7 |
| Species | Common Name | ≥30 cm DBH | 10–19 cm DBH | ||
|---|---|---|---|---|---|
| n | Percent | n | Percent | ||
| Acer rubrum | Red maple | 39 | 1.2 | 318 | 9.1 |
| Acer saccharum | Sugar maple | 519 | 16.5 | 2160 | 62.1 |
| Carya glabra | Pignut hickory | 155 | 4.9 | 67 | 1.9 |
| Fagus grandifolia | American beech | 70 | 2.2 | 610 | 17.5 |
| Liriodendron tulipifera | Tulip poplar | 35 | 1.1 | 4 | 0.1 |
| Nyssa sylvatica | Blackgum | 43 | 1.4 | 72 | 2.1 |
| Quercus alba | White oak | 194 | 6.2 | 20 | 0.6 |
| Quercus montana | Chestnut oak | 1551 | 49.4 | 79 | 2.3 |
| Quercus rubra | Northern red oak | 176 | 5.6 | 1 | <0.1 |
| Quercus velutina | Black oak | 202 | 6.4 | 2 | 0.1 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dyer, J.M. A GIS-Based Water Balance Approach Using a LiDAR-Derived DEM Captures Fine-Scale Vegetation Patterns. Remote Sens. 2019, 11, 2385. https://doi.org/10.3390/rs11202385
Dyer JM. A GIS-Based Water Balance Approach Using a LiDAR-Derived DEM Captures Fine-Scale Vegetation Patterns. Remote Sensing. 2019; 11(20):2385. https://doi.org/10.3390/rs11202385
Chicago/Turabian StyleDyer, James M. 2019. "A GIS-Based Water Balance Approach Using a LiDAR-Derived DEM Captures Fine-Scale Vegetation Patterns" Remote Sensing 11, no. 20: 2385. https://doi.org/10.3390/rs11202385
APA StyleDyer, J. M. (2019). A GIS-Based Water Balance Approach Using a LiDAR-Derived DEM Captures Fine-Scale Vegetation Patterns. Remote Sensing, 11(20), 2385. https://doi.org/10.3390/rs11202385