Fully Convolutional Networks and Geographic Object-Based Image Analysis for the Classification of VHR Imagery
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Description
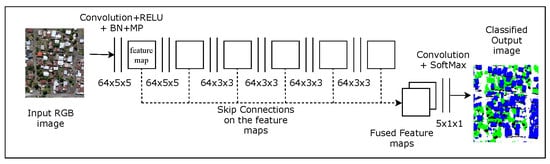
2.2. FCN with Dilated Convolutions and Skip Architecture
2.3. GEOBIA Semi-Automatic Processing Chain
2.4. Refining FCN Maps Using GEOBIA Segments
2.5. FCN_dec and Patch-Based CNN
2.6. Overview of Abbreviations
2.7. Computation of Accuracy Metrics and Other Area Metrics
3. Results
4. Discussion
4.1. FCN_dec and PB-CNN
4.2. FCN vs. GEOBIA
4.3. FCN_skip vs. FCN_noskip
4.4. FCN_skip vs. FCN_obia
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hay, G.J.; Castilla, G. Geographic Object-Based Image Analysis ( GEOBIA ): A new name for a new discipline. In Object-Based Image Analysis. Lecture Notes in Geoinformation and Cartography; Blaschke, T., Lang, S., Hay, G.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2012; pp. 1097–1105. ISBN 9781627480031. [Google Scholar]
- Bergado, J.R.; Persello, C.; Gevaert, C. A deep learning approach to the classification of sub-decimeter resolution aerial images. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1516–1519. Available online: https://ieeexplore.ieee.org/abstract/document/7729387 (accessed on 1 January 2019).
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Volpi, M.; Tuia, D. Dense semantic labeling of sub-decimeter resolution images with convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 881–893. [Google Scholar] [CrossRef]
- Persello, C.; Stein, A. Deep Fully Convolutional Networks for the Detection of Informal Settlements in VHR Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2325–2329. [Google Scholar] [CrossRef]
- Sherrah, J. Fully Convolutional Networks for Dense Semantic Labelling of High-Resolution Aerial Imagery. Available online: https://arxiv.org/abs/1606.02585 (accessed on 1 January 2019).
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: a review. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2014, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Koltun, V. Multi-scale Context Aggregation By Dilated Convolutions. In Proceedings of the International Conference on Learning and Representations, San Juan, PR, USA, 2–4 May 2016; pp. 1–13. [Google Scholar]
- Chen, L.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1–14. [Google Scholar] [CrossRef]
- Marmanis, D.; Datcu, M.; Esch, T.; Stilla, U. Deep learning earth observation classification using ImageNet pretrained networks. IEEE Geosci. Remote Sens. Lett. 2016, 13, 105–109. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Marmanis, D.; Schindler, K.; Wegner, J.D.; Galliani, S.; Datcu, M.; Stilla, U. Classification with an edge: Improving semantic image segmentation with boundary detection. ISPRS J. Photogramm. Remote Sens. 2018, 135, 158–172. [Google Scholar] [CrossRef]
- Guirado, E.; Tabik, S. Deep-learning Versus OBIA for Scattered Shrub Detection with Google Earth Imagery: Ziziphus lotus as Case Study. Remote Sens. 2017, 9, 1220. [Google Scholar] [CrossRef]
- Liu, T.; Abd-Elrahman, A.; Jon, M.; Wilhelm, V.L. Comparing Fully Convolutional Networks, Random Forest, Support Vector Machine, and Patch-based Deep Convolutional Neural Networks for Object-based Wetland Mapping using Images from small Unmanned Aircraft System. GIScience Remote Sens. 2018, 55, 243–264. [Google Scholar] [CrossRef]
- Liu, T.; Abd-Elrahman, A. An Object-Based Image Analysis Method for Enhancing Classification of Land Covers Using Fully Convolutional Networks and Multi-View Images of Small Unmanned Aerial System. Remote Sens. 2018, 10, 457. [Google Scholar] [CrossRef]
- Längkvist, M.; Kiselev, A.; Alirezaie, M.; Loutfi, A. Classification and Segmentation of Satellite Orthoimagery Using Convolutional Neural Networks. Remote Sens. 2016, 8, 329. [Google Scholar] [CrossRef]
- Fu, T.; Ma, L.; Li, M.; Johnson, B.A. Using convolutional neural network to identify irregular segmentation objects from very high-resolution remote sensing imagery. J. Appl. Remote Sens. 2018, 12, 1. [Google Scholar] [CrossRef]
- Lv, X.; Ming, D.; Lu, T.; Zhou, K.; Wang, M.; Bao, H. A New Method for Region-Based Majority Voting CNNs for Very High Resolution Image Classification. Remote Sens. 2018, 10, 1946. [Google Scholar] [CrossRef]
- Zhang, C.; Sargent, I.; Pan, X.; Li, H.; Gardiner, A.; Hare, J.; Atkinson, P.M. An object-based convolutional neural network (OCNN) for urban land use classification. Remote Sens. Environ. 2018, 216, 57–70. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S.; Emery, W.J. Object-Based Convolutional Neural Network for High-Resolution Imagery Classification Object-Based Convolutional Neural Network for High-Resolution Imagery Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017. [Google Scholar] [CrossRef]
- Mboga, N.; Georganos, S.; Grippa, T.; Lennert, M.; Vanhuysse, S.; Wolff, E. Fully convolutional networks for the classification of aerial VHR imagery. In Proceedings of the GEOBIA 2018—Geobia in a Changing World, Montpellier, France, 18–22 June 2018; pp. 1–12. [Google Scholar]
- Grippa, T.; Lennert, M.; Beaumont, B.; Vanhuysse, S.; Stephenne, N.; Wolff, E. An open-source semi-automated processing chain for urban object-based classification. Remote Sens. 2017, 9, 358. [Google Scholar] [CrossRef]
- Michellier, C.; Pigeon, P.; Kervyn, F.; Wolff, E. Contextualizing vulnerability assessment: A support to geo-risk management in central Africa. Nat. Hazards 2016, 82, 27–42. [Google Scholar] [CrossRef]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; Volume 9, pp. 249–256. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. Available online: https://arxiv.org/abs/1502.03167 (accessed on 1 January 2019).
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of the COMPSTAT’2010; Physica-Verlag HD: Heidelberg, Germany, 2010; pp. 177–186. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Theano Development Team Theano: A {Python} Framework for Fast Computation of Mathematical Expressions. Available online: http://adsabs.harvard.edu/abs/arXiv:1605.02688 (accessed on 1 January 2019).
- Chollet, F.; Others Keras. Github Repos. 2015. Available online: https://github.com/fchollet/keras. (accessed on 28 November 2017).
- Neteler, M.; Bowman, M.H.; Landa, M.; Metz, M. GRASS GIS: A multi-purpose open source GIS. Environ. Model. Softw. 2012, 31, 124–130. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Momsen, E.; Metz, M. Grass Development Team Module i.segment. In Geographic Resources Analysis Support System (GRASS) Software; Version 7.0; GRASS Development Team: Bonn, Germany, 2015. [Google Scholar]
- Haralick, R.M.; Shapiro, L.G. Image Segmentation Techniques. Comput. Vision, Graph. Image Process. 1985, 29, 100–132. [Google Scholar] [CrossRef]
- Espindola, G.M.; Camara, G.; Reis, I.A.; Bins, L.S.; Monteiro, A.M. Parameter selection for region-growing image segmentation algorithms using spatial autocorrelation. Int. J. Remote Sens. 2006, 27, 3035–3040. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Lennert, M.; Vanhuysse, S.; Johnson, B.A.; Wolff, E. Scale Matters: Spatially Partitioned Unsupervised Segmentation Parameter Optimization for Large and Heterogeneous Satellite Images. Remote Sens. 2018, 10, 1440. [Google Scholar] [CrossRef]
- Johnson, B.; Xie, Z. Unsupervised image segmentation evaluation and refinement using a multi-scale approach. ISPRS J. Photogramm. Remote Sens. 2011, 66, 473–483. [Google Scholar] [CrossRef]
- Lennert, M.; Team, G.D. Addon i.segment.uspo. In Geographic Resources Analysis Support System (GRASS) Software; Version 7.3; GRASS Development Team: Bonn, Germany, 2016. [Google Scholar]
- Georganos, S.; Grippa, T.; Vanhuysse, S.; Lennert, M.; Shimoni, M.; Kalogirou, S.; Wolff, E. Less is more: Optimizing classification performance through feature selection in a very-high-resolution remote sensing object-based urban application. GIScience Remote Sens. 2017, 1–22. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Vanhuysse, S.; Lennert, M.; Shimoni, M.; Wolff, E. Very High Resolution Object-Based Land Use-Land Cover Urban Classification Using Extreme Gradient Boosting. IEEE Geosci. Remote Sens. Lett. 2018, 15. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S.; Wang, Q.; Emery, W.J. Contextually guided very-high-resolution imagery classification with semantic segments. ISPRS J. Photogramm. Remote Sens. 2017, 132, 48–60. [Google Scholar] [CrossRef]
- Noh, H.; Hong, S.; Han, B. Learning deconvolution network for semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Las Vegas, NV, USA, 11–18 December 2016; pp. 1520–1528. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. Available online: https://arxiv.org/abs/1409.1556 (accessed on 1 January 2019).
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Sermanet, P.; Eigen, D.; Zhang, X.; Mathieu, M.; Fergus, R.; LeCun, Y. OverFeat: Integrated Recognition, Localization and Detection using Convolutional Networks. Available online: https://arxiv.org/abs/1312.6229 (accessed on 1 January 2019).
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Queiroz Feitosa, R.; van der Meer, F.; van der Werff, H.; van Coillie, F.; et al. Geographic Object-Based Image Analysis—Towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Semantic Image Segmentation with Deep Convolutional Nets and Fully Connected CRFs. Available online: https://arxiv.org/abs/1412.7062 (accessed on 1 January 2019).
- Bergado, J.R.; Persello, C.; Stein, A. Recurrent Multiresolution Convolutional Networks for VHR Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, X, 1–14. [Google Scholar] [CrossRef]
- Roscher, R.; Waske, B. Superpixel-based classification of hyperspectral data using sparse representation and conditional random fields. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 3674–3677. [Google Scholar]
- Dao, M.; Kwan, C.; Koperski, K.; Marchisio, G. A joint sparsity approach to tunnel activity monitoring using high resolution satellite images. In Proceedings of the 2017 IEEE 8th Annual Ubiquitous Computing, Electronics and Mobile Communication Conference (UEMCON), New York, NY, USA, 19–21 October 2017; pp. 322–328. [Google Scholar]




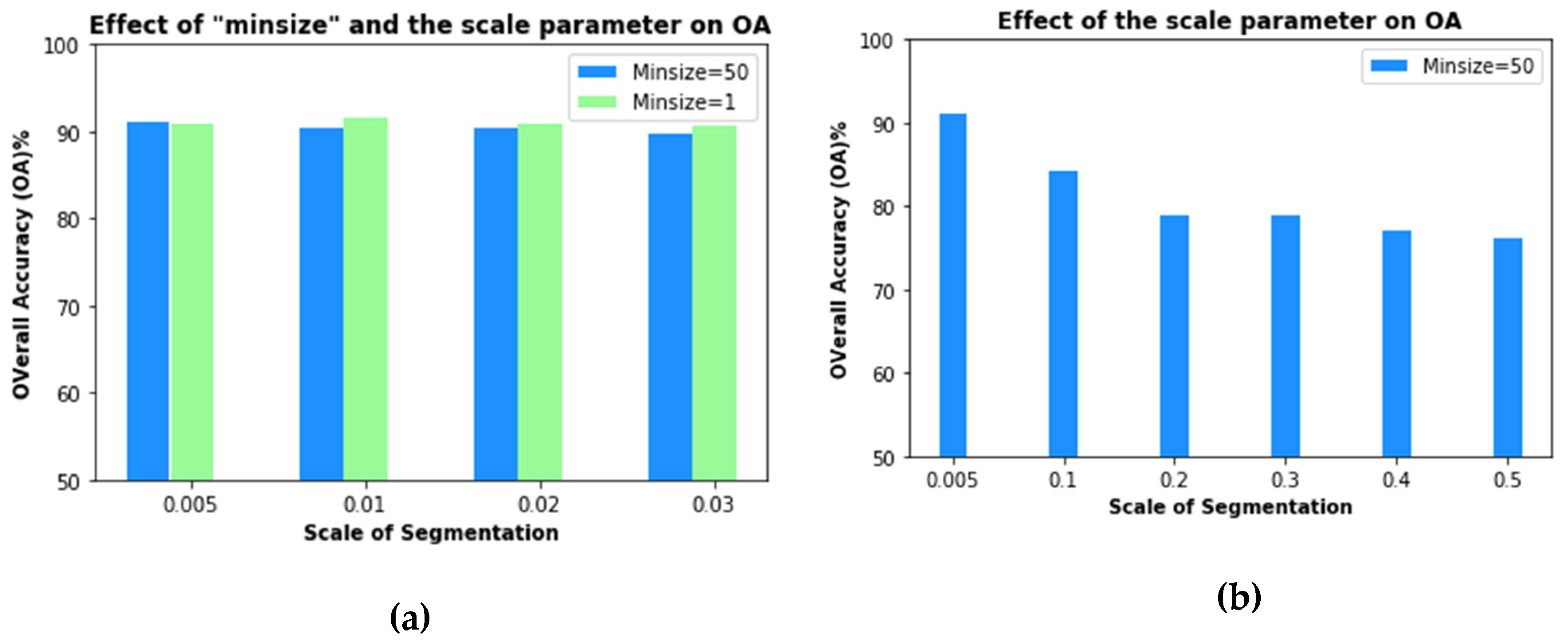



| Scale (threshold) | Minsize = 1 | Minsize = 50 |
|---|---|---|
| 0.005 | FCN_obia_051 | FCN_obia_055 |
| 0.010 | FCN_obia_101 | FCN_obia_105 |
| 0.020 | FCN_obia_201 | FCN_obia_205 |
| 0.030 | FCN_obia_301 | FCN_obia_305 |
| 0.018 | FCN_obia_181 | FCN_obia_185 |
| BD % | VG % | BS % | IS % | SH % | OA % | F1% | ||
|---|---|---|---|---|---|---|---|---|
| XGB_obia | UA | 90.03 | 91.62 | 83.19 | 88.51 | 94.74 | 89.50 | 90.18 |
| PA | 90.32 | 92.66 | 84.61 | 88.22 | 90.91 | |||
| PB-CNN | UA | 88.15 | 94.41 | 98.68 | 78.61 | 92.86 | 86.90 | 80.37 |
| PA | 92.94 | 92.35 | 66.37 | 94.97 | 55.32 | |||
| FCN_dec | UA | 92.71 | 92.90 | 90.11 | 78.27 | 90.78 | 87.20 | 91.21 |
| PA | 89.74 | 92.90 | 72.57 | 94.30 | 62.76 | |||
| FCN_noskip | UA | 92.56 | 88.77 | 96.25 | 80.22 | 97.33 | 88.20 | 92.41 |
| PA | 92.26 | 93.79 | 65.81 | 94.28 | 73.74 | |||
| FCN_skip | UA | 93.93 | 90.96 | 96.70 | 85.49 | 98.81 | 91.30 | 94.38 |
| PA | 94.84 | 96.61 | 75.21 | 93.27 | 83.84 | |||
| FCN_obia_055 | UA | 94.27 | 90.37 | 98.80 | 85.24 | 98.81 | 91.30 | 94.87 |
| PA | 95.48 | 95.48 | 70.09 | 95.29 | 83.84 | |||
| FCN_obia_105 | UA | 93.08 | 89.84 | 100 | 84.08 | 98.75 | 90.5 | 94.27 |
| PA | 95.48 | 94.91 | 70.09 | 94.28 | 79.78 | |||
| FCN_obia_185 | UA | 94.86 | 89.42 | 100 | 82.18 | 98.70 | 90.01 | 95.01 |
| PA | 95.16 | 95.48 | 64.10 | 96.30 | 76.77 | |||
| FCN_obia_205 | UA | 94.21 | 88.48 | 100 | 84.37 | 96.30 | 90.40 | 94.36 |
| PA | 94.52 | 95.48 | 66.67 | 96.30 | 78.79 | |||
| FCN_obia_305 | UA | 94.82 | 90.81 | 100 | 81.02 | 97.44 | 89.80 | 94.67 |
| PA | 94.52 | 94.92 | 64.10 | 96.30 | 76.77 | |||
| FCN_obia_051 | UA | 93.93 | 90.96 | 97.75 | 84.97 | 98.81 | 91.20 | 94.38 |
| PA | 94.84 | 96.61 | 74.36 | 93.27 | 83.84 | |||
| FCN_obia_101 | UA | 93.97 | 90.48 | 98.88 | 85.76 | 98.81 | 91.50 | 94.72 |
| PA | 95.48 | 96.61 | 75.21 | 93.27 | 83.84 | |||
| FCN_obia_181 | UA | 94.87 | 90.91 | 100 | 84.68 | 98.80 | 91.50 | 95.18 |
| PA | 95.48 | 96.05 | 72.65 | 95.95 | 82.83 | |||
| FCN_obia_201 | UA | 93.97 | 89.89 | 100 | 84.59 | 97.62 | 90.9 | 94.72 |
| PA | 95.48 | 95.48 | 70.09 | 94.28 | 82.83 | |||
| FCN_obia_301 | UA | 93.95 | 90.96 | 100 | 83.28 | 97.62 | 90.60 | 94.55 |
| PA | 95.16 | 96.61 | 67.52 | 93.94 | 82.83 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mboga, N.; Georganos, S.; Grippa, T.; Lennert, M.; Vanhuysse, S.; Wolff, E. Fully Convolutional Networks and Geographic Object-Based Image Analysis for the Classification of VHR Imagery. Remote Sens. 2019, 11, 597. https://doi.org/10.3390/rs11050597
Mboga N, Georganos S, Grippa T, Lennert M, Vanhuysse S, Wolff E. Fully Convolutional Networks and Geographic Object-Based Image Analysis for the Classification of VHR Imagery. Remote Sensing. 2019; 11(5):597. https://doi.org/10.3390/rs11050597
Chicago/Turabian StyleMboga, Nicholus, Stefanos Georganos, Tais Grippa, Moritz Lennert, Sabine Vanhuysse, and Eléonore Wolff. 2019. "Fully Convolutional Networks and Geographic Object-Based Image Analysis for the Classification of VHR Imagery" Remote Sensing 11, no. 5: 597. https://doi.org/10.3390/rs11050597
APA StyleMboga, N., Georganos, S., Grippa, T., Lennert, M., Vanhuysse, S., & Wolff, E. (2019). Fully Convolutional Networks and Geographic Object-Based Image Analysis for the Classification of VHR Imagery. Remote Sensing, 11(5), 597. https://doi.org/10.3390/rs11050597