Ground Validation of GPM IMERG Precipitation Products over Iran
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Datasets
2.2.1. Satellite-Based Precipitation (GPM IMERG)
2.2.2. Ground-Based Precipitation
2.3. Evaluation Processes and Indices
2.3.1. Data Preparation
2.3.2. Error Analysis of IMERG Products
2.3.3. Analysis of Statistical Distribution
2.3.4. Geospatial and Temporal Analysis
3. Results and Discussion
3.1. General Comparison of Precipitation Datasets
3.2. Error Analyses of IMERG Products
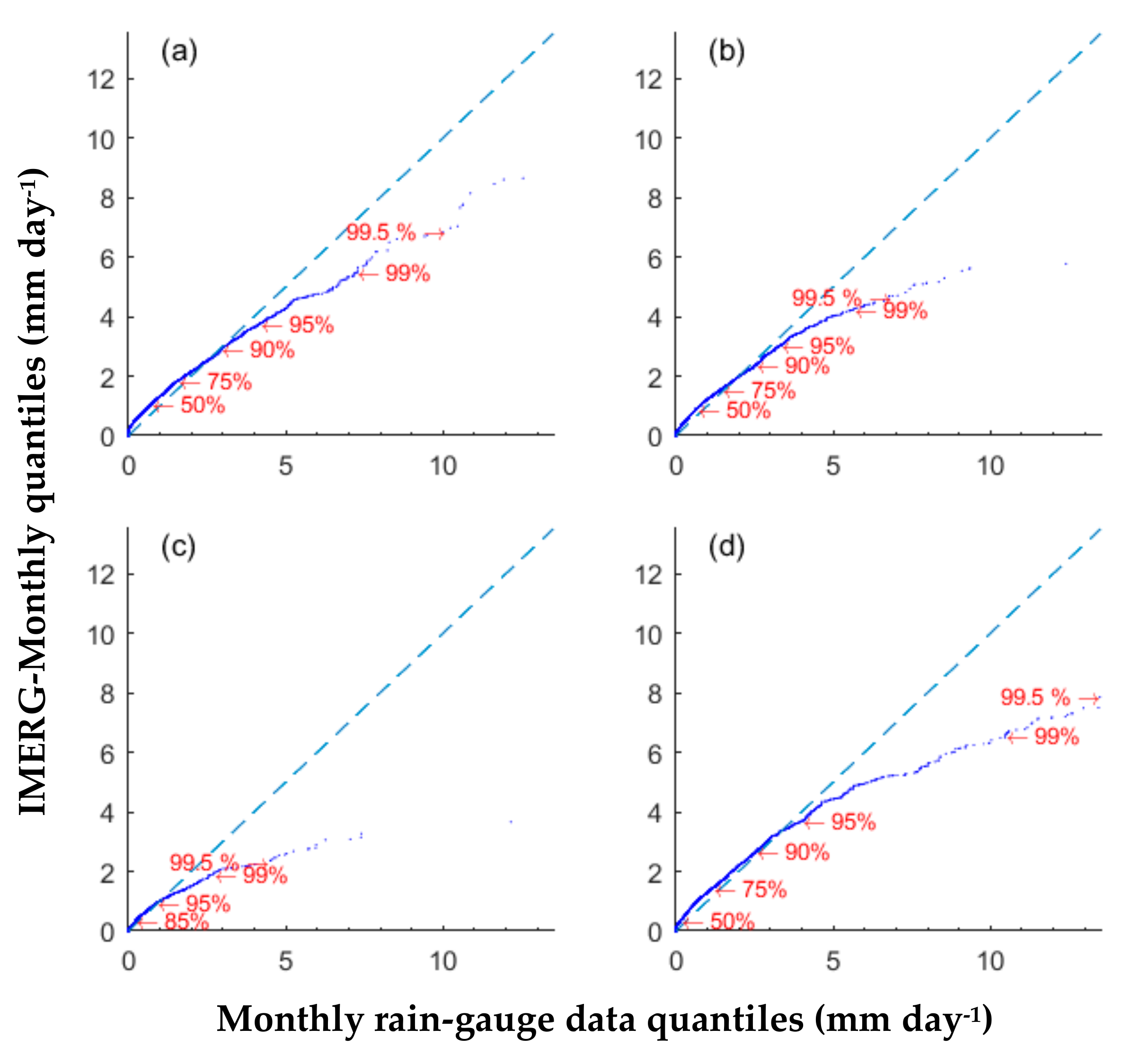
3.3. Evaluation of Statistical Distribution of IMERG Products
3.4. Temporal Performance of IMERG Products
3.5. Geospatial Performance of IMERG Products
Relation to Location-Specific Rainfall
3.6. Spatiotemporal Distribution of Rainfall Detection Ability
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Katiraie-Boroujerdy, P.S.; Nasrollahi, N.; Hsu, K.L.; Sorooshian, S. Evaluation of satellite-based precipitation estimation over Iran. J. Arid Environ. 2013, 97, 205–219. [Google Scholar] [CrossRef] [Green Version]
- Mahmoud, M.T.; Al-Zahrani, M.A.; Sharif, H.O. Assessment of global precipitation measurement satellite products over Saudi Arabia. J. Hydrol. 2018, 559, 1–12. [Google Scholar] [CrossRef]
- Sun, W.; Sun, Y.; Li, X.; Wang, T.; Wang, Y.; Qiu, Q.; Deng, Z. Evaluation and Correction of GPM IMERG Precipitation Products over the Capital Circle in Northeast China at Multiple Spatiotemporal Scales. Adv. Meteorol. 2018, 2018, 4714173. [Google Scholar] [CrossRef]
- Tan, M.; Duan, Z. Assessment of GPM and TRMM Precipitation Products over Singapore. Remote Sens. 2017, 9, 720. [Google Scholar] [CrossRef] [Green Version]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Assessment of GPM-IMERG and other precipitation products against gauge data under different topographic and climatic conditions in Iran: Preliminary results. Remote Sens. 2016, 135. [Google Scholar] [CrossRef] [Green Version]
- Islam, T.; Rico-Ramirez, M.A.; Han, D.; Srivastava, P.K.; Ishak, A.M. Performance evaluation of the TRMM precipitation estimation using ground-based radars from the GPM validation network. J. Atmos. Sol. Terr. Phys. 2012, 77, 194–208. [Google Scholar] [CrossRef]
- Kim, K.; Park, J.; Baik, J.; Choi, M. Evaluation of topographical and seasonal feature using GPM IMERG and TRMM 3B42 over Far-East Asia. Atmos. Res. 2017, 187, 95–105. [Google Scholar] [CrossRef]
- De Coning, E. Optimizing satellite-based precipitation estimation for nowcasting of rainfall and flash flood events over the South African domain. Remote Sens. 2013, 5, 5702–5724. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Yang, B.; Yang, S.; Huang, Y.; Dong, G.; Bai, J.; Wang, Z. Systematical estimation of GPM-based global satellite mapping of precipitation products over China. Atmos. Res. 2018, 201, 206–217. [Google Scholar] [CrossRef]
- Khodadoust Siuki, S.; Saghafian, B.; Moazami, S. Comprehensive evaluation of 3-hourly TRMM and half-hourly GPM-IMERG satellite precipitation products. Int. J. Remote Sens. 2017, 38, 558–571. [Google Scholar] [CrossRef]
- Dembélé, M.; Zwart, S.J. Evaluation and comparison of satellite-based rainfall products in Burkina Faso, West Africa. Int. J. Remote Sens. 2016, 37, 3995–4014. [Google Scholar] [CrossRef] [Green Version]
- Mondal, A.; Lakshmi, V.; Hashemi, H. Intercomparison of trend analysis of Multisatellite Monthly Precipitation Products and Gauge Measurements for River Basins of India. J. Hydrol. 2018, 565, 779–790. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, R.; Lai, C.; Chen, J. Evaluation of the GPM IMERG satellite-based precipitation products and the hydrological utility. Atmos. Res. 2017, 196, 151–163. [Google Scholar] [CrossRef]
- Beria, H.; Nanda, T.; Bisht, D.S.; Chatterjee, C. Does the GPM mission improve the systematic error component in satellite rainfall estimates over TRMM? An evaluation at a pan-India scale. Hydrol. Earth Syst. Sci. 2017, 21, 6117–6134. [Google Scholar] [CrossRef] [Green Version]
- Yuan, F.; Zhang, L.; Wah, K.; Win, W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Assessment of GPM and TRMM Multi-Satellite Precipitation Products in Streamflow Simulations in a Data-Sparse Mountainous Watershed in Myanmar. Remote Sens. 2017, 9, 302. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Chen, Q.; Duan, Z.; Zhang, J.; Mo, K.; Li, Z.; Tang, G. Multiscale comparative evaluation of the GPM IMERG v5 and TRMM 3B42 v7 precipitation products from 2015 to 2017 over a climate transition area of China. Remote Sens. 2018, 10, 944. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Liu, J.; Wang, J.; Qiao, X.; Zhang, J. Evaluation of GPM IMERG V05B and TRMM 3B42V7 Precipitation Products over High Mountainous Tributaries in Lhasa with Dense Rain Gauges. Remote Sens. 2019, 11, 2080. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Zhang, Z.; Huang, Y.; Jin, Q.; Chen, X.; Chang, J. Evaluation of the GPM IMERG v5 and TRMM 3B42 v7 Precipitation Products in the Yangtze River Basin, China. Water 2019, 11, 1459. [Google Scholar] [CrossRef] [Green Version]
- Tang, G.; Long, D.; Hong, Y.; Gao, J.; Wan, W. Documentation of multifactorial relationships between precipitation and topography of the Tibetan Plateau using spaceborne precipitation radars. Remote Sens. Environ. 2018, 208, 82–96. [Google Scholar] [CrossRef]
- Jiang, L.; Bauer-Gottwein, P. How do GPM IMERG precipitation estimates perform as hydrological model forcing? Evaluation for 300 catchments across Mainland China. J. Hydrol. 2019, 572, 486–500. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, J.; Huang, Y.; Chen, X.; Chen, S. Hydrologic Evaluation of TRMM and GPM IMERG Satellite-Based Precipitation in a Humid Basin of China. Remote Sens. 2019, 431. [Google Scholar] [CrossRef] [Green Version]
- Mayor, Y.G.; Tereshchenko, I.; Fonseca-Hernández, M.; Pantoja, D.A.; Montes, J.M. Evaluation of error in IMERG precipitation estimates under different topographic conditions and temporal scales over Mexico. Remote Sens. 2017, 9, 503. [Google Scholar] [CrossRef] [Green Version]
- Sungmin, O.; Foelsche, U.; Kirchengast, G.; Fuchsberger, J.; Tan, J.; Petersen, W.A. Evaluation of GPM IMERG Early, Late, and Final rainfall estimates using WegenerNet gauge data in southeastern Austria. Hydrol. Earth Syst. Sci. 2017, 21, 6559–6572. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.R.; Chang, Y.H.; Liu, P.Y. Assessment of IMERG precipitation over Taiwan at multiple timescales. Atmos. Res. 2018, 214, 239–249. [Google Scholar] [CrossRef]
- Boluwade, A.; Stadnyk, T.; Fortin, V.; Roy, G. Assimilation of precipitation Estimates from the Integrated Multisatellite Retrievals for GPM (IMERG, early Run) in the Canadian Precipitation Analysis (CaPA). J. Hydrol. Reg. Stud. 2017, 14, 10–22. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S. Assessment of Satellite-Based Precipitation Measurement Products over the Hot Desert Climate of Egypt. Remote Sens. 2019, 555. [Google Scholar] [CrossRef] [Green Version]
- Anjum, M.N.; Ahmad, I.; Ding, Y.; Shangguan, D.; Zaman, M.; Ijaz, M.W.; Sarwar, K.; Han, H.; Yang, M. Assessment of IMERG-V06 Precipitation Product over Di ff erent Hydro-Climatic Regimes in the Tianshan. Remote Sens. 2019, 11, 2314. [Google Scholar] [CrossRef] [Green Version]
- Lu, M.A. Evaluation of the integrated multi-satellite retrievals for global precipitation measurement over the Tibetan Plateau. J. Mt. Sci. 2019, 16, 1500–1514. [Google Scholar]
- Turini, N.; Thies, B.; Bendix, J. Estimating High Spatio-Temporal Resolution Rainfall from MSG1 and GPM IMERG Based on Machine Learning: Case Study of Iran. Remote Sens. 2019, 11, 2307. [Google Scholar] [CrossRef] [Green Version]
- Darand, M.; Amanollahi, J.; Zandkarimi, S. Evaluation of the performance of TRMM Multi-satellite Precipitation Analysis (TMPA) estimation over Iran. Atmos. Res. 2017, 190, 121–127. [Google Scholar] [CrossRef]
- Ghorbani, M.; Deposits, M.; Resources, N. The Economic Geology of Iran; Springer: Dordrecht, the Netherlands, 2013; ISBN 9789400756243. [Google Scholar]
- Balling, R.C.; Keikhosravi Kiany, M.S.; Sen Roy, S.; Khoshhal, J. Trends in Extreme Precipitation Indices in Iran: 1951–2007. Adv. Meteorol. 2016, 2016. [Google Scholar] [CrossRef] [Green Version]
- Alizadeh-Choobari, O.; Najafi, M.S. Extreme weather events in Iran under a changing climate. Clim. Dyn. 2018, 50, 249–260. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. Integrated Multi-satellitE Retrievals for GPM (IMERG) Technical Documentation. IMERG Tech. Doc. 2017, 1–60. [Google Scholar] [CrossRef] [Green Version]
- Hashemi, H.; Nordin, M.; Lakshmi, V.; Huffman, G.J.; Knight, R. Bias correction of long-term satellite monthly precipitation product (TRMM 3B43) over the conterminous United States. J. Hydrometeorol. 2017, 18, 2491–2509. [Google Scholar] [CrossRef]
- Hosseini, S.H. Disastrous floods after prolonged droughts have challenged Iran. FUF Bladet 2019, 2019, 30–33. [Google Scholar]
- Hashemi, H.; Berndtsson, R.; Persson, M. Floodwater harvesting for artificial recharge and spate irrigation in arid area. J. Water Manag. Res. 2013, 69, 93–100. [Google Scholar]
- Tan, M.L.; Santo, H. Comparison of GPM IMERG, TMPA 3B42 and PERSIANN-CDR satellite precipitation products over Malaysia. Atmos. Res. 2018, 202, 63–76. [Google Scholar] [CrossRef]












| Criteria | IMERG-Monthly | IMERG-Early | IMERG-Late | IMERG-Final | |||
|---|---|---|---|---|---|---|---|
| Monthly | Monthly | Daily | Monthly | Daily | Monthly | Daily | |
| CC | 0.68 | 0.49 | 0.41 | 0.50 | 0.41 | 0.65 | 0.47 |
| MAE (mm day−1) | 0.44 | 0.62 | 1.14 | 0.60 | 1.10 | 0.43 | 1.03 |
| rBIAS | 0.05 | 0.04 | 0.09 | −0.01 | 0.03 | −0.04 | 0.00 |
| POD (%) | 99.8 | 97.9 | 67.6 | 98.3 | 68.0 | 98.3 | 67.9 |
| FAR (%) | 22.7 | 14.6 | 60.1 | 15.5 | 59.9 | 15.5 | 59.6 |
| Over (%) | 34.9 | 38.7 | 46.2 | 35.6 | 44.9 | 31.1 | 46.1 |
| Equal (%) | 47.1 | 36.3 | 12.0 | 38.2 | 12.7 | 48.3 | 13.2 |
| Under (%) | 18.0 | 25.0 | 41.8 | 26.3 | 42.3 | 20.6 | 40.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maghsood, F.F.; Hashemi, H.; Hosseini, S.H.; Berndtsson, R. Ground Validation of GPM IMERG Precipitation Products over Iran. Remote Sens. 2020, 12, 48. https://doi.org/10.3390/rs12010048
Maghsood FF, Hashemi H, Hosseini SH, Berndtsson R. Ground Validation of GPM IMERG Precipitation Products over Iran. Remote Sensing. 2020; 12(1):48. https://doi.org/10.3390/rs12010048
Chicago/Turabian StyleMaghsood, Fatemeh Fadia, Hossein Hashemi, Seyyed Hasan Hosseini, and Ronny Berndtsson. 2020. "Ground Validation of GPM IMERG Precipitation Products over Iran" Remote Sensing 12, no. 1: 48. https://doi.org/10.3390/rs12010048
APA StyleMaghsood, F. F., Hashemi, H., Hosseini, S. H., & Berndtsson, R. (2020). Ground Validation of GPM IMERG Precipitation Products over Iran. Remote Sensing, 12(1), 48. https://doi.org/10.3390/rs12010048