Field Intercomparison of Radiometer Measurements for Ocean Colour Validation
Abstract
:1. Introduction
- Hyperspectral (five above-water TriOS-RAMSES, two Seabird-HyperSAS, one Pan-and-Tilt System with TriOS-RAMSES sensors (PANTHYR), one in-water TriOS-RAMSES system) and multispectral (one in-water Biospherical-C-OPS) sensors.
- In-water and above-water measurement systems.
2. Materials and Methods
2.1. Determination of Water-Leaving Radiance: Above-Water
2.2. Determination of Water-Leaving Radiance: In-Water
2.3. Determination of Remote-Sensing Reflectance and Normalized Water-Leaving Radiance
2.4. Simulation of Ocean and Land Colour Instrument (OLCI) Bands
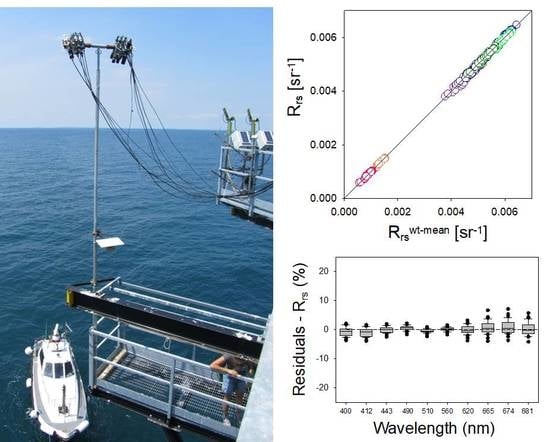
2.5. The Field Intercomparison
2.6. Participants and Data Submission
2.7. Radiometer Set-Up and Experimental Design
2.8. Above-Water Measurement Methods
2.8.1. TriOS-RAMSES
2.8.2. TriOS Data Processing
2.8.3. Seabird-HyperSAS
2.8.4. Seabird HyperSAS Data Processing
2.8.5. The Pan-and-Tilt Hyperspectral Radiometer System (PANTHYR)
2.8.6. PANTHYR Data Processing
2.8.7. SeaPRISM AERONET-OC
2.9. In-Water Methods
2.9.1. Compact Optical Profiling System (C-OPS)
2.9.2. In-Water TriOS-RAMSES
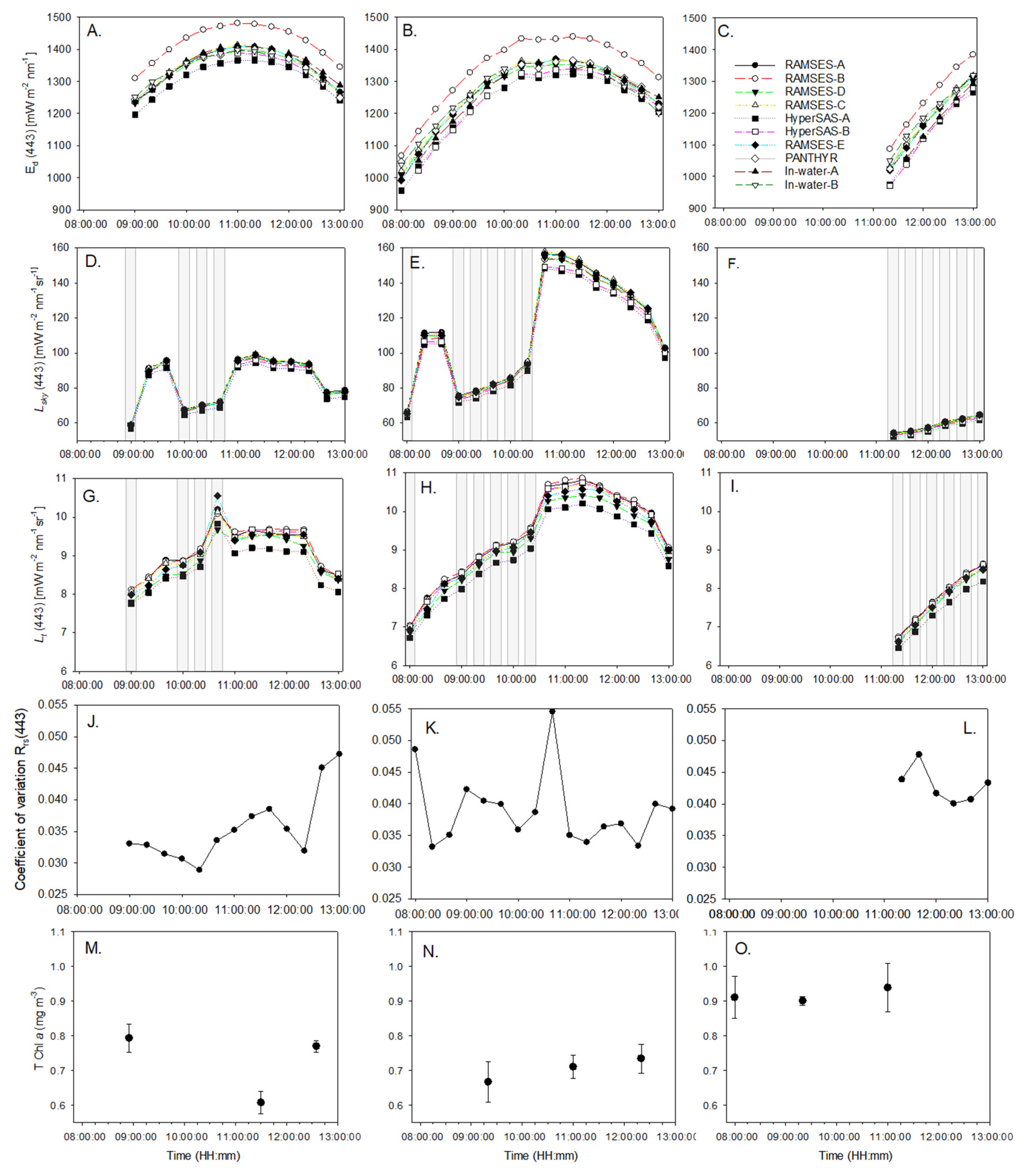
2.10. Environmental Conditions and Selection of Casts
2.11. Inherent Optical Properties and Biogeochemical Concentrations
2.12. Statistical Analyses
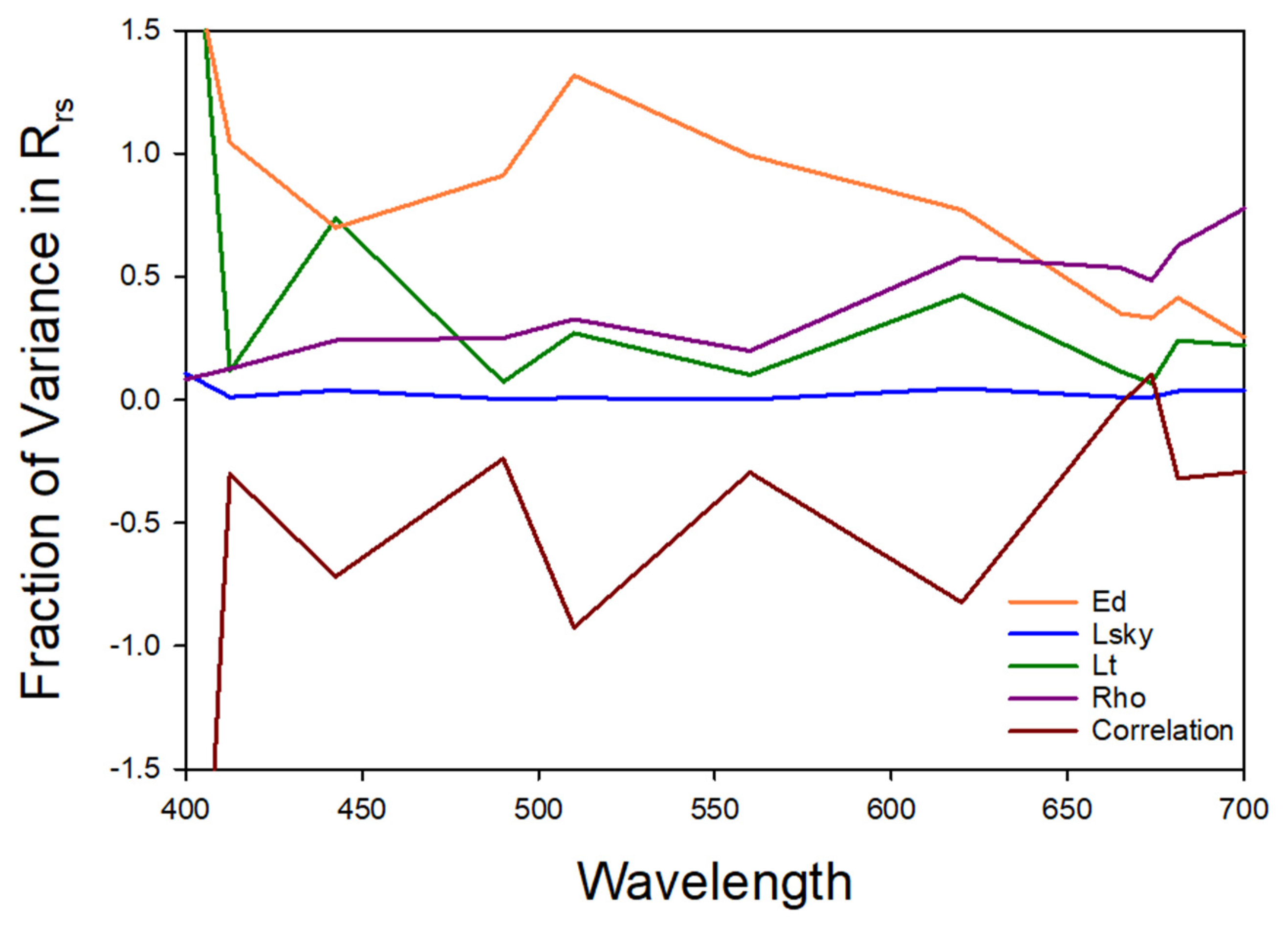
2.13. Sources of Variability in
3. Results
3.1. Data Submission
3.2. Inherent Optical Properties (IOPs) and Biogeochemical Concentrations
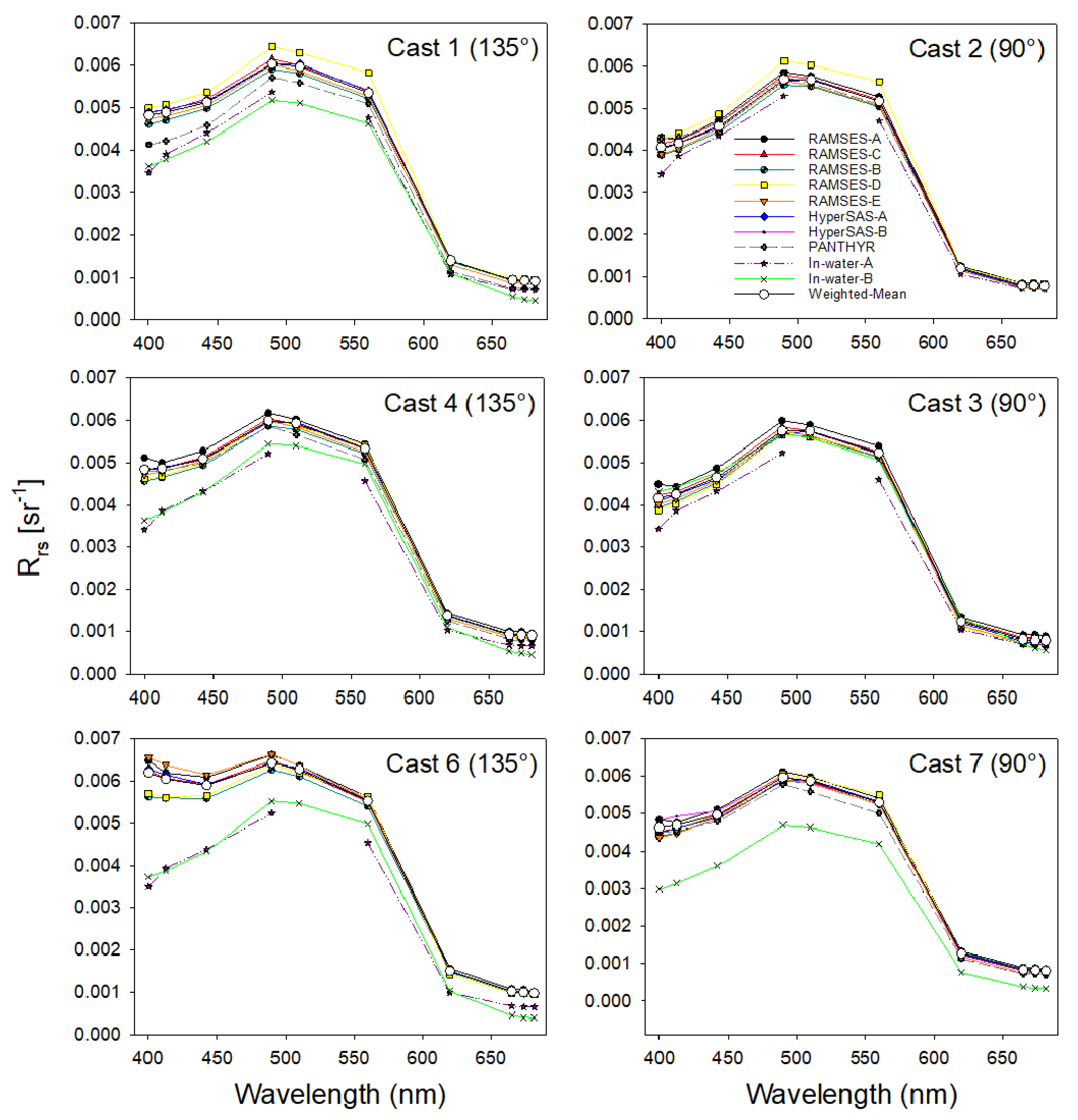
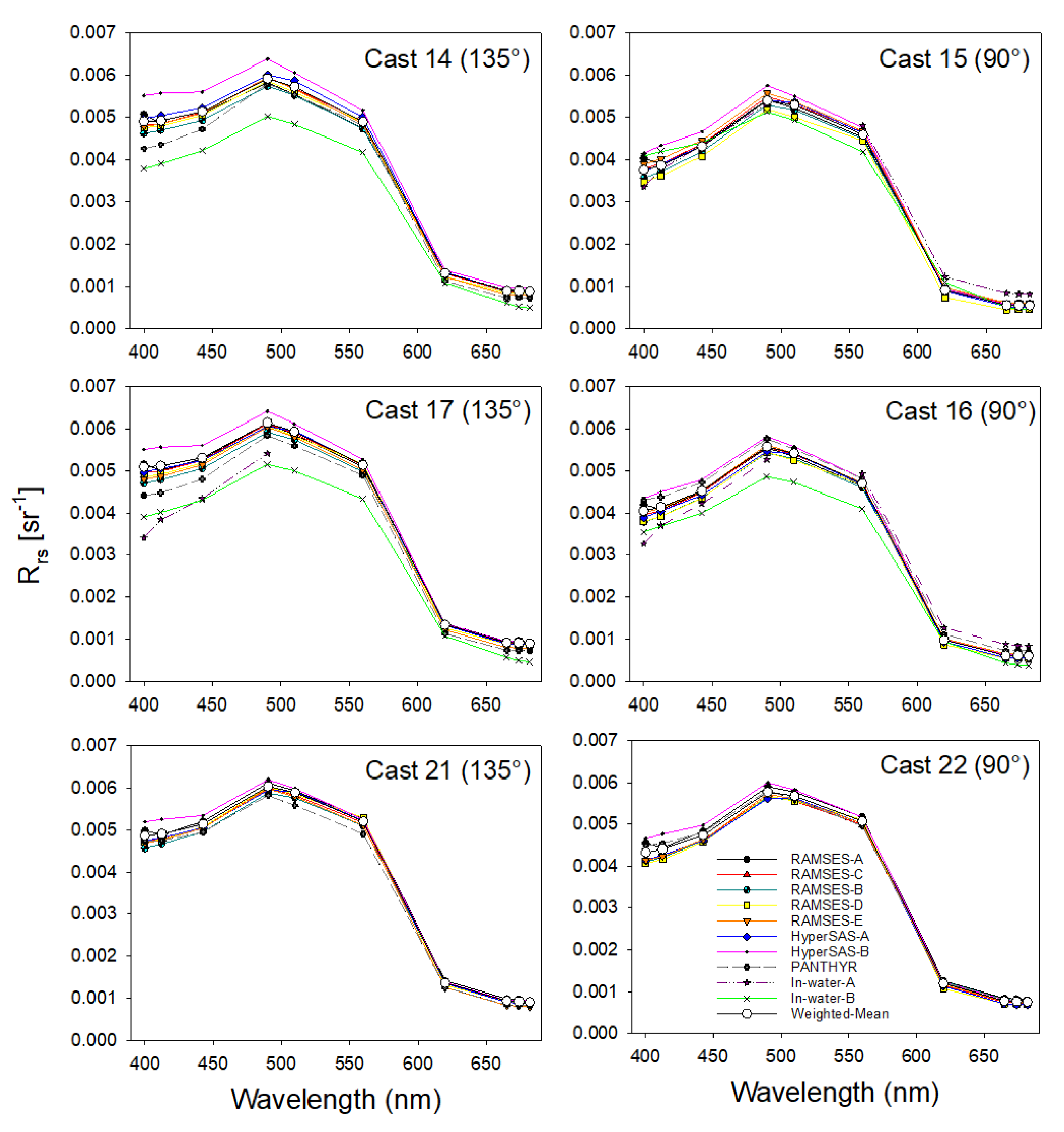
3.3. Intercomparison of , , ,
4. Discussion
4.1. Sources of Uncertainty
4.1.1. Effects of Sensor Absolute Calibration
4.1.2. Differences in Cosine Response
4.1.3. Differences in Field of View (FOV) of Radiance Sensors
4.1.4. Temperature Effects
4.1.5. Differences Due to Data Processing
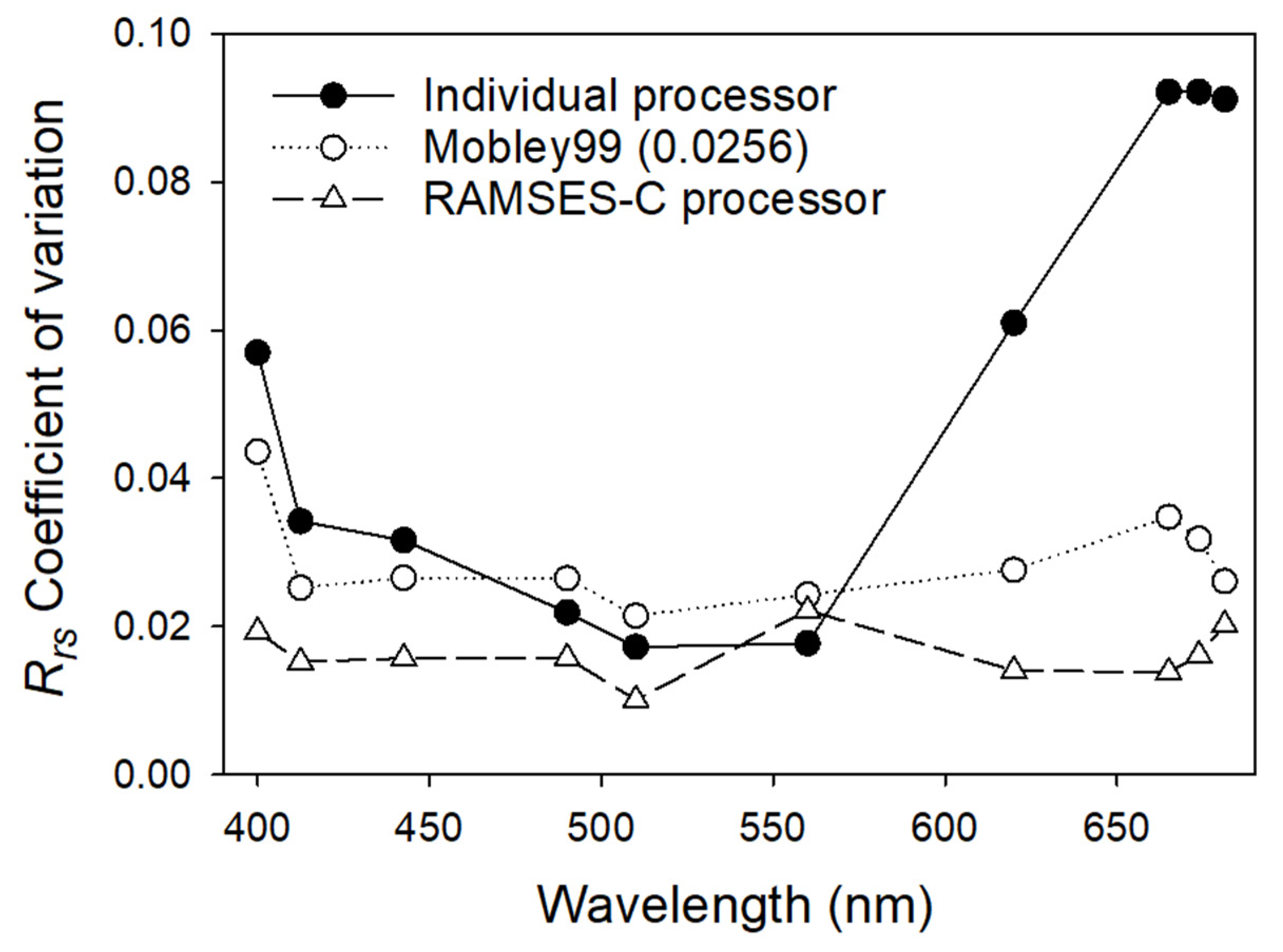
4.1.6. Differences between Case 1 and Case 2 Water-Type Processors
4.1.7. Other Effects
4.2. Differences in and
4.3. Propagation of Errors in , and to
- For both above- and in-water systems, the cosine collector of the sensor needs to be carefully characterised to ensure the most accurate measurements are made.
- We found that above-water Fresnel reflectance factor caused a high variability between processing chains which was greater than other differences between processors, as demonstrated by using a single community processor. Future studies should assess further differences between above and in-water systems and the resulting under a range of environmental conditions and on moving vessels.
- The experimental design should be carefully considered in order to balance between representative sensor types of different above-water, in-water, and new technological systems whilst capturing a broad international range of participants that are active in satellite ocean colour validation.
- This intercomparison focused mainly on differences within and between TriOS-RAMSES systems. Differences within RAMSES systems were low. Future intercomparisons should include a wider range of sensors and systems to capture a further cross-section of the community, rather than just RAMSES systems.
- A more detailed characterisation of stray light, cosine response, linearity, temperature response and polarization sensitivity of individual instruments should be made to assess the contribution of each of these factors to the overall measurement uncertainty. Once these have been assessed, it is recommended to compute a full uncertainty budget as demonstrated in [4,17,73], to evaluate relative differences in uncertainty between instruments.
- Differences between sensors with varying FOV should be further investigated under non-homogeneous sky and sea conditions. In particular the use of a large FOV may be suboptimal when viewing the sea surface which has strong angular variability at the viewing nadir angle of 40°.
- Further intercomparisons of this nature are required from other types of platforms, such as on moving ships as in [74], and under non-ideal environmental conditions such as high sea states and partially cloudy skies when the errors between sensors are expected to increase.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B


Appendix C

Appendix D

References
- Vabson, V.; Kuusk, J.; Ansko, I.; Vendt, R.; Alikas, K.; Ruddick, K.; Ansper, A.; Bresciani, M.; Burmester, H.; Costa, M.; et al. Laboratory intercomparison of radiometers used for satellite validation in the 400–900 nm range. Remote Sens. 2019, 11, 1101. [Google Scholar] [CrossRef] [Green Version]
- JCGM. Guide to the Expression of Uncertainty in Measurement—JCGM 100:2008 (GUM 1995 with Minor Corrections—Evaluation of Measurement Data; Joint Committee for Guides in Metrology, 2008; pp. 1–134. [Google Scholar]
- Zibordi, G.; Donlon, C.J. In Situ Measurement Strategies. In Experimental Methods in the Physical Sciences; Zibordi, G., Donlon, C.J., Parr, A.C., Eds.; Academic Press: Cambridge, MA, USA, 2014; Chapter 5; Volume 47, pp. 527–529. [Google Scholar]
- Vabson, V.; Kuusk, J.; Ansko, I.; Vendt, R.; Alikas, K.; Ansper, A.; Bresciani, M.; Burmeister, H.; Costa, M.; D’Alimonte, D.; et al. Field intercomparison of radiometers used for satellite validation in the 400–900 nm range. Remote Sens. 2019, 11, 1129. [Google Scholar] [CrossRef] [Green Version]
- Mueller, J.L. Above-water radiance and remote sensing reflectance measurements and analysis protocols. In Ocean Optics Protocols for Satellite Ocean Color Sensor Validation; Fargion, G.S., Mueller, J.L., Eds.; National Aeronautical and Space Administration: Washington, DC, USA, 2000. [Google Scholar]
- Tilstone, G.H.; Moore, G.F.; Sorensen, K.; Doerffer, R.; Rottgers, R.; Ruddick, K.G.; Jorgensen, P.V.; Pasterkamp, R. Regional Validation of MERIS Chlorophyll Products in North Sea Coastal Waters: REVAMP Protocols. In ENVISAT Validation Workshop; European Space Agency: Frascatti, Italy, 2004; Available online: http://envisat.esa.int/workshops/mavt_2003/ (accessed on 13 May 2020).
- Ruddick, K.G.; Voss, K.; Boss, E.; Castagna, A.; Frouin, R.; Gilerson, A.; Hieronymi, M.; Johnson, B.C.; Kuusk, J.; Lee, Z.; et al. A Review of Protocols for Fiducial Reference Measurements of Water-leaving Radiance for the Validation of Satellite Remote Sensing Data over Water. Remote Sens. 2019, 11, 2198. [Google Scholar] [CrossRef] [Green Version]
- Ruddick, K.G.; Voss, K.; Banks, A.C.; Boss, E.; Castagna, A.; Frouin, R.; Hieronymi, M.; Jamet, C.; Johnson, B.C.; Kuusk, J.; et al. A Review of Protocols for Fiducial Reference Measurements of Downwelling Irradiance for the Validation of Satellite Remote Sensing Data over Water. Remote Sens. 2019, 11, 1742. [Google Scholar] [CrossRef] [Green Version]
- Hooker, S.B.; Lazin, G.; Zibordi, G.; McClean, S. An evaluation of above- and in-water methods for determining water leaving radiances. J. Atmos. Ocean. Tech. 2002, 19, 486–515. [Google Scholar] [CrossRef]
- Hooker, S.B.; McLean, S.; Sherman, J.; Small, M.; Lazin, G.; Zibordi, G.; Brown, J.W. The Seventh SeaWiFS Intercalibration Round-Robin Experiment (SIRREX-7), March 1999. NASA Tech. Memo; NASA/TM-2002-206892/VOL17; NASA Goddard Space Flight Center: Prince George’s County, MD, USA, 2002; p. 78. [Google Scholar]
- Johnson, B.C.; Yoon, H.W.; Bruce, S.S.; Shaw, P.-S.; Thompson, A.; Hooker, S.B.; Eplee, R.E.; Barnes, R.A., Jr.; Maritorena, S.; Mueller, J.L. The fifth SeaWiFS Intercalibration Round Robin Experiment (SIRREX-5), July 1996; NASA Tech Memo. 1999-206892; Hooker, S.B., Firestone, E.R., Eds.; NASA Goddard Space Flight Center: Prince George’s County, MD, USA, 1999; Volume 7, p. 75. [Google Scholar]
- Meister, G.; Abel, P.; McClain, C.; Barnes, R.; Fargion, G.; Cooper, J.; Davis, C.; Korwan, D.; Godin, M.; Maffione, R. The First SIMBIOS Radiometric Intercomparison (SIMRIC-1), April–September 2001; National Aeronautics and Space Administration, Goddard Space Flight: Greenbelt, MD, USA, 2002. [Google Scholar]
- Meister, G.; Abel, P.; Carder, K.; Chapin, A.; Clark, D.; Cooper, J.; Davis, C.; English, D.; Fargion, G.; Feinholtz, M.; et al. The Second SIMBIOS Radiometric Intercomparison (SIMRIC-2), March–November 2002; NASA Technical Memorandum; National Aeronautics and Space Administration, Goddard Space Flight Center: Prince George’s County, MD, USA, 2003; Volume 210006, pp. 1–65. [Google Scholar]
- Tilstone, G.H.; Moore, G.F.; Sorensen, K.; Doerffer, R.; Rottgers, R.; Ruddick, K.G.; Pasterkamp, R. Protocols for the validation of MERIS products in Case 2 waters. In Proceedings of the ENVISAT MAVT Conference, Frascatti, Italy, 20–24 October 2003. [Google Scholar]
- Moore, G.F.; Icely, J.D.; Kratzer, S. Field Inter-comparison and validation of in-water radiometer and sun photometers for MERIS validation. In Proceedings of the ESA Living Planet Symposium, Bergen, Norway, 28 June–2 July 2010. [Google Scholar]
- Zibordi, G.; D’Alimonte, D.; van der Linde, D.; Berthon, J.-F.; Hooker, S.B.; Mueller, J.-L.; Lazin, G.; McLean, S. The Eighth SeaWiFS Intercalibration Round-Robin Exercise (SIRREX-8), September–December 2001. NASA Tech Memo. 2002-206892; Hooker, S.B., Firesetone, E.R., Eds.; NASA Goddard Space: Prince George’s County, MD, USA, 2002; Volume 20, p. 39. [Google Scholar]
- Zibordi, G.; Ruddick, K.; Ansko, I.; Moore, G.; Kratzer, S.; Icely, J.; Reinart, A. In situ determination of the remote sensing reflectance: An intercomparison. Ocean Sci. 2012, 8, 567–586. [Google Scholar] [CrossRef] [Green Version]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef]
- Deschamps, P.-Y.; Fougnie, B.; Frouin, R.; Lecomte, P.; Verwaerde, C. SIMBAD: A field radiometer for satellite ocean-color validation. Appl. Opt. 2004, 43, 4055–4069. [Google Scholar] [CrossRef]
- Zibordi, G.; Melin, F.; Hooker, S.B.; D’Alimonte, D.; Holben, B. An autonomous above-water system for the validation of ocean color radiance data. IEEE Trans. Geosc. Rem. Sens. 2004, 42, 401–415. [Google Scholar] [CrossRef]
- Hooker, S.B.; Lazin, G. The SeaBOARR-99 Field Campaign; NASA: Greenbelt, MD, USA, 2000; p. 46. [Google Scholar]
- Waters, K.J.; Smith, R.C.; Lewis, M.R. Avoiding ship-induced light-field perturbation in the determination of oceanic optical properties. Oceanography 1990, 3, 18–21. [Google Scholar] [CrossRef] [Green Version]
- Leymarie, E.; Penkerc’h, C.; Vellucci, V.; Lerebourg, C.; Antoine, D.; Boss, E.; Lewis, M.R.; d’Ortenzio, F.; Claustre, H. ProVal: A new autonomous profiling float for high quality radiometric measurements. Front. Mar. Sci. 2018, 5, 437. [Google Scholar] [CrossRef] [Green Version]
- Clark, D.K.; Yarbrough, M.A.; Feinholz, M.; Flora, S.; Broenkow, W.; Kim, Y.S.; Johnson, B.C.; Brown, S.W.; Yuen, M.; Mueller, J.L. MOBY, a Radiometric Buoy for Performance Monitoring and Vicarious Calibration of Satellite Ocean Color Sensors: Measurement and Data Analysis Protocols; National Aeronautics and Space Administration, Goddard Space Flight: Greenbelt, MD, USA, 2003; Chapter 2. [Google Scholar]
- Morel, A. Résultats expérimentaux concernant la pénétration de la lumière du jour dans les eaux Méditerranéennes. Cah. Océanograph. 1965, 17, 177–184. [Google Scholar]
- Gordon, H.R. Normalized water-leaving radiance: Revisiting the influence of surface roughness. Appl. Opt. 2005, 44, 241–248. [Google Scholar] [CrossRef] [PubMed]
- Thuillier, G.; Floyd, L.; Woods, T.N.; Cebula, R.; Hilsenrath, E.; Herse, M.; Labs, D. Solar irradiance reference spectra for two solar active levels. Adv. Space Res. 2004, 34, 256–261. [Google Scholar] [CrossRef]
- Morel, A.; Antoine, D.; Gentili, B. Bidirectional reflectance of oceanic waters: Accounting for Raman emission and varying particle phase function. Appl. Opt. 2002, 41, 6289–6306. [Google Scholar] [CrossRef]
- Berthon, J.F.; Zibordi, Z. Bio-optical relationships for the northern Adriatic Sea. Int. J. Remote. Sens. 2004, 25, 1527–1532. [Google Scholar] [CrossRef]
- OLCI spectral response functions. In Technical Guide; European Space Agency, ESRIN: Frascatti, Italy, 2016.
- Melin, F.; Scleps, G. Band shifting for ocean color multi-spectral reflectance data. Opt. Express 2015, 23, 2262–2279. [Google Scholar] [CrossRef]
- Zibordi, G.; Melin, F.; Berthon, J.-F. Comparison of SeaWiFS, MODIS and MERIS radiometric products at a coastal site. Geophys. Res. Lett. 2006, 33, L06617. [Google Scholar] [CrossRef]
- Zibordi, G.; Berthon, J.-F.; M’elin, F.; D’Alimonte, D.; Kaitala, S. Validation of satellite ocean color primary products at optically complex coastal sites: Northern Adriatic Sea, Northern Baltic Proper and Gulf of Finland. Remote Sens. Environ. 2009, 113, 2574–2591. [Google Scholar] [CrossRef]
- Zibordi, G.; D’Alimonte, D.; Berthon, J.-F. An evaluation of depth resolution requirements for optical profiling in coastal waters. J. Atmos. Ocean. Tech. 2004, 21, 1059–1073. [Google Scholar] [CrossRef]
- Zibordi, G.; Mélin, F.; Berthon, J.; Holben, B.; Slutsker, I.; Giles, D.; D’Alimonte, D.; Vandemark, D.; Feng, H.; Schuster, G. AERONET-OC: A Network for the Validation of Ocean Color Primary Products. J. Atmos. Ocean. Tech. 2009, 26, 1634–1651. [Google Scholar] [CrossRef]
- Zibordi, G.; Hooker, S.B.; Berthon, J.-F.; D’Alimonte, D. Autonomous above–water radiance measurement from an offshore platform: A. field assessment. J. Atmos. Ocean. Tech. 2002, 19, 808–819. [Google Scholar] [CrossRef]
- Artegiani, A.; Bregant, D.; Paschini, E.; Pinardi, N.; Raicich, F.; Russo, A. The Adriatic Sea general circulation. Part I: Air-sea interactions and water mass structure. J. Phys. Oceanogr. 1997, 27, 1492–1514. [Google Scholar] [CrossRef]
- Zavatarelli, M.; Pinardi, N.; Kourafalou, V.H.; Maggiore, A. Diagnostic and prognostic model studies of the Adriatic Sea general circulation: Seasonal variability. J. Geophys. Res. 2002, 107, 3004. [Google Scholar] [CrossRef] [Green Version]
- D’Alimonte, D.; Zibordi, G.; Kajiyama, T. Effects of integration time on in-water radiometric profiles. Opt. Express 2018, 26, 5908–5939. [Google Scholar] [CrossRef]
- Uudeberg, K.; Ansko, I.; Põru, G.; Ansper, A.; Reinart, A. Using Optical Water Types to Monitor Changes in Optically Complex Inland and Coastal Waters. Remote Sens. 2019, 11, 2297. [Google Scholar] [CrossRef] [Green Version]
- Hieronymi, M. Polarized reflectance and transmittance distribution functions of the ocean surface. Opt. Express 2016, 24, A1045–A1068. [Google Scholar] [CrossRef]
- Theis, A. Validation of MERIS, MODIS and SeaWiFS Level-2 Products with Ground Based in-situ Measurements in Atlantic Case 1 Waters. Mater’s Thesis, University of Bremen, Bremen, Germany, 2009; pp. 1–91. Available online: https://epic.awi.de/21447/1/The2009a.pdf (accessed on 13 May 2020).
- Ruddick, K.; Cauwer, V.D.; van Mol, B. Use of the near infrared similarity spectrum for the quality control of remote sensing data. In Proceedings of the SPIE International conference on Remote Sensing of the Coastal Oceanic Environment, San Diego, CA, USA, 23 August 2005; Volume 5885, p. 588501. [Google Scholar]
- Ruddick, K.; De Cauwer, V.; Park, Y.-J. Seaborne measurements of near infra-red water leaving reflectance: The similarity spectrum for turbid waters. Limnol. Oceanogr. 2006, 51, 1167–1179. [Google Scholar] [CrossRef] [Green Version]
- Brewin, R.J.W.; Dall’Olmo, G.; Pardo, S.; van Dongen-Vogel, V.; Boss, E.S. Underway spectrophotometry along the Atlantic Meridional Transect reveals remarkable performance in satellite chlorophyll data. Remote Sens. Environ. 2016, 183, 82–97. [Google Scholar] [CrossRef] [Green Version]
- Carswell, T.; Costa, M.; Young, E.; Komick, N.; Gower, J.; Sweeting, R. Evaluation of MODIS-Aqua Atmospheric Correction and Chlorophyll Products of Western North American Coastal Waters Based on 13 Years of Data. Remote Sens. 2017, 9, 1063. [Google Scholar] [CrossRef] [Green Version]
- Vansteenwegen, D.; Ruddick, K.; Cattrijsse, A.; Vanhellemont, Q.; Beck, M. The Pan-and-Tilt Hyperspectral Radiometer System (PANTHYR) for Autonomous Satellite Validation Measurements—Prototype Design and Testing. Remote Sens. 2019, 11, 1360. [Google Scholar] [CrossRef] [Green Version]
- Morrow, J.H.; Hooker, S.B.; Booth, C.R.; Bernhard, G.; Lind, R.N.; Brown, J.W. Advances in Measuring the Apparent Optical Properties (AOPs) of Optically Complex Waters; NASA/TM-2010-215856; NASA: Greenbelt, MD, USA, 2010. [Google Scholar]
- Taylor, B.B.; Torrecilla, E.; Bernhardt, A.; Taylor, M.H.; Peeken, I.; Röttgers, R.; Piera, J.; Bracher, A. Bio-optical provinces in the eastern Atlantic Ocean and their biogeographical relevance. Biogeosciences 2011, 8, 3609–3629. [Google Scholar] [CrossRef] [Green Version]
- Mueller, J.L.; Giulietta, S.; Fargion, C.; McClain, R. Ocean Optics Protocols For Satellite Ocean Color Sensor Validation; Revision 5; Biogeochemical and Bio-Optical Measurements and Data Analysis Protocols National Aeronautical and Space Administration: Washington, DC, USA, 2003; Volume V. [Google Scholar]
- Ebuchi, N.; Kizu, S. Probability Distribution of Surface Wave Slope Derived Using Sun Glitter Images from Geostationary Meteorological Satellite and Surface Vector Winds from Scatterometers. J. Oceanogr. 2002, 58, 477–486. [Google Scholar] [CrossRef]
- Zibordi, G. Experimental evaluation of theoretical sea surface reflectance factors relevant to above-water radiometry. Opt. Express 2016, 24, A446. [Google Scholar] [CrossRef] [PubMed]
- Mobley, C.D. Polarized reflectance and transmittance properties of windblown sea surfaces. Appl. Opt. 2015, 54, 4828–4849. [Google Scholar] [CrossRef]
- Bracher, A.; Taylor, M.; Taylor, B.B.; Dinter, T.; Röttgers, R.; Steinmetz, F. Using empirical orthogonal functions derived from remote sensing reflectance for the prediction of phytoplankton pigment concentrations. Ocean Sci. 2015, 11, 139–158. [Google Scholar] [CrossRef] [Green Version]
- Mueller, J.L.; Fargion, G.S.; McClain, C.R. Ocean Optics Protocols for Satellite Ocean Color Sensor Validation; Revision 4; Radiometric Measurements and Data Analysis Protocols; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2003; Volume III. [Google Scholar]
- IOCCG Protocol Series; Protocols for Satellite Ocean Colour Data Validation: In situ Optical Radiometry. In IOCCG Ocean Optics and Biogeochemistry Protocols for Satellite Ocean Colour Sensor Validation; Zibordi, G.; Voss, K.J.; Johnson, B.C.; Mueller, J.L. (Eds.) IOCCG: Dartmouth, NS, Canada, 2019; Volume 3.0. [Google Scholar]
- Gould, R.W.; Arnone, R.A.; Sydor, M. Absorption, scattering, and remote sensing reflectance relationships in coastal waters: Testing a new inversion algorithm. J. Coastal Res. 2001, 17, 328–341. [Google Scholar]
- Hooker, S.B.; Zibordi, G.; Berthon, J.-F.; Brown, J.W. Above-Water Radiometry in shallow coastal waters. Appl. Opt. 2004, 43, 4254–4268. [Google Scholar] [CrossRef]
- Hooker, S.B.; Morrow, J.H.; Matsuoka, A. Apparent optical properties of the Canadian Beaufort Sea—Part 2: The 1% and 1 cm perspective in deriving and validating AOP data products. Biogeosciences 2013, 10, 4511–4527. [Google Scholar] [CrossRef] [Green Version]
- Morel, A.; Maritorena, S. Bio-optical properties of oceanic waters: A reappraisal. J. Geophys. Res. 2001, 106, 7163–7180. [Google Scholar] [CrossRef] [Green Version]
- Gregg, W.W.; Carder, K.L. A simple spectral solar irradiance model for cloudless maritime atmospheres. Limnol. Oceanogr. 1990, 35, 1657–1675. [Google Scholar] [CrossRef]
- Stramski, D.; Reynolds, R.A.; Babin, M.; Kaczmarek, S.; Lewis, M.R.; Röttgers, R.; Sciandra, A.; Stramska, M.; Twardowski, M.S.; Franz, B.A.; et al. Relationships between the surfaceconcentration of particulate organic carbon and optical properties in the eastern South Pacific and eastern Atlantic Oceans. Biogeosciences 2008, 5, 171–201. [Google Scholar] [CrossRef] [Green Version]
- Chance, J.; Kurucz, R.L. An improved high-resolution solar reference spectrum for earth’s atmosphere measurements in the ultraviolet, visible, and near infrared. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1289–1295. [Google Scholar] [CrossRef]
- Barlow, R.G.; Cummings, D.G.; Gibb, S.W. Improved resolution of mono-and divinyl chlorophylls a and b and zeaxanthin and lutein in phytoplankton extracts using reverse phase C-8 HPLC. Mar. Ecol. Prog. Ser. 1997, 161, 303–307. [Google Scholar] [CrossRef]
- Aiken, J.; Pradhan, Y.; Barlow, R.; Lavender, S.; Poulton, A.; Holligan, P.; Hardman-Mountford, N. Phytoplankton pigments and functional types in the Atlantic Ocean: A decadal assessment, 1995–2005. Deep-Sea Res. Part II Top. Stud. Oceanogr. 2009, 56, 899–917. [Google Scholar] [CrossRef]
- Mekaoui, S.; Zibordi, G. Cosine error for a class of hyperspectral irradiance sensors. Metrologia 2013, 50, 187. [Google Scholar] [CrossRef]
- Sea-Bird Scientific. Specifications for HyperOCR Radiometer. 2019. Available online: https://www.seabird.com/hyperspectral-radiometers/hyperocr-radiometer/family?productCategoryId=54627869935 (accessed on 13 May 2020).
- TriOS. RAMSES Technische Spezifikationen, TriOS Mess- und Datentechnik. 2019. Available online: https://www.trios.de/ramses.html (accessed on 13 May 2020).
- Zibordi, G.; Talone, M.; Jankowski, L. Response to Temperature of a Class of In Situ Hyperspectral Radiometers. J. Atmos. Ocean. Technol. 2017, 34, 1795–1805. [Google Scholar] [CrossRef]
- Burggraaff, O. Biases from incorrect reflectance convolution. Opt. Express 2020, 28, 13801. [Google Scholar] [CrossRef]
- Gordon, H.; Ding, K. Self-shading of in-water optical measurements. Limnol. Oceanogr. 1992, 37, 491–500. [Google Scholar]
- Talone, M.; Zibordi, G. Spectral assessment of deployment platform perturbations on above-water radiometry. Opt. Express 2019, 27, A878–A889. [Google Scholar] [CrossRef]
- Białek, A.; Douglas, S.; Kuusk, J.; Ansko, I.; Vabson, V.; Vendt, R.; Casal, T. Example of Monte Carlo Method Uncertainty Evaluation for Above-Water Ocean Colour Radiometry. Remote Sens. 2020, 12, 780. [Google Scholar] [CrossRef] [Green Version]
- Alikas, K.; Vabson, V.; Ansko, I.; Tilstone, G.H.; Dall’Olmo, G.; Vendt, R.; Donlon, C.; Casal, T. Comparison of above-water Seabird and TriOS radiometers along an Atlantic Meridional Transect. Remote Sens. 2020. (in revision). [Google Scholar]











| Method (Identifier) | Radiometers | Reference | Institute | |
|---|---|---|---|---|
| 1 | Above-water (RAMSES-A) | TriOS-RAMSES | [39] | University of Algarve, Portugal |
| 2 | Above-water (RAMSES-B) | TriOS-RAMSES | [40] | University of Tartu, Estonia |
| 3 | Above-water (RAMSES-C) | TriOS-RAMSES | [41] | Helmholtz-Zentrum Geesthacht, Germany |
| 4 | Above-water (RAMSES-D) | TriOS-RAMSES | [42] | Alfred Wegener Institute, Germany |
| 5 | Above-water (RAMSES-E) | TriOS-RAMSES | [43,44] | Royal Belgian Institute of Natural Sciences |
| 6 | Above-water (HyperSAS-A) | Seabird | [45] | Plymouth Marine Laboratory, United Kingdom |
| 7 | Above-water (HyperSAS-B) | Seabird | [46] | University of Victoria, Canada |
| 8 | Above-water (PANTHYR) | TriOS-RAMSES + pan and tilt | [47] | Flanders Marine Institute, Belgium |
| 9 | Above-water (SeaPRISM) | SeaPRISM | [11] | Joint Research Centre, Italy |
| 10 | In-water C-OPS (in-water A) | Biospherical microradiometers | [48] | Institut de la Mer de Villefranche, France |
| 11 | In-water TriOS (in-water B) | TriOS-RAMSES | [49] | Alfred Wegener Institute, Germany |
| Sensor Type | Year | N | N | N | QC Flag | FOV | |
|---|---|---|---|---|---|---|---|
| RAMSES-A | 2015, 2015, 2015 | 3–30 | 3–30 | 3–30 | Visual QC | 7° | [18] |
| RAMSES-B | 2004, 2006, 2010 | 3–30 | 3–30 | 3–30 | Visual QC | 7° | [18] |
| RAMSES-C | 2006, 2006, 2006 | 117–140 | 116–140 | 102–140 | 5 min scans | 7° | [18,41] * |
| RAMSES-D | 2007, 2006 **, 2011 | 123–141 | 4–90 | 4–54 | < 1.5%; < 0.5% of min. | 7° | [18] |
| RAMSES-E | 2008, 2001, 2001 | 1st 5 QC | 1st 5 QC | 1st 5 QC | 1st 5 scans *** | 7° | [43,44] |
| HyperSAS-A | 2006, 2006, 2006 | 280–345 | 284–398 | 93–198 | 5 min scans | 6° | [18,45] † |
| HyperSAS-B | 2004, 2004, 2004 | ~130 | ~86 | ~86 | lower 20% | 6° | [18,46] |
| PANTHYR | 2016, 2016 # | 2*3 | 2*3 | 11 | See [45] | 7° | [18,47] |
| In-water A | 2010, N/A, 2010 | 3–4 | N/A | 3–4 | Visual QC | N/A | [18] |
| In-water B | 2007, N/A, 2010 | 150–200 | N/A | ‡ | ~86 | 7° | [52] |
| Quantity [Units] | Median ± abs Dev | Min–Max Range |
|---|---|---|
| (440) [m−1] | 0.079 ± 0.014 | 0.063–0.092 |
| (412) [m−1] | 0.112 ± 0.010 | 0.107–0.131 |
| (440) [m−1] | 0.080 ± 0.009 | 0.070–0.091 |
| (440) [m−1] | 0.929 ± 0.166 | 0.856–1.229 |
| [m−1] | 0.0063 ± 0.001 | N/A |
| (440) [m−1] | 0.004 ± 0.001 | N/A |
| TChl a [mg m−3] | 0.77 ± 0.12 | 0.61–0.94 |
| Sensor Type | N | RMS 443 | RPD 443 | RMS 560 | RPD 560 | RMS 665 | RPD 665 |
|---|---|---|---|---|---|---|---|
| RAMSES-A | 34 | 0.007 | −1.55 | 0.023 | −4.88 | 0.027 | −5.74 |
| RAMSES-B | 35 | 0.029 | 6.64 | 0.014 | 3.01 | 0.017 | 3.76 |
| RAMSES-C | 35 | 0.006 | 1.13 | 0.005 | −0.92 | 0.004 | −0.28 |
| RAMSES-D S1 | 35 | 0.034 | −7.92 | 0.046 | −9.66 | 0.048 | −10.58 |
| RAMSES-D S2 | 35 | 0.004 | 0.35 | 0.009 | −1.64 | 0.007 | −1.03 |
| RAMSES-E | 35 | 0.004 | 0.73 | 0.005 | −1.03 | 0.003 | −0.24 |
| PANTHYR | 30 | 0.007 | 0.85 | 0.011 | 2.18 | 0.018 | 4.07 |
| HyperSAS-A | 35 | 0.011 | −2.30 | 0.008 | 1.61 | 0.004 | 0.78 |
| HyperSAS-B | 27 | 0.009 | −1.79 | 0.005 | −0.19 | 0.006 | 0.65 |
| In-water A | 28 | 0.005 | 0.03 | 0.014 | −2.90 | 0.005 | 0.03 |
| In-water B S1 | 28 | 0.032 | −6.64 | 0.044 | −9.04 | 0.046 | −9.55 |
| In-water B S2 | 28 | 0.010 | 1.21 | 0.011 | −0.82 | 0.010 | −0.22 |
| Sensor Type | N | RMS 443 | RPD 443 | RMS 560 | RPD 560 | RMS 665 | RPD 665 |
|---|---|---|---|---|---|---|---|
| RAMSES-A | 34 | 0.011 | 2.42 | 0.003 | 0.19 | 0.003 | 0.38 |
| RAMSES-B | 35 | 0.003 | 0.65 | 0.003 | −0.26 | 0.004 | −0.38 |
| RAMSES-C | 35 | 0.011 | 2.37 | 0.004 | 0.41 | 0.005 | 0.93 |
| RAMSES-D | 35 | 0.004 | 0.46 | 0.004 | −0.49 | 0.005 | −0.41 |
| RAMSES-E | 35 | 0.008 | 1.78 | 0.007 | 1.23 | 0.008 | 1.27 |
| HyperSAS-A | 35 | 0.011 | −2.47 | 0.007 | 1.43 | 0.0041 | −1.31 |
| HyperSAS-B | 27 | 0.005 | −0.82 | 0.012 | −2.49 | 0.010 | −1.88 |
| Sensor Type | N | RMS 443 | RPD 443 | RMS 560 | RPD 560 | RMS 665 | RPD 665 |
|---|---|---|---|---|---|---|---|
| RAMSES-A | 34 | 0.007 | 1.57 | 0.004 | −0.83 | 0.003 | 0.31 |
| RAMSES-B | 35 | 0.009 | 3.00 | 0.002 | 0.97 | 0.008 | 2.97 |
| RAMSES-C | 35 | 0.005 | 0.86 | 0.006 | −1.21 | 0.003 | −0.12 |
| RAMSES-D | 35 | 0.006 | −0.57 | 0.005 | −0.33 | 0.015 | −2.66 |
| RAMSES-E | 35 | 0.005 | 0.39 | 0.007 | −0.56 | 0.006 | −0.37 |
| HyperSAS-A | 35 | 0.015 | −2.35 | 0.006 | 1.23 | 0.005 | −0.8 |
| HyperSAS-B | 27 | 0.006 | 1.26 | 0.003 | −0.24 | 0.004 | 0.06 |
| Sensor Type | N | RMS 443 | RPD 443 | RMS 560 | RPD 560 | RMS 665 | RPD 665 |
|---|---|---|---|---|---|---|---|
| RAMSES-A | 34 | 0.010 | 1.89 | 0.008 | 0.98 | 0.026 | 5.55 |
| RAMSES-B | 35 | 0.016 | −3.39 | 0.011 | −2.23 | 0.011 | 0.39 |
| RAMSES-C | 35 | 0.006 | 0.01 | 0.005 | 0.19 | 0.004 | 0.75 |
| RAMSES-D S1 | 35 | 0.038 | 8.79 | 0.049 | 11.61 | 0.045 | 10.30 |
| RAMSES-D S2 | 35 | 0.010 | −1.63 | 0.008 | 1.34 | 0.027 | −4.01 |
| RAMSES-E | 35 | 0.010 | −1.46 | 0.004 | −1.42 | 0.023 | −7.42 |
| HyperSAS-A | 35 | 0.032 | −1.15 | 0.008 | −0.01 | 0.042 | −4.02 |
| HyperSAS-B | 27 | 0.023 | 5.04 | 0.009 | 1.49 | 0.015 | 2.14 |
| PANTHYR | 29 | 0.032 | −5.58 | 0.026 | −5.00 | 0.077 | −13.22 |
| In-water A | 27 | 0.065 | −12.07 | 0.051 | −8.20 | 0.097 | −8.85 |
| In-water B S1 | 28 | 0.066 | −10.09 | 0.034 | −4.39 | 0.19 | −29.98 |
| In-water B S2 | 28 | 0.096 | −17.05 | 0.065 | −12.30 | 0.229 | −36.59 |
| Sensor Type | N | RMS 441 | RPD 441 | RMS 551 | RPD 551 | RMS 667 | RPD 667 |
|---|---|---|---|---|---|---|---|
| RAMSES-A | 9 | 0.046 | −6.32 | 0.009 | −0.83 | 0.057 | 9.45 |
| RAMSES-B | 9 | 0.051 | −7.89 | 0.031 | −5.82 | 0.046 | 2.55 |
| RAMSES-C | 9 | 0.011 | −3.49 | 0.004 | −3.69 | 0.005 | 4.73 |
| RAMSES-D S1 | 9 | 0.037 | 1.22 | 0.027 | 5.10 | 0.064 | 9.00 |
| RAMSES-D S2 | 9 | 0.048 | −6.00 | 0.020 | −2.59 | 0.052 | −0.10 |
| RAMSES-E | 9 | 0.052 | −5.65 | 0.030 | −5.62 | 0.055 | −5.90 |
| HyperSAS-A | 9 | 0.048 | −5.52 | 0.021 | −3.94 | 0.064 | −4.81 |
| HyperSAS-B | 6 | 0.025 | −1.39 | 0.041 | −7.37 | 0.058 | 3.99 |
| In-water A | 8 | 0.063 | −11.51 | 0.051 | −10.25 | 0.071 | −9.06 |
| In-water B S1 | 6 | 0.039 | −3.38 | 0.036 | −3.18 | 0.164 | −17.44 |
| In-water B S2 | 6 | 0.069 | −10.49 | 0.043 | −4.71 | 0.200 | −24.67 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tilstone, G.; Dall’Olmo, G.; Hieronymi, M.; Ruddick, K.; Beck, M.; Ligi, M.; Costa, M.; D’Alimonte, D.; Vellucci, V.; Vansteenwegen, D.; et al. Field Intercomparison of Radiometer Measurements for Ocean Colour Validation. Remote Sens. 2020, 12, 1587. https://doi.org/10.3390/rs12101587
Tilstone G, Dall’Olmo G, Hieronymi M, Ruddick K, Beck M, Ligi M, Costa M, D’Alimonte D, Vellucci V, Vansteenwegen D, et al. Field Intercomparison of Radiometer Measurements for Ocean Colour Validation. Remote Sensing. 2020; 12(10):1587. https://doi.org/10.3390/rs12101587
Chicago/Turabian StyleTilstone, Gavin, Giorgio Dall’Olmo, Martin Hieronymi, Kevin Ruddick, Matthew Beck, Martin Ligi, Maycira Costa, Davide D’Alimonte, Vincenzo Vellucci, Dieter Vansteenwegen, and et al. 2020. "Field Intercomparison of Radiometer Measurements for Ocean Colour Validation" Remote Sensing 12, no. 10: 1587. https://doi.org/10.3390/rs12101587
APA StyleTilstone, G., Dall’Olmo, G., Hieronymi, M., Ruddick, K., Beck, M., Ligi, M., Costa, M., D’Alimonte, D., Vellucci, V., Vansteenwegen, D., Bracher, A., Wiegmann, S., Kuusk, J., Vabson, V., Ansko, I., Vendt, R., Donlon, C., & Casal, T. (2020). Field Intercomparison of Radiometer Measurements for Ocean Colour Validation. Remote Sensing, 12(10), 1587. https://doi.org/10.3390/rs12101587