Winter Wheat Yield Prediction at County Level and Uncertainty Analysis in Main Wheat-Producing Regions of China with Deep Learning Approaches
Abstract
:1. Introduction
2. Materials and Methods
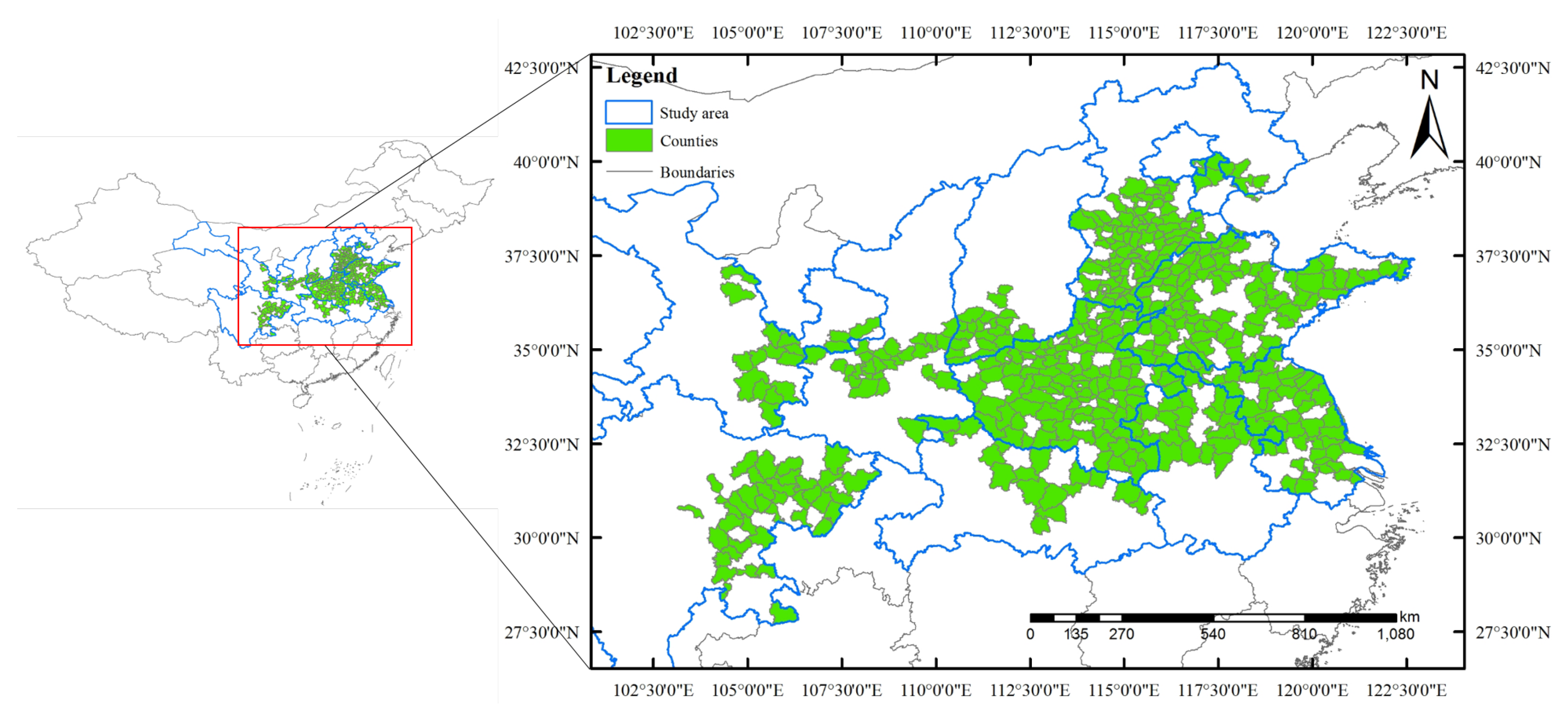
2.1. Study Area
2.2. Datasets and Preprocessing
2.2.1. Satellite Data
2.2.2. Meteorological Data
2.2.3. Soil Data
2.2.4. Cropland Data
2.2.5. Yield Data and Detrending
2.2.6. Data Preprocessing
2.3. Model Development
2.3.1. Deep Neural Network Structure
2.3.2. Quantification of Prediction Uncertainty
2.3.3. Implementation Details
2.4. Model Evaluation Metrics
3. Results
3.1. Model Accuracy
3.2. Impact of Different Data Sources on Model Accuracy
3.3. Improvement in Yield Detrending
3.4. Comparison with Machine Learning Methods
3.5. Quantified Uncertainty
3.6. Yield Forecast Ability
4. Discussion
4.1. Uncertainty Changes Caused by Yield Detrending
4.2. Impact of Agricultural Policies
4.3. Potential for Integrating Prior Knowledge
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LAI | Leaf Area Index |
| ET | Evapotranspiration |
| LSTM | Long Short-Term Memory |
| CNN | Convolution Neural Networks |
| AVHRR | Advanced Very High Resolution Radiometer |
| NDVI | Normalized Difference Vegetation Index |
| GEE | Google Earth Engine |
| GDAL | The Geospatial Data Abstraction Library |
| RMSE | Root Mean Square Error |
| NRMSE | Normalized Root Mean Square Error |
| R | Coefficient Of Determination |
| MAPE | Mean Absolute Percentage Error |
References
- Lobell, D.B.; Cassman, K.G.; Field, C.B. Crop yield gaps: Their importance, magnitudes, and causes. Annu. Rev. Environ. Resour. 2009, 34, 179–204. [Google Scholar] [CrossRef] [Green Version]
- Basso, B.; Cammarano, D.; Carfagna, E. Review of crop yield forecasting methods and early warning systems. In Proceedings of the First Meeting of the Scientific Advisory Committee of the Global Strategy to Improve Agricultural and Rural Statistics, Rome, Italy, 18 July 2013; Volume 41. [Google Scholar]
- Schlenker, W.; Roberts, M.J. Nonlinear effects of weather on corn yields. Rev. Agric. Econ. 2006, 28, 391–398. [Google Scholar] [CrossRef]
- Huang, J.; Tian, L.; Liang, S.; Ma, H.; Becker-Reshef, I.; Huang, Y.; Su, W.; Zhang, X.; Zhu, D.; Wu, W. Improving winter wheat yield estimation by assimilation of the leaf area index from Landsat TM and MODIS data into the WOFOST model. Agric. For. Meteorol. 2015, 204, 106–121. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Sedano, F.; Huang, Y.; Ma, H.; Li, X.; Liang, S.; Tian, L.; Zhang, X.; Fan, J.; Wu, W. Assimilating a synthetic Kalman filter leaf area index series into the WOFOST model to improve regional winter wheat yield estimation. Agric. For. Meteorol. 2016, 216, 188–202. [Google Scholar] [CrossRef]
- Huang, J.; Ma, H.; Sedano, F.; Lewis, P.; Liang, S.; Wu, Q.; Su, W.; Zhang, X.; Zhu, D. Evaluation of regional estimates of winter wheat yield by assimilating three remotely sensed reflectance datasets into the coupled WOFOST–PROSAIL model. Eur. J. Agron. 2019, 102, 1–13. [Google Scholar] [CrossRef]
- Zhuo, W.; Huang, J.; Li, L.; Zhang, X.; Ma, H.; Gao, X.; Huang, H.; Xu, B.; Xiao, X. Assimilating soil moisture retrieved from Sentinel-1 and Sentinel-2 data into WOFOST model to improve winter wheat yield estimation. Remote Sens. 2019, 11, 1618. [Google Scholar] [CrossRef] [Green Version]
- Moriondo, M.; Maselli, F.; Bindi, M. A simple model of regional wheat yield based on NDVI data. Eur. J. Agron. 2007, 26, 266–274. [Google Scholar] [CrossRef]
- Dubey, R.; Ajwani, N.; Kalubarme, M.; Sridhar, V.; Navalgund, R.; Mahey, R.; Sidhu, S.; Jhorar, O.; Cheema, S.; Na Rang, R. Pre-harvest wheat yield and production estimation for the Punjab, India. Int. J. Remote Sens. 1994, 15, 2137–2144. [Google Scholar] [CrossRef]
- Huang, J.; Gómez-Dans, J.L.; Huang, H.; Ma, H.; Wu, Q.; Lewis, P.E.; Liang, S.; Chen, Z.; Xue, J.H.; Wu, Y.; et al. Assimilation of remote sensing into crop growth models: Current status and perspectives. Agric. For. Meteorol. 2019, 276, 107609. [Google Scholar] [CrossRef]
- Wall, L.; Larocque, D.; Léger, P.M. The early explanatory power of NDVI in crop yield modelling. Int. J. Remote Sens. 2008, 29, 2211–2225. [Google Scholar] [CrossRef]
- Becker-Reshef, I.; Vermote, E.; Lindeman, M.; Justice, C. A generalized regression-based model for forecasting winter wheat yields in Kansas and Ukraine using MODIS data. Remote Sens. Environ. 2010, 114, 1312–1323. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.; Becker-Reshef, I.; Claverie, M.; Huang, J.; Zhang, J.; Justice, C.; Sobrino, J. Improving the timeliness of winter wheat production forecast in the United States of America, Ukraine and China using MODIS data and NCAR Growing Degree Day information. Remote Sens. Environ. 2015, 161, 131–148. [Google Scholar] [CrossRef]
- Doraiswamy, P.C.; Moulin, S.; Cook, P.W.; Stern, A. Crop yield assessment from remote sensing. Photogramm. Eng. Remote Sens. 2003, 69, 665–674. [Google Scholar] [CrossRef]
- Patrício, D.I.; Rieder, R. Computer vision and artificial intelligence in precision agriculture for grain crops: A systematic review. Comput. Electron. Agric. 2018, 153, 69–81. [Google Scholar] [CrossRef] [Green Version]
- Feng, Q.; Liu, J.; Gong, J. UAV remote sensing for urban vegetation mapping using random forest and texture analysis. Remote Sens. 2015, 7, 1074–1094. [Google Scholar] [CrossRef] [Green Version]
- Feng, Q.; Liu, J.; Gong, J. Urban flood mapping based on unmanned aerial vehicle remote sensing and random forest classifier—A case of Yuyao, China. Water 2015, 7, 1437–1455. [Google Scholar] [CrossRef]
- Ali, I.; Greifeneder, F.; Stamenkovic, J.; Neumann, M.; Notarnicola, C. Review of machine learning approaches for biomass and soil moisture retrievals from remote sensing data. Remote Sens. 2015, 7, 16398–16421. [Google Scholar] [CrossRef] [Green Version]
- Ip, R.H.; Ang, L.M.; Seng, K.P.; Broster, J.; Pratley, J. Big data and machine learning for crop protection. Comput. Electron. Agric. 2018, 151, 376–383. [Google Scholar] [CrossRef]
- Jeong, J.H.; Resop, J.P.; Mueller, N.D.; Fleisher, D.H.; Yun, K.; Butler, E.E.; Timlin, D.J.; Shim, K.M.; Gerber, J.S.; Reddy, V.R.; et al. Random forests for global and regional crop yield predictions. PLoS ONE 2016, 11, e0156571. [Google Scholar] [CrossRef]
- Han, J.; Zhang, Z.; Cao, J.; Luo, Y.; Zhang, L.; Li, Z.; Zhang, J. Prediction of Winter Wheat Yield Based on Multi-Source Data and Machine Learning in China. Remote Sens. 2020, 12, 236. [Google Scholar] [CrossRef] [Green Version]
- Kuwata, K.; Shibasaki, R. Estimating corn yield in the united states with modis evi and machine learning methods. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3. [Google Scholar] [CrossRef] [Green Version]
- Kim, N.; Lee, Y.W. Machine learning approaches to corn yield estimation using satellite images and climate data: A case of Iowa State. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2016, 34, 383–390. [Google Scholar] [CrossRef]
- Feng, Q.; Yang, J.; Zhu, D.; Liu, J.; Guo, H.; Bayartungalag, B.; Li, B. Integrating Multitemporal Sentinel-1/2 Data for Coastal Land Cover Classification Using a Multibranch Convolutional Neural Network: A Case of the Yellow River Delta. Remote Sens. 2019, 11, 1006. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- You, J.; Li, X.; Low, M.; Lobell, D.; Ermon, S. Deep gaussian process for crop yield prediction based on remote sensing data. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Wang, A.X.; Tran, C.; Desai, N.; Lobell, D.; Ermon, S. Deep transfer learning for crop yield prediction with remote sensing data. In Proceedings of the 1st ACM SIGCAS Conference on Computing and Sustainable Societies, Menlo Park and San Jose, CA, USA, 20–22 June 2018; pp. 1–5. [Google Scholar]
- Wolanin, A.; Mateo-García, G.; Camps-Valls, G.; Gómez-Chova, L.; Meroni, M.; Duveiller, G.; Liangzhi, Y.; Guanter, L. Estimating and understanding crop yields with explainable deep learning in the Indian Wheat Belt. Environ. Res. Lett. 2020, 15, 024019. [Google Scholar] [CrossRef]
- Jiang, Z.; Liu, C.; Hendricks, N.P.; Ganapathysubramanian, B.; Hayes, D.J.; Sarkar, S. Predicting county level corn yields using deep long short term memory models. arXiv 2018, arXiv:1805.12044. [Google Scholar]
- Oliveira, I.; Cunha, R.L.; Silva, B.; Netto, M.A. A scalable machine learning system for pre-season agriculture yield forecast. arXiv 2018, arXiv:1806.09244. [Google Scholar]
- Qin, X.; Zhang, F.; Liu, C.; Yu, H.; Cao, B.; Tian, S.; Liao, Y.; Siddique, K.H. Wheat yield improvements in China: Past trends and future directions. Field Crops Res. 2015, 177, 117–124. [Google Scholar] [CrossRef]
- Wang, F.; He, Z.; Sayre, K.; Li, S.; Si, J.; Feng, B.; Kong, L. Wheat cropping systems and technologies in China. Field Crops Res. 2009, 111, 181–188. [Google Scholar] [CrossRef]
- Li, X.; Liu, N.; You, L.; Ke, X.; Liu, H.; Huang, M.; Waddington, S.R. Patterns of cereal yield growth across China from 1980 to 2010 and their implications for food production and food security. PLoS ONE 2016, 11, e0159061. [Google Scholar] [CrossRef]
- Quiring, S.M.; Papakryiakou, T.N. An evaluation of agricultural drought indices for the Canadian prairies. Agric. For. Meteorol. 2003, 118, 49–62. [Google Scholar] [CrossRef]
- Michel, L.; Makowski, D. Comparison of statistical models for analyzing wheat yield time series. PLoS ONE 2013, 8, e78615. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, J.; Carbone, G.J.; Gao, P. Detrending crop yield data for spatial visualization of drought impacts in the United States, 1895–2014. Agric. For. Meteorol. 2017, 237, 196–208. [Google Scholar] [CrossRef]
- Kendall, A.; Gal, Y. What uncertainties do we need in Bayesian deep learning for computer vision? In Proceedings of the NIPS 2017—2017 Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5575–5585. [Google Scholar]
- Vermote, E.; Justice, C.; Csiszar, I.; Eidenshink, J.; Myneni, R.; Baret, F.; Masuoka, E.; Wolfe, R.; Claverie, M. NOAA Climate Data Record (CDR) of AVHRR Surface Reflectance, Version 5; NOAA National Centers for Environmental Information: Washington, DC, USA, 2019. Available online: https://doi.org/10.7289/V53776Z4 (accessed on 1 December 2019).
- Chen, Y.; Yang, K.; He, J.; Qin, J.; Shi, J.; Du, J.; He, Q. Improving land surface temperature modeling for dry land of China. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Yang, K.; He, J.; Tang, W.; Qin, J.; Cheng, C.C. On downward shortwave and longwave radiations over high altitude regions: Observation and modeling in the Tibetan Plateau. Agric. For. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- Kun, Y. China Meteorological Forcing Dataset (1979–2018); National Tibetan Plateau Data Center, Institute of Tibetan Plateau Research, Chinese Academy of Sciences: Beijing, China, 2018. [Google Scholar] [CrossRef]
- Hengl, T.; de Jesus, J.M.; Heuvelink, G.B.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [Green Version]
- Hengl, T.; de Jesus, J.M.; MacMillan, R.A.; Batjes, N.H.; Heuvelink, G.B.; Ribeiro, E.; Samuel-Rosa, A.; Kempen, B.; Leenaars, J.G.; Walsh, M.G.; et al. SoilGrids1km—Global soil information based on automated mapping. PLoS ONE 2014, 9, e105992. [Google Scholar] [CrossRef] [Green Version]
- Shao, Y.; Campbell, J.B.; Taff, G.N.; Zheng, B. An analysis of cropland mask choice and ancillary data for annual corn yield forecasting using MODIS data. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 78–87. [Google Scholar] [CrossRef]
- Zhang, Y.; Chipanshi, A.; Daneshfar, B.; Koiter, L.; Champagne, C.; Davidson, A.; Reichert, G.; Bédard, F. Effect of using crop specific masks on earth observation based crop yield forecasting across Canada. Remote Sens. Appl. Soc. Environ. 2019, 13, 121–137. [Google Scholar] [CrossRef]
- Liu, J.; Shang, J.; Qian, B.; Huffman, T.; Zhang, Y.; Dong, T.; Jing, Q.; Martin, T. Crop Yield Estimation Using Time-Series MODIS Data and the Effects of Cropland Masks in Ontario, Canada. Remote Sens. 2019, 11, 2419. [Google Scholar] [CrossRef] [Green Version]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Kiureghian, A.D.; Ditlevsen, O. Aleatory or epistemic? Does it matter? Struct. Saf. 2009, 31, 105–112. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the 33rd International Conference on Machine Learning, ICML 2016, New York, NY, USA, 19–24 June 2016; Volume 3, pp. 1651–1660. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: tensorflow.org (accessed on 11 July 2019).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Schut, A.; Stephens, D.; Stovold, R.; Adams, M.; Craig, R. Improved wheat yield and production forecasting with a moisture stress index, AVHRR and MODIS data. Crop Pasture Sci. 2009, 60, 60–70. [Google Scholar] [CrossRef]
- Mkhabela, M.; Bullock, P.; Raj, S.; Wang, S.; Yang, Y. Crop yield forecasting on the Canadian Prairies using MODIS NDVI data. Agric. For. Meteorol. 2011, 151, 385–393. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Breiman, L. Statistical modeling: The two cultures (with comments and a rejoinder by the author). Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Gal, Y. Uncertainty in Deep Learning. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2016. [Google Scholar]
- Zhu, X. Analysis of China’s Grain Supply and Demand Balance. Probl. Agric. Econ. 2004, 4, 12–19. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, W.; Ma, L.; Wu, L.; Shen, J.; Davies, W.J.; Oenema, O.; Zhang, F.; Dou, Z. An analysis of China’s grain production: Looking back and looking forward. Food Energy Secur. 2014, 3, 19–32. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, P.; Zhang, S.; Tao, F.; Liu, X. Spatio-temporal changes of agrometrorological disasters for wheat production across China since 1990. Acta Geogr. Sin. 2013, 68. [Google Scholar] [CrossRef]
- Yu, C.; Huang, X.; Chen, H.; Huang, G.; Ni, S.; Wright, J.S.; Hall, J.; Ciais, P.; Zhang, J.; Xiao, Y.; et al. Assessing the Impacts of Extreme Agricultural Droughts in China Under Climate and Socioeconomic Changes. Earth’s Future 2018, 6, 689–703. [Google Scholar] [CrossRef]
- Schölkopf, B. Causality for Machine Learning. arXiv 2019, arXiv:cs.LG/1911.10500. [Google Scholar]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Jia, X.; Willard, J.; Karpatne, A.; Read, J.; Zwart, J.; Steinbach, M.; Kumar, V. Physics guided RNNs for modeling dynamical systems: A case study in simulating lake temperature profiles. In Proceedings of the 2019 SIAM International Conference on Data Mining, Calgary, AB, Canada, 2–4 May 2019; pp. 558–566. [Google Scholar]












| Data Source | Feature Name | Unit | Description |
|---|---|---|---|
| Remote sensing data of AVHRR | SREFL_CH1 | Surface reflectance (640 nm) | |
| SREFL_CH2 | Surface reflectance (860 nm) | ||
| SREFL_CH3 | Surface reflectance (3750 nm) | ||
| NDVI | Normalized Difference Vegetation Index | ||
| Meteorological data | TEMP | K | Instantaneous near surface (2 m) air temperature |
| PREC | mm hr | Precipitation rate | |
| PRES | Pa | Instantaneous near surface (2 m) air pressure | |
| SHUM | kg kg | Instantaneous near surface (2 m) air specific humidity | |
| LRAD | W m | Surface downward longwave radiation | |
| SRAD | W m | Surface downward shortwave radiation | |
| WIND | m s | Instantaneous near surface (10 m) wind speed | |
| Soil data | BLDFIE | kg m | Bulk density (fine earth) |
| CECSOL | cmolc kg | Cation exchange capacity of soil | |
| CLYPPT | % | Clay content (0–2 micrometer) mass fraction | |
| CRFVOL | % | Coarse fragments volumetric | |
| ORCDRC | g kg | Soil organic carbon content (fine earth fraction) | |
| PHIHOX | PH × 10 in H2O | ||
| PHIKCL | PH × 10 in KCL | ||
| SLTPPT | % | Silt content (2-50 micrometer) mass fraction | |
| SNDPPT | % | Sand content (50-2000 micrometer) mass fraction |
| Combination of Data Sources | R | RMSE (kg/hm) | MAPE |
|---|---|---|---|
| Remote sensing data | 0.58 | 969 | 21.04% |
| Meteorological data | 0.50 | 1051 | 22.20% |
| Remote sensing data, Meteorological data | 0.60 | 945 | 19.94% |
| Remote sensing data, Meteorological data and soil data | 0.77 | 721 | 15.28% |
| Round | Dataset | R | RMSE (kg/ha) | MAPE (%) |
|---|---|---|---|---|
| train | 0.82 | 643 | 13.03 | |
| 1 | test | 0.75 | 706 | 14.81 |
| change | −0.07 | +63 | +1.78 | |
| train | 0.82 | 630 | 13.03 | |
| 2 | test | 0.77 | 758 | 16.04 |
| change | −0.05 | +128 | +3.01 | |
| train | 0.85 | 588 | 12.15 | |
| 4 | test | 0.74 | 727 | 15.15 |
| change | −0.11 | +139 | +3.00 | |
| train | 0.83 | 608 | 12.84 | |
| 5 | test | 0.81 | 668 | 13.85 |
| change | −0.02 | +60 | +1.01 | |
| train | 0.84 | 607 | 12.87 | |
| 6 | test | 0.73 | 753 | 15.08 |
| change | −0.11 | +146 | +2.21 | |
| train | 0.84 | 609 | 12.17 | |
| 7 | test | 0.79 | 665 | 14.45 |
| change | −0.05 | +56 | +2.28 | |
| train | 0.83 | 631 | 13.08 | |
| 8 | test | 0.76 | 681 | 13.85 |
| change | −0.07 | +50 | +0.77 | |
| train | 0.84 | 595 | 12.83 | |
| 9 | test | 0.74 | 740 | 13.83 |
| change | −0.1 | +145 | +1.00 | |
| train | 0.83 | 618 | 13.17 | |
| 10 | test | 0.76 | 724 | 15.34 |
| change | −0.07 | +106 | +2.17 | |
| train | 0.83 | 614 | 12.77 | |
| Average | test | 0.76 | 712 | 14.63 |
| change | −0.07 | +98 | +1.86 |
| Method | R | RMSE (kg/hm) | MAPE |
|---|---|---|---|
| Proposed | 0.77 | 721 | 15.28% |
| Random Forest | 0.72 | 792 | 17.03% |
| Support Vector Machine | 0.57 | 981 | 20.30% |
| Lasso Regression | 0.60 | 949 | 20.52% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Huang, J.; Feng, Q.; Yin, D. Winter Wheat Yield Prediction at County Level and Uncertainty Analysis in Main Wheat-Producing Regions of China with Deep Learning Approaches. Remote Sens. 2020, 12, 1744. https://doi.org/10.3390/rs12111744
Wang X, Huang J, Feng Q, Yin D. Winter Wheat Yield Prediction at County Level and Uncertainty Analysis in Main Wheat-Producing Regions of China with Deep Learning Approaches. Remote Sensing. 2020; 12(11):1744. https://doi.org/10.3390/rs12111744
Chicago/Turabian StyleWang, Xinlei, Jianxi Huang, Quanlong Feng, and Dongqin Yin. 2020. "Winter Wheat Yield Prediction at County Level and Uncertainty Analysis in Main Wheat-Producing Regions of China with Deep Learning Approaches" Remote Sensing 12, no. 11: 1744. https://doi.org/10.3390/rs12111744
APA StyleWang, X., Huang, J., Feng, Q., & Yin, D. (2020). Winter Wheat Yield Prediction at County Level and Uncertainty Analysis in Main Wheat-Producing Regions of China with Deep Learning Approaches. Remote Sensing, 12(11), 1744. https://doi.org/10.3390/rs12111744







