Water Balance Standardization Approach for Reconstructing Runoff Using GPS at the Basin Upstream
Abstract
:1. Introduction
2. Data and Processing Strategies
2.1. Time Series of In-Situ Estuarine Discharge Gauges
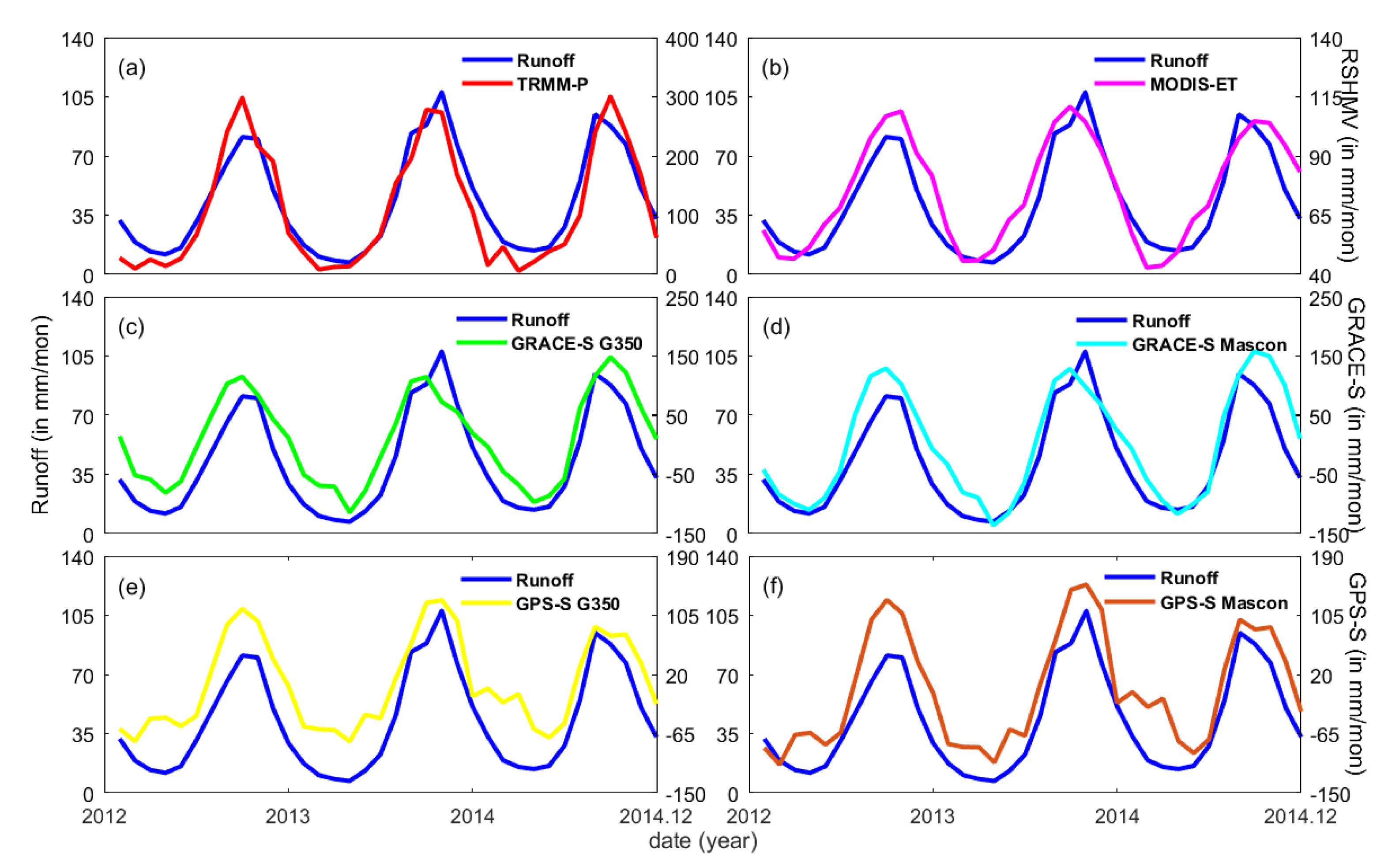
2.2. Remotely-Sensed Water Balance Variables
2.3. Data Processing for GPS-Determined VCD and its Conversion into Water Storage (S)
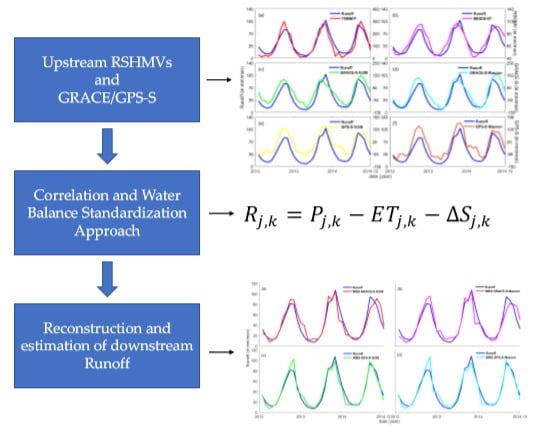
3. Methodology
3.1. Reconstruction Based on Correlation and Water Balance Standardization
3.2. Performance Indicators
4. Results and Evaluation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sichangi, A.; Wang, L.; Yang, K.; Chen, D.; Wang, Z.; Li, X.; Zhou, J.; Liu, W.; Kuria, D. Estimating continental river basin discharges using multiple remote sensing data sets. Remote Sens. Environ. 2016, 179, 36–53. [Google Scholar] [CrossRef] [Green Version]
- Dai, A.; Qian, T.; Trenberth, K.E.; Milliman, J.D. Changes in Continental Freshwater Discharge from 1948 to 2004. J. Clim. 2009, 22, 2773–2792. [Google Scholar] [CrossRef]
- Adamson, P.; Bird, J. The Mekong: A Drought-prone Tropical Environment? Int. J. Water Resour. Dev. 2010, 26, 579–594. [Google Scholar] [CrossRef]
- Kreins, P.; Henseler, M.; Anter, J.; Herrmann, F.; Wendland, F. Quantification of Climate Change Impact on Regional Agricultural Irrigation and Groundwater Demand. Water Resour. Manag. 2015, 29, 3585–3600. [Google Scholar] [CrossRef]
- Pavelic, P.; Srisuk, K.; Saraphirom, P.; Nadee, S.; Pholkern, K.; Chusanathas, S.; Munyou, S.; Tangsutthinon, T.; Intarasut, T.; Smakhtin, V. Balancing-out floods and droughts: Opportunities to utilize floodwater harvesting and groundwater storage for agricultural development in Thailand. J. Hydrol. 2012, 470, 55–64. [Google Scholar] [CrossRef]
- Thilakarathne, M.; Sridhar, V. Characterization of future drought conditions in the Lower Mekong River Basin. Weather Clim. Extrem. 2017, 17, 47–58. [Google Scholar] [CrossRef]
- Fekete, B.M.; Robarts, R.D.; Kumagai, M.; Nachtnebel, H.-P.; Odada, E.; Zhulidov, A.V. Time for in situ renaissance. Science 2015, 349, 685–686. [Google Scholar] [CrossRef]
- Dai, A.; Trenberth, K.E. Estimates of freshwater discharge from continents: Latitudinal and seasonal variations. J. Hydrometeorol. 2002, 3, 660–687. [Google Scholar] [CrossRef] [Green Version]
- Gleason, C.J.; Smith, L.C. Toward global mapping of river discharge using satellite images and at-many-stations hydraulic geometry. Proc. Natl. Acad. Sci. USA 2014, 111, 4788–4791. [Google Scholar] [CrossRef] [Green Version]
- Overton, I. Modelling floodplain inundation on a regulated river: Integrating GIS, remote sensing and hydrological models. River Res. Appl. 2005, 21, 991–1001. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Sobrino, J.A.; Jimenez, J.C.; Paolini, L. Land surface temperature retrieval from LANDSAT TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Fok, H.S.; He, Q. Water Level Reconstruction Based on Satellite Gravimetry in the Yangtze River Basin. ISPRS Int. J. Geo Inf. 2018, 7, 286. [Google Scholar] [CrossRef] [Green Version]
- Birkinshaw, S.J.; Moore, P.; Kilsby, C.; O’Donnell, G.M.; Hardy, A.; Berry, P.A.M. Daily discharge estimation at ungauged river sites using remote sensing. Hydrol. Process. 2012, 28, 1043–1054. [Google Scholar] [CrossRef]
- Zhou, L.; Fok, H.S.; Ma, Z.; Chen, Q. Upstream Remotely-Sensed Hydrological Variables and Their Standardization for Surface Runoff Reconstruction and Estimation of the Entire Mekong River Basin. Remote Sens. 2019, 11, 1064. [Google Scholar] [CrossRef] [Green Version]
- Brakenridge, G.R.; Cohen, S.; Kettner, A.J.; De Groeve, T.; Nghiem, S.; Syvitski, J.P.; Fekete, B.M. Calibration of satellite measurements of river discharge using a global hydrology model. J. Hydrol. 2012, 475, 123–136. [Google Scholar] [CrossRef]
- Papa, F.; Prigent, C.; Rossow, W.B. Monitoring Flood and Discharge Variations in the Large Siberian Rivers From a Multi-Satellite Technique. Surv. Geophys. 2008, 29, 297–317. [Google Scholar] [CrossRef]
- Biancamaria, S.; Frappart, F.; Leleu, A.-S.; Marieu, V.; Blumstein, D.; Desjonquères, J.-D.; Boy, F.; Sottolichio, A.; Valle-Levinson, A. Satellite radar altimetry water elevations performance over a 200 m wide river: Evaluation over the Garonne River. Adv. Space Res. 2017, 59, 128–146. [Google Scholar] [CrossRef] [Green Version]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [Green Version]
- Han, S.-C.; Kim, H.; Yeo, I.-Y.; Yeh, P.J.-F.; Oki, T.; Seo, K.-W.; Alsdorf, D.; Luthcke, S.B. Dynamics of surface water storage in the Amazon inferred from measurements of inter-satellite distance change. Geophys. Res. Lett. 2009, 36, 09403. [Google Scholar] [CrossRef] [Green Version]
- Sproles, E.; Leibowitz, S.G.; Reager, J.T.; Wigington, P.J.; Famiglietti, J.; Patil, S. GRACE storage-runoff hystereses reveal the dynamics of regional watersheds. Hydrol. Earth Syst. Sci. 2015, 19, 3253–3272. [Google Scholar] [CrossRef] [Green Version]
- Jones, P.D.; Hulme, M. Calculating regional climatic time series for temperature and precipitation: Methods and illustrations. Int. J. Clim. 1996, 16, 361–377. [Google Scholar] [CrossRef]
- Fok, H.S.; He, Q.; Chun, K.P.; Zhou, Z.; Chu, T. Application of ENSO and Drought Indices for Water Level Reconstruction and Prediction: A Case Study in the Lower Mekong River Estuary. Water 2018, 10, 58. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Heflin, M.B.; Ivins, E.R.; Argus, D.F.; Webb, F.H. Large-scale global surface mass variations inferred from GPS measurements of load-induced deformation. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Argus, D.F.; Landerer, F. GPS as an independent measurement to estimate terrestrial water storage variations in Washington and Oregon. J. Geophys. Res. Solid Earth 2015, 120, 552–566. [Google Scholar] [CrossRef]
- Fok, H.S.; Liu, Y. An Improved GPS-Inferred Seasonal Terrestrial Water Storage Using Terrain-Corrected Vertical Crustal Displacements Constrained by GRACE. Remote Sens. 2019, 11, 1433. [Google Scholar] [CrossRef] [Green Version]
- Tregoning, P.; Watson, C.S.; Ramillien, G.; McQueen, H.; Zhang, J. Detecting hydrologic deformation using GRACE and GPS. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Freymueller, J.; Jensen, T.E. Seasonal hydrological loading in southern Alaska observed by GPS and GRACE. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- Zhan, W.; Li, F.; Hao, W.; Yan, J. Regional characteristics and influencing factors of seasonal vertical crustal motions in Yunnan, China. Geophys. J. Int. 2017, 210, 1295–1304. [Google Scholar] [CrossRef]
- Ferreira, V.; Montecino, H.; Ndehedehe, C.E.; Del Rio, R.A.; Cuevas, A.; De Freitas, S.R.C. Determining seasonal displacements of Earth’s crust in South America using observations from space-borne geodetic sensors and surface-loading models. Earth Planets Space 2019, 71, 84. [Google Scholar] [CrossRef] [Green Version]
- Chanard, K.; Avouac, J.-P.; Ramillien, G.; Genrich, J. Modeling deformation induced by seasonal variations of continental water in the Himalaya region: Sensitivity to Earth elastic structure. J. Geophys. Res. Solid Earth 2014, 119, 5097–5113. [Google Scholar] [CrossRef] [Green Version]
- Pan, Y.; Shen, W.; Shum, C.; Pan, Y. Spatially varying surface seasonal oscillations and 3-D crustal deformation of the Tibetan Plateau derived from GPS and GRACE data. Earth Planet. Sci. Lett. 2018, 502, 12–22. [Google Scholar] [CrossRef]
- Peixoto, J.P.; Oort, A.H.; Covey, C.; Taylor, K. Physics of Climate. Phys. Today 1992, 45, 67. [Google Scholar] [CrossRef]
- MRC (Mekong River Commission). Overview of the Hydrology of the Mekong Basin; Mekong River Commission: Vientiane, Laos, 2005; Volume 82. [Google Scholar]
- Manh, N.V.; Dung, N.V.; Hung, N.N.; Merz, B.; Apel, H. Large-scale suspended sediment transport and sediment deposition in the Mekong Delta. Hydrol. Earth Syst. Sci. 2014, 18, 3033–3053. [Google Scholar] [CrossRef] [Green Version]
- Nowacki, D.J.; Ogston, A.S.; Nittrouer, C.A.; Fricke, A.; Van, P.D.T.; Tri, V.P.D. Sediment dynamics in the lower M ekong R iver: Transition from tidal river to estuary. J. Geophys. Res. Oceans 2015, 120, 6363–6383. [Google Scholar] [CrossRef] [Green Version]
- Dang, T.D.; Cochrane, T.A.; Arias, M.E.; Tri, V.P.D. Future hydrological alterations in the Mekong Delta under the impact of water resources development, land subsidence and sea level rise. J. Hydrol. Reg. Stud. 2018, 15, 119–133. [Google Scholar] [CrossRef]
- Arias, M.E.; Cochrane, T.A.; Piman, T.; Kummu, M.; Caruso, B.S.; Killeen, T.J. Quantifying changes in flooding and habitats in the Tonle Sap Lake (Cambodia) caused by water infrastructure development and climate change in the Mekong Basin. J. Environ. Manag. 2012, 112, 53–66. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, W.-K.; Gui, S.; Tao, Y.; Cao, J. Rainy season precipitation variation in the Mekong River basin and its relationship to the Indian and East Asian summer monsoons. Clim. Dyn. 2018, 52, 5691–5708. [Google Scholar] [CrossRef] [Green Version]
- Pokhrel, Y.; Shin, S.; Lin, Z.; Yamazaki, D.; Qi, J. Potential Disruption of Flood Dynamics in the Lower Mekong River Basin Due to Upstream Flow Regulation. Sci. Rep. 2018, 8, 17767. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Amarnath, G.; Brocca, L.; Massari, C.; Moramarco, T. Discharge estimation and forecasting by MODIS and altimetry data in Niger-Benue River. Remote Sens. Environ. 2017, 195, 96–106. [Google Scholar] [CrossRef]
- Li, D.; Long, D.; Zhao, J.; Lu, H.; Hong, Y. Observed changes in flow regimes in the Mekong River basin. J. Hydrol. 2017, 551, 217–232. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.P.; Saito, Y.; Nguyen, V.L. Recent evolution of the Mekong Delta and the impacts of dams. Earth Sci. Rev. 2017, 175, 1–17. [Google Scholar] [CrossRef]
- Ferguson, J.W.; Healey, M.; Dugan, P.; Barlow, C. Potential Effects of Dams on Migratory Fish in the Mekong River: Lessons from Salmon in the Fraser and Columbia Rivers. Environ. Manag. 2010, 47, 141–159. [Google Scholar] [CrossRef] [PubMed]
- Onishi, K. Reassessing Water Security in the Mekong: The Chinese Rapprochement with Southeast Asia. J. Nat. Resour. Policy Res. 2011, 3, 393–412. [Google Scholar] [CrossRef]
- Adamson, P.T.; Rutherfurd, I.D.; Peel, M.C.; Conlan, I.A. The Hydrology of the Mekong River. In The Mekong; Elsevier BV: Amsterdam, The Netherlands, 2009; pp. 53–76. [Google Scholar]
- Hecht, J.S.; Lacombe, G.; Arias, M.E.; Dang, T.D.; Piman, T. Hydropower dams of the Mekong River basin: A review of their hydrological impacts. J. Hydrol. 2019, 568, 285–300. [Google Scholar] [CrossRef]
- Liu, Z.; Ostrenga, D.; Teng, W.; Kempler, S. Tropical Rainfall Measuring Mission (TRMM) Precipitation Data and Services for Research and Applications. Bull. Am. Meteorol. Soc. 2012, 93, 1317–1325. [Google Scholar] [CrossRef] [Green Version]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM Multi-satellite Precipitation Analysis: Quasi-Global, Multi-Year, Combined-Sensor Precipitation Estimates at Fine Scale. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote. Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Wu, X.; Ray, J.; Van Dam, T. Geocenter motion and its geodetic and geophysical implications. J. Geodyn. 2012, 58, 44–61. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J. The unexpected signal in GRACE estimates of C20. J. Geod. 2017, 91, 897–914. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Herring, T.; King, R.; McClusky, S. GAMIT Reference Manual, Release 10.4; Massachusetts Institute Technology Cambridge: Cambridge, MA, USA, 2010; Available online: http://www-gpsg.mit.edu/~simon/gtgk/GAMIT_Ref.pdf (accessed on 10 July 2016).
- Böhm, J.; Moeller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2014, 19, 433–441. [Google Scholar] [CrossRef] [Green Version]
- Petit, G.; Luzum, B. IERS Conventions (2010); Bureau International Des Poids et Mesures Sevres (France). 2010. Available online: https://www.iers.org (accessed on 12 May 2019).
- Zhu, Z.; Zhou, X.; Deng, L.; Wang, K.; Zhou, B. Quantitative analysis of geophysical sources of common mode component in CMONOC GPS coordinate time series. Adv. Space Res. 2017, 60, 2896–2909. [Google Scholar] [CrossRef]
- Haines, B.J.; Bertiger, W.I.; Desai, S.D.; Harvey, N.; Sibois, A.; Weiss, J.P.; Bar-Sever, Y.E. Realizing a terrestrial reference frame using the Global Positioning System. J. Geophys. Res. Solid Earth 2015, 120, 5911–5939. [Google Scholar] [CrossRef] [Green Version]
- Wahr, J.; Khan, S.A.; Van Dam, T.; Liu, L.; Van Angelen, J.H.; Broeke, M.R.V.D.; Meertens, C. The use of GPS horizontals for loading studies, with applications to northern California and southeast Greenland. J. Geophys. Res. Solid Earth 2013, 118, 1795–1806. [Google Scholar] [CrossRef] [Green Version]
- Bevis, M.; Kendrick, E.; Cser, A.; Smalley, R., Jr. Geodetic measurement of the local elastic response to the changing mass of water in Lago Laja, Chile. Phys. Earth Planet. Inter. 2004, 141, 71–78. [Google Scholar] [CrossRef]
- Pokhrel, Y.; Burbano, M.; Roush, J.; Kang, H.; Sridhar, V.; Hyndman, D.W. A Review of the Integrated Effects of Changing Climate, Land Use, and Dams on Mekong River Hydrology. Water 2018, 10, 266. [Google Scholar] [CrossRef] [Green Version]
- Veldkamp, T.I.; Eisner, S.; Wada, Y.; Aerts, J.C.J.H.; Ward, P.J. Sensitivity of water scarcity events to ENSO-driven climate variability at the global scale. Hydrol. Earth Syst. Sci. 2015, 19, 4081–4098. [Google Scholar] [CrossRef] [Green Version]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]





| GPS S | (/mon) | (mm/mon) |
|---|---|---|
| RL06-G350 | −8.4453 ± 0.7394 | 14.6906 ± 5.6426 |
| RL06-mascon | −10.6587 ± 0.8392 | 6.4034 ± 6.2864 |
| Station | Variables | PCC | NRMSE | NSE | |
|---|---|---|---|---|---|
| CT-MT station reconstruction | RSHMVs | TRMM-P | 0.945 | 0.096 | 0.893 |
| MODIS-ET | 0.920 | 0.114 | 0.847 | ||
| GRACE-S | RL06-G350 | 0.933 | 0.105 | 0.871 | |
| RL06-mascon | 0.938 | 0.101 | 0.879 | ||
| GPS-S | RL06-G350 | 0.945 | 0.096 | 0.892 | |
| RL06-mascon | 0.942 | 0.097 | 0.888 | ||
| WBS-GRACE | RL06-G350 | 0.965 | 0.076 | 0.932 | |
| RL06-mascon | 0.965 | 0.076 | 0.932 | ||
| WBS-GPS | RL06-G350 | 0.974 | 0.067 | 0.948 | |
| RL06-mascon | 0.974 | 0.066 | 0.950 | ||
| CT-MT station estimates TC-CD station | RSHMVs | TRMM-P | 0.921 | 0.135 | 0.824 |
| MODIS-ET | 0.935 | 0.120 | 0.860 | ||
| GRACE-S | RL06-G350 | 0.932 | 0.124 | 0.851 | |
| RL06-mascon | 0.927 | 0.129 | 0.839 | ||
| GPS-S | RL06-G350 | 0.915 | 0.140 | 0.810 | |
| RL06-mascon | 0.910 | 0.144 | 0.800 | ||
| WBS-GRACE | RL06-G350 | 0.954 | 0.108 | 0.888 | |
| RL06-mascon | 0.954 | 0.107 | 0.889 | ||
| WBS-GPS | RL06-G350 | 0.961 | 0.101 | 0.900 | |
| RL06-mascon | 0.961 | 0.101 | 0.900 | ||
| Station | Variables | PCC | NRMSE | NSE | |
|---|---|---|---|---|---|
| TC-CD station reconstruction | RSHMVs | TRMM-P | 0.921 | 0.125 | 0.849 |
| MODIS-ET | 0.935 | 0.114 | 0.874 | ||
| GRACE-S | RL06-G350 | 0.932 | 0.116 | 0.869 | |
| RL06-mascon | 0.927 | 0.120 | 0.860 | ||
| GPS-S | RL06-G350 | 0.915 | 0.130 | 0.837 | |
| RL06-mascon | 0.910 | 0.133 | 0.828 | ||
| WBS-GRACE | RL06-G350 | 0.966 | 0.083 | 0.933 | |
| RL06-mascon | 0.964 | 0.085 | 0.929 | ||
| WBS-GPS | RL06-G350 | 0.967 | 0.082 | 0.935 | |
| RL06-mascon | 0.966 | 0.082 | 0.934 | ||
| TC-CD station estimates CT-MT station | RSHMVs | TRMM-P | 0.945 | 0.104 | 0.874 |
| MODIS-ET | 0.920 | 0.118 | 0.837 | ||
| GRACE-S | RL06-G350 | 0.933 | 0.110 | 0.857 | |
| RL06-mascon | 0.938 | 0.108 | 0.863 | ||
| GPS-S | RL06-G350 | 0.945 | 0.104 | 0.872 | |
| RL06-mascon | 0.942 | 0.106 | 0.867 | ||
| WBS-GRACE | RL06-G350 | 0.956 | 0.092 | 0.901 | |
| RL06-mascon | 0.955 | 0.092 | 0.900 | ||
| WBS-GPS | RL06-G350 | 0.959 | 0.089 | 0.907 | |
| RL06-mascon | 0.959 | 0.089 | 0.907 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fok, H.S.; Zhou, L.; Liu, Y.; Tenzer, R.; Ma, Z.; Zou, F. Water Balance Standardization Approach for Reconstructing Runoff Using GPS at the Basin Upstream. Remote Sens. 2020, 12, 1767. https://doi.org/10.3390/rs12111767
Fok HS, Zhou L, Liu Y, Tenzer R, Ma Z, Zou F. Water Balance Standardization Approach for Reconstructing Runoff Using GPS at the Basin Upstream. Remote Sensing. 2020; 12(11):1767. https://doi.org/10.3390/rs12111767
Chicago/Turabian StyleFok, Hok Sum, Linghao Zhou, Yongxin Liu, Robert Tenzer, Zhongtian Ma, and Fang Zou. 2020. "Water Balance Standardization Approach for Reconstructing Runoff Using GPS at the Basin Upstream" Remote Sensing 12, no. 11: 1767. https://doi.org/10.3390/rs12111767
APA StyleFok, H. S., Zhou, L., Liu, Y., Tenzer, R., Ma, Z., & Zou, F. (2020). Water Balance Standardization Approach for Reconstructing Runoff Using GPS at the Basin Upstream. Remote Sensing, 12(11), 1767. https://doi.org/10.3390/rs12111767