1. Introduction
With the completion of the construction of China’s BeiDou navigation satellite system (BDS) in 2020, all global navigation satellite systems will be capable of offering global service [
1]. Along with two regional navigation satellite systems—the quasi-zenith satellite system (QZSS) from Japan and navigation with Indian constellation (NavIC) from India—medium/geosynchronous/inclined geosynchronous orbit satellites, whose altitudes are approximately 20,000 km, constitute the satellite navigation system. However, due to the weak signals of these satellites, the positioning, navigation and timing (PNT) services, on which many critical infrastructures are heavily dependent, are easily disrupted in a deeply attenuated environment or can be interfered with by a jammer [
2]. To avoid this limitation, the low Earth orbit (LEO)-augmented global navigation satellite system (GNSS) has attracted increased attention. Experimental results from a satellite time and location (STL) service carried out by Iridium show that, even on the lowest floor inside a building, the carrier-to-noise density power ratio (C/N0) from Iridium satellites ranges between 35 and 55 dB-Hz, which is approximately the same as GPS in an open sky environment [
3]. Stronger signals would make GNSS more resilient and resistant to jamming. In addition, simulation results show that the swifter motion of LEO satellites significantly reduces by 70%~90% the convergence time of the precise point positioning (PPP), and the tracking data of GNSS satellites from LEO satellites improves the accuracy of the precise orbit determination of GNSS by 70% [
4,
5,
6]. Thus, the LEO-augmented GNSS promises to make a considerable contribution to PNT services.
The prerequisite of the LEO-augmented GNSS service is a well-distributed LEO satellite constellation augmentation or a standalone backup navigation system. LEO satellite constellations consist of small satellites. Small satellites have greater component capabilities and low developing, building and launching costs. Small satellites have led to the wider application of large constellations in space missions, such as in telecommunication, the survey of resources and climate and sustaining global information networks, as well as navigation [
7,
8,
9,
10]. The construction of LEO constellations consisting of small satellites can be completed within a short time. However, because of the LEO’s much smaller footprint than the medium Earth orbit (MEO) satellite, many more satellites would be needed in order to provide the same coverage as an MEO [
11]. The emerging mega-constellations proposed by SpaceX, Telesat and OneWeb for internet broadband are great opportunities for integrating communication and navigation, but their huge costs and redundancy make these constellations less attractive [
12]. With the first successful launch of a trial satellite, China’s LEO-based augmentation system—Hongyan—is under construction [
13]. Therefore, the entire design routine of a well-distributed LEO global coverage constellation is important and in urgent demand.
Among all the existing navigation constellations, the Walker configuration is widely used in the global positioning system (GPS), Galileo, and global navigation satellite system (GLONASS), as well as the third-generation system of BDS (BDS-3) because of its symmetrical configuration and favourable global coverage. Walker configuration is denoted as N/P/F, where N represents the total number of satellites in a constellation, P is the number of orbital planes and F is an inter-plane phase parameter, signifying the relative location of the satellites in the adjacent plane [
14]. Besides this, many other configurations have also been figured out since the last century. Luders et al. introduced the streets-of-coverage design, in which the inclined circular orbit satellites were placed at the same altitude in a single plane, and several different planes were selected to achieve local or global coverage [
15]. Mortari et al. introduced a flower-constellation methodology which was generally characterized by repeatable ground tracks [
16]. The orbits in a flower constellation can be elliptical or circular, and the constellation can have zonal or global coverage, depending on the specific mission requirements. The satellites in the constellation share the same repeating ground track, perigee altitude, inclination and argument of perigee. Traditionally, analytical methods were mainly adopted in early constellation designs due to only a few satellites and the need for simple earth coverage. However, now, with hundreds or even thousands of satellites and the requirements of different tasks in a constellation, there is always a set of optimal solutions rather than one best solution. Therefore, constellation design has become a non-linear and multi-objective optimization problem.
Multi-objective optimization problems mean there is always a trade-off between objectives like the number of satellites and earth coverage. One of the tools which has proved to be effective in solving this problem is the genetic algorithm (GA). By combining several weighted objective functions into a single function, Ely et al. applied the GA for zonal elliptical streets of coverage in constellation design [
17]. However, the results of the GA were highly related to weight, which was always difficult to choose. Thus, instead of a single objective optimization, Ferringer et al. implemented a multi-objective evolutionary algorithm—the non-dominated sorting genetic algorithm-II (NSGA-II)—to generate sets of constellations. The results demonstrated that this was effective in searching for the complex trade-off spaces in satellite constellation design. Compared to an enumerative analysis, the NSGA-II enabled great cost saving in computational resources. Furthermore, the results of multi-objective evolutionary algorithm paradigms based on the two parallel processes of master–slave and island models showed excellent approximations of the true Pareto frontier [
18,
19].
Aiming at LEO satellites, Lang developed a LEO satellite constellation specifically for continuous coverage of the mid-latitude band [
20]. A regional augmentation system aiming at Chinese cities was designed by Zhang et al. in which the flower and Walker configurations with a restricted phasing scheme, as well as deployment strategies, were compared [
21]. Furthermore, Shtark et al. proposed an optimization algorithm for regional positioning using a LEO satellite constellation [
22]. The differences and similarities in the system architecture among three large broadband constellations—SpaceX, OneWeb and Telesat—were compared, and the total system throughput and minimum ground stations to support the system throughput were calculated by Portillo ID et al. [
12]. Aiming at LEO-based even global coverage augmentation systems, Ma et al. designed an optimal hybrid configuration of 100 LEO satellites. Besides this, the necessary number of satellites for different visible satellites and the elevation mask angle were studied using the GA [
23]. In the future, a LEO satellite constellation could either be an augmentation system in the environment, where the GNSS PNT service degrades, or a stand-alone backup navigation system, where the GNSS PNT service is not available. Therefore, it is essential to design LEO satellite constellations to fulfil both aspects.
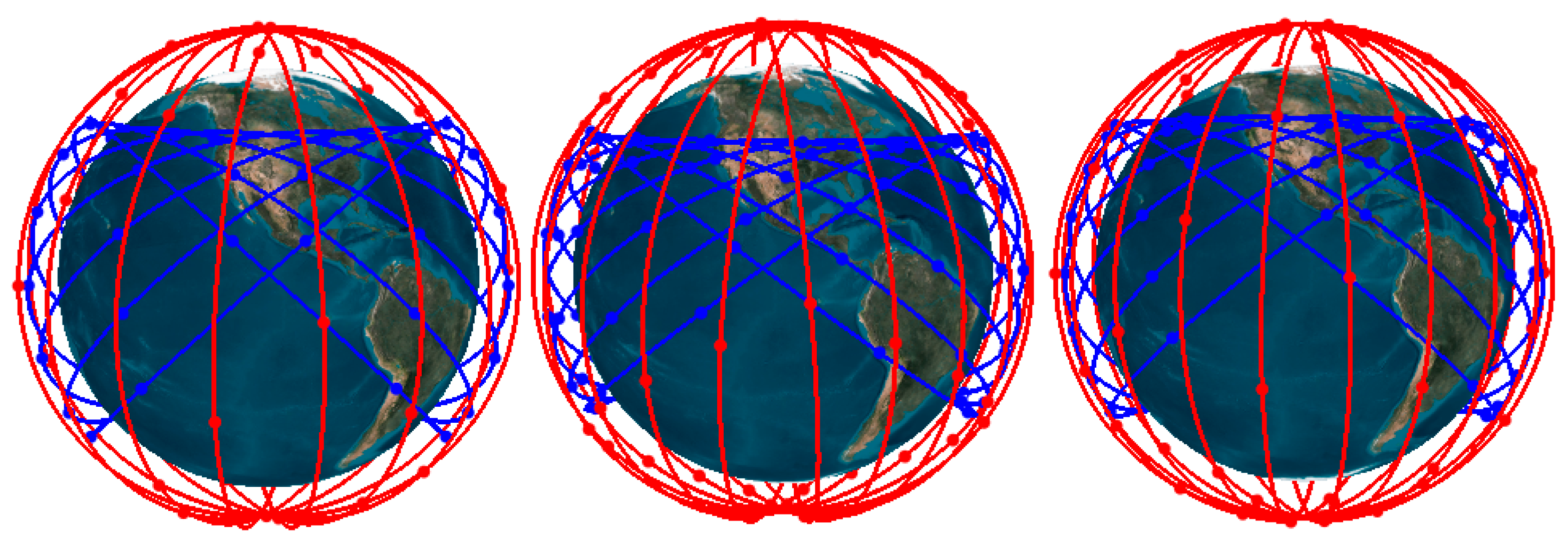
The Walker constellation is preferred for navigation because of its symmetrical configuration. For a LEO-based global navigation constellation, a polar or near-polar inclination is required. A polar constellation might increase the chance of collision in the polar region, especially in a large constellation. Consequently, a near-polar Walker constellation is adopted in this paper. With the near-polar Walker constellation, a global navigation constellation solely consisting of LEO satellites is designed under two situations: one is the two-objective optimization case, including the geometric dilution of precision (GDOP), measuring the constellation geometry and number of satellites, and the other is the three-objective optimization case including the number of satellites, the GDOP and satellite altitude. The NSGA-III, a reference-based NSGA-II, is used for the two- and three-objective navigation constellation design. For any LEO-augmented constellation with a specific altitude, the single objective is the global average of visible satellites; therefore, the GA is adopted for the augmented constellation design. Since it is hard to achieve an even global coverage with a single near-polar Walker constellation, a hybrid constellation with Walker/Walker constellation is designed for an even global coverage. Furthermore, the Walker/Walker LEO constellation is designed with the consideration of GNSS satellites, and the GDOPs of GNSS with and without LEO constellation are compared. Since the constellation design process is time-consuming, a parallel processing method is adopted in order to improve computing efficiency.
This paper mainly gives solutions to LEO navigation constellation design every 100 km for altitudes of 900 km~1500 km. Besides this, LEO augmentation constellations are designed every 100 km for altitudes of 900 km~1500 km from the global average visible satellites perspective. In addition, the GDOPs of the GNSS with and without LEO constellation are compared. From the search results, we prove that NSGA-III is able to give optimal fronts of constellation design. The paper is organized as follows:
Section 2 describes the problem and the methodology, the results and analysis are presented in
Section 3; and the conclusions and discussion are presented in the last section.
2. Problem Description and Methodology
2.1. Problem Description
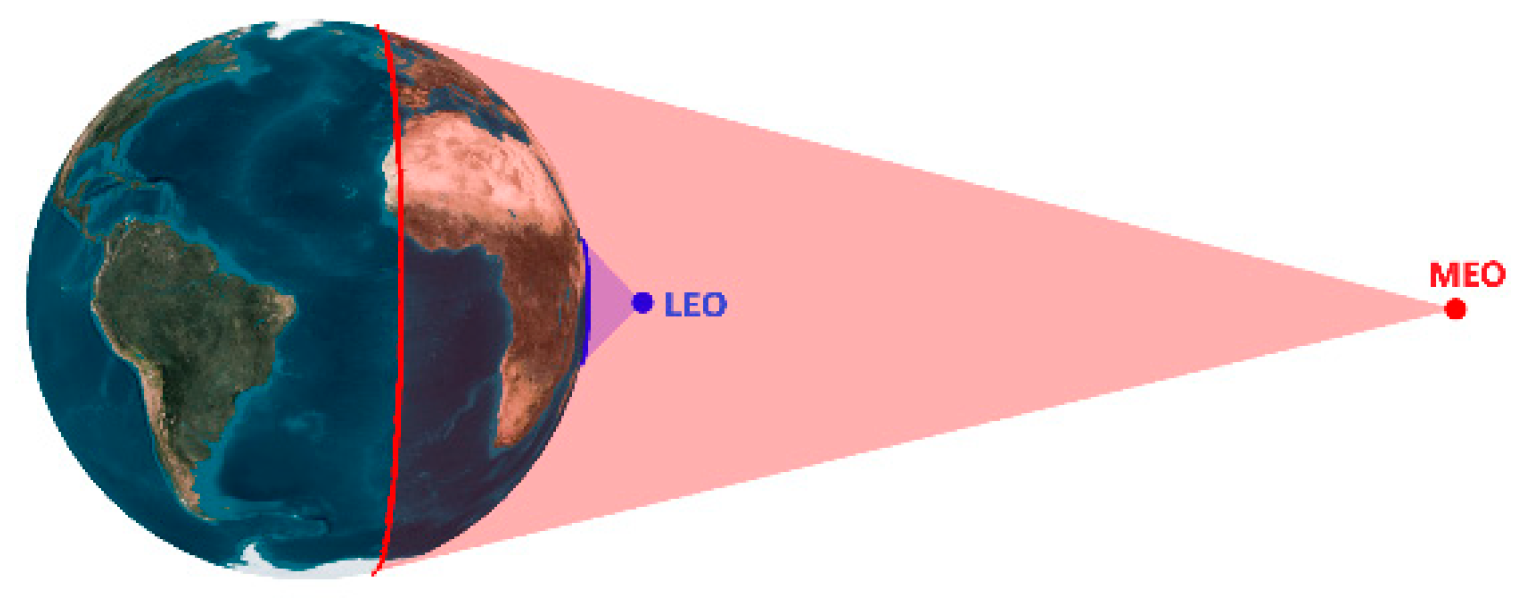
A Walker configuration has been widely used in navigation systems due to its symmetrical distribution and favourable global coverage. Owing to a remarkable difference in the footprints of a LEO and MEO, as shown in
Figure 1, many more satellites would be required in order to provide global coverage. The nadir-pointing coverage circle area
of a satellite is calculated as
;
(6378.14 km) is the radius of Earth and
is the satellite altitude. For instance, taking the MEO altitude as 20,200 km and the LEO altitude as 900 km, the ratio of the footprint areas of MEO/LEO is 6.146.
In the problem description section, the Walker configuration and the factor-GDOP of measuring the positioning performance for a satellite constellation are described.
2.1.1. Walker Pattern
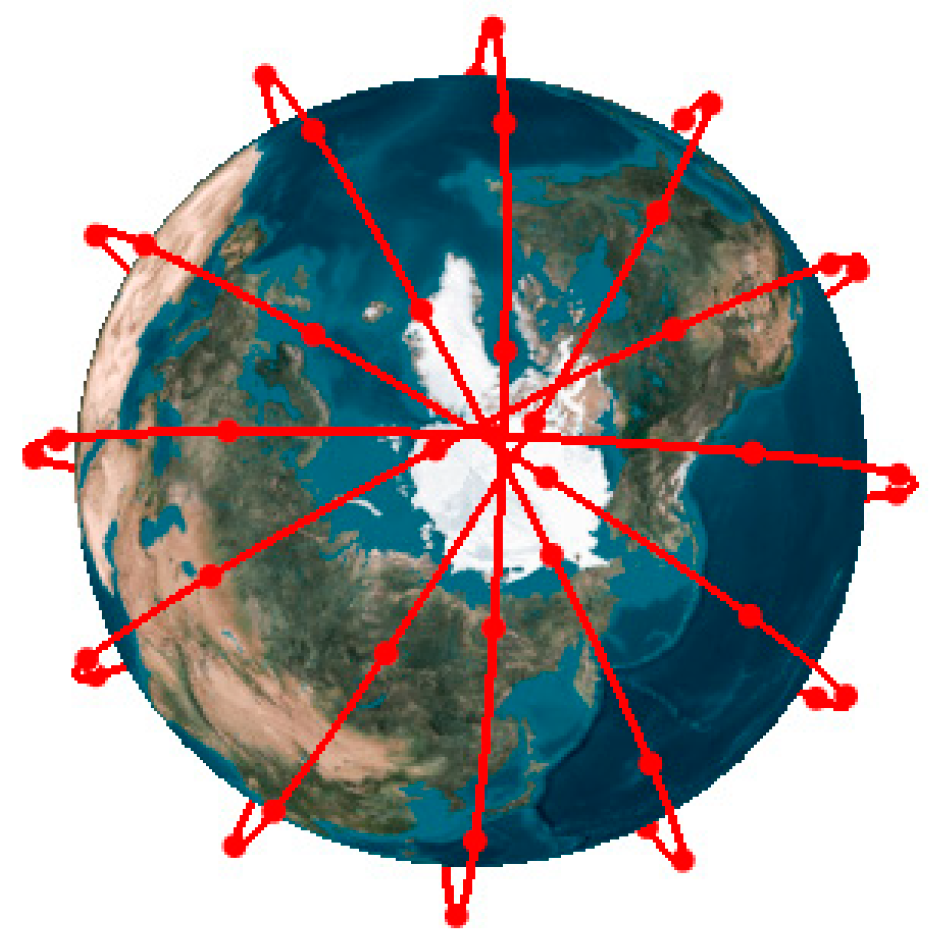
A Walker pattern constellation is described by three integers as N/P/F, where N denotes the total number of satellites in the constellation, P is the number of orbital planes and F is the phasing parameter, which defines the relative position of the satellites in the adjacent plane and values between 0 and P-1. Satellites in a Walker constellation are uniformly distributed in space. For instance, the distribution of satellites in the Iridium system, which is a Walker constellation, is depicted in
Figure 2. These satellites share the same semi-major axis, inclination, eccentricity and argument of perigee. The right ascension of the ascending nodes (RAAN) and the mean anomaly of the j-th satellites on the i-th plane are described by the following formulas [
24]:
where
represents the number of satellites per plane,
is the
and
is the mean anomaly. As such, satellites in a Walker configuration are specifically located.
2.1.2. GDOP
The problem of determining the user position, which concerns three unknown variables (i.e., Cartesian coordinates x, y, z), is solved through the known positions of navigation satellites. Usually, there is a time offset for the receiver clock; so, there are four unknown variables instead of three, meaning that there should be at least four satellites in sight at any time for determining the position of the user. The user position error is described as [
25]:
where the GDOP solely depends on the relative locations of the satellites and the user.
is the pseudo-range error factor, mainly including the effects of the satellite clock, ionosphere error, troposphere error, receiver noise and multi-path. GDOP ranges from zero to infinity (∞), and the geometry is ideal when GDOP tends towards 0. The larger the GDOP value is, the poorer the geometry of the satellite constellation.
2.2. Methods
In order to get the optimal parameters to describe a Walker constellation, NSGA-III, one of the GAs, is used in this paper. GA mimics Darwin’s theory of evolution, creating offspring through a procedure of cross, mutation and fitness selection. The procedure begins by producing a random population, and each individual, coded by a chromosome, represents a possible solution to the problem. The chromosome could be binary-coded or real-coded. For a binary-coded chromosome, cross techniques may be a one-point or two-point crossover. With a cross probability, two parent chromosomes exchange the bits after the point with one-point crossover and the bits between the points with two-point crossover to create two new offspring. With the new offspring, a mutation technique changes a random gene of the chromosome to create a new offspring with a mutation probability. For a binary-coded chromosome, the gene changes from 0 to 1 or from 1 to 0. A mutation technique introduces new members to the population and prevents prematurity. Better individuals are preserved to the next generation in accordance with their fitness functions. For a minimum problem, individuals with smaller fitness functions are carried on to the next generation. This loop of cross, mutation and fitness functions stops when the maximum generation or a stop criterion is met. For a multi-objective problem, the results achieve a Pareto frontier, which means no solution in this set can be better than the current one in some objective function without worsening the other objective function.
NSGA-III is a reference-point based NSGA-II [
26,
27]. In NSGA-II, crowding distance sorting is adopted to ensure population diversity. We will give an overview of crowding distance sorting in advance in order to get a better understanding of reference point distance sorting. The routine of crowding distance sorting is as follows: firstly, objective functions are sorted for individuals in every non-domination layer. The maximum and minimum for the m-th objective function are denoted as
and
, respectively. Next, crowding distance
is calculated as
. An individual with a larger crowding distance is sent to the next generation. With a fast non-dominating and crowding distance sorting, the NSGA-II is able to reduce the computational complexity of the NSGA and preserve elitism. However, with an increase in objectives, on the one hand, the identification of neighbors could be rather difficult, which means crowding distance sorting lacks diversity preservation; on the other hand, the searching process could be rather time-consuming. With a strategy change in reference point distance sorting, the NSGA-III is able to alleviate the problems of sticking to multiple local fronts, the computationally expensive identification of neighbours and the difficulty in creating new solutions when it concerns an increase in the number of objectives. More comparisons of the NSGA-II and NSGA-III are listed in the reference section [
28]. For NSGA-III, the algorithm starts with a random population
of size
, and after being sorted by non-domination, each member in this population is assigned a rank. Then, the main loop starts with an offspring
created from
by the usual cross and mutation operators. After this,
combines with its offspring
to form a population
of size
.
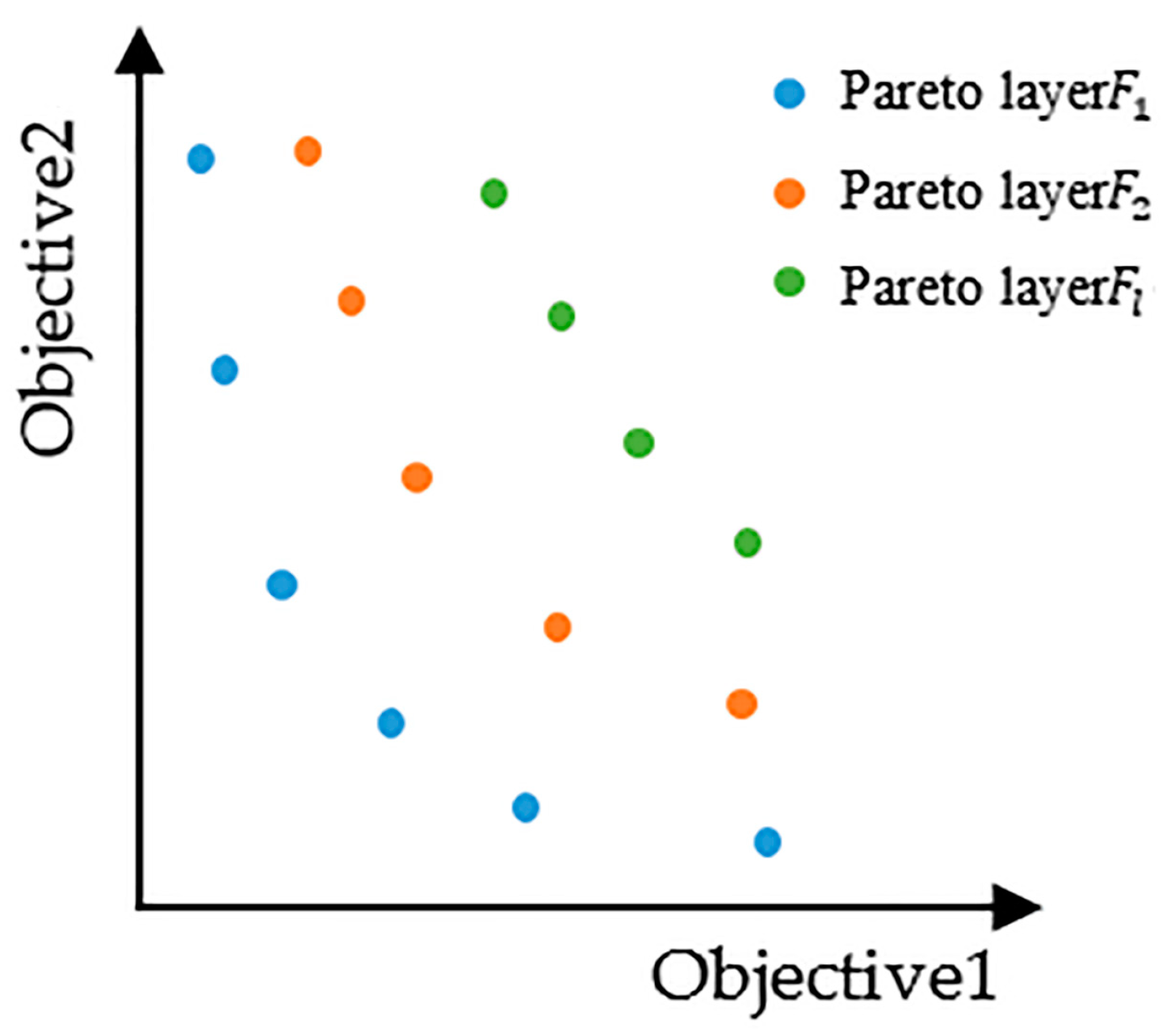
undergoes a routine of fast non-dominated sorting and reference point distance sorting. Fast non-dominated sorting sorts individuals in
into
layers such as
,
, …,
, as shown in
Figure 3, for two-objective optimization. Individuals in the same layer are non-dominated by each other; otherwise, for a minimum optimization problem, individuals in
are dominated by individuals in
, i.e., individuals in
dominate individuals in
.
After fast non-dominated sorting, individuals with lower non-dominated ranks are merged into until the size of is greater than or equal to N. If the size of is greater than N, and the procedure moves into the next generation. Otherwise, and individuals are selected from , .
Reference point distance sorting is performed on individuals in
to determine which
individuals are selected. Reference point distance sorting includes four sections: determination of reference points on a hyper-plane, adaptive normalization of population members, association operation and niche-preservation operation. Firstly, for a three-objective problem with four divisions, widely distributed reference points are chosen for each objective axis which are produced using Das and Dennis’s systematic approach [
29]. These reference points are deemed ideally well distributed in space, and the size of population must be the same as the number of reference points. Secondly, as the objectives are always in different units, they are normalized. Each minimum for
objective functions
are found to get them translated into objectives
. With
, extreme points are calculated as:
Then,
extreme objective vectors
are made to constitute a linear hyper-plane. With this hyper-plane, the intercept
of extreme vectors on the i-th objective axis can be computed. Therefore, the objective functions can be normalized using the following equation:
After this normalization, the perpendicular distance of each individual in is calculated from each of the reference lines, which is joined by the reference point with the origin on the hyper-plane. Then, the reference point with the smallest distance is associated with the individual. The niche count of a reference point is calculated, except for the last-domination layer, i.e., , and the niche count can be zero or more than one. Individuals associated with the reference point that has the lowest niche count should be preserved to ensure population diversity. The reference point with the lowest niche count is selected to find out whether this point is associated with the individuals in . If not, another reference point is selected until at least one individual in is associated. If none of the individuals in are associated with the selected reference point, the individual with the minimum perpendicular distance in is selected; otherwise, a random individual in is selected since the population diversity has already been assured. The niche preservation operation stops once individuals are selected in . As such, the size of is N, and the one loop of mutation, cross, non-dominated sorting and reference point distance sorting completes. This loop continues until the maximum generation or a stop criterion has been met.
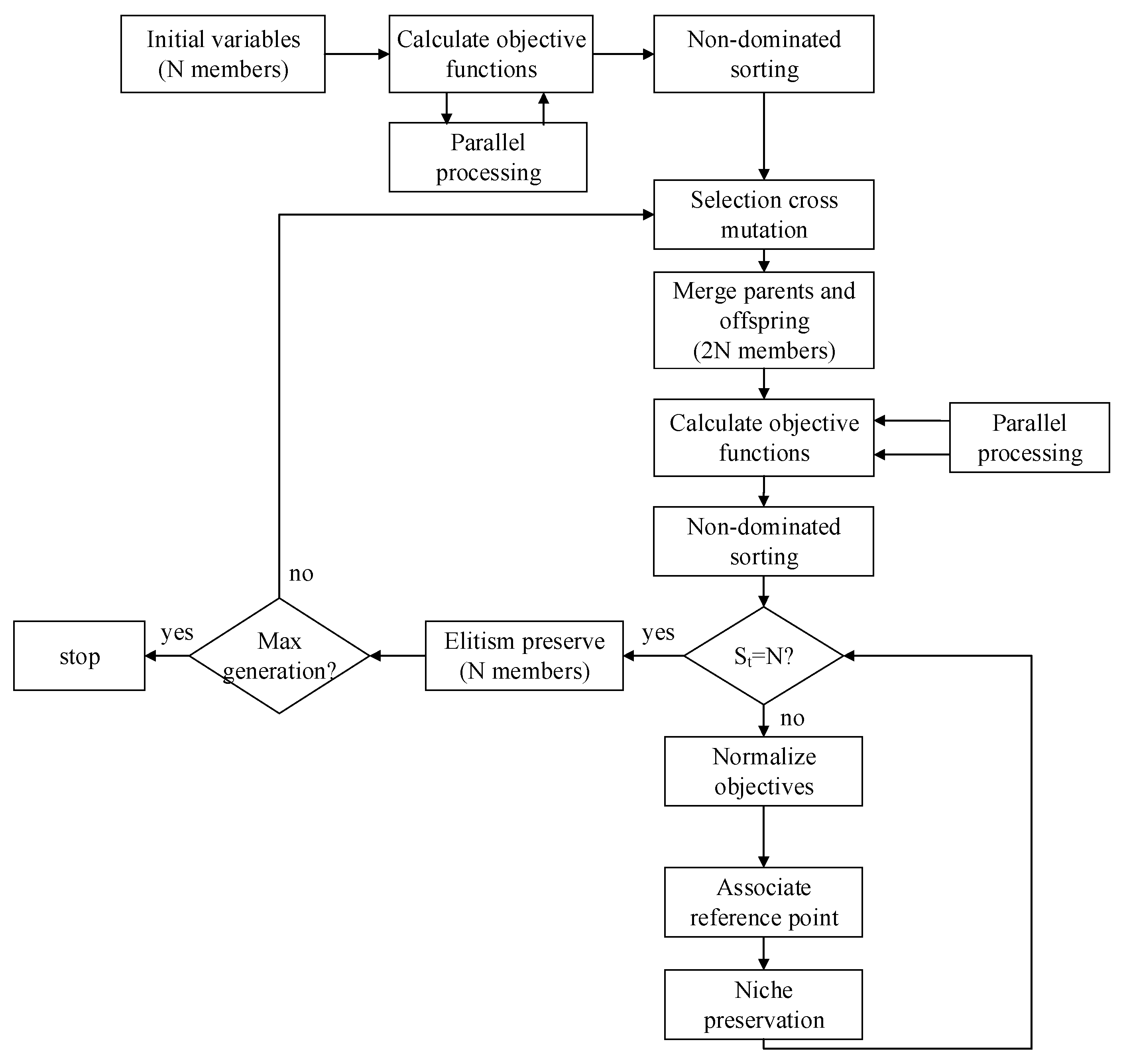
A flow chart of the NSGA-III in parallel processing is presented in
Figure 4.
4. Conclusions
The premise of a LEO navigation system or a LEO-augmented GNSS system is a well-distributed global coverage LEO constellation. For a LEO-based navigation constellation, the GDOP and the number of satellites need to be considered. For a LEO-based global augmentation constellation, the global average of visible satellites is required. With one Walker configuration, it was hard to get even global coverage. Therefore, a hybrid Walker/Walker constellation was designed. The GDOPs of the GNSS with and without LEO satellites were compared.
To achieve a suitable altitude for the LEO constellation, the air drag effects on satellites at altitudes of 500 km to 1100 km were evaluated. The results showed that air drag had a great effect mainly on the semi-major axes of the satellites, whose altitudes were lower than 900 km. For satellites with an altitude of 500 km, the semi-major axis decreased by 8 km in 20 days. The semi-major axis decreased by 31 meters for satellites with an altitude of 900 km.
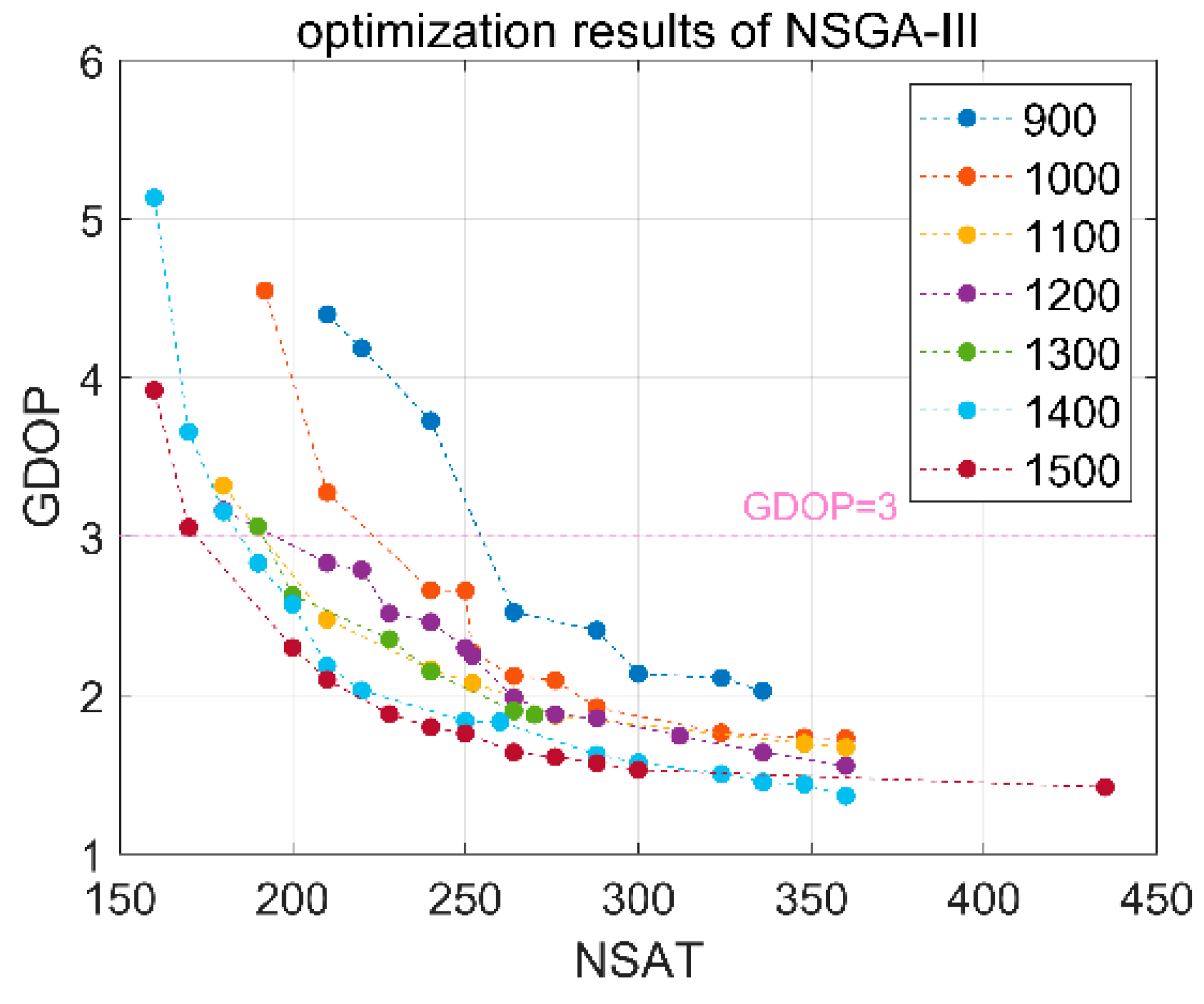
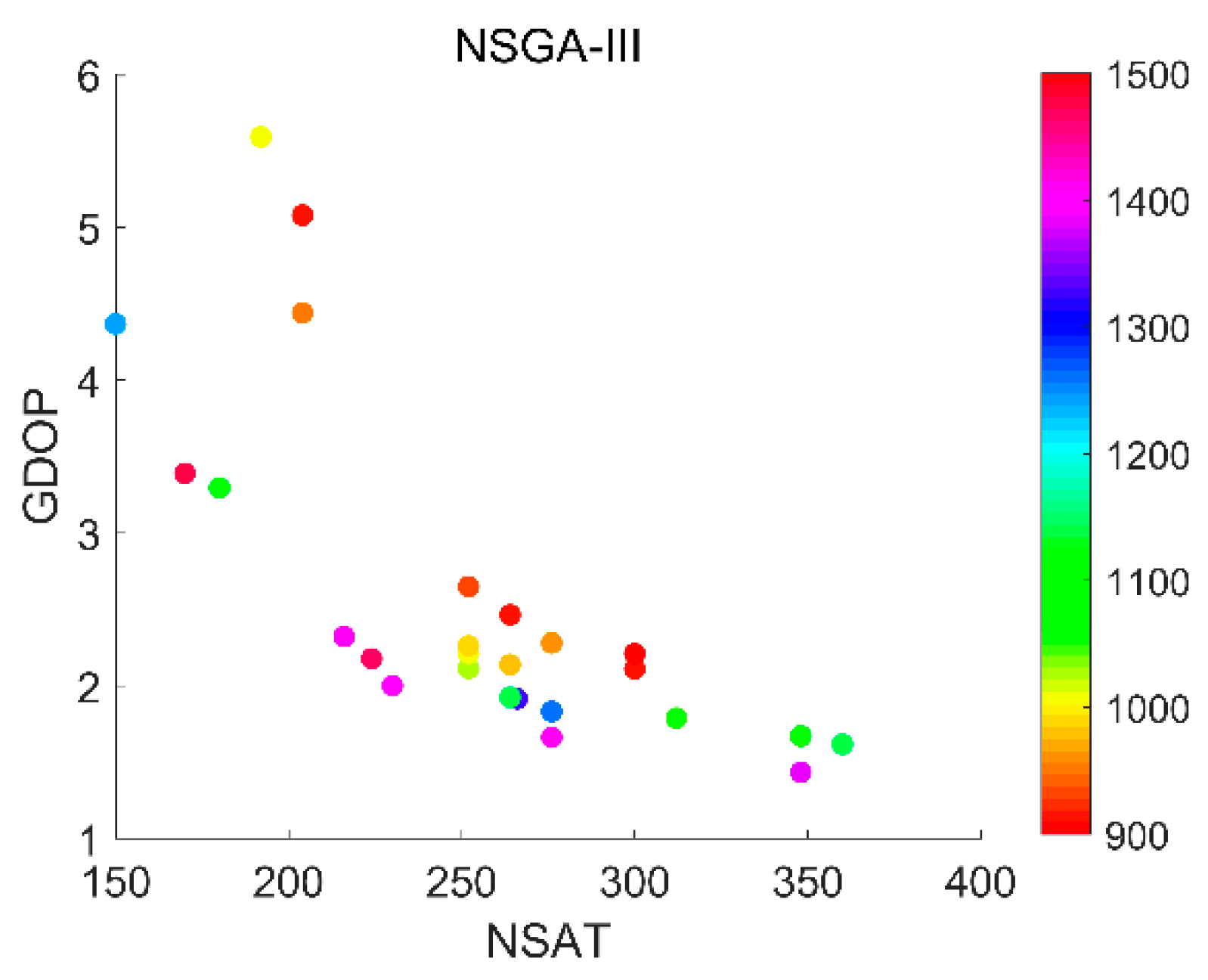
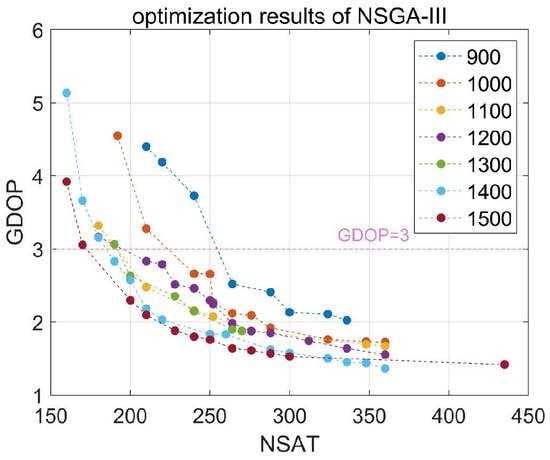
With a suitable altitude range, global navigation constellations were designed with two-objective and three-objective optimization. The results demonstrate that the following configurations are recommended for two-objective optimization: for an altitude of 900 km, the configuration of W264/12/1 with an inclination of 88.54°; for an altitude of 1000 km, W240/10/9 with an inclination of 85.64°; for an altitude of 1100 km, W210/10/7 with an inclination of 85.64°; for an altitude of 1200 km, W210/10/8 with an inclination of 85.64°; for an altitude of 1300 km, W200/10/1 with an inclination of 86.72°; for an altitude of 1400 km, W190/10/8 with an inclination of 88.55°; and for an altitude of 1500 km, W180/10/1 with an inclination of 85.64°. For global navigation with three-objective optimization, a configuration of W252/12/1 with an inclination of 85.64° and altitude of 1008.23 km is recommended.
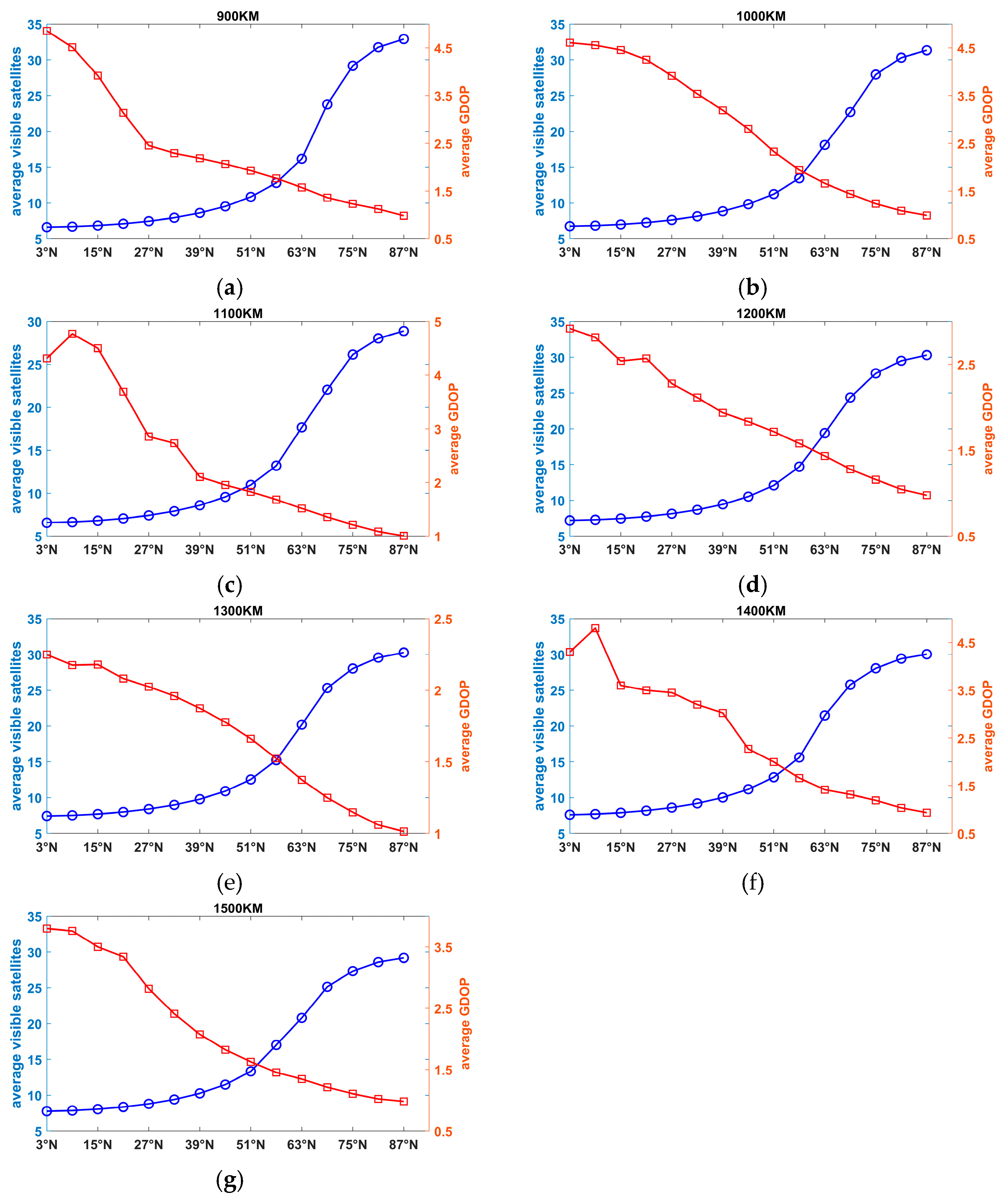
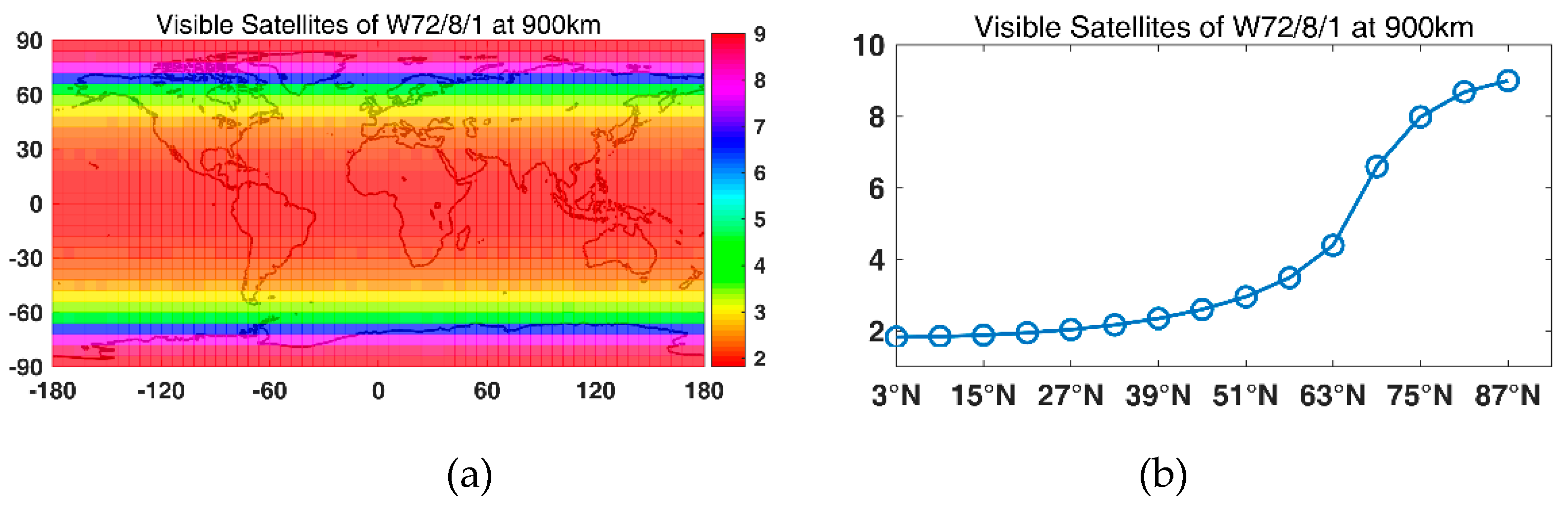
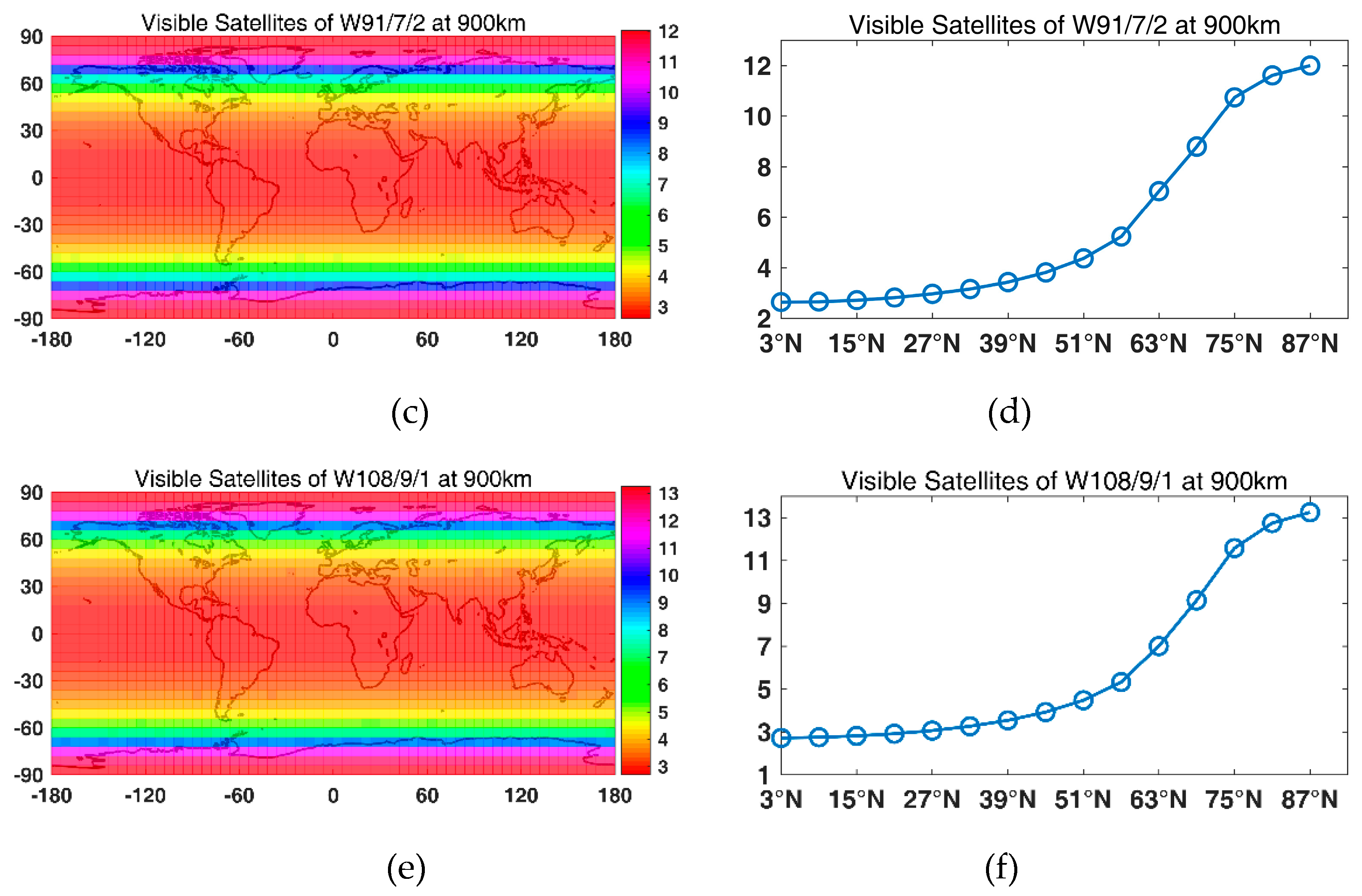
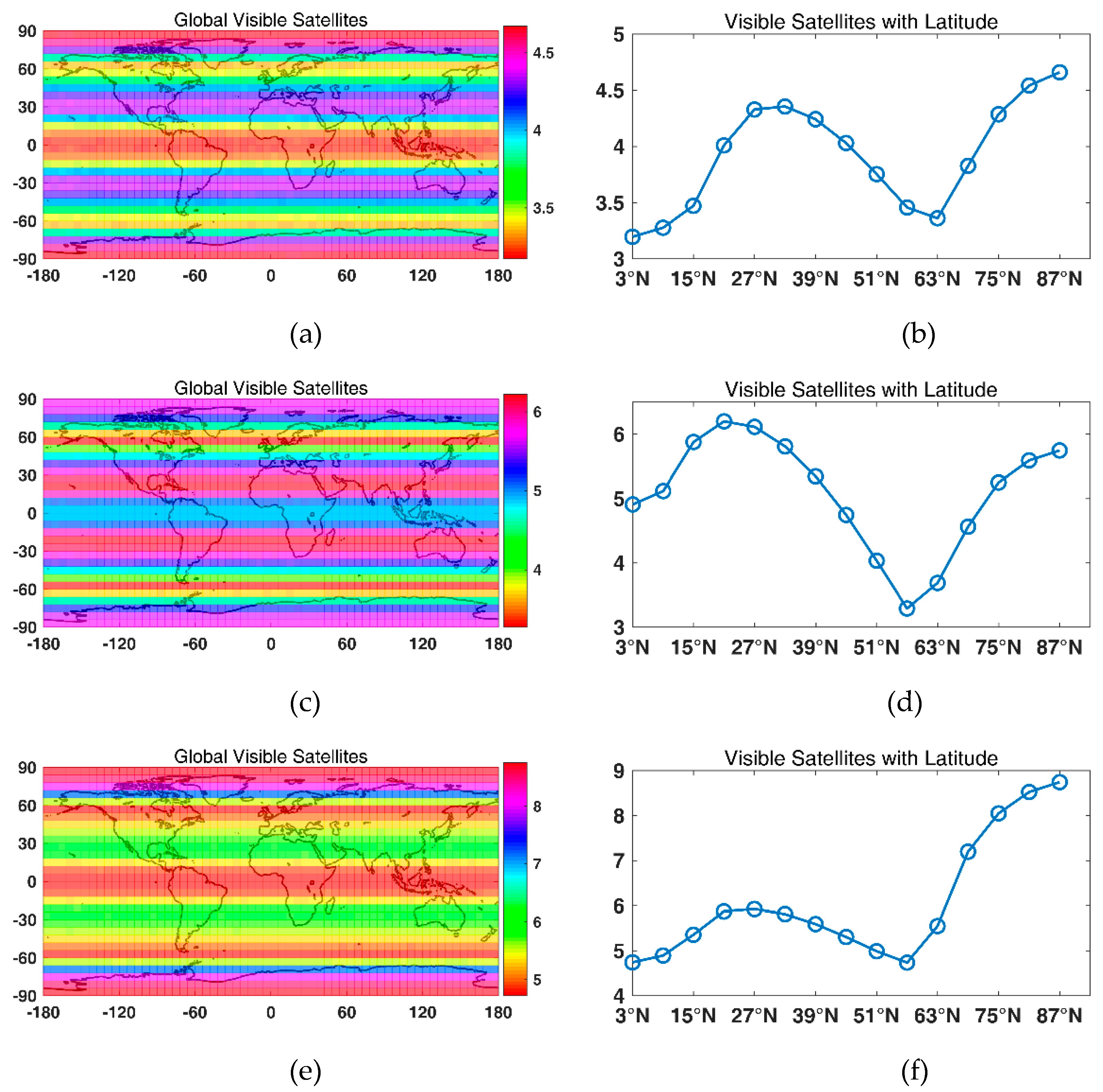
Then, LEO-based augmentation constellations were designed using the GA. First, a constellation with one Walker constellation was designed. For a global average of four visible satellites, 72/65/63/56/52/50/48 satellites were needed for altitudes of 900 km/1000 km/1100 km/1200 km/1300 km/1400 km/ and 1500 km, respectively. For a global average of five visible satellites, 91/84/77/70/66/60/56 satellites were needed for altitudes of 900 km/1000 km/1100 km/1200 km/1300 km/1400 km/ and 1500 km, respectively. For a global average of six visible satellites, 108/100/91/90/78/75/70 satellites were needed for altitudes of 900 km/1000 km/1100 km/1200 km/1300 km/1400 km/ and 1500 km, respectively. With the global average of visible satellites increasing from four to five and six, the available percentage for navigation increased approximately from 40% to 50% and 60%. Note that it was hard to achieve even global coverage with one constellation. Therefore, a Walker/Walker hybrid constellation was designed. The results show that a more even global coverage could be achieved with two constellations, and the available percentage of navigation of an average of six visible satellites was 95.58%.
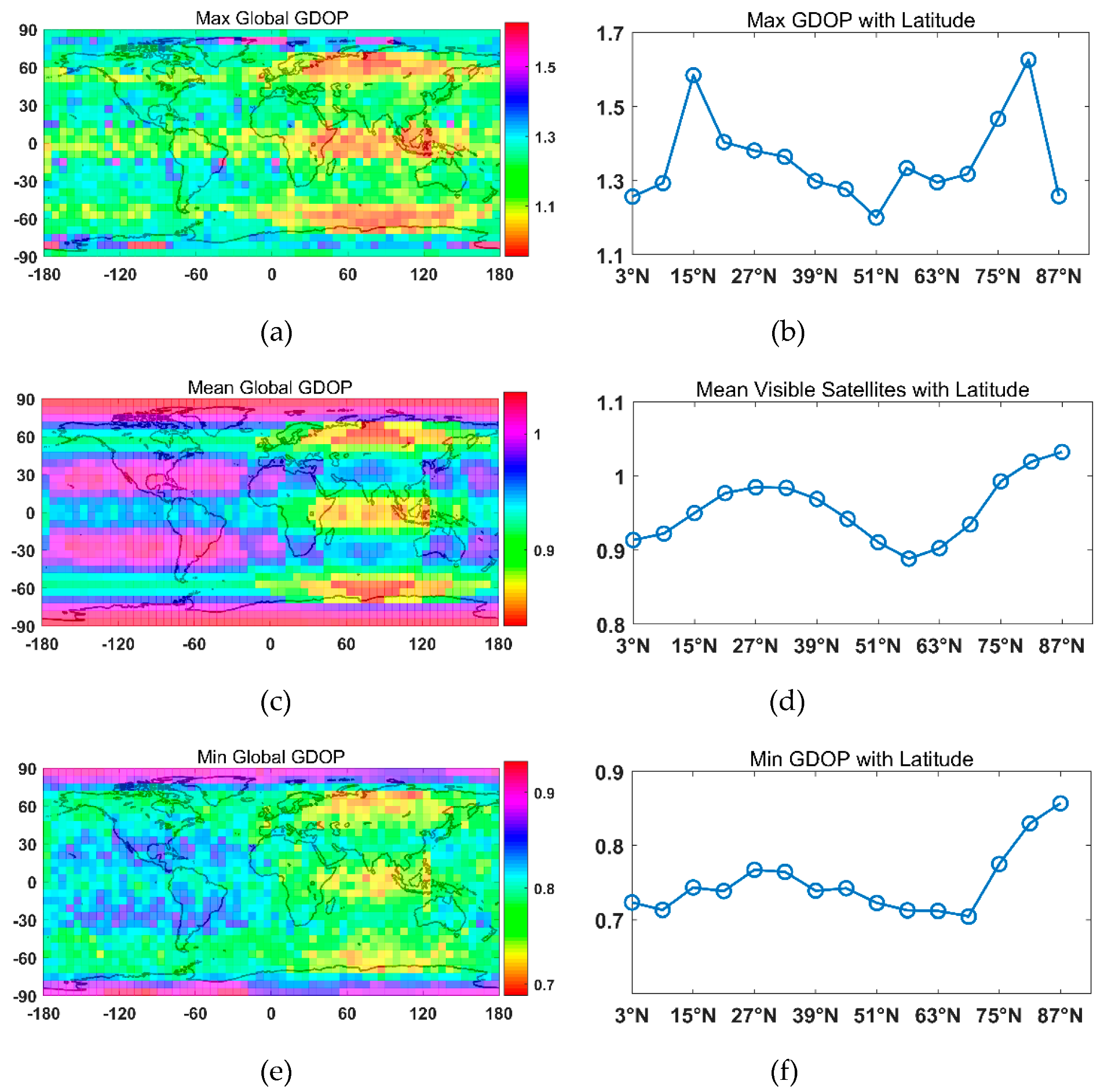
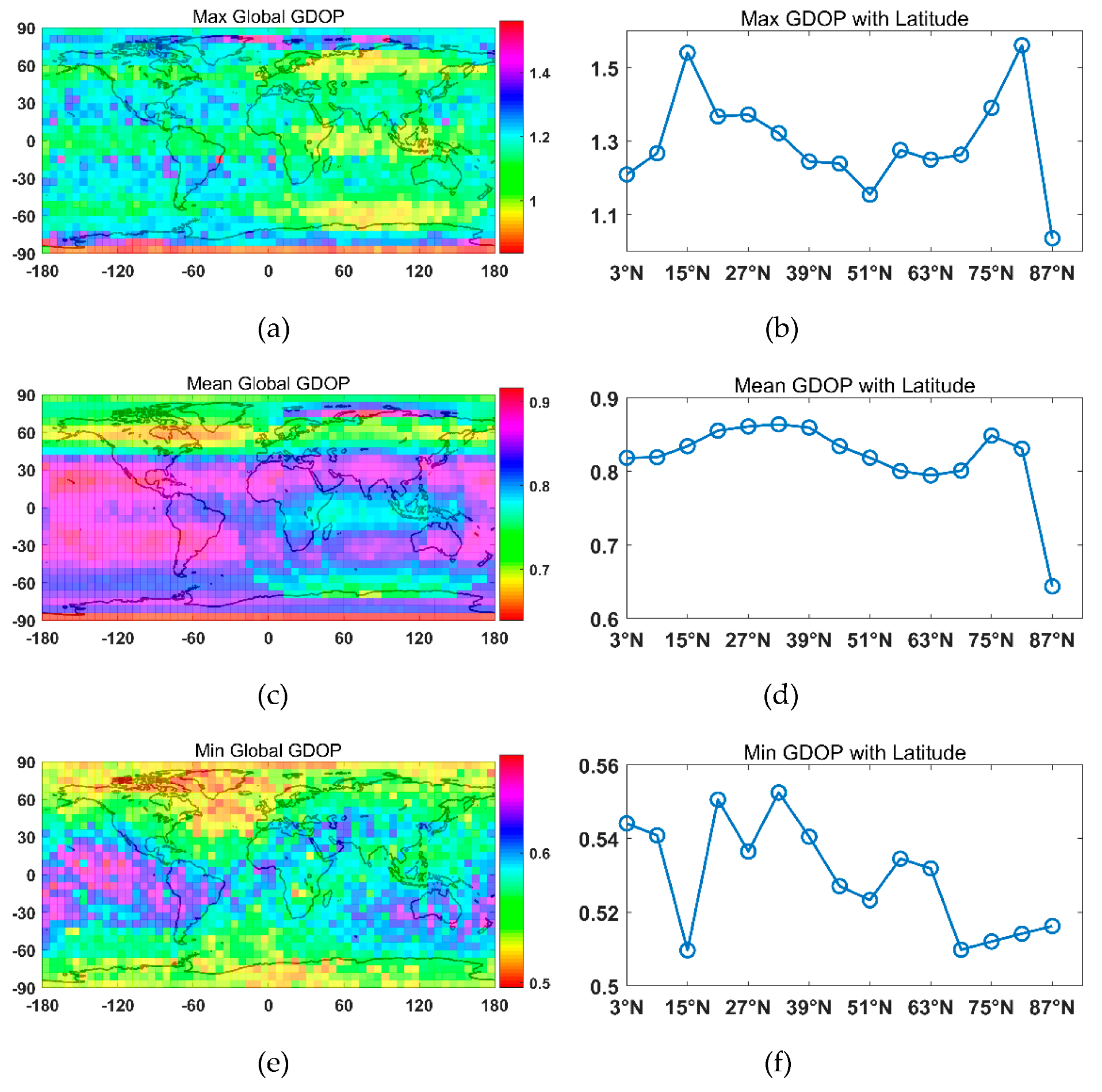
A hybrid Walker/Walker LEO constellation along with GNSS satellites was designed using the NSGA-III with two-objective optimization. The results show that with the 56 LEO satellites introduced in the GNSS, the global mean GDOP of the GNSS decreased from 0.9549 to 0.8048; the global maximum GDOP of the GNSS decreased from 1.6264 to 1.5611; and the global minimum GDOP of the GNSS decreased from 0.6880 to 0.4962. Note that even though only a small range of GDOP was improved, the main contribution of LEO satellites was to reduce the convergence time of the GNSS PPP and provide a backup PNT service where GNSS signals were blocked or interfered with.
The results above were obtained by using NSGA-III and GA. It can be seen that the NSGA-III was able to find the optimal front of constellation design. Parallel computing shortens the running time considerably. With parallel computing, the NSGA-III under a 1400 km altitude and three-objective optimization runs 27.3 and 28.16 times faster, respectively, than serial computing.
In summary, LEO-based navigation constellations with a Walker configuration need 180~264 satellites for altitudes of 1500 km~900 km in order to achieve a global average GDOP of less than three; LEO-based augmentation constellations with a Walker configuration need fewer satellites than navigation constellation to realize global averages of four, five and six visible satellites. Nevertheless, due to the constraint of global coverage, LEO-based augmentation constellations with a single Walker configuration find it hard to achieve even global even coverage. Instead of a single Walker configuration, a hybrid Walker/Walker constellation is able to achieve a more even global coverage.