WaterNet: A Convolutional Neural Network for Chlorophyll-a Concentration Retrieval
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Datasets
2.2. CNN-Based Chl-a Concentration Model
2.2.1. Data Preprocessing and Normalization
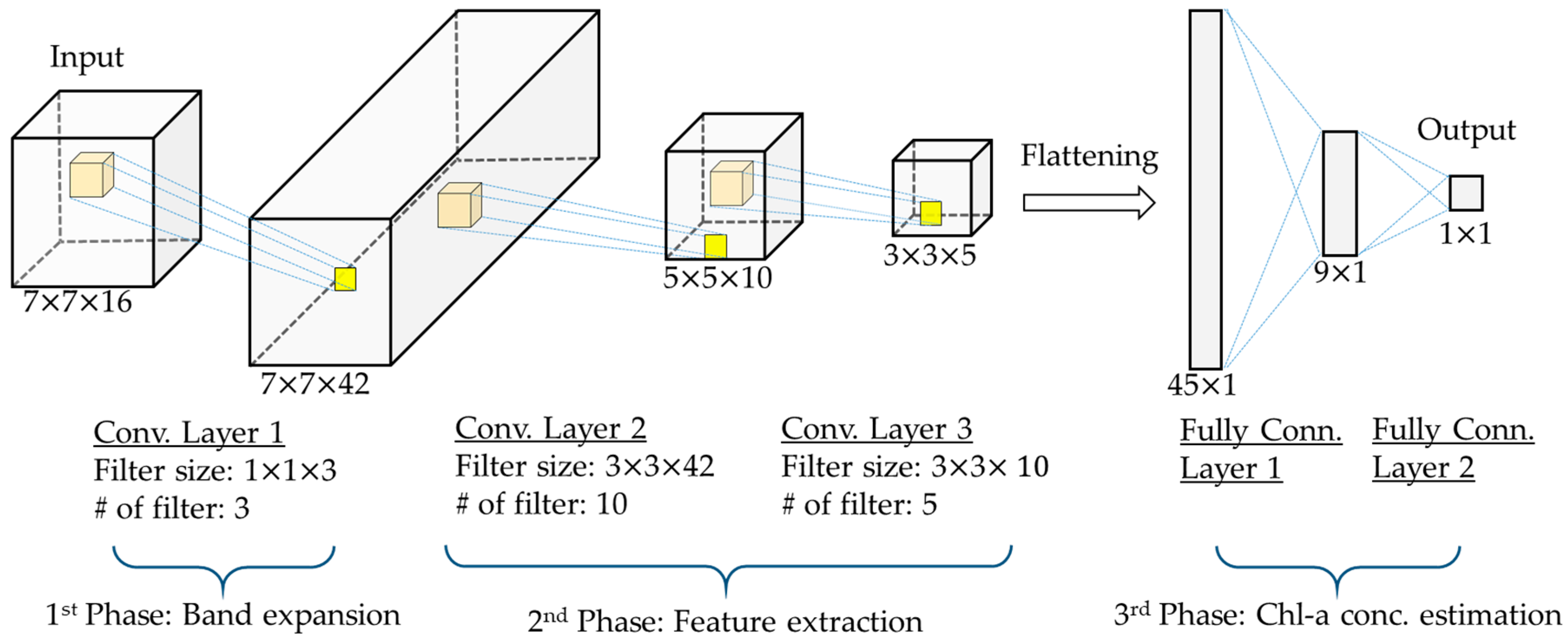
2.2.2. Network Structure of WaterNet
2.2.3. Two-Stage Training
2.2.4. Postprocessing of WaterNet
3. Experimental Results
WaterNet Performance Evaluation
4. Discussion
4.1. Comparison Between WaterNet and Feedforward Neural Networks
4.2. Comparison of WaterNet and Related Chl-a Concentration Models
5. Conclusions and Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Francis, G. Poisonous Australian lake. Nature 1878, 18, 11–12. [Google Scholar] [CrossRef] [Green Version]
- Shumwey, S.E. A review of the effects of algal blooms on shellfish and aquaculture. J. World Aquac. Soc. 1990, 21, 65–104. [Google Scholar] [CrossRef]
- Hoagland, A.P.; Anderson, D.M.; Kaoru, Y.; White, A.W.; Hoaglandl, P. The economic effects of harmful algal blooms in the United States: Estimates, assessment issues, and information. Assessment 2012, 25, 819–837. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, X.; Cheng, X.; Wang, C. Remote estimation of chlorophyll-a concentrations in Taihu Lake during cyanobacterial algae bloom outbreak. In Proceedings of the 2011 19th International Conference on Geoinformatics, Shanghai, China, 24–26 June 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Ha, N.T.T.; Koike, K.; Nhuan, M.T.; Canh, B.D.; Thao, N.T.P.; Parsons, M. Landsat 8/OLI Two bands ratio algorithm for chlorophyll-a concentration mapping in hypertrophic waters: An application to west lake in Hanoi (Vietnam). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4919–4929. [Google Scholar] [CrossRef]
- Kown, Y.S.; Baek, S.H.; Lim, Y.K.; Pyo, J.C.; Ligaray, M.; Park, Y.; Cho, K.H. Monitoring coastal chlorophyll-a concentrations in coastal areas using machine learning models. Water 2018, 10, 1020. [Google Scholar] [CrossRef] [Green Version]
- Van Nguyen, M.; Lin, C.H.; Chu, H.J.; Jaelani, L.M.; Syariz, M.A. Spectral feature selection optimization for water quality estimation. Int. J. Environ. Res. Public Health 2020, 17, 272. [Google Scholar] [CrossRef] [Green Version]
- González Vilas, L.; Spyrakos, E.; Torres Palenzuela, J.M. Neural network estimation of chlorophyll a from MERIS full resolution data for the coastal waters of Galician rias (NW Spain). Remote Sens. Environ. 2011, 115, 524–535. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Q.; Wu, C.; Zhao, S.; Xu, X.; Wang, Y.; Huang, C. Estimation of chlorophyll a concentration using NIR/Red bands of MERIS and classification procedure in inland turbid water. IEEE Trans. Geosci. Remote Sens. 2012, 50, 988–997. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Shen, Q.; Zhang, B.; Tian, L.; Ye, H.; Wang, S.; Lu, Z. A soft-classification-based chlorophyll-a estimation method using MERIS data in the highly turbid and eutrophic Taihu Lake. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 138–149. [Google Scholar] [CrossRef]
- Cristina, S.; Fragoso, B.; Icely, J.; Grant, J. Aquaspace Project Document. 2018. Available online: http://www.aquaspace-h2020.eu/wp-content/uploads/2018/09/AquaSpaceMM-07-RS-27Aug18.pdf (accessed on 14 May 2020).
- Toming, K.; Kutser, T.; Uiboupin, R.; Arikas, A.; Vahter, K.; Paavel, B. Mapping water quality parameters with Sentinel-3 ocean and land colour instrument imagery in the Baltic Sea. Remote Sens. 2017, 9, 1070. [Google Scholar] [CrossRef] [Green Version]
- Kravitz, J.; Matthews, M.; Bernard, S.; Griffith, D. Application of Sentinel 3 OLCI for chl-a retrieval over small inland water targets: Successes and challenges. Remote Sens. Environ. 2020, 237. [Google Scholar] [CrossRef]
- Pahlevan, N.; Lee, Z.; Wei, J.; Schaaf, C.B.; Schott, J.R.; Berk, A. On-orbit radiometric characterization of OLI (Landsat-8) for applications in aquatic remote sensing. Remote Sens. Environ. 2014, 154, 272–284. [Google Scholar] [CrossRef]
- Bernardo, N.; Watanabe, F.; Rodrigues, T.; Alcântara, E. An investigation into the effectiveness of relative and absolute atmospheric correction for retrieval the TSM concentration in inland waters. Model. Earth Syst. Environ. 2016, 2. [Google Scholar] [CrossRef] [Green Version]
- Du, Y.; Teillet, P.M.; Cihlar, J. Radiometric normalization of multitemporal high-resolution satellite images with quality control for land cover change detection. Remote Sens. Environ. 2002, 82, 123–134. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Vitti, A.; Lyzenga, D.R. Multiple optimal depth predictors analysis (MODPA) for river bathymetry: Findings from spectroradiometry, simulations, and satellite imagery. Remote Sens. Environ. 2018, 218, 132–147. [Google Scholar] [CrossRef]
- Wang, D.; Ma, R.; Xue, K.; Loiselle, S.A. The assessment of landsat-8 OLI atmospheric correction algorithms for inland waters. Remote Sens. 2019, 11, 169. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.; Carder, K.L.; Muller-Karger, F.E. Atmospheric correction of SeaWiFS imagery over turbid coastal waters: A practical method. Remote Sens. Environ. 2000, 74, 195–206. [Google Scholar] [CrossRef]
- Denaro, L.G.; Lin, B.-Y.; Syariz, M.A.; Jaelani, L.M.; Lin, C.-H. Pseudoinvariant feature selection for cross-sensor optical satellite images. J. Appl. Remote Sens. 2018, 12. [Google Scholar] [CrossRef]
- Lin, B.-Y.; Wang, Z.-J.; Syariz, M.A.; Denaro, L.G.; Lin, C.-H. Pseudoinvariant feature selection using multitemporal MAD for optical satellite images. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1353–1357. [Google Scholar] [CrossRef]
- Syariz, M.A.; Lin, B.Y.; Denaro, L.G.; Jaelani, L.M.; Van Nguyen, M.; Lin, C.H. Spectral-consistent relative radiometric normalization for multitemporal Landsat 8 imagery. ISPRS J. Photogramm. Remote Sens. 2019, 147, 56–64. [Google Scholar] [CrossRef]
- Guindon, B. Assessing the radiometric fidelity of high resolution satellite image mosaics. ISPRS J. Photogramm. Remote Sens. 1997, 52, 229–243. [Google Scholar] [CrossRef]
- Li, J.; Gao, M.; Feng, L.; Zhao, H.; Shen, Q.; Zhang, F.; Wang, S.; Zhang, B. Estimation of chlorophyll-a concentrations in a highly turbid eutrophic lake using a classification-based MODIS land-band algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3769–3783. [Google Scholar] [CrossRef]
- Tao, M.; Duan, H.; Cao, Z.; Loiselle, S.A.; Ma, R. A Hybrid EOF algorithm to improve MODIS cyanobacteria phycocyanin data quality in a highly turbid lake: Bloom and nonbloom condition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4430–4444. [Google Scholar] [CrossRef]
- Igamberdiev, R.M.; Grenzdoerffer, G.; Bill, R.; Schubert, H.; Bachmann, M.; Lennartz, B. Determination of chlorophyll content of small water bodies (kettle holes) using hyperspectral airborne data. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 912–921. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Gitelson, A.A. Effect of bio-optical parameter variability and uncertainties in reflectance measurements on the remote estimation of chlorophyll-a concentration in turbid productive waters: Modeling results. Appl. Opt. 2006, 45, 3577. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Al Shehhi, M.R.; Gherboudj, I.; Zhao, J.; Ghedira, H. Improved atmospheric correction and chlorophyll-a remote sensing models for turbid waters in a dusty environment. ISPRS J. Photogramm. Remote Sens. 2017, 133, 46–60. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Dall’Olmo, G.; Moses, W.; Rundquist, D.C.; Barrow, T.; Fisher, T.R.; Gurlin, D.; Holz, J. A simple semi-analytical model for remote estimation of chlorophyll-a in turbid waters: Validation. Remote Sens. Environ. 2008, 112, 3582–3593. [Google Scholar] [CrossRef]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Povazhnyy, V. Satellite estimation of chlorophyll-a concentration using the red and NIR bands of MERIS—The Azov sea case study. IEEE Geosci. Remote Sens. Lett. 2009, 6, 845–849. [Google Scholar] [CrossRef]
- Barnes, B.B.; Hu, C.; Cannizzaro, J.P.; Craig, S.E.; Hallock, P.; Jones, D.L.; Lehrter, J.C.; Melo, N.; Schaeffer, B.A.; Zepp, R. Estimation of diffuse attenuation of ultraviolet light in optically shallow Florida Keys waters from MODIS measurements. Remote Sens. Environ. 2014, 140, 519–532. [Google Scholar] [CrossRef]
- Andrzej Urbanski, J.; Wochna, A.; Bubak, I.; Grzybowski, W.; Lukawska-Matuszewska, K.; Łącka, M.; Śliwińska, S.; Wojtasiewicz, B.; Zajączkowski, M. Application of Landsat 8 imagery to regional-scale assessment of lake water quality. Int. J. Appl. Earth Obs. Geoinf. 2016, 51, 28–36. [Google Scholar] [CrossRef]
- Niroumand-jadidi, M.; Bovolo, F.; Bruzzone, L. Novel spectra-derived features for empirical retrieval of water quality parameters: Demonstrations for OLI, MSI, and OLCI sensors. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10285–10300. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Ding, J. Evaluation of water quality based on a machine learning algorithm and water quality index for the Ebinur Lake Watershed. Sci. Rep. 2017, 1–18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carder, K.L.; Chen, F.R.; Lee, Z.P.; Hawes, S.K.; Kamykowski, D. Semianalytic moderate-resolution imaging spectrometer algorithm for chlorophyll-a and absorption with bio-optical domains based on nitrate-depletion temperatures. J. Geophys. Res. 1999, 104, 5403–5421. [Google Scholar] [CrossRef]
- Garver, S.A.; Siegel, D.A. Inherent optical property inversion of ocean color spectra and its biogeochemical interpretation 1. Time series from the Sargassio Sea. J. Geophys. Res. 1997, 102, 18607–18625. [Google Scholar] [CrossRef]
- Ioannou, I.; Gilerson, A.; Gross, B.; Moshary, F.; Ahmed, S. Neural network approach to retrieve the inherent optical properties of the ocean from observations of MODIS. Appl. Opt. 2011, 50, 3168. [Google Scholar] [CrossRef] [PubMed]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef] [Green Version]
- Tsagkatakis, G.; Aidini, A.; Fotiadou, K.; Giannopoulos, M.; Pentari, A.; Tsakalides, P. Survey of deep-learning approaches for remote sensing observation enhancement. Sensors 2019, 19, 3929. [Google Scholar] [CrossRef] [Green Version]
- Syariz, M.A.; Lin, C.; Blanco, A.C. Chlorophyll-a concentration retrieval using convolutional neural networks in Laugna Lake, Philippines. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII, 14–15. [Google Scholar]
- Ioannou, I.; Gilerson, A.; Gross, B.; Moshary, F.; Ahmed, S. Deriving ocean color products using neural networks. Remote Sens. Environ. 2013, 134, 78–91. [Google Scholar] [CrossRef]
- Buckton, D.; O’Mongain, E.; Danaher, S. The use of neural networks for the estimation of oceanic constituents based on the MERIS instrument. Int. J. Remote Sens. 1999, 20, 1841–1851. [Google Scholar] [CrossRef]
- Hafeez, S.; Wong, M.; Ho, H.; Nazeer, M.; Nichol, J.; Abbas, S.; Tang, D.; Lee, K.; Pun, L. Comparison of machine learning algorithms for retrieval of water quality indicators in case-II waters: A case study of Hong Kong. Remote Sens. 2019, 11, 617. [Google Scholar] [CrossRef] [Green Version]
- El-habashi, A.; El-habashi, A.; Ahmed, S.; Ondrusek, M.; Lovko, V. Analyses of satellite ocean color retrievals show advantage of neural network approaches and algorithms that avoid deep blue bands. J. Appl. Remote Sens. 2020, 13. [Google Scholar] [CrossRef]
- Herrera, E.; Nadaoka, K.; Blanco, A.C.; Hernandez, E.C. Hydrodynamic investigation of a shallow lake environment (Laguna Lake, Philippines) and associated implications for eutrophic vulnerability. ASEAN Eng. J. Part C 2015, 4, 48–62. [Google Scholar]
- Lasco, R.D.; Javier, E.Q. Laguna de Bay: Case Study for Sustainable Fisheries Development; National Academy of Science and Technology: Washington, DC, USA, 2018. [Google Scholar]
- Bricaud, A.; Morel, A.; Babin, M.; Allali, K.; Claustre, H. Variations of light absorption by suspended particles with chlorophyll A concentration in oceanic (case 1) waters: Analysis and implications for bio-optical models. J. Geophys. Res. 1998, 103, 31033–31044. [Google Scholar] [CrossRef]
- Morel, A.; Maritorena, S. Bio-optical properties of oceanic waters: A reappraisal. J. Geophys. Res. Ocean. 2001, 106, 7163–7180. [Google Scholar] [CrossRef] [Green Version]
- Ha, N.T.T.; Koike, K.; Nhuan, M.T. Improved accuracy of chlorophyll-a concentration estimates from MODIS Imagery using a two-band ratio algorithm and geostatistics: As applied to the monitoring of eutrophication processes over Tien Yen Bay (Northern Vietnam). Remote Sens. 2013, 6, 421–442. [Google Scholar] [CrossRef] [Green Version]
- Menon, H.B.; Adhikari, A. Remote sensing of chlorophyll-A in case II waters: A novel approach with improved accuracy over widely implemented turbid water indices. J. Geophys. Res. Ocean. 2018, 123, 8138–8158. [Google Scholar] [CrossRef]
- GKSS Research Center. OLCI Level 2 Algorithm Theoretical Basis Document Ocean Colour Turbid Water; GKSS: Geesthacht, Germany, 2010. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Mishra, S.; Mishra, D.R. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll-a concentration in turbid productive waters. Remote Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]
- Gower, J.F.R.; Doerffer, R.; Borstad, G.A. Interpretation of the 685nm peak in water-leaving radiance spectra in terms of fluorescence, absorption and scattering, and its observation by MERIS. Int. J. Remote Sens. 1999, 20, 1771–1786. [Google Scholar] [CrossRef]







| Campaign | Date | Region | Samples # | Chl-a Conc. (μg/L) |
|---|---|---|---|---|
| 1st | January 11 | West | 35 | 11.339 ± 0.592 |
| 2nd | March 29 | Center | 74 | 7.906 ± 0.165 |
| 3rd | April 6 | West | 98 | 8.483 ± 1.230 |
| 4th | April 26 | Center | 22 | 7.254 ± 0.323 |
| 5th | April 30 | West | 48 | 9.598 ± 0.822 |
| Total samples | 257 | 8.639 ± 1.538 | ||
| Campaign # | # of Patches | Chl-a Conc. (μg/L) at Center Pixel | |
|---|---|---|---|
| IRTM-NN | OC4Me | ||
| 1st | 1008 | 1.348 ± 0.034 | 0.983 ± 0.052 |
| 2nd | 4715 | 1.321 ± 0.022 | 0.993 ± 0.069 |
| 3rd | 5681 | 1.327 ± 0.039 | 0.987 ± 0.104 |
| 4th | 1809 | 1.236 ± 0.060 | 1.138 ± 0.156 |
| 5th | 2582 | 1.210 ± 0.082 | 1.095 ± 0.176 |
| All samples | 20,565 | 1.299 ± 0.072 | 1.055 ± 0.106 |
| Campaign | In Situ Samples (μg/L) | RMSE (μg/L) | ||
|---|---|---|---|---|
| # of Samples | Chl-a Conc. | IRTM-NN | OC4Me | |
| 1st | 35 | 11.339 ± 0.592 | 10.008 | 10.361 |
| 2nd | 74 | 7.906 ± 0.165 | 6.591 | 6.917 |
| 3rd | 98 | 8.483 ± 1.230 | 7.251 | 7.613 |
| 4th | 22 | 7.254 ± 0.323 | 6.109 | 5.856 |
| 5th | 48 | 9.598 ± 0.822 | 8.420 | 8.538 |
| Average | 8.639 ± 1.538 | 7.676 | 7.857 | |
| Fold ID | Chl-a Conc. (μg/L) | |||
|---|---|---|---|---|
| Mean | Std. | Max. | Min. | |
| 1 | 9.134 | 1.617 | 12.463 | 6.753 |
| 2 | 9.043 | 1.532 | 12.150 | 6.840 |
| 3 | 8.936 | 1.389 | 11.586 | 6.932 |
| 4 | 8.980 | 1.399 | 11.692 | 7.079 |
| 5 | 8.980 | 1.354 | 11.552 | 7.139 |
| 6 | 8.956 | 1.348 | 11.488 | 7.099 |
| 7 | 8.968 | 1.362 | 11.847 | 7.099 |
| 8 | 8.928 | 1.446 | 11.916 | 6.738 |
| 9 | 8.939 | 1.401 | 11.756 | 6.731 |
| 10 | 8.996 | 1.435 | 11.654 | 6.741 |
| Fold No. | RMSE (μg/L) of WaterNet | ||
|---|---|---|---|
| Two-Stage Training | First Stage Only | Second Stage Only | |
| 1 | 0.837 | 2.396 | 1.219 |
| 2 | 0.975 | 2.390 | 1.709 |
| 3 | 0.522 | 2.396 | 1.643 |
| 4 | 0.509 | 2.357 | 0.962 |
| 5 | 0.691 | 2.189 | 0.962 |
| 6 | 0.937 | 2.316 | 2.181 |
| 7 | 0.858 | 2.355 | 1.410 |
| 8 | 0.588 | 2.406 | 0.716 |
| 9 | 0.844 | 2.492 | 1.214 |
| 10 | 0.755 | 2.354 | 0.968 |
| Ave. | 0.752 | 2.365 | 1.298 |
| Std. | 0.168 | 0.078 | 0.443 |
WaterNet  | Feed-Forward NN (1 Hidden Layer)  | Feed-Forward NN (2 Hidden Layers)  | Feed-Forward NN (3 Hidden Layers)  | |
|---|---|---|---|---|
| Unknowns | 4753 | 4753 | 4791 | 4753 |
| Fold ID | RMSE (μg/L) | |||
| #1 | 0.837 | 1.534 | 1.590 | 1.560 |
| #2 | 0.975 | 1.442 | 1.484 | 1.486 |
| #3 | 0.522 | 1.331 | 1.448 | 1.335 |
| #4 | 0.509 | 1.327 | 1.352 | 1.356 |
| #5 | 0.691 | 1.295 | 1.440 | 1.304 |
| #6 | 0.936 | 1.305 | 1.407 | 1.321 |
| #7 | 0.858 | 1.301 | 1.380 | 1.312 |
| #8 | 0.588 | 1.392 | 1.361 | 1.359 |
| #9 | 0.844 | 1.389 | 1.389 | 1.361 |
| #10 | 0.755 | 1.377 | 1.436 | 1.347 |
| Ave. | 0.752 | 1.369 | 1.429 | 1.374 |
| Std. | 0.168 | 0.075 | 0.067 | 0.078 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Syariz, M.A.; Lin, C.-H.; Nguyen, M.V.; Jaelani, L.M.; Blanco, A.C. WaterNet: A Convolutional Neural Network for Chlorophyll-a Concentration Retrieval. Remote Sens. 2020, 12, 1966. https://doi.org/10.3390/rs12121966
Syariz MA, Lin C-H, Nguyen MV, Jaelani LM, Blanco AC. WaterNet: A Convolutional Neural Network for Chlorophyll-a Concentration Retrieval. Remote Sensing. 2020; 12(12):1966. https://doi.org/10.3390/rs12121966
Chicago/Turabian StyleSyariz, Muhammad Aldila, Chao-Hung Lin, Manh Van Nguyen, Lalu Muhamad Jaelani, and Ariel C. Blanco. 2020. "WaterNet: A Convolutional Neural Network for Chlorophyll-a Concentration Retrieval" Remote Sensing 12, no. 12: 1966. https://doi.org/10.3390/rs12121966







