Position-Domain Non-Gaussian Error Overbounding for ARAIM
Abstract
:1. Introduction
2. Problem Definition
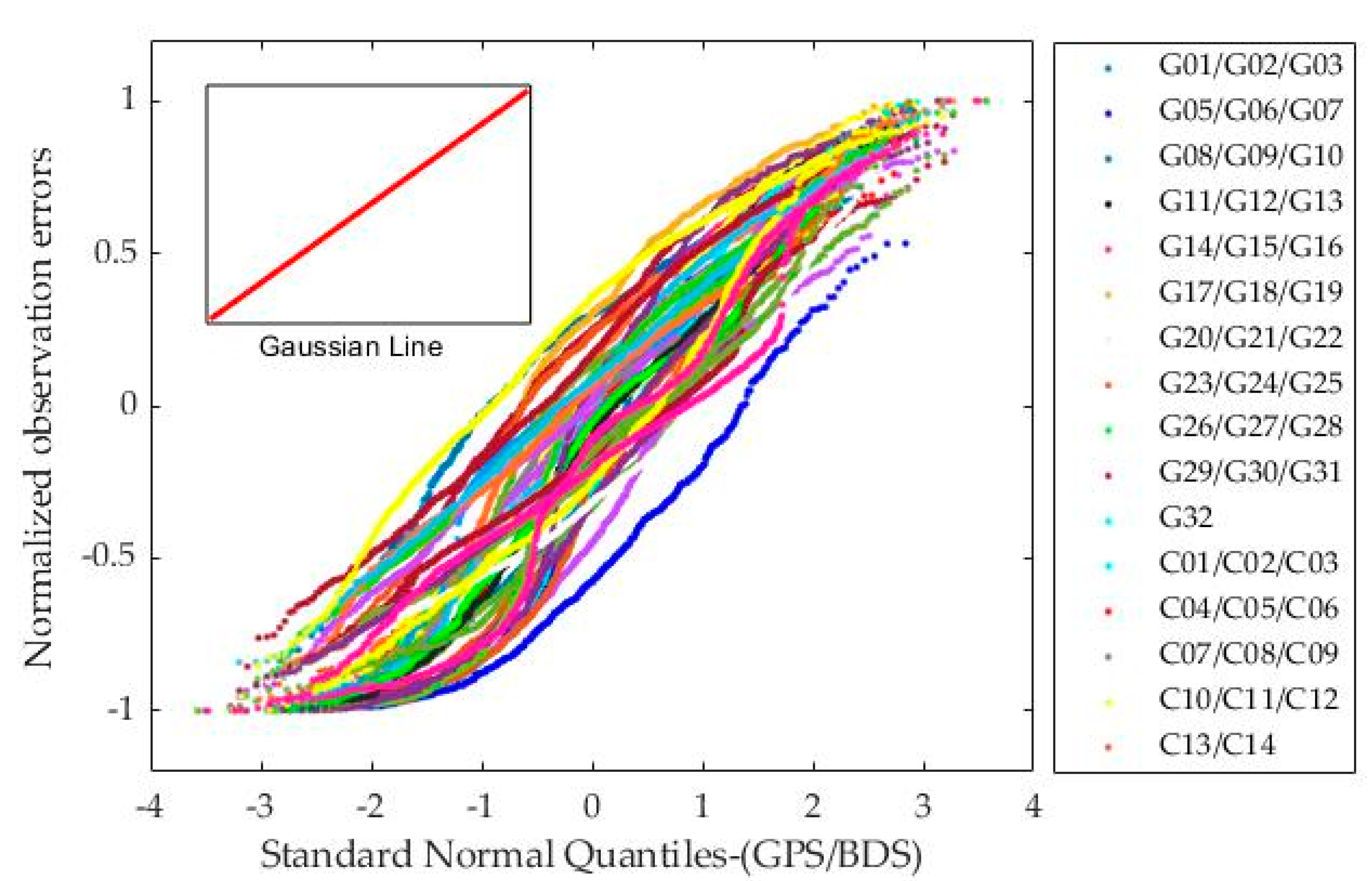
2.1. Non-Gaussian Effect
2.2. Limitations of Traditional Method
2.2.1. Traditional Method
2.2.2. Limitations
3. Position-Domain Overbounding for ARAIM
3.1. Methodology
3.2. Integrity Proof
3.3. Overbounding Boundary for Continuity
4. Experiment and Discussion
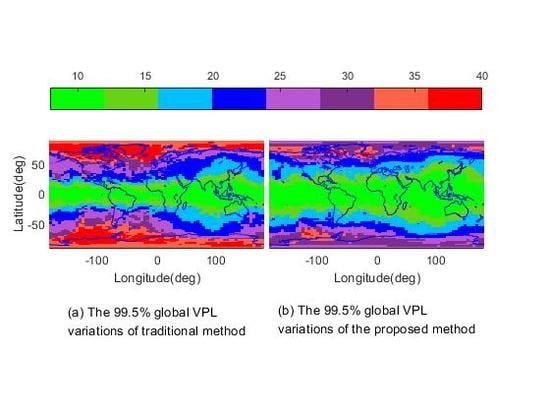
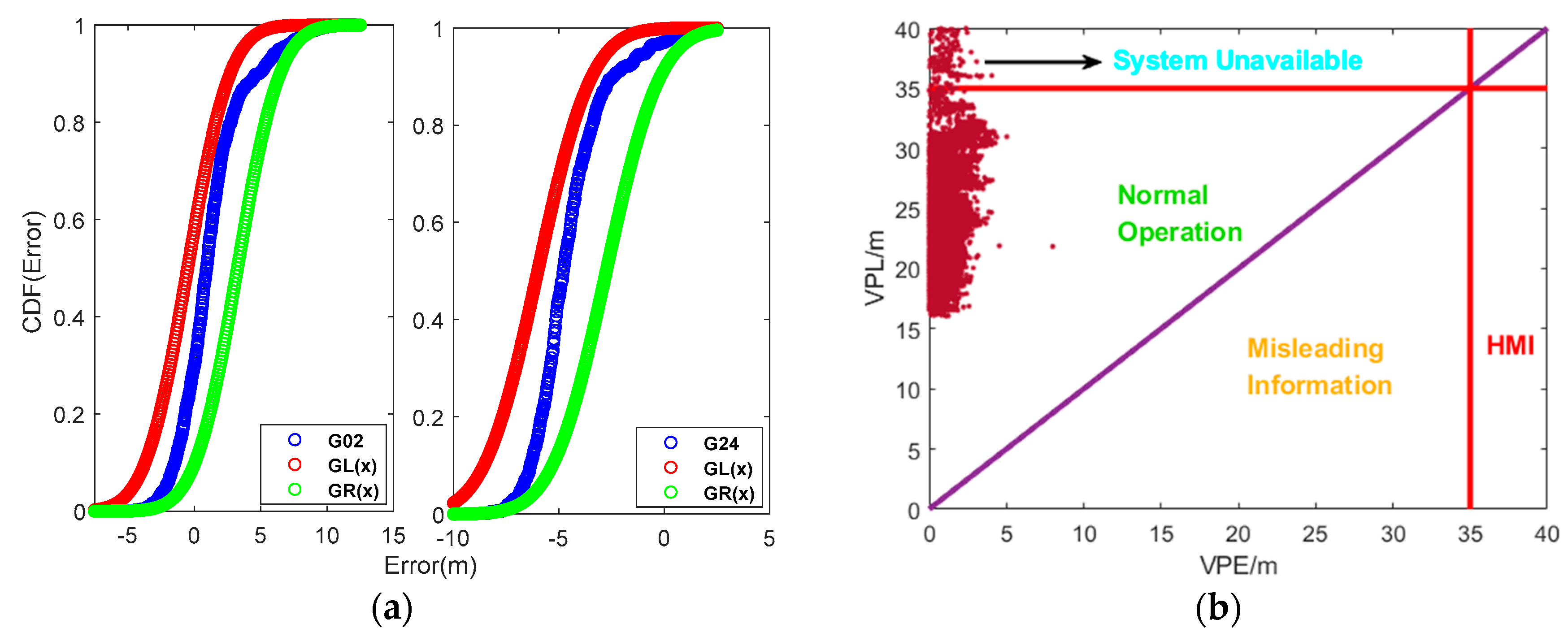
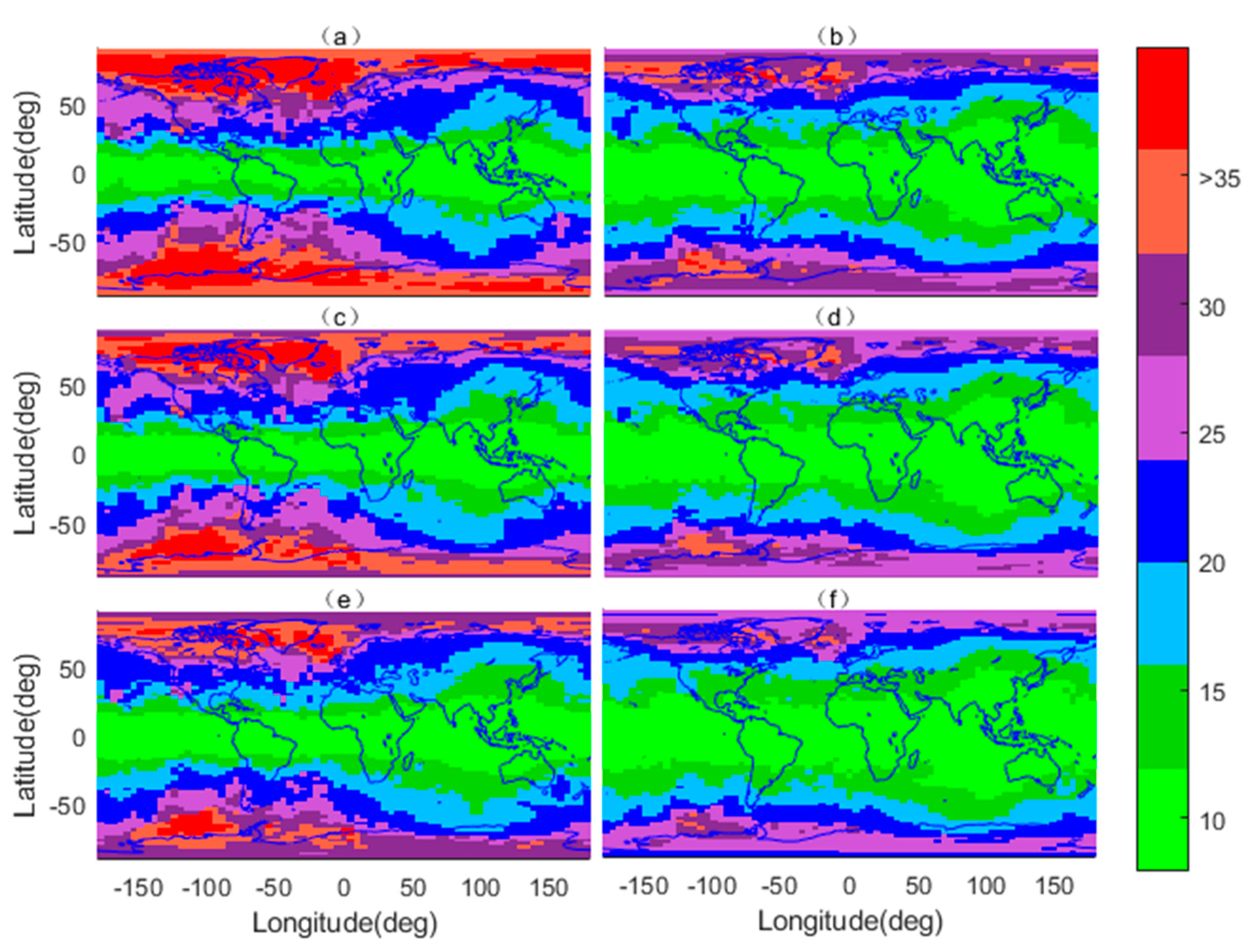
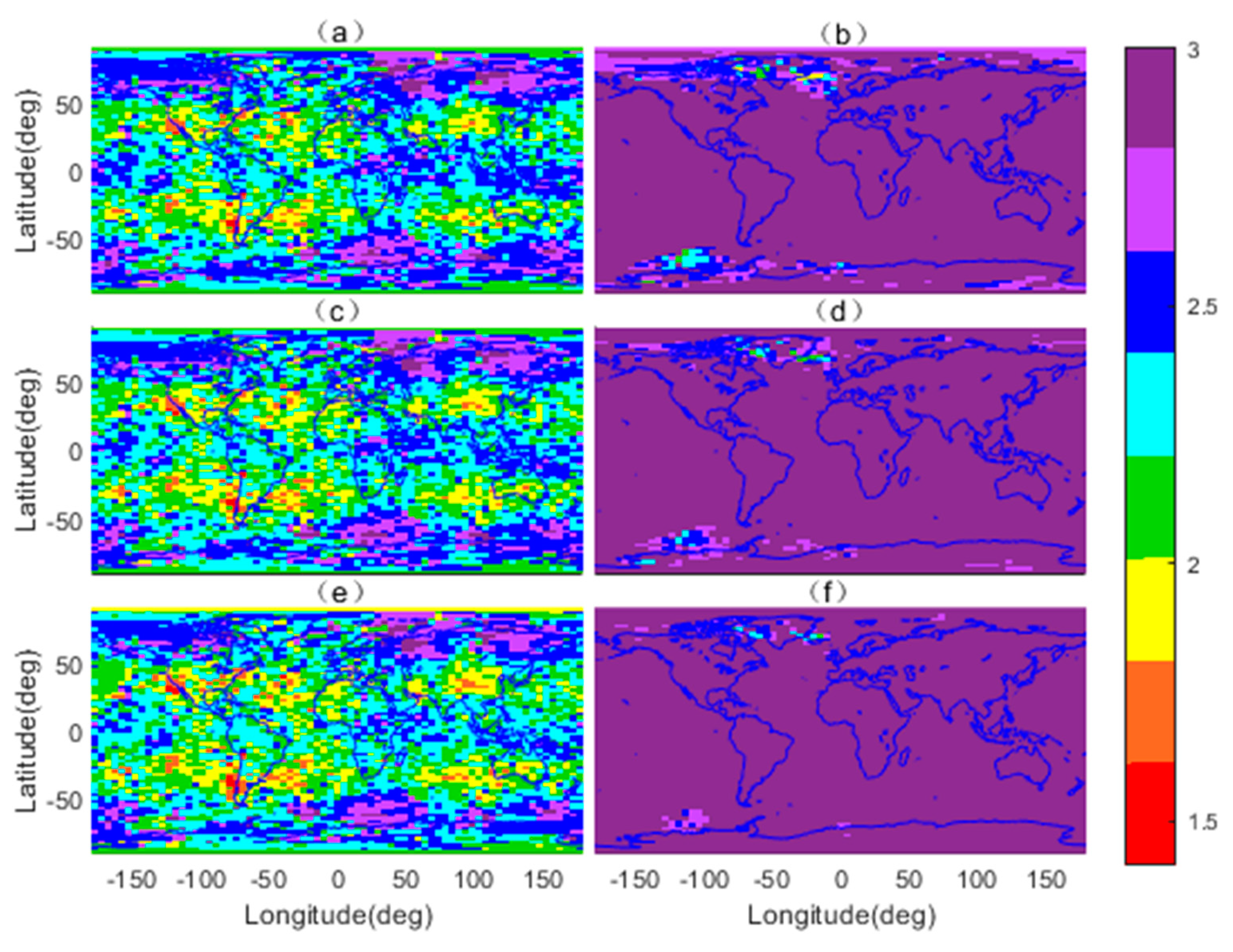
4.1. Simulation Result
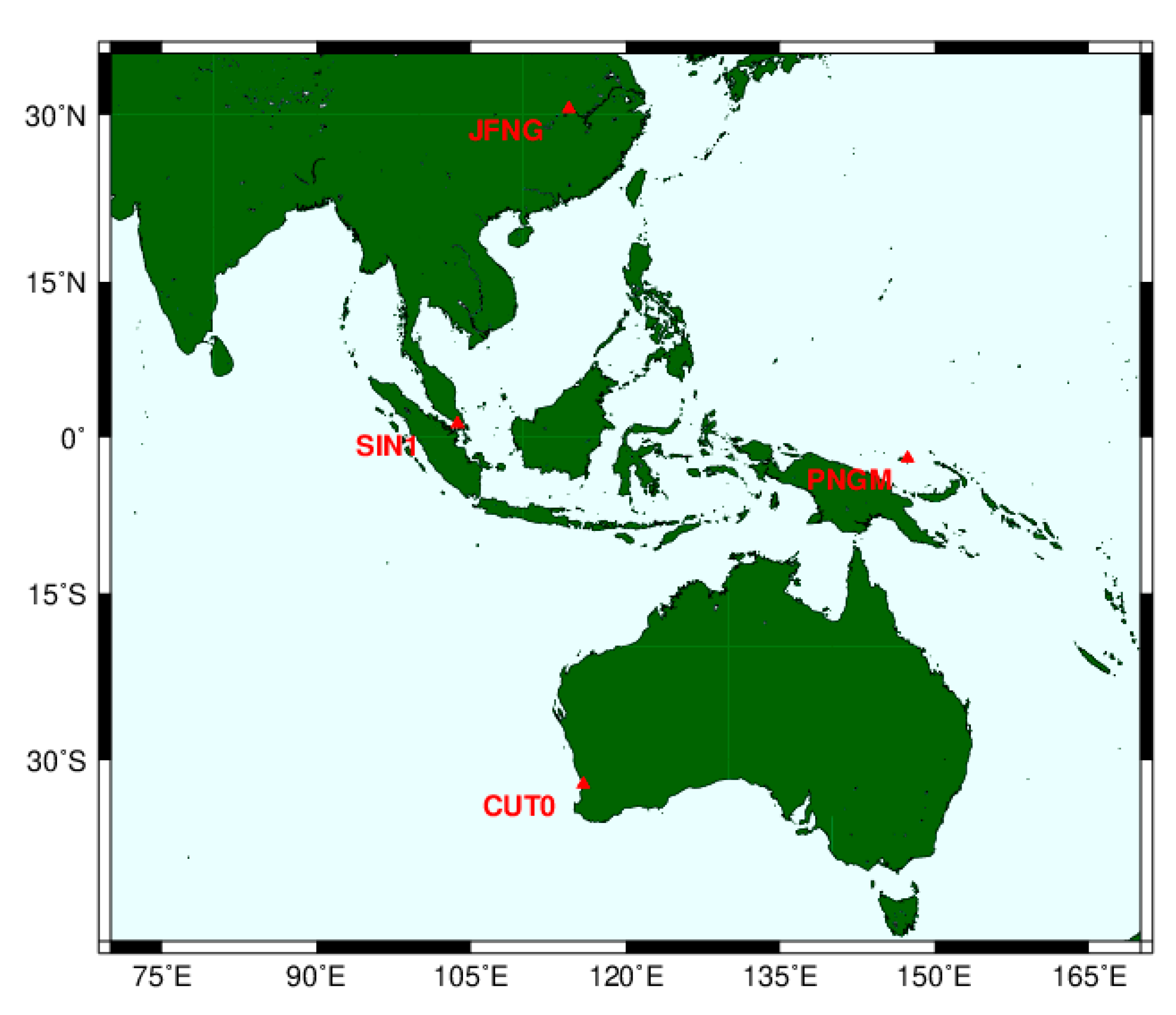
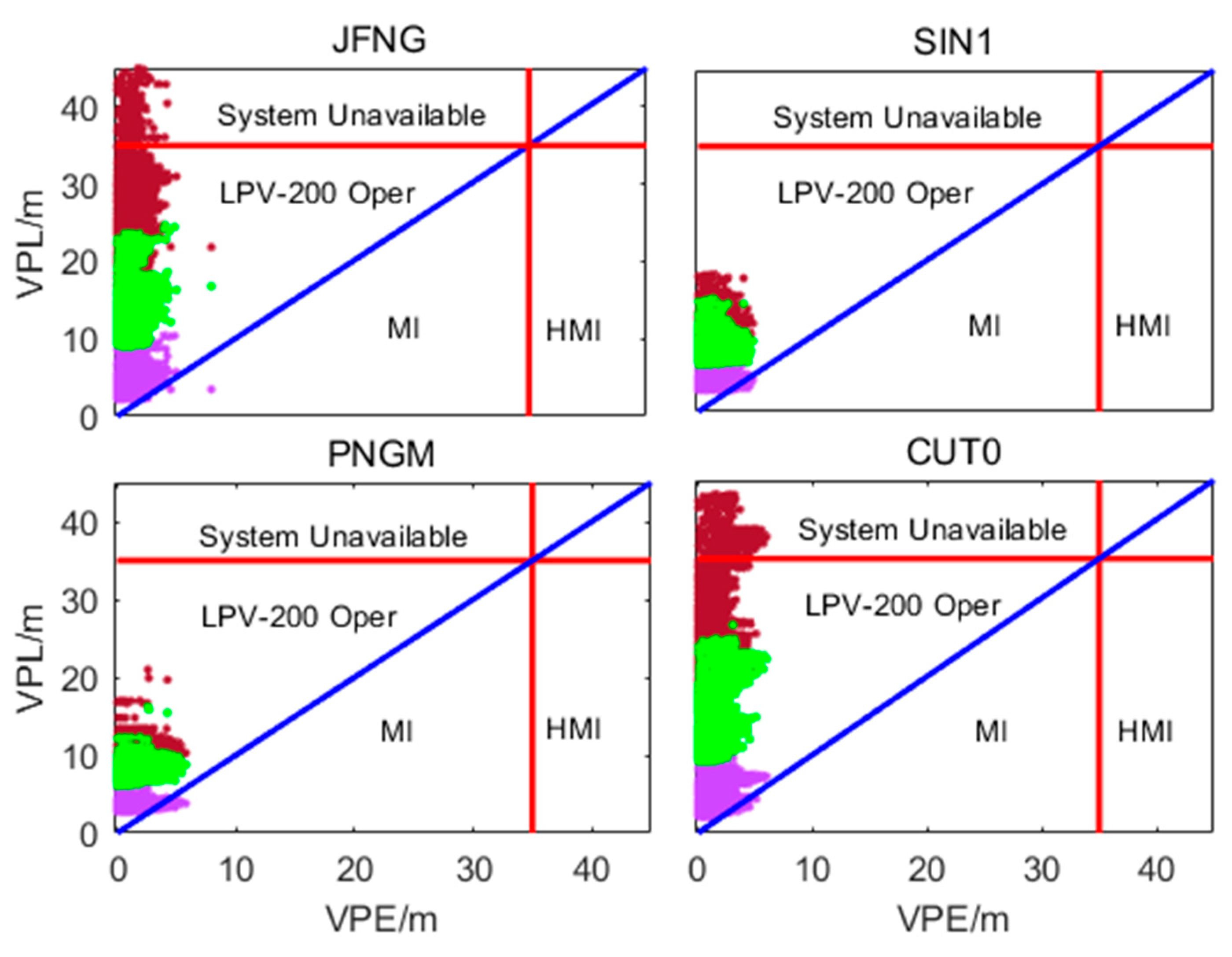
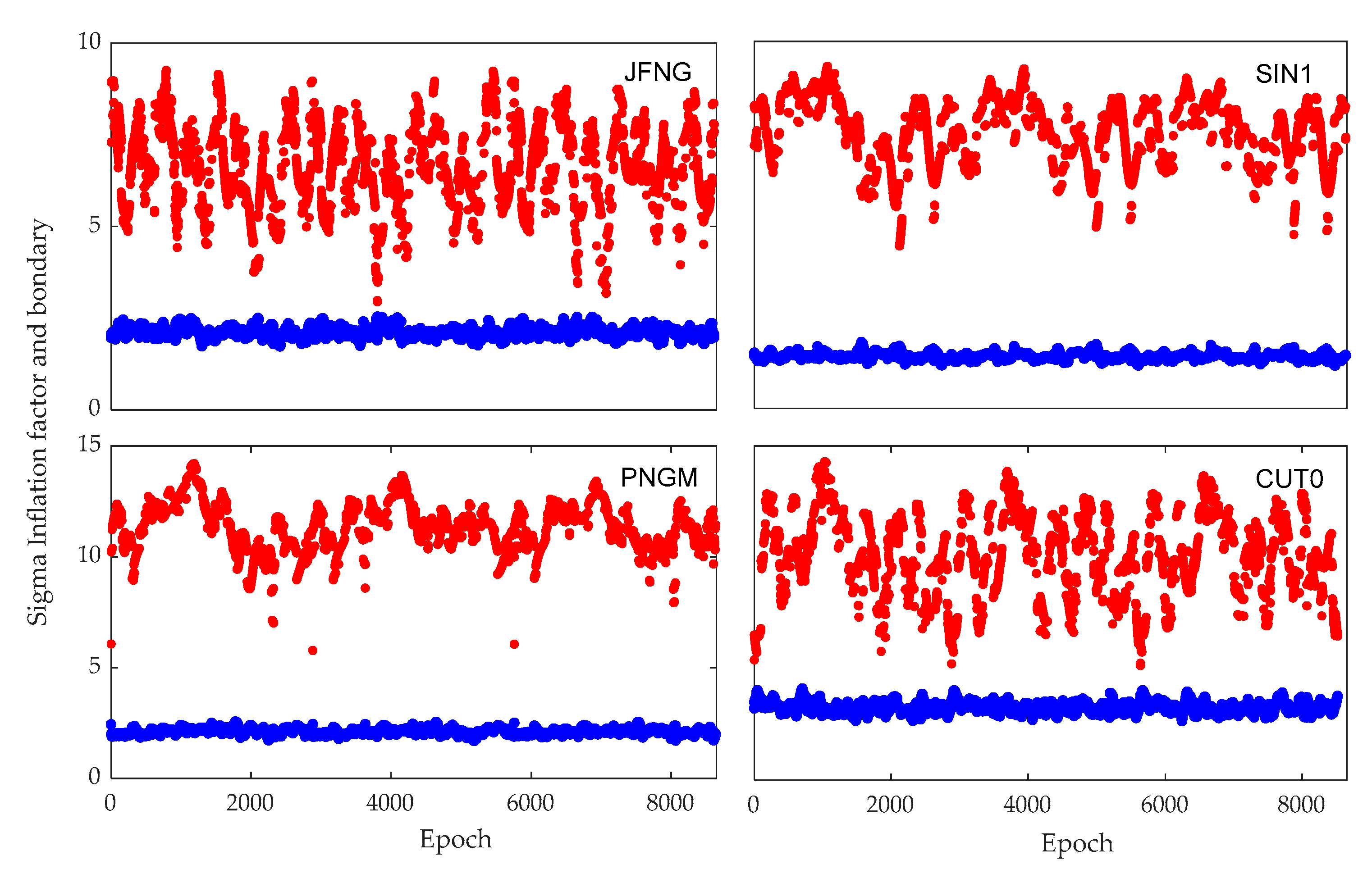
4.2. Real-World Data Result
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, Y.C. New advance RAIM with improved availability for detecting constellation-wide faults, using two independent constellations. Navig. J. Inst. Navig. 2013, 60, 71–83. [Google Scholar] [CrossRef]
- Nikiforov, I.; Roturier, B. Advanced RAIM algorithms: First results. In Proceedings of the 18th ITM of the Satellite Division of The Institute of Navigation (IONGNSS2005), Long-Beach, CA, USA, 13–16 September 2005; pp. 789–1800. [Google Scholar]
- Ene, A.; Blanch, J.; Powell, J.D. Fault detection and elimination for Galileo-GPS vertical guidance. In Proceedings of the ION NTM, San Diego, CA, USA, 22–24 January 2007; pp. 1244–1254. [Google Scholar]
- Lee, Y.C.; Braff, R.; Fernow, J.P.; Hashemi, D.; McLaughlin, M.P.; O’Laughlin, D. GPS and Galileo with RAIM or WAAS for vertically guided approaches. In Proceedings of the ION GNSS 2005, Long Beach, CA, USA, 13–16 September 2005; pp. 1801–1825. [Google Scholar]
- Blanch, J.; Walter, T.; Enge, P.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A.; Kropp, V. Baseline Advanced RAIM User Algorithm and Possible Improvements. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 713–732. [Google Scholar] [CrossRef]
- Blanch, J.; Walter, T.; Enge, P. Optimal positioning for advanced RAIM. Navig. J. Inst. Navig. 2013, 60, 279–289. [Google Scholar] [CrossRef]
- Blanch, J.; Walter, T.; Enge, P. RAIM with optimal integrity and continuity allocations under multiple failures. IEEE Trans. Aerosp Electron. Syst. 2010, 46, 1235–1247. [Google Scholar] [CrossRef]
- Brown, R.G. A baseline GPS RAIM scheme and a note on the equivalence of three RAIM methods. Navigation 1992, 39, 301–306. [Google Scholar] [CrossRef]
- Li, L.; Quddus, M.; Ison, S.; Zhao, L. Multiple reference consistency check for LAAS: A novel position domain approach. GPS Solut. 2012, 16, 209–220. [Google Scholar] [CrossRef] [Green Version]
- Angus, J. RAIM with multiple faults. Navigation 2006, 53, 249–257. [Google Scholar] [CrossRef]
- Walter, T.; Blanch, J. Characterization of GNSS clock and ephemeris errors to support ARAIM. In Proceedings of the Institute of Navigation, Pacific PNT Meeting, Honolulu, HI, USA, 20–23 April 2015; pp. 920–931. [Google Scholar]
- Misra, P.; Rife, J. RAIM with non-Gaussian errors. In Proceedings of the 26th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2013), Nashville, TN, USA, 16–20 September 2013; pp. 2664–2671. [Google Scholar]
- DiLellio, J. A hybrid GNSS integrity design leveraging a priori signal noise characteristics. J.Navig. 2010, 63, 513–526. [Google Scholar] [CrossRef]
- Perea, S.; Meurer, M.; Rippl, M.; Belabbas, B.; Joerger, M. URA/SISA analysis for GPS and Galileo to support ARAIM. Navig. J. Inst. Navig. 2017, 64, 237–254. [Google Scholar] [CrossRef]
- DeCleene, B. Defining pseudorange integrity-Overbounding. In Proceedings of the 13th International Techn. Meeting Satellite Division of the Institute of Navigation, Salt Lake City, UT, USA, 19–22 September 2000; pp. 1916–1924. [Google Scholar]
- Rife, J.; Pervan, B. Overbounding Revisited: Discrete Error Distribution Modeling for Safety Critical GPS Navigation. IEEE Trans. Aerosp Electron. Syst. 2012, 48, 1237–1251. [Google Scholar] [CrossRef]
- Walter, T.; Gunning, K.; Eric Phelts, R.; Blanch, J. Validation of the unfaulted error bounds for ARAIM. Navig. J. Inst. Navig. 2018, 65, 117–133. [Google Scholar] [CrossRef]
- Langel, S.E.; Khanafseh, S.M.; Pervan, B.S. Bounding integrity risk for sequential state estimators with stochastic modeling uncertainty. J. Guidance Control Dyn. 2014, 37, 36–46. [Google Scholar] [CrossRef]
- Rife, J.; Pullen, S.; Pervan, B.; Enge, P. Paired overbounding for nonideal LAAS and WAAS error distributions. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 1386–1395. [Google Scholar] [CrossRef]
- Rife, J. Core overbounding and its implications for LAAS integrity. In Proceedings of the ION GNSS 2004, Long Beach, CA, USA, 21–24 September 2004; pp. 2810–2821. [Google Scholar]
- Rife, J.; Walter, T.; Blanch, J. Overbounding SBAS and GBAS error distributions with excess-mass functions. In Proceedings of the International Symposium GPS/GNSS, Sydney, Australia, 6–8 December 2004. [Google Scholar]
- Rife, J.; Pullen, S. The impact of measurement biases on availability for CAT III LAAS. Navigation 2005, 52, 215–228. [Google Scholar] [CrossRef]
- Larson, J.D.; Gebre-Egziabher, D.; Rife, J.H. Gaussian-Pareto overbounding of DGNSS pseudoranges from CORS. Navig. J. Inst. Navig. 2018, 66, 139–150. [Google Scholar] [CrossRef] [Green Version]
- Pervan, B.; Khanafseh, S.; Patel, J. Test Statistic Auto- and Cross-correlation Effects on Monitor False Alert and Missed Detection Probabilities. In Proceedings of the 2017 International Technical Meeting of The Institute of Navigation, Monterey, CA, USA, 30 January–2 February 2017; pp. 562–590. [Google Scholar]
- Pervan, B.; Sayim, I. Sigma inflation for the local area augmentation of GPS. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 1301–1311. [Google Scholar] [CrossRef]
- Rife, J.; Gebre-Egziabher, D. Symmetric overbounding of correlated errors. Navigation 2007, 54, 109–124. [Google Scholar] [CrossRef]
- Li, L.; Zhao, L.; Ding, J.; Gao, S. A new inflation integrity monitoring algorithm for improving availability of LASS signal-in-space. Acta Aeronaut. Astronaut. Sin. 2011, 32, 664–671. [Google Scholar]
- Lee, J.; Pullen, S. Sigma overbounding using a position-domain method for the local area augmentation of GPS. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1262–1274. [Google Scholar]
- Braff, R. A method for LAAS fault-free error overbounding using a position domain monitor. In Proceedings of the ION National Technical Meeting, Anaheim, CA, USA, 22–24 January 2003; pp. 326–388. [Google Scholar]
- Fang, K.; Zhu, Y.; Xue, R.; Wang, Z. A Novel Position Domain Overbounding Method Using Pseudorange Error Model Based on Extreme Value Theory. In Proceedings of the ION 2015 Pacific PNT Meeting, Honolulu, HI, USA, 20–23 April 2015; pp. 912–919. [Google Scholar]
- Blanch, J.; Walter, T.; Enge, P. Gaussian bounds of sample distributions for integrity analysis. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1806–1815. [Google Scholar] [CrossRef]
- Blanch, J.; Walter, T.; Enge, P. A MATLAB toolset to determine strict Gaussian bounding distributions of a sample distribution. In Proceedings of the 30th International Technical Meeting Satellite Division of the Institute of Navigation, Portland, OR, USA, 25–29 September 2017; pp. 4236–4247. [Google Scholar]
- Li, L.; Wang, H.; Jia, C.; Zhao, L.; Zhao, Y. Integrity and continuity allocation for the RAIM with multiple constellations. GPS Solut. 2017, 21, 1503–1513. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| (integrity) | 0.5 m |
| (continuity) | 0.25 m |
| (integrity) | 0.9 m |
| (continuity) | 0.45 m |
| (integrity) | 0.75 m |
| (continuity) | 0.1 m |
| integrity risk | |
| continuity risk | |
| (GPS) | |
| (BDS) |
| Category | PB-RAIM | PDM-ARAIM | |
|---|---|---|---|
| Average 99.5% VPL/m | 20.67 | 16.62 | |
| Availability | 96.06% | 99.99% | |
| Average 99.5% VPL/m | 22.52 | 17.86 | |
| Availability | 89.96% | 99.74% | |
| Average 99.5% VPL/m | 24.16 | 18.96 | |
| Availability | 82.53% | 98.89% |
| Station | JFNG | SIN1 | PNGM | CUT0 | |
|---|---|---|---|---|---|
| NARAIM | PMI | 0.57% | 0.91% | 1.65% | 0.36% |
| Availability | 100% | 100% | 100% | 100% | |
| PB-RAIM | PMI | 0% | 0% | 0% | 0% |
| Availability | 96.41% | 100% | 100% | 95.72% | |
| PDM-ARAIM | PMI | 0% | 0% | 0% | 0% |
| Availability | 99.99% | 100% | 100% | 100% | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Zhang, J.; Li, L.; Yang, F.; Liu, X. Position-Domain Non-Gaussian Error Overbounding for ARAIM. Remote Sens. 2020, 12, 1992. https://doi.org/10.3390/rs12121992
Zhao L, Zhang J, Li L, Yang F, Liu X. Position-Domain Non-Gaussian Error Overbounding for ARAIM. Remote Sensing. 2020; 12(12):1992. https://doi.org/10.3390/rs12121992
Chicago/Turabian StyleZhao, Lin, Jie Zhang, Liang Li, Fuxin Yang, and Xiaosong Liu. 2020. "Position-Domain Non-Gaussian Error Overbounding for ARAIM" Remote Sensing 12, no. 12: 1992. https://doi.org/10.3390/rs12121992
APA StyleZhao, L., Zhang, J., Li, L., Yang, F., & Liu, X. (2020). Position-Domain Non-Gaussian Error Overbounding for ARAIM. Remote Sensing, 12(12), 1992. https://doi.org/10.3390/rs12121992