A Global Gravity Reconstruction Method for Mercury Employing Deep Convolutional Neural Network
Abstract
1. Introduction
2. Data and Spatial Structure Similarity Analysis
2.1. Mercury’s Datasets
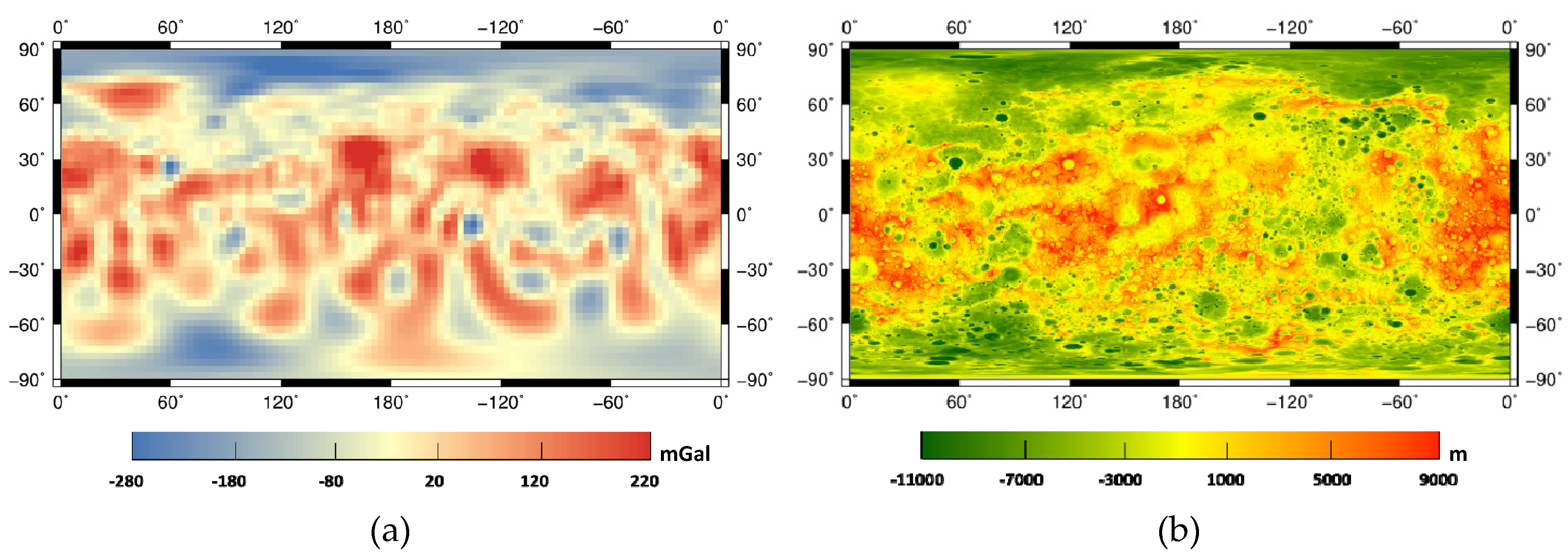
2.1.1. Gravity Field Data of Mercury
2.1.2. Mercury’s Global DEM
2.2. Lunar Datasets
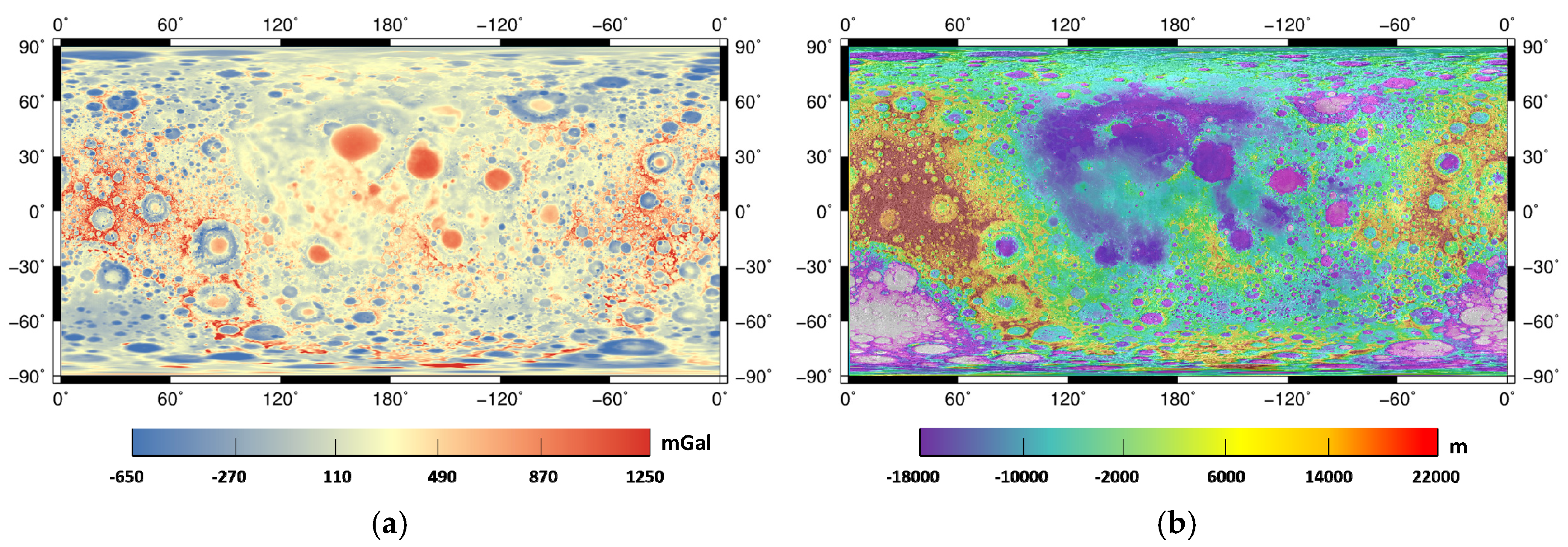
2.2.1. Gravity Field Data of the Moon
2.2.2. Lunar Global DEM
2.3. Spatial Structure Similarity Analysis of Gravity Data and DEM
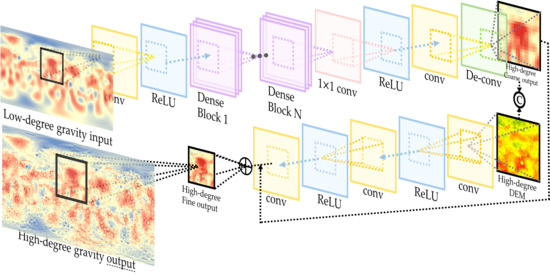
3. Methodology
3.1. Gravity Field Data Reconstruction Network
3.2. DEM Refining Network
4. Experiments and Discussion
4.1. Experimental Settings
4.1.1. Parameter Setting and Network Training
4.1.2. Quantitative Evaluation Indicators
4.1.3. Compared Method
4.2. Experimental Results
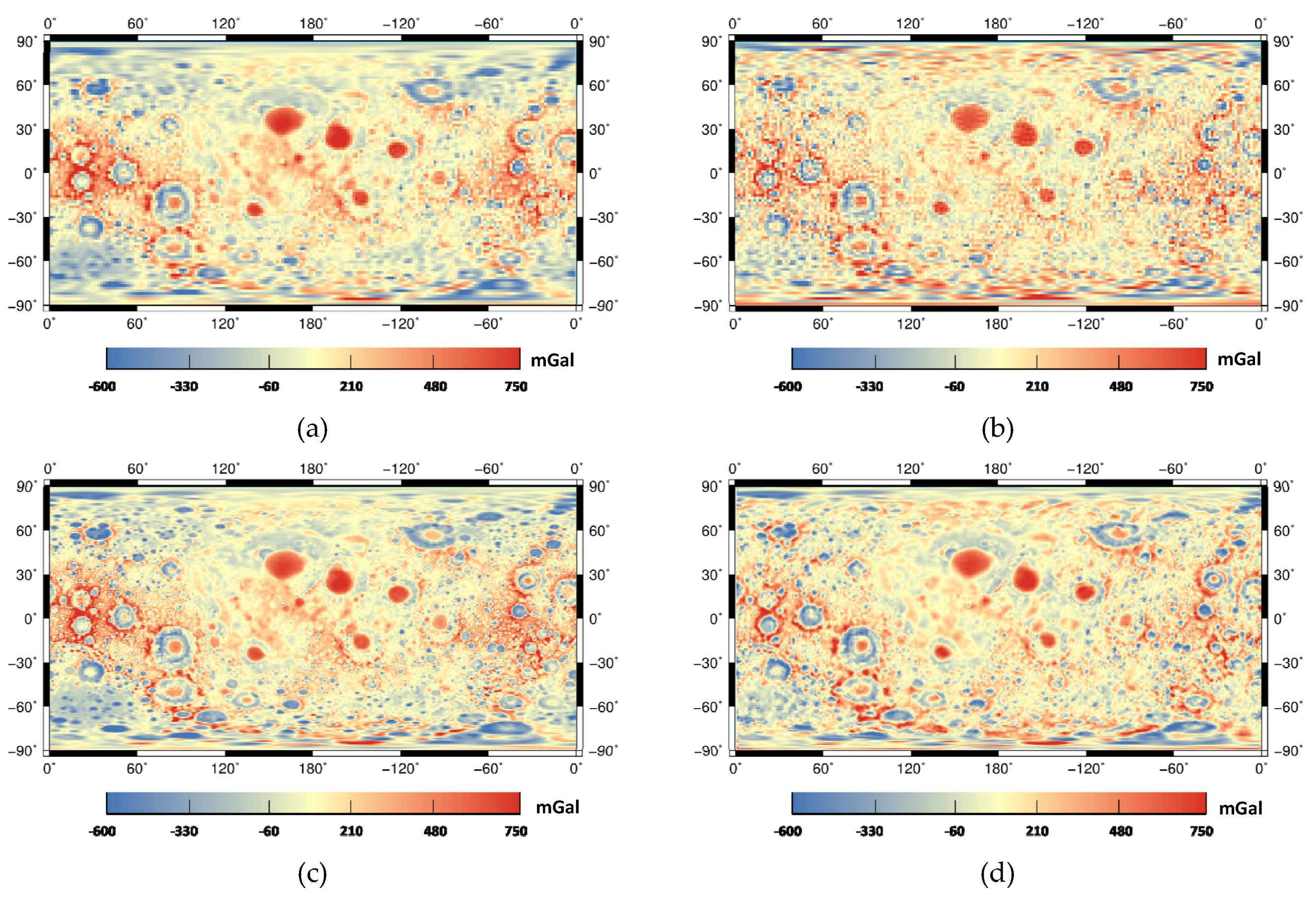
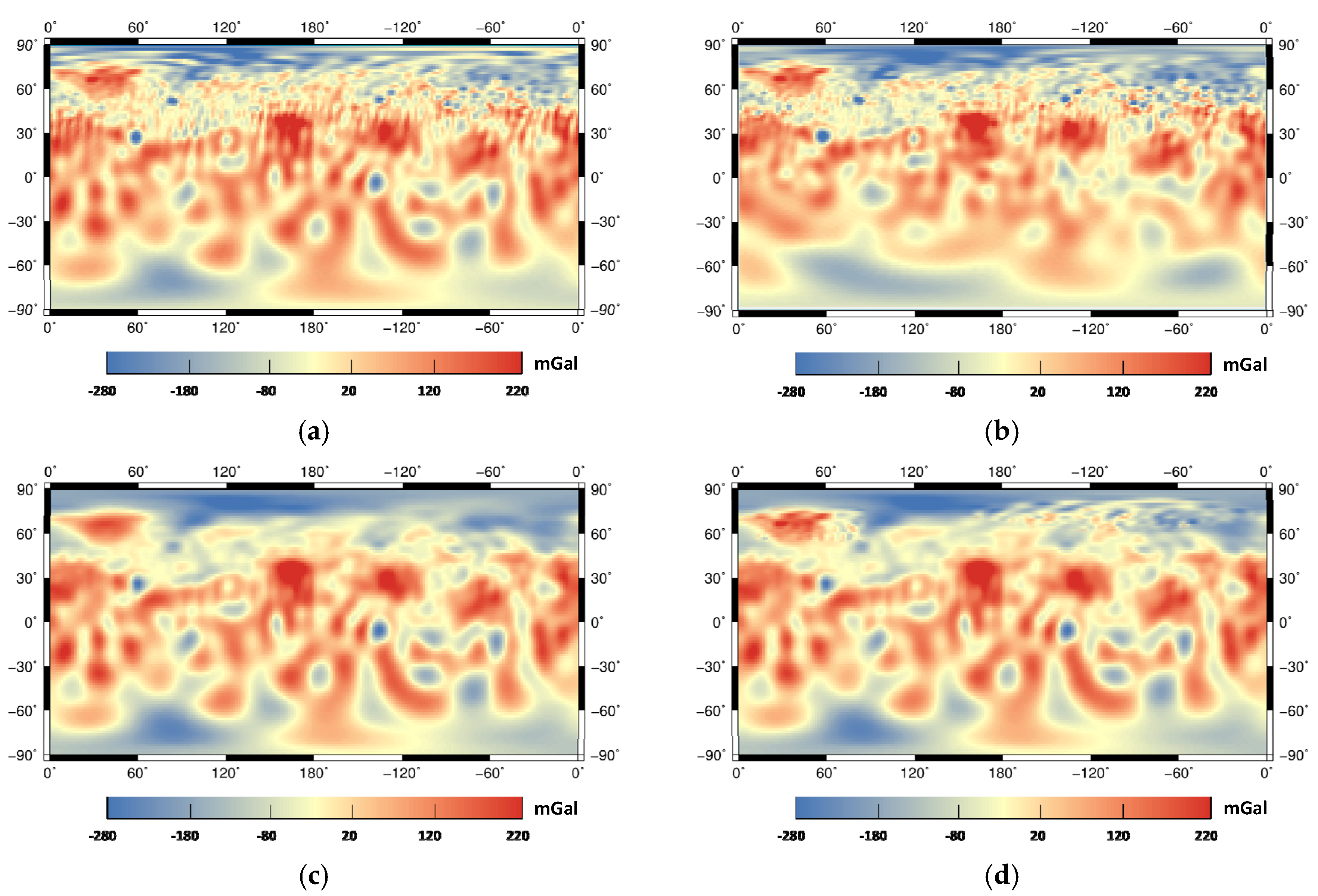
4.2.1. Experiment 1: The Feasibility of the Proposed Network
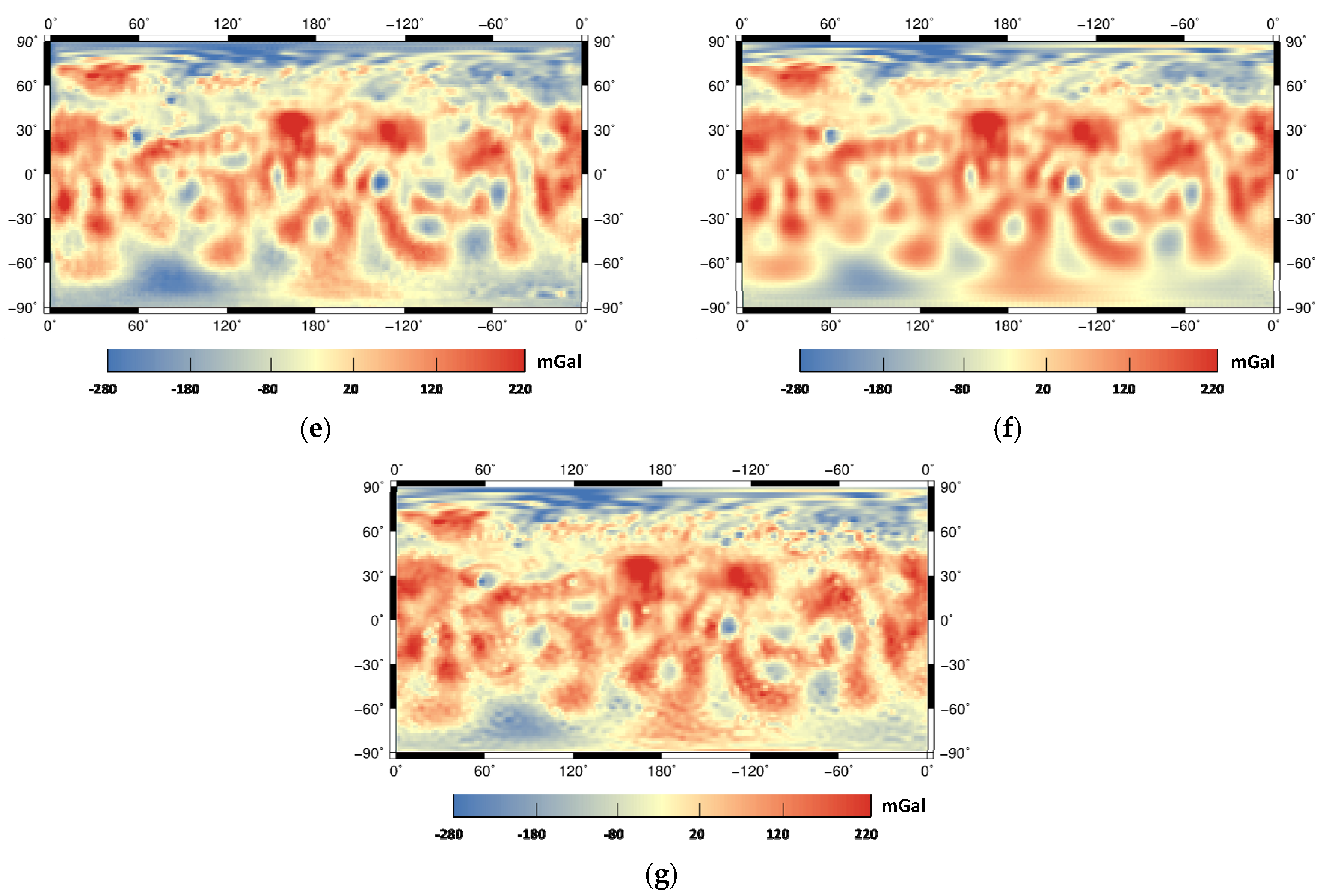
4.2.2. Experiment 2: The Transferability between the Lunar and the Mercury Data
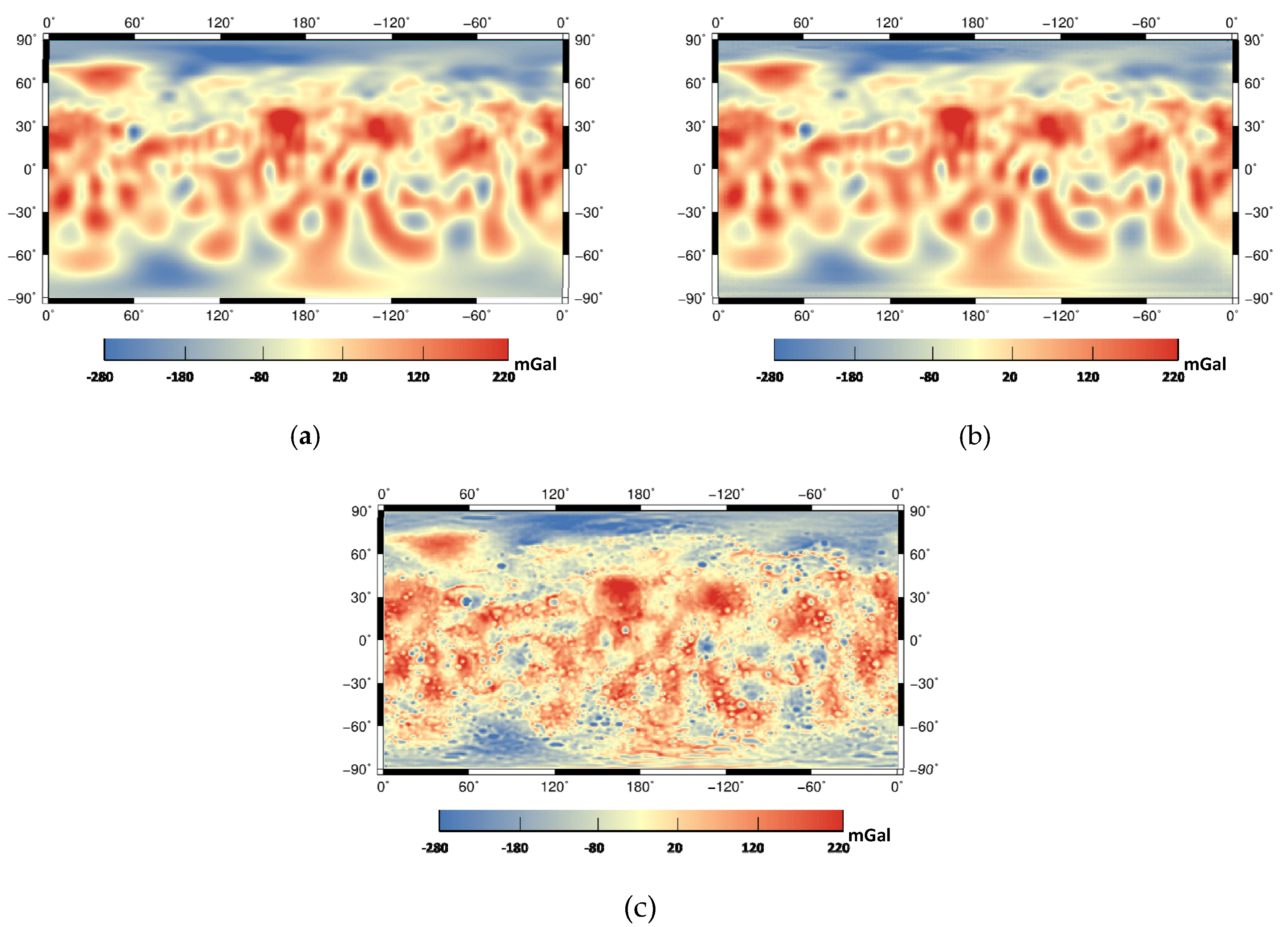
4.2.3. Experiment 3: The Fourfold Downscaling Accuracy
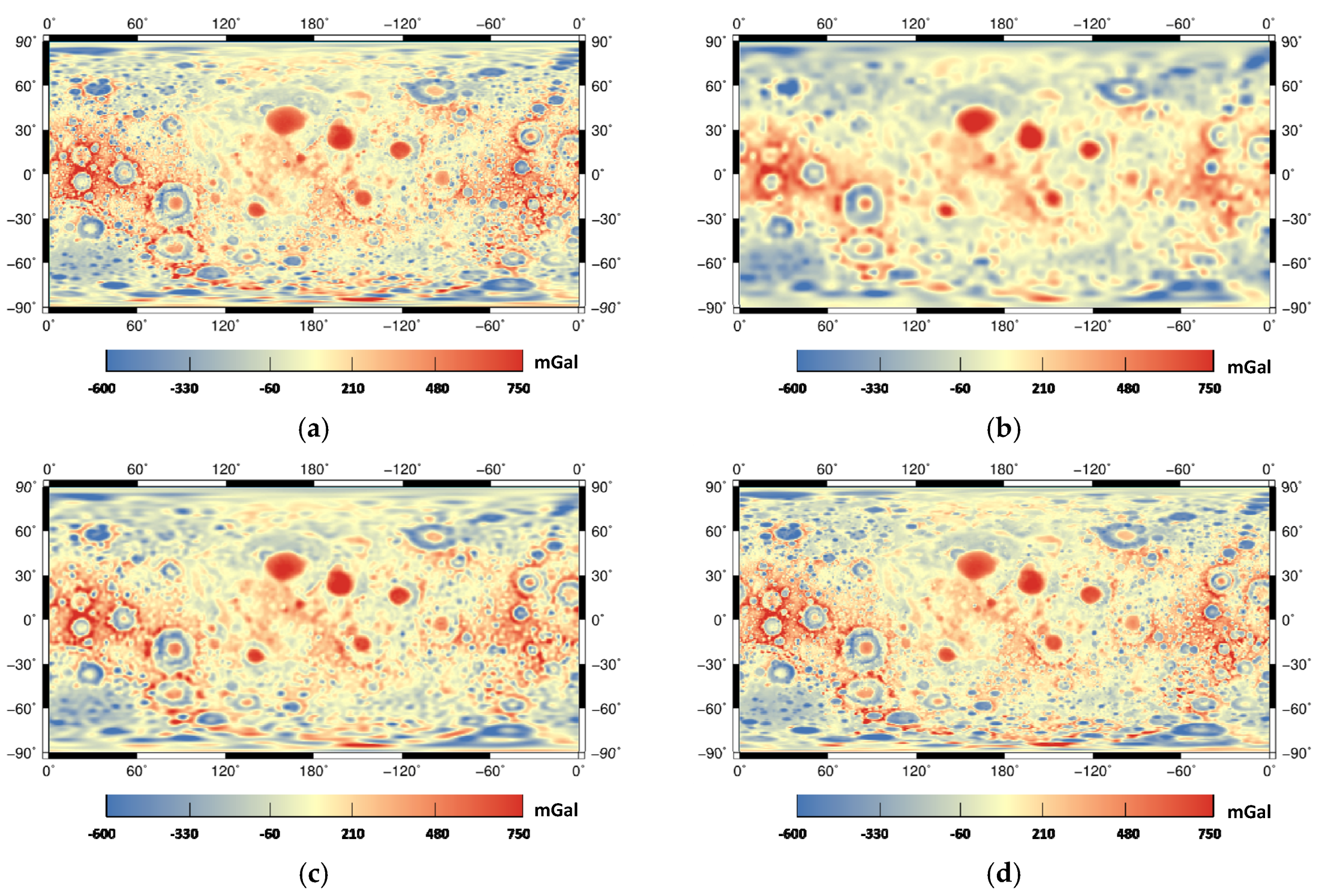
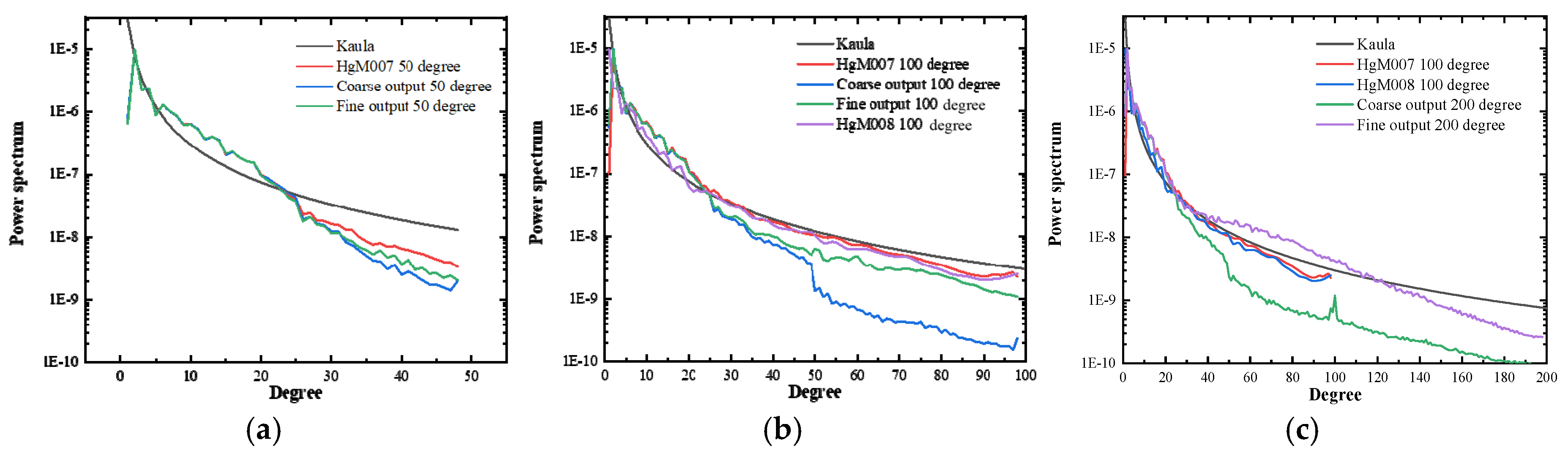
4.3. Power Spectrum Analysis and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chapman, C.R. Mercury: Introduction to an end-member planet. In Mercury; University of Arizona Press: Tucson, AZ, USA, 1988; pp. 1–23. [Google Scholar]
- Solomon, S.C. Mercury: The enigmatic innermost planet. Earth Planet. Sci. Lett. 2003, 216, 441–455. [Google Scholar] [CrossRef]
- Nelson, R.M. Mercury: The Forgotten Planet. Sci. Am. 1997, 277, 28–35. [Google Scholar] [CrossRef]
- Strom, R.G. Mercury: The Elusive Planet; Cambridge University Press: Cambridge, UK, 1987; Volume 1. [Google Scholar]
- Ness, N.; Behannon, K.; Lepping, R.; Whang, Y.; Schatten, K. Magnetic field observations near Mercury: Preliminary results from Mariner 10. Science 1974, 185, 151–160. [Google Scholar] [CrossRef]
- Hapke, B.; Danielson, G.E.; Klaasen, K.; Wilson, L. Photometric observations of Mercury from Mariner 10. J. Geophys. Res. 1975, 80, 2431–2443. [Google Scholar] [CrossRef]
- Rava, B.; Hapke, B. An analysis of the Mariner 10 color ratio map of Mercury. Icarus 1987, 71, 397–429. [Google Scholar] [CrossRef]
- Stark, A.; Oberst, J.; Preusker, F.; Burmeister, S.; Steinbrügge, G.; Hussmann, H. The reference frames of Mercury after the MESSENGER mission. J. Geod. 2018, 92, 949–961. [Google Scholar] [CrossRef]
- Deng, Q.; Li, F.; Yan, J.; Xiao, Z.; Rodriguez, J.A.P. Buried Impact Features on Mercury as Revealed by Gravity Data. J. Geophys. Res. Planets 2018, 123, 3005–3019. [Google Scholar]
- Forsberg, R.; Tscherning, C.C. The use of height data in gravity field approximation by collocation. J. Geophys. Res. Solid Earth 1981, 86, 7843–7854. [Google Scholar] [CrossRef]
- Padovan, S.; Wieczorek, M.A.; Margot, J.-L.; Tosi, N.; Solomon, S.C. Thickness of the crust of Mercury from geoid-to-topography ratios. Geophys. Res. Lett. 2015, 42, 1029. [Google Scholar] [CrossRef]
- Forsberg, R. A Study of Terrain Reductions, Density Anomalies and Geophysical Inversion Methods in Gravity Field Modelling; Ohio State Univ Columbus Dept of Geodetic Science and Surveying: Columbus, OH, USA, 1984. [Google Scholar]
- Hirt, C. Prediction of vertical deflections from high-degree spherical harmonic synthesis and residual terrain model data. J. Geod. 2010, 84, 179–190. [Google Scholar] [CrossRef]
- Hirt, C.; Claessens, S.J.; Kuhn, M.; Featherstone, W.E. Kilometer-resolution gravity field of Mars: MGM2011. Planet. Space Sci. 2012, 67, 147–154. [Google Scholar] [CrossRef]
- Hirt, C.; Featherstone, W.E. A 1.5 km-resolution gravity field model of the Moon. Earth Planet. Sci. Lett. 2012, 329, 22–30. [Google Scholar] [CrossRef]
- Li, F.; Yan, J.; Xu, L.; Jin, S.; Rodriguez, J.A.P.; Dohm, J.H. A 10 km-resolution synthetic Venus gravity field model based on topography. Icarus 2015, 247, 103–111. [Google Scholar] [CrossRef]
- Kucinskas, A.B.; Turcotte, D.L. Isostatic Compensation of Equatorial Highlands on Venus. Icarus 1994, 112, 104–116. [Google Scholar] [CrossRef]
- Kucinskas, A.B.; Turcotte, D.L.; Arkani-Hamed, J. Isostatic compensation of Ishtar Terra, Venus. J. Geophys. Res. 1996, 101, 4725–4736. [Google Scholar] [CrossRef]
- Grimm, R.E.; Hess, P.C. The Crust of Venus; University of Arizona Press: Tucson, AZ, USA, 1997. [Google Scholar]
- Bedini, P.D.; Solomon, S.C.; Finnegan, E.J.; Calloway, A.B.; Ensor, S.L.; McNutt, R.L.; Anderson, B.J.; Prockter, L.M. MESSENGER at Mercury: A mid-term report. Acta Astronaut. 2012, 81, 369–379. [Google Scholar] [CrossRef]
- Solomon, S.C.; McNutt, R.L.; Gold, R.E.; Domingue, D.L. MESSENGER Mission Overview. Space Sci. Rev. 2007, 131, 3–39. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Phillips, R.J.; Solomon, S.C.; Hauck, S.A.; Lemoine, F.G.; Mazarico, E.; Neumann, G.A.; Peale, S.J.; Margot, J.-L.; et al. Gravity Field and Internal Structure of Mercury from MESSENGER. Science 2012, 336, 214. [Google Scholar] [CrossRef]
- Mazarico, E.; Genova, A.; Goossens, S.; Lemoine, F.G.; Neumann, G.A.; Zuber, M.T.; Smith, D.E.; Solomon, S.C. The gravity field, orientation, and ephemeris of Mercury from MESSENGER observations after three years in orbit. J. Geophys. Res. Planets 2014, 119, 2417–2436. [Google Scholar] [CrossRef]
- Genova, A.; Goossens, S.; Lemoine, F.G.; Mazarico, E.; Neumann, G.A.; Smith, D.E.; Zuber, M.T. Seasonal and static gravity field of Mars from MGS, Mars Odyssey and MRO radio science. Icarus 2016, 272, 228–245. [Google Scholar] [CrossRef]
- Becker, K.J.; Robinson, M.S.; Becker, T.L.; Weller, L.A.; Edmundson, K.L.; Neumann, G.A.; Perry, M.E.; Solomon, S.C. First Global Digital Elevation Model of Mercury. In Proceedings of the Lunar & Planetary Science Conference, Houston, TX, USA, 13–17 March 2006. [Google Scholar]
- Hawkins, S.E.; Boldt, J.D.; Darlington, E.H.; Espiritu, R.; Gold, R.E.; Gotwols, B.; Grey, M.P.; Hash, C.D.; Hayes, J.R.; Jaskulek, S.E. The Mercury Dual Imaging System on the MESSENGER Spacecraft. Space Sci. Rev. 2007, 131, 247–338. [Google Scholar] [CrossRef]
- Solomon, S.C.; McNutt, R.L., Jr.; Gold, R.E.; Acuña, M.H.; Baker, D.N.; Boynton, W.V.; Chapman, C.R.; Cheng, A.F.; Gloeckler, G.; Head, J.W., III. The MESSENGER mission to Mercury: Scientific objectives and implementation. Planet. Space Sci. 2001, 49, 1445–1465. [Google Scholar] [CrossRef]
- Di, K.; Wei, L.; Yue, Z.; Sun, Y.; Liu, Y. A machine learning approach to crater detection from topographic data. Adv. Space Res. 2019, 54, 2419–2429. [Google Scholar] [CrossRef]
- Zuber, M.T.; Smith, D.E.; Watkins, M.M.; Asmar, S.W.; Konopliv, A.S.; Lemoine, F.G.; Melosh, H.J.; Neumann, G.A.; Phillips, R.J.; Solomon, S.C. Gravity Field of the Moon from the Gravity Recovery and Interior Laboratory (GRAIL) Mission. Science 2013, 339, 668–671. [Google Scholar] [CrossRef]
- Zuber, M.T.; Smith, D.E.; Lehman, D.H.; Hoffman, T.L. Gravity Recovery and Interior Laboratory (GRAIL): Mapping the Lunar Interior from Crust to Core. Space Sci. Rev. 2013, 178, 3–24. [Google Scholar] [CrossRef]
- Šprlák, M.; Han, S.-C.; Featherstone, W. Forward modelling of global gravity fields with 3D density structures and an application to the high-resolution (~2 km) gravity fields of the Moon. J. Geod. 2018, 92, 847–862. [Google Scholar] [CrossRef]
- Namiki, N.; Iwata, T.; Matsumoto, K.; Hanada, H.; Noda, H.; Goossens, S.; Ogawa, M.; Kawano, N.; Asari, K.; Tsuruta, S.-I. Farside gravity field of the Moon from four-way Doppler measurements of SELENE (Kaguya). Science 2009, 323, 900–905. [Google Scholar] [CrossRef]
- Konopliv, A.S.; Park, R.S.; Yuan, D.N.; Asmar, S.W.; Watkins, M.M.; Williams, J.G.; Fahnestock, E.; Kruizinga, G.; Paik, M.; Strekalov, D. High-resolution lunar gravity fields from the GRAIL Primary and Extended Missions. Geophys. Res. Lett. 2014, 41, 1452–1458. [Google Scholar] [CrossRef]
- Li, F.; Zhu, C.; Hao, W.; Yan, J.; Ye, M.; Barriot, J.-P.; Cheng, Q.; Sun, T. An Improved Digital Elevation Model of the Lunar Mons Rümker Region Based on Multisource Altimeter Data. Remote Sens. 2018, 10, 1442. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Lemoine, F.G.; Mazarico, E.; Torrence, M.H.; McGarry, J.F.; Rowlands, D.D.; Head, J.W.; Duxbury, T.H.; et al. Initial observations from the Lunar Orbiter Laser Altimeter (LOLA). Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Mazarico, E.; Rowlands, D.; Neumann, G.; Smith, D.; Torrence, M.; Lemoine, F.; Zuber, M. Orbit determination of the lunar reconnaissance orbiter. J. Geod. 2012, 86, 193–207. [Google Scholar] [CrossRef]
- Rowlands, D.; Lemoine, F.; Chinn, D.; Luthcke, S. A simulation study of multi-beam altimetry for lunar reconnaissance orbiter and other planetary missions. J. Geod. 2009, 83, 709. [Google Scholar] [CrossRef]
- Zuber, M.T.; Smith, D.E.; Phillips, R.J.; Solomon, S.C.; Neumann, G.A.; Hauck, S.A.; Peale, S.J.; Barnouin, O.S.; Head, J.W.; Johnson, C.L. Topography of the northern hemisphere of Mercury from MESSENGER laser altimetry. Science 2012, 336, 217–220. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans Image Process 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Maaten, L.V.D.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 22–25 July 2017. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NY, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Genova, A.; Goossens, S.; Mazarico, E.; Lemoine, F.G.; Neumann, G.A.; Kuang, W.; Sabaka, T.J.; Hauck, I.; Steven, A.; Smith, D.E.; et al. Geodetic evidence that Mercury has a solid inner core. Geophys. Res. Lett. 2019, 46, 3625–3633. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Jian, S. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Keys, R.G. Cubic convolution interpolation for digital image processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, Z.; Yi, W.; Gui, Q.; Hou, W.; Ding, M. Deep gradient prior network for DEM super-resolution: Transfer learning from image to DEM. ISPRS J. Photogramm. Remote Sens. 2019, 150, 80–90. [Google Scholar] [CrossRef]
- Wieczorek, M.A.; Meschede, M. SHTools: Tools for Working with Spherical Harmonics. Geochem. Geophys. Geosyst. 2018, 19, 2574–2592. [Google Scholar] [CrossRef]
- Mazarico, E.; Genova, A.; Goossens, S.; Lemoine, F.G.; Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Solomon, S.C. The Gravity Field of Mercury After the MESSENGER Low-Altitude Campaign. In Proceedings of the Lunar and Planetary Science Conference, The Woodlands, TX, USA, 16–20 March 2015; p. 1385. [Google Scholar]
- Kaula, W.M. An introduction to planetary physics. The terrestrial planets. Earth Sci. Rev. 1968, 5, A203–A204. [Google Scholar]



| Mercury | ||||||
| Resolution | 25 Degree | 50 Degree | 100 Degree | |||
| . | 6692 | 0.6464 | 0.6153 | |||
| SSIM | 0.9673 | 0.9663 | 0.9647 | |||
| Moon | ||||||
| Resolution | 25 Degree | 50 Degree | 100 Degree | 200 Degree | 400 Degree | 800 Degree |
| . | 5201 | 0.5072 | 0.4737 | 0.4985 | 0.5179 | 0.5695 |
| SSIM | 0.9651 | 0.9647 | 0.9650 | 0.9652 | 0.9658 | 0.9657 |
| Lunar 25–50 Degree | ||||
| Method | Scale | r | SSIM | RMSE |
| Bicubic | 2 | 0.9701 | 0.9712 | 5.6842 |
| Coarse Output | 2 | 0.9728 | 0.9735 | 4.5789 |
| Fine Output | 2 | 0.9740 | 0.9742 | 4.0011 |
| Lunar 50–100 Degree | ||||
| Bicubic | 2 | 0.9320 | 0.9313 | 7.9650 |
| Coarse Output | 2 | 0.9366 | 0.9354 | 7.2486 |
| Fine Output | 2 | 0.9408 | 0.9412 | 6.5304 |
| Lunar 400–800 Degree | ||||
| Bicubic | 2 | 0.8746 | 0.8751 | 14.0251 |
| Coarse Output | 2 | 0.8876 | 0.8820 | 11.1050 |
| Fine Output | 2 | 0.9115 | 0.9136 | 9.3142 |
| 100-Degree Original SELENE Compared with 100-Degree GRAIL | |||
| Scale | r | SSIM | RMSE |
| . | 0.7085 | 0.8812 | 43.044 |
| 200-Degree Reconstructed SELENE Compared with 200-Degree GRAIL | |||
| 2 | 0.8246 | 0.9389 | 40.8355 |
| Mercury’s 25–50 Degrees | ||||
| Method | Scale | . | IM | RMSE |
| Bicubic | 2 | 0.9725 | 0.9710 | 4.7988 |
| Coarse Output | 2 | 0.9753 | 0.9739 | 3.9971 |
| Fine Output | 2 | 0.9788 | 0.9799 | 3.6548 |
| Mercury’s 50–100 Degrees | ||||
| Bicubic | 2 | 0.9049 | 0.9028 | 8.7884 |
| Coarse Output | 2 | 0.9119 | 0.9113 | 8.5412 |
| Fine Output | 2 | 0.9170 | 0.9179 | 7.2164 |
| Fine-Tuned 50–100 Degrees | ||||
| Coarse Output | 2 | 0.9127 | 0.9118 | 8.3125 |
| Fine Output | 2 | 0.9216 | 0.9185 | 6.7743 |
| 100-Degree Fine-Tuned Results Compared with HgM008 | ||||
| The original HgM007 | / | 0.8561 | 0.8197 | 14.8108 |
| Bicubic | 2 | 0.8427 | 0.8386 | 11.7451 |
| Coarse Output | 2 | 0.8508 | 0.8495 | 10.5847 |
| Fine Output | 2 | 0.8898 | 0.8876 | 9.8873 |
| Compared with 100-Degree Fine-Tuned Result in 0~45°N Region | |||
|---|---|---|---|
| Data | r | SSIM | RMSE |
| HgM007 100 Degree | 0.8825 | 0.8780 | 10.0102 |
| HgM008 100 Degree | 0.9072 | 0.8995 | 9.3155 |
| Lunar 50–200 Degree | ||||
|---|---|---|---|---|
| Method | Scale | r | SSIM | RMSE |
| Bicubic | 4 | 0.9233 | 0.9213 | 10.9855 |
| Coarse Output | 4 | 0.9306 | 0.9297 | 8.6765 |
| Fine Output | 4 | 0.9368 | 0.9354 | 6.8764 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Liu, D.; Yuan, Q.; Li, J. A Global Gravity Reconstruction Method for Mercury Employing Deep Convolutional Neural Network. Remote Sens. 2020, 12, 2293. https://doi.org/10.3390/rs12142293
Zhao S, Liu D, Yuan Q, Li J. A Global Gravity Reconstruction Method for Mercury Employing Deep Convolutional Neural Network. Remote Sensing. 2020; 12(14):2293. https://doi.org/10.3390/rs12142293
Chicago/Turabian StyleZhao, Shuheng, Denghong Liu, Qiangqiang Yuan, and Jie Li. 2020. "A Global Gravity Reconstruction Method for Mercury Employing Deep Convolutional Neural Network" Remote Sensing 12, no. 14: 2293. https://doi.org/10.3390/rs12142293
APA StyleZhao, S., Liu, D., Yuan, Q., & Li, J. (2020). A Global Gravity Reconstruction Method for Mercury Employing Deep Convolutional Neural Network. Remote Sensing, 12(14), 2293. https://doi.org/10.3390/rs12142293