Obtaining Gradients of XCO2 in Atmosphere Using the Constrained Linear Least-Squares Technique and Multi-Wavelength IPDA LiDAR
Abstract
:1. Introduction
2. Methods
2.1. IPDA Inversion Algorithm
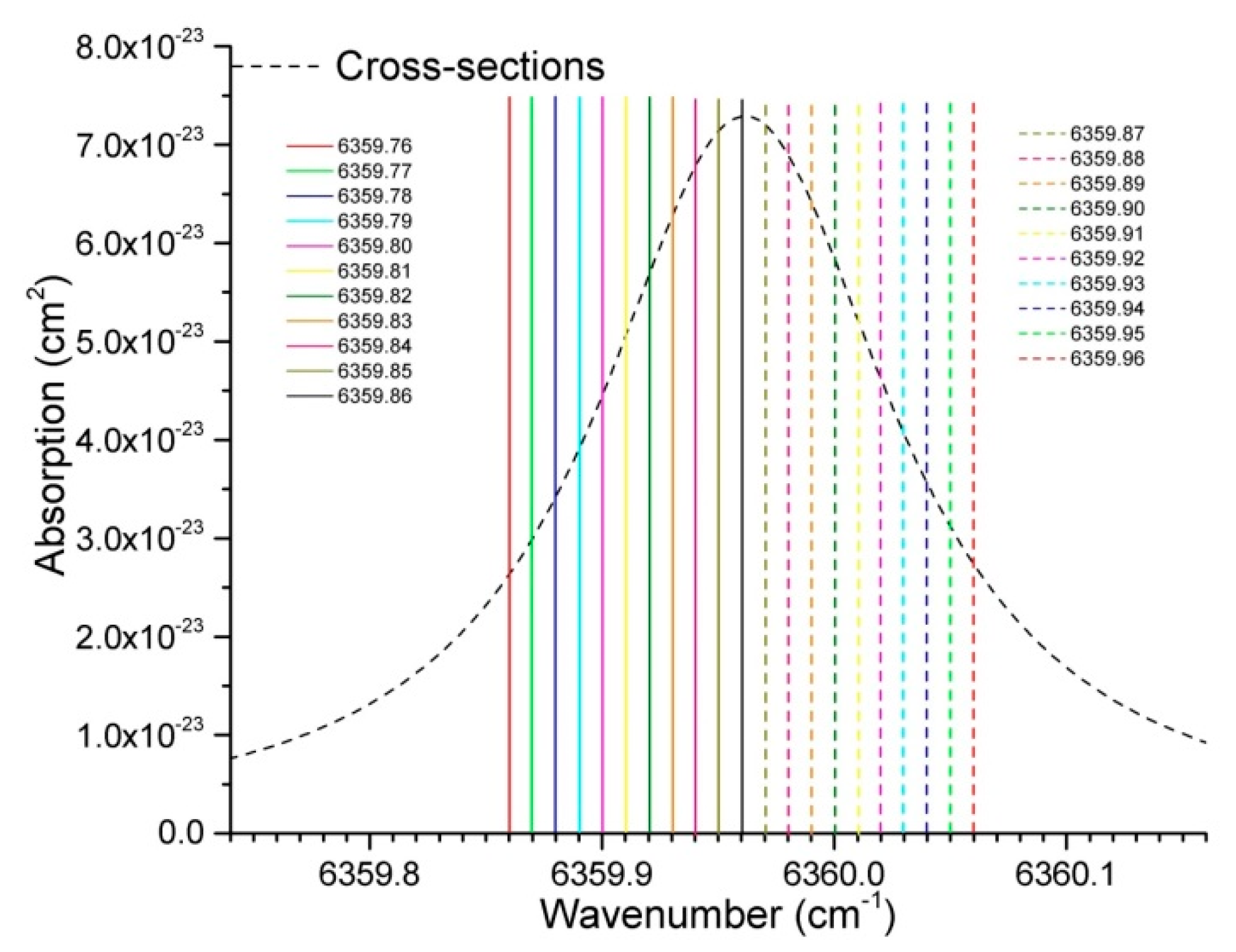
2.2. Multi-Wavelength Inversion Framework
3. Results
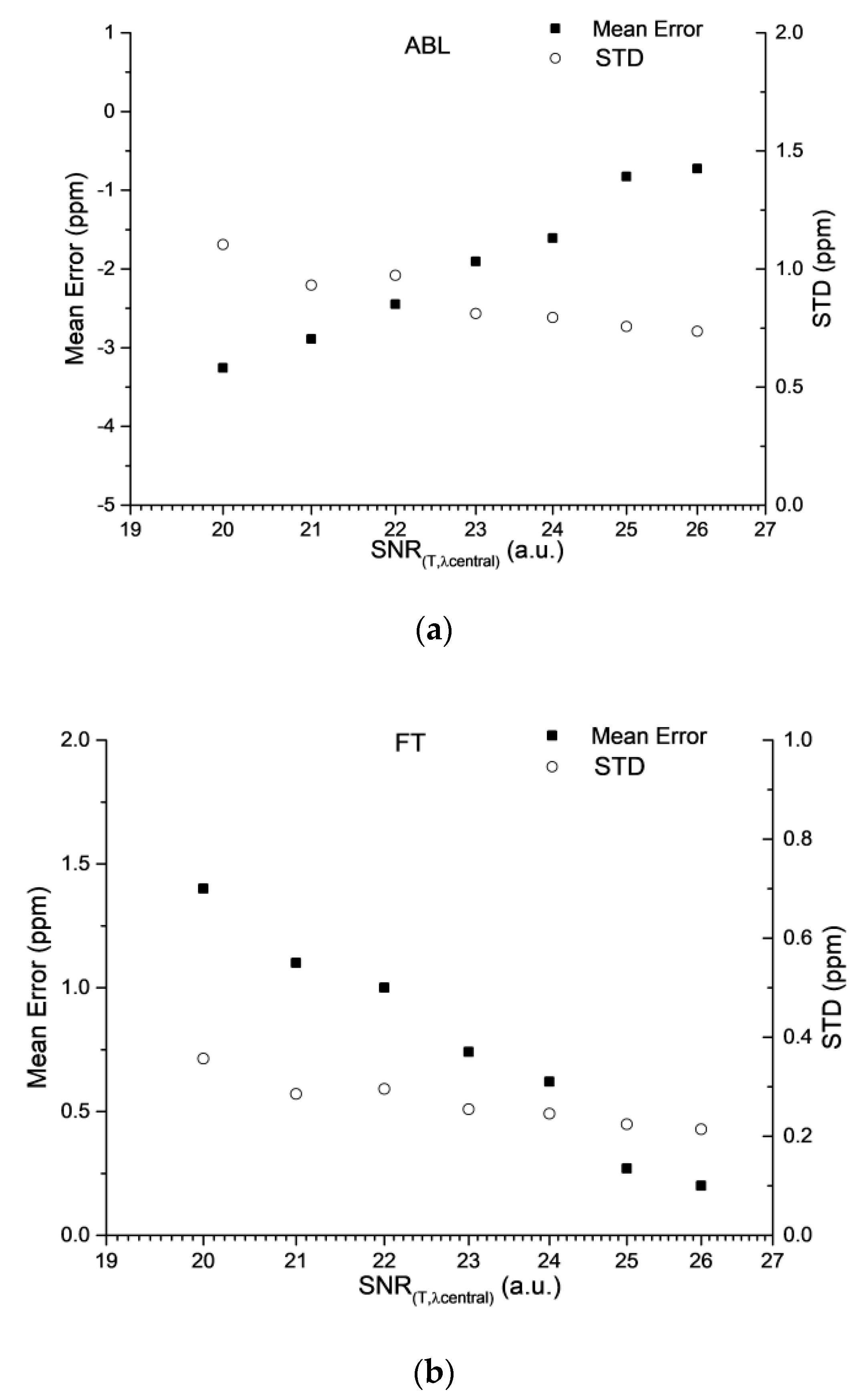
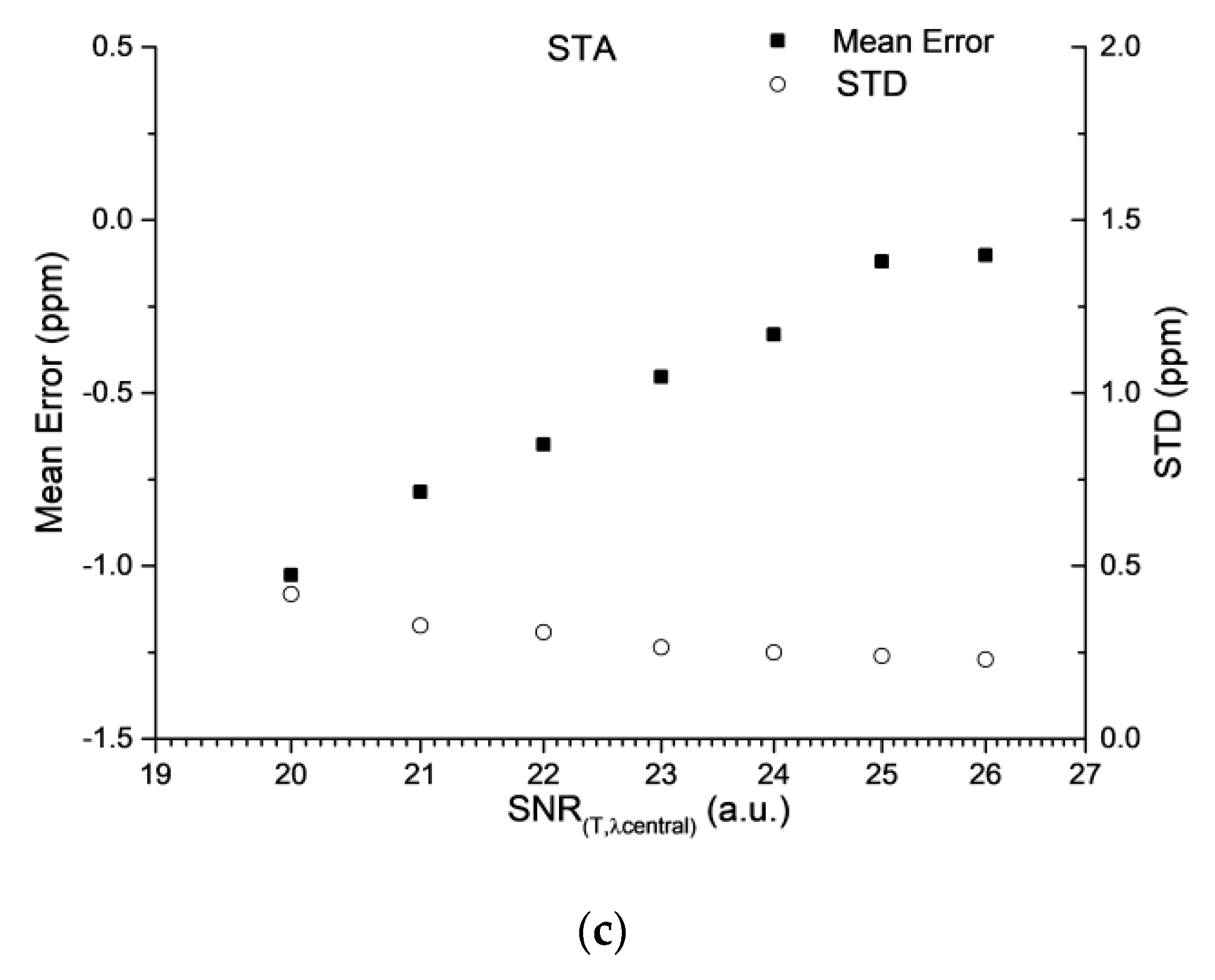
3.1. Effect of Signal-to-Noise Ratio
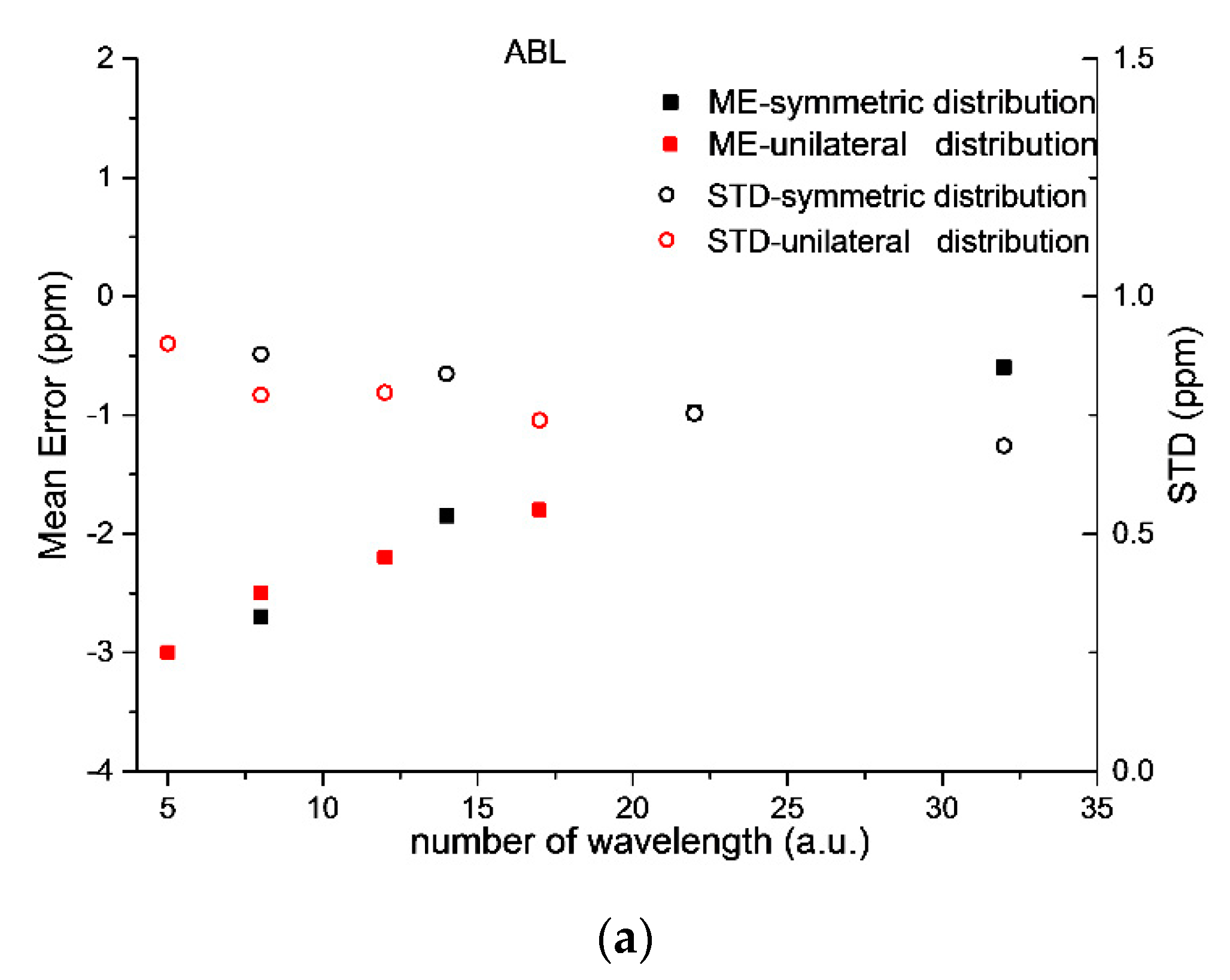
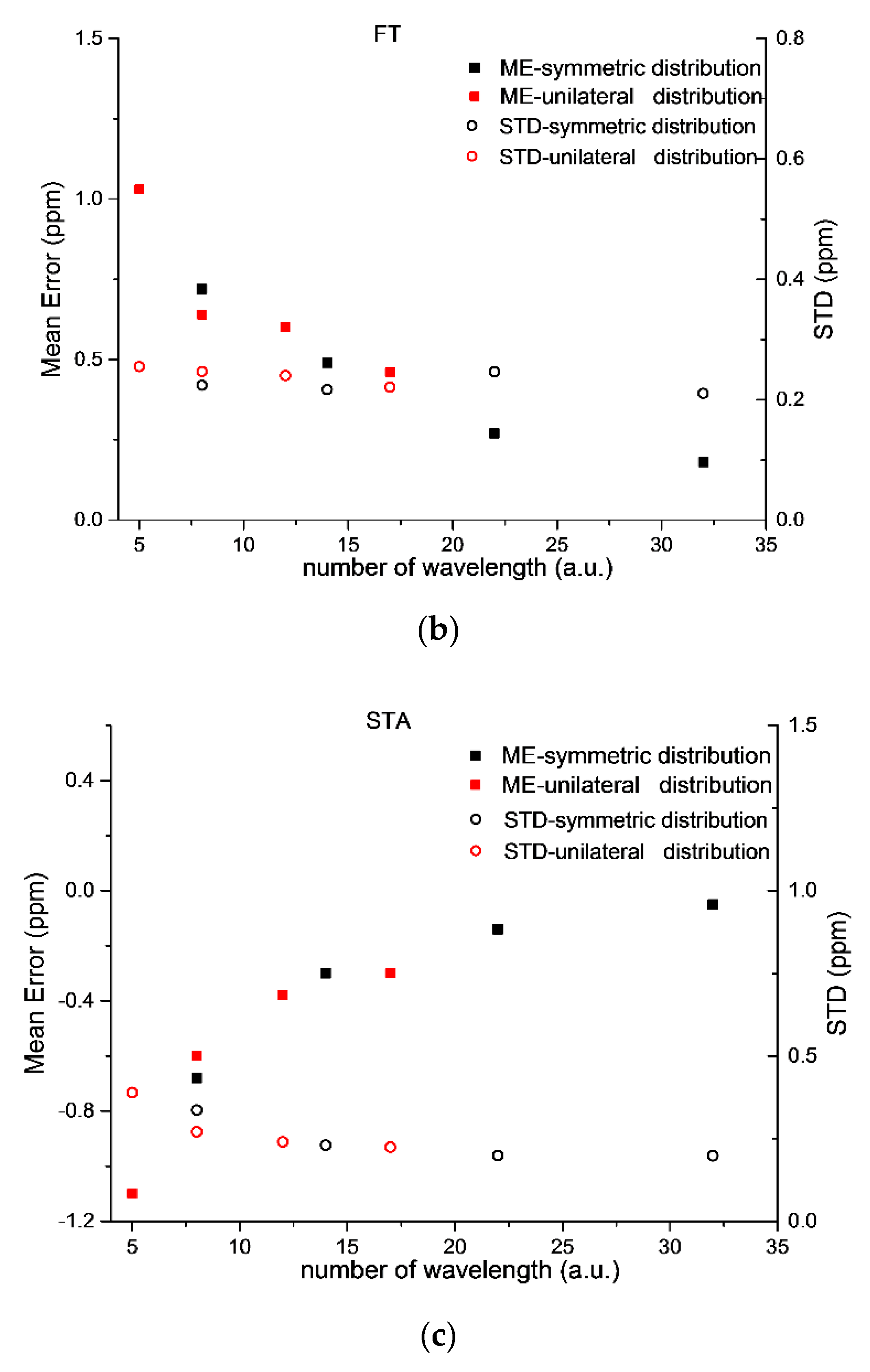
3.2. Effect of the Number of Wavelengths and Selecting Modes
3.3. Effect of the Number of Layers
3.4. Effect of the Atmospheric Boundary Layer Height (ABLH)
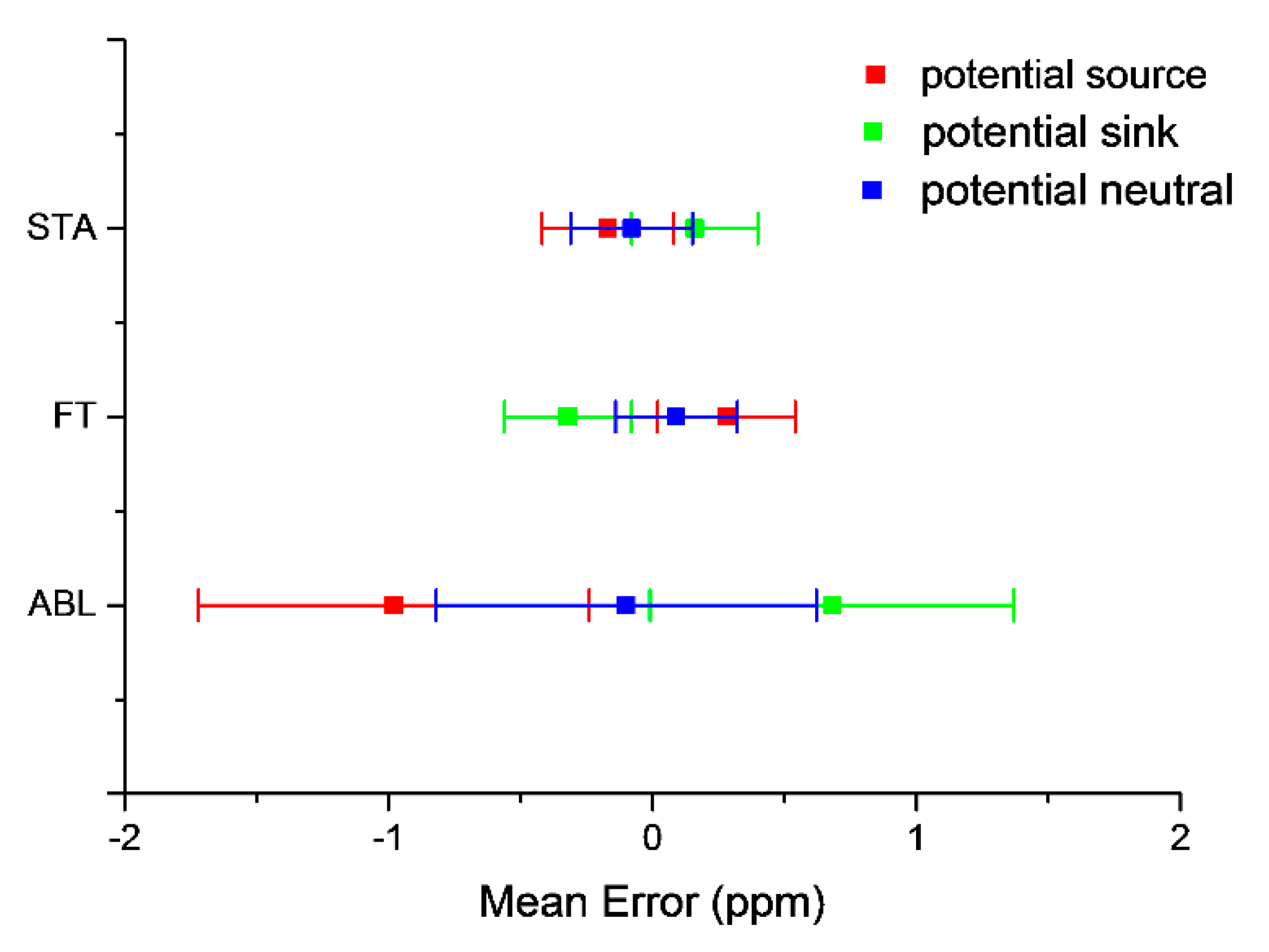
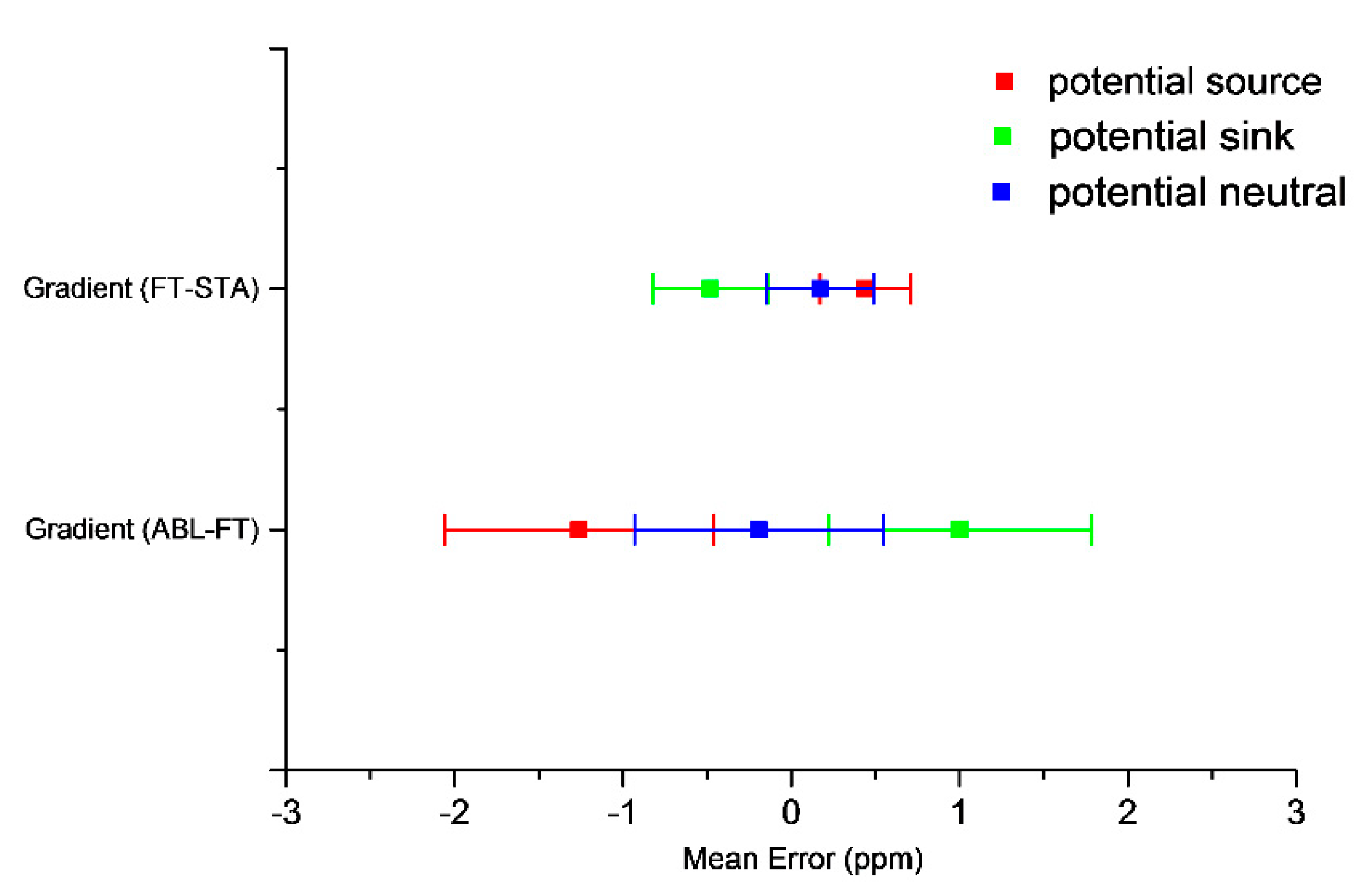
3.5. Ability to Retrieve Gradients of xCO2
4. Discussion
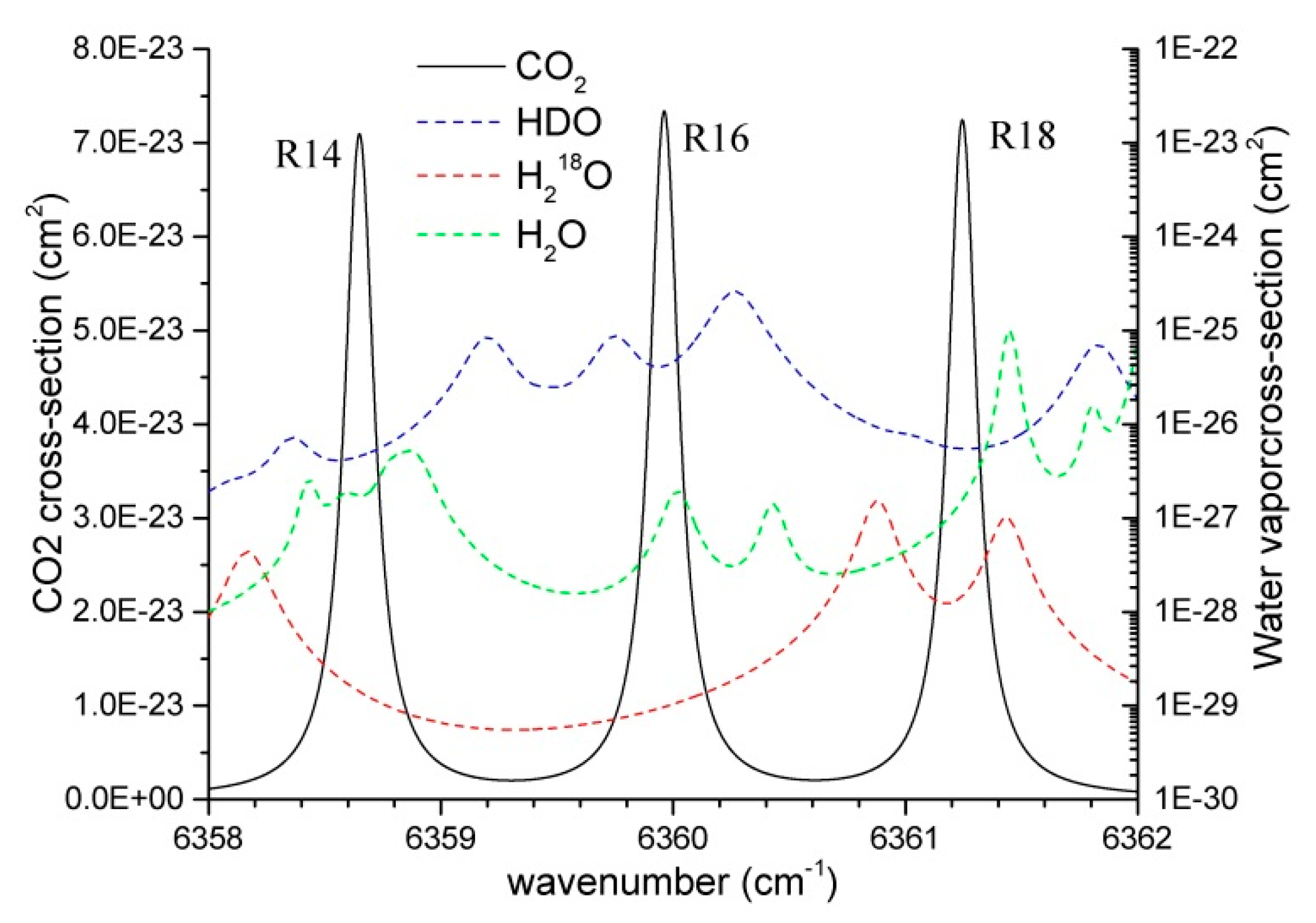
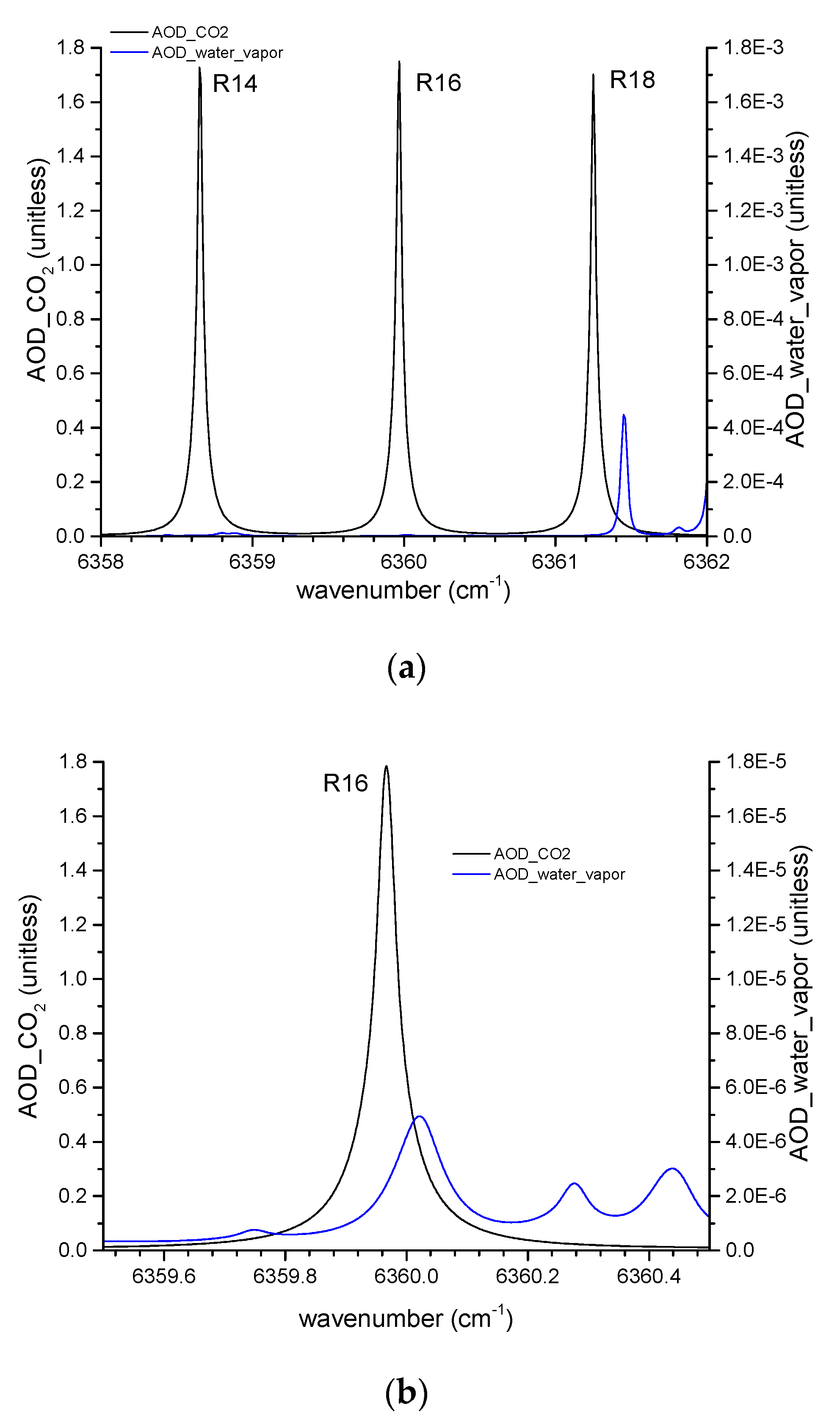
4.1. Interference of Water Vapor in the Absorb Spectrum
4.2. The Influence of Water Vapor on the Value of Dry-Air Mixing Ratio of CO2
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Sabine, C.L.; Feely, R.A.; Gruber, N.; Key, R.M.; Lee, K.; Bullister, J.L.; Wanninkhof, R.; Wong, C.S.; Wallace, D.W.R.; Tilbrook, B.; et al. The oceanic sink for anthropogenic CO2. Science 2004, 305, 367–371. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rayner, P.; O’Brien, D. The utility of remotely sensed CO2 concentration data in surface source inversions. Geophys. Res. Lett. 2001, 28, 175–178. [Google Scholar] [CrossRef] [Green Version]
- Qiu, R.; Han, G.; Ma, X.; Sha, Z.; Shi, T.; Xu, H.; Zhang, M. CO2 concentration, a critical factor influencing the relationship between solar-induced chlorophyll fluorescence and gross primary productivity. Remote Sens. 2020, 12, 1377. [Google Scholar] [CrossRef]
- Liang, A.; Han, G.; Gong, W.; Yang, J.; Xiang, C. Comparison of global XCO2 concentrations from OCO-2 with tccon data in terms of latitude zones. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2491–2498. [Google Scholar] [CrossRef]
- Abshire, J.B.; Ramanathan, A.; Riris, H.; Mao, J.P.; Allan, G.R.; Hasselbrack, W.E.; Weaver, C.J.; Browell, E.V. Airborne measurements of CO2 column concentration and range using a pulsed direct-detection ipda lidar. Remote Sens. 2014, 6, 443–469. [Google Scholar] [CrossRef] [Green Version]
- Amediek, A.; Ehret, G.; Fix, A.; Wirth, M.; Budenbender, C.; Quatrevalet, M.; Kiemle, C.; Gerbig, C. Charm-f-a new airborne integrated-path differential-absorption lidar for carbon dioxide and methane observations: Measurement performance and quantification of strong point source emissions. Appl. Opt. 2017, 56, 5182–5197. [Google Scholar] [CrossRef]
- Amediek, A.; Fix, A.; Wirth, M.; Ehret, G. Development of an opo system at 1.57 μm for integrated path dial measurement of atmospheric carbon dioxide. Appl. Phys. B 2008, 92, 295–302. [Google Scholar] [CrossRef] [Green Version]
- Ehret, G.; Kiemle, C.; Wirth, M.; Amediek, A.; Fix, A.; Houweling, S. Space-borne remote sensing of CO2, ch4, and n2o by integrated path differential absorption lidar: A sensitivity analysis. Appl. Phys. B 2008, 90, 593–608. [Google Scholar] [CrossRef] [Green Version]
- Kiemle, C.; Ehret, G.; Amediek, A.; Fix, A.; Quatrevalet, M.; Wirth, M. Potential of spaceborne lidar measurements of carbon dioxide and methane emissions from strong point sources. Remote Sens. 2017, 9, 1137. [Google Scholar] [CrossRef] [Green Version]
- Han, G.; Xu, H.; Gong, W.; Liu, J.; Du, J.; Ma, X.; Liang, A. Feasibility study on measuring atmospheric CO2 in urban areas using spaceborne CO2-ipda lidar. Remote Sens. 2018, 10, 985. [Google Scholar] [CrossRef] [Green Version]
- Du, J.; Zhu, Y.D.; Li, S.G.; Zhang, J.X.; Sun, Y.G.; Zang, H.G.; Liu, D.; Ma, X.H.; Bi, D.C.; Liu, J.Q.; et al. Double-pulse 1.57 mu m integrated path differential absorption lidar ground validation for atmospheric carbon dioxide measurement. Appl. Opt. 2017, 56, 7053–7058. [Google Scholar] [CrossRef] [PubMed]
- Lin, B.; Nehrir, A.R.; Harrison, F.W.; Browell, E.V.; Ismail, S.; Obland, M.D.; Campbell, J.; Dobler, J.; Meadows, B.; Fan, T.-F.; et al. Atmospheric CO2 column measurements in cloudy conditions using intensity-modulated continuous-wave lidar at 1.57 micron. Opt. Express 2015, 23, A582–A593. [Google Scholar] [CrossRef] [PubMed]
- Mao, J.; Ramanathan, A.; Abshire, J.B.; Kawa, S.R.; Riris, H.; Allan, G.R.; Rodriguez, M.; Hasselbrack, W.E.; Sun, X.; Numata, K. Measurement of atmospheric CO2 column concentrations to cloud tops with a pulsed multi-wavelength airborne lidar. Atmos. Meas. Tech. 2018, 11, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Shi, T.; Han, G.; Ma, X.; Zhang, M.; Pei, Z.; Xu, H.; Qiu, R.; Zhang, H.; Gong, W. An inversion method for estimating strong point carbon dioxide emissions using a differential absorption lidar. J. Clean. Prod. 2020, 271, 122434. [Google Scholar] [CrossRef]
- Shi, T.; Ma, X.; Han, G.; Xu, H.; Qiu, R.; He, B.; Gong, W. Measurement of CO2 rectifier effect during summer and winter using ground-based differential absorption lidar. Atmos. Environ. 2020, 220, 117097. [Google Scholar] [CrossRef]
- Helliker, B.R.; Berry, J.A.; Betts, A.K.; Bakwin, P.S.; Davis, K.J.; Denning, A.S.; Ehleringer, J.R.; Miller, J.B.; Butler, M.P.; Ricciuto, D.M. Estimates of net CO2 flux by application of equilibrium boundary layer concepts to CO2 and water vapor measurements from a tall tower. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar]
- Gatti, L.V.; Gloor, M.; Miller, J.B.; Doughty, C.E.; Malhi, Y.; Domingues, L.G.; Basso, L.S.; Martinewski, A.; Correia, C.S.C.; Borges, V.F.; et al. Drought sensitivity of amazonian carbon balance revealed by atmospheric measurements. Nature 2014, 506, 76–80. [Google Scholar] [CrossRef]
- Han, G.; Gong, W.; Ma, X.; Xiang, C.Z.; Liang, A.L.; Zheng, Y.X. A ground-based differential absorption lidar for atmospheric vertical CO2 profiling. Acta Phys. Sin. 2015, 6, 244206. [Google Scholar]
- Qiu, R.; Han, G.; Ma, X.; Xu, H.; Shi, T.; Zhang, M. A comparison of OCO-2 sif, modis gpp, and gosif data from gross primary production (gpp) estimation and seasonal cycles in north america. Remote Sens. 2020, 12, 258. [Google Scholar] [CrossRef] [Green Version]
- Aiuppa, A.; Fiorani, L.; Santoro, S.; Parracino, S.; Nuvoli, M.; Chiodini, G.; Minopoli, C.; Tamburello, G. New ground-based lidar enables volcanic CO2 flux measurements. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [Green Version]
- Gibert, F.; Edouart, D.; Cenac, C.; Le Mounier, F.; Dumas, A. 2-mu m ho emitter-based coherent dial for CO2 profiling in the atmosphere. Opt. Lett. 2015, 40, 3093–3096. [Google Scholar] [CrossRef] [PubMed]
- Warren, R.E. Detection and discrimination using multiple-wavelength differential absorption lidar. Appl. Opt. 1985, 24, 3541–3545. [Google Scholar] [CrossRef] [PubMed]
- Fukuchi, T.; Goto, N.; Fujii, T.; Nemoto, K. Error analysis of so2 measurement by multiwavelength differential absorption lidar. Opt. Eng. 1999, 38, 141–145. [Google Scholar] [CrossRef]
- Fujii, T.; Fukuchi, T.; Cao, N.W.; Nemoto, K.; Takeuchi, N. Trace atmospheric SO2 measurement by multiwavelength curve-fitting and wavelength-optimized dual differential absorption lidar. Appl. Opt. 2002, 41, 524–531. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.R.; Numata, K.; Wu, S.T. Error reduction in retrievals of atmospheric species from symmetrically measured lidar sounding absorption spectra. Opt. Express 2014, 22, 26055–26075. [Google Scholar] [CrossRef] [PubMed]
- Xiang, C.; Ma, X.; Liang, A.; Han, G.; Gong, W.; Yan, F. Feasibility study of multi-wavelength differential absorption lidar for CO2 monitoring. Atmosphere 2016, 7, 89. [Google Scholar] [CrossRef] [Green Version]
- Han, G.; Xu, H.; Gong, W.; Ma, X.; Liang, A. Simulations of a multi-wavelength differential absorption lidar method for CO2 measurement. Appl. Opt. 2017, 56, 8532–8540. [Google Scholar] [CrossRef] [PubMed]
- Ramanathan, A.K.; Mao, J.P.; Abshire, J.B.; Allan, G.R. Remote sensing measurements of the CO2 mixing ratio in the planetary boundary layer using cloud slicing with airborne lidar. Geophys. Res. Lett. 2015, 42, 2055–2062. [Google Scholar] [CrossRef]
- Tedeschi, L.O. Assessment of the adequacy of mathematical models. Agric. Syst. 2006, 89, 225–247. [Google Scholar] [CrossRef]
- Han, G.; Cui, X.; Liang, A.; Ma, X.; Zhang, T.; Gong, W. A CO2 profile retrieving method based on chebyshev fitting for ground-based dial. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6099–6110. [Google Scholar] [CrossRef]
- Chan, K.L.; Ning, Z.; Westerdahl, D.; Wong, K.C.; Sun, Y.W.; Hartl, A.; Wenig, M.O. Dispersive infrared spectroscopy measurements of atmospheric CO2 using a fabry-perot interferometer sensor. Sci. Total Environ. 2014, 472, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Heinz, D.C.; Chang, C.I. Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 529–545. [Google Scholar] [CrossRef] [Green Version]
- LAI, C.T.; Schauer, A.J.; Owensby, C.; Ham, J.M.; Helliker, B.; Tans, P.P.; Ehleringer, J.R. Regional CO2 fluxes inferred from mixing ratio measurements: Estimates from flask air samples in central kansas, USA. Tellus B 2006, 58, 523–536. [Google Scholar] [CrossRef]
- Gong, W.; Liang, A.; Han, G.; Ma, X.; Xiang, C. Sensitivity of on-line wavelength during retrieval of atmospheric CO2 vertical profile. Photonics Res. 2015, 3, 146–152. [Google Scholar] [CrossRef]
- Han, G.; Gong, W.; Lin, H.; Ma, X.; Xiang, Z. Study on influences of atmospheric factors on vertical profile retrieving from ground-based dial at 1.6 μm. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3221–3234. [Google Scholar] [CrossRef]
- Stephens, B.B.; Gurney, K.R.; Tans, P.P.; Sweeney, C.; Peters, W.; Bruhwiler, L.; Ciais, P.; Ramonet, M.; Bousquet, P.; Nakazawa, T. Weak northern and strong tropical land carbon uptake from vertical profiles of atmospheric CO2. Science 2007, 316, 1732–1735. [Google Scholar] [CrossRef] [Green Version]
- Gatti, L.V.; Miller, J.B.; D’Amelio, M.T.S.; Martinewski, A.; Basso, L.S.; Gloor, M.E.; Wofsy, S.; Tans, P. Vertical profiles of CO2 above eastern amazonia suggest a net carbon flux to the atmosphere and balanced biosphere between 2000 and 2009. Tellus Ser. B-Chem. Phys. Meteorol. 2010, 62, 581–594. [Google Scholar] [CrossRef] [Green Version]
- Han, G.; Ma, X.; Liang, A.; Zhang, T.; Zhao, Y.; Zhang, M.; Gong, W. Performance evaluation for China’s planned CO2-ipda. Remote Sens. 2017, 9, 768. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Yang, J.; Chen, X.; Zhu, X.; Zhang, J.; Li, S.; Sun, Y.; Hou, X.; Bi, D.; Bu, L.; et al. Airborne validation experiment of 1.57-μm double-pulse ipda lidar for atmospheric carbon dioxide measurement. Remote Sens. 2020, 12, 1999. [Google Scholar] [CrossRef]
- Gong, W.; Han, G.; Ma, X.; Lin, H. Multi-points scanning method for wavelength locking in CO2 differential absorption lidar. Opt. Commun. 2013, 305, 180–184. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hill, C.; Kochanov, R.V.; Tan, Y.; Bernath, P.F.; Birk, M.; Boudon, V.; Campargue, A.; Chance, K.V. The hitran2016 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2017, 130, 4–50. [Google Scholar] [CrossRef]
- Ingmann, P.; Bensi, P.; Durand, Y. A-Scope-Advanced Space Carbon and Climate Observation of Planet Erath; Report for Assessment; 2008; pp. SP-1311, 1313. [Google Scholar]
- Wexler, A. Vapor pressure formulation for water in range 0 to 100 °C. A revision. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1976, 80A, 775–785. [Google Scholar] [CrossRef] [PubMed]
| Abbreviation | Range (km) | xCO2 (ppm) |
|---|---|---|
| ABL | 0–1.5 | 410 |
| FT | 1.5–12 | 402 |
| STA | >12 | 395 |
| Mode | Symmetric | Unilateral | ||||||
|---|---|---|---|---|---|---|---|---|
| range(nm) | 1572.305–1572.365 | 1572.305–1572.335 | ||||||
| number | 32 | 22 | 14 | 8 | 17 | 12 | 8 | 5 |
| step(pm) | 2 | 3 | 5 | 10 | 2 | 3 | 5 | 10 |
| Number of Layers | Range (km) | Pseudo-Truth of xCO2 (ppm) | Mean Error (ppm) | STD (ppm) |
|---|---|---|---|---|
| 2 | 0–1.5 | 410 | −0.46 | 0.37 |
| >1.5 | 400 | 0.11 | 0.15 | |
| 3 | 0–1.5 | 410 | −0.96 | 0.81 |
| 1.5-12 | 402 | 0.33 | 0.32 | |
| 12 | 395 | −0.18 | 0.30 | |
| 4 | 0–1.5 | 410 | −1.77 | 1.02 |
| 1.5–7.5 | 403 | 1.20 | 0.43 | |
| 7.5–12 | 399 | −1.70 | 0.81 | |
| >12 | 395 | 0.20 | 0.52 |
| Mean Error (ppm) | STD (ppm) | |||||
|---|---|---|---|---|---|---|
| ABLH (km) | ABL | FT | STA | ABL | FT | STA |
| 2.0 | −0.84 | 0.31 | −0.20 | 0.58 | 0.24 | 0.21 |
| 1.5 | −0.98 | 0.27 | −0.15 | 0.74 | 0.24 | 0.24 |
| 1.0 | −1.76 | 0.29 | −0.20 | 0.91 | 0.18 | 0.23 |
| Layers | xCO2 (ppm) | ||
|---|---|---|---|
| Potential Source | Potential Sink | Potential Neutral | |
| ABL | 410 | 390 | 402 |
| FT | 402 | 402 | 402 |
| STA | 395 | 395 | 395 |
| Layers | Accuracy of Water Vapor | ||||
|---|---|---|---|---|---|
| 0% | +1% | −1% | +5% | −5% | |
| ABL (xCO2) | 409.02 | 409.03 | 409.00 | 409.07 | 408.96 |
| FT (xCO2) | 402.27 | 402.27 | 402.27 | 402.28 | 402.26 |
| STA (xCO2) | 394.85 | 394.85 | 394.85 | 394.85 | 394.85 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, G.; Shi, T.; Ma, X.; Xu, H.; Zhang, M.; Liu, Q.; Gong, W. Obtaining Gradients of XCO2 in Atmosphere Using the Constrained Linear Least-Squares Technique and Multi-Wavelength IPDA LiDAR. Remote Sens. 2020, 12, 2395. https://doi.org/10.3390/rs12152395
Han G, Shi T, Ma X, Xu H, Zhang M, Liu Q, Gong W. Obtaining Gradients of XCO2 in Atmosphere Using the Constrained Linear Least-Squares Technique and Multi-Wavelength IPDA LiDAR. Remote Sensing. 2020; 12(15):2395. https://doi.org/10.3390/rs12152395
Chicago/Turabian StyleHan, Ge, Tianqi Shi, Xin Ma, Hao Xu, Miao Zhang, Qi Liu, and Wei Gong. 2020. "Obtaining Gradients of XCO2 in Atmosphere Using the Constrained Linear Least-Squares Technique and Multi-Wavelength IPDA LiDAR" Remote Sensing 12, no. 15: 2395. https://doi.org/10.3390/rs12152395
APA StyleHan, G., Shi, T., Ma, X., Xu, H., Zhang, M., Liu, Q., & Gong, W. (2020). Obtaining Gradients of XCO2 in Atmosphere Using the Constrained Linear Least-Squares Technique and Multi-Wavelength IPDA LiDAR. Remote Sensing, 12(15), 2395. https://doi.org/10.3390/rs12152395








