Linear and Non-Linear Models for Remotely-Sensed Hyperspectral Image Visualization

Abstract

The visualization of hyperspectral images still constitutes an open question and may have an important impact on the consequent analysis tasks. The existing techniques fall mainly in the following categories: band selection, PCA-based approaches, linear approaches, approaches based on digital image processing techniques and machine/deep learning methods. In this article, we propose the usage of a linear model for color formation, to emulate the image acquisition process by a digital color camera. We show how the choice of spectral sensitivity curves has an impact on the visualization of hyperspectral images as RGB color images. In addition, we propose a non-linear model based on an artificial neural network. We objectively assess the impact and the intrinsic quality of the hyperspectral image visualization from the point of view of the amount of information and complexity: (i) in order to objectively quantify the amount of information present in the image, we use the color entropy as a metric; (ii) for the evaluation of the complexity of the scene we employ the color fractal dimension, as an indication of detail and texture characteristics of the image. For comparison, we use several state-of-the-art visualization techniques. We present experimental results on visualization using both the linear and non-linear color formation models, in comparison with four other methods and report on the superiority of the proposed non-linear model.

1. Introduction

Hyperspectral imaging captures high-resolution spectral information covering the visible and the infrared wavelength spectra, and thus can provide a high-level understanding of the land cover objects [1]. It is used in a wide variety of applications, such as agriculture [2,3], forest management [4,5], geology [6,7] and military/defense applications [8,9]. Human interaction with hyperspectral images is very important for image interpretation and analysis as the visualization is very often the first step in an image analysis chain [10]. However, displaying a hyperspectral image poses the problem of reducing the large number of bands to just three color RGB channels in order for it to be rendered on a monitor, with the information being meaningful from a human point of view. In order to address this problem, a series of hyperspectral image visualization techniques have been developed, which can be included in the following broad categories: band selection, PCA-based approaches, linear approaches, approaches based on digital image processing techniques and machine/deep learning methods.

Band selection methods consist of a mechanism of picking three spectral channels from the hyperspectral image and mapping them as the red, green and blue channels in the color composite. Commercial geospatial image analysis software products such as ENVI [11] offer the possibility to visualize a hyperspectral image by manually selecting the three channels to be displayed. More complex unsupervised band selection approaches have been developed, based on the one-bit transform (1BT) [12], normalized information (NI) [13], linear prediction (LP) or the minimum endmember abundance covariance (MEAC) [14].

Another family of hyperspectral visualization techniques consists of methods that use principal component analysis (PCA) for dimension reduction of the data. A straightforward visualization technique is to map a set of three principal components (usually the first three) to the R, G and B channels of the color image [15]. Other methods use PCA as part of a more complex approach. For instance, the method presented in [16] is an interactive visualization technique based on PCA, followed by convex optimization. The authors of [17] obtain the color composite by fusing the spectral bands with saliency maps obtained before and after applying PCA. In [1], the image is first decomposed into two different layers (base and detail) through edge-preserving filtering; dimension reduction is achieved through PCA applied on the base layer and a weighted averaging-based fusion on the detail layer, with the final result being a combination of the two layers.

In the case of the linear method described in [18,19], the values of each output color channel are computed as projections of the hyperspectral pixel values on a vector basis. Examples of such bases include one consisting of a stretched version of the CIE 1964 color matching functions (CMFs), a constant-luma disc basis or an unwrapped cosine basis.

A set of hyperspectral image visualization approaches are based on digital image processing techniques. In [20], dimension reduction is achieved using multidimensional scaling, followed by detail enhancement using a Laplacian pyramid. The approach presented in [21] uses the averaging method in order to the number of bands to 9; a decolorization algorithm is then applied on groups of three adjacent channels, which produces the final color image. The technique described in [22] is based on t-distributed stochastic neighbor embedding (t-SNE) and bilateral filtering. The method in [23] is also based on bilateral filtering, together with high dynamic range (HDR) processing techniques, while in [24] a pairwise-distances-analysis-driven visualization technique is described.

Machine/deep learning-based methods used for hyperspectral image visualization generally rely on a geographically-matched RGB image, either obtained through band selection or captured by a color image sensor. Approaches include constrained manifold learning [25], a method based on self-organizing maps [26], a moving least squares framework [10], a technique based on a multichannel pulse-coupled neural network [27] or methods based on convolutional neural networks (CNNs) [28,29].

In this paper, our goal is to produce natural-looking visualization results (i.e., depicting colors close to the real ones in the scene) with the highest possible amount of information and complexity. We propose the usage of a linear color formation model based on a widely-used linear model in colorimetry, based on spectral sensitivity curves. We study the impact on visualization of the choice of spectral sensitivity curves and the amount of overlapping between them, which induces the correlation between the three color channels used for visualization. Besides Gaussian functions, we use spectral sensitivity functions of digital camera sensors, the main idea behind the approach being to emulate the result of capturing the scene with a consumer-grade digital camera sensor instead of a hyperspectral one. Alternatively, we also developed a non-linear visualization method based on an artificial neural network, trained using the spectral signatures of a 24-sample color checker, also often used in colorimetry. By using the proposed approaches, we address the following question: what is the impact of the choice of visualization technique on the amount of information and complexity of a scene? The amount of information in a hyperspectral image should be preserved as much as possible after the visualization. The entropy is often used to measure the amount of information contained by a signal [30] and is one of the metrics that are used for the objective assessment of the visualization result [10,21,31]. The complexity of a scene is related to the texture and object characteristics preservation in the process of visualization. The color fractal dimension is a multi-scale measure capable of globally assessing the complexity of a color image, which can be useful to evaluate both the amount of detail and the object-level content in the image. We perform both a qualitative and a quantitative evaluation (using color entropy and color fractal dimension) of the described techniques in comparison with four other state-of-the-art methods, employing five widely used hyperspectral test images.

The rest of the paper is organized as follows: Section 2 presents the five hyperspectral images used in our experiments, the proposed approaches (both linear and non-linear) and the two embraced measures for the objective evaluation of the performance of the proposed approaches, Section 3 depicts the experimental results, Section 4 the discussion on the various aspects related to the proposed approaches, as well as possible further investigation paths, and Section 5 presents our conclusions.

2. Data and Methods

In this section we briefly describe the five hyperspectral images used in our experiments, the linear and non-linear models proposed and used to visualize the respective hyperspectral images, as well as the two quality metrics deployed to objectively evaluate the experimental results—the color entropy and the color fractal dimension.

2.1. Hyperspectral Images

The hyperspectral images used in our experiments are Pavia University, Pavia Centre, Indian Pines, SalinasA and Cuprite [32]. The first two were acquired by the ROSIS-3 sensor [33], while the other three were acquired by the AVIRIS sensor [34]. Figure 1 depicts RGB representations of the five test images.

Pavia University (Figure 1a) is a 610 × 340 image, with a resolution of 1.3 m. The image has 103 bands in the 430–860 nm range. The scene in the image contains a number of 9 materials according to the provided ground truth, both natural and man-made. Pavia Centre (Figure 1b) is a 1096 × 715, 102-band image with the same characteristics as Pavia University. In both cases, the 10th, 31st and 46th bands were used for generating the RGB representations [25].

The third test image, Indian Pines (Figure 1c), is a 145 × 145 image, having 224 spectral reflectance bands in the 400–2500 nm range with a 20 m resolution. The water absorption bands were removed, resulting in a total of 200 bands. The image contains 16 classes, mostly vegetation/crops.

SalinasA (Figure 1d), is an 86 × 83 sub-scene of the Salinas image. After removing the water absorption bands, the image has 204 spectral reflectance bands in the 400–2500 nm range with a spatial resolution of 3.7 m. This image exhibits 6 types of agricultural crops.

The fifth image, Cuprite (Figure 1e), is of size 512 × 614, with 188 spectral reflectance bands in the 400–2500 nm range remaining after removing noisy and water absorption channels. This image contains 14 types of minerals.

For the last three images, the RGB representations were generated by selecting the 6th, 17th, and 36th bands [25].

2.2. Linear Color Formation Model

Considering the formation process of an RGB image, we embraced a linear model given by Equation (1) [35]. In colorimetry, the linear model is used as a standard model for the color formation, but usually the XYZ coordinates of colors are used as an intermediate step before computing the RGB final color coordinates [36]. In the embraced approach, for a pixel at any position $(x,y)$ in the resulting RGB color image, the scalar value on each channel of the RGB triplet is computed as the integral of the product between the spectral reflectance $R\left(\lambda \right)$ of the $(x,y)$ point in the real scene, the power spectral distribution $L\left(\lambda \right)$ of the illuminant and the spectral sensitivity $C\left(\lambda \right)$ of the imaging sensor:

$$I_k(x,y)=\underset{{\lambda }_{min}}{\overset{{\lambda }_{max}}{\int }}{C}_k\left(\lambda \right)L\left(\lambda \right)R_{(x,y)}\left(\lambda \right)d\lambda ,k=R,G,B$$

(1)

For the spectral sensitivity curves of the imaging sensor one can use theoretical or ideal curves, in order to simulate the image formation process. An alternative would be to use the actual sensitivity curves of a specific sensor, which can be measured according to the approach proposed in [35].

The illuminant can be also characterized, either by considering a standard illuminant or measuring the real one by means of spectrophotometry. In colorimetry, a D65 illuminant is very often preferred, as it corresponds to a bright summer day light. For remotely-sensed images, one may know the illuminant as the direct sun light incident to the Earth’s surface, as the position of the sun with respect to the position of the satellite is known. The use of the illuminant in the model from Equation (1) represents merely an unbalanced weighting of the three sensitivities, favoring the blue channel (lower wavelengths) over green and red. The classical D65 illuminant is depicted in Figure 2, in support of this statement. However, in this article we assume that the illuminant is constant across all wavelengths, as we are mostly interested in the effect of the image sensor sensitivity curves on the vizualization process. Thus, the influence of the illuminant $L\left(\lambda \right)$ in Equation (1) is basically null and it can be removed from the integral. Consequently, the equation is basically reduced to the following:

$$I_k(x,y)=\underset{{\lambda }_{min}}{\overset{{\lambda }_{max}}{\int }}{C}_k\left(\lambda \right)R_{(x,y)}\left(\lambda \right)d\lambda ,k=R,G,B$$

(2)

This is the linear model we consider for the experimental results presented in Section 3. In order to apply Equation (2) on a hyperspectral image, we extract from it only the bands corresponding to the range $[{\lambda }_{min},{\lambda }_{max}]$, covered by the sensitivity curves, which corresponds to the visible spectrum. This is the main difference between the proposed model and the linear model presented in [18], which uses all of the bands of the hyperspectral image and the weighting functions are stretched in order to cover the entire range of wavelenghts of the hyperspectral image. Since both the sensitivity functions and the reflectances are discrete, an interpolation of the pixel values of the hyperspectral image is done in order to match the wavelengths and number of values of the sensitivity functions.

Given the embraced linear model and sensitivity functions, our study is limited to the visible spectrum. The extension beyond the visible range could be done either by (i) stretching the sensitivity functions [18] or (ii) adding a fourth color channel, given that one of the latest trends in color display technologies is to add a fourth channel (such as a yellow channel) besides the RGB primaries [37]. However, both approaches would lead to unnatural-looking visualization results, which is not the goal of this study.

2.3. Spectral Sensitivity Functions

As the main objective of visualization is very often the interpretation of the image by humans, we start by considering the spectral sensitivity of the human visual system, which is actually the paradigm for RGB-based color image acquisition and display systems. Figure 3 presents the spectral sensitivities of the human cone cells in the retina, based on the data from [38]. The spectral sensitivity is a function of the wavelength of signal relative to detection of color. These spectral sensitivities are labeled in three categories, depending on the peak value: short (S), medium (M) and long (L). The cone cells are called $\beta$ for the S group with the range that corresponds to the perception of the blue color. Similarly, the range of the M group ($\gamma$ cells) corresponds to green and the L group ($\rho$) corresponds to red.

The RGB color digital cameras are characterized by their sensor spectral sensitivity functions, which define the performance of the respective system. The sensor sensitivity functions for consumer-grade cameras have a similar shape to the spectral sensitivities of human cone cells, since the aim of these products is to capture a representation of the scene that is as accurate as possible from the point of view of human perception. The five digital camera sensor spectral sensitivity functions used in our experiments, taken from [35], are presented in Figure 4.

Starting from the spectral sensitivities of the Canon 5D camera sensor, for our experiments we modeled a set of spectral sensitivities consisting of three Gaussian functions with the mean equal to the wavelength corresponding to the three peaks in Figure 4a and with increasing standard deviation. The functions are depicted in Figure 5. Figure 5a depicts Gaussian functions with a standard deviation of 0, which represent basically unit impulses. In this case, the linear model is reduced to a band selection approach (BS). The standard deviation is gradually increased in the next graphs, resulting in an increasing degree of overlapping between the three functions: no overlap (NOL), small overlap (SOL), medium overlap (MOL) and high overlap (HOL). In this way, we emulate the various levels of correlation between the three RGB color channels of the considered sensor model—from zero correlation, corresponding to a complete separation between the color channels for an ideal imaging sensor, to high overlap, corresponding to a low-performance imaging sensor.

2.4. Non-Linear Color Formation Model

The non-linear color formation model that we propose is based on an Artificial Neural Network (ANN) [39], with the input feature vector consisting of a spectral reflectance curve and the output being the corresponding RGB value. The architecture of the fully connected 5-layer network is depicted in Figure 6. The network uses the Exponential Linear Unit (ELU) [40] as an activation function instead of the more standard Rectified Linear Unit (ReLU), in order to overcome the problem of having a multitude of deactivated neurons (also referred to as “dying neurons” [41]). The implementation was done using the PyTorch library [42].

For the supervised training of the ANN, we chose to use a standard set of 24 colors widely-used in colorimetry–the McBeth color chart [43], depicted in Figure 7. In Figure 8 we show the spectral reflectance curves of the color patches for each row in the McBeth color chart, with their original designations in the legend of the plots. For each color, the RGB triplet is known and we used the measurements provided by [44]. The wavelength range covered by the reflectance curves is 380–780 nm. The reason for choosing this McBeth standard color set is twofold: (i) the spectral reflectance curves of the colors are specified regardless of the illuminant, therefore they can be used as references both in ideal or real conditions; and (ii) this particular color set was determined independently from the domain of remote sensing, thus it can be seen as a neutral set of colors compared to the existing data set of material spectral signatures, such as the ASTER spectral library [45]. In addition, the chosen color set does not require the mapping between the spectral curves and corresponding RGB colors. The training of the ANN is done via the classical backpropagation algorithm, with the mean squared error (MSE) being used as a cost function and Adam used as the optimizer.

As in the case of the linear model, only the bands covered by the spectral reflectance curves of the McBeth color set are used from the hyperspectral image. Concretely, the common range between the Pavia University image and the McBeth curves is 430–780 nm. This range is covered by 83 bands of the image and 71 values of the spectral reflectance curves. The 83 bands of the image are reduced to 71 through interpolation, such as to match the McBeth spectral reflectance curves, giving the size of the input feature vector in Figure 6.

After training with the 24 reflectance curves, the network is applied on a pixel-by-pixel basis; thus, for each pixel in the input image (a vector of 71 values in the case of Pavia University), the 3 output values (R, G and B) are obtained and placed in the corresponding position in the visualization result.

2.5. Quality Metrics

A commonly used objective quality metric for hyperspectral image visualization is the entropy, which is a measure of the degree of information preservation in the resulting image [1]. The most common definition of entropy is the Shannon entropy (see Equation (3)) which measures the average level of information present in a signal with N quantization levels [30].

$$H=-\sum _{i=1}^N{p}_i{log}_2{p}_i$$

(3)

where $p_i$ represents the probability to find a certain level in the signal (or color i in a given subset, in context of color images). From the Shannon definition, various other definitions were developed: Rényi entropy (as a generalization), Hartley entropy, collision entropy and min-entropy, or the Kolmogorov entropy, which is another generic definition of entropy [46]. The original Shannon entropy was embraced by Haralick as one of his thirteen features proposed for texture characterization [47]. In our experiments, we use the extension of the entropy to color images from [48].

Additionally, we use the fractal dimension from fractal geometry [49] to assess the complexity of the color images resulting in the process of hyperspectral image visualization. The fractal dimension, also called similarity dimension, is a measure of the variations, irregularities or wiggliness of a fractal object [50]. This multi-scale measure is often used in practice for the discrimination between various signals or patterns exhibiting fractal properties, such as textures [51]. In [52] the fractal dimension was linked to the visual complexity of a color image, more specifically to the perceived beauty of the visual art. Consequently, we use it in this article to both objectively assess the color image content at multiple scales and the appealing of the visualization from a human perception point of view.

The theoretical fractal dimension is the Hausdorff dimension [53], which is comprised in the interval $[E,E+1]$, where E is the topological dimension of that object (thus, for gray-scale images the fractal dimension is comprised between 2 and 3.). Because it was defined for continuous objects, equivalent fractal dimension estimates were defined and used: the probability measure [54,55], the Minkowski or box-counting dimension [53], the $\delta$-parallel body method [56], the gliding box-counting algorithm [57] etc. The fractal dimension estimation was extended to the color image domain, like the marginal color analysis [58] or the fully vectorial probabilistic box-counting [59]. More recent attempts in defining the fractal dimension for color images exist [60,61]. For an RGB color image, the estimated color fractal dimension should be comprised in the interval $[2,5]$ [59].

In our experiments, we used the probabilistic box-counting approach defined color images in [59] for the estimation of the fractal dimension of the visualization results. The classical box-counting method consists of covering the image with grids at different scales and counting the number of boxes that cover the image pixels in each grid. The fractal dimension $FD$ is then computed as [62]:

$$FD=\underset{r\to 0}{lim}\frac{log{N}_r}{logr}$$

(4)

where $N_r$ is the number of boxes and r is the scale.

$FD$ is defined and computed for binary and grayscale images (considering the $z=f(x,y)$ image model, where z is the luminance and x and y are the spatial coordinates). The extension of $FD$ to color images, the color fractal dimension ($CFD$), is defined by considering the color image as a surface in a 5-dimensional hyperspace ($RGBxy$) [59] and 5D hyper-boxes instead of 3D regular ones. For the experimental results presented in Section 3, the stable $CFD$ estimator proposed in [63] was used, which minimizes the variance of the nine regression line estimators used in the process of fractal dimension estimation. See [64] for reference color fractal images and the Matlab implementation of the baseline CFD estimation approach.

3. Experimental Results

Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 depict the visualization results for the five hyperspectral test images presented in Section 2. Each figure is organized as follows: on the top row, the results obtained with the proposed linear approach using the Gaussian functions (Figure 5); on the middle row, the results obtained with the linear approach using camera spectral sensitivity functions (Figure 4); on the bottom row, the results obtained using the proposed ANN approach (Section 2.4), the approach based on the PCA to RGB mapping [15], the linear approach based on the stretched color matching functions (CMF) [18] and two recent approaches, constrained manifold learning (CML) [25] and decolorization-based hyperspectral visualization (DHV) [21].

For the Gaussian approaches, it can be noticed that, as the degree of overlapping between the three functions increases, the vizualization results tend to come closer to grayscale images, as expected. In the case of the camera functions, the difference between the results is not significant, proving that the choice of a particular camera model over the other does not have a large impact on the visualization results. Moreover, there is no significant difference in the visualization results between the two cases of the proposed linear approach. The proposed ANN approach obtains satisfying results in terms of both color and contrast, while the other depicted methods, particularly PCA and DHV, do not tend to give natural-looking results.

The corresponding values for the color entropy H and color fractal dimension $CFD$ are depicted in

Table 1. Entropy and fractal dimension for the visualization results in Figure 9 and Figure 10. The values in bold represent the highest values for the respective image.

		Pavia University		Pavia Centre
Method		$\mathit{H}$	$\mathit{CFD}$	$\mathit{H}$	$\mathit{CFD}$
Linear Gaussian (proposed)	BS	13.22	2.41	13.48	2.44
	NOL	12.81	2.39	13.08	2.39
	SOL	12.68	2.38	12.96	2.38
	MOL	12.45	2.37	12.70	2.37
	HOL	10.79	2.35	10.82	2.36
Linear Camera (proposed)	Canon 5D	12.03	2.37	12.10	2.36
	Canon 1D	12.23	2.37	12.31	2.37
	Hasselblad H2	12.25	2.38	12.25	2.37
	Nikon D3X	12.30	2.38	12.34	2.37
	Nikon D50	12.45	2.38	12.49	2.38
ANN (proposed)		15.38	3.02	15.28	2.87
PCA [15]		15.20	2.84	14.58	2.75
CMF [18]		14.98	2.51	15.11	2.63
CML [25]		12.79	2.80	12.94	2.63
DHV [21]		15.31	2.84	15.21	2.77

and

Table 2. Entropy and fractal dimension for the visualization results in Figure 11, Figure 12 and Figure 13. The values in bold represent the highest values for the respective image.

		Indian Pines		Salinas A		Cuprite
Method		$\mathit{H}$	$\mathit{CFD}$	$\mathit{H}$	$\mathit{CFD}$	$\mathit{H}$	$\mathit{CFD}$
Linear Gaussian (proposed)	BS	13.22	2.41	12.01	2.38	13.71	2.84
	NOL	11.76	2.51	11.29	2.29	13.31	2.80
	SOL	11.53	2.56	11.16	2.28	13.19	2.79
	MOL	11.31	2.46	10.97	2.27	12.84	2.79
	HOL	10.29	2.42	9.84	2.36	10.99	2.73
Linear Camera (proposed)	Canon 5D	12.03	2.37	11.06	2.43	12.13	2.76
	Canon 1D	11.28	2.46	10.51	2.26	12.32	2.77
	Hasselblad H2	11.40	2.46	10.47	2.25	12.36	2.76
	Nikon D3X	11.34	2.45	10.52	2.25	12.35	2.77
	Nikon D50	11.50	2.46	10.69	2.27	12.56	2.78
ANN (proposed)		13.89	3.24	11.50	2.75	15.76	3.00
PCA [15]		14.24	3.19	11.04	2.38	17.40	3.37
CMF [18]		12.51	3.17	10.36	1.86	8.00	2.77
CML [25]		12.81	2.68	11.10	2.14	13.66	2.67
DHV [21]		14.13	3.03	12.29	2.44	16.22	3.06

. One may note that, for the set of Linear Gaussian approaches, both the color entropy and color fractal dimension are maximum for the band selection, with one exception for the SalinasA image, and they both decrease with the increase of the correlation between the three Gaussian functions, as the color content tends to gray-scale and thus complexity diminishes. For the set of Linear Camera proposed approaches, the two quality measures have similar values, basically there is no noticeable difference in the visualization results. For both the Linear Gaussian and Linear Camera approaches, the two quality measures exhibit relatively modest values, which indicate that the visualization result does neither contain the highest information, nor is the most complex. The highest amount of information, measured through the color entropy, is obtained using the proposed non-linear ANN approach for the Pavia University and Pavia Centre images, the PCA approach for the Indian Pines and Cuprite images, and DHV for the SalinasA image. For the three latter images, the proposed ANN-based non-linear approach obtains the third (Indian Pines, Cuprite) and second (SalinasA) best visualization from the point of view of entropy. The highest complexity, measured through the color fractal dimension, is revealed when the hyperspectral images are visualized using the non-linear approach based on ANN, with the exception of the Cuprite image, in which case the PCA approach proves to be superior. The main advantage of the ANN method is that basically any out-of-the-box artificial neural network model can be used, by changing the input layer only in order to match the hyperspectral image under analysis.

Table 3. Independent data used by the methods under comparison.

Method	Independent Data
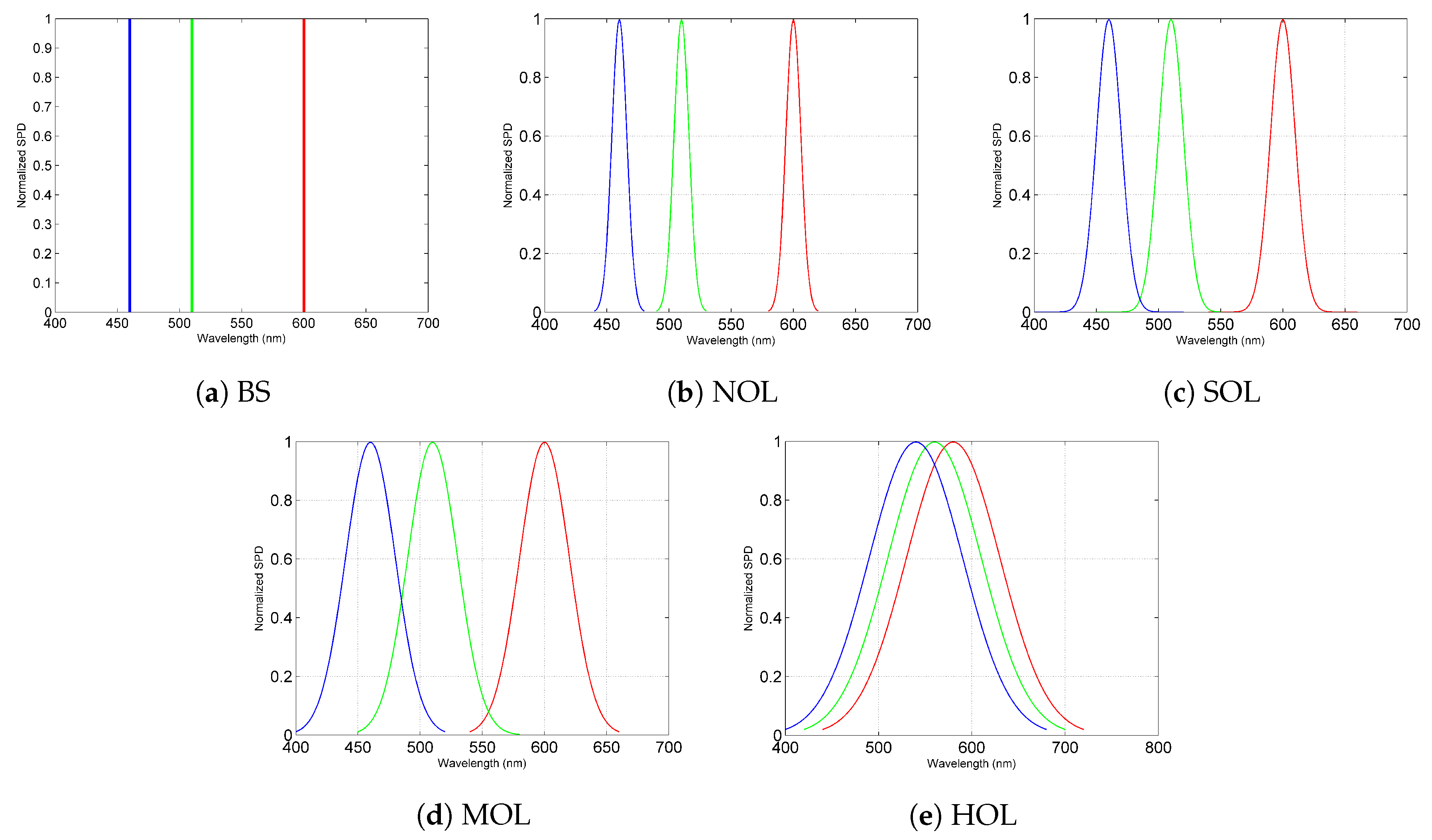
Linear Gaussian	Gaussian sensitivity functions (Figure 5)
Linear Camera	Camera sensitivity functions (Figure 4)
ANN	McBeth spectral reflectance curves (Figure 8)
PCA [15]	none
CMF [18]	Stretched CIE 1964 color matching functions
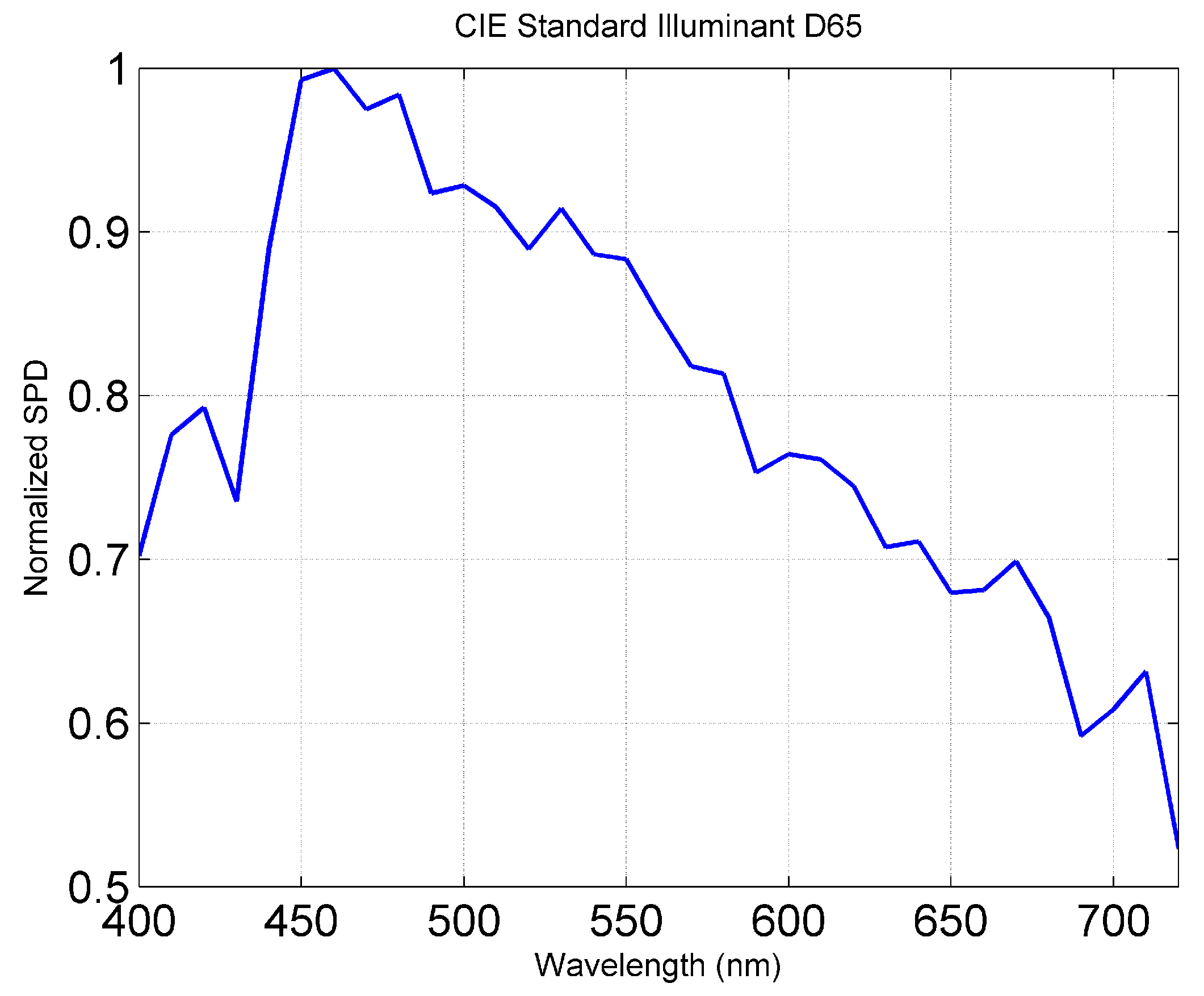
CML [25]	Geographically-matched RGB image (Figure 1)
DHV [21]	none

lists, for each visualization method, the independent data used in addition to the hyperspectral images. In the case of the CML approach, the geographically-matched RGB image was obtained through band selection from the original image; the images used are depicted in Figure 1, while the specific bands chosen are listed in Section 2.1.

4. Discussion

First of all, other measures can be considered for the assessment of the complexity of color images, like the Naive Complexity Measure [65]. For the evaluation of the information present in a color image, one could use the Pearson correlation coefficient between the color channels of the resulting RGB color image [63] as an indication of the overlapping between the information on the three RGB color channels. In the presence of a reference or ground truth, similarity indexes like Structural Similarity Index Measure [66] can be used. Nevertheless, the ultimate criteria for the evaluation of the performance of the hyperspectral image visualization approaches are dictated by the specific application and its objectives.

The best experimental results were obtained using the proposed non-linear ANN-based model, despite the extremely reduced training set—only 24 spectral reflectance curves and the corresponding RGB triplets. One should investigate the effects of increasing the size of the training set, in order to assess and reduce the overfitting effect [67] which may occur in our experiments. Extending the training set implies the realization of more color references, characterized both by their hyperspectral signatures (e.g., by using a spectrophotometer) and RGB triplets (e.g., by using a calibrated digital color image acquisition system). The non-linear model itself could be developed further by considering the wavelengths outside the visible range and taking into account the possibility to display the image with more than 3 color channels, including various choices for the mapping between the hyperspectral signatures and RGB triplets.

The linear models used to obtain the experimental results can be useful in understanding both the capabilities and limitations of current or new imaging sensors. The full characterization of the imaging sensors is mandatory in order to predict the imaging process outcome.

5. Conclusions

In this article, we proposed the usage of a linear model for the color formation based on spectral sensitivity curves in order to visualize hyperspectral images by rendering them as RGB color images. We deployed both Gaussian and real digital camera sensitivity curves and showed that, as the correlation between the RGB color channels increases, similar to the overlapping of the curves for both the human visual system and commercially-available digital cameras, the resulting color images tend to go to gray-scale and to exhibit both a smaller amount of information and complexity. We also proposed a non-linear color formation model based on an artificial neural network which was trained with the colors of the McBeth color chart widely used in colorimetry. The training was supervised as the 24 colors of the McBeth chart are specified both by their spectral reflectance curves and RGB triplets. Given their construction, both proposed linear and non-linear approaches generate color images with natural colors.

For the objective assessment of the quality of the hyperspectral image visualization results, we deployed the widely-used measure of entropy, as it is an indicator of the amount of information contained by a signal. We also proposed the usage of the fractal dimension, which is a multi-scale measure usually employed to assess the complexity of color images, but also their beauty and appeal according to some studies. The fractal dimension is an indicator of the amount of details present in the image along multiple analysis scales.

In our experiments, we compared the proposed approaches with four other visualization techniques, using five remotely-sensed hyperspectral images. In the case of the Gaussian functions, our results show that, as the degree of overlapping between functions increases, the visualization results come closer to a grayscale image. With regards to the camera sensitivity functions, we show that the specific choice of a camera model does not have a significant impact on the visualization result. Our experiments also show that the proposed non-linear model achieves the best visualization results from the point of view of the complexity of the resulting color images. We envisage further development by investigating the possible overfitting effect occurring in the case of the ANN approach, extending the approach beyond the visible range and by using a fourth color channel. We underline that for the choice of the most appropriate visualization technique, one may need to consider three important aspects: the naturalness of the resulting colors, the amount of information present in the resulting color image and the complexity along multiple scales.