Remote Sensing Analysis of Surface Temperature from Heterogeneous Data in a Maize Field and Related Water Stress
Abstract
:1. Introduction
2. Materials
2.1. Study Site
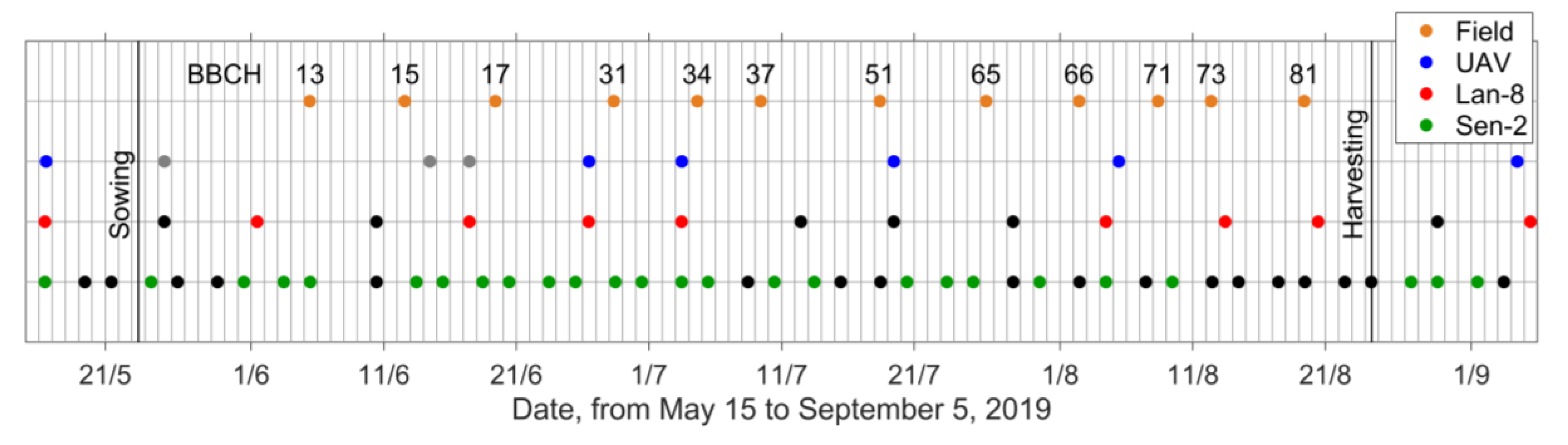
2.2. Imagery Surveyed from UAV and Satellites
2.3. UAV Thermal and Optical Surveys
2.4. Acquisition of Satellite Data
2.5. Ground Temperature Acquisition for Validation
2.6. Irrigation Water Management
3. Methods
3.1. UAV Imagery Pre-Processing
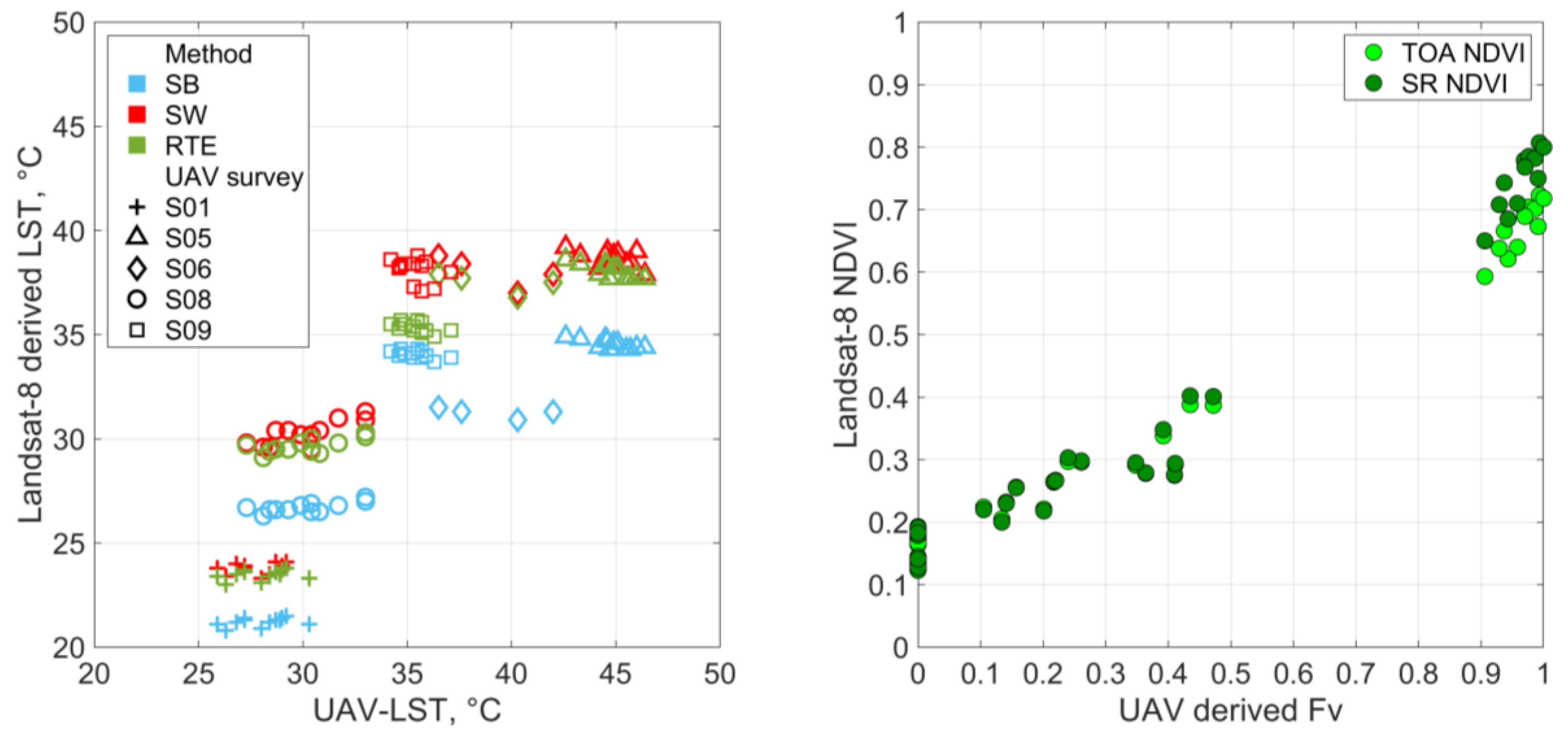
3.2. Relation between UAV Measured LST and Landsat Derived One
3.2.1. LST from Artis and Carnahan Equation
3.2.2. LST from the Radiative Transfer Equation Based Method
3.2.3. LST from the Split Window Algorithm
3.3. Actual Evapotranspiration and Crop Water Stress
- a hot or dry pixel, representing zero ETa conditions, and
- a cold or wet pixel, representing areas where ETa equals the potential value as LST equals air temperature canceling sensible heat flux convected to the air.
3.3.1. Surface Energy Balance Algorithm for Land (SEBAL)
- Net Radiation
- 2.
- Soil heat flux
- 3.
- Sensible heat flux
- dT from and Equation (32);
- H from dT and Equation (27);
- finally, λE from H and the energy balance (Equation (18)).
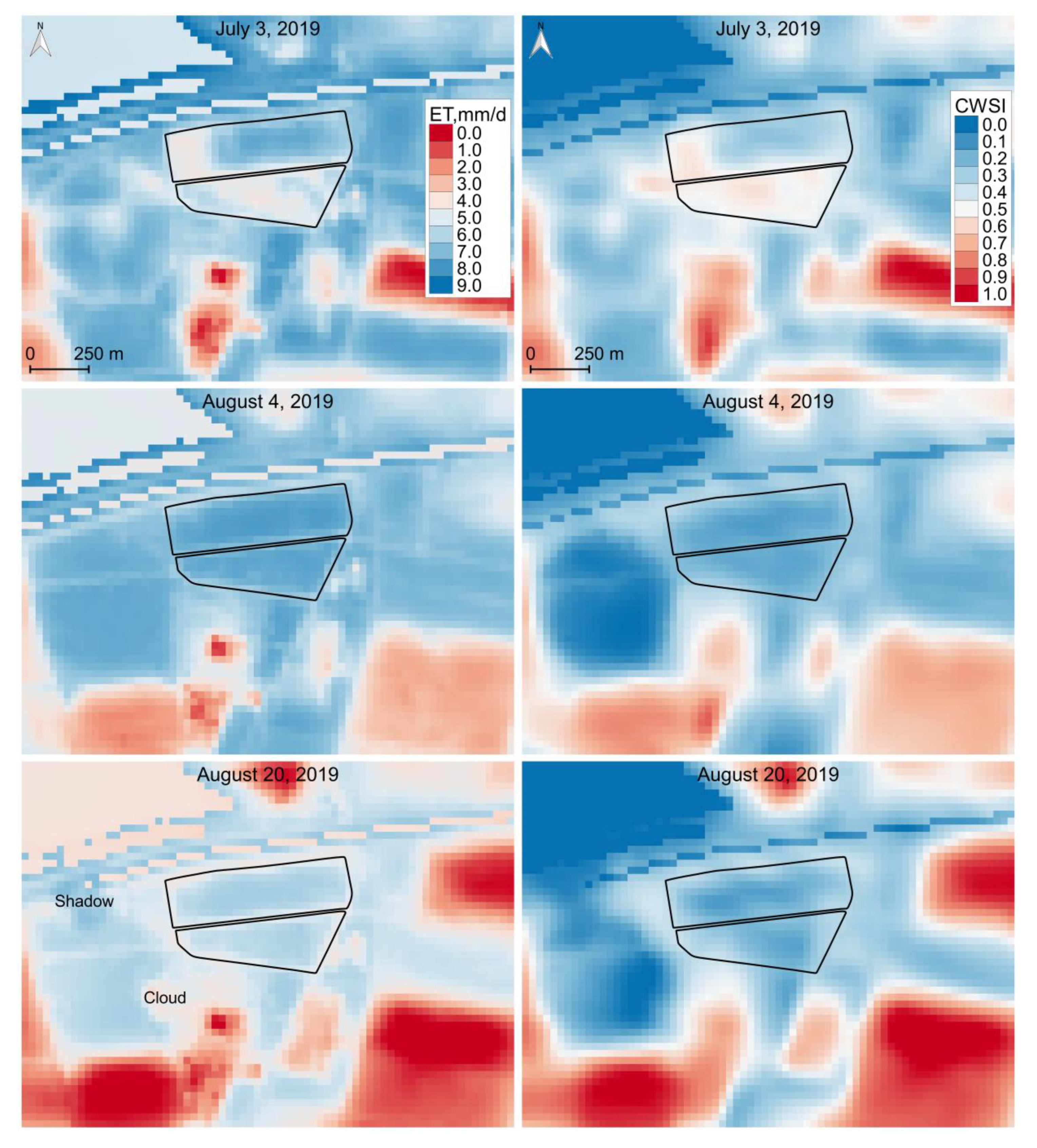
3.3.2. Crop Water Stress Index (CWSI)
4. Results
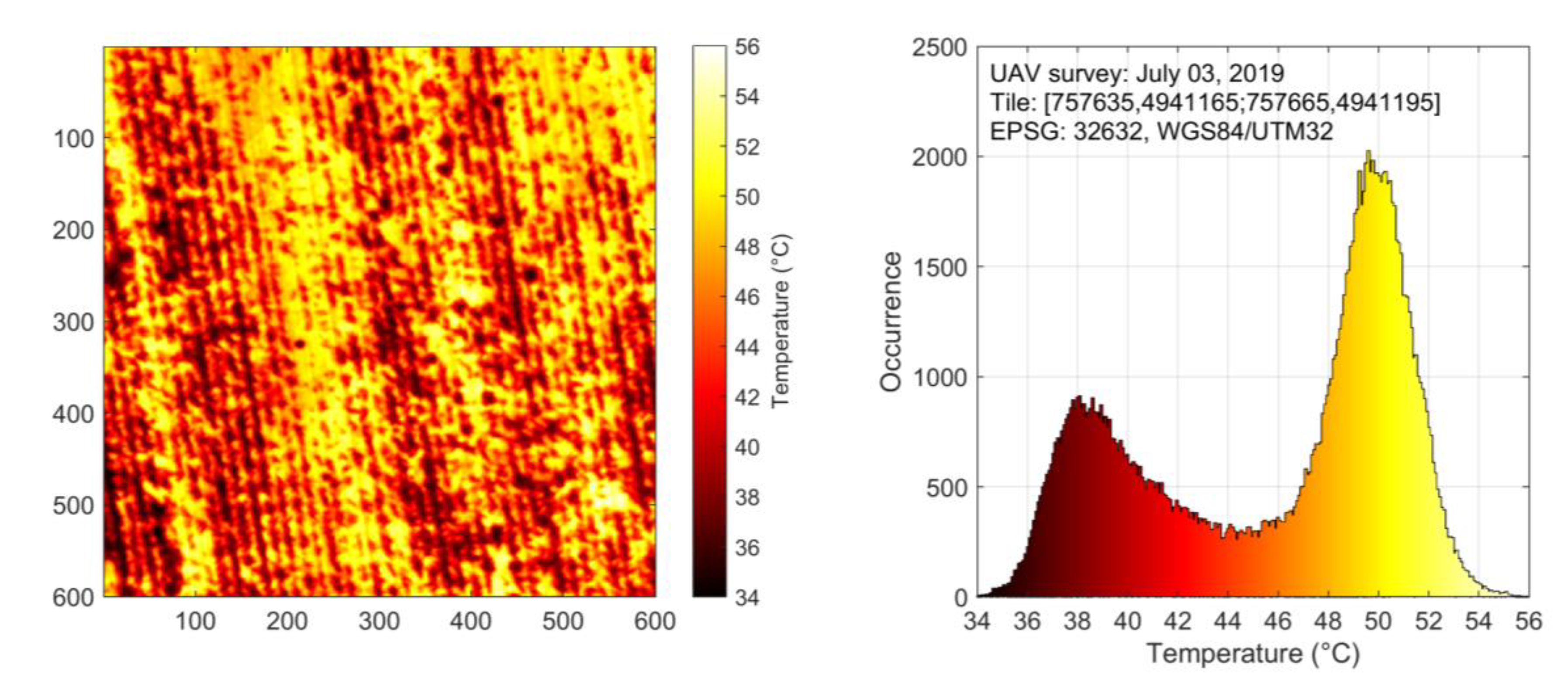
4.1. Tile and Pixel Data
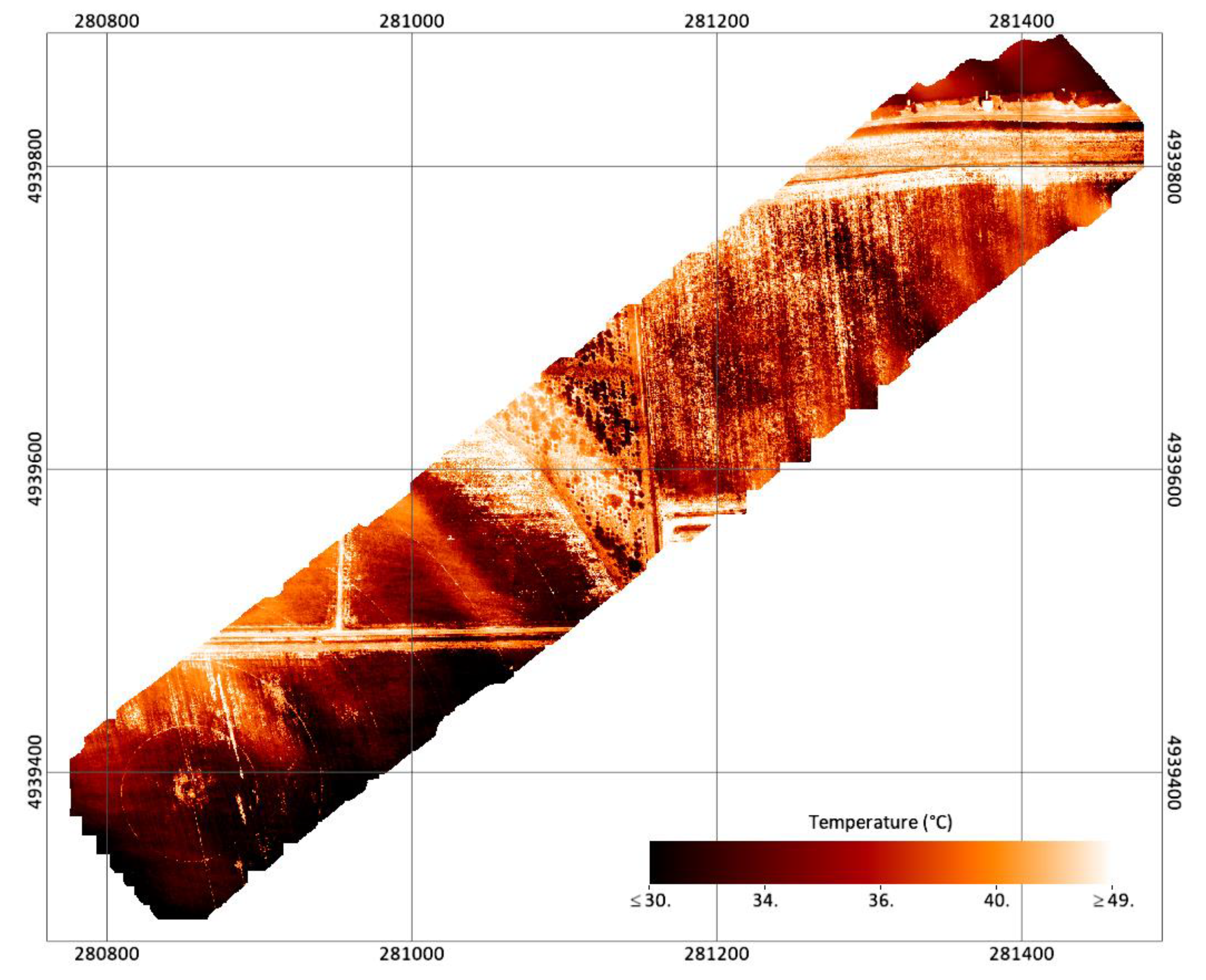
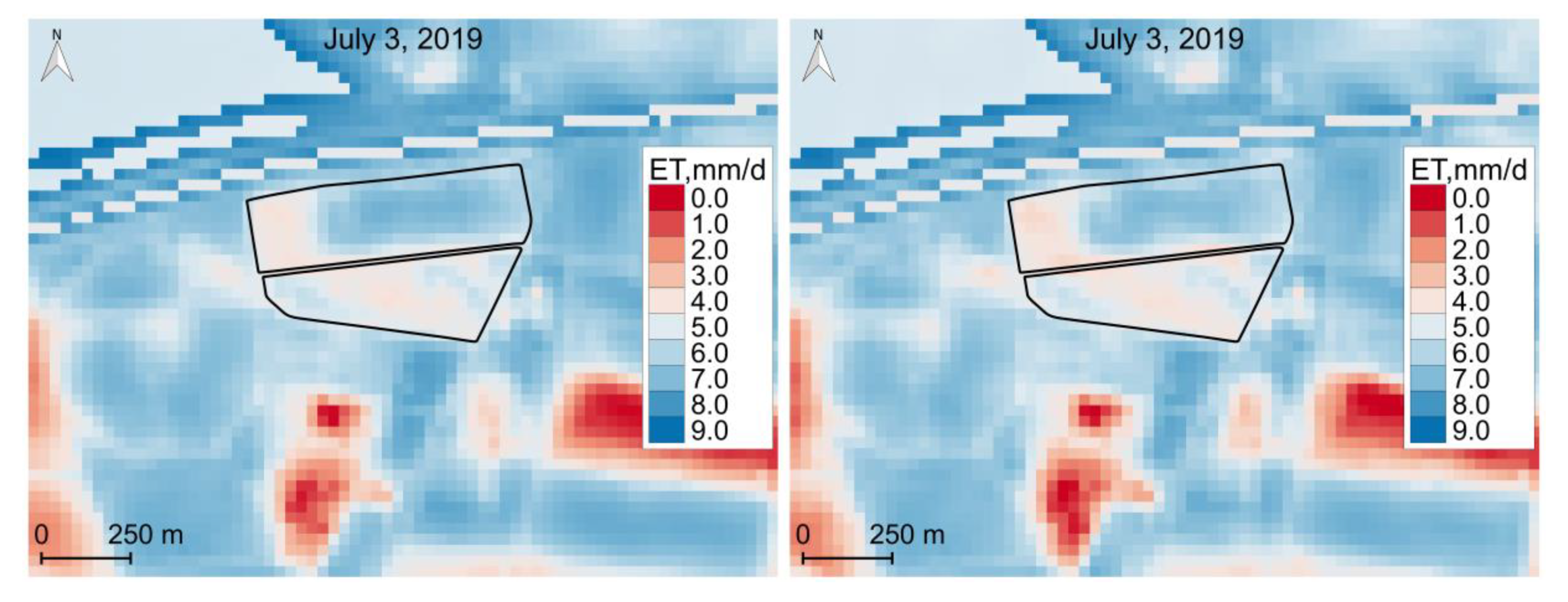
4.2. Surface Temperature Maps
4.3. Evapotranspiration and Water Stress Maps
5. Discussion and Perspectives
- the long revisit interval of Landsat-8 (see Figure 3) and the frequent presence of cloud cover or atmospheric haze, which reduce dramatically the quality of satellite observations, limit the temporal resolution of useful images (around two useful passages per month) compared to irrigation frequency (one to three events per month); as a consequence the probability of not having the necessary information, when one needs it, is relevant so that the present technique, when used for irrigation management, may lead to disappointment;
- the fact that soil storage capacity, groundwater conditions and groundwater dynamics should be known with a balanced reliability; soil in particular is not changing quickly so that information about its properties can be cumulated from a sequence of maps under several hydrologic conditions.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gebbers, R.; Adamchuk, V.I. Precision Agriculture and Food Security. Science 2010, 327, 828–831. [Google Scholar] [CrossRef] [PubMed]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Bansod, B.; Singh, R.; Thakur, R.; Singhal, G. A comparision between satellite based and drone based remote sensing technology to achieve sustainable development: A review. J. Agric. Environ. Int. Dev. (JAEID) 2017, 111, 383–407. [Google Scholar]
- Kayad, A.; Sozzi, M.; Gatto, S.; Marinello, F.; Pirotti, F. Monitoring within-field variability of corn yield using Sentinel-2 and machine learning techniques. Remote Sens. 2019, 11, 2873. [Google Scholar] [CrossRef] [Green Version]
- Khanal, S.; Fulton, J.; Shearer, S. An overview of current and potential applications of thermal remote sensing in precision agriculture. Comput. Electron. Agric. 2017, 139, 22–32. [Google Scholar] [CrossRef]
- Hassler, S.C.; Baysal-Gurel, F. Unmanned aircraft system (UAS) technology and applications in agriculture. Agronomy 2019, 9, 618. [Google Scholar] [CrossRef] [Green Version]
- Mandanici, E.; Bitelli, G. Preliminary comparison of Sentinel-2 and Landsat 8 imagery for a combined use. Remote Sens. 2016, 8, 1014. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Han, W.; Zhang, L. UAV multispectral imagery combined with the FAO-56 dual approach for maize evapotranspiration mapping in the North China plain. Remote Sens. 2019, 11, 2519. [Google Scholar] [CrossRef] [Green Version]
- Tsouros, D.C.; Bibi, S.; Sarigiannidis, P.G. A review on UAV-based applications for precision agriculture. Information 2019, 10, 349. [Google Scholar] [CrossRef] [Green Version]
- Santesteban, L.G.; Di Gennaro, S.F.; Herrero-Langreo, A.; Miranda, C.; Royo, J.B.; Matese, A. High-resolution UAV-based thermal imaging to estimate the instantaneous and seasonal variability of plant water status within a vineyard. Agric. Water Manag. 2017, 183, 49–59. [Google Scholar] [CrossRef]
- Maes, W.H.; Huete, A.R.; Steppe, K. Optimizing the processing of UAV-based thermal imagery. Remote Sens. 2017, 9, 476. [Google Scholar] [CrossRef] [Green Version]
- Carlson, T. An overview of the “triangle method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar] [CrossRef] [Green Version]
- Liou, Y.-A.; Kar, S.K. Evapotranspiration estimation with remote sensing and various surface energy balance algorithms—A review. Energies 2014, 7, 2821–2849. [Google Scholar] [CrossRef] [Green Version]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Teatini, P.; Ferronato, M.; Gambolati, G.; Bertoni, W.; Gonella, M. A century of land subsidence in Ravenna, Italy. Environ. Geol. 2005, 47, 831–846. [Google Scholar] [CrossRef]
- Masina, M.; Lamberti, A. A nonstationary analysis for the Northern Adriatic extreme sea levels. J. Geophys. Res. Oceans 2013, 118, 3999–4016. [Google Scholar] [CrossRef]
- Bitelli, G.; Bonsignore, F.; Del Conte, S.; Franci, F.; Lambertini, A.; Novali, F.; Severi, P.; Vittuari, L. Updating the subsidence map of Emilia-Romagna region (Italy) by integration of SAR interferometry and GNSS time series: The 2011-2016 period. Proc. Int. Assoc. Hydrol. Sci. 2020, 382, 39–44. [Google Scholar] [CrossRef] [Green Version]
- Antonellini, M.; Mollema, P.; Giambastiani, B.; Bishop, K.; Caruso, L.; Minchio, A.; Pellegrini, L.; Sabia, M.; Ulazzi, E.; Gabbianelli, G. Salt water intrusion in the coastal aquifer of the southern Po Plain, Italy. Hydrogeol. J. 2008, 16, 1541–1556. [Google Scholar] [CrossRef]
- Masina, M.; Calone, R.; Barbanti, L.; Mazzotti, C.; Lamberti, A.; Speranza, M. Smart water and soil-salinity management in agro-wetlands. Environ. Eng. Manag. J. 2019, 18, 2273–2285. [Google Scholar]
- Lamberti, A.; Masina, M.; Lambertini, A.; Borgatti, L. La contaminazione salina nella fascia costiera tra i fiumi Reno e Lamone: l’influenza delle condizioni geomorfologiche per l’ingressione di acqua marina. In Proceedings of the XXXVI Italian Conference on “Water Engineering”, Ancona, Italy, 12–14 September 2018; p. 317. [Google Scholar]
- Lionello, P.; Malanotte-Rizzoli, P.; Boscolo, R.; Alpert, P.; Artale, V.; Li, L.; Luterbacher, J.; May, W.; Trigo, R.; Tsimplis, M.; et al. The Mediterranean climate: An overview of the main characteristics and issues. Dev. Earth Environ. Sci. 2006, 4, 1–26. [Google Scholar]
- Antolini, G.; Pavan, V.; Tomozeiu, R.; Marletto, V. Atlante climatico dell’Emilia-Romagna 1961–2015, edizione 2017; ARPAE Emilia-Romagna, Servizio IdroMeteoClima; Casma Tipolito srl: Bologna, Italy, 2017. [Google Scholar]
- ARPAE Emilia-Romagna, Servizio Idro-Meteo-Clima. Monthly Agro-Climatic Bulletin, May 2019. Available online: https://www.arpae.it/sim/datiiningresso/Agrometeo/mensile/anno_2019/bollagro_2019_05.pdf (accessed on 12 May 2020).
- Copernicus Climate Change Service. State-of-the-European-Climate: June 2019. Available online: https://surfobs.climate.copernicus.eu/stateoftheclimate/june2019.php (accessed on 12 May 2020).
- Meier, U. Growth Stages of Mono- and Dicotyledonous Plants. BBCH Monograph, 2nd ed.; Federal Biological Research Centre for Agriculture and Forestry: Berlin/Braunschweig, Germany, 2001; Available online: https://www.politicheagricole.it/flex/AppData/WebLive/Agrometeo/MIEPFY800/BBCHengl2001.pdf (accessed on 12 May 2020).
- Zanutta, A.; Lambertini, A.; Vittuari, L. UAV photogrammetry and ground surveys as a mapping tool for quickly monitoring shoreline and beach changes. J. Mar. Sci. Eng. 2020, 8, 52. [Google Scholar] [CrossRef] [Green Version]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef] [PubMed]
- Department of the Interior U.S. Geological Survey. Landsat8 (L8) Data Users Handbook, Version 5.0; EROS: Sioux Falls, SD, USA, 2019. [Google Scholar]
- European Space Agency. Sentinel-2 User Handbook; ESA Standard Document; European Space Agency: Paris, France, 2015. [Google Scholar]
- Aguzzi, M.; Bonsignore, F.; De Nigris, N.; Morelli, M.; Paccagnella, T.; Romagnoli, C.; Unguendoli, S. Stato del Litorale Emiliano-Romagnolo al 2012. Erosione e Interventi di Difesa; I quaderni di ARPAE, ARPAE Emilia-Romagna: Bologna, Italy, 2016. [Google Scholar]
- Šimůnek, J.; Šejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat and Multiple Solutes in Variably-Saturated Media; Version 4.17; Department of Environmental Sciences, University of California Riverside: Riverside, CA, USA, June 2013. [Google Scholar]
- Cipolla, S.S.; Maglionico, M.; Masina, M.; Lamberti, A.; Daprà, I. Real time monitoring of water quality in an agricultural area with salinity problems. Environ. Eng. Manag. J. 2019, 18, 2229–2240. [Google Scholar]
- Steduto, P.; Hsiao, T.C.; Raes, D.; Fereres, E. AquaCrop−The FAO crop model to simulate yield response to water: I. Concepts and underlying principles. Agron. J. 2009, 101, 426–437. [Google Scholar] [CrossRef] [Green Version]
- Raes, D.; Steduto, P.; Hsiao, T.C.; Fereres, E. AquaCrop−The FAO crop model to simulate yield response to water: II. Main algorithms and software description. Agron. J. 2009, 101, 438–447. [Google Scholar] [CrossRef] [Green Version]
- Artis, D.A.; Carnahan, W.H. Survey of emissivity variability in thermography of urban areas. Remote Sens. Environ. 1982, 12, 313–329. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef] [Green Version]
- García-Santos, V.; Cuxart, J.; Martínez-Villagrasa, D.; Jiménez, M.A.; Simó, G. Comparison of three methods for estimating land surface temperature from Landsat 8-TIRS sensor data. Remote Sens. 2018, 10, 1450. [Google Scholar] [CrossRef] [Green Version]
- Costa, J.O.; Coelho, R.D.; Wolff, W.; José, J.V.; Folegatti, M.V.; Ferraz, S.F.B. Spatial variability of coffee plant water consumption based on the SEBAL algorithm. Sci. Agric. 2019, 76, 93–101. [Google Scholar] [CrossRef]
- Wolff, W. Script to Calculate Daily Evapotranspiration for Landsat Images in GRASS GIS 7.X. Available online: https://github.com/wwolff7/SEBAL_GRASS (accessed on 3 October 2019).
- Waters, R.; Allen, R.; Tasumi, M.; Trezza, R.; Bastiaanssen, W. SEBAL Surface Energy Balance Algorithms for Land-Advanced Training and Users Manual-Idaho Implementation; Version 1.0; 2002; Available online: http://www.posmet.ufv.br/wp-content/uploads/2016/09/MET-479-Waters-et-al-SEBAL.pdf (accessed on 9 October 2019).
- Ottle, C.; Stoll, M. Effect of atmospheric absorption and surface emissivity on the determination of land surface temperature from infrared satellite data. Int. J. Remote Sens. 1993, 14, 2025–2037. [Google Scholar] [CrossRef]
- Barsi, J.A.; Barker, J.L.; Schott, J.R. An Atmospheric Correction Parameter Calculator for a single thermal band earth-sensing instrument. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003. [Google Scholar]
- Barsi, J.A.; Schott, J.R.; Palluconi, F.D.; Hook, S.J. Validation of a web-based atmospheric correction tool for single thermal band instruments. In Proceedings of the SPIE Vol. 5882, Earth Observing Systems X, San Diego, CA, USA, 22 August 2005. [Google Scholar]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Sòria, G.; Romaguera, M.; Guanter, L.; Moreno, J.; Plaza, A.; Martínez, P. Land surface emissivity retrieval from different VNIR and TIRS sensors. IEEE Trans. Geosci. Remote Sens. 2008, 46, 316–327. [Google Scholar] [CrossRef]
- Skoković, D.; Sobrino, J.A.; Jiménez-Muñoz, J.C.; Sòria, G.; Julien, Y.; Mattar, C.; Cristóbal, J. Calibration and validation of land surface temperature for Landsat8-TIRS sensor. In Proceedings of the Land Product Validation and Evolution, ESA/ESRIN, Frascati, Italy, 28–30 January 2014. [Google Scholar]
- Cristóbal, J.; Jiménez-Muñoz, J.C.; Sobrino, J.A.; Ninyerola, M.; Pons, X. Improvements in land surface temperature retrieval from the Landsat series thermal band using water vapor and air temperature. J. Geophys. Res. Atmos. 2009, 114, D08103. [Google Scholar] [CrossRef]
- Yu, X.; Guo, X.; Wu, Z. Land Surface Temperature Retrieval from Landsat 8 TIRS-Comparison between Radiative Transfer Equation-Based Method, Split Window Algorithm and Single Channel Method. Remote Sens. 2014, 6, 9829–9852. [Google Scholar] [CrossRef] [Green Version]
- Jiménez-Muñoz, J.C.; Sobrino, J.A.; Skoković, D.; Mattar, C.; Cristóbal, J. Land surface temperature retrieval methods from Landsat-8 thermal infrared sensor data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1840–1843. [Google Scholar] [CrossRef]
- Kamran, K.V.; Pirnazar, M.; Bansouleh, V.F. Land surface temperature retrieval from Landsat 8 TIRS: Comparison between split window algorithm and SEBAL method. In Proceedings of the SPIE Vol. 9535, Third International Conference on Remote Sensing and Geoinformation of the Environment, Paphos, Cyprus, 19 June 2015. [Google Scholar]
- Skoković, D.; Sobrino, J.A.; Jiménez, J.C.; Sòria, G.; Julien, Y.; Gomis-Cebolla, J.; García-Monteiro, S. Vicarious calibration of Landsat-8 thermal data collections and its influence on split-window algorithm validation. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22−27 July 2018; pp. 4312–4315. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)-Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Allen, R.; Irmak, A.; Trezza, R.; Hendrickx, J.M.H.; Bastiaanssen, W.; Kjaersgaard, J. Satellite-based ET estimation in agriculture using SEBAL and METRIC. Hydrol. Process. 2011, 25, 4011–4027. [Google Scholar] [CrossRef]
- ASCE-EWRI. The ASCE Standardized Reference Evapotranspiration Equation. In Technical Committee on Standardization of Reference Evapotranspiration; Allen, R.G., Walter, I.A., Elliot, R.L., Howell, T.A., Itenfisu, D., Jensen, M.E., Snyder, R.L., Eds.; Environmental and Water Resources Institute of the American Society of Civil Engineers: Reston, VA, USA, 2005. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper No. 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Bastiaanssen, W.G.M. SEBAL-based sensible and latent heat fluxes in the irrigated Gediz Basin, Turkey. J. Hydrol. 2000, 229, 87–100. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Noordman, E.J.M.; Pelgrum, H.; Davids, G.; Thoreson, B.P.; Allen, R.G. SEBAL model with remotely sensed data to improve water-resources management under actual field conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar] [CrossRef]
- Mekonnen, S.C. Assessment of Catchment Water Balance Using GIS and Remote Sensing; Roxo, Portugal. Master’s Thesis, International Institute for Geo-Information Science and Earth Observation Enschede, Enschede, The Netherlands, March 2005. [Google Scholar]
- Allen, R.G. Ref-ET: Reference Evapotranspiration Calculator for Support of ASCE Manual 70 (1990, 2016) and 2005 ASCE Standardization and FAO Irrigation and Drainage Paper No. 56: Crop Evapotranspiration; Version 4.1; University of Idaho, Research and Extension Center: Kimberly, ID, USA, 2016. [Google Scholar]
- Irmak, S.; Haman, D.Z.; Bastug, R. Determination of Crop Water Stress Index for Irrigation Timing and Yield Estimation of Corn. Agron. J. 2000, 92, 1221–1227. [Google Scholar] [CrossRef]
- Meron, M.; Tsipris, J.; Orlov, V.; Alchanatis, V.; Cohen, Y. Crop water stress mapping for site-specific irrigation by thermal imagery and artificial reference surfaces. Precis. Agric. 2010, 11, 148–162. [Google Scholar] [CrossRef]
- Veysi, S.; Naseri, A.A.; Hamzeh, S.; Bartholomeus, H. A satellite based crop water stress index for irrigation scheduling in sugarcane fields. Agric. Water Manag. 2017, 189, 70–86. [Google Scholar] [CrossRef]
- Gao, B.-C. NDWI-A Normalized Difference Water Index for Remote Sensing of Vegetation Liquid Water from Space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Brodu, N. Super-Resolving Multiresolution Images With Band-Independent Geometry of Multispectral Pixels. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4610–4617. [Google Scholar] [CrossRef] [Green Version]




| UAV | Landsat-8 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Survey | FV [] | TV °C | TS °C | TLS °C | DTa °C | Tab °C | TSB °C | TRTE °C | TSW °C | NDVId [] | wc g/cm2 | Tab °C |
| S01 | 0.00 | 30.5 | 30.5 | 2.5 | 16.8 | 21.2 | 23.5 | 23.7 | 0.13 | 2.0 | 16.3 | |
| 0.00 | 1.3 | 1.3 | 0.2 | 0.2 | 0.3 | 0.01 | ||||||
| S05 | 0.25 | 39.9 | 47.8 | 45.8 | 1.0 | 31.2 | 34.5 | 38.1 | 38.7 | 0.26 | 3.0 | 31.1 |
| 0.11 | 1.6 | 1.6 | 1.1 | 0.2 | 0.3 | 0.4 | 0.03 | |||||
| S06 | 0.39 | 34.0 | 44.0 | 40.1 | 1.0 | 30.6 | 31.2 | 37.4 | 38.0 | 0.35 | 4.0 | 30.3 |
| 0.10 | 1.9 | 1.5 | 2.5 | 0.3 | 0.5 | 0.7 | 0.04 | |||||
| S08 | 0.96 | 28.7 | 38.3 | 29.1 | −1.0 | 28.7 | 26.7 | 29.7 | 30.3 | 0.67 | 3.6 | 28.0 |
| 0.03 | 1.6 | 1.6 | 1.8 | 0.2 | 0.4 | 0.6 | 0.04 | |||||
| S09 | 0.00 | 33.7 | 33.7 | −1.7 | 25.2 | 34.0 | 35.4 | 38.1 | 0.17 | 2.5 | 25.6 | |
| 0.00 | 0.8 | 0.8 | 0.2 | 0.2 | 0.6 | 0.00 | ||||||
| TLS | TSB | TRTE | TSW | |
| TLS | −0.15 ± 0.62 | −0.16 ± 0.62 | −0.17 ± 0.61 | |
| TSB | 5.9 ± 1.6 | +1.00 | +0.78 ± 0.09 | |
| TRTE | 2.7 ± 1.6 | −3.3 ± 0.1 | +0.78 ± 0.13 | |
| TSW | 1.7 ± 1.7 | −4.2 ± 0.4 | −0.9 ± 0.3 |
| TW | TSB | TRTE | TSW | |
| TW | +0.90 | +0.91 | +0.94 | |
| TSB | +1.0 ± 1.6 | +0.92 | +0.96 | |
| TRTE | −1.7 ± 1.6 | −2.7 ± 1.9 | +0.98 | |
| TSW | −2.3 ± 1.5 | −3.3 ± 1.3 | −0.6 ± 1.0 |
| TSB | TRTE | TSW | |
| TSB | +0.991 | +0.984 | |
| TRTE | −4.7 ± 1.6 | +0.994 | |
| TSW | −5.4 ± 1.6 | −0.7 ± 0.5 |
| ESB | ERTE | ESW | |
| ESB | 0.999 | 0.991 | |
| ERTE | 0.260 | 0.992 | |
| ESW | 0.409 | 0.149 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masina, M.; Lambertini, A.; Daprà, I.; Mandanici, E.; Lamberti, A. Remote Sensing Analysis of Surface Temperature from Heterogeneous Data in a Maize Field and Related Water Stress. Remote Sens. 2020, 12, 2506. https://doi.org/10.3390/rs12152506
Masina M, Lambertini A, Daprà I, Mandanici E, Lamberti A. Remote Sensing Analysis of Surface Temperature from Heterogeneous Data in a Maize Field and Related Water Stress. Remote Sensing. 2020; 12(15):2506. https://doi.org/10.3390/rs12152506
Chicago/Turabian StyleMasina, Marinella, Alessandro Lambertini, Irene Daprà, Emanuele Mandanici, and Alberto Lamberti. 2020. "Remote Sensing Analysis of Surface Temperature from Heterogeneous Data in a Maize Field and Related Water Stress" Remote Sensing 12, no. 15: 2506. https://doi.org/10.3390/rs12152506
APA StyleMasina, M., Lambertini, A., Daprà, I., Mandanici, E., & Lamberti, A. (2020). Remote Sensing Analysis of Surface Temperature from Heterogeneous Data in a Maize Field and Related Water Stress. Remote Sensing, 12(15), 2506. https://doi.org/10.3390/rs12152506







