A Bistatic Analytical Approximation Model for Doppler Rate Estimation Error from Real-Time Spaceborne SAR Onboard Orbit Determination Data

Abstract

Real-time spaceborne bistatic SAR imaging could significantly reduce the whole processing time and can enhance the spaceborne SAR mission availability. Onboard real-time SAR imaging relies on the Doppler parameters estimated from the real-time onboard orbit determination system (OODS) measurement, whose accuracy level is not comparable to the orbit ephemeris data in ground-based SAR processing. The investigation of the impact of error in real-time OODS measurements on bistatic SAR image quality is necessary, and it can help to clarify the key parameter limits of the real-time OODS. The monostatic analytical approximation model (MonoAAM) for spaceborne SAR reduces simulation complexity and processing time compared to the widely used numerical simulation method. However, due to the different configurations between spaceborne bistatic and monostatic SAR, simply applying the MonoAAM on spaceborne bistatic SAR cannot guarantee the desired result. A bistatic analytical approximation model (BiAAM) for Doppler rate estimation error from real-time OODS measurement in real-time spaceborne bistatic SAR imaging is proposed for characterizing the estimation error. Selecting quadratic phase error (QPE) as an evaluation variable, the proposed BiAAM model can provide QPE estimation results for each position of the satellite in its orbit and the maximum QPE estimation for the whole orbit, while revealing the different process of OODS measurement error transferring to QPE in spaceborne bistatic SAR. The correctness and reliability of BiAAM are evaluated by comparing the result with a Monte Carlo numerical simulation method. With the supporting result from BiAAM, the concept and early-stage development of a real-time onboard bistatic SAR imaging mission could be possibly benefited.

1. Introduction

Spaceborne bistatic synthetic aperture radar (SAR) has always been a research focus and bistatic SAR imaging provides different observation geometry compared to the spaceborne monostatic SAR [1,2,3,4,5]. Spaceborne monostatic SAR works like observing the area of interest using a flashlight in a completely dark environment, while spaceborne bistatic SAR is more like that in spaceborne optical imaging, as the radiation source is not at the identical position of the observer. Hence, spaceborne bistatic SAR may provide some unique information and benefit the interferometric SAR mission [6,7,8]. Spaceborne bistatic SAR satellites are always in formation, and there are formations like the HELIX formation [9], interferometric cartwheel [10], trinodal pendulum [11], etc. Real-time SAR imaging is also an interesting topic in selected applications, as it could significantly reduce the whole processing time from a single observation to the final SAR image product and can enhance the spaceborne SAR mission availability. It is a relatively established technique in real-time airborne SAR imaging [12,13,14,15,16] and in unmanned aerial vehicle (UAV) real-time SAR sensing [17,18,19]. As for real-time spaceborne SAR imaging, due to its extremely large data rate and limited onboard computation capabilities, there is no real-time SAR imaging system on orbit, whereas related research on real-time digital imaging [20,21,22] and real-time optical imaging [23] indicate its feasibility. Combining the spaceborne bistatic SAR configuration with real-time onboard SAR imaging capability could be beneficial to selected applications such as quick response rescue operation after severe earthquakes. Related research suggests if the interferometric SAR (InSAR) measured scale of terrain changes after an earthquake significantly lower from the previous ones with similar seismic magnitude scales, it is more likely to have short time severe aftershocks just after the main earthquake [24,25]. The real-time onboard spaceborne bistatic SAR imaging product can provide opportune support to the quick reaction rescue forces heading to the earthquake epicenter. For those entities who cannot access a global satellite data receiving network, a spaceborne bistatic SAR mission with real-time onboard SAR imaging could be a feasible choice to obtain important information about the earthquake-stricken region in a relatively short time.

Real-time onboard spaceborne bistatic SAR imaging requires relevant high precision and accurate Doppler parameters, and those Doppler parameters can only be estimated from accurate state vectors of the payload platform, i.e., the position and velocity vectors. A Typical spaceborne SAR mission has a ground-based processing center for applying downlink echo data from the satellite to the imaging algorithm to get the final SAR imaging product. During this process, high accuracy orbit ephemeris is available, but orbit ephemeris with high accuracy can only be generated at least several hours or days after the observation process [26]. This means for real-time onboard spaceborne SAR imaging, high accuracy orbit ephemeris is not available. Thus, the real-time onboard orbit determination system (OODS) based on GNSS receivers and appropriate algorithms [27,28] is equipped on the satellite platform to provide the measurement of the state vectors, which is necessary for Doppler parameter. It is obvious that GNSS-based real-time OODS has comparatively inadequate accuracy in the measurements of the state vector of the payload platform, compared with the high accuracy orbit ephemeris in the processing procedure on the ground. However, it could be the only solution that is available for real-time onboard spaceborne bistatic SAR imaging.

The fact must be taken into account for SAR mission designers that error in the measurement from GNSS-based real-time OODS will have an undesired effect on the performance of the SAR product as the error results in an inaccurate Doppler parameter estimation. Although autofocusing algorithms have been developed to improve the quality of the SAR image processed with an inaccurate Doppler parameter, these algorithms are time consuming and cannot guarantee significant SAR image quality improvement for each attempt. Real-time spaceborne bistatic SAR imaging is undoubtedly time sensitive because following signal analysis, such as onboard InSAR deformation location and monitoring or moving target identification and recognition, requires the product of the real-time SAR imaging. Thus, the autofocusing algorithm should not be a build-in block in the SAR imaging algorithm because it cannot guarantee real-time performance. Different SAR imaging modes have different Doppler rate histories and integration times, which means that even the same Doppler rate error performs differently in different SAR imaging modes. Hence, quadrature phase error (QPE) is selected as an evaluation parameter of the error in the measurement from the real-time OODS equipped on the real-time spaceborne bistatic SAR satellite. Certain QPE has a direct relationship with the azimuth impulse response width of the point target, and it is even more easy to assess the influence of the inaccuracy of onboard orbit determination data.

A certain probability distribution with corresponding parameters is used to model the error in the measurement from real-time OODS, and the Gaussian distribution is widely used based on engineering experience. Typically, the probability distribution of real-time OODS has a zero expected value and a non-zero standard deviation $\sigma$. As the input is a kind of probability distribution, the probability distribution of QPE with its parameters is selected as an evaluation variable of the BiAAM. The extreme value method, the Monte Carlo numerical simulation, method and estimation based on the monostatic analytical approximation model (MonoAAM) are often applied to QPE evaluation. The extreme value method has an intuitive evaluation to investigate QPE, as the maximum error is brought in the estimation. In this way, the probability distribution of the error is ignored as it only cares about the maximum error. This method cannot provide any result about the probability distribution of QPE as such a situation is not going to happen at any time. Instead, the Monte Carlo numerical simulation method [29] can provide the details about the probability distribution of QPE. However, when applying the Monte Carlo method, it requires repeating experiments and a large amount of generated error samples corresponding to the probability distribution of the error. The MonoAAM can significantly reduce the calculation amount and the requirements of the estimation of the statistic parameter of QPE [30], but it only aims at the spaceborne monostatic SAR mission. This MonoAAM cannot be applied directly to the spaceborne bistatic SAR missions, as the relative motion between the transmitter and receiver satellites in the bistatic SAR formation is not taken into consideration in the MonoAAM.

In this paper, a bistatic analytical approximation model (BiAAM) for Doppler rate estimation error from real-time OODS data in real-time spaceborne bistatic SAR imaging is proposed. As an upgraded version of the MonoAAM, the BiAAM extends the application of the analytical approximation model from a monostatic configuration to a bistatic one. The evaluation result of BiAAM is the probability distribution of QPE to the satellite’s mean anomaly. In the meantime, BiAAM can also provide the maximum of the parameters of the probability distribution of QPE during one track in the orbit as a more easy-to-use result. An a priori probability of the error in the real-time OODS is mandatory for BiAAM, together with SAR satellite orbit elements for both the transmitter and receiver satellites in the spaceborne bistatic SAR formation and the parameters of the observing geometry of the spaceborne SAR payload as the remaining input parameters.

This paper is structured as follows. Section 2 introduces the coordinate systems in BiAAM and the limitations of applying the MonoAAM in spaceborne bistatic SAR. Section 3 presents the detailed derivation and applied approximations in the BiAAM. Following this, Section 4 describes the evaluation model of the BiAAM, selecting the Monte Carlo numerical simulation and MonoAAM results as references. Section 5 contains relevant discussions about BiAAM and real-time onboard spaceborne bistatic SAR imaging. Finally, Section 6 summarizes the above with a brief conclusion.

2. Coordinate Systems and the Limitations of the MonoAAM in Spaceborne Bistatic SAR

The coordinate systems are important in the estimation of QPE, and in this section, they will be introduced. The limitations of applying the MonoAAM in spaceborne bistatic SAR are also described in this section.

2.1. Coordinate Systems

The BiAAM relies on the derivations in three coordinate systems. Different coordinate system has its unique role in the BiAAM; either can be helpful in the description of SAR observation geometry or the relative movement from the receiver satellite to the transmitter satellite.

2.1.1. Orbital Plane Coordinate System

The six Keplerian elements are the traditional orbital elements that are used to describe the movement of the satellite in space. However, in the orbital plane (OP) coordinate system, only three are used to describe the satellite movement in it. The semi-major axis a and eccentricity e determine the overall shape of the elliptical orbit, and true anomaly $\nu$ completes the satellite’s unique position on the orbit. The rest in the Keplerian elements are the inclination i, the right ascension of the ascending node (RAAN) Ω, and the argument of periapsis $\omega$, and these three elements are necessary to generate the transformation matrix from the OP coordinate system to the celestial reference system, which will be discussed in Section 2.1.2.

In this OP coordinate system, the satellite can be regarded as a mass point, and it is traveling around the Earth, which locates at one of the foci of the elliptical orbit. Given certain a, e, and $\nu$, there is a set expressions of unique state vectors of the satellite in the OP coordinate system.

2.1.2. Celestial Reference System

The celestial reference system (CRS), also known as the Earth centered inertial (ECI), is applied to characterize satellite motion relative to the Earth in 3D space. There are two main choices of the celestial reference system in the satellite project. They are the J2000 and International Celestial Reference frame (ICRF). The J2000 has its origin in the Earth’s center of mass, its fundamental plane being the mean Equatorial plane (containing the geocenter) of the epoch J2000.0, and the principal axis points to the mean Vernal equinox of epoch J2000.0 [31]. The ICRF is a realization of a more recent celestial reference system, and with the improvement to the J2000 frame, the ICRF has better performance. There is only a very small difference between the ICRF and J2000 frame as the definition indicates the J2000 frame rotating very slowly instead of being stationary.

In one certain satellite project, either of the two mentioned celestial reference systems can be chosen as the realization of an ECI system. In order to simplify the whole description of the proposed BiAAM, in the following paper, we use ECI as a representative of a certain celestial reference system.

2.1.3. Local Vertical, Local Horizontal Coordinate System

In the bistatic SAR satellite formation, there exists the need to describe the relative motion between the transmitter satellite and the receiver satellite. The intuitive expression of relative motion can be expressed in the local vertical, local horizontal (LVLH) coordinate system with the appropriate linearization method.

The LVLH is defined by the unit vector ${\mathbf{e}}_R$ along the radial direction (positive outwards), the unit vector ${\mathbf{e}}_T$ in the along-trace (tangential) direction of the satellite motion, and the unit vector ${\mathbf{e}}_N$ normal to the orbital plane in the direction to the positive angular momentum vector (cross track) [32].

The relationship of the ECI, OP and LVLH coordinate systems is given in Figure 1.

2.2. Brief Introduction to the MonoAAM

The MonoAAM introduced in [30] can be summarized as follows

Step 1:

Setup input for the MonoAAM: The input parameters of the MonoAAM are: (a) the a priori probability of the error in real-time OODS, (b) the satellite Keplerian parameters, and (c) the SAR payload configurations.

Step 2:

Estimation of the Doppler frequency rate: The estimation procedure produces the expression of the expected value $\mathbb{E}\left[f_r\right]$ and standard deviation $\sigma \left[f_r\right]$ of the estimated Doppler frequency rate from the real-time OODS measurement, respectively.

Step 3:

Estimation of QPE: The tolerance of the Doppler frequency rate error varies in different imaging modes. QPE can be a valuable variable to evaluate the Doppler frequency rate error in a certain imaging mode, as the calculation of QPE requires the integration time. This estimation produces the expression of the expected value $\mathbb{E}\left[\mathrm{QPE}\right]$ and standard deviation of QPE $\sigma \left[\mathrm{QPE}\right]$, individually.

The real-time OODS measurement is presented in the corresponding reference system of the selected GNSS and can be transformed into ECI. The measurement vector consists of two parts, i.e., the true state vector and the error vector. A new operation mark $\mathrm{\Delta }•$ represents the operator difference $\left({•}_e-{•}_{ori}\right)$. The subscript e and $ori$ represent the element with and without errors, respectively. We assume that the measurement error of the state vector of the satellite follows a Gaussian distribution with the excepted value of zero, and the error vectors in the measurement can be described as:

$$\begin{array}{cc}\hfill \mathrm{\Delta }\mathbf{P}& =\left[\begin{array}{c}\mathrm{\Delta }{p}_x\\ \mathrm{\Delta }{p}_y\\ \mathrm{\Delta }{p}_z\end{array}\right]\sim \left[\begin{array}{c}N\left(0,{\sigma }_{p,x}^2\right)\\ N\left(0,{\sigma }_{p,y}^2\right)\\ N\left(0,{\sigma }_{p,z}^2\right)\end{array}\right],\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \mathrm{\Delta }\mathbf{V}& =\left[\begin{array}{c}\mathrm{\Delta }{v}_x\\ \mathrm{\Delta }{v}_y\\ \mathrm{\Delta }{v}_z\end{array}\right]\sim \left[\begin{array}{c}N\left(0,{\sigma }_{v,x}^2\right)\\ N\left(0,{\sigma }_{v,y}^2\right)\\ N\left(0,{\sigma }_{v,z}^2\right)\end{array}\right].\hfill \end{array}$$

(2)

The expression of QPE in radians is [33]:

$$\begin{array}{cc}\hfill \mathrm{QPE}& =\pi ·\mathrm{\Delta }{f}_r·{\left({\displaystyle \frac{T_{int}}{2}}\right)}^2,\hfill \end{array}$$

(3)

in which $\mathrm{\Delta }{f}_r$ is the Doppler rate estimation error and $T_{int}$ represents the integration time. In SAR imaging geometry, the integration time indicates the time of the point of interest within the full 3 dB area of the beam of the transmitting antenna.

The MonoAAM works with the input of the statistic distribution of $\mathrm{\Delta }\mathbf{P}$ and $\mathrm{\Delta }\mathbf{V}$, together with other required parameters. The MonoAAM gives the expression of the expected value and standard deviation of estimated QPE, i.e., $\mathbb{E}\left[\mathrm{QPE}\right]$ and $\sigma \left[\mathrm{QPE}\right]$, respectively.

2.3. Limitations of the MonoAAM in Spaceborne Bistatic SAR

Applying the MonoAAM directly in spaceborne bistatic SAR missions is not an ideal way to investigate the QPE in real-time spaceborne bistatic SAR imaging caused by real-time orbit determination error. For spaceborne bistatic SAR satellite formation flying, the transmitter and receiver satellite pair have slightly different motions, resulting in a different Doppler frequency rate history compared to the monostatic SAR mission. The SAR imaging algorithm requires high accuracy estimated Doppler parameters, and the imaging algorithm is sensitive to Doppler frequency rate changes.

In bistatic SAR imaging, one possible way to apply the monostatic SAR imaging algorithm is to get a virtual phase center of the transmitter and receiver antenna phase center [5]. This works when the trajectories of the transmitter and receiver are translationally invariant. Then, the movement parameters of the virtual phase center can be modeled, and using these parameters, the bistatic imaging can be achieved. It can get a fairly good result in certain situations, especially in airborne bistatic SAR systems. However, the movements of the transmitter and of the receiver SAR satellite platform are not identical to the ones in the airborne platform. In the LVLH coordinate system of the transmitter satellite, the receiver satellite usually flies in an elliptical orbit. In this case, the movement is more complex than the ones in the airborne bistatic SAR systems. Besides, the movement of the virtual phase center is not easy to get in ECI, when given the Keplerian elements of the satellites in the spaceborne bistatic SAR formation.

The relative distance between the transmitter and receiver satellites usually is no more than dozens of kilometers in the formation like the trinodal pendulum in order to achieve a high coherent signal. Even though the slant range, i.e., the distance from the transmitter antenna phase center to the antenna aiming point on the surface of the Earth, is within hundreds of kilometers, the relative distance between the satellites cannot be neglected. Hence, replacing all the receiver-target vectors with transmitter-target vectors in the MonoAAM cannot guarantee an acceptable result. The MonoAAM should be upgraded to have a better estimation performance for a spaceborne bistatic SAR satellite formation.

3. The BiAAM: An Upgraded Model Based on the MonoAAM

Starting with the Doppler rate of the echo signal of a certain point of interest in the imaging scenario, which is an important value to be estimated for the SAR imaging procedure. The variables ${\mathbf{R}}_{tp}$, ${\mathbf{V}}_{tp}$, ${\mathbf{A}}_{tp}$ and ${\mathbf{R}}_{rp}$, ${\mathbf{V}}_{rp}$, ${\mathbf{A}}_{rp}$ represent the relative position, velocity, and acceleration vector of the spaceborne transmitter and receiver SAR satellite to the point of interest, respectively. In the ECI system, the Doppler rate $f_r$ in stripmap mode with zero squint angle is [6]:

$$\begin{array}{cc}\hfill f_{r,bi}& ={\displaystyle \frac{1}{\lambda }}\left[{\displaystyle \frac{{\mathbf{V}}_{tp}·{\mathbf{V}}_{tp}}{\left|{\mathbf{R}}_{tp}\right|}}+{\displaystyle \frac{{\mathbf{A}}_{tp}·{\mathbf{R}}_{tp}}{\left|{\mathbf{R}}_{tp}\right|}}+{\displaystyle \frac{{\mathbf{V}}_{rp}·{\mathbf{V}}_{rp}}{\left|{\mathbf{R}}_{rp}\right|}}+{\displaystyle \frac{{\mathbf{A}}_{rp}·{\mathbf{R}}_{rp}}{\left|{\mathbf{R}}_{rp}\right|}}\right].\hfill \end{array}$$

(4)

The $f_{r,bi}$ expression in Equation (4) is an approximation expression in the bistatic configuration, and it can achieve even better accuracy if more high order terms remain. Only the terms in Equation (4) are discussed in the BiAAM, and this carries the simple analysis of the model while preserving an acceptable accuracy.

Since the BiAAM is an approximation model, there are several approximations in the model list as below,

• The eccentricity e of spaceborne SAR satellites is small, such that we assume $e\approx 0$ in the BiAAM.
• The errors from the real-time OODS contribute most of the error vectors, and there are $\mathrm{\Delta }{\mathbf{V}}_{tp}\approx \mathrm{\Delta }{\mathbf{V}}_t$, $\mathrm{\Delta }{\mathbf{R}}_{tp}\approx \mathrm{\Delta }{\mathbf{R}}_t$, and $\mathrm{\Delta }{\mathbf{A}}_{tp}\approx \mathrm{\Delta }{\mathbf{A}}_t$ for the transmitter satellite. The same approximations also work for the receiver satellites.
• The variance of each axis of the error vector in Equations (1) and (2) is the same, i.e., ${\sigma }_{p,x}^2={\sigma }_{p,y}^2={\sigma }_{p,z}^2={\sigma }_p^2$ and ${\sigma }_{v,x}^2={\sigma }_{v,y}^2={\sigma }_{v,z}^2={\sigma }_v^2$.

In the bistatic formation like the trinodal pendulum, the separation of the transmitter and receiver satellite usually is no more than dozens of kilometers, resulting in a relatively small difference in ${\mathbf{R}}_{tp}$ and ${\mathbf{R}}_{rp}$. Thus, we have another approximation $\rho \approx \left|{\mathbf{R}}_{tp}\right|\approx \left|{\mathbf{R}}_{rp}\right|$. From basic geometry, we can get ${\mathbf{V}}_{rp}={\mathbf{V}}_{rt}+{\mathbf{V}}_{tp}$ and ${\mathbf{R}}_{rp}={\mathbf{R}}_{rt}+{\mathbf{R}}_{tp}$, and together with Equation (4), the difference between the estimated $f_{r,bi,e}$ (contains estimation error) and the true $f_{r,bi}$ value (contains no error) is:

$$\begin{array}{cc}\hfill \mathrm{\Delta }{f}_{r,bi}& ={\displaystyle \frac{1}{\lambda \rho }}\left[2\mathrm{\Delta }{\mathbf{V}}_t·{\mathbf{V}}_t+\mathrm{\Delta }{\mathbf{A}}_t·{\mathbf{R}}_{tp}+2\mathrm{\Delta }{\mathbf{V}}_r·{\mathbf{V}}_r+\mathrm{\Delta }{\mathbf{A}}_r·{\mathbf{R}}_{tp}+{\mathbf{A}}_r·\mathrm{\Delta }{\mathbf{R}}_{rt}+\mathrm{\Delta }{\mathbf{A}}_r·{\mathbf{R}}_{rt}\right].\hfill \end{array}$$

(5)

In Equation (5), the terms that have the form $\mathrm{\Delta }·\mathrm{\Delta }$ are neglected as we assume the errors in real-time orbit determination to be reasonably small.

For spaceborne bistatic SAR satellites that share the same type of real-time OODS, the variations in Equations (1) and (2) are almost the same. Therefore, we assume they have the same value in the BiAAM approximations. It is worth pointing out that at a certain time, $\mathrm{\Delta }{\mathbf{P}}_t$ and $\mathrm{\Delta }{\mathbf{P}}_r$ are not identical. They are independent and identically distributed (i.i.d.). $\mathrm{\Delta }{\mathbf{V}}_t$ and $\mathrm{\Delta }{\mathbf{V}}_r$ are also i.i.d.

Applying the same the approximations in the MonoAAM, the corresponding Doppler frequency rate error is written as:

$$\begin{array}{cc}\hfill \mathrm{\Delta }{f}_{r,mono}& ={\displaystyle \frac{2}{\lambda \rho }}\left[2\mathrm{\Delta }{\mathbf{V}}_t·{\mathbf{V}}_t+\mathrm{\Delta }{\mathbf{A}}_t·{\mathbf{R}}_{tp}\right].\hfill \end{array}$$

(6)

Here, we give some detailed explanation of why we introduce ${\mathbf{R}}_{rp}={\mathbf{R}}_{rt}+{\mathbf{R}}_{tp}$. Let us have a close look at Equations (5) and (6). It seems that if the ${\mathbf{R}}_{rp}={\mathbf{R}}_{rt}+{\mathbf{R}}_{tp}$ relationship is not introduced, one can just use the MonoAAM twice with the parameters from the transmitter and receiver satellite separately and then combine the result in a statistical way to get $\mathbb{E}\left[\mathrm{QPE}\right]$ and $\sigma \left[\mathrm{QPE}\right]$. However, this is not the right way if we have a close look at the detail of the MonoAAM. In the MonoAAM, the steering angle plays an important role in calculating the key parameters. In spaceborne bistatic SAR satellite missions, the steering angle of transmitter and receiver satellites are linked, but not identical. If we use the method mentioned above, there exists the problem that the two antenna footprints may not overlap with each other. There are multiple strategies available to calculate the steering angle of the transmitter and receiver satellites to make the antenna footprint perfectly overlapped [34]. In the BiAAM, we introduce ${\mathbf{R}}_{rp}={\mathbf{R}}_{rt}+{\mathbf{R}}_{tp}$ together with other approximations to make things equivalent to the situation when the centers of two antenna footprints coincide. Though this introduced relationship may not be able to guarantee the line of sight of the two antenna footprints being parallel, it is a simple way to build the BiAAM and make it easy to use with comparatively acceptable accuracy.

Now, it is clear that the statistic parameters of the first two terms in Equation (5) can be calculated using the MonoAAM, just with different amplitudes. If we take the approximation replacing ${\mathbf{R}}_{tp}$ in the forth term in Equation (5) with ${\mathbf{R}}_{rp}$, the third and forth terms can also be calculated using the MonoAAM with the parameters of the receiver satellite. The remaining two terms are key to the BiAAM, as they try to maintain a relatively high accuracy after we take the approximation in the forth term. The key question is to find a relatively easy way to deal with the remaining two terms in order to keep the BiAAM as easy to use as the MonoAAM while maintaining relatively high accuracy.

The terms ${\mathbf{A}}_r·\mathrm{\Delta }{\mathbf{R}}_{rt}$ and $\mathrm{\Delta }{\mathbf{A}}_r·{\mathbf{R}}_{rt}$ are named as A-DR and DA-R for convenience in the following pages.

3.1. The Term A-DR

The term A-DR consists of two parts, the acceleration vector of the receiver satellite ${\mathbf{A}}_r$ and the error vector of the relative distance of the transmitter and receiver satellite $\mathrm{\Delta }{\mathbf{R}}_{rt}$. In real-time spaceborne bistatic SAR imaging, the acceleration vectors are not measured with real sensors, but instead calculated from the real-time orbit determination data, as any acceleration sensor onboard a satellite platform is in a weightless environment. In order to get the acceleration vectors, the true anomaly $\nu$ should be derived from platform state vectors measured from real-time OODS. If the measurement of the real-time OODS contains an error, the calculated true anomaly $\nu$ also has an error in it, and this error will be transferred to the acceleration vectors. In term A-DR, the acceleration vector contains no error in it. The one that contains the error from the true anomaly is discussed for term DA-R in Section 3.2.

In the OP coordinate system, the acceleration vector of the receiver satellite is written as:

$$\begin{array}{cc}\hfill {\mathbf{A}}_r& =-{\displaystyle \frac{\mu }{p^2}}\left[\begin{array}{c}cos\nu \\ sin\nu \\ 0\end{array}\right],\hfill \end{array}$$

(7)

where $\nu$ is the true anomaly, $\mu$ is the Earth’s standard gravitational parameter, and $p=a\left(1-e^2\right)$ is the semi-latus rectum of the satellite elliptical orbit.

The error vector $\mathrm{\Delta }{\mathbf{R}}_{rt}$ includes the errors of the position measurement from both the transmitter and receiver satellites. As mentioned above, $\mathrm{\Delta }{\mathbf{P}}_t$ and $\mathrm{\Delta }{\mathbf{P}}_r$ are i.i.d., and each axis fits a Gaussian distribution with the expected value of zero and variance ${\sigma }_p^2$. Hence, the error vector $\mathrm{\Delta }{\mathbf{R}}_{rt}$ is written as:

$$\begin{array}{cc}\hfill \mathrm{\Delta }{\mathbf{R}}_{rt}& =\left[\begin{array}{c}\mathrm{\Delta }{R}_{rt,x}\\ \mathrm{\Delta }{R}_{rt,y}\\ \mathrm{\Delta }{R}_{rt,z}\end{array}\right]\sim \left[\begin{array}{c}N\left(0,2{\sigma }_p^2\right)\\ N\left(0,2{\sigma }_p^2\right)\\ N\left(0,2{\sigma }_p^2\right)\end{array}\right].\hfill \end{array}$$

(8)

It is easy to obtain the expected value and the standard deviation of term A-DR:

$$\begin{array}{cc}\hfill \mathbb{E}\left[{\mathbf{A}}_r·\mathrm{\Delta }{\mathbf{R}}_{rt}\right]& =0,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \sigma \left[{\mathbf{A}}_r·\mathrm{\Delta }{\mathbf{R}}_{rt}\right]& ={\displaystyle \frac{\sqrt{2}{\sigma }_p\mu }{p^2}}.\hfill \end{array}$$

(10)

Since $\sigma \left[{\mathbf{A}}_r·\mathrm{\Delta }{\mathbf{R}}_{rt}\right]$ is a constant value, which means it does not vary with the true anomaly, the maximum value of the standard deviation of the term A-DR is:

$$\begin{array}{c}\hfill \sigma {\left[{\mathbf{A}}_r·\mathrm{\Delta }{\mathbf{R}}_{rt}\right]}_{max}=\sigma \left[{\mathbf{A}}_r·\mathrm{\Delta }{\mathbf{R}}_{rt}\right].\end{array}$$

(11)

3.2. The Term DA-R

The term A-DR consists of two parts, the error vector of the acceleration vector of the receiver satellite $\mathrm{\Delta }{\mathbf{A}}_r$ and the state vector of the relative distance of the transmitter and receiver satellite ${\mathbf{R}}_{rt}$. The true anomaly with error results in the acceleration vector of the receiver satellite also contains an error in it. True anomaly $\nu$ is estimated using the state vector measurements from real-time OODS. A widely used method to estimate $\nu$ is [35]:

$$\begin{array}{c}\hfill \nu =\mathrm{atan}2\left(\sqrt{{\displaystyle \frac{p}{\mu }}}\left({\mathbf{V}}_{sat,ECI}·{\mathbf{R}}_{sat,ECI}\right),p-\left|{\mathbf{R}}_{sat,ECI}\right|\right),\end{array}$$

(12)

where the $\mathrm{atan}2\left(Y,X\right)$ function is an unambiguous version of $arctan\left(Y,X\right)$, and it calculates the result in $\left(-\pi ,\pi \right]$. Hence, the estimated true anomaly ${\nu }_e$ from state vectors ${\mathbf{P}}_{sat,ECI,e}$ and ${\mathbf{V}}_{sat,ECI,e}$ certainly contains estimation error.

With the approximations introduced in the BiAAM and the fact that the error vector of true anomaly $\mathrm{\Delta }\nu$ is relatively small, the error vector of the acceleration vector of the receiver satellite $\mathrm{\Delta }{\mathbf{A}}_r$ in OP can be expressed as:

$$\begin{array}{cc}\hfill \mathrm{\Delta }{\mathbf{A}}_{r,OP}& ={\displaystyle \frac{\mu }{p^2}}·\mathrm{\Delta }\nu ·\left(-{\displaystyle \frac{{\mathbf{V}}_{r,OP}}{\left|{\mathbf{V}}_{r,OP}\right|}}\right)\hfill \\ \hfill & ={\displaystyle \frac{\mu }{p^2}}·\mathrm{\Delta }\nu ·\left[\begin{array}{c}sin\nu \\ -cos\nu \\ 0\end{array}\right].\hfill \end{array}$$

(13)

Equation (13) indicates that $\mathrm{\Delta }{\mathbf{A}}_{r,OP}$ parallels the opposite direction of the receiver satellite velocity vector.

To get the expression of the state vector of the relative distance of the transmitter and receiver satellite, ${\mathbf{R}}_{rt}$ is not a straightforward task. In ECI, the orbits of the transmitter and receiver SAR satellites are determined by two sets of Keplerian elements with quite small differences compared to each other in order to form a flying formation configuration; that is to say, the expression of ${\mathbf{R}}_{rt}$ in ECI is a function of twelve different variables at most, which means this is not a simple way to get the expression. In OP, things become a little simpler, with three variables to describe the orbit of one satellite. However, the transmitter and receiver SAR satellites run in different orbital planes. If one would like to get the expression of ${\mathbf{R}}_{rt}$ in OP, the variable that characterizes the two different orbital planes shall be a necessary part. The two orbital planes of transmitter and receiver SAR satellites share the same origin of the coordinate system, and it requires at least two more variables to identify the amplitude and phase of the difference of the two orbital planes.

A comparatively straightforward way to get the expression of ${\mathbf{R}}_{rt}$ is to analyze it in the LVLH coordinate system. The spaceborne bistatic SAR formation usually applies eccentricity/inclination vector separation for continuous and safe operation [32,36,37]. A detailed explanation of the theory of eccentricity/inclination vector separation can be found in [32], and for convenience, here, in the BiAAM, only the related expressions are presented.

Relative inclination vector $\mathrm{\Delta }\mathbf{i}$ is controlled by the inclination i and RAANΩ, describing the out-of-plane motion of the receiver satellite. It can be written as follows:

$$\begin{array}{cc}\hfill \mathrm{\Delta }\mathbf{i}& =\left[\begin{array}{c}\mathrm{\Delta }{i}_x\\ \mathrm{\Delta }{i}_y\end{array}\right]=sin\left(\delta i\right)\left[\begin{array}{c}cos\theta \\ sin\theta \end{array}\right]\approx \left[\begin{array}{c}\mathrm{\Delta }i\\ \mathrm{\Delta }\mathrm{\Omega }sini\end{array}\right],\hfill \end{array}$$

(14)

where $\delta i$ is the angle between the two orbital planes of the satellite and $\theta$ represents the argument of the latitude at which the receiver satellite crosses the orbital plane of the transmitter satellite in the ascending direction. $\mathrm{\Delta }i$ and $\mathrm{\Delta }\mathrm{\Omega }$ are the variations in the inclination and right ascension of the ascending node, respectively [32].

Relative eccentricity vector $\mathrm{\Delta }\mathbf{e}$ indicates the movement in the orbital plane. An eccentricity vector $\mathbf{e}$ usually has the form:

$$\begin{array}{cc}\hfill \mathbf{e}& =\left[\begin{array}{c}{e}_x\\ e_y\end{array}\right]=e·\left[\begin{array}{c}cos\omega \\ sin\omega \end{array}\right].\hfill \end{array}$$

(15)

The difference between the two eccentricity vector gives the relative eccentricity vector:

$$\begin{array}{cc}\hfill \mathrm{\Delta }\mathbf{e}& ={\mathbf{e}}_2-{\mathbf{e}}_1=\left[\begin{array}{c}\mathrm{\Delta }{e}_x\\ \mathrm{\Delta }{e}_y\end{array}\right]=\delta e·\left[\begin{array}{c}cos\varphi \\ sin\varphi \end{array}\right],\hfill \end{array}$$

(16)

where $\mathrm{\Delta }e$ and $\mathrm{\Delta }\omega$ represent the differences in the eccentricity and the argument of perigee.

By linearizing HCWequations, there exists the equations of relative motion in LVLH [38]:

$$\begin{array}{cc}\hfill {\mathbf{R}}_{rt,LVLH}& =\left[\begin{array}{c}{\mathbf{r}}_R\\ {\mathbf{r}}_T\\ {\mathbf{r}}_N\end{array}\right]=a\left[\begin{array}{c}-\delta ecos\left(u-\varphi \right)\\ 2\delta esin\left(u-\varphi \right)+\mathrm{\Delta }l\\ \delta isin\left(u-\theta \right)\end{array}\right],\hfill \end{array}$$

(17)

where $u=\omega +M$ represents the mean argument of latitude and M is the mean anomaly. Considering the approximation that eccentricity e equals zero, there will be $M=\nu$ in the BiAAM. $\mathrm{\Delta }l=\mathrm{\Delta }u-\mathrm{\Delta }\theta \approx \mathrm{\Delta }u+\mathrm{\Delta }\mathrm{\Omega }·cosi$ stands for the difference of the mean orbital longitudes of both satellites.

Now, since we have $\mathrm{\Delta }{\mathbf{A}}_r$ in OP and ${\mathbf{R}}_{rt}$ in LVLH, both should be transferred to the same coordinate system to get the term DA-R. With the approximations given in the previous pages, the transformation matrix from LVLH to OP is:

$$\begin{array}{cc}\hfill {\mathbf{A}}_{L2O}& =\left[\begin{array}{ccc}cos\nu & -sin\nu & 0\\ sin\nu & cos\nu & 0\\ 0& 0& 1\end{array}\right].\hfill \end{array}$$

(18)

Now, we can give the expression of term DA-R in OP:

$$\begin{array}{cc}\hfill \mathrm{\Delta }{\mathbf{A}}_{r,OP}·{\mathbf{R}}_{rt,OP}& =\mathrm{\Delta }{\mathbf{A}}_{r,OP}·{\mathbf{A}}_{L2O}·{\mathbf{R}}_{rt,LVLH}\hfill \\ \hfill & =-{\displaystyle \frac{\mu }{p^2}}·\mathrm{\Delta }\nu ·\left[\mathrm{\Delta }l+2\delta esin\left(\nu +\omega -\varphi \right)\right].\hfill \end{array}$$

(19)

Therefore, the statistic parameters of term DA-R are:

$$\begin{array}{cc}\hfill \mathbb{E}\left[\mathrm{\Delta }{\mathbf{A}}_r·{\mathbf{R}}_{rt}\right]& =0,\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill \sigma \left[\mathrm{\Delta }{\mathbf{A}}_r·{\mathbf{R}}_{rt}\right]& ={\displaystyle \frac{\mu }{p^2}}·\sigma \left[\mathrm{\Delta }\nu \right]·\left[\mathrm{\Delta }l+2\delta esin\left(\nu +\omega -\varphi \right)\right],\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill \sigma {\left[\mathrm{\Delta }{\mathbf{A}}_r·{\mathbf{R}}_{rt}\right]}_{max}& ={\displaystyle \frac{\mu }{p^2}}·\sigma {\left[\mathrm{\Delta }\nu \right]}_{\mathrm{Max}}·\left(\mathrm{\Delta }l+2\delta e\right).\hfill \end{array}$$

(22)

3.3. The QPE in the BiAAM

The output of the BiAAM is the expression of the expected value and standard deviation of QPE, i.e., $\mathbb{E}\left[\mathrm{QPE}\right]$ and $\sigma \left[\mathrm{QPE}\right]$, respectively. Actually, $\mathbb{E}\left[\mathrm{QPE}\right]$ and $\sigma \left[\mathrm{QPE}\right]$ are given as functions of mean anomaly M. Furthermore, the maximum of QPE, $\sigma {\left[\mathrm{QPE}\right]}_{Max}$, is also available in the BiAAM to all $M\in \left[0,2\pi \right]$. Equation (3) indicates the definition of QPE, and it is obvious that it requires $T_{int}$ as a variable.

In the BiAAM, the integration time $T_{int}$ and slant range $\rho$ are required in both the accurate value and in the approximation. The accurate values are applied to estimate the QPE to each mean anomaly point, while the approximations are required in estimating the maximum parameters of the probability distribution of the estimated QPE.

In the calculations with accurate values, the slant range is obtained by solving the following quadratic equation:

$$\begin{array}{c}\hfill {\displaystyle \frac{{\left(\rho {\widehat{u}}_{a,ECI,x}+R_{sat,ECI,x}\right)}^2+{\left(\rho {\widehat{u}}_{a,ECI,y}+R_{sat,ECI,y}\right)}^2}{E_a^2}}+{\displaystyle \frac{{\left(\rho {\widehat{u}}_{a,ECI,z}+R_{sat,ECI,z}\right)}^2}{E_b^2}}=1,\end{array}$$

(23)

where the semi-major axis and semi-minor axis of the Earth’s surface ellipsoid are $E_a=$ 6,378,137.000 m and $E_b=$ 6,356,752.314 m. The vector ${\widehat{u}}_{a,ECI}=\left[{\widehat{u}}_{a,ECI,x},{\widehat{u}}_{a,ECI,y},{\widehat{u}}_{a,ECI,z}\right]$ is the antenna direction vector, which has the same definition as the MonoAAM. Then, the integration time is:

$$\begin{array}{cc}\hfill T_{int}& ={\displaystyle \frac{\lambda }{L_a}}{\displaystyle \frac{\left|{\mathbf{R}}_{tp}\right|}{\left|{\mathbf{V}}_{tp}\right|}}{\displaystyle \frac{\left|{\mathbf{R}}_t\right|}{\left|{\mathbf{R}}_p\right|}}.\hfill \end{array}$$

(24)

In the estimation of the maximum of the parameters of the probability distribution of QPE, the mean slant range is determined on the circular Earth’s surface with the radius of $E_{mean}=\left(2E_a+E_b\right)/3$ and:

$$\begin{array}{c}\hfill {\rho }_{mean}=E_{mean}{\displaystyle \frac{sin\left[{\theta }_L+\pi -arcsin\left(asin{\theta }_L/E_{mean}\right)\right]}{sin{\theta }_L}},\end{array}$$

(25)

where ${\theta }_L$ is the center off-nadir angle of a certain beam in SAR observation geometry.

The mean integration time $T_{int,mean}$ is presented with the satellite velocity at apogee only, together with semi-major axis a of the satellite instead of $\left|{\mathbf{R}}_t\right|$ as follows,

$$\begin{array}{cc}\hfill T_{int,mean}& ={\displaystyle \frac{a\lambda {\rho }_{mean}}{E_{mean}{L}_a}}\sqrt{{\displaystyle \frac{a\left(1+e\right)}{\mu \left(1-e\right)}}}.\hfill \end{array}$$

(26)

Based on the derivation from Section 3.1 and Section 3.2, the static parameters of QPE result from the term A-DR $\left({\mathbf{A}}_r·\mathrm{\Delta }{\mathbf{R}}_{rt}\right)$ and the term AD-R $\left(\mathrm{\Delta }{\mathbf{A}}_r·{\mathbf{R}}_{rt}\right)$ as:

$$\begin{array}{cc}\hfill \mathbb{E}{\left[\mathrm{QPE}\right]}_{\mathrm{A}-\mathrm{DR},\mathrm{DA}-\mathrm{R}}& ={\displaystyle \frac{\pi }{\lambda \rho }}\left(\mathbb{E}\left[{\mathbf{A}}_r·\mathrm{\Delta }{\mathbf{R}}_{rt}\right]+\mathbb{E}\left[\mathrm{\Delta }{\mathbf{A}}_r·{\mathbf{R}}_{rt}\right]\right){\left({\displaystyle \frac{T_{int}}{2}}\right)}^2,\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill \sigma {\left[\mathrm{QPE}\right]}_{\mathrm{A}-\mathrm{DR},\mathrm{DA}-\mathrm{R}}& ={\displaystyle \frac{\pi }{\lambda \rho }}\sqrt{{\sigma }^2\left[{\mathbf{A}}_r·\mathrm{\Delta }{\mathbf{R}}_{rt}\right]+{\sigma }^2\left[\mathrm{\Delta }{\mathbf{A}}_r·{\mathbf{R}}_{rt}\right]}{\left({\displaystyle \frac{T_{int}}{2}}\right)}^2,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill \sigma {\left[\mathrm{QPE}\right]}_{\mathrm{A}-\mathrm{DR},\mathrm{DA}-\mathrm{R},max}& ={\displaystyle \frac{\pi }{\lambda {\rho }_{mean}}}\sqrt{{\sigma }^2{\left[{\mathbf{A}}_r·\mathrm{\Delta }{\mathbf{R}}_{rt}\right]}_{max}+{\sigma }^2{\left[\mathrm{\Delta }{\mathbf{A}}_r·{\mathbf{R}}_{rt}\right]}_{max}}{\left({\displaystyle \frac{T_{int,mean}}{2}}\right)}^2.\hfill \end{array}$$

(29)

For convenience, we take a second look at the result from the MonoAAM and mark it as follows:

$$\begin{array}{cc}\hfill \mathbb{E}{\left[\mathrm{QPE}\right]}_{\mathrm{MonoAAM}}& =\pi \mathbb{E}\left[\mathrm{\Delta }{f}_{r,a}\right]{\left({\displaystyle \frac{T_{int}}{2}}\right)}^2,\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill \sigma {\left[\mathrm{QPE}\right]}_{\mathrm{MonoAAM}}& =\pi \sqrt{{\sigma }^2\left[\mathrm{\Delta }{f}_{r,v}\right]+{\sigma }^2\left[\mathrm{\Delta }{f}_{r,a}\right]}{\left({\displaystyle \frac{T_{int}}{2}}\right)}^2,\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill \sigma {\left[\mathrm{QPE}\right]}_{\mathrm{MonoAAM},max}& =\pi \sqrt{{\sigma }^2{\left[\mathrm{\Delta }{f}_{r,v}\right]}_{max}+{\sigma }^2{\left[\mathrm{\Delta }{f}_{r,a}\right]}_{max}}{\left({\displaystyle \frac{T_{int,mean}}{2}}\right)}^2.\hfill \end{array}$$

(32)

The detailed expression of $\sigma \left[\mathrm{\Delta }{f}_{r,v}\right]$ and $\sigma \left[\mathrm{\Delta }{f}_{r,a}\right]$, together with their maximum value expressions, can be found exactly in [30]. Here, we do not plan to provide them in order to avoid redundancy.

Thus, we have the expressions of the probability distribution of QPE to the satellite’s mean anomaly. The maximum of the probability distribution parameters of QPE for the whole track in typical spaceborne bistatic SAR formation is:

$$\begin{array}{cc}\hfill & \mathbb{E}{\left[\mathrm{QPE}\right]}_{\mathrm{BiAAM}}={\displaystyle \frac{\mathbb{E}{\left[\mathrm{QPE}\right]}_{\mathrm{MonoAAM},\mathrm{t}}+\mathbb{E}{\left[\mathrm{QPE}\right]}_{\mathrm{MonoAAM},\mathrm{r}}+\mathbb{E}{\left[\mathrm{QPE}\right]}_{\mathrm{A}-\mathrm{DR},\mathrm{DA}-\mathrm{R}}}{2}},\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & \sigma {\left[\mathrm{QPE}\right]}_{\mathrm{BiAAM}}={\displaystyle \frac{\sqrt{{\sigma }^2{\left[\mathrm{QPE}\right]}_{\mathrm{MonoAAM},\mathrm{t}}+{\sigma }^2{\left[\mathrm{QPE}\right]}_{\mathrm{MonoAAM},\mathrm{r}}+{\sigma }^2{\left[\mathrm{QPE}\right]}_{\mathrm{A}-\mathrm{DR},\mathrm{DA}-\mathrm{R}}}}{2}},\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & \sigma {\left[\mathrm{QPE}\right]}_{\mathrm{BiAAM},max}={\displaystyle \frac{\sqrt{{\sigma }^2{\left[\mathrm{QPE}\right]}_{\mathrm{MonoAAM},\mathrm{t},\max }+{\sigma }^2{\left[\mathrm{QPE}\right]}_{\mathrm{MonoAAM},\mathrm{r},\max }+{\sigma }^2{\left[\mathrm{QPE}\right]}_{\mathrm{A}-\mathrm{DR},\mathrm{DA}-\mathrm{R},\max }}}{2}}.\hfill \end{array}$$

(35)

where subscripts t and r identify either the transmitter or receiver SAR satellite parameters the should be applied in the parameter calculations, respectively.

4. Evaluation Model and Results

The evaluation model of BiAAM is presented in this section, selecting the Monte Carlo numerical simulation and the MonoAAM results as a reference. A detailed comparison between the MonoAAM and BiAAM is also given.

4.1. Evaluation Model

The Monte Carlo numerical simulation model could be a solid reference to evaluate the correctness and reliability evaluation of the BiAAM, with the MonoAAM as another reference.

The Monte Carlo numerical simulation generates multiple samples of error data, which fit the specified probability distribution of the error in real-time OODS. The Monte Carlo numerical simulation generates 30,000 error samples of the state vector measurements per mean anomaly, and there are 1000 mean anomaly estimation points in $M\in \left[0,2\pi \right]$. For each mean anomaly estimation point, the Monte Carlo numerical simulation estimates the Doppler rate with and without the measurement errors, resulting in the real Doppler rate and estimated Doppler rate with error. The difference between the real Doppler rate and estimated Doppler rate is then recorded, and a probability analysis is conducted to get the model of the probability distribution and corresponding parameters. When the probability analysis for all the mean anomaly estimation points is finished, the curves of the expected value of QPE $\mathbb{E}\left[\mathrm{QPE}\right]$ and the standard deviation of QPE $\sigma \left[\mathrm{QPE}\right]$ are presented.

The Monte Carlo numerical simulation applies no approximations that are applied in the BiAAM, aiming to provide a trustable reference. Currently, the BiAAM focuses on the changes of the parameters of the probability distribution of QPE in one track, and there exists no perturbed terms in the state vector calculation. In addition, the Monte Carlo numerical simulation implements a total zero Doppler beam steering method described in [39], for which the key idea is not only using yaw steering, but also applying pitch steering to minimize the Doppler centroid residence of the transmitter satellite. The surface of the Earth is defined with the ellipsoid reference in WGS 84. The Monte Carlo numerical simulation uses the mean anomaly because it is linear with time, while the true anomaly does not. The true anomaly has a certain relation to the mean anomaly. The MonoAAM and BiAAM use the true anomaly, but based on the approximation, that eccentricity equals zero, and the true anomaly equals mean anomaly.

The simulation parameters for the Monte Carlo numerical simulation, MonoAAM, and BiAAM are provided in

Table 1. Simulation parameters.

Parameter	Transmitter Satellite	Receiver Satellite
$E_a$	6,378,137.000 m
$E_b$	6,356,752.314 m
a	7,007,137.000 m
i	97.93°
$\omega$	90°
e	0.00114	0.001216
$\mathrm{\Omega }$	0°	0.09325°
$f_0$	9.60 GHz
${\theta }_L$	33.8°
$L_a$	1.92 m
${\sigma }_p$	3 m
${\sigma }_v$	0.1 m/s

. The Earth’s physical parameters $E_a$ and $E_b$ have the same definition compared to the ones in Section 3.3. The satellite Keplerian parameters include the semi-major axes a of the orbit, the orbital inclination i, the argument of periapsis $\omega$, the eccentricity e, and the RAAN $\mathrm{\Omega }$. The orbit parameters of the transmitter and receiver satellite are from the trinodal pendulum formation in [11], with proper eccentricity and RAAN separations for safe formation operation. The center frequency of the transmitting signal $f_0$, the center off-nadir angle ${\theta }_L$, and the azimuth length of the antenna $L_a$ are the key parameters of the SAR payload. Finally, the probability distribution parameters of the error in the real-time OODS measurements contain ${\sigma }_p$ and ${\sigma }_v$, which are the standard deviations of the measurement error in the position and velocity vector. The measurement error usually has an unbiased Gaussian distribution with zero expected value. The simulation value of ${\sigma }_p$ is determined with an equivalent value to the 3D positioning residuals (RMS) within around 1.5 m in the reference [28], and here, in the simulation, a 3 m standard deviation is applied. The ${\sigma }_v$ is also chosen based on a comparison with the result in [27]. These parameters are identical to the ones used in the evaluation of the MonoAAM.

4.2. Comparison of the MonoAAM and BiAAM

In spaceborne bistatic SAR missions, the relative movement of the receiver satellite to the transmitter satellite brings additional characteristics of the Doppler parameter. Significant estimation error exists when applying the MonoAAM directly to the spaceborne bistatic SAR missions. Selecting $\sigma \left[\mathrm{QPE}\right]$ of the receiver satellite as the comparison parameter, Figure 2 presents the Monte Carlo simulation result (in blue), the MonoAAM estimation result (in orange), and the BiAAM estimation result (in red).

In common practice, engineers always focus on the maxima standard deviation of the estimated QPE, and both MonoAAM and BiAAM should provide an estimation with tolerance, i.e., the maxima of the standard deviation of the estimated QPE should be just a little more than the upper bound of the ones from the Monte Carlo numerical simulation. As Figure 2 indicates, around the mean anomaly M at around 210°, the Monte Carlo numerical simulation result is greater than the MonoAAM results, which means applying the MonoAAM directly to the spaceborne bistatic SAR missions cannot guarantee the desired result it is designed to obtain. The BiAAM, in the meantime, can provide a reliable result of the maxima of the standard deviation of the estimated QPE for all mean anomalies in one orbit.

4.3. QPE Approximation of BiAAM

The Monte Carlo numerical simulation and BiAAM results are illustrated in Figure 3. The estimation results in blue are from the Monte Carlo numerical simulation, and those in red are from the proposed BiAAM. Figure 3a,b show almost exactly the same result of $\mathbb{E}\left[\mathrm{QPE}\right]$ between the Monte Carlo simulation and the BiAAM of transmitter and receiver satellites in the spaceborne bistatic SAR formation, represented with blue and red lines, respectively. The results of $\sigma \left[\mathrm{QPE}\right]$ of the transmitter and receiver satellites are in Figure 3c,d on an individual basis.

The dashed magenta lines in Figure 3c,d represent the maximum estimation of the standard deviation of QPE ($\sigma {\left[\mathrm{QPE}\right]}_{max}$) from the BiAAM for all the positions in one track of the satellite. It is necessary to indicate that this maximum estimation is not identical to the exact global maxima of $\sigma \left[\mathrm{QPE}\right]$. In fact, the relative error of the $\sigma \left[\mathrm{QPE}\right]$ of the transmitter and receiver satellite is $0.59\%$ and $0.77\%$ with the given simulation parameters in Figure 3c,d, respectively. The advantage of presenting $\sigma {\left[\mathrm{QPE}\right]}_{max}$ is that it can be calculated very easily even with only a calculator and the appropriate parameters. In this process, the error transfer routine is very clear.

5. Discussion

We propose the BiAAM, a bistatic analytical approximation model for Doppler rate estimation error from real-time OODS measurement in real-time spaceborne bistatic SAR imaging. The BiAAM aims to reduce the process and calculation, while providing a reliable method for investigating the OODS measurement error from real-time OODS onto the SAR image. The concept and early-stage development for a real-time onboard spaceborne bistatic SAR imaging mission likely benefit from the proposed BiAAM.

The SAR imaging algorithm requires the Doppler centroid and Doppler rate, which are estimated with the relative state vectors between the radar antenna phase center and targets. The “real-time” requirement of one spaceborne bistatic SAR mission varies from minutes to hours, as long as it has a significantly reduced processing time from the observation to finishing the SAR imaging procedure compared to the ones transmitting sampled data to the ground processing center. Typically, in the ground processing center for SAR imaging, the high accuracy orbit determination data can guarantee also high accuracy Doppler parameters, and this kind of parameter has a very limited negative impact on the quality of the SAR image. However, this high accuracy orbit determination data really need time to be obtained, usually at least several hours or more. Considering the real-time prerequisite, only the real-time OODS measurement could be useful for real-time onboard SAR imaging.

The ongoing trend of a SAR payload onboard a small satellite, lead by the MirrorSAR proposed by the DLR [40], makes it more challenging to obtain acceptable real-time onboard orbit determination data, as a small satellite platform is not as steady as professional SAR satellite platform. In this case, the performance of real-time OODS is more important, and it should be evaluated to identify whether it meets the requirement of real-time onboard SAR imaging.

Spaceborne bistatic SAR missions often have more tolerance for real-time orbit determination error than spaceborne monostatic SAR missions, as the transmitter and receiver satellites have different measured errors at the same time. In this case, it seems that the spaceborne bistatic SAR missions could have a relatively lowered requirement for real-time OODS. Besides, the relative motion of the receiver satellite to the transmitter satellite adds more challenges in evaluating the influence of the measurement error from real-time OODS in the real-time SAR imaging procedure.

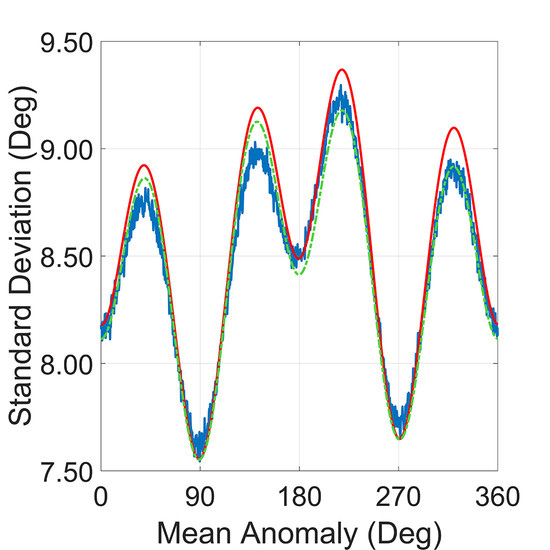
Both MonoAAM and BiAAM are designed to have a relatively simple way to estimate the QPE with the given parameters. System designers could evaluate these results and make updated equipment requirements during the design procedure. In common practice, designers always focus on the maxima standard deviation of the estimated QPE, and both MonoAAM and BiAAM should provide an estimation with tolerance, i.e., the maximum of standard deviation of the estimated QPE should be just a little more than the upper bound of the ones from the Monte Carlo numerical simulation. As Section 4.2 indicates, applying the MonoAAM directly to the spaceborne bistatic SAR missions cannot guarantee the desired result as designed. The BiAAM, in the meantime, can provide a reliable result of the maximum of the standard deviation of the estimated QPE for all mean anomalies in one orbit. Compared to the Monte Carlo numerical simulation method, the proposed BiAAM has significant advantages in the total process and calculations. For an error sample number of A in each calculation of the mean anomaly M point and the total number of mean anomaly points B, the calculation of the Monte Carlo simulation is $O\left(AB\right)$, while the BiAAM is only $O\left(B\right)$ with the given parameters and equations and generates no error samples. Normally, in order to get better Monte Carlo numerical simulation results, the number A is relatively large, and in this paper, it is $A=$ 30,000.

QPE can be a design requirement for different processing blocks in the SAR processing system, as any block of the system can bring in new errors to the Doppler rate. Based on the previous experience of designing a processing system, a QPE of no more than $0.25\pi$ (45.00°) is acceptable for one single processing block, and this equals a broadened azimuth impulse response width of no more than 1.02 [33]. With the BiAAM result in Section 4 and the 68–95–99.7 rule, it is obvious that, with the given simulation parameters and $\mathbb{E}\left[\mathrm{\Delta }{f}_{r,a}\right]$ being detached during the Doppler rate estimation, the QPE introduced by the measurement error from the real-time OODS of the transmitter and receiver satellites will be less than 28.10°, within the 99.73% confidence interval. This result indicates a broadened azimuth impulse response width of less than 2% within the 99.73% confidence interval, and this meets the acceptable limitation of one processing block.

Currently, the attitude error is not considered in the proposed BiAAM. The following step of the BiAAM can be investigating the attitude error in order to examine the coupled performance of the orbit determination error and the attitude error. Another worthy direction is to apply different steering strategies in the BiAAM, as there are multiply steering strategies available for spaceborne bistatic SAR missions.

6. Conclusions

As the measurement error from the orbit determination system onboard the spaceborne bistatic SAR satellites could have a negative impact on real-time SAR imaging quality, this paper proposes the BiAAM, a bistatic analytical approximation model for Doppler rate estimation error from real-time OODS measurement in real-time spaceborne bistatic SAR imaging. The proposed BiAAM model can provide QPE estimation results for each position of the satellite in its orbit and the maximum QPE estimation for the whole orbit, while revealing the different processes of orbit determination error transferred to QPE in spaceborne bistatic SAR. With a comparison to the Monte Carlo numerical simulation result and the existing analytical approximation model for spaceborne monostatic SAR, the proposed BiAAM reduces the total process and calculation, while maintaining relatively high accuracy. Real-time spaceborne bistatic SAR imaging mission architects and engineers can quickly identify the probability distribution parameters of estimated QPE with the BiAAM. The BiAAM will likely accelerate the concept and early-stage development of a real-time onboard SAR imaging mission to a certain extent and provide substantial evidence of the practicability of spaceborne bistatic SAR with real-time imaging capability.