Feature Dimension Reduction Using Stacked Sparse Auto-Encoders for Crop Classification with Multi-Temporal, Quad-Pol SAR Data

Abstract

Crop classification in agriculture is one of important applications for polarimetric synthetic aperture radar (PolSAR) data. For agricultural crop discrimination, compared with single-temporal data, multi-temporal data can dramatically increase crop classification accuracies since the same crop shows different external phenomena as it grows up. In practice, the utilization of multi-temporal data encounters a serious problem known as a “dimension disaster”. Aiming to solve this problem and raise the classification accuracy, this study developed a feature dimension reduction method using stacked sparse auto-encoders (S-SAEs) for crop classification. First, various incoherent scattering decomposition algorithms were employed to extract a variety of detailed and quantitative parameters from multi-temporal PolSAR data. Second, based on analyzing the configuration and main parameters for constructing an S-SAE, a three-hidden-layer S-SAE network was built to reduce the dimensionality and extract effective features to manage the “dimension disaster” caused by excessive scattering parameters, especially for multi-temporal, quad-pol SAR images. Third, a convolutional neural network (CNN) was constructed and employed to further enhance the crop classification performance. Finally, the performances of the proposed strategy were assessed with the simulated multi-temporal Sentinel-1 data for two experimental sites established by the European Space Agency (ESA). The experimental results showed that the overall accuracy with the proposed method was raised by at least 17% compared with the long short-term memory (LSTM) method in the case of a 1% training ratio. Meanwhile, for a CNN classifier, the overall accuracy was almost 4% higher than those of the principle component analysis (PCA) and locally linear embedded (LLE) methods. The comparison studies clearly demonstrated the advantage of the proposed multi-temporal crop classification methodology in terms of classification accuracy, even with small training ratios.

1. Introduction

It is very important to acquire crop type information in crop growing monitoring, biomass estimation, crop yield prediction, etc. [1,2,3]. Different from the conventional optical remote sensing, polarimetric synthetic aperture radar (PolSAR) is an active remote sensing technology that can work in all weather and all time conditions. During the past few decades, crop classification with PolSAR data has attracted strongly increasing research interest [4,5,6].

Currently, a variety of classification algorithms have been proposed and developed for PolSAR data. Generally, the development mainly underwent the following three phases [7]: 1) Lee investigated the regularities of distribution and applied statistical models to discriminate different objects [8]. 2) With the deeper research on the mechanisms of PolSAR data, the scattering mechanisms of electromagnetic waves were introduced into the analysis and application of PolSAR data [9,10]. Many studies have proved that retrieved polarimetric features by both coherent and incoherent decomposition algorithms can improve the recognition and classification accuracy [11,12], especially for quad-pol SAR images [13,14]. 3) Currently, several deep learning architectures have been developed and notable results were attained [15,16]. These knowledge-based algorithms [17,18] have opened a new horizon in this area. However, most of existing methods only concentrate on single-date PolSAR data. For agricultural-crop-type discrimination, single-temporal PolSAR images cannot provide sufficient information since the same crop shows different external phenomena as it grows up [19]. Additionally, the date of data collection is quite crucial. For instance, it is very challenging to discriminate different crops within the sowing periods. Accordingly, it is necessary to take the advantage of multi-temporal PolSAR images to produce classification results with a high accuracy [14]. Fortunately, with the rapid developments of SAR techniques, increasing numbers of spaceborne SAR systems have been launched and operate in orbits, which can collect a large amount of multi-temporal SAR data for Earth observations. Nowadays, several representative systems are available for civilian applications, including C-band Sentinel-1 systems [20,21], RADARSAT-2 and Radarsat Constellation Mission (RCM) [22,23], L-band Advanced Land Observing Satellite (ALOS) ALOS-PALSAR/PALSAR-2 [24,25], X-band Tandem-X [26], and X-band Constellation of Small Satellites for Mediterranean basin Observation (COMSMO) COMSMO -SkyMed constellation [27]. Based on these operational systems, large amounts of multi-temporal PolSAR data can be collected and adopted for use in crop classification and other applications [28,29,30,31,32,33,34,35,36].

For multi-temporal remote sensing data, a key point is how to take full advantage of the wealth of multi-temporal characteristics. Currently, a variety of classification algorithms with time-series information have been proposed. These algorithms can be mainly split into two methods: on one hand, long short-term memory (LSTM) networks have been adopted for the recognition and classification of multi-temporal data. For instance, Teimouri et al. combined an Fully Convolutional Networks (FCN) and a ConvLSTM network to classify and map land covers with multi-temporal Sentinel-1 data [29]. In order to further raise the performances of LSTM, the input features of LSTM are artificially modified with the fusion of high-resolution optical and SAR images. Zhou et al. used extracted SAR features in multiple deep convolutional networks (DCNs) as the input features of LSTM to improve the classification accuracy [30]. On the other hand, time-series or multi-temporal information is extracted manually from multi-temporal and multi-source data [31,32,33,34,35,36]. For example, Zhong et al. designed a one-dimensional convolution network to extract time-series features and discriminate different ground objects [31]. Yang et al. combined Normalized Difference Vegetation Index (NDVI) of optical images with SAR data to raise the accuracy of classifying paddy-rice in mountainous areas [32]. Guo et al. defined a new parameter based on differential characteristics of Cloude scattering parameters to improve the crop classification accuracy [33]. It can be seen that there is a rapid development in the analysis and application of multi-temporal optical and SAR data. These existing methods have the following limitations: First, it is difficult to discriminate multiple crop types by only using the time-series information due to the similarity between various crops. Second, the performances of the LSTM networks depend heavily on the input features and excessive features or sparse time-series data seriously deteriorate its performances. Consequently, for both the LSTM networks and time-series-information-based methods, most of the algorithms still concentrate on extracting more effective features. However, since SAR data represent the compositive interaction between radar signals and vegetation and soil [21], a variety of famous decomposition algorithms have been proposed to efficiently extract polarimetric scattering features [37,38,39,40]. However, direct utilization of many polarimetric features will cause a “dimension disaster” for most of the classification methods. Therefore, effective feature dimension reduction from these redundant ones is a very important task.

In the area of data dimension reduction, early representative algorithms mainly include principle component analysis (PCA) [41] and locally linear embedded (LLE) methods [42]. However, since most engineering problems are nonlinear, PCA performs poorly due to its assumption that the processed data are linear [43]. In addition, LLE can automatically extract low-dimensional nonlinear feature representations from high-dimensional data and is easy to implement, but they are not robust to outliers [44]. More recently, artificial neural network (ANN) and deep learning theory have realized considerable development in terms of image classification [45], target recognition [46], data dimensionality reduction [47], and other machine vision fields. With more than three hidden layers, deep learning models contain sufficient complexity to learn effective features from the data itself [4]. Currently, deep learning has also been proven to be an extremely powerful tool in remote sensing data analysis [48]. For instance, convolutional neural networks (CNN) and deep stack auto-encoder (S-AE) are the most successful network architectures, showing excellent performances in image classification and feature learning [16,49,50].

To make full use of multi-temporal PolSAR images and manage the serious problem of a “dimension disaster”, this study first employed several common scattering decomposition algorithms to extract detailed and quantitative parameters. Second, a three-hidden-layer stacked sparse auto-encoder (S-SAE) network was built to effectively extract polarimetric features and reduce the feature dimensionality. Third, the architecture of a deep CNN classifier was proposed to enhance the crop classification performance with limited training ratios. The main contribution of this paper was to apply S-SAEs to effectively reduce the feature dimension for crop classification improvements with multi-temporal, quad-pol SAR images.

The remaining sections are arranged as follows. Section 2 reviews the PolSAR data structure and polarimetric feature extraction. Furthermore, the main concept of an S-SAE and the architecture of CNN classifier is also proposed and discussed in this section. In Section 3, the main configuration and optimization of an S-SAE are analyzed and the performances of the proposed processing framework are assessed using simulated Sentinel-1 data. Section 4 is the conclusion of this paper.

2. Methodology

For the purpose of crop classification with multi-temporal remote sensing data, this study employed stacked sparse auto-encoders to learn low-dimensional features from a number of decomposed scattering signatures, which were fed to CNN classifiers to achieve classification results with high accuracies. The flowchart of the proposed method is shown in Figure 1, which was mainly composed of three steps including scattering feature extraction, feature dimensionality reduction with an S-SAE, and crop classification with CNN. It should be emphasized that the second step was the key of this study. Its aim was to acquire the optimal low-dimension features to represent sufficient information contained in the original multi-temporal data. In this section, the PolSAR data structure and features, along with the stacked sparse auto-encoders, are reviewed, and the architecture of a proposed deep CNN classifier is proposed and discussed.

2.1. PolSAR Data Structure and Features

In quad-pol SAR systems, the measured vector data can be expressed using a 2 × 2 complex scattering matrix as the following format:

$$S=\left[\begin{array}{cc}{S}_{HH}& S_{HV}\\ S_{VH}& S_{VV}\end{array}\right],$$

(1)

where $S_{HH}$, $S_{VH}$, $S_{HV}$, and $S_{VV}$ are the four scattering elements from four independent polarization channels, with “H” and “V” standing for the horizontal and vertical linear polarizations. With the assumption of reciprocal backscattering, $S_{HV}$ is approximately equal to $S_{VH}$ and the polarimetric scattering matrix can be rewritten as the Lexicographic basis vector:

$$\mathit{h}={\left[\begin{array}{ccc}{S}_{HH}& \sqrt{2}{S}_{HV}& S_{VV}\end{array}\right]}^{\mathrm{T}},$$

(2)

where the superscript “T” is the matrix transpose. Then, a covariance matrix can be constructed as:

$$\mathit{C}=\mathit{h}{\mathit{h}}^{*\mathrm{T}}.$$

(3)

Additionally, the Pauli-based scattering matrix can also be obtained as:

$${\mathit{k}}_m=\frac{1}{\sqrt{2}}{\left[S_{HH}+S_{VV},S_{HH}-S_{VV},2S_{HV}\right]}^{\mathrm{T}},$$

(4)

$${\mathit{T}}_m={\mathit{k}}_m{\mathit{k}}_m^{*\mathrm{T}}$$

(5)

where ${\mathit{T}}_m$ is the one-look coherency matrix for the mth pixel, where ${(\cdot )}^{*}$ denotes conjugate complex of $(\cdot )$. Actually, PolSAR images are multi-look processed to suppress speckles such that the coherency matrix is spatially averaged to become:

$$\langle \mathit{T}\rangle =\frac{1}{N}{\displaystyle \sum _{m=1}^N{\mathit{k}}_m{\mathit{k}}_m^{*\mathrm{T}}},$$

(6)

where $N$ indicates the number of equivalent looks. It has also been proven that the covariance and coherency matrices are linearly related and can be easily converted to each other [51].

According to the covariance and coherency matrices, several obvious features, including the polarization intensities of $\left|S_{HH}\right|$, $\left|S_{HV}\right|$, and $\left|S_{VV}\right|$, can be directly obtained, where $\left|\cdot \right|$ denotes the absolute value of $\cdot$. With the deeper research on the mechanisms of PolSAR data, various coherent and incoherent scattering decomposition algorithms based on the covariance and coherency matrices have been employed to extract a variety of detailed and quantitative parameters from multi-temporal PolSAR data. Consequently, several features can be extracted for single and multiple temporal PolSAR images. Bai summarized a 123-dimensional feature vector extracted from single temporal quad-pol SAR images [52]. Furthermore, some new features have also been proposed recently [15]. These tremendous features encounter the great difficulty of the curse of dimensionality at high dimensionalities. To take full advantage of the wealth of multiple temporal PolSAR images for crop classification, feature dimension reduction is essential and important.

2.2. Auto-Encoder

In the past few years, feature learning with neural network architectures has attracted increasing attention, which can be used to extract optimal features from high-dimension data. An auto-encoder (AE) is an unsupervised learning algorithm and its goal is to set the target values to be approximately equal to the inputs. A single-layer AE network comprises three main steps (i.e., encoder, activation, and decoder), having one visible input layer ($x$) of $w$ units, one hidden layer ($y$) of $s$ units, and one reconstruction layer ($z$) of $w$ units, which is shown in Figure 2, where $f(\cdot )$ and $g(\cdot )$ denote the activation functions.

Considering the input data $x_i\in R^w$, where $i$ is the index of $i$th data point, the AE network first maps it to the latent representation $y_i\in R^s$. This process is named the encoding step and can be mathematically represented as:

$$y_i=f(W_y{x}_i+b_y),$$

(7)

where $W_y\in R^{s\times w}$ is the encoding matrix and $b_y\in R^s$ is the bias. Here, the logistic sigmoid function of $f(I)={(1+e^{-I})}^{-1}$ is adopted.

The decoder has a similar structure to the encoder and maps the compressed data to a reconstruction $z_i\in R^w$ with the weight matrix $W_z\in R^{w\times s}$, bias $b_z\in R^w$, and an activation function $g(I)=f(I)={(1+e^{-I})}^{-1}$, which can be represented as:

$$z_i=g(W_z{y}_i+b_z).$$

(8)

For simplification, the assumption of the weights strategy $W_y=W_z^T=W$ is used. Consequently, the three parameters $\left\{W,b_y,b_z\right\}$ need to determined. An auto-encoder can be trained by minimizing the cost function (i.e., the error between the inputs and reconstructed ones):

$$\psi (x,z)=\arg \underset{W,b_y,b_z}{\min }\frac{1}{2n}{\displaystyle \sum _{i=1}^n{\Vert x_i-z_i\Vert }^2},$$

(9)

where $n$ is the number of training samples. In addition, a weight attenuation term can be added in the cost function to control the degree of the weight reduction such that the term inhibits the influence of noise on the irrelevant components in the target and weight vector, significantly improves the generalization ability of the network, and effectively avoids over fitting. The cost function is defined as:

$$\tau (x,z,\lambda )=\psi (x,z)+\lambda \cdot {\Omega }_{weights},$$

(10)

$${\Omega }_{weights}=\frac{1}{2}{\displaystyle \sum _{l=1}^u{\displaystyle \sum _{i=1}^s{\displaystyle \sum _{j=1}^w(W_{ij}^{(l)}{)}^2}}},$$

(11)

where $\lambda$ is used to control the regularization strength, $u$ is the number of hidden layers, and ${\Omega }_{weights}$ is the weight attenuation term named L2 regularization. By using the Stochastic gradient descent (SGD) algorithm, the weight matrix and bias are trained and optimized [53].

2.3. Stacked Sparse Auto-Encoder

A sparse auto-encoder is the foundation of an S-SAE, which is developed from an AE. By adding sparsity constraints to an AE, the sparsity constraints act on hidden layer units. This method can preferably express high-dimensional features [54]. In order to realize the inhibitory effects, an SAE uses a Kullback-Leibler (KL) divergence to force it to be close to a given sparse value $\rho$ (sparsity parameter) by constraining the average activation value $\widehat{\rho }$ of the hidden layer neuron output. KL divergence is added to the cost function as a penalty term. Therefore, the cost function of an SAE can be updated in accordance with Equation (11). Furthermore, the penalty term is called a sparse regularization term, which is expressed in Equation (12).

$$E(x,\lambda ,\beta ,\rho )=\frac{1}{2n}{\displaystyle \sum _{n=1}^n{\Vert x_i-z_i\Vert }^2}+\lambda \cdot {\Omega }_{weights}+\beta \cdot {\Omega }_{sparsity}$$

(12)

$${\Omega }_{sparsity}={\displaystyle \sum _{i=1}^{D}KL(\rho \Vert {\widehat{\rho }}_i)}={\displaystyle \sum _{i=1}^D\rho \log (\frac{\rho }{{\widehat{\rho }}_i})}+(1-\rho )\log (\frac{1-\rho }{1-{\widehat{\rho }}_i})$$

(13)

In Equation (12), the average activation values ${\widehat{\rho }}_i$ of all training samples on neurons $i$ of the hidden layer are defined as:

$${\widehat{\rho }}_i=\frac{1}{n}{\displaystyle \sum _{j=1}^{n}f(w_i^{(1)}{x}_j+b_i^{(1)})},$$

(14)

where $x_j$ is the $j$th training samples, $w_i^{(1)}$ is $i$th row of the weight matrix $W$ in the first layer, and $b_i^{(1)}$ is the $i$th entry of the bias vector.

KL divergence is adopted because it can measure the difference between two different distributions wel. If ${\widehat{\rho }}_i={\rho }_i$, $KL\left({\widehat{\rho }}_i\Vert {\rho }_i\right)=0$. If the difference between $\rho$ and $\widehat{\rho }$ is large, KL divergence will force them to be close. In Equation (11), $\beta$ ($0<\beta <1$) is used to control the weight of the sparse regularization term. In order to inhibit most neurons, the value is generally close to 0. If the value is 0.03, the average activation value of each neuron on the SAE will be close to 0.03 through this constraint.

S-SAE is a deep learning architecture constructed by linking several sparse auto-encoders in series, in which the outputs of each layer are fed to the following layer. The training of an S-SAE is through greedy training layer by layer. An S-SAE with the Softmax regression neural network [49] can train and adjust network parameters again, which is called fine-tuning. The structure and training process of an S-SAE are given in Figure 3 and Figure 4, respectively.

In the network, the number of labels is equal to the dimension of the output vector $y^{(u)}$. Here, $W^{(l)}$ and $b^{(l)}$, $l\in \left\{1,2,3\dots u\right\}$, are the parameters of the $l$th layer, where $W^{(l)}$ is the weight matrix of the $l$th layer and $b^{(l)}$ is the bias vector. According to the known labels, the whole S-SAE network is finely tuned to determine the parameters of $W$ and $b$ using backpropagation.

2.4. Architecture of the Proposed Deep CNN Classifier

A convolutional neural network (CNN) is one of the most successful network architectures in deep learning methods. The learning process of CNNs is computationally efficient and insensitive to shifts in data like image translation, making CNN a leading model to recognize 2D patterns in images [31]. In remote sensing studies, a deep learning network based on CNN has been widely used in remote sensing, such as in large-scale image recognition, semantic segmentation, and target classification [48]. In the field of remote sensing target classification, since the ground truth data collection is always a hard task, the aim of this paper was to construct a lightweight CNN network to achieve classification results with a high accuracy and the classical LetNet was selected as the basic structure. Additionally, it is difficult to obtain better classification performance by deepening the network due to the small size of the input data cubic. Consequently, this paper promoted the LetNet configuration using two parallel branches inspired by the characteristics of GoogLeNet [55]. The proposed structure of a CNN classifier is given in Figure 5. It mainly comprises four convolutional layers, one average-pooling layer, one addlayer layer, one fully connected layer, and a Softmax classifier. Basically, it retains the same elements as GoogLeNet and utilizes the average pooling layer to reduce the number of fully connected layers. Furthermore, the network uses two convolution branches with different depths and the addlayer structure to fuse the features from different depths, enhancing the relevant features to achieve a fast convergence. The dimension of the input data is 15 × 15 × M where M indicates the number of input features. First, the input is through one convolution layer with 32 filters whose size is 5 × 5 and the stride is 1. The dimension of the generated feature cubic is 15 × 15 × 32 using zero padding. Second, the generated feature maps are fed into two pathways, where one pathway contains two convolution layers and another is one convolution layer. These three convolution layers have the same 64 filters with the same size of 3 × 3 and the strides are 2, 1, and 2. Third, the feature maps from the upper pathway are activated using a Rectified Linear Unit (ReLU) function and combined with the feature from the lower pathway. Thus, the feature maps with dimension of 8 × 8 × 64 are obtained. Fourth, the combined maps are downsampled by one average-pooling layer with the size of 2 × 2 and the stride is 2. Finally, in order to use Softmax to calculate the probability for each class, one fully connected layer is applied to map the data to a vector.

3. Experiments and Results

3.1. Experimental Sites and PolSAR Data

The performances of the proposed method were assessed with two data sets from two experimental sites. The first experimental site was an approximate 14 km × 19 km rectangular region located in the town of Indian Head (103°66′87.3″W, 50°53′18.1″N) in southeastern Saskatchewan, Canada [56,57]. The second one was a 13 km × 9 km rectangular region located in Flevoland (5°33′53.67″W, 52°26′45.73″N), Netherlands. The location maps of the study areas are shown in Figure 6. These two sites were established by the European Space Agency (ESA) to evaluate the performances of crop classification with Sentinel-1 data. Both study sites contained various crop types. There are mainly 14 classes of crops and the corresponding planting areas are summarized in

Table 1. Data acquisition dates and basic information of the main crops in the experimental sites.

Experimental Sites	Acquisition Dates	Category Code	Crop Type	Number of Pixels	Proportion
Indian Head(Canada)	21 April 15 May 8 June 2 July 26 July 19 August 12 September	H1	Lentil	215,659	10.62%
		H2	Durum Wheat	98,927	4.87%
		H3	Spring Wheat	571,205	28.13%
		H4	Field Pea	252,277	12.43%
		H5	Oat	70,541	3.47%
		H6	Canola	452,068	22.27%
		H7	Grass	23,452	1.16%
		H8	Mixed Pasture	14,608	0.72%
		H9	Mixed Hay	27,135	1.34%
		H10	Barley	106,022	5.22%
		H11	Summer fallow	22,067	1.09%
		H12	Flax	127,757	6.29%
		H13	Canary seed	45,915	2.26%
		H14	Chemical fallow	2682	0.13%
Flevoland(Netherlands)	21 April 15 May 8 June 2 July 26 July 19 August 12 September	F1	Carrots	440	0.1%
		F2	Flower bulbs	11,499	2.58%
		F3	Fruit	10,198	2.29%
		F4	Grass	33,787	7.58%
		F5	Lucerne	2255	0.51%
		F6	Maize	18,253	4.09%
		F7	Misc	31,573	7.08%
		F8	Onions	41,001	9.19%
		F9	Peas	7105	1.59%
		F10	Potato	100,040	22.43%
		F11	Spring barley	6340	1.42%
		F12	Spring wheat	17,991	4.03%
		F13	Sugarbeet	58,403	13.09%
		F14	Winter wheat	107,142	24.02%

.

The two experimental PolSAR data sets were both simulated with Sentinel-1 system parameters from real RADARSAT-2 data by ESA before launching real Sentinel-1 systems. The real RADARSAT-2 data were collected from April to September (i.e., Indian Head data set: 21 April, 15 May, 8 June, 2 July, 26 July, 19 August, and 12 September; Flevoland data set: 7 April, 1 May, 25 May, 12 June, 5 July, 29 August, and 22 September) in 2009, almost covering the whole growing cycles of the main crops. The multi-temporal images have already been coregistered and filtered for speckle noise suppression using an averaged structure Lee filter [58]. For the performance evaluation, optical images of high resolutions and ground surveys were combined to establish the ground truth maps, which are shown in Figure 7.

3.2. Results and Analysis for the Indian Head Site

3.2.1. Polarimetric Feature Extraction

For the subsequent experiments, polarimetric scattering features were first derived from seven time-series PolSAR images separately using various methods. Some of these features were based on the measured data and directly obtained, and others were calculated with Freeman decomposition [37], Huynen decomposition [38], Yamaguchi decomposition [39], and Cloude decomposition [40]. It should be noted that the parameter “A” from Cloude decomposition was substituted by the theta parameter proposed in Ji et al. [34] and the null angle parameters were from Chen and Tao [15]. In total, 252 features from 7 time series were prepared, which are summarized in

Table 2. The 36 dimensional features from a single temporal PolSAR image.

Feature Extraction Methods	Features	Dimension
Features based on measured data	Polarization intensities($\left|S_{HH}\right|$, $\left|S_{HV}\right|$, $\left|S_{VV}\right|$)	3
	Amplitude of HH-VV correlation($\left|S_{VV}{S}_{HV}^{\ast }/\sqrt{{\left|S_{HH}\right|}^2\cdot {\left|S_{VV}\right|}^2}\right|$)	1
	Phase difference of HH-VV($\mathrm{atan}\left[\mathrm{Im}\left(S_{HH}{S}_{VV}^{\ast }\right)/\mathrm{Re}\left(S_{HH}{S}_{VV}^{\ast }\right)\right]$)	1
	Co-polarized ratio($10{\log }_{10}\left({\left|S_{HV}\right|}^2/{\left|S_{VV}\right|}^2\right)$)	1
	Cross-polarized ratio($10{\log }_{10}\left({\left|S_{VV}\right|}^2/{\left|S_{HH}\right|}^2\right)$)	1
	Co-polarization ratio($10{\log }_{10}\left({\left|S_{HV}\right|}^2/{\left|S_{HH}\right|}^2\right)$)	1
	Degrees of polarization(${\left|S_{HV}\right|}^2/\left({\left|S_{HH}\right|}^2+{\left|S_{VV}\right|}^2\right)$,${\left|S_{VV}\right|}^2/\left({\left|S_{HH}\right|}^2+{\left|S_{HV}\right|}^2\right)$)	2
Incoherent decomposition	Freeman decomposition	5
	Yamaguchi decomposition	7
	Cloude decomposition	3
	Huynen decomposition	9
Other Decomposition	Null angle parameters	2
Sum	36

* $\mathrm{Re}[·]$ and $\mathrm{Im}[·]$ are the real and imaginary parts, respectively.

and some typical features (i.e., amplitude of HH-VV correlation where HH and VV stands for the complex SAR images from horizontal and vertical channels respectively, phase difference of HH-VV, co-polarized ratio, and null angle parameters) are shown in Figure 8.

3.2.2. S-SAE Configuration and Optimization

1. Selection of unsupervised training samples for pretraining the parameters of an S-SAE item

Unsupervised pretraining is the first key step to constructing an S-SAE. The ratio of selected training samples significantly affects the performance and computation time. For simplification, a single-layer sparse auto-encoder with the regularization term $\lambda$ of 0.001, sparsity regularization term $\beta$ of 4.5, and the sparsity parameter $\rho$ of 0.25 was used to compress 252 input features down to 9 features. To investigate the performances of an S-SAE with different training samples, this section compares the performances of different training sample ratios of 0.3%, 1%, 5%, 10%, 20%, and 50%. The pretraining epochs were 400. After the dimensionality reduction, the nine reduced features were fed into a support vector machine (SVM) classifier. The ratio of the supervised training samples for the SVM classifier was 1% and randomly selected, and the remaining 99% were for testing. In the experiments, crop classifications were carried out ten times and the averaged classification accuracy was utilized for the evaluation. The overall accuracy (OA) and kappa coefficient of the classification results are plotted in Figure 9a. Figure 9b gives the training calculation time with different ratios of unsupervised training samples. From Figure 9, it can be seen that the classification accuracy increased with the increase of unsupervised pretraining samples. For the case of a 50% training ratio, the OA and kappa were raised by about 6% and 5%, respectively, relative to those for the 0.3% training ratio. However, the training time also became longer. Therefore, taking the computational efficiency into account, the ratio of the unsupervised pretraining samples was fixed to 0.3%, 1%, and 5% in the following experiments.

2. Depth and supervised fine-tuning of the parameters of an S-SAE

In order to investigate the performance of an S-SAE with different depths, this section sets five AEs with one to five layers (i.e., AE, S-AE2, S-AE3, S-AE4, and S-AE5), where AE is a single layer auto-encoder, S-AE is stack auto-encoder. These five S-SAEs were first pretrained, as discussed in the last section, and then finely tuned with supervised training samples. The ratios of the pretraining samples were 0.3%, 1% and 5%. The ratio of the supervised training samples for fine-tuning was set to be 1%. In order to reduce the disturbance of other parameters, $\lambda$, $\beta$, and $\rho$ of the five S-AEs were all set to 0.001, 0, and 0. The number of epochs of pretraining and fine-tuning training were 400 and 800, respectively. Again, the nine reduced features were fed into the SVM classifier after the dimensionality reduction. The OA and kappa of the classification results with five different S-AEs are shown in Figure 10 (1% pretraining ratio), and the evaluation parameter values were calculated and are listed in

Table 3. Classification accuracy using S-SAEs with different depths.

Algorithm	Architecture	Method	Classification Accuracy (%)
			0.3% PRA Ratio		1% PRA Ratio		5% PRA Ratio
			OA	Kappa	OA	Kappa	OA	Kappa
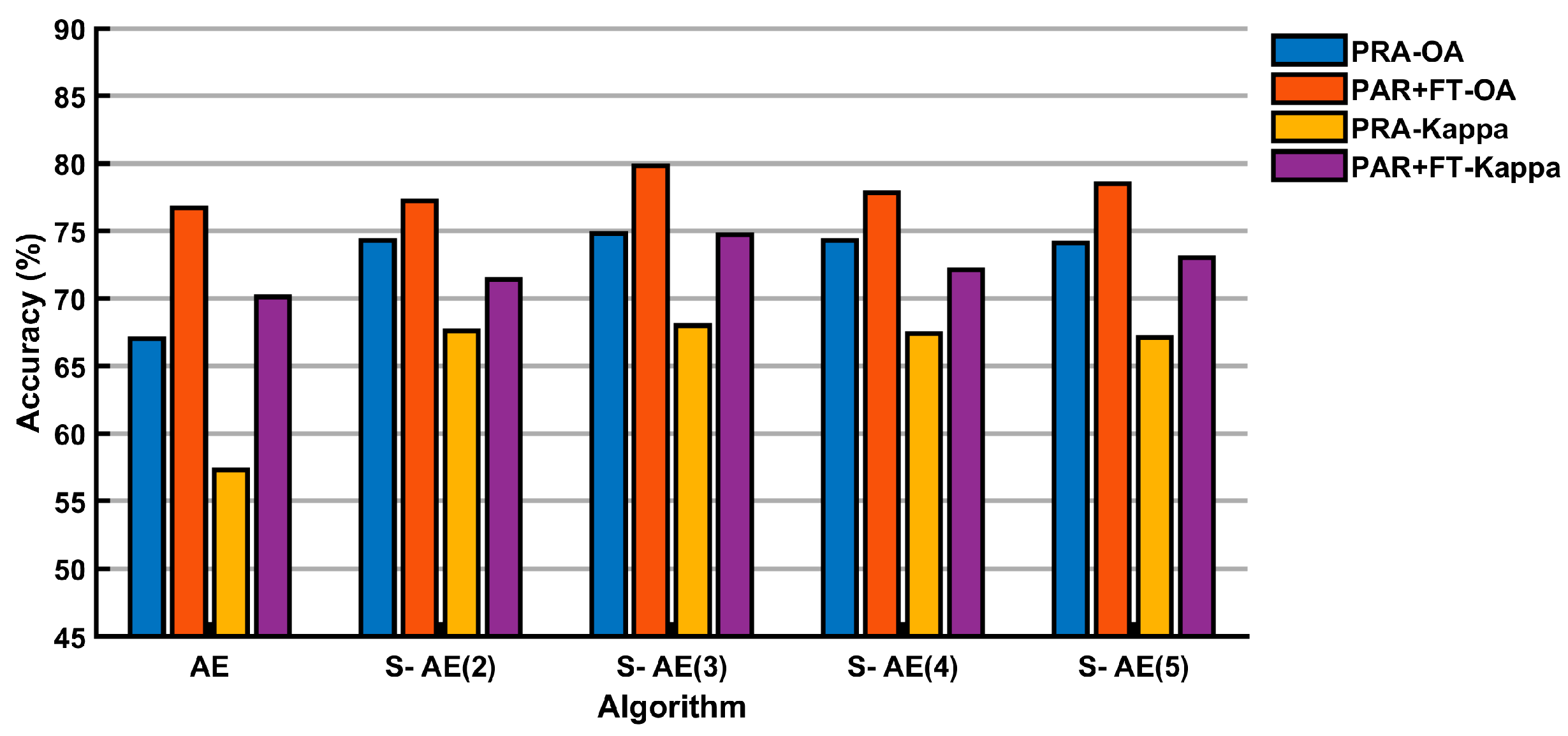
AE	252 - 9	PRA	63.61	52.30	67.01	57.26	70.35	62.01
		PRA+FT	73.10	65.75	76.74	70.51	78.91	73.55
S-AE2	252 - 100 - 9	PRA	73.09	65.83	74.34	67.57	76.23	70.12
		PRA+FT	76.42	70.31	77.23	71.35	77.74	72.05
S-AE3	252 - 100 - 50 - 9	PRA	73.08	65.79	74.77	68.01	76.56	70.48
		PRA+FT	76.45	70.27	79.75	74.67	79.31	74.07
S-AE4	252 - 100 - 50 -110 - 9	PRA	72.91	65.56	74.30	67.38	77.00	71.03
		PRA+FT	74.16	67.23	77.82	72.13	77.51	71.73
S-AE5	252 - 100 - 50 -110 - 30 - 9	PRA	72.37	64.83	74.12	67.14	76.47	70.73
		PRA+FT	75.91	69.58	78.46	73.00	78.14	72.56

PRA stands for pretraining, PRA+FT stands for pretraining and fine-tuning, OA stands for overall accuracy.

. From Figure 10 and Table 3, it is clear to see that: 1) The accuracy of the classification results increased with the increase of pretraining samples, which is consistent with the conclusion of previous step. 2) Comparing Table 3 and Figure 9a, the parameters of $\lambda$, $\beta$, and $\rho$ improved the accuracy, especially in the case of the 0.3% pretraining samples. 3) The fine-tuning of S-SAE raised the classification accuracy dramatically. However, the power of improvement became weaker with the increase of pretraining samples, which was mainly due to the insufficient training caused by the decreased ratio of fine-tuning samples to pretraining ones. 4) As the number of layers increased, the classification accuracies became gradually higher [55]. However, when the network contained more than three layers, the performance did not increase. Therefore, the network architecture of 252-100-50-9 was configured as the optimal one and used in the following experiments.

3. Size of the hidden layers

For an AE network, the number of learned features is decided by the hidden layer. To investigate the effects of the hidden layers on crop classification, a group of experiments were conducted. Here, the goal was still to reduce the 252 input features to 9, where the optimal network with the hidden neurons of 252-100-50-9 in the previous step was chosen as the original network configuration. Let $L_1$ and $L_2$ denote the number of units contained in the two hidden layers and the searching intervals were [35, 260] and [20, 200], respectively. In the experiment, the grid search strategy with a step of 15 was employed to determine the optimal number of hidden neurons. The values of $\lambda$, $\beta$, and $\rho$ were still set to 0.001, 0, and 0. The nine compressed features were fed into the SVM classifiers trained with 1% supervised samples. The OA and kappa of the classification results are shown in Figure 11. From Figure 11, it is clear that the effects of the size of the hidden layer were strong. The highest OA was approximately 10% higher than the lowest. The zone with the higher classification accuracy was mainly distributed in the top-left area, appearing as an inverted triangle, marked by a yellow line in Figure 11. In this area, the optimal interval for the size of the second hidden layer shrunk gradually with the decrease of the size of the first hidden layer. Consequently, the size of the first hidden layer was much bigger than that of the second one. In addition, when the size of the first hidden layer was close to the size of the input data, a better performance of the dimension reduction was obtained, which was mainly because having more neurons could raise the ability of feature learning and improve the performance of the whole S-SAE. Finally, the best classification accuracy with an OA of 80.45% and kappa of 75.42% was achieved when $L_1$ and $L_2$ were 215 and 95, and thus the S-SAE with the structure of 252-215-95-9 was the optimal configuration.

4. Parameters of $\lambda$, $\beta$, and $\rho$

The determination of $\lambda$, $\beta$, and $\rho$ is the final step to constructing an optimal S-SAE. In order to study the effects of these three parameters, this study carried out some comparison experiments for a single-layer AE network.

For $\lambda$, the grid search of $\Delta {\log }_{10}\lambda$ was carried out with a stride of 1 and an interval of [−7, 1]. The other remaining implementation was similar with that in the previous step. The OA and kappa of the classification results with an SVM classifier are plotted in Figure 12, where the highest accuracy was obtained with a $\lambda$ of 0.1 (i.e., ${\log }_{10}\lambda =-1$), and a $\lambda$ of 10 generated the lowest accuracy.

For $\beta$ and $\rho$, two groups of experiments with a ${\log }_{10}\lambda$ of −2 and −1 were compared. For $\beta$, the searching interval and step were [0.5, 4.5] and 1. For $\rho$, the searching interval and step were set to [0.05, 0.45] and 0.1. The AEs were configured with these parameters and the reduced features were fed into the SVM classifiers. The OA and kappa were charted in Figure 13, where it was evident that: 1) the values of $\lambda$, $\beta$, and $\rho$ had a great impact on the recognition performances; and 2) the best results were generated when $\lambda$, $\beta$, and $\rho$ were set to 0.1, 2.5, and 0.45. The highest OA and kappa were 80.62% and 75.84%, which were both 5% higher than that of an SAE with the original parameters (i.e., $\lambda$ = 0.001, $\beta$ = 0, $\rho$ = 0). Additionally, clear regulations during the process of determining optimal parameters were not found in these experiments.

Finally, after a variety of experiments, a group of optimal parameters were determined and are listed in

Table 4. Optimal parameter settings of each layer in an S-SAE for the Indian Head site.

Parameters	${\mathbf{L}}_1$	${\mathbf{L}}_2$	${\mathbf{L}}_3$
$\lambda$	0.0024	0.02	0.001
$\beta$	0.6	0.2	0.4
$\rho$	0.5	0.55	0.25

for the S-SAE with the structure of 252-215-95-9. Consequently, the OA and kappa of the classification results with the SVM were 81.77% and 77.20%, which were slightly higher than those in the previous section.

3.2.3. Comparison of Classification Results with the Different Methods

In this section, nine reduced features were extracted from the original 252 multi-temporal features using different methods, including PCA, LLE, a single-layer AE(1) of 252-9, a finely tuned AE(2) of 252-9, a finely tuned S-AE(1) of 252-100-50-9, a finely tuned S-AE(2) of 252-215-95-9, and a finely tuned S-SAE of 252-215-95-9 with the optimal parameters listed in Table 4. The $\lambda$, $\beta$, and $\rho$ of AE(1), AE(2), S-AE(1), and S-AE(2) were all set to 0.001, 0, and 0. The ratio of the supervised fine-tuning samples for AE was 1%. For LLE, the number of neighbors was 300 and the max embedding dimensionality was 9. Then, the extracted nine-dimensional features were fed into the SVM and the proposed CNN classifiers. For the CNN classifier, the initial parameters were randomly selected and renewed with a learning rate of 0.01, momentum parameter of 0.9, and weight decay of 0.0004.

First, the ratio of the training samples for the SVM and CNN classifiers were 1% and the other 99% were for testing. The 14 types of crops were classified, including lentil, durum wheat, spring wheat, field pea, oat, canola, grass, mixed pasture, mixed hay, barley, summer fallow, flax, canary seed, and chemical fallow. Compared with the ground truth, some of the classification results along with the error map are shown in Figure 14, and the OA and kappa for the SVM and CNN classifiers, along with the correct classification ratio for each class, were calculated and are summarized in

Table 5. Comparison of the support vector machine (SVM) classification accuracy with different dimension reduction methods for the Indian Head site. PCA: Principle component analysis.

Methods	OA (%)	Kappa (%)	Classification Accuracy of the 14 Crops (%)
			H1	H2	H3	H4	H5	H6	H7	H8	H9	H10	H11	H12	H13	H14
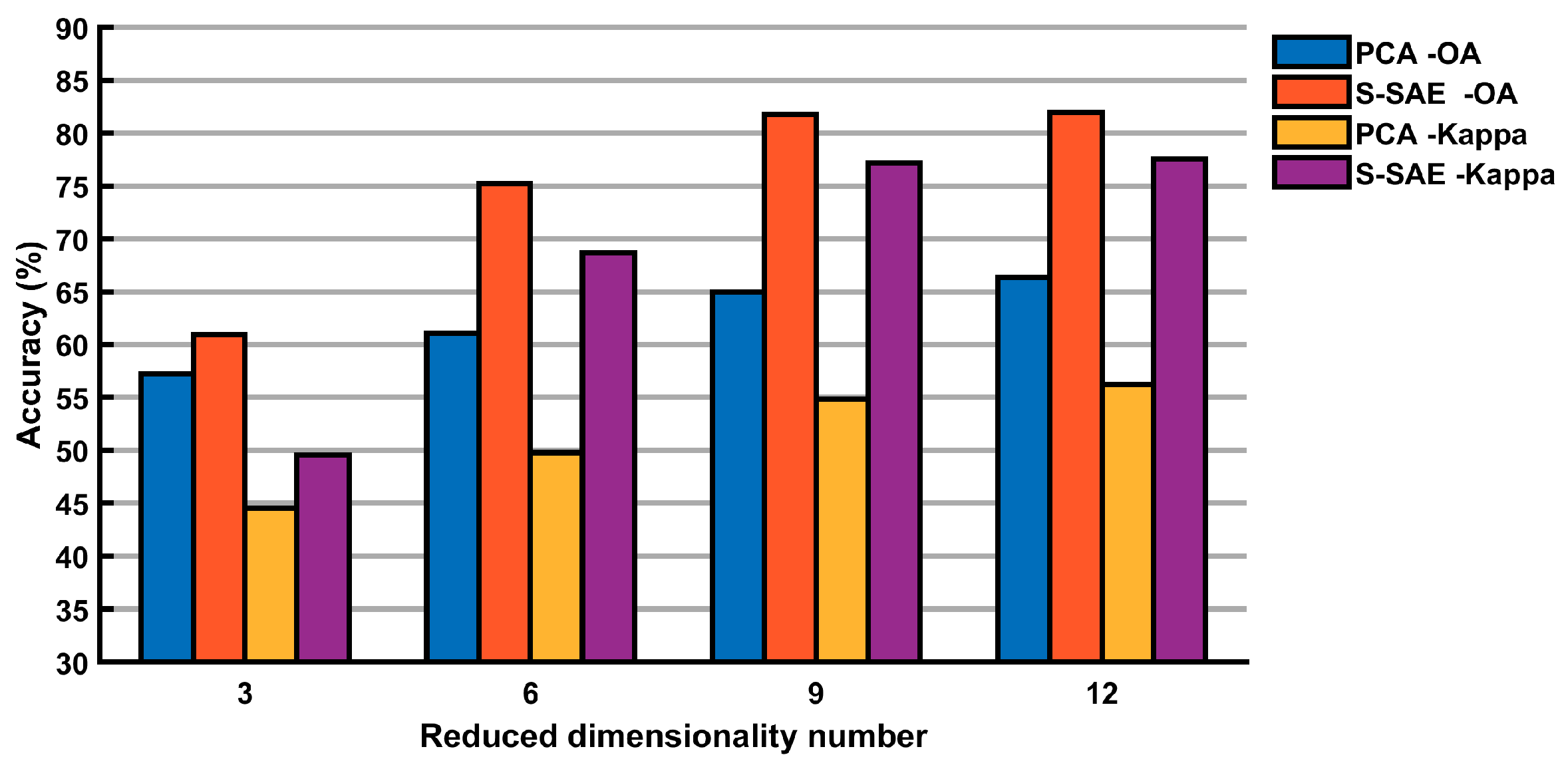
PCA	65.00	54.88	88	1	96	48	1	90	44	2	33	1	8	18	1	0
LLE	65.19	55.23	90	1	96	48	1	89	48	3	36	1	19	21	1	0
AE(1)	67.21	57.55	83	1	97	83	3	90	4	6	37	3	25	23	1	0
AE(2)	76.74	70.51	88	2	98	92	22	94	35	7	37	29	35	56	29	2
S-AE(3)	79.75	74.67	90	5	98	93	26	95	62	2	57	40	43	65	34	0
S-AE(4)	80.47	75.62	92	5	98	94	24	94	68	3	59	43	49	65	44	0
S-SAE	81.77	77.20	92	7	98	94	31	96	72	7	48	41	58	69	53	25

and

Table 6. Comparison of the CNN classification accuracy with different dimension reduction methods in Indian Head site.

Methods	OA (%)	Kappa (%)	Classification Accuracy of the 14 Crops (%)
			H1	H2	H3	H4	H5	H6	H7	H8	H9	H10	H11	H12	H13	H14
PCA	87.59	84.87	96	55	96	92	56	98	78	50	79	61	76	80	49	23
LLE	88.30	85.80	97	51	94	94	62	99	76	62	79	63	86	84	60	61
AE(1)	87.86	85.29	91	44	92	97	63	99	88	59	71	70	89	79	75	31
AE(2)	93.03	91.58	96	70	96	99	79	99	88	55	83	80	89	87	86	92
S-AE(3)	94.74	93.65	98	69	97	99	81	100	85	58	88	84	95	94	93	61
S-AE(4)	94.95	93.92	98	71	97	99	81	100	83	59	82	92	91	94	98	79
S-SAE	95.44	94.51	99	78	97	99	80	100	89	57	86	88	97	94	94	75

, respectively. The crop classification results showed that the optimal S-SAE had the best performances for both the SVM and CNN classifiers. For the SVM classifier, OA from the S-SAE was 16.77% and 14.56% higher than those from PCA and AE(1). For the CNN classifier, OA from the S-SAE was raised by 7.55% and 7.58% relative to those from PCA and AE(1). The combination of S-SAE and CNN achieved the best classification results, of which the OA and kappa were up to 95.44% and 94.51%

Second, the classification methods with different training ratios (i.e., 1%, 5%, and 10%) for training the SVM and CNN classifiers were compared. The quantitative evaluation parameters were calculated and are listed in

Table 7. Classification accuracy with different methods and training ratios for the Indian Head site.

Methods	1%		5%		10%
	OA (%)	Kappa (%)	OA (%)	Kappa (%)	OA (%)	Kappa (%)
Complex Wishart	60.86	55.89	61.05	56.08	61.26	56.28
LLE + SVM	65.19	55.23	69.93	61.60	72.75	65.35
S-SAE + SVM	81.77	77.20	82..35	78.01	84.06	80.17
Chen + SVM	66.99	57.45	71.61	63.77	72.13	64.47
Chen + CNN	91.74	90.04	96.35	95.55	97.93	97.51
LSTM	69.67	61.31	80.74	76.07	82.83	78.76
LLE + CNN	88.30	85.80	96..66	96.00	99.23	98.95
S-SAE + CNN	95.44	94.51	99.08	98.89	99.61	99.53

. Meanwhile, some results with the conventional Complex Wishart classifier, LSTM in Zhong et al. [31] and Chen method [15] are also included. The 36 × 7 decomposed features were the input of the LSTM and 14 decomposed roll-invariant features from 7 time series were taken as the input of the Chen method.

From Figure 14, we can conclude that: 1) for feature dimension reduction, the SVM and CNN with nine features from the S-SAE achieved the best classification results; 2) with the increase of the training ratio, the recognition accuracy for all methods became better, as expected; 3) compared with the SVM classifier, the CNN classifier improved the classification performance of the dimensionality reduction features, especially for the crops with small planting areas; 4) among all the compared methods, the proposed method achieved the highest classification accuracy. The LSTM wass not effective in discriminating crop species with similar external morphologies, such as barley and durum wheat. Moreover, the proposed method of S-SAE + CNN achieved excellent crop classification accuracies, even with finite training ratios.

3.2.4. Comparison of the Dimensionality Reduction Features with Different Methods

In order to further demonstrate the advantages of this method regarding feature extraction, this section compares the dimensionality reduction features with different dimensionality reduction methods for the following two aspects. First, according to the contribution of PCA and visual quality of LLE and S-SAE, the first four extracted features from these three methods were visualized and are shown in Figure 15, from which it can be seen that the features with S-SAE exhibited the best visual effects. Second, the values of the standard deviation between different crops and within the same class were calculated for quantitative comparison. The six main crops with the highest planting area in the Indian Head site were selected for comparison: lentil, spring wheat, field pea, canola, barley, and flax. Then, six local windows with the size of 100 × 100 were used to choose samples for the six main crops, and the standard deviations of the optimal feature (i.e., the first column in Figure 15) from each method were calculated and plotted in Figure 16 (in Figure 16a, the number of the horizontal ordinate stands for the six selected crops; in Figure 16b, the number of the horizontal ordinate stands for three crops, including the current and neighboring crops), which shows the maximum standard deviation between different crops and the minimum within the same crop. Consequently, the features with the S-SAE had a better classification ability and are expected to improve the accuracy of crop recognition and classification.

3.3. Results and Analysis for the Flevoland Site

In order to further verify the reliability of the proposed method, another experiment with multi-temporal data from Flevoland was carried out and is reported on in this section. The methods of dimensionality reduction and classification maintained the same setup as the previous one. For a fair comparison, according to the contribution rate (i.e., more than 90%) of reduced parameters using PCA method, the original 252 features were all reduced to 12 features.

First, various dimensionality reduction methods, including PCA, LLE, a single-layer AE(1) of 252-12, a finely tuned AE(2) of 252-12, a finely tuned S-AE(1) of 252-100-50-12, a finely tuned S-AE(2) of 252-215-95-12, and an S-SAE of 252-215-95-12 were used to extract 12 low-dimension features from the original 252 multi-temporal features. In addition, the comparison methods also included a finely tuned SAE of 252-12 with $\lambda$, $\beta$, and $\rho$ being 0.1, 2.5, and 0.45. The determined optimal parameters of an S-SAE of 252-215-95-12 are listed in

Table 8. Optimal parameter settings of each layer in the S-SAE for the Flevoland site.

Parameters	${\mathbf{L}}_1$	${\mathbf{L}}_2$	${\mathbf{L}}_3$
$\lambda$	0.001	0.02	0.001
$\beta$	0.6	0.2	0.4
$\rho$	0.25	0.55	0.25

. Compared with the ground truth, some of the classification results and the error maps are shown in Figure 17, and the OA and kappa, along with the correct classification ratio for each class, were calculated and are summarized in

Table 9. Comparison of CNN classification accuracy with different dimension reduction methods in Flevoland site.

Methods	OA (%)	Kappa (%)	Classification Accuracy of the 14 Crops (%)
			F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13	F14
PCA	87.30	84.94	0	94	91	89	64	83	70	87	59	95	57	32	90	96
LLE	87.90	85.69	5	95	79	92	62	86	67	89	80	94	56	32	94	97
AE(1)	86.62	84.16	12	93	92	82	45	84	72	84	79	96	46	18	95	94
AE(2)	88.09	85.89	13	94	88	90	50	87	70	88	68	95	49	34	93	97
S-AE(3)	88.98	86.95	0	98	86	86	82	74	74	86	81	96	62	39	97	98
S-AE(4)	89.93	87.98	3	97	91	87	36	87	80	88	63	97	74	40	94	98
SAE	91.09	89.47	34	96	92	91	55	91	79	90	80	98	64	44	95	97
S-SAE	91.63	90.11	35	97	92	93	67	90	77	87	85	98	86	41	97	98

, from which it can be seen that the optimal S-SAE still had the best performances. The combination of the S-SAE and CNN achieved the best classification results, of which OA and kappa were up to 91.63% and 90.11%, respectively. Furthermore, the AE with a deeper structure and fine-tuning parameters improved the data dimensionality reduction ability.

Secondly, the classification methods with different training ratios (i.e., 1%, 5% and 10%) for training SVM and CNN classifiers are compared. The quantitative evaluation parameters are calculated and listed in

Table 10. Classification accuracy with the different methods and training ratios for the Flevoland site.

Methods	1%		5%		10%
	OA (%)	Kappa (%)	OA (%)	Kappa (%)	OA (%)	Kappa (%)
Complex Wishart	77.50	73.92	76.74	73.08	76.11	72.34
LLE + SVM	80.22	76.07	82.63	77.59	84.15	79.24
S-SAE + SVM	82.66	79.22	84.81	81.83	86.06	83.36
Chen + SVM	75.42	72.33	78.37	75.01	80.24	78.55
Chen + CNN	81.19	77.62	93.57	92.40	96.41	95.76
LSTM	73.93	68.51	76.52	71.72	79.77	75.71
LLE + CNN	87.90	85.69	94.99	94.09	97.28	96.30
S-SAE + CNN	91.63	90.11	95.90	95.17	97.57	97.14

. The experimental results show that the classification accuracy with Chen method is a little lower than that in Indian Head data. Other main conclusions are the same as those in the first study site.

4. Discussions

The accuracy of the crop recognition and classification can be raised dramatically with multi-temporal quad-pol SAR data. Recently, an increasing number of spaceborne SAR systems launched into orbit around the Earth can acquire a large amount of real data, providing a great opportunity for multi-temporal data analysis [28]. Meanwhile, deep learning has shown powerful abilities in the fields of remote sensing [48]. Based on these two considerations, this study attempted to combine the effective feature dimension methods of AE and CNN classifiers to achieve crop classification results with a high accuracy. Based on the theoretical analysis and experimental results above, we provide the following discussions.

4.1. Contribution of Multi-Temporal SAR Data and Decomposed Features

Different from other ground objects, agricultural crops usually hold a stable and regular growing cycle. Generally, the crop categories would not change during various growing stages. In this case, single-temporal PolSAR images cannot provide sufficient information since the same crop shows different external phenomena as it grows up. Compared with single temporal data, multi-temporal remote sensing data can provide much richer information to improve the classification accuracy [29,30].

In order to better understand the polarimetric scattering mechanisms of various objects, a variety of polarimetric feature decomposition techniques have been developed [37,38,39,40,59]. With these polarimetric decomposition algorithms, a huge number of features can be extracted from PolSAR data that are used to raise the classification accuracy. For multi-temporal data from M time series, the number of features becomes M times greater. If a deep learning algorithm is directly applied, these tremendous features encounter the serious difficulty of the curse of dimensionality at high dimensionality [50], especially for quad-pol SAR images. Therefore, data dimension reduction and effective feature extraction are very essential and important issues.

4.2. Network Construction and Parameter Optimization of an S-SAE

In this study, the S-SAE was employed to extract effective features from multi-temporal polarimetric features. Furthermore, the effects of the training ratios, network configurations, size of the hidden layers, and main parameters were studied in Section 3.2.2.

For the training ratios, the increasing training ratio of unsupervised training samples increased the performances of S-SAE. However, the power of improvement became weaker with the increase in pretraining samples, which was mainly due to the insufficient training caused by the decreased ratio of fine-tuning samples to pretraining ones. In addition, the increasing training samples brought about a heavy computation burden. Therefore, an appropriate training ratio is of paramount importance.

For network depths and the size of hidden layers, as the network deepened, the classification accuracies became higher. However, the network depth was not as deep as possible [50,53]. When the network contained more than three layers, the performance did not increase any more. Additionally, by setting the step size of the searching grid to be smaller, this study provided new discoveries. If the number of neurons in the first hidden layer approximated the number of input features and the number of neurons in the second hidden layer kept a certain gap with the former and following layers, a better performance of the data dimension reduction could be obtained.

For the parameters of λ, β and ρ, the regularization of λ and the sparsity terms of β and ρ had uncertain impacts on the performances of the S-SAE. Appropriate values of these parameters improved the OA of classification results by 5%, which was even higher than that of the optimal structure of 252-215-95-9. Unfortunately, clear regulations were not found in these experiments, which needs further study in the future.

4.3. Differences from Existing Works

Regarding the purpose of classification with multi-temporal PolSAR data, Lee investigated the regularities of distribution and applied statistical models to discriminate between different objects [8]. The proposed complex Wishart classifier only uses the statistical distribution of the covariance matrix and can be easily extended to the case of multi-band or multi-temporal PolSAR images.

With the development of polarimetric decomposition theory, various decomposed features can be calculated, and it has been proven that the performances of target recognition and classification can be improved greatly with these meaningful parameters [15,33]. Meanwhile, the CNN classifier was also applied to classification with PolSAR images since it has shown great success in computer vision and other fields [15,48]. In order to take full advantage of the polarimetric decomposition and the CNN classifier, a feature dimension reduction was necessary. In this case, the conventional PCA and LLE were used to extract effective information expressed by the reduced parameters.

In Section 3.2.3, for fair comparison, according to the contribution rate of the reduced parameters using the PCA method, the original 252 features were all reduced to 9 features. The experimental results show that the S-SAE performed best and the accuracy of the classification result obtained using the S-SAE+CNN was the highest. For further comparison, PCA and S-SAE were used to reduce the original 252 features to 3, 6, 9, and 12 low-dimensional features for the Indian Head site, and then the reduced features were fed into the SVM classifier. The OA and kappa with different reduced features are shown in Figure 18. It can be seen clearly that the classification accuracy increased as the number of reduced features increased, as we expected. Regardless of the dimension of the reduced features, S-SAE had a better performance than the conventional PCA method.

4.4. Limitations and Future Work

First, only a limited number of polarimetric decomposition algorithms for quad-pol SAR images were used in this paper. Polarimetric decomposition is still a rapidly developing area and many other algorithms can also be used together to form a rather high-dimensional feature vector [52]. Second, the proposed S-SAE feature dimension reduction method had a heavy computation burden, although it performed much better than PCA. Third, the training ratio, network depth, size of the hidden layer, and other main parameters can impact the performances of data dimension reduction, especially for a multi-layer deep S-SAE. Finally, the proposed method was only assessed with Sentinel-1 data. The performances with multiple SAR sensors and combination of SAR and optical data will be investigated in future work.

5. Conclusions

To deal with the problem of the dimension disaster, this paper proposed an S-SAE to reduce the data dimension of scattering features extracted from multi-temporal PolSAR images. To validate the performances of the proposed S-SAE + CNN strategy, the Sentinel-1 data, along with the established ground truth maps for two experimental sites, were used. Combined with the traditional SVM and constructed CNN classifiers, the classification results were compared and evaluated. The experimental results showed that the S-SAE could extract low-dimension features from original ones. For the CNN classifier, this method could significantly improve the classification accuracy of small sample crops compared with the traditional methods. With the increasing availability of PolSAR data, the proposed method also provides an efficient way for crop classification with multi-temporal PolSAR data.

In order to construct an optimal S-SAE, this paper also investigated the effects of the training ratio, network depth, size of the hidden layer, network configuration, and other main parameters. The experimental results showed that these factors could greatly impact the performance of the feature dimension reduction. For this specific purpose, the configuration and main parameters of an S-SAE should be optimized. It should be noted that the single-layer SAE could achieve a dimension reduction performance that was close to the optimized S-SAE when the training parameters were set properly. Due to the complexity of optimizing the parameters of a multi-layer S-SAE, the potential of multi-layer S-SAE is not fully utilized. Methods to effectively determine the configuration and parameters for constructing an optimal S-SAE will be discussed in a separate paper.