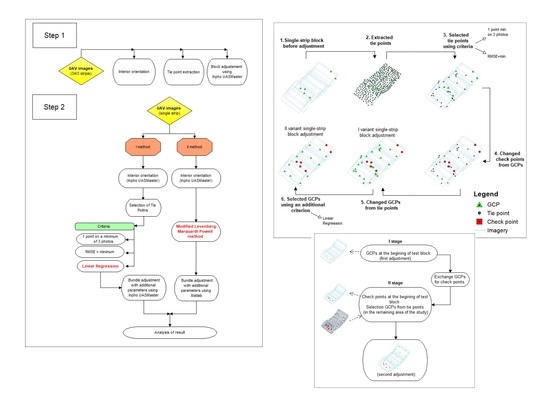
Methodology of Processing Single-Strip Blocks of Imagery with Reduction and Optimization Number of Ground Control Points in UAV Photogrammetry

Abstract

Unmanned aerial vehicle (UAV) systems are often used to collect high-resolution imagery. Data obtained from UAVs are now widely used for both military and civilian purposes. This article discusses the issues related to the use of UAVs for the imaging of restricted areas. Two methods of developing single-strip blocks with the optimal number of ground control points are presented. The proposed methodology is based on a modified linear regression model and an empirically modified Levenberg–Marquardt–Powell algorithm. The effectiveness of the proposed methods of adjusting a single-strip block were verified based on several test sets. For method I, the mean square errors (RMSE) values for the X, Y, Z coordinates of the control points were within the range of 0.03–0.13 m/0.08–0.09 m, and for the second method, 0.03–0.04 m/0.06–0.07 m. For independent control points, the RMSE values were 0.07–0.12 m/0.06–0.07 m for the first method and 0.07–0.12 m/0.07–0.09 m for the second method. The results of the single-strip block adjustment showed that the use of the modified Levenberg–Marquardt–Powell method improved the adjustment accuracy by 13% and 16%, respectively.

1. Introduction

In recent years, the intensity of use of unmanned aerial vehicles (UAVs) in photogrammetric and remote sensing applications has been constantly growing. Miniature unmanned aerial vehicles can be a cheap and effective alternative for acquiring imagery for the purpose of classic aerial photogrammetry. UAVs, which were initially created for the needs of the military, have also found civilian use—for example, to study the natural environment. It is worth noting that UAV imaging also meets needs related to aviation. A good example is the so-called securing of an off-airport landing strip, where the selection of the landing site is made based on preliminary field reconnaissance or based on landing zone maps. It seems reasonable to use UAVs to collect data to facilitate the choice of the location for such a landing strip. This can be justified in many ways, such as low cost of operation, the ability to provide geospatial data with high spatial resolution, the small size of the flying platform, low airspace occupancy (e.g., low flight altitude), ease of preparation for flight and quick recovery of readiness to perform the task. Therefore, UAVs can also be used to obtain data from hard-to-reach areas. Conducting a flight over an area with restricted access is associated with the problem of an incomplete photogrammetric control network, which should be evenly distributed throughout the area of study. It is worth noting that despite the emergence of a more precise positioning system (e.g., real-time kinematic (RTK)), many low-cost UAVs are still equipped with single-frequency global positioning system (GPS) receivers [1]. In comparison with previously used global navigation satellite systems (GNSS) methods, the RTK positioning method uses a wider frequency band. There is, therefore, a greater likelihood of improper navigation of the UAV using RTK in the vicinity of other radiation sources. This is mainly due to the phenomenon of electromagnetic wave interference from various devices. Therefore, it seems more appropriate to use a UAV positioning method which utilizes a narrower frequency band, i.e., GPS.

1.1. Related Works

Obtaining geospatial data from unmanned aerial systems is becoming more and more popular [2]. UAVs have become a widely used aerial platform in the field of photogrammetry and remote sensing [3]. Currently, a gradual replacement of classical aerial photogrammetry with low-altitude photogrammetry can be observed [4]. UAV s platforms have many advantages, including low costs and ease of use [5]. UAVs were created mainly for the needs of the military: for exercises, observation, reconnaissance, and offensive operations [6]. Increasingly, however, unmanned aerial vehicles are being used for civilian applications, such as for researching the natural environment, among others [7,8,9,10]. UAVs may be remotely controlled (e.g., piloted from a ground control station) or can fly autonomously using a pre-programmed flight plan [11]. UAVs can be equipped with optical sensors, thermal sensors, multispectral sensors, and Lidar sensors [12,13]. They can be used for mapping artificial objects and 3D modeling of natural objects [14,15]. Compared to traditional aerial photogrammetry, UAVs can acquire higher spatial resolution images for the production of orthophotos [16], digital surface models [17], and others [18].

Unmanned aerial vehicles can be used for imaging the earth’s surface to create air navigation obstacle maps [19,20,21]. The location of objects (aviation obstacles) affects the course and safety of the flight during its critical stages (take-off, landing). There are cases of a so-called improvised landing where the landing site selection can be made based on terrain reconnaissance. Such an area is called an off-airport take-off and landing area [21,22]. The basic criterion for selecting such a site is the ability to perform a safe landing and take-off in accordance with the conditions and limitations specified in the operation manual of a given type of aircraft [23]. An important parameter is the slope angle of the landing area and the type of coverage. Due to the low cost of operation, small size, low flight altitude, ease of storage and implementation, and the ability to provide geospatial data with a high spatial resolution with a higher data collection rate and relatively short data processing time, it is reasonable to obtain imagery data using UAV platforms [24,25,26,27]. Another area that may be used in the future for the so-called accidental landing are highway strips. The use of unmanned aerial vehicles can facilitate the control of the current condition of road sections used as emergency landing strips.

UAV imagery has become a commonly used tool for the observation of restricted areas [28,29]. While the imaging of the inaccessible area seems easy to perform with the use of UAV platforms, setting up and measuring a photogrammetric control network in the study area may be impossible (Figure 1).

The general consensus in photogrammetry is to ensure an even distribution of control points [30] and check points throughout the study area [31,32,33]. It is worth noticing the issues related to the processing of data obtained from UAVs and determining how the accuracy of photogrammetric products changes depending on the distribution of ground control points (GCPs), especially with a small number of GCPs [34]. Unfortunately, there is no consensus on what best practice is, and questions remain as to whether GCPs should be mainly on the periphery or in the middle of the area, and what is the best placement rule for them. The number of GCPs to be used in traditional aerial photogrammetry has previously been discussed in the photogrammetric literature. It is well known that an increase in the number of ground control points (GCPs) results in an improvement in the accuracy of the developed data [33]. There is little published work on the impact of the number of GCPs on the accuracy of UAV-derived photogrammetric products, and many conclusions are ambiguous or even contradictory. For example, Mancini et al. [35], Yang et al. [36] and Saporano at al. [37] found that the number of used GCPs can be further reduced without significant loss of accuracy. Tmušić et al. [38] state that the required GCP deployment will also depend on the image content (e.g., vegetation and surface type), terrain characteristics, survey design, and camera characteristics, which influence the potential for systematic error to develop within the image block. The optimal number of GCPs and their spatial distribution is one of the most important issues in indirect georeferencing. In their research, Harwin et al. [34] use different subsets of GCPs, suggesting that the number of GCPs is an important parameter in the resulting accuracy. By contrast, Tahar et al. [39] analyses the accuracy of different configurations using from four to 12 GCPs, with the authors concluding that the error range decreased after using seven or more GCPs. Shahbazi et al. [40] analyze the results using three to 22 GCPs. They recommend providing a large number of well-distributed GCPs to maximize accuracy but also state that with a minimum number of GCPs that are well distributed and with high overlap, similar results can be obtained. In their research, Oniga et al. [41] determined that the RMSE can be reduced down to 50% when switching from four to 20 GCPs, whereas a higher number of GCPs only slightly improves the results. In the study aimed at determining the optimal number of GCPs conducted by Yu et al. [42] the alignment results were analyzed in three study sites with different areas according to the number of GCPs. The results showed that the optimal number of GCPs was 12 for small and medium sites (7 and 39 ha) and 18 for large sites (342 ha) based on the overall accuracy. Agüera-Vega et al. [43] showed in their research that both the horizontal and vertical accuracy improves with an increase in the number of GCPs.

Currently, the integration of the increasingly popular RTK system with the aircraft allows for the reduction of the number of control points, and in some cases, even their complete exclusion. Caution should be exercised when abandoning the field survey. If we do not have the coordinates of even a few check points, we are deprived of the possibility of controlling the obtained results [44]. As it is known, the accuracy of determining the position of an unmanned aerial vehicle for a single-frequency GPS receiver is about 10 m [1]. At the same time, Shahbazi et al. [40] in his research shows the possibility of achieving high accuracy from UAVs equipped with GPS receivers.

The use of the RTK system in the vicinity of certain devices may affect its operation. Airports are equipped with a large amount of flight inspection system equipment (instrument landing system (ILS), primary surveillance radar (PSR), secondary surveillance radar (SSR), VHF omnidirectional range (VOR), tactical air navigation (TACAN), radio communication), the proper operation of which is based on electromagnetic wave propagation in a wide range of frequencies and with different types of modulation. In addition, military airfields and aircraft based there may be equipped with jamming, spoofing, or radiation protection devices. To reduce the likelihood of navigation errors of an unmanned aerial vehicle performing a task near an airfield, it is reasonable to use a positioning method which utilizes a more narrow frequency band, i.e., GPS. The use of “traditional” GNSS technology may have a smaller impact on the operation of the airport devices themselves compared to RTK technology (e.g., transmitting antenna—rover), which directly translates into the safety of air operations. UAVs with a GPS module can also perform better during a conflict. The arguments for this are higher system reliability and, as previously mentioned, fewer frequencies. Moreover, UAVs with GPS do not require the presence of an operator (reference station) directly in the study area. An example of use may be checking the suitability of a highway strip or other takeoff and landing site in inaccessible terrain or during a conflict.

In photogrammetric triangulation approaches, bundle adjustment (BA) is a commonly used process to simultaneously refine the X, Y, Z coordinates of the scene points, the exterior orientation points (EOPs) of the involved images, and/or the interior orientation parameters (IOPs) of the utilized cameras [45,46]. The classic photogrammetric bundle adjustment is based on the collinearity equations [47]. It can be formulated as a nonlinear least-squares problem, which aims at minimizing the total back-projection error between the observed image point coordinates and predicated feature locations [48]. Recently, bundle adjustment has been further expanded to deal with a wide variety of situations, such as the utilization of different features (e.g., line [49,50], curves [51], etc.), the reconstruction of dynamic scene objects [52], and the employment of non-quadratic error models [53]. Readers wishing to know more details regarding modern bundle adjustment techniques [54,55], should refer to the review conducted by Triggs et al. [53]. The most popular programs processing the low-ceiling photogrammetric data are Agisoft Photoscan, Inpho UASMaster, Pix4D, and EnsoMosaic [45].

In literature, there are studies on the processing of a single block of images. One can especially find many detailed descriptions of adjusting blocks of imagery using the independent model method [56,57]. A methodology of processing a single block of imagery collected by a UAV had been described by Forlani et al. [58], where an auxiliary block obtained from the flight at a higher altitude is used to adjust a single strip block. Another approach to developing a single-strip block from a UAV is presented by Jiang et al. [59], where, to determine the accuracy of the adjustment of a single-strip block, images were additionally taken as part of a two-strip block.

1.2. Research Purpose

In this research work, the hypothesis is: taking into account additional parameters in the aerotriangulation process makes it possible to increase the accuracy of the adjustment of a single-strip block with a limited number of control points for inaccessible areas, using sensors installed onboard low-cost unmanned aerial vehicles using single-frequency GPS receivers.

The research aimed to develop a methodology of adjusting single-strip blocks of low altitude imagery depicting highway landing strips, taking into account limited access to the entire study area. Based on the research hypothesis, as part of the research, a methodology was proposed based on a modified linear regression model and a modified Levenberg–Marquardt–Powell algorithm (empirically modified ranges for the region size ∆_k depending on the size ρ_k were taken into account). The effectiveness of the proposed methods of adjusting a single-strip block was verified based on several test sets.

The paper is structured as follows: in Section 2, the test data are introduced. In Section 3, the research method is explained. Section 4 presents the results of the conducted experiments. In Section 5, the results are discussed. Finally, Section 6 provides a brief summary of this work.

2. Materials

2.1. Study Area

The research was carried out on two test blocks carried out as two separate missions. The first block—set I Łagiewniki—covered the area along a road section, a highway landing strip, located in southwestern Poland, in the town of Łagiewniki (50°47′27″N; 16°50′40″E) (Figure 2). The imaged area covered an area of approximately 0.34 km².

The second test block—set II Nadarzyce—covered an area of the Central Aviation Training Range in Nadarzyce (53°27’18″N; 16°29’24″E) in northwestern Poland (Figure 2).

2.2. Description of Data Sets

Set I—Łagiewniki: The source data for aerotriangulation was obtained using the Trimble UX-5 airframe (Figure 3a), equipped with a Sony a7R camera. The aerial platform was equipped with a single-frequency GPS receiver, recording data at a frequency of 10 Hz.

The flight was carried out in the test area in July 2017. The imaging conditions were good, i.e., the sky was partially covered by cumulus clouds and the average wind speed was about 2 m/s. The camera settings were defined in manual mode, while the focus of the lens was set to infinity. The selected test area was the vicinity of the village of Łagiewniki, covering the area along the highway landing strip. The entire test block consisted of 811 images in 34 rows, obtained from an altitude of 250 m above the ground. The flight was conducted in the east-west direction, assuming that the transverse and longitudinal coverage was 75%. In the area of the study, 22 signaled control points were designed and measured (Figure 3b). All points were measured using the RTK technique in the GNSS system. The field coordinates of the control points were determined with the mean error m_x,y,z = ±0.03 m.

Set II—Nadarzyce: The source data for aerotriangulation was obtained using the VTOL WingtraOne system (Figure 4a), equipped with a Sony RX1R II camera. The aerial platform was equipped with a single-frequency GPS receiver, recording data at a frequency of 10 Hz. As part of the research analysis, the GNSS data recorded by an AsteRx-m2 UAS receiver placed on the Tailsitter unmanned platform was used. The Tailsitter platform is a type of VTOL aircraft.

The flight was carried out in the test area in August 2019. The imaging conditions were good. The selected test area was an airport located at the 21st Central Aviation Training Grounds. The entire test block consisted of 97 images in three rows, obtained from an altitude of 250 m above the ground. The flight was conducted in the east-west direction, assuming that the transverse and longitudinal coverage was 75%. In the test area, nine signaled control points were measured (Figure 4b) using the RTK technique in the GNSS system. The accuracy of determining the field coordinates of the control points was 0.03 m. In addition, in order to perform further verification of the results, a re-raid of the Wingtra platform was carried out with precise recording of the platform’s flight trajectory in the post-processing kinematic (PPK) mode.

2.3. Data Characteristics

For set I—Łagiewniki, the test block consisted of 34 strips (

Table 1. Characteristics of the test block in Łagiewniki.

Number of Strips	34
Camera/lens focal length [mm]	Sony a7R/36.34
Average longitudinal/transverse coverage [%]	75/75
Flight altitude [m]	250
Number of control points	4
Number of independent check points	18
a priori standard deviation of the control points and check points X, Y, Z [m]	0.03, 0.03, 0.03
Theoretical pixel size [m]	0.04

), which consisted of 811 images. The images were referenced to PUWG 2000PL zone V (Cartesian 2D coordinate system marked with the symbol “2000”, based on the ellipsoid GRS80 according to the Gauss–Krüger mapping theory [60].

For set II—Nadarzyce, test block I consisted of three strips made up of 97 images. The images were referenced to PUWG 2000PL zone VI. Block characteristics are presented in the table below (

Table 2. Characteristics of the test block in Nadarzyce.

Number of Rows	3
Camera/lens focal length [mm]	Sony RX1R II/35.0
Average longitudinal/transverse coverage [%]	75/75
Flight altitude [m]	250
Number of control points	4
Number of independent check points	5
a priori standard deviation of the control points and check points X, Y, Z [m]	0.03, 0.03, 0.03
Theoretical pixel size [m]	0.04

).

3. Methods

This chapter presents and describes the mathematical models which can be used for the adjustment of a single-strip block of UAV images. The block diagram of the adjustment process is shown in the figure below (Figure 5). It shows two methods of adjusting a test block. The common point of both methods is the first step, i.e., the adjustment of the entire block of images using Inpho UASMaster software. The second step is to develop a single-strip block of images using two methods, taking additional parameters into account.

Method I was based on the densification of the photogrammetric network with tie points generated during the adjustment of the entire block (step I). From among the tie points, a certain number of them had been selected based on the following criteria:

• One point on at least three images
• Points with the lowest mean square error (RMSE = minimum)
• Points evenly distributed within the area of development (linear regression method [61]).

Method II is the adjustment of the single-strip block of images using nonlinear optimization in MATLAB. In this case, the empirically modified Levenberg–Marquardt–Powell (LMP) method was used. A ready, generally available toolbox was used—the damped bundled adjustment toolbox (DBAT) [62], to which the input data file was implemented. The toolbox includes tools for developing various nonlinear optimization strategies [63,64]. For the bundle adjustment process, the DBAT toolbox with self-calibration was selected. In this toolbox, the fixed and weighted prior observations, control points and camera stations, and check points are all supported. The parameters to be estimated by the bundle are selectable at the parameter level, for individual camera parameters. Furthermore, the parameters can be block-invariant (the same for a whole block), image-variant (individual for each image), or anything in between. Multiple damping schemes may be used to avoid divergence due to poor initial values of the modified Levenberg–Marquardt–Powell [63].

3.1. Modified Linear Regression with Additional Parameters

Using the linear relationship between the data, a classic linear regression model was used to ensure an even distribution of tie points in the study area.

Due to the restricted access to the area, only a small number of control points were measured in the study area. Hence, for the purpose of this research, tie points generated through digital aerotriangulation of the entire block were used. The adjustment was performed in Inpho UASMaster software. These points were randomly distributed throughout the test area. To ensure an even distribution of the tie points in the study area, a linear regression method was used, based on a linear relationship in which the curve was fitted to the data, i.e., the coordinates of the tie points.

The linear regression model [61,65,66,67] used is defined by the following formula:

y_i=ax_i+b;i = 1, 2, …, n,

(1)

where a and b are the parameters of the line that had to be adapted to our data using the least-squares method [68,69,70,71]. Using the least-squares method, the best fit line can be found by minimizing the sum of the squares of the vertical distance from a data point to a point on the line [72].

The point selection criterion: one point on at least three images, points with the smallest errors, and points evenly distributed throughout the area of study.

To select the tie points, the least-squares method was used, thanks to which the line y = a₁x + b₁ (Figure 11a).

The parameters of the line defined by the equation y_i = ax_i + b were determined using the formulas:

$$a=\frac{n{{\displaystyle \sum }}_{i=1}^n{x}_i{y}_i-{{\displaystyle \sum }}_{i=1}^n{x}_i{{\displaystyle \sum }}_{i=1}^n{y}_i}{n{{\displaystyle \sum }}_{i=1}^n{x}_i^2-{\left({{\displaystyle \sum }}_{i=1}^n{x}_i\right)}^2}$$

(2)

$$b=\frac{{{\displaystyle \sum }}_{i=1}^n{y}_i{{\displaystyle \sum }}_{i=1}^n{x}_i^2-{{\displaystyle \sum }}_{i=1}^n{x}_i{{\displaystyle \sum }}_{i=1}^n{x}_i{y}_i}{n{{\displaystyle \sum }}_{i=1}^n{x}_i^2-{\left({{\displaystyle \sum }}_{i=1}^n{x}_i\right)}^2}=\frac{1}{n}({\displaystyle \sum }_{i=1}^n{y}_i-a{\displaystyle \sum }_{i=1}^n{x}_i),$$

(3)

where a and b are the determined linear coefficients; n is the number of tie points; and x_i and y_i are the coordinates of the tie point.

3.2. Modified Bundle Adjustment with Additional Parameters

This section describes the block adjustment with additional parameters methodology. Studies presented by Börlin et al. [63] and Lourakis et al. [73] served as the basis for writing this subsection.

3.2.1. Problem-Specific Damping

In the algorithm shown below (Figure 6), a trial point t_k is calculated and tested at each iteration. If t_k does not improve on the current point, it is rejected and another point is tried according to an algorithm-specific scheme. The quality of t_k is judged by the reduction of the objective function value. However, it is possible to add a problem-specific veto condition to disqualify “illegal” trial points. For the BA problem, an illegal trial point t_k may, for instance, violate the chirality constraint (each object point should be in front of each camera in which the object point was measured). The veto condition would be added to steps 4, 5, and 6 of algorithms 4, 5, and 6, respectively (Figure 6). Thus, in the case of the veto condition, the trial point will be accepted only when the value of the objective function is reduced and the trial point satisfies the veto condition. Importantly, for the veto addition to work, the initial values must satisfy the veto condition [63].

In this method, a combination of the camera model and the least-squares adjustment (LSA) algorithm is called a BA algorithm. The algorithm assumes fixed, known IO parameters and does not perform any outlier detection during the least-squares iterations. The choice of ∆₀ = ‖x₀‖ for the Levenberg–Marquardt–Powell method is based on the assumption that the initial values are correct to within one order of magnitude [63].

3.2.2. Non-Linear Optimization

In order to increase the accuracy of adjustment, non-linear optimization based on a function called the objective function was used.

The GN method may be modified to converge under a large set of circumstances [74]. The basic modification is to require that every value is “better” than the previous one. The logical choice is to at least require that the objective function must decrease so that

$$F\left(x_{k+1}\right)< F\left(x_{k }\right),$$

(4)

Algorithms satisfying the descent condition (4) are called descent methods.

The modifications to make GN a descent method are of two types, line search and trust-region [74]. The line search strategy uses the same linear model in

$$r\left(x_k + s\right)\approx r_{k } + {\mathrm{J}}_{k}s,$$

(5)

that was used to calculate s_k to decide when a new point is good enough. The trust-region approach works with the quadratic approximation in

$$min \frac{1}{2}||r_{k } + {\mathrm{J}}_{k}s{||}_w^2 = min \frac{1}{2}{\left(r_{k } + {\mathrm{J}}_k{s}_k\right)}^{T}W\left(r_{k } + {\mathrm{J}}_k{s}_k\right),$$

(6)

of the objective function for the same purpose. Both methods may be seen as attempts to avoid taking “too long” steps, since when the Jacobian $F\left(x_{k }\right)$ is ill-conditioned, the norm of the update can become arbitrarily large. The line search strategy is now considered; the trust-region is discussed in a later section on the Levenberg–Marquardt–Powell method.

3.2.3. The Levenberg–Marquardt–Powell Method (Trust-Region)

It is possible to interpret the LM method [75,76,77,78,79,80,81] geometrically as a trust-region method (Figure 7) [74]. In this interpretation, the method relies on the same quadratic model (6) as the GN method

$${\mathsf{\Phi }}_k\left(s_k\right)= \frac{1}{2}||r_{k } + {\mathrm{J}}_k{s}_k{||}_w^2 = \frac{1}{2}{r}_{k }W{r}_{k } + s_k^T{J}_k^T{\mathrm{Wr}}_k+\frac{1}{2}{s}_k^T{J}_k^T{\mathrm{WJ}}_k{\mathrm{s}}_k,$$

(7)

The quadratic model is trusted only within a region of trust $\Vert s_k\Vert \le {\Delta }_k$ around the current approximation x_k. Thus, at each iteration, we consider the constrained sub-problem

$$\begin{gathered} min\frac{1}{2}{r}_{k }W{r}_{k } + s_k^T{J}_k^T{\mathrm{Wr}}_k+\frac{1}{2}{s}_k^T{J}_k^T{\mathrm{WJ}}_k{\mathrm{s}}_k, \\ \mathrm{subject}\mathrm{to}\Vert s_k\Vert \le {\Delta }_k \end{gathered}$$

(8)

Mathematically, the solution of Problem (8) is given by

$$({\mathrm{J}}^T{\mathrm{WJ}}_k+{\lambda }_{k}I)\lambda s_k= - {\mathrm{J}}^{T}W{r}_k,$$

(9)

for some value of the Lagrange multiplier λ_k≥ 0. Indeed, Equation (9) may be seen as a way to solve the Problem (8).

3.2.4. Modified Powell Dogleg Method

Similarly to the LM algorithm, the Powell dogleg algorithm [82] for unconstrained minimization tries combinations of the Gauss–Newton and steepest descent directions [73]. In the case of DL, however, this is explicitly controlled via the use of a trust region. Trust region methods have been studied during the last few decades and have given rise to numerical algorithms that are reliable and robust, possessing strong convergence properties and being applicable even to ill-conditioned problems [83,84].

The method of Powell may be used to solve the problem (7) without any knowledge of the ${\lambda }_k$ value. The method is called dogleg due to the shape of the piecewise linear path used to approximate the ${\mathrm{s}}_{LM}\left(\lambda \right)$ curve. The dogleg path goes from the current point, via the Cauchy point ${\mathrm{s}}_{CP}$, to the GN search direction ${\mathrm{s}}_{GN}.$ The Cauchy point is defined as

$${\mathrm{s}}_{CP}=\frac{{\mathrm{g}}_k^T{\mathrm{g}}_k}{{\mathrm{g}}_k^T{\mathrm{J}}_k^T{\mathrm{WJ}}_k{\mathrm{g}}_k}\left(-{\mathrm{g}}_k\right),$$

(10)

where ${\mathrm{g}}_k = \nabla \left\{\backslash displaystyle \backslash nabla \right\} \mathrm{F} \left(x_k\right)={\mathrm{J}}_k^T{\mathrm{Wr}}_k$ is the minimizer of the quadratic model ${\mathsf{\Phi }}_k\left(s_k\right)$ in the direction of the negative gradient. Given the current value of ${\Delta }_k$, the dogleg point is found as the intersection of the dogleg path with the circle $\Vert s_k\Vert ={\Delta }_k$. If $\Vert s_k\Vert <{\Delta }_k$, the dogleg point is chosen as ${\mathrm{s}}_{GN}$. During the iterations, the trust region size ${\Delta }_k$ is adaptively modified based on how well the quadratic model predicts the reduction of the objective function. The gain ratio ρ between the actual and predicted reductions is defined as

$$\rho =\frac{F \left(x_k\right)-F \left(x_k+s_k\right)}{{\mathsf{\Phi }}_k\left(0\right)-{\mathsf{\Phi }}_k\left(s_k\right)},$$

(11)

If ρ is high enough, the step is accepted and the region size ∆ is increased. If ρ is too low, the step is discarded and the region size ∆ is decreased.

4. Experiments and Results

In this section, we present research experiments and the corresponding results obtained in the aerotriangulation process. The aerotriangulation process of the low altitude image block was performed in the Inpho UASMaster software. Tie points were generated automatically using Dense Image Matching algorithms [85]. After the adjustment, manual correction of the measured points in the images was made by the operator and points with the number of ties less than three were eliminated in order to increase the reliability of the network.

4.1. Set I—Łagiewniki

In the first step of the research, four main work areas were specified (Figure 8). Each of them consisted of a different test block: test block I–IV, each of which was then identified as separate study areas (Figure 9).

The basis for the entire processing was the initial part of the algorithm, i.e., the adjustment of the entire block, which consisted of 34 strips of imagery. The images were taken along the road section (approx. 2 km long). The four main work areas mentioned earlier are test block I, test block II, test block III, test block IV, (Figure 8), all within the area of development of the entire block. Each of these workspaces is a special case image block—a single strip block. Test block I, II, and IV consisted of images taken over straight sections of road about 300–450 m long. Test block III is a study area covering the section of the road on the curve (length about 350 m).

4.1.1. Step I

Test block 0

The bundle adjustment in Inpho UASMaster process starts with defining the internal orientation elements based on the results of the Sony a7R camera calibration. Four control points and 18 independent check points were identified in the study area. The tie points were generated automatically using a digital image correlation strategy based on the least-squares method. The results of the aerotriangulation are presented in

Table 3. Summary of blocks adjustment.

Description		Test Block 0	Test Block I	Test Block II	Test Block III	Test Block IV
			Variant I/Variant II	Variant I/Variant II	Variant I/Variant II	after 2 Stages
Weather Conditions		Scattered Cloud
Number of images		811	12	25	13	12
σ0 [μm]/[pix]		7.5/1.5	7.0/1.4 6.3/1.3	7.3/1.5 6.9/1.4	7.9/1.6 7.5/1.5	5.5/1.1
Number of GCPs		4	26/13	43/17	46/17	12
Number of check points		18	6	4	4	5
Number of tie points		51,092	1509/1545	2483/2604	2422/2450	1694
Average a priori error for GCPs and check points X, Y, Z [m]	X	0.03	0.03	0.03	0.03	0.03
	Y	0.03	0.03	0.03	0.03	0.03
	Z	0.03	0.03	0.03	0.03	0.03
Standard deviation X, Y, Z [m]	X	0.07	0.12/0.09	0.12/0.12	0.19/0.14	0.27
	Y	0.09	0.14/0.12	0.13/0.11	0.16/0.14	0.32
	Z	0.08	0.05/0.04	0.05/0.05	0.09/0.05	0.36
GCPs X, Y, Z [m] RMS	X	0.02	0.04/0.04	0.04/0.03	0.04/0.03	0.04
	Y	0.10	0.04/0.03	0.05/0.04	0.05/0.05	0.03
	Z	0.15	0.19/0.17	0.18/0.17	0.22/0.19	0.13
Check points X, Y, Z [m] RMS	X	0.06	0.05/0.02	0.05/0.03	0.04/0.02	0.07
	Y	0.04	0.03/0.01	0.08/0.05	0.08/0.02	0.09
	Z	0.15	0.22/0.09	0.16/0.09	0.14/0.10	0.12
MX0 [m]		0.11	0.13/0.12	0.12/0.09	0.09/0.09	0.08
MY0 [m]		0.13	0.11/0.09	0.10/0.08	0.11/0.08	0.09
MZ0 [m]		0.13	0.08/0.09	0.08/0.08	0.12/0.10	0.11
Mω [°]		0.034	0.054/0.043	0.047/0.042	0.056/0.054	0.083
Mφ [°]		0.026	0.046/0.036	0.040/0.040	0.066/0.046	0.085
Mκ [°]		0.006	0.011/0.009	0.009/0.009	0.014/0.008	0.021

.

As a result of adjusting the entire block, the average error of a typical observation was 7.5 µm (1.5 pixels). The mean square errors (calculated from the equalization corrections) for the X, Y, and Z coordinates of the control points were within the range of 0.02–0.15 m. As a result of the adjustment of the large block, good results were obtained in determining the coordinates of the centres of projection X₀, Y₀, Z₀. The values of standard deviations ranged from 0.07–0.10 m. However, the accuracy of determining the angular elements of the external orientation ω, φ, κ was between 0.006° and 0.034°. On the basis of the analysis of the adjusting results of the entire block, it was noticed that four control points in the study area gave satisfactory accuracy results. The mean square errors of the horizontal coordinates fluctuates on the level of a few cm. The height coordinates are affected by errors of several cm. The decrease in accuracy for the Z coordinates is due to the fact that some of the tie points were on the canopy of trees and shrubs.

4.1.2. Step II—I Method

Test block I

The first fundamental area of the study was the adjustment of a single-strip block, which consisted of 12 images. This area was included in the area of the entire block (test block 0). The adjustment was performed in two variants. The first variant is to adjust one strip by measuring 26 control points and six check points (Figure 10a). The control points were the points of the measured photogrammetric network, while the control points were selected from among the tie points generated during the adjustment of the entire block. The selection of control points in the first variant was made based on two criteria: one tie point on a minimum of three images and points with the lowest mean square errors. After automatic selection of the tie points, a visual selection was performed. Points located in characteristic places, clearly identifiable in the images, were selected for further study. The second variant (Figure 10b), is to adjust the same block as in the first variant, using the same six check points. 13 control points were selected based on an additional linear regression criterion (Figure 11b). The use of the linear relationship ensured the uniformity of the distribution of GCPs in the area of study, with particular emphasis on the edges. The process of adjusting a single-strip block is shown in the diagram below (Figure 12). The results of the adjustment are presented in Table 3.

As a result of the block adjustment in two variants, the mean error of a typical observation was 7.0 µm (1.4 pixels) for the first variant and 6.3 µm (1.3 pixels) for the second variant. The mean square errors for the X, Y, Z coordinates of the control points were within the range of 0.04–0.19 m for the first variant and 0.03–0.17 m for the second variant. For independent check points, the mean square errors were 0.03–0.22 m for the first variant and 0.01–0.09 m for the second variant. The values of standard deviations were within the range of 0.08–0.13 m for the first variant and 0.09–0.12 m for the second variant. However, the accuracy of determining the angular elements of the exterior orientation ω, φ, κ was from 0.011° to 0.054° for the first variant and 0.009°–0.043° for the second variant. Variant II provides better adjustment accuracy of a single-strip block. The mean square errors both at control points and independent check points are smaller by a few mm for variant II. Better accuracy was ensured by the optimal number of control points. 13 GCPs were necessary to obtain the correct geometry of a single-strip block of images. It was found that a large number of GCPs did not improve the adjustment results. Only reduction and even distribution of control points guarantee improved results. The results of the block adjustment in variant II improved the accuracy by an average of 28%.

Test block II

The second area of the study was a single-strip block consisting of 25 images. The block adjustment was also conducted in two variants. The first variant is the adjustment of one strip when measuring 43 control points and four check points (Figure 13a). Check points are points that are part of the photogrammetric control network, measured in the study area. Control points were selected based on tie points generated when adjusting the entire block. The criterion for selecting points from among the tie points: one point on at least three images, points with the smallest mean square errors (a method similar to test block I—variant I). The second variant is the adjustment of the same block, by measuring 17 control points and four check points (Figure 13b). The check points used are the same checkpoints as in the first variant. The control points were selected from the tie points based on an additional linear regression parameter. The results of the adjustment are presented in Table 3.

As a result of the block adjustment in two variants, the mean error of a typical observation was 7.3 µm (1.5 pixels) for the first variant and 6.9 µm (1.4 pixels) for the second variant. The mean square errors for the X, Y, Z coordinates of the control points were within the range of 0.04–0.18 m for the first variant and 0.03–0.17 m for the second variant. For independent check points, the mean square errors were 0.05–0.16 m for the first variant and 0.03–0.09 m for the second variant. The values of standard deviations were within the range of 0.08–0.12 m for the first variant and 0.08–0.09 m for the second variant. However, the accuracy of determining the angular elements of the exterior orientation ω, φ, κ was from 0.009° to 0.047° for the first variant and 0.009°–0.042° for the second variant. The results of the Test block II adjustment in two variants correspond to the results of the Test block I adjustment. It was noticed that variant II increased the adjusting accuracy by an average of 23%. Thus, it is confirmed that striving for an even distribution of GCPs in the developed areas is justified. Based on the analysis of the results of the research experiment, it can be noticed that the RMS values for the horizontal coordinates was only a few cm. The mean square errors Z, on the other hand, reach several cm. The obtained accuracy values result from the large leveling of the terrain in the test area.

Test block III

The next stage was the adjustment of a single-strip block (road curve), which consisted of 21 images. This area was within the area of the entire block. The adjustment was performed in two variants. The first is the adjustment of the single-strip by measuring 46 control points and four check points (Figure 14a). The selection of control points and check points was carried out based on the previously measured photogrammetric network and on the basis of the tie points generated during the adjustment of the entire block.

The criterion for selecting points from among the tie points: one point on at least three images, points with the smallest mean square errors.

The second variant is to adjust the single strip by measuring five control points and 31 check points (Figure 14b). The selection of control points and check points was carried out based on the previously measured photogrammetric network and on the basis of the tie points generated during the adjustment of the entire block. In order to filter the binding points, a method similar to that of test block I—variant II, was used. From the tie points, control points and check points were selected and the single-strip block was adjusted.

As a result of the block adjustment in two variants, the mean error of a typical observation was 7.9 µm (1.6 pixels) for the first variant and 7.5 µm (1.5 pixels) for the second variant. The mean square errors for the X, Y, Z coordinates of the control points were within the range of 0.04–0.22 m for the first variant and 0.03–0.19 m for the second variant. For independent check points, the mean square errors were 0.04–0.14 m for the first variant and 0.02–0.10 m for the second variant. The values of standard deviations were within the range of 0.09–0.12 m for the first variant and 0.08–0.11 m for the second variant. However, the accuracy of determining the angular elements of the exterior orientation ω, φ, κ was from 0.014° to 0.066° for the first variant and 0.008°–0.054° for the second variant. Variant I is block adjustment with 46 GCPs. The distribution of the control points was completely random, which translated into the results of the equalization. Variant II showed that ensuring the optimal number of GCPs turned out to be as important as ensuring their proper distribution in the test area. As a result of GCPs optimization satisfactory equalization results were obtained, where the mean square errors were a few cm for the horizontal coordinates and a dozen or so for the elevation coordinate. The accuracy of determining the linear elements of EO and the accuracy of determining the angles elements of EO turned out to be sufficient to ensure the correct geometry of the block. The results of the block adjustment in variant II improved the accuracy by an average of 27%.

An analysis of the results of the adjustment of blocks: test block I, test block II, test block III with filtered tie points showed that the second variant of the adjustment, which uses linear regression as an additional parameter in the selection of tie points, significantly improves the accuracy of the adjustment. For test block I, the accuracy increased on average by 28%, for test block II by 23% and for test block III by 27%. For further study, the tie point selection method was used according to the following three criteria:

• One point on minimum three images
• RMSE = minimum
• Linear regression

Test block IV

The fourth study area was focused on the adjustment of a block for an area with restricted access, where it is impossible to establish a photogrammetric network for the entire studied area. The selected test area is a single-strip block consisting of 13 images. The adjustment took place in two closely related stages. The first stage is the adjustment of the block with five control points on the edge of the study. In the second stage, the control points from the first stage were turned into check points, and the control points were selected from among the tie points from the development of the entire block (selection according to three criteria: one point on and minimum three images, RMSE = minimum, linear regression). To sum up, the second step is the adjustment of the test block with 16 control points and five check points (Figure 15). The results of the adjustment are presented in (Table 3).

The sequence of processes in the adjustment of a single-strip block in areas with restricted access is presented in the diagram below (Figure 16).

As a result of the two-step block adjustment, the following results were obtained: the mean error of the typical observation for stage I/stage II was 6.4 µm/5.5 µm, respectively. The mean square errors for the X, Y, Z coordinates of the control points were in the range 0.20–0.85 m/0.03–0.13 m. For independent check points, the mean square errors were 0.14–0.16 m/0.07–0.09 m. The values of standard deviations were within the range of 0.11–0.15 m/0.08–0.11 m. In contrast, the accuracy of determining the angular elements of the exterior orientation ω, φ, κ was 0.094–0.336°/0.021–0.085°. On the basis of the obtained results, it was noticed that the X, Y coordinates were affected by errors of a few cm. The highest values of the mean square errors for GCPs and check points occur for the Z coordinate. The mentioned dependence was noticed in the research experiment for test block 0, test block I, test block II, and test block III. One of the reasons for this regularity is the high leveling of the terrain in the studied area. The block alignment at 12 GCPs allowed to obtain accuracy on the level from a few to several cm for both the X, Y, Z coordinates. The summary of the adjustment results for the areas of study: test block 0, test block I, test block II, test block III, and test block IV is presented in the table below (Table 3).

4.1.3. Step II—Method II

This section presents the experimental use of the modified Levenberg–Marquardt–Powell algorithm for single-strip block adjustment. For this process, the same study area was selected as in test block IV (consisting of 13 images). A working project was set up, in which the initial parameters of the adjustment were defined. Next, two control points and three check points were manually measured on the images. Control points and check points located on the edge of the block were points of the photogrammetric network. The bundle adjustment was done in MATLAB. The self-calibrating DBAT toolbox was selected for this adjustment. The camera parameters, control points, and check points were input directly into the program. The same camera parameters were selected for the entire block. After auto-calibration, the bundle with damping using modified Levenberg–Marquardt–Powell was selected. The initial values for bundle adjustment:

• Start with initial values x₀ of the parameters and k₀ = 0 (a maximum number of iterations = 10)
• Select an initial value of ∆₀, such as ∆₀ = ‖x₀‖

The threshold values for ρ were selected on the basis of the adjustment results for several variants (0.10 < ρ < 0.90, 0.20 < ρ < 0.80, 0.25 < ρ < 0.75, 0.30 < ρ < 0.70, 0.35 < ρ < 0.65). The range which gave the best adjustment accuracy was selected.

The modified range for the gain ratio:

• If ρ < 0.30 (the prediction is bad)—the trust region size -> ∆ + 1 = ∆k/4
• If ρ > 0.70 (the prediction is fair)—the trust region size -> ∆k + 1 = ∆k
• If the prediction is good the trust region size -> ∆k + 1 = ∆4k.

The results of the adjustment are presented in

Table 4. Compare of bundle block adjustment—method II, method I.

Description		Method II—Test Block IV	Method I—Test Block IV
			after II Stages
Weather conditions		scattered cloud
Number of images		12	12
σ0 [μm]/[pix]		4.2/0.9	5.5/1.1
Number of GCPs		2	12
Number of check points		3	5
Number of tie points		1515	1694
Average a priori error for GCPs and check points X, Y, Z [m]	X	0.03	0.03
	Y	0.03	0.03
	Z	0.03	0.03
Standard deviation X, Y, Z [m]	X	0.21	0.27
	Y	0.18	0.32
	Z	0.20	0.36
GCPs X, Y, Z [m] RMS	X	0.03	0.04
	Y	0.03	0.03
	Z	0.04	0.13
Check points X, Y, Z [m] RMS	X	0.07	0.07
	Y	0.08	0.09
	Z	0.12	0.12
MX0 [m]		0.09	0.08
MY0 [m]		0.08	0.09
MZ0 [m]		0.11	0.11
Mω [°]		0.076	0.083
Mφ [°]		0.073	0.085
Mκ [°]		0.018	0.021

. To analyze the accuracy of the adjustment, the table summarizes the results of the adjustment using method I and II.

As a result of the test block IV adjustment using method II, the mean error of a typical observation σ₀ was at a level of 4.2 μm. The mean square error value for the X, Y, Z coordinates of the control points reached the value of 0.03–0.04 m. For independent check points, the mean square errors were 0.07–0.12 m. The values of standard deviations were within 0.18–0.21 m. Whereas the angular elements of the exterior orientation ω, φ, κ obtain values in the range from 0.018°–0.076°. The second adjustment method allowed to obtain the mean square error value for the X, Y, Z coordinates of the control points and the independent check points at the level of several cm. The accuracy of the determination of the linear elements of EO was from a few to several cm. The values of standard deviations for the angle elements of EO also allowed to obtain a good alignment accuracy.

For the adjustment using method II, the mean square errors decreased slightly. The results presented in the table below (

Table 5. Summary of the percentage accuracy of adjustment results—test block IV (method II).

Name of Test Area	Increase in Accuracy [%]
	σ0	GCPs			Check Points			Linear Elements of EO	Angles Elements of EO
		RMS X	RMS Y	RMS Z	RMS X	RMS Y	RMS Z	MX0, MY0, MZ0	Mω, Mφ, Mκ
test block IV	24	25	0	69	0	14	0	3	12

) represent the relative percentage change in accuracy in relation to the results of block adjustment conducted using method I. When considering the increase of the adjustment accuracy, the assessment of the error value σ₀, the determination of terrain coordinates for control points and independent check points, as well as elements of exterior orientation, were taken into account. Based on the results of the adjustment, a slight increase in accuracy in the second method was noticed—an average increase in accuracy by 16%.

4.1.4. A Statistical Significance Test of Results—Data Set I

In order to confirm the reliability of the obtained results of the block adjustment using two methods, a statistical analysis of the results was performed. For this purpose, confidence intervals with a probability of 95% [86] were determined for the obtained mean square errors of the X, Y, Z coordinates of the control points and check points. The confidence interval was determined for the mean of the population with a normal distribution N(m, σ). The confidence interval for the m parameter of this distribution was calculated from the formula:

$$P(\overline{X} –t_{\alpha ,n-1}\frac{S\left(x\right)}{\sqrt{n - 1 }} < m <\overline{X}+t_{\alpha ,n-1}\left(\frac{S\left(x\right)}{\sqrt{n - 1 }}\right) =1 – \alpha$$

(12)

where: n is the size of the random sample, $\overline{X}$ is the mean of the random sample, S is the standard deviation of the sample, $t_{\alpha }$ is the Student’s t-distribution with n − 1 degrees of freedom.

For the first method, based on the modified linear regression method, the GCPs X RMSE confidence interval was calculated with the number of trials n = 12. It was calculated that the confidence interval was within the limits: 0.04 < m < 0.07. For the Y coordinate, with the same number of trials, the confidence interval was 0.03 < m < 0.06. For the Z coordinate, the confidence interval is 0.09 < m < 0.13. Confidence intervals were also calculated for the X, Y, Z RMSE check points with the number of trials n = 8. It was calculated that the confidence interval for RMSE X was within the limits: 0.04 < m < 0.08. For the Y coordinate, with the same number of trials, the confidence interval was 0.02 < m < 0.12. For the Z coordinate, the confidence interval is 0.09 < m < 0.15. The common rule in photogrammetry confirms that the mean square errors for the Z coordinate are greater than for the horizontal X, Y coordinates. Additionally, the RMSE values for the control points are lower than for the check points.

For the second method, based on the modified Levenberg–Marquardt–Powell algorithm, the RMSE confidence interval was calculated for the X coordinates of the control points with the number of trials n = 2. It was calculated that the confidence interval was within the limits −0.10 < m < 0.15. For the Y coordinate, with the same number of trials, the confidence interval was −0.09 < m < 0.16. For the Z coordinate, the confidence interval is −0.21 < m < 0.29. Confidence intervals were also calculated for the check points X, Y, Z RMSE with the number of trials n = 3. It was calculated that the confidence interval for RMSE X was within the limits: 0.04 < m < 0.10. For the Y coordinate, with the same number of trials, the confidence interval was 0.02 < m < 0.14. For the Z coordinate, the confidence interval is 0.11 < m < 0.15. Similarly to the first method, the second method also confirms the common rule that the mean square errors for the Z coordinate are greater than for the horizontal X, Y coordinates. The confidence intervals for the RMSE values of the control points are greater than for the check points. This is due to the fact that there are fewer trials for the control points.

4.2. Set II—Nadarzyce

Processing of the second data set was divided into two main areas: test block I and test block II (Figure 17). The basis for the study was the first area, i.e., the entire block (Figure 18).

The first area was the entire test block, which consisted of three strips of imagery, with evenly distributed control points. The second working area is a single-strip block with an incomplete photogrammetric network, located on the edge of the study.

4.2.1. Step I

Test Block I

The first study area was processed using UASMaster software. The bundle adjustment process began by defining the interior orientation elements based on the results of the Sony RX1R II camera calibration. Four control points and five independent check points were identified in the study area. The tie points were generated automatically using a digital image correlation strategy based on the least-squares method. The results of the aerotriangulation are summarized in

Table 6. Summary of blocks adjustment.

Description		Test Block I	Test Block II
			After Stage II
Weather conditions		scattered clouds
Number of images		97	22
σ0 [μm]/[pix]		3.6/0.8	3.8/0.9
Number of GCPs		4	16
Number of check points		5	5
Number of tie points		2231	1199
Average a priori error for GCPs and check points X, Y, Z [m]	X	0.03	0.03
	Y	0.03	0.03
	Z	0.03	0.03
Standard deviation X, Y, Z [m]	X	0.09	0.62
	Y	0.08	0.07
	Z	0.26	0.10
GCPs X, Y, Z [m] RMS	X	0.15	0.08
	Y	0.10	0.08
	Z	0.15	0.09
Check points X, Y, Z [m] RMS	X	0.17	0.08
	Y	0.19	0.09
	Z	0.16	0.10
MX0 [m]		0.09	0.10
MY0 [m]		0.08	0.10
MZ0 [m]		0.11	0.13
Mω [°]		0.076	0.051
Mφ [°]		0.073	0.043
Mκ [°]		0.018	0.026

.

As a result of adjusting the entire block, the mean error of a typical observation was 3.6 µm (0.8 pixels). The mean square errors (calculated from the equalization corrections) for the X, Y, and Z coordinates of the control points were within the range of 0.10–0.15 m. For the independent check points, the mean square errors were 0.17–0.19 m. The values of standard deviations were within the range of 0.11–0.13 m. Whereas the accuracy of determining the angular elements of the exterior orientation ω, φ, κ was from 0.018° to 0.051°. Adjustment of a block consisting of three strips performed at four control points allowed to obtain mean square errors for the X, Y, Z of the control points and the independent check points at the level of several centimeters. No significant deterioration of the accuracy for the horizontal coordinates and the Z coordinate was noticed. The studied area covered the airport area, where the ground leveling was a few cm maximum. The values of standard deviations of the coordinates of the linear elements of EO are several cm. The accuracy of the angle elements of EO proves good block geometry. The highest value of the standard deviation of angle elements of EO was obtained for the kappa angle.

4.2.2. Step II—Method I

Test Block II

The processing of the second study area was carried out in two stages. The first stage included the adjustment of the block using five control points on the edge of the study. Stage II is the adjustment of the test block with 16 control points and five check points. At this stage, the control points were selected from the tie points generated during the test block I adjustment. The criterion from the first method of adjusting the image block was used: one point on a minimum three images, RMSE = minimum, linear regression. The sequence of processes in the adjustment of a single-strip block with a small number of points of the photogrammetric network is shown in the diagram (Figure 16). The final distribution of the control points and check points is presented below (Figure 19).

As a result of the two-stage block adjustment, the following results were obtained: the mean error of a typical observation for stage I/stage II was 3.9 µm/3.8 µm, respectively. The mean square errors for the X, Y, Z coordinates of the control points were at in the range of 0.56–0.92 m/0.08–0.09 m. For the independent check points, the mean square errors were 0.11–0.18 m/0.08–0.10 m. The values of standard deviations ranged from 0.11–0.14 m/0.10–0.13 m. However, the accuracy of determining the angular elements of the exterior orientation ω, φ, κ was 0.061–0.144°/0.026–051°. The analysis of the results of the adjustment of a single-strip block confirms the need to select the appropriate number of GCPs (16) and, above all, to ensure their proper distribution, with particular emphasis on the edge of the block. A summary of the adjustment results for the study areas: test block I and test block II is presented in the table below (Table 6).

4.2.3. Step II—Method II

This section presents the experimental use of the modified Levenberg–Marquardt–Powell algorithm for single-strip block adjustment. The same study area was selected for this research as in test block II (consisting of 22 images). A working project was set up, in which the initial parameters of the adjustment were defined. Next, two control points and three check points were manually measured on the images. Control points and check points located on the edge of the block were points of the photogrammetric network. The bundle adjustment was done in MATLAB. The self-calibrating DBAT toolbox was selected for this adjustment. The camera parameters, control points, and check points were input directly into the program. The same camera parameters were selected for the entire block. After auto-calibration, the bundle with damping using modified Levenberg–Marquardt–Powell was selected. The initial values for bundle adjustment:

• Start with initial values x₀ of the parameters and k₀ = 0 (a maximum number of iterations = 10)
• Select an initial value of ∆₀, such as ∆₀ = ‖x₀‖

The threshold values for ρ were selected on the basis of the equalization results for several variants (0.10 < ρ < 0.90, 0.20 < ρ < 0.80, 0.25 < ρ < 0.75, 0.30 < ρ < 0.70, 0.35 < ρ < 0.65). The range which gave the best adjustment accuracy was selected.

The modified range for the gain ratio:

• If ρ < 0.30 (the prediction is bad)—the trust region size -> ∆_k+1 = ∆_k/4
• If ρ > 0.70 (the prediction is fair)—the trust region size -> ∆_k+1 = ∆_k

If the prediction is good the trust region size -> ∆_k+1 = ∆4_k.

The results of the adjustment are presented in

Table 7. Comparison of bundle block adjustment—method II, method I.

Description		MethodII—Test Block II	Method I—Test Block II
			after Stage II
Weather conditions		scattered clouds
Number of images		22	22
σ0 [μm]/[pix]		3.0/0.6	3.8/0.9
Number of GCPs		2	16
Number of check points		4	5
Number of tie points		2218	1199
Average a priori error for GCPs and check points X, Y, Z [m]	X	0.03	0.03
	Y	0.03	0.03
	Z	0.03	0.03
Standard deviation X, Y, Z [m]	X	0.12	0.03
	Y	0.14	0.03
	Z	0.13	0.03
GCPs X, Y, Z [m] RMS	X	0.06	0.62
	Y	0.07	0.07
	Z	0.07	0.10
Check points X, Y, Z [m] RMS	X	0.07	0.08
	Y	0.08	0.08
	Z	0.09	0.09
MX0 [m]		0.09	0.10
MY0 [m]	0.09	0.10
MZ0 [m]		0.12	0.13
Mω [°]		0.044	0.051
Mφ [°]		0.038	0.043
Mκ [°]		0.024	0.026

. To analyze the accuracy of the adjustment, the table presents the results of the adjustment methods I and II.

As a result of performing the adjustment of test block II using method II, the mean error of a typical observation σ₀ was at a level of 3.2 μm. The mean square error value for the X, Y, Z coordinates of the control points reached the value of 0.06–0.07 m. For independent check points, the mean square errors were 0.07–0.09 m. The values of standard deviations were within 0.09–0.12 m. Whereas the angular elements of the exterior orientation ω, φ, κ obtain values in the range from 0.024°–0.044°. The second adjustment method allowed to obtain the mean square error value for the X, Y, Z coordinates of the control points and the independent check points at the level of several cm. No significant deterioration of the accuracy for the Z coordinate was noticed. The accuracy of the linear elements of EO was determined at the level from a few to several cm. The LMP method provided low values of standard deviation for angles elements of EO.

For the adjustment in which method II was used, the mean square errors decreased slightly. The results presented in the table below (

Table 8. Summary of the percentage accuracy of adjustment results—test block II (method II).

Name of Test Area	Increase in Accuracy [%]
	σ0	GCPs			Check Points			Linear Elements of EO	Angles Elements of EO
		RMS X	RMS Y	RMS Z	RMS X	RMS Y	RMS Z	MX0, MY0, MZ0	Mω, Mφ, Mκ
Test block II	21	25	12	22	12	20	11	9	11

) represent the relative percentage change in accuracy in relation to the results of the block adjustment using method I. When considering the increase of the adjustment accuracy, the assessment of the error value σ_0, the determination of terrain coordinates for control points and independent check points, as well as elements of exterior orientation, were taken into account. Based on the results of the adjustment, a slight increase in accuracy in the second method was noticed—an average increase in accuracy by 13%.

4.2.4. A Statistical Significance Test of Results—Data Set II

The statistical analysis of the equalization results was also performed for the second data set. Confidence intervals of 95% [86] were determined for the obtained mean square errors of the X, Y, Z coordinates of the control points and check points. The confidence interval was determined for the mean of the population with a normal distribution N (m, σ) based on formula (14).

For the first method, based on the modified linear regression method, the GCPs X RMSE confidence interval was calculated with the number of trials n = 12 (the number of trials is the same as the number of control points). It was calculated that the confidence interval was within the limits: 0.05 < m < 0.11. This means that the RMSE mean value is within the calculated range with a probability of 95%. For the Y coordinate, with the same number of trials, the confidence interval was 0.05 < m < 0.11. For the Z coordinate, the confidence interval is 0.06 < m < 0.13. Confidence intervals were also calculated for the X, Y, Z RMSE check points with the number of trials n = 8. It was calculated that the confidence interval for RMSE X was within the limits: 0.04 < m < 0.12. For the Y coordinate, with the same number of trials, the confidence interval was 0.05 < m < 0.14. For the Z coordinate, the confidence interval is 0.05 < m < 0.14. The common rule in photogrammetry confirms that the mean square errors for the Z coordinate are greater than for the horizontal X, Y coordinates. Additionally, the RMSE values for the control points are lower than for the check points.

For the second method based on the modified Levenberg–Marquardt–Powell algorithm, the confidence interval of GCPs X RMSE was determined with the number of trials n = 2. It was calculated that the confidence interval was within the limits: −0.07 < m < 0.19. For the Y coordinate, with the same number of trials, the confidence interval was −0.06 < m < 0.20. For the Z coordinate, the confidence interval is −0.18 < m < 0.32. Confidence intervals were also calculated for the X, Y, Z RMSE check points with the number of trials n = 3. It was calculated that the confidence interval for RMSE X was within the limits: 0.04 < m < 0.10. For the Y coordinate, with the same number of trials, the confidence interval was 0.02 < m < 0.10. For the Z coordinate, the confidence interval is 0.01 < m < 0.13. In method II, one can also observe the regularity that the mean square errors for the Z coordinate are greater than for the horizontal X, Y coordinates. The greater confidence interval for the RMSE value of the control points is due to a smaller number of trials than in the case of the control point analysis.

4.2.5. Comparison of the Results of BBA using LMP Algorithm and with Precision Positioning Trajectory of UAV

The results of the BBA of a single-strip block from the Set II—Nadarzyce research area, were compared with the results of a research experiment using precision positioning technology using post-processing kinematic (PPK). The exact coordinates of the UAV platform linear elements of EO were determined. The results are shown in the table below (

Table 9. Comparison of bundle block adjustment—LMP, PPK.

Description		LMP—Test Block II	PPK—Test Block II
Weather conditions		scattered clouds
Number of images		22	22
σ0 [μm]/[pix]		3.0/0.6	2.0/0.4
Number of GCPs		2	2
Number of check points		4	4
Number of tie points		2218	8346
Average a priori error for GCPs and check points X, Y, Z [m]	X	0.03	0.03
	Y	0.03	0.03
	Z	0.03	0.03
Standard deviation X, Y, Z [m]	X	0.12	0.04
	Y	0.14	0.05
	Z	0.13	0.05
GCPs X, Y, Z [m] RMS	X	0.06	0.04
	Y	0.07	0.04
	Z	0.07	0.05
Check points X, Y, Z [m] RMS	X	0.07	0.04
	Y	0.08	0.04
	Z	0.09	0.05
MX0 [m]		0.09	0.04
MY0 [m]		0.09	0.03
MZ0 [m]		0.12	0.05
Mω [°]		0.044	0.008
Mφ [°]		0.038	0.010
Mκ [°]		0.024	0.005

).

An additional research experiment gave the following results: the mean error of a typical observation was 2.0 µm, respectively. The mean square errors for the X, Y, Z coordinates of the control points were at in the range of 0.04–0.05 m. For the independent check points, the mean square errors were 0.04–0.05 m. The values of standard deviations ranged from 0.03–0.05 m. However, the accuracy of determining the angular elements of the exterior orientation ω, φ, κ was 0.008–0.010°. Based on the analysis of the results, it was found that the accuracy of the single-strip BBA using precision positioning technology increased by 40%. A significant increase in accuracy has been observed for the linear elements of EO (60%) and angles elements of EO φ, ω, κ (70%).

5. Discussion

This article presents the methodology for processing a single-strip block of images of highway landing strips obtained from low altitudes. The study area was a restricted area, so the photogrammetric network covered only a small part of it. This article presents two methods of processing a single-strip block. The first method met the iron rule of ensuring an even distribution of GCPs and check points in the study area [31,32,33]. Because a special case of block adjustment was considered—the one-strip block, attention was also paid to ensuring that the block edges had both control points and check points [39,86]. The proposed first method of adjustment, based on the selection of tie points according to selected criteria, significantly improved the accuracy of aerotriangulation for the data set I. The mean error value of a typical observation σ₀ decreased by 0.90 μm. RMSE for the control points decreased by 0.17 m on average, and by 0.13 m for check points. However, the accuracy of determining the angular elements of the exterior orientation ω, φ, κ increased by an average of 0.176°. For the second data set, the use of the first method also increased the accuracy of the block adjustment. The value of σ₀ decreased by 0.10 μm. The RMSE for control points decreased on average by 0.06 m, for control points by 0.02 m. On the other hand, the accuracy of determining the angular elements of the external orientation ω, φ, κ increased by an average of 0.080°. Similar results were obtained in the research of Casella et al. [86], where the authors present bundle adjustment in three different configurations of GCPs and check points, using five different types of software. The use of additional adjustment parameters improves the adjustment results. Similar conclusions are presented in the article by Rango et al. [87].

Within the photogrammetric community, ref. [88] compared the undamped GM method with the LM method on the spatial resection problem. On the BA problem, Börlin et al. [89] suggested the GNA algorithm and compared it to the GM method on a problem with two cameras. The conclusion was that the GNA method reduced the number of convergence failures compared to GM at an insignificant extra computational cost. Later, ref. [73] applied the LM and LMP (called DL) algorithms on the BA problem and concluded that LMP was faster than LM.

The second method of single-strip block adjustment using the modified Levenberg–Marquardt–Powell algorithm allowed for a slight increase in the adjustment accuracy. For data set I—Łagiewniki, the mean error of a typical observation σ₀ decreased by 1.30 μm. The RMSE for control points and check points was not improved. However, the accuracy of determining the angular elements of the exterior orientation ω, φ, κ increased by an average of 0.007°. For the second data set, the value of σ₀ decreased by 0.80 μm. The RMSE for the control points decreased by 0.02 m on average, and by 0.01 m for check points. However, the accuracy of determining the angular elements of the exterior orientation ω, φ, κ increased by 0.005°.

The legitimacy of using the LMP algorithm for bundle adjustment has already been confirmed [63,73].

The obtained test results prove the universality of the presented approach for the adjustment of a single-strip block with a limited number of control points in areas with restricted access. The presented research shows the validity of using both the modified linear regression method and the empirically modified Levenberg–Marquardt–Powell method for block compensation. The linear regression method ensures an even distribution of control points in the study area, with particular emphasis on the outer edges of the images. The limitation of this method may be the lengthy and complex filtering process of the tie points. The modified LMP method does not ensure an even distribution of the GCPs.

The approach proposed by the authors may be a new direction in the orientation of low altitude imagery from low-cost UAVs. The presented approach based on the modified Levenberg–Marquardt–Powell algorithm made it possible to increase the accuracy of the adjustment regardless of the input data (two different UAV systems were used), which proves the universality of the proposed methodology. Ongoing research also revealed some imperfections in the orientation of single-strip blocks, suggesting the need to develop a new approach to facilitate a more reliable assessment. Compared to the traditional bundle adjustment method, the BA with Levenberg–Marquardt–Powell process allows for a noticeable increase in the accuracy of determining the coordinates of projection centers with low accuracy GNSS and with a limited number of GCPs.

The developed method of adjustment of single-strip block does not reduce the accuracy in relation to the latest methods with precise registration of flight trajectory. This method is recommended for the orientation of images obtained by low-cost UAVs because the single-frequency GNSS receivers installed onboard them will not allow for more accurate registration of the linear elements of exterior orientation. Low-cost UAVs are also particularly sensitive to wind, and in this case, the negative impact of the rotation angles will be significant. The conducted research also showed that the proposed method can use the advantages of the on-board GNSS/IMU receiver with the additional condition of using an optimized method of selecting tie points at the adjustment stage. This results in an improved processing method that reduces the values of the final processing errors.

A limitation of the presented method is that it may not improve the accuracy of adjustment on blocks consisting of images with irregular geometry (e.g., high tilt angles for the images—above 6°) or blocks with asymmetric coverage between images—below 70%. In addition, for blocks with images of an irregular shape or atypical distribution of GCPs, the use of the developed methodology may even cause a decrease in accuracy

6. Conclusions

The article presents the results of experiments and analyses concerning the adjustment of a single-strip block. The main objective of the research was to develop a methodology of adjusting single-strip blocks of low altitude imagery of highway landing strips, taking into account the limited access to the entire study area. The research was based on two methods. The first one, presenting a proprietary approach to the use of tie points in the adjustment process, was based on a modified linear regression method. The second method was based on a linear optimization method—the modified Levenberg–Marquardt–Powell algorithm. Based on the conducted analyses, it was found that the use of both methods to adjust a single-strip block improve adjustment results. It was noticed that the RMSE error values for the X, Y coordinates were smaller than for the Z coordinates, which confirms the common rule in photogrammetry. It was also noticed that an even distribution of GCPs significantly improves the accuracy of the adjustment (on average by 50%). Locating the GCPs on the edge of the block improves the accuracy for the angular elements of the exterior orientation ω, φ, κ (on average by 25%). Based on the comparative analysis of the first and second methods, it was found that the second method improved the accuracy of the adjustment by 16% for the flight carried out in Łagiewniki and by 13% for the mission carried out in Nadarzyce.

In the future, research is planned on the methodology of developing landing approach maps based on data obtained from UAVs.