A Model-Based Volume Estimator that Accounts for Both Land Cover Misclassification and Model Prediction Uncertainty
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. Spanish National Forest Inventory (SNFI)
2.2.2. Multispectral and Auxiliary Data
2.2.3. Airborne Laser Scanning (ALS) Data
2.3. Statistical Techniques
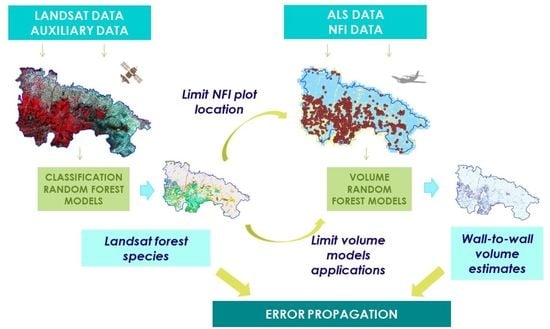
2.3.1. Overview
2.3.2. Random Forests (RF)
2.3.3. Model-Based (MB) Estimation
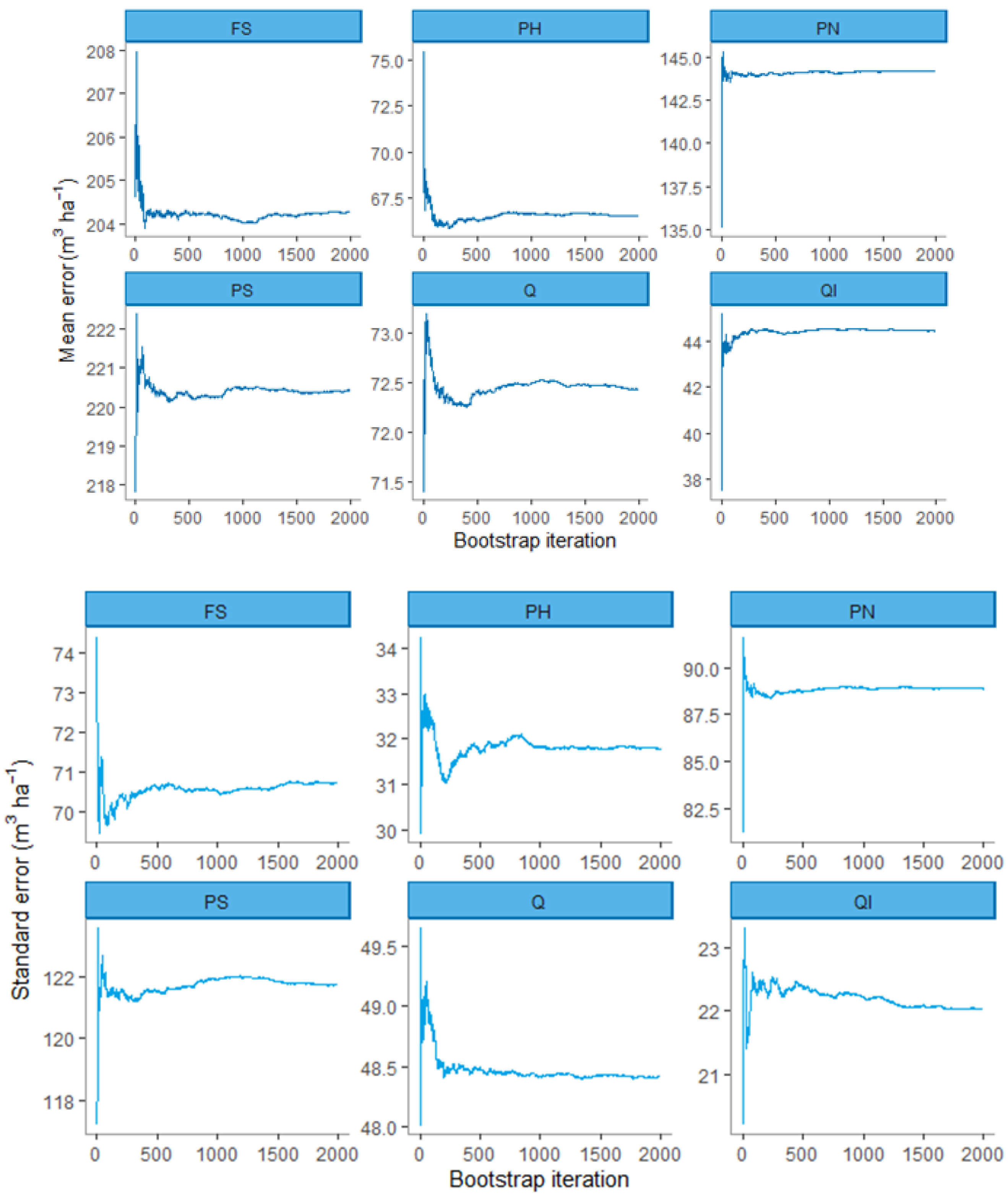
2.3.4. Bootstrapping
2.4. Analyses
2.4.1. Overview
2.4.2. The Forest Species Map and the Effects of Its Uncertainty on Area Estimates
- (1)
- A pairs bootstrap resample was selected from the training data used to calibrate the RF classification model,
- (2)
- A new Landsat forest species map was constructed by applying a new RF classification model based on the resample from step (1),
- (3)
- The area for each of the dominant forest species, k, for each bootstrap iteration, b, was estimated as the product of the number of pixels classified as the species and the pixel area and was denoted where the subscript “p” indicates that pairs bootstrapping was used,
- (4)
- Steps (1)–(3) were replicated 2000 times,
- (5)
- The MB estimates of species-specific areas and their SEs were estimated as,andwhere the subscript “map” indicates that only the uncertainty in the Landsat forest species map was incorporated into Equation (3), and the subscript “b” indexes the bootstrap resamples.
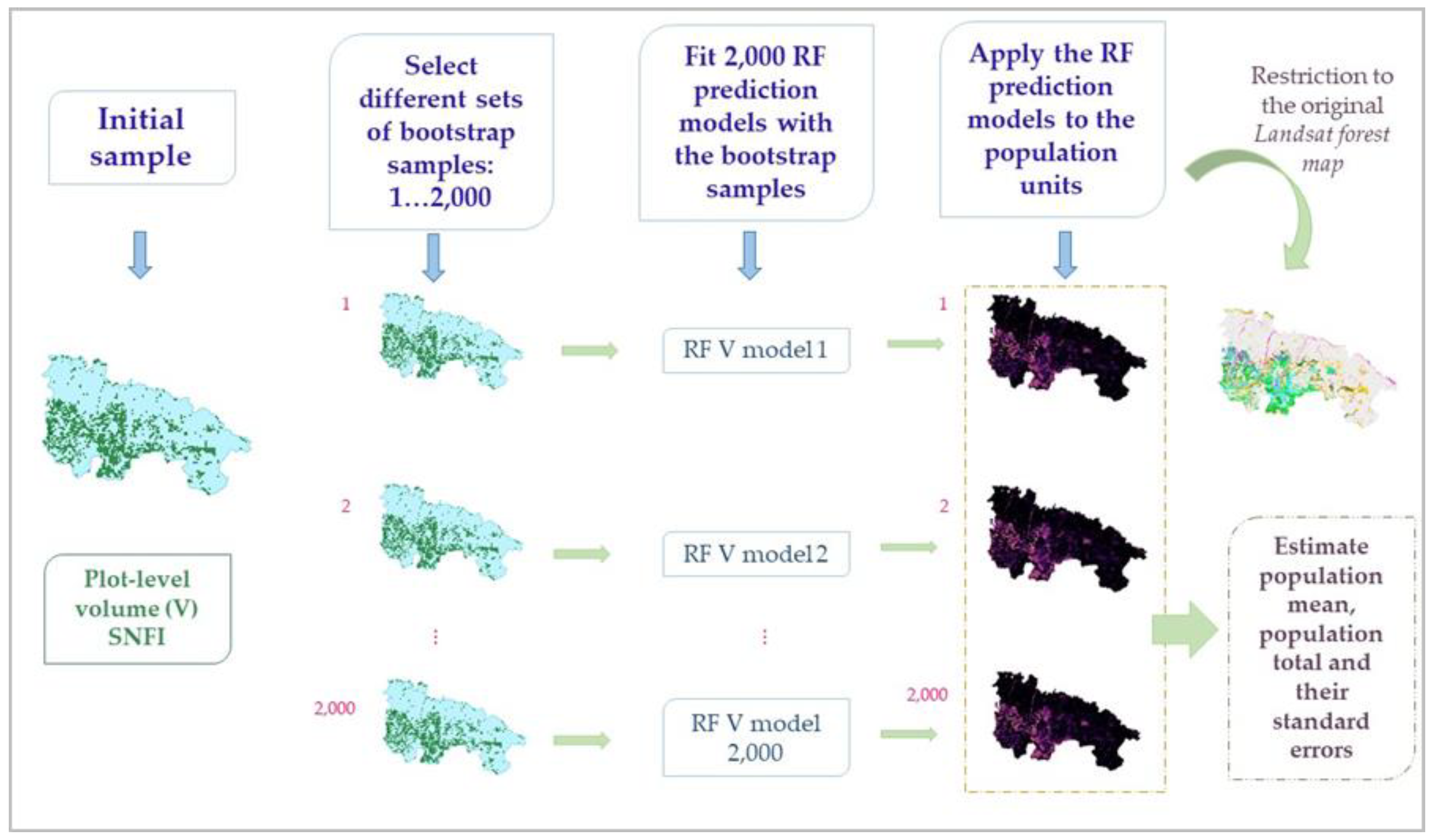
2.4.3. The Effects of Sampling Variability in the Volume Model Calibration Data on Volume Estimates
- (1)
- Select a wild bootstrap resample from the SNFI field plot dataset subject to the two previously noted constraints,
- (2)
- Calibrate the species-specific RF V models,
- (3)
- For each species, k, predict V for all population units classified as that species in the original Landsat forest species map,
- (4)
- Estimate mean species-specific V as using Equation (1) and total V, , as the product of the estimates of mean V and the area, , from the original Landsat forest species map,where the subscript “w” indicates that wild bootstrapping was used.
- (5)
- Repeat steps (1)–(4) 2000 times,
- (6)
- Estimate species-specific mean V and its SE as,with
- (7)
- Estimate species-specific total V and its SE as,withwhere the subscript “plot” indicates that only the effects of sampling variability in the RF model calibration dataset are incorporated into Equations (6) and (8).
2.4.4. The Effects of Uncertainty in the Forest Species Map on Volume Estimates
- (1)
- Select a pairs bootstrap resample of the training areas used to calibrate the RF classification model,
- (2)
- Construct a new Landsat forest species map and for each species, k, estimate the area, . The oob error estimation for each RF classification model, recalibrated in each bootstrap iteration with the resample from step (1), was recorded to estimate the average user’s and producer’s accuracy for each of the classified forest species and to estimate the standard error of the user’s and producer’s accuracy,
- (3)
- Select the subset of the SNFI field plot dataset located in the forest portion of the new Landsat forest species map,
- (4)
- Construct new species-specific RF V prediction models using data for that species determined from the plot data, not the map species classification for plot,
- (5)
- For each species, apply the model constructed in (4) to each pixel classified as that species in the map constructed in step (2),
- (6)
- For each species, k, estimate mean V for each bootstrap iteration, b, as using Equation (1) and total V, , as the product of the estimates of mean V and the area from step (2):
- (7)
- Replicate steps (1)–(6) 2000 times,
- (8)
- Estimate species-specific mean V and its SE as,with
- (9)
- Estimate species-specific total V and its SE as,withwhere the subscript “map” indicates that only the effects of uncertainty in the Landsat forest species map were incorporated into Equations (11) and (13).
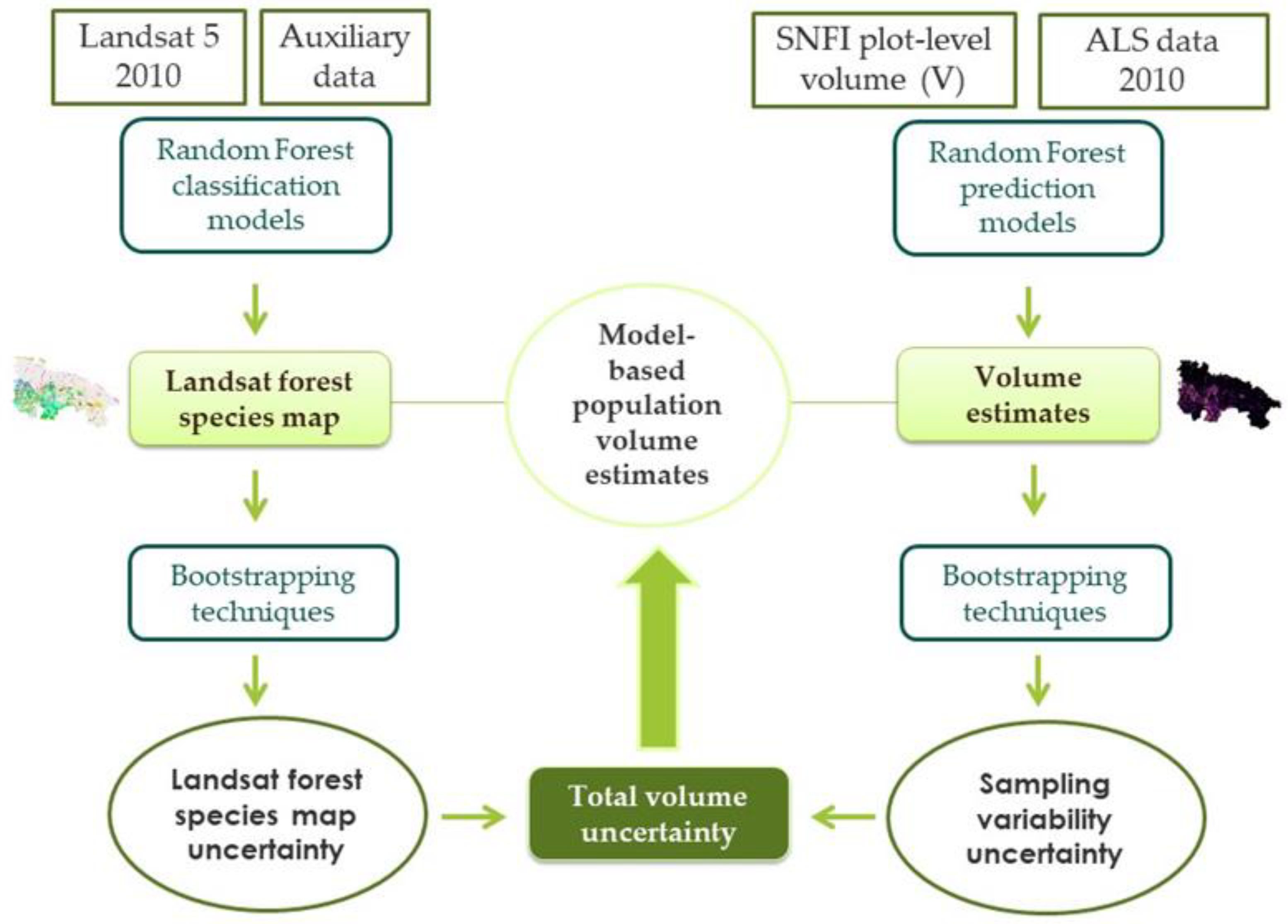
2.4.5. Total Uncertainty
3. Results
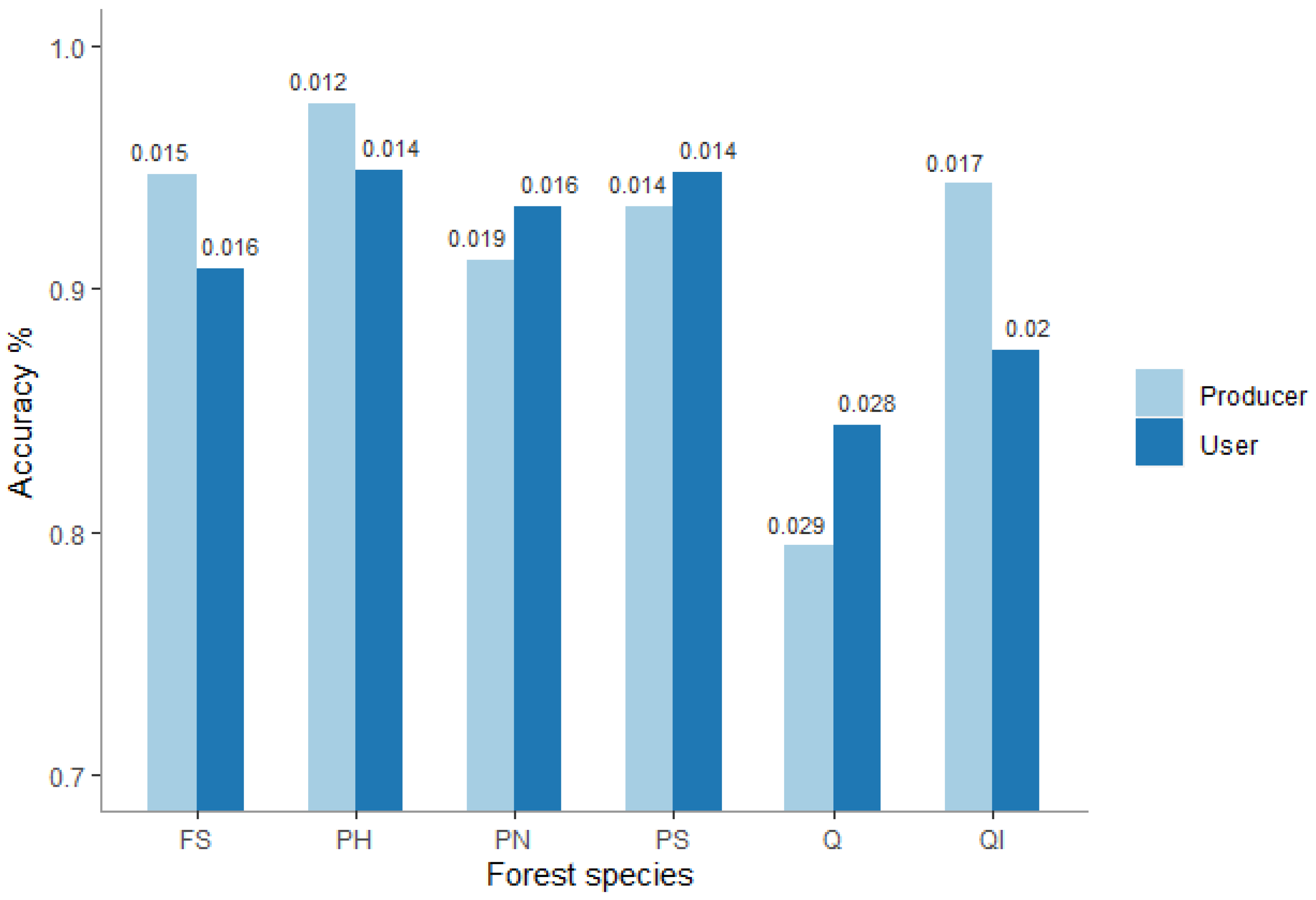
3.1. Accuracy Assessment
3.1.1. Forest Species Map Accuracy
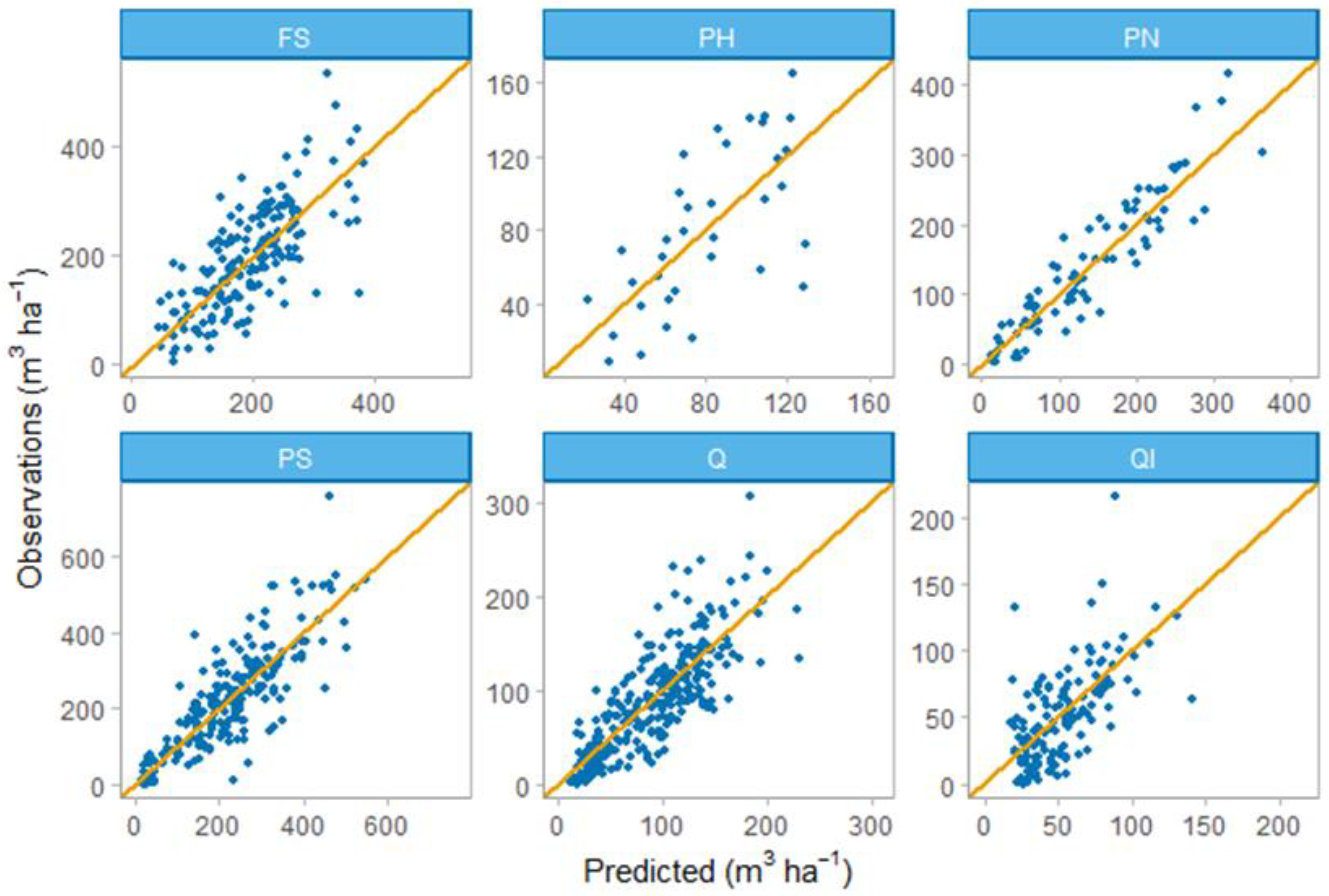
3.1.2. RF Volume Models
3.2. Uncertainty Assessment
3.2.1. The Effects of Uncertainty in the Landsat Forest Species Map on Area Estimates
3.2.2. The Effects of Uncertainty in the Landsat Forest Species Map on Volume Estimates
3.2.3. The Effects of Sampling Variability in the Model Calibration Dataset on Volume Estimates
3.3. Total Uncertainty
4. Discussion
4.1. The Statistical Techniques
4.2. Effects of Uncertainty in the Landsat Forest Species Map
4.3. Effects of Sampling Variability for the Model Calibration Datas
4.4. Total Uncertainty
4.5. Operational Consequences
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Full Description |
| ALS | Airborne laser scanning |
| crr | ALS canopy relief ratio |
| cv | ALS height coefficient of variation |
| DBH | Diameter at breast height |
| FS | Fagus sylvatica |
| IPCC | Intergovernmental Panel on Climate Change |
| iq | ALS height interquartile range |
| kurto | ALS height kurtosis |
| lfcc | Forest canopy cover |
| MB | Model-based |
| MSE | Mean square error |
| NBR | Normalized Burn Ratio |
| NDMI | Normalized Difference Moisture Index |
| NDVI | Normalized Difference Vegetation Index |
| NFI | National Forest Inventory |
| NIR | Near infrared |
| OB | Other broadleaves |
| OC | Other coniferous |
| oob | Out-of-bag |
| p1-p99 | ALS percentiles (ranging from the 1st to 99th percentile) |
| PH | Pinus halepensis |
| PN | Pinus nigra |
| PS | Pinus sylvestris |
| Q | Quercus faginea or Quercus pyrenaica |
| QI | Quercus ilex |
| RF | Random forest |
| RMSE | Root mean square error |
| rRMSE | Relative root mean square error |
| RS | Remote sensing |
| SE | Standard error |
| SNFI | Spanish National Forest Inventory |
| SNFM | Spanish National Forest Map |
| stdev | ALS height standard deviation |
| TM | Thematic Mapper |
| V | Mean volume per hectare |
| varia | ALS height variance |
Appendix A
| Forest Species * | % Variance Explained | MSE (m3/ha) | RMSE (m3/ha) | rRMSE (%) |
|---|---|---|---|---|
| FS | 52.62 | 4081.84 | 63.89 | 33.27 |
| PH | 44.37 | 973.24 | 31.20 | 38.72 |
| PN | 85.64 | 1279.01 | 35.76 | 25.97 |
| PS | 69.26 | 5665.13 | 75.27 | 33.43 |
| Q | 64.47 | 1084.85 | 32.94 | 36.47 |
| QI | 36.38 | 769.52 | 27.74 | 52.43 |
| Forest Species * | NF | FS | PH | PN | PS | Q | QI | OB | OC |
|---|---|---|---|---|---|---|---|---|---|
| NF | 158 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| FS | 0 | 146 | 1 | 3 | 1 | 0 | 1 | 2 | 3 |
| PH | 1 | 0 | 104 | 0 | 0 | 1 | 0 | 0 | 1 |
| PN | 0 | 2 | 3 | 100 | 0 | 6 | 1 | 0 | 0 |
| PS | 0 | 1 | 0 | 0 | 84 | 5 | 13 | 6 | 0 |
| Q | 3 | 0 | 1 | 1 | 4 | 128 | 0 | 1 | 3 |
| QI | 2 | 1 | 0 | 1 | 9 | 6 | 89 | 12 | 5 |
| OB | 0 | 0 | 0 | 0 | 2 | 0 | 7 | 161 | 0 |
| OC | 6 | 2 | 1 | 1 | 0 | 7 | 4 | 2 | 97 |
References
- Food and Agriculture Organizations of the United Nations. State of Europe’s Forests 2015 Report. 2015. Available online: https://foresteurope.org/state-europes-forests-2015-report/ (accessed on 12 October 2020).
- McRoberts, R.E.; Tomppo, E.O.; Næsset, E. Advances and emerging issues in national forest inventories. Scand. J. For. Res. 2010, 25, 368–381. [Google Scholar] [CrossRef]
- Vidal, C.; Alberdi, I.; Redmond, J.; Vestman, M.; Lanz, A.; Schadauer, K. The role of European National Forest Inventories for international forestry reporting a Legally Binding Agreement. Ann. For. Sci. 2016, 73, 793–806. [Google Scholar] [CrossRef] [Green Version]
- Alberdi, I.; Vallejo, R.; Álvarez-González, J.G.; Condés, S.; González-Ferreiro, E.; Guerrero, S.; Hernández, L.; Martínez-Jauregui, M.; Montes, F.; Oliveira, N.; et al. The multi-objective Spanish National Forest Inventory. For. Syst. 2017, 26, 1–17. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Westfall, J.A. Propagating uncertainty through individual tree volume model predictions to large-area volume estimates. Ann. For. Sci. 2016, 73, 625–633. [Google Scholar] [CrossRef] [Green Version]
- Grafstörm, A.; Saarela, S.; Ene, L. Efficient sampling strategies for forest inventories by spreading the sample in auxiliary space. Can. J. For. Res. 2014, 44, 1156–1164. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Cohen, W.B.; Erik, N.; Stehman, S.V.; Tomppo, E.O. Using remotely sensed data to construct and assess forest attribute maps and related spatial products. Scand. J. For. Res. 2010, 25, 340–367. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Sannier, C.; Stehman, S.V.; Tomppo, E.O. Remote sensing support for the gain-loss approach for greenhouse gas inventories. Remote Sens. 2020, 12, 1891. [Google Scholar] [CrossRef]
- Tomppo, E.; Gschwantner, T.; Lawrence, M.; McRoberts, R.E. National Forest Inventories: Pathways for Common Reporting; Springer: Dordrecht, The Netherlands, 2010; ISBN 978-90-481-3233-1. [Google Scholar]
- Alberdi, I.; Cañellas, I.; Vallejo Bombín, R. The Spanish National Forest Inventory: History, development, challenges and perspectives. Pesqui. Florest. Bras. 2017, 37, 361. [Google Scholar] [CrossRef]
- Gomez, C.; Alejandro, P.; Hermosilla, T.; Montes, F.; Pascual, C.; Ruiz, L.Á.; Alvarez-taboada, F.; Tanase, M.A.; Valbuena, R. Remote sensing for the Spanish forests in the 21 st century: A review of advances, needs, and opportunities. For. Syst. 2019, 28, eR001. [Google Scholar]
- Saarela, S.; Wästlund, A.; Holmström, E.; Mensah, A.A.; Holm, S.; Nilsson, M.; Fridman, J.; Ståhl, G. Mapping aboveground biomass and its prediction uncertainty using LiDAR and field data, accounting for tree-level allometric and LiDAR model errors. For. Ecosyst. 2020, 7, 43. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Tomppo, E.O. Remote sensing support for national forest inventories. Remote Sens. Environ. 2007, 110, 412–419. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote Sensing Technologies for Enhancing Forest Inventories: A Review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef] [Green Version]
- Ståhl, G.; Saarela, S.; Schnell, S.; Holm, S.; Breidenbach, J.; Healey, S.P.; Patterson, P.L.; Magnussen, S.; Næsset, E.; McRoberts, R.E.; et al. Use of models in large-area forest surveys: Comparing model-assisted, model-based and hybrid estimation. For. Ecosyst. 2016, 3, 5. [Google Scholar] [CrossRef] [Green Version]
- McRoberts, R.E.; Moser, P.; Zimermann Oliveira, L.; Vibrans, A.C. A general method for assessing the effects of uncertainty in individual-tree volume model predictions on large-area volume estimates with a subtropical forest illustration. Can. J. For. Res. 2014, 45, 44–51. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T. Estimation for inaccessible and non-sampled forest areas using model-based inference and remotely sensed auxiliary information. Remote Sens. Environ. 2014, 154, 226–233. [Google Scholar] [CrossRef]
- Hansen, M.H.; Madow, W.G.; Tepping, B.J. An evaluation of model-dependent and probability-sampling inferences in sample surveys. J. Am. Stat. Assoc. 1983, 78, 776–793. [Google Scholar] [CrossRef]
- Royall, R.M.; Herson, J. Robust Estimation in Finite Populations I. J. Am. Stat. Assoc. 1973, 68, 880–889. [Google Scholar] [CrossRef]
- Shettles, M.; Temesgen, H.; Gray, A.N.; Hilker, T. Comparison of uncertainty in per unit area estimates of aboveground biomass for two selected model sets. For. Ecol. Manag. 2015, 354, 18–25. [Google Scholar] [CrossRef]
- Urbazaev, M.; Thiel, C.; Cremer, F.; Dubayah, R.; Migliavacca, M.; Reichstein, M.; Schmullius, C. Estimation of forest aboveground biomass and uncertainties by integration of field measurements, airborne LiDAR, and SAR and optical satellite data in Mexico. Carbon Balance Manag. 2018, 13, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez-Veiga, P.; Saatchi, S.; Tansey, K.; Balzter, H. Magnitude, spatial distribution and uncertainty of forest biomass stocks in Mexico. Remote Sens. Environ. 2016, 183, 265–281. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Messina, J.P.; Moore, N.J.; Fan, P.; Shortridge, A.M. MODIS land cover uncertainty in regional climate simulations. Clim. Dyn. 2017, 49, 4047–4059. [Google Scholar] [CrossRef] [Green Version]
- IPCC. Volume 4: Agriculture, Forestry and other land use. In Refinement to the 2006 IPCC Guidelines for National Greenhouse Gas Inventories; Calvo Buendia, E., Tanabe, K., Kranjc, A., Baasansuren, J., Fukuda, M., Ngarize, S., Osako, A., Pyrozhenko, Y., Shermanau, P., Federici, S., Eds.; IPCC: Geneva, Switzerland, 2019; Available online: https://www.ipcc-nggip.iges.or.jp/public/2019rf/index.html (accessed on 12 October 2020).
- Bravo, F.; Guijarro, M.; Cámara, A.; Balteiro, L.D.; Fernández-Rebollo, P.; Pajares, J.A.; Pemán, J.; Ruiz-Peinado, R. Informe de Situación de los bosques y sector forestal en España—ISFE 2017. Sociedad Española de Ciencias Forestales. 2017. Available online: http://secforestales.org/sites/default/files/archivos/7cfe_avance_isfe_final.pdf (accessed on 12 October 2020).
- Cuarto Inventario Forestal Nacional La Rioja. Edited by Ministerio de Agricultura, Alimentación y Medio Ambiente. Available online: https://docplayer.es/4459716-Cuarto-inventario-forestal-nacional-la-rioja.html (accessed on 12 October 2020).
- Álvarez-González, J.G.; Cañellas, I.; Alberdi, I.; Gadow, K.V.; Ruiz-González, A.D. National Forest Inventory and forest observational studies in Spain: Applications to forest modeling. For. Ecol. Manag. 2014, 316, 54–64. [Google Scholar] [CrossRef]
- Fernández-Landa, A.; Fernández-Moya, J.; Tomé, J.L.; Algeet-Abarquero, N.; Guillén-Climent, M.L.; Vallejo, R.; Sandoval, V.; Marchamalo, M. High resolution forest inventory of pure and mixed stands at regional level combining National Forest Inventory field plots, Landsat, and low density lidar. Int. J. Remote Sens. 2018, 39, 4830–4844. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- McGaughey, R.; Forester, R.; Carson, W. Fusing LIDAR data, photographs, and other data using 2D and 3D visualization techniques. Proc. Terrain Data Appl. Vis. Connect. 2003, 28–30, 16–24. [Google Scholar]
- Næsset, E.; Bollandsås, O.M.; Gobakken, T.; Solberg, S.; McRoberts, R.E. The effects of field plot size on model-assisted estimation of aboveground biomass change using multitemporal interferometric SAR and airborne laser scanning data. Remote Sens. Environ. 2015, 168, 252–264. [Google Scholar] [CrossRef]
- Saarela, S.; Grafström, A.; Ståhl, G.; Kangas, A.; Holopainen, M.; Tuominen, S.; Nordkvist, K.; Hyyppä, J. Model-assisted estimation of growing stock volume using different combinations of LiDAR and Landsat data as auxiliary information. Remote Sens. Environ. 2015, 158, 431–440. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Chen, Q.; Domke, G.M.; Ståhl, G.; Saarela, S.; Westfall, J.A. Hybrid estimators for mean aboveground carbon per unit area. For. Ecol. Manag. 2016, 378, 44–56. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Shataee, S.; Kalbi, S.; Fallah, A.; Pelz, D. Forest attribute imputation using machine-learning methods and ASTER data: Comparison of k-NN, SVR and random forest regression algorithms. Int. J. Remote Sens. 2012, 33, 6254–6280. [Google Scholar] [CrossRef]
- Penner, M.; Pitt, D.G.; Woods, M.E. Parametric vs. nonparametric LiDAR models for operational forest inventory in boreal Ontario. Can. J. Remote Sens. 2013, 39, 426–443. [Google Scholar]
- Rodriguez-Galiano, V.F.; Chica-Rivas, M. Evaluation of different machine learning methods for land cover mapping of a Mediterranean area using multi-seasonal Landsat images and Digital Terrain Models. Int. J. Digit. Earth 2012, 7, 492–509. [Google Scholar] [CrossRef]
- Grinand, C.; Rakotomalala, F.; Gond, V.; Vaudry, R.; Bernoux, M.; Vieilledent, G. Estimating deforestation in tropical humid and dry forests in Madagascar from 2000 to 2010 using multi-date Landsat satellite images and the random forests classifier. Remote Sens. Environ. 2013, 139, 68–80. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Moser, P.; Vibrans, A.C.; McRoberts, R.E.; Næsset, E.; Gobakken, T.; Chirici, G.; Mura, M.; Marchetti, M. Methods for variable selection in LiDAR-assisted forest inventories. Forestry 2016, 90, 112–124. [Google Scholar] [CrossRef] [Green Version]
- Navarro, J.A.; Algeet, N.; Fernández-Landa, A.; Esteban, J.; Rodríguez-Noriega, P.; Guillén-Climent, M.L. Integration of UAV, Sentinel-1, and Sentinel-2 data for mangrove plantation aboveground biomass monitoring in Senegal. Remote Sens. 2019, 11, 77. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- McRoberts, R.E.; Næsset, E.; Gobakken, T.; Chirici, G.; Condés, S.; Hou, Z.; Saarela, S.; Chen, Q.; Ståhl, G.; Walters, B.F. Assessing components of the model-based mean square error estimator for remote sensing assisted forest applications. Can. J. For. Res. 2018, 48, 642–649. [Google Scholar] [CrossRef]
- Condés, S.; McRoberts, R.E. Updating national forest inventory estimates of growing stock volume using hybrid inference. For. Ecol. Manag. 2017, 400, 48–57. [Google Scholar] [CrossRef]
- Hou, Z.; Xu, Q.; McRoberts, R.E.; Greenberg, J.A.; Liu, J.; Heiskanen, J.; Pitkänen, S.; Packalen, P. Effects of temporally external auxiliary data on model-based inference. Remote Sens. Environ. 2017, 198, 150–159. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Magnussen, S.; Tomppo, E.O.; Chirici, G. Parametric, bootstrap, and jackknife variance estimators for the k-Nearest Neighbors technique with illustrations using forest inventory and satellite image data. Remote Sens. Environ. 2011, 115, 3165–3174. [Google Scholar] [CrossRef]
- Hou, Z.; McRoberts, R.E.; Ståhl, G.; Packalen, P.; Greenberg, J.A.; Xu, Q. How much can natural resource inventory benefit from finer resolution auxiliary data? Remote Sens. Environ. 2018, 209, 31–40. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall: New York, NY, USA, 1994. [Google Scholar]
- Liu, R. Bootstrap Procedures under some Non-I.I.D. Models. Ann.Stat. 1988, 16, 1696–1708. [Google Scholar] [CrossRef]
- Carpenter, J.; Bithell, J. Bootstrap confidence intervals: When, which, what? A practical guide for medical statisticians. Stat. Med. 2000, 19, 1141–1164. [Google Scholar] [CrossRef]
- Diaconis, P.; Efron, B. Computer-Intensive Methods in Statistics. Sci. Am. 1983, 248, 116–130. [Google Scholar] [CrossRef]
- Ranalli, M.G.; Mecatti, F. Comparing Recent Approaches For Bootstrapping Sample Survey Data: A First Step Towards A Unified Approach. Proc. Surv. Res. Methods Sect. Am. Stat. Assoc. 2012, 4088–4099. Available online: http://boa.unimib.it/retrieve/handle/10281/41947/62652/Ranalli_Mecatti_Proc2013.pdf (accessed on 12 October 2020).
- Flachaire, E. Bootstrapping heteroskedastic regression models: Wild bootstrap vs. pairs bootstrap. Comput. Stat. Data Anal. 2005, 49, 361–376. [Google Scholar] [CrossRef] [Green Version]
- Freedman, D.A. Bootstrapping Regression Models. Ann. Stat. 1981, 6, 1218–1228. [Google Scholar] [CrossRef]
- Esteban, J.; McRoberts, R.E.; Fernández-Landa, A.; Tomé, J.L.; Næsset, E. Estimating forest volume and biomass and their changes using random forests and remotely sensed data. Remote Sens. 2019, 11, 1944. [Google Scholar] [CrossRef] [Green Version]
- Domingo, D.; Alonso, R.; de la Riva, J.; Lamelas, M.T.; Rodríguez, F.; Montealegre, A.L. Temporal Transferability of Pine Forest Attributes Modeling Using Low-Density Airborne Laser Scanning Data. Remote Sens. 2019, 11, 261. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Galiano, V.; Chica-Olmo, M. Land cover change analysis of a Mediterranean area in Spain using different sources of data: Multi-seasonal Landsat images, land surface temperature, digital terrain models and texture. Appl. Geogr. 2012, 35, 208–218. [Google Scholar] [CrossRef]
- Stavrakoudis, D.G.; Dragozi, E.; Gitas, I.Z.; Karydas, C.G. Decision Fusion Based on Hyperspectral and Multispectral Satellite Imagery for Accurate Forest Species Mapping. Remote Sens. 2014, 6, 6897–6928. [Google Scholar] [CrossRef] [Green Version]
- Pesaresi, S.; Mancini, A.; Quattrini, G.; Casavecchia, S. Mapping Mediterranean Forest Plant Associations and Habitats with Functional Principal Component Analysis Using Landsat 8 NDVI Time Series. Remote Sens. 2020, 12, 1132. [Google Scholar] [CrossRef] [Green Version]
- Valbuena, R.; Mauro, F.; Rodriguez-Solano, R.; Manzanera, J.A. Accuracy and precision of GPS receivers under forest canopies in a mountainous environment. Span. J. Agric. Res. 2013, 8, 1047. [Google Scholar] [CrossRef]
- Chen, Q.; Vaglio Laurin, G.; Valentini, R. Uncertainty of remotely sensed aboveground biomass over an African tropical forest: Propagating errors from trees to plots to pixels. Remote Sens. Environ. 2015, 160, 134–143. [Google Scholar] [CrossRef]
- Breidenbach, J.; Astrup, R. Small area estimation of forest attributes in the Norwegian National Forest Inventory. Eur. J. For. Res. 2012, 131, 1255–1267. [Google Scholar] [CrossRef]
- Chirici, G.; Giannetti, F.; McRoberts, R.E.; Travaglini, D.; Pecchi, M.; Maselli, F.; Chiesi, M.; Corona, P. Wall-to-wall spatial prediction of growing stock volume based on Italian National Forest Inventory plots and remotely sensed data. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101959. [Google Scholar] [CrossRef]
- Irulappa-Pillai-Vijayakumar, D.B.; Renaud, J.P.; Morneau, F.; McRoberts, R.E.; Vega, C. Increasing precision for French forest inventory estimates using the k-NN technique with optical and photogrammetric data and model-assisted estimators. Remote Sens. 2019, 11, 991. [Google Scholar] [CrossRef] [Green Version]
- Maselli, F.; Chiesi, M.; Mura, M.; Marchetti, M.; Corona, P.; Chirici, G. Combination of optical and LiDAR satellite imagery with forest inventory data to improve wall-to-wall assessment of growing stock in Italy. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 377–386. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T. Inference for lidar-assisted estimation of forest growing stock volume. Remote Sens. Environ. 2013, 128, 268–275. [Google Scholar] [CrossRef]



| Forest Species * | Number of SNFI Plots | Mean | Standard Deviation | Minimum | Maximum |
|---|---|---|---|---|---|
| FS | 182 | 192.62 | 93.07 | 5.89 | 530.81 |
| PH | 35 | 80.58 | 42.44 | 9.06 | 164.24 |
| PN | 82 | 137.69 | 94.96 | 3.71 | 415.36 |
| PS | 199 | 225.12 | 136.10 | 2.53 | 756.76 |
| Q | 272 | 90.31 | 55.36 | 1.44 | 305.75 |
| QI | 136 | 52.91 | 34.99 | 0.00 | 215.51 |
| Forest Species * | User’s Accuracy (%) | Commission Error (%) | Producer’s Accuracy (%) | Omission Error (%) |
|---|---|---|---|---|
| NF | 98 | 2 | 93 | 7 |
| FS | 95 | 5 | 88 | 13 |
| PH | 97 | 3 | 94 | 6 |
| PN | 89 | 11 | 93 | 7 |
| PS | 93 | 7 | 96 | 4 |
| Q | 77 | 23 | 84 | 16 |
| QI | 91 | 9 | 84 | 16 |
| OB | 71 | 29 | 77 | 23 |
| OC | 81 | 19 | 88 | 12 |
| Forest Species * | Area Estimates | Standard Errors | Stability | |||
|---|---|---|---|---|---|---|
| (ha) | (ha) | (ha) | (%) | % of Stable Pixels | % of Stable Plots | |
| See Footnote (**) | Equation (2) | Equation (3) | Equations (2) and (3) | |||
| FS | 2.10 × 104 | 2.24 × 104 | 552.66 | 2.47 | 94.20 | 100.00 |
| PH | 1.09 × 104 | 0.97 × 104 | 2132.26 | 22.07 | 66.85 | 72.97 |
| PN | 0.67 × 104 | 0.63 × 104 | 779.12 | 12.27 | 79.52 | 86.59 |
| PS | 1.79 × 104 | 1.86 × 104 | 1243.83 | 6.67 | 92.01 | 96.48 |
| Q | 5.51 × 104 | 5.06 × 104 | 2664.66 | 5.27 | 83.54 | 95.96 |
| QI | 3.53 × 104 | 3.61 × 104 | 3202.95 | 8.84 | 84.51 | 86.76 |
| Forest Species * | Mean Volume (m3/ha) | Total Volume (m3) | |||
|---|---|---|---|---|---|
| (%) | |||||
| Equation (10) | Equation (11) | Equation (12) | Equation (13) | Equations (12) and (13) | |
| FS | 204.05 | 5.46 | 4.57 × 106 | 1.45 × 105 | 3.17 |
| PH | 67.38 | 7.91 | 0.65 × 106 | 1.42 × 105 | 21.95 |
| PN | 144.05 | 8.75 | 0.91 × 106 | 0.79 × 105 | 8.71 |
| PS | 216.28 | 8.62 | 4.02 × 106 | 1.87 × 105 | 4.65 |
| Q | 70.50 | 2.80 | 3.56 × 106 | 1.66 × 105 | 4.66 |
| QI | 44.63 | 4.10 | 1.62 × 106 | 1.95 × 105 | 12.05 |
| Forest Species * | Mean Volume (m3/ha) | Total Volume (m3) | |||||
|---|---|---|---|---|---|---|---|
| (%) | (%) | ||||||
| Equation (1) | Equation (5) | Equation (6) | See Footnote (**) | Equation (7) | Equation (8) | Equations (7) and (8) | |
| FS | 203.70 | 204.29 | 5.02 | 4.28 × 106 | 4.29 × 106 | 1.06 × 105 | 2.46 |
| PH | 61.52 | 66.49 | 7.47 | 0.67 × 106 | 0.73 × 106 | 0.82 × 105 | 11.23 |
| PN | 146.96 | 144.22 | 4.25 | 0.99 × 106 | 0.97 × 106 | 0.28 × 105 | 2.94 |
| PS | 223.08 | 220.43 | 5.22 | 3.99 × 106 | 3.95 × 106 | 0.94 × 105 | 2.37 |
| Q | 70.84 | 72.43 | 2.06 | 3.90 × 106 | 3.99 × 106 | 1.13 × 105 | 2.84 |
| QI | 43.27 | 44.46 | 4.03 | 1.53 × 106 | 1.57 × 106 | 1.43 × 105 | 9.07 |
| Forest Species * | Uncertainty in the Landsat Forest Species Map | Sampling Variability in Model Calibration Data | Total Uncertainty |
|---|---|---|---|
| (%) | (%) | (%) | |
| Equations (12) and (13) | Equations (7) and (8) | Equation (14) | |
| FS | 3.17 | 2.46 | 4.01 |
| PH | 21.95 | 11.23 | 24.66 |
| PN | 8.71 | 2.94 | 9.19 |
| PS | 4.65 | 2.37 | 5.22 |
| Q | 4.66 | 2.84 | 5.46 |
| QI | 12.05 | 9.07 | 15.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esteban, J.; McRoberts, R.E.; Fernández-Landa, A.; Tomé, J.L.; Marchamalo, M. A Model-Based Volume Estimator that Accounts for Both Land Cover Misclassification and Model Prediction Uncertainty. Remote Sens. 2020, 12, 3360. https://doi.org/10.3390/rs12203360
Esteban J, McRoberts RE, Fernández-Landa A, Tomé JL, Marchamalo M. A Model-Based Volume Estimator that Accounts for Both Land Cover Misclassification and Model Prediction Uncertainty. Remote Sensing. 2020; 12(20):3360. https://doi.org/10.3390/rs12203360
Chicago/Turabian StyleEsteban, Jessica, Ronald E. McRoberts, Alfredo Fernández-Landa, José Luis Tomé, and Miguel Marchamalo. 2020. "A Model-Based Volume Estimator that Accounts for Both Land Cover Misclassification and Model Prediction Uncertainty" Remote Sensing 12, no. 20: 3360. https://doi.org/10.3390/rs12203360
APA StyleEsteban, J., McRoberts, R. E., Fernández-Landa, A., Tomé, J. L., & Marchamalo, M. (2020). A Model-Based Volume Estimator that Accounts for Both Land Cover Misclassification and Model Prediction Uncertainty. Remote Sensing, 12(20), 3360. https://doi.org/10.3390/rs12203360